 Journal of Modern Physics, 2011, 2, 392-397 doi:10.4236/jmp.2011.25048 Published Online May 2011 (http://www.SciRP.org/journal/jmp) Copyright © 2011 SciRes. JMP Modeling and Numerical Simulation of Wings Effect on Turbulent Flow between Two Contra-Rotating Cylinders Maher Raddaoui Unit “Materials, Energy and Renewable Energies: MÉÉR”, Faculty of Science, University of Gafsa, Zarroug, Tunisia E-mail: maherzohra@yahoo.fr Received September 20, 2010; revised March 6, 2011; accepted March 28, 2011 Abstract Many industries in the world take part in the pollution of the environment. This pollution often comes from the reactions of combustion. To optimize these reactions and to minimize pollution, turbulence is a funda- mental tool. Several factors are at the origin of turbulence in the complex flows, among these factors, we can quote the effect of wings in the rotating flows. The interest of this work is to model and to simulate numeri- cally the effect of wings on the level of turbulence in the flow between two contra-rotating cylinders. We have fixed on these two cylinders eight wings uniformly distributed and we have varied the height of the wings to have six values from 2 mm to 20 mm by maintaining the same Reynolds number of rotation. The numerical tool is based on a statistical model in a point using the closing of the second order of the transport equations of the Reynolds stresses (Reynolds Stress Model: RSM). We have modelled wings effect on the flow by a source term added to the equation tangential speed. The results of the numerical simulation showed that all the average and fluctuating variables are affected the value of the kinetic energy of turbulence as those of Reynolds stresses increase with the height of the wings. Keywords: Pollution, Turbulence, Combustion, Wing, Modeling, Numerical Simulation, Contra-Rotating Cylinders, Reynolds Stress Model, Source Term 1. Introduction 1.1. Former work It is just in the years 1970’s that the first models for tur- bulence in rotation saw the day, Morse [1,2] used a model of the k- type to small Reynolds number, but the author noticed the existence of an abnormally important laminar zone. He proposes then a modified version which takes into account the anisotropy of turbulence close to the walls. The study of Iacovides and Toum- panakis [3], in which four models of turbulence are tested, shows that the model of transport of the tensions of Reynolds is the suitable level of closing to envisage such complex flows. Schiestel, et al. [4] used an alge- braic model (ASM) in the central heart of the flow. Later, Elena and Schiestel [5] used a model of transport of the tensions of Reynolds that was derived from the model from Launder and Tselepidakis [6]. This model is more satisfactory than that of Hanjalic and Launder [7] and than model ASM. But there too, the authors note a too large laminarisation of the flow compared with the ex- perimental results of Itoh, et al. [8]. Hence, many im- provements are appeared like those of Elena and Schi- estel [9] which proposed an alternative of the model of transport equations of the tensions of Reynolds (RSM), who takes into account the implicit effects of rotation on the turbulent field and whom they compare with more traditional models. Iacovides and Theofanopoulos [10] used an approach based on an algebraic model of the tensions of Reynolds in the zone of fully developed tur- bulence and an assumption length of mixture close to walls. A complete review of the various studies con- cerning the models of turbulence for the flows in rotation was made by Schiestel [11] and Elena [12]. Taking into account the complexity of the flows which we study (ro- tation, containment, flow, laminarized zone, anisotropy…), it is about the adequate level of closing. Elena [12] suc- cessively used three models of the second order of the type RSM (Reynolds Stress Model). The last version is a model of the second order to small Reynolds number, who accounts better for the effects of the rotatio n and the  M. RADDAOUI393 physics of these flows. This model will be thus selected for all our numerical study. The experimental study of the flows confined between revolving discs interested these last years several re- searchers, in Marseilles (group of P. Le Gal in the IR- PHE), in Lille (group of D. Buisine to the LML), in Paris area (group of P. Queré to the LIMSI, and of O. Stew at the University of Evry) and laboratory FAST in Orsay which studied in experiments the instability of this kind of flow, it proved the existence of two typ es of instab ility which exist only for ratios of very weak aspect and which start to appear if the number of rotation increases: an instability in time making the flow non stationary and an instability in space destroying the axisymètrie. In 2008, Poncet, Schiestel and Monchaux [13] studied the flow of Von Karman corresponding to the two contra- rotating discs for smooth discs and discs with wings, these authors primarily were interested in the average sizes without taking several values height of the wings. Our present numerical study supplements this old work by taking many heights of wings and especially it puts the point on the turbu lent sizes lik e th e turbulence k inetic energy and the Reynolds stresses. 2. Experimental Installation The geometrical characteristics of rotating cylinders are displayed in Figure 1, it consists in two fixed discs en- closed by two moving cylinders. These cylinders move in opposite side. The value of interior ray is R1 = 100 mm and the external ray is R2 = 200 mm, the two cylinders are of the same length h = 200 mm, which corresponds to an aspect ratio G = 2.0. The axis of z corresponds to the axis of rotation. We define the Reynolds number of the rotation R based on the external ray of the cavity by 2 2 RR . All the simu- lations considered here correspond to a Reynolds number of rotation R = 2 105. On each cylinder, we placed 8 wings uniformly distributed with a thickness equal to 2 mm and a height a whi ch c o rresp onds to a parameter h* = a/h, the length of each wing is equal to the height of the a 2 Fixed walls Wings 1 Fluid Mobile walls h Figure 1. Experimental installation. cylinder. Our study is made with 6 different heights of wing correspondent to h* = 0.01, 0.02, 0.04, 0.06, 0.08 and 0.1. The flu id cons idered in annular space is income- pressible and the flow is steady and isotherm. 3. Numerical Scheme 3.1. Statistical Modeling The instantaneous velocity (and respectively the pres- sure) is decomposed into a mean part Vi (P) and a fluctu- ating part vi (p), for turbulent mean flow prediction, the governing equations for the conservation of mass and momentum are deduced by statistical averaging from Navier-Stokes equations using the Reynolds decomposi- tion: ,, , , ,0 ijijij ij i jj VP VVV vv t V (1) The equations fluctuating speeds are then written with difference of this last equation and Navier-Stokes equa- tions: ,,, , , , ijijjijjijiji j i vP VvvV vvvvv t (2) with iji j Rvv denotes the Reynolds stress t ensor. Our approach is based on one-point statistical model- ling using a low Reynolds number second-order full stress transport closure derived from the Launder and Tselepidakis model [6] and sensitized to rotation effects [5,14]. Previous works [15] have shown that this level of closure was adequate in such flow configurations, while the usual k- model, which is blind to any rotation effect, presents serious deficiencies. This approach allows for a detailed description of near-wall turbulence and is free from any eddy viscosity hypothesis. An example of these models is the RSM model based on the resolution of the following transport eq uation of Reynolds stress: d d ij ijijij ijij ij RP t D T (3) where Pij, ij, ij, ij, Dij and Tij respectively denote the production, the source term of Coriolis, pressure-strain correlation, dissipation, diffusion and extra terms of rota- tion. The equation of dissipation rate is proposed by Laun- der and Tselepidakis [6]: 1,2 ,, , 3,,4, , d- diji jijjii jkijli klii k cRVcf cR tk k cRVVck kk (4) Copyright © 2011 SciRes. JMP 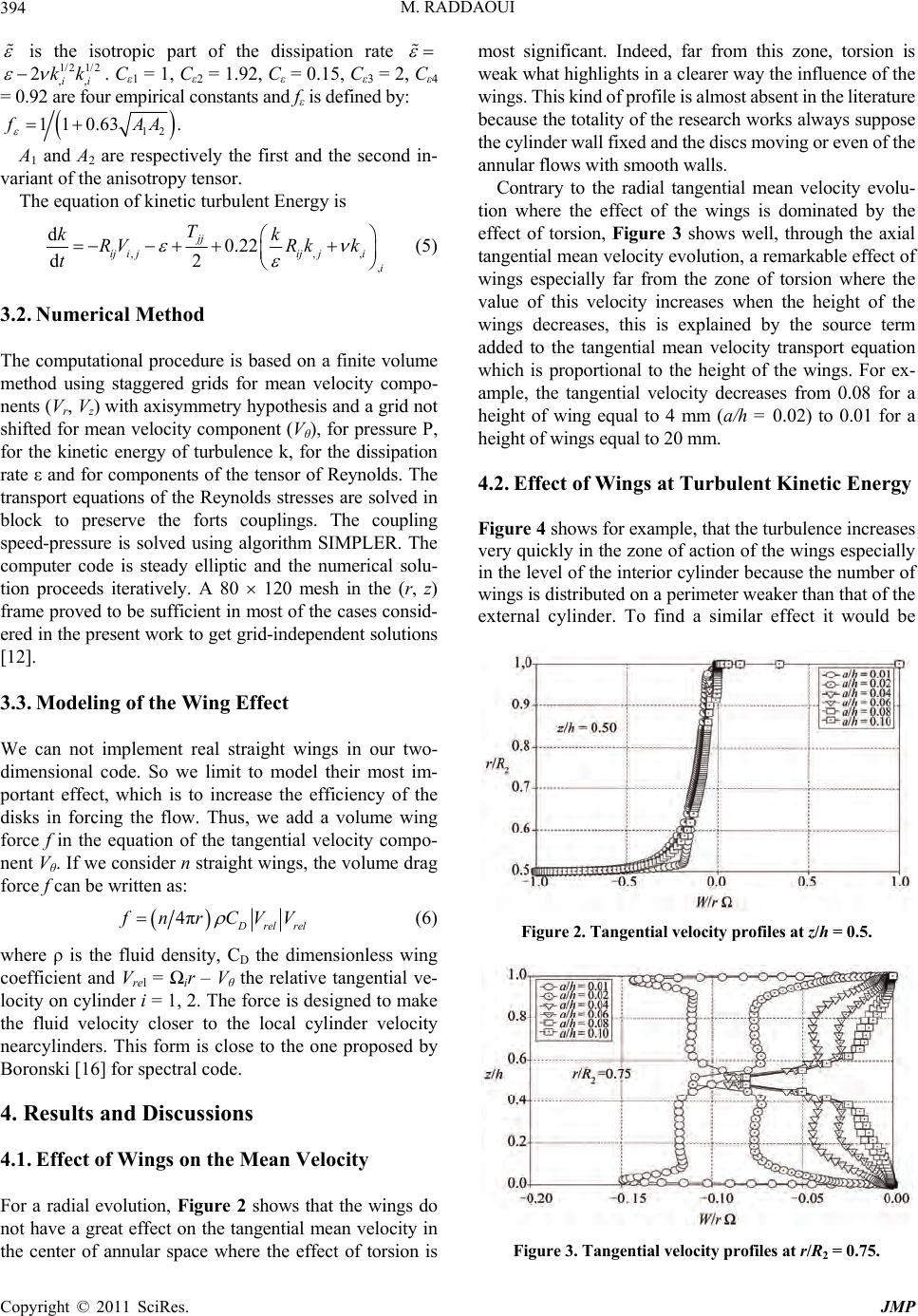 M. RADDAOUI 394 is the isotropic part of the dissipation rate . C1 = 1, C2 = 1.92, C = 0.15, C3 = 2, C4 = 0.92 are four empirical constants and f i s defi ned by: 1/21/2 ,, 2ii kk 12 1 10.63. AA A1 and A2 are respectively the first and the second in- variant of the anisotrop y tensor. The equation of kinetic turbu lent Energy is ,, d0.22 d2 jj iji jijjii T kk RVRkk t ,, (5) 3.2. Numerical Method The computational procedure is based on a finite volume method using staggered grids for mean velocity compo- nents (Vr, Vz) with axisymmetry hypothesis and a grid not shifted for mean velocity co mponent (V), for pressure P, for the kinetic energy of turbulence k, for the dissipation rate and for components of the tensor of Reynolds. The transport equations of the Reynolds stresses are solved in block to preserve the forts couplings. The coupling speed-pressure is solved using algorithm SIMPLER. The computer code is steady elliptic and the numerical solu- tion proceeds iteratively. A 80 120 mesh in the (r, z) frame proved to be sufficient in most of the cases consid- ered in the present work to get gr id-independent solution s [12]. 3.3. Modeling of the Wing Effect We can not implement real straight wings in our two- dimensional code. So we limit to model their most im- portant effect, which is to increase the efficiency of the disks in forcing the flow. Thus, we add a volume wing force f in the equation of the tangential velocity compo- nent V. If we consider n straight wing s, the volume drag force f can be written as: 4 rel rel nrCVV (6) where is the fluid density, CD the dimensionless wing coefficient and Vrel = ir – V the relative tangential ve- locity on cylinder i = 1, 2. The force is designed to make the fluid velocity closer to the local cylinder velocity nearcylinders. This form is close to the one proposed by Boronski [1 6] for spectral co de. 4. Results and Discussions 4.1. Effect of Wings on the Mean Velocity For a radial evolution, Figure 2 shows that the wings do not have a great effect on the tangential mean velocity in the center of annular space where the effect of torsion is most significant. Indeed, far from this zone, torsion is weak what highlights in a clearer way the influence of the wings. This kind of profile is almost absent in the literature because the totality of the research works always suppose the cylinder wall fixed and the discs m oving or even of t he annular flows with sm ooth wal ls . Contrary to the radial tangential mean velocity evolu- tion where the effect of the wings is dominated by the effect of torsion, Figure 3 shows well, through the axial tangential mean velocity evolu tion, a remarkable effect of wings especially far from the zone of torsion where the value of this velocity increases when the height of the wings decreases, this is explained by the source term added to the tangential mean velocity transport equation which is proportional to the height of the wings. For ex- ample, the tangential velocity decreases from 0.08 for a height of wing equal to 4 mm (a/h = 0.02) to 0.01 for a height of wing s equal to 2 0 mm. 4.2. Effect of Wings at Turbulent Kinetic Energy Figure 4 shows for example, that the turbulence increases very quickly in the zone of action of the wings especially in the level of the interior cylinder because the number of wings is distributed on a perimeter weaker than that of the external cylinder. To find a similar effect it would be Figure 2. Tangential velocity profiles at z/h = 0.5. Figure 3. Tangential velocity profiles at r/R2 = 0.75. Copyright © 2011 SciRes. JMP 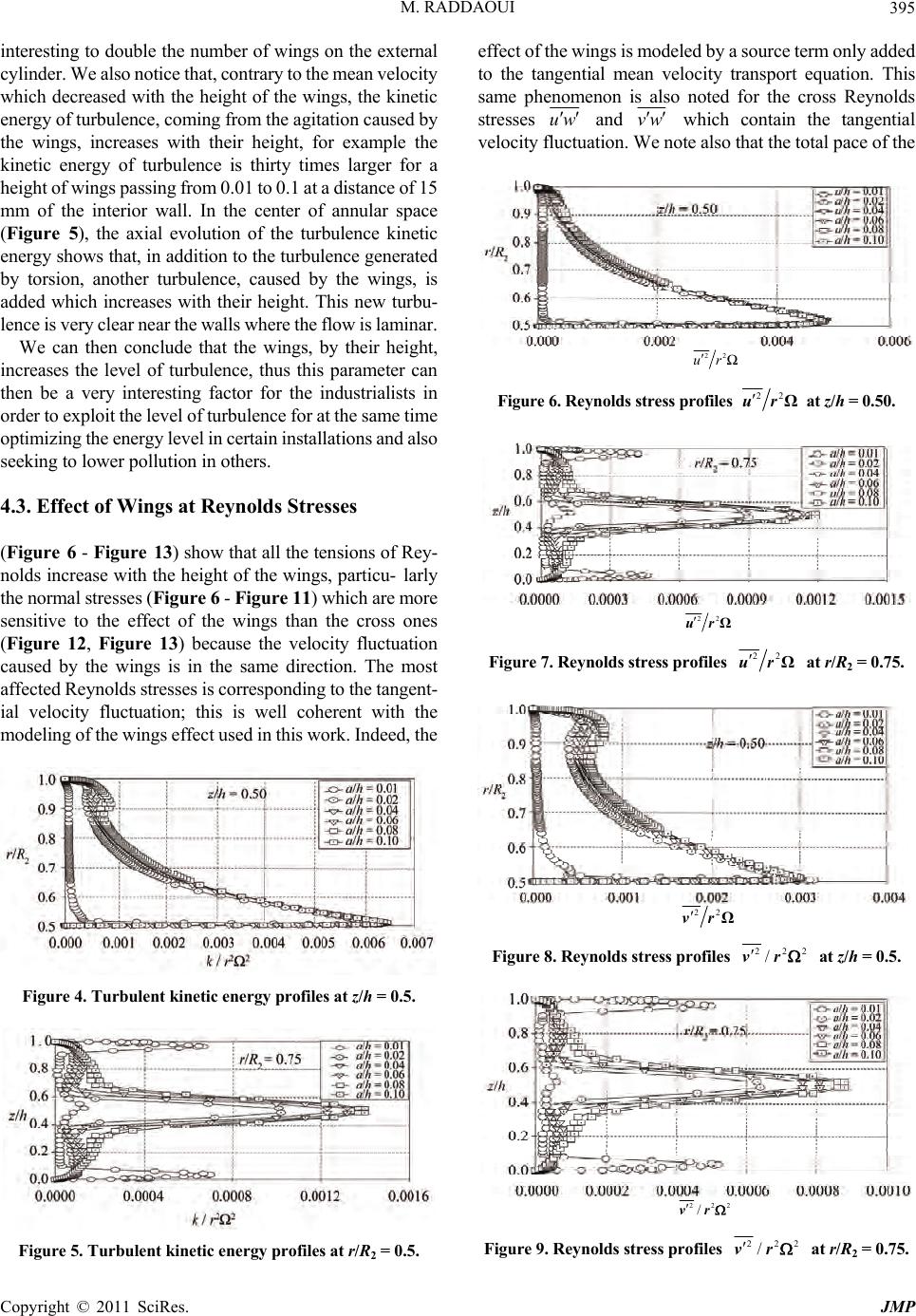 M. RADDAOUI395 interesting to do uble the number of wings on the external cylinder. We also notice that, c ontrary to the mean velocity which decreased with the height of the wings, the kinetic energy of turbulence, coming from the agitation cause d by the wings, increases with their height, for example the kinetic energy of turbulence is thirty times larger for a height of wings passing from 0.01 to 0.1 at a dist ance of 15 mm of the interior wall. In the center of annular space (Figure 5), the axial evolution of the turbulence kinetic energy shows that, in additio n to the turbulence g enerated by torsion, another turbulence, caused by the wings, is added which increases with their height. This new turbu- lence is very clear near the walls where the flow is laminar. We can then conclude that the wings, by their height, increases the level of turbulence, thus this parameter can then be a very interesting factor for the industrialists in order to exploit t he level of turbulence for at the sam e time optimizing the energy level in certain installations and also seeking to lower pollution in others. 4.3. Effect of Wings at Reynolds Stresses (Figure 6 - Figure 13) show that al l the tens ions of Rey- nolds increase with the height of the wings, particu- larly the normal stresses (Figure 6 - Figure 11) which are more sensitive to the effect of the wings than the cross ones (Figure 12, Figure 13) because the velocity fluctuation caused by the wings is in the same direction. The most affected Reynolds stresses is corresponding to the tangent- ial velocity fluctuation; this is well coherent with the modeling of th e wings effect used in this work. I ndeed, the Figure 4. Turbulent kin etic en ergy profiles at z/h = 0.5. Figure 5. Turbulent kin etic en ergy profiles at r/R2 = 0.5. effect of the wings is model ed by a source term only added to the tangential mean velocity transport equation. This same phenomenon is also noted for the cross Reynolds stresses uw and vw which contain the tangential velocity fluctuation. We note also that the total pace of the 22 ur Figure 6. Reynolds stress profiles 22 Ωur at z/h = 0.50. 22 Ωur Figure 7. Reynolds stress profiles 22 Ωur at r/R2 = 0.75. 22 Ωur 22 Ωvr Figure 8. Reynolds stress profiles 22 / vr2 at z/h = 0.5. 222 / vr Figure 9. Reynolds stress profiles 22 / vr2 at r/R2 = 0.75. Copyright © 2011 SciRes. JMP 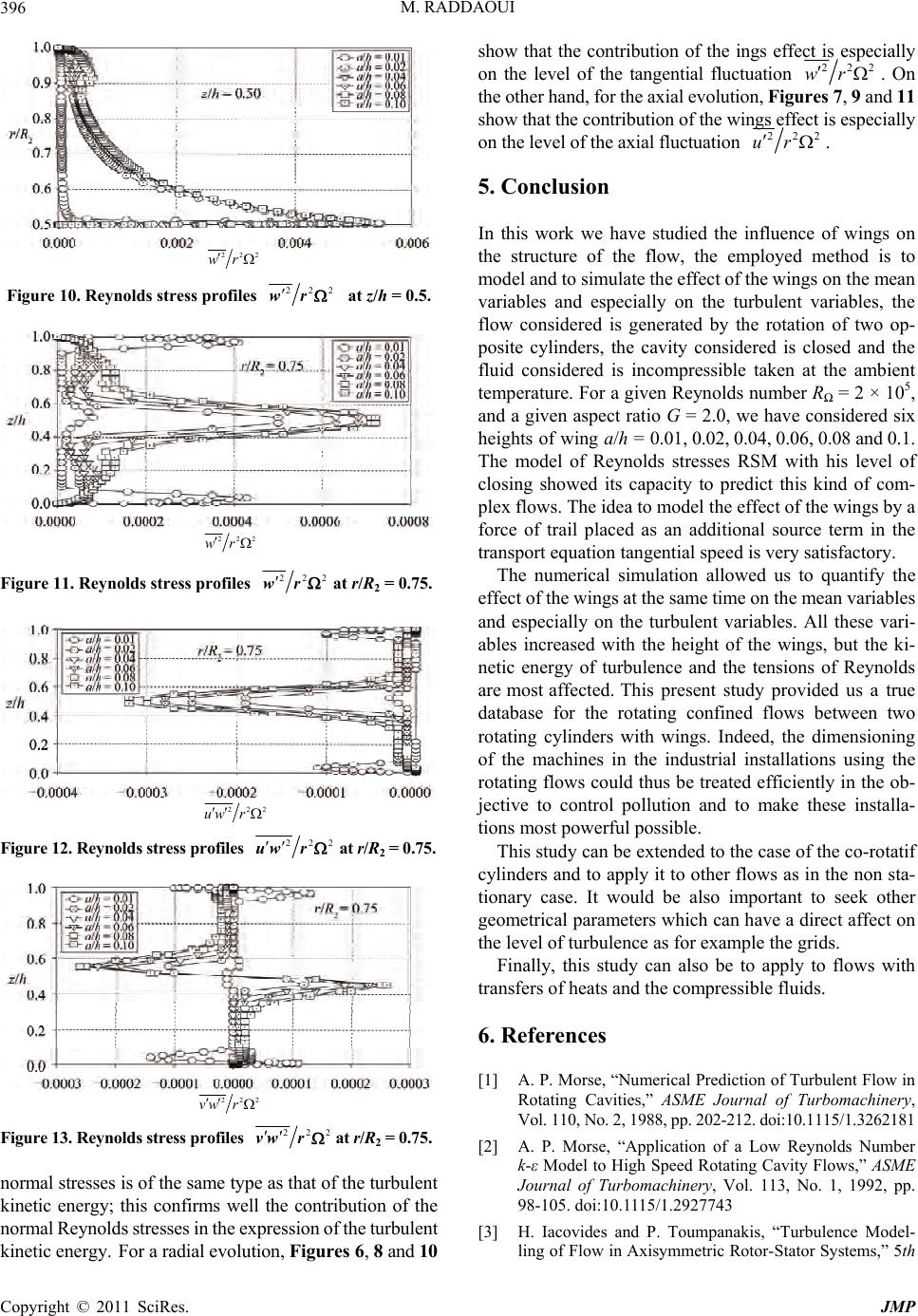 M. RADDAOUI 396 222 wr Figure 10. Reynolds stress profiles 222 wr at z/h = 0.5. 222 wr Figure 11. Reynolds stress profiles 222 wrat r/R2 = 0.75. 222 uw r Figure 12. Reynolds stress profiles 222 uwrat r/R2 = 0. 75. 222 vw r Figure 13. Reynolds stress profiles 222 vwr at r/R2 = 0.75. normal stresses is of the same type as that o f the turb ulent kinetic energy; this confirms well the contribution of the normal Reynolds st resses in the expression of the turbulent kinetic energy. For a radial evolution, Figures 6, 8 and 10 show that the contribution of the ings effect is especially on the level of the tangential fluctuation 222 wr . On the other hand, for the axial evol ution, Figures 7, 9 and 11 show that the cont ri but i on of the wings effect is especially on the level of the axial fluctuation 222 ur . 5. Conclusion In this work we have studied the influence of wings on the structure of the flow, the employed method is to model and to simulate the effect of the wings on the mean variables and especially on the turbulent variables, the flow considered is generated by the rotation of two op- posite cylinders, the cavity considered is closed and the fluid considered is incompressible taken at the ambient temperature. For a given Reynolds number R = 2 × 105, and a given aspect ratio G = 2.0, we have considered six heights of wing a/h = 0.01, 0.02, 0.04, 0.06, 0.08 and 0.1. The model of Reynolds stresses RSM with his level of closing showed its capacity to predict this kind of com- plex flows. The idea to m odel the effect of the wings by a force of trail placed as an additional source term in the transport equa tion tangential speed is very satisfactory. The numerical simulation allowed us to quantify the effect of the w ings at the sam e tim e on the mean variables and especially on the turbulent variables. All these vari- ables increased with the height of the wings, but the ki- netic energy of turbulence and the tensions of Reynolds are most affected. This present study provided us a true database for the rotating confined flows between two rotating cylinders with wings. Indeed, the dimensioning of the machines in the industrial installations using the rotating flows could thus be treated efficiently in the ob- jective to control pollution and to make these installa- tions most powerful possible. This study can be extend ed to the case of the co-rotatif cylinders and to apply it to other flows as in the non sta- tionary case. It would be also important to seek other geometrical parameters which can have a direct affect on the level of turbulence as for example the grids. Finally, this study can also be to apply to flows with transfers of heats and the compressible fluids. 6. References [1] A. P. Morse, “Numerical Prediction of Turbulent Flow in Rotating Cavities,” ASME Journal of Turbomachinery, Vol. 110, No. 2, 1988, pp. 202-212. doi:10.1115/1.3262181 [2] A. P. Morse, “Application of a Low Reynolds Number k- Model to High Speed Rotating Cavity Flows,” ASME Journal of Turbomachinery, Vol. 113, No. 1, 1992, pp. 98-105. doi:10.1115/1.2927743 [3] H. Iacovides and P. Toumpanakis, “Turbulence Model- ling of Flow in Axisymmetric Rotor-Stator Systems,” 5th Copyright © 2011 SciRes. JMP  M. RADDAOUI Copyright © 2011 SciRes. JMP 397 International Symposium on Refined Flow Modelling and Turbulence Measurements, Presses de l’Ecole Nationale des Ponts et Chaussées, Paris, September 1993, pp. 7-10. [4] R. Schiestel, L. Elena and T. Rezoug, “Numerical Mod- eling of Turbulent Flow and Heat Transfer in Rotating Cavities,” Numerical Heat Transfer, Part A, Vol. 24, No. 1, 1995, pp. 45-65. doi:10.1080/10407789308902602 [5] L. Elena and R. Schiestel, “Turbulence Modeling of Con- fined Flow in Rotating Disk Systems,” AIAA Journal, Vol. 33, No. 5, 1995, pp. 812-821. doi:10.2514/3.12800 [6] B. E. Launder and D. P. Tselepidakis, “Application of a New Second-moment Closure to Turbulent Channel Flow Rotating in Orthogonal Mode,” International Journal of Heat and Fluid Flow, Vol. 15, No. 1, 1994, pp. 2-10. doi:10.1016/0142-727X(94)90025-6 [7] K. Hanjalic and B. E. Launder, “Contribution towards a Reynolds-Stress Closure for Low-Reynolds Number Tur- bulence,” Journal of Fluid Mechanics, Vol. 74, No. 4, 1976, pp. 593-610. doi:10.1017/S0022112076001961 [8] M. Itoh, Y. Yamada, S. Imao and M. Gonda, “Experi- ments on Turbulent Flow Due to an Enclosed Rotating Disk,” In: W. Rodi and E. N. Ganic, Eds., Engineering Turbulence Modeling and Experiments, Elsevier, New York, 1990, pp. 659-668. [9] L. Elena and R. Schiestel, “Turbulence Modeling of Ro- tating Confined Flows,” International Journal of Heat and Fluid Flow, Vol. 17, No. 3, 1996, pp. 283-289. doi:10.1016/0142-727X(96)00032-X [10] H. Iacovides and I. P. Theofanopoulos, “Turbulence Modeling of Axisymmetric Flow Inside Rotating Cavi- ties,” International Journal of Heat and Fluid Flow, Vol. 12, No. 1, 1991, pp. 2-11. doi:10.1016/0142-727X(91)90002-D [11] R. Schiestel, “Les Ecoulements Turbulents,” 2nd Edition, Hermès, Paris, 1998. [12] L. Elena, “Modélisation de la Turbulence Inhomogène en Présence de Rotation,” Ph. D, Université Aix-Marseille I-II, 1994. [13] S. Poncet, R. Schiestel and R. Monchaux, “Turbulence Modeling off the Von Karman Flow: Viscous and Inertial Stirrings,” International Journal of Heat and Fluid Flow, Vol. 29, No. 1, 2008, pp. 62-74. doi:10.1016/j.ijheatfluidflow.2007.07.005 [14] R. Schiestel and L. Elena., “Modeling of Anisotropic Turbulence in Rapid Rotation,” Aerospace Science and Technology, Vol. 1, No. 7, 1997, pp. 441-451. doi:10.1016/S1270-9638(97)90006-7 [15] S. Poncet, R. Schiestel and M. P. Chauve, “Turbulence Modelling and Measurements in a Rotor-Stator System with Throughflow,” ERCOFTAC International Sympo- siu m o n E n gine er i ng T u rbul e nce Modelling and Measure- ments, Sardinia, Italy, 2005. [16] P. Boronski, “Méthode des Potentiels Poloïdal-Toroïdal Appliquée à l’écoulement de Von Karman en Cylindre Fini,” Ph. D, Ecole Polytechnique, 2005. Nomenclature R1 : Radius of interior cylinder (m) R2 : Radius of external cylinder (m) h : Height of cylinder (m) a : Height of wings (m) h’ : Length of wings (m) b : Thickness of wings (m) Dimensionless G : Aspect ratio of the cavity R : Rotational Reynolds number U : Mean axial velocity V : Mean radial velocity W : Mean tangential velocity u’ : Axial velocity fluctuation v’ : Radial velocity fluctuation w’ : Tangential velocity fluctuation P : Pressure p’ : Pressure fluctuation h* : Height of wings Greek letters : Density of fluid (kg·m-3) : Kinematics viscosity of fluid (m2·s–1) : Rotating velocity of disks (rad·s–1)
|