Journal of Modern Physics, 2011, 2, 404-415
doi:10.4236/jmp.2011.25050 Published Online May 2011 (http://www.SciRP.org/journal/jmp)
The Liquid-Bridge with Large Gap in Micro
Structural Systems
Shiqiao Gao, Lei Jin, Jingqing Du, Haipeng Liu
School of Mechatronic Engineering, Beijing Institute of Technology, Beijing, China
Received April 8, 2010; revised March 12, 2011; accepted March 17, 2011
Abstract
Based on the analysis of the total free energy of the liquid-bridge, several methods are presented to analyze
the pull-off force of liquid-bridge. For the liquid bridge system with a large gap width, accurate solutions of
a two-plate liquid bridge and a sphere-plane liquid bridge are given. In addition, the edge-effect resulting
from the profile of the top solid in the liquid-bridge system is analyzed and calculated. It is proved by the
subsequent tests.
Keywords: Liquid-Bridge, MEMS, Capillary, Pull-Off Force
1. Introduction
When a small amount of liquid is introduced at the small
gap between two solid surfaces, a liquid-bridging phe-
nomenon can be observed. Such a liquid-bridging phe-
nomenon occurs in many cases. For example, a small
water between the tip and the substrate surface of atomic
force microscopy (AFM) will form a liquid-bridge [1,2],
some water films or other liquids will cause a liq-
uid-bridge between the tip and sample of the scanning
force microscope (SFM) [3], a protective lubricant thin-
film used over the surface of the disk to separate the head
slider from the disk can also cause meniscus rings around
contacting asperities and liquid bridg es between the head
and the disk [4], an adsorbed water droplet due to hu-
midity between the cantilever beam and the substrate of
micro accelerator (or RF-MEMS) will result in a liq-
uid-bridge [5], similarly many liquid-bridges between
combs and substrate or between the neighbor combs of
micro gyroscope will be formed when there is some wa-
ter. With miniaturization of system and microminiaturi-
zation of the structures and objects, adhesion caused by
capillary appears to be one major problem during the
assembly and/or fabrication of micro-components and
the operation of system.
The liquid-bridge will cause a capillary interaction
between the solid surface and th e liquid. To separate two
solid surfaces in a liquid-bridge system, a force is needed
to overcome the capillary attractive force caused by the
liquid. This force is usually called as pull-off force or
capillary force (or adhesion force). Such a cap illary force
is too insignificant for normal macro mechanical system
to consider. But it will play a significant role in a micro
scale system, especially in a nanoscale system. This is
because surface forces become more and more important
when size diminishes and the objects are scaled down.
Capillary force is one of the adhesion forces. Capillary
force can cause the thin polymer beams of the 3D micro-
structures to deflect and collapse during the evaporative
drying of structures from liquid resin [6]. Adhesion can
also prevent micro structures like RF-MEMS, micro
sensor, micro gyroscope, or any high aspect ratio struc-
tures from normal functioning.
Of course, from another point of view, capillary force
between two objects can be also used to manipulate small
object [7]. In such a case, the capillary force applied on to
the object should be controllable. Nevertheless, the major
opposing forc e to picking up and releasing parts becomes
adhesion. In assembly, it is as important to pick up as to
release the object. In macro-assembly, this problem does
not exist, because usual grippers can be closed (i.e. the
part is locked between the digits of the gripper) or open
(and the gripping force falls to zero). In micro-assembly,
adhesion provides a very small value for the “gripping”
force. If the weight of the object is smaller than adhesion,
the object cannot be released. Conversely, if adhesion is
smaller than the object weight, the object cannot be
picked up.
The liquid of a liquid-bridge may exist originally (i.e.
placed previously or remained after fabrication). It may

S. Q. GAO ET AL.405
be also subsequently formed by the phase transition from
a condensable vapor near saturation to liquid. Therefore,
for a micro structural system, especially for a nano-
structural system, whether there is original liquid or not,
it is possible for a liquid-bridge to be formed when am-
bient humidity is relatively large. To avoid the formation
of a liquid-bridge for a micro system or a nanoscale sys-
tem, an appropriate packing with sufficient drying vac-
uum is necessary.
In order to understand the liquid-bridging phenome-
non, much effort has been made by earlier researchers
[8-11]. In the aspect of theoretical studies, there are two
ways to establish the models. One app roach to determin-
ing force is the macroscopic Laplace-Kelvin Equation
based on the meniscus theory. The other way is to make
numerical computations based on the molecular theories,
including molecular dynamics and Monte Carlo simula-
tions, integral Equation and density functional theories.
The profile of the liquid shows meniscus. According to
the Laplace-Young Equation, a negative pressure differ-
ence between the inside and the outside of the meniscus
will be formed. This negative pressure difference will be
also applied on the wetted surface of solids in terms of
the Pascal’s law that no pressure gradient can exist for
static liquids. This macroscopic approach usually as-
sumes that the meniscus shape can be described by two
principal radii, and its volume remains unchanged as the
gap width chan ges. Even though this approach is simple,
it has been validated for relative large scale structures.
However, for nanoscale problems, this approach is not
appropriate because of finite molecular size effects that
give large fluctuations in meniscus size and shape. To
study the capillary force in such a nanoscale case, some
analyses based on the molecular theory are needed. For
micro scale problem, this conventional simple approach
can not be directly used either. Orr, Scriven and Rivas
[12] presented a detailed literature survey on the earlier
work related to the meniscus properties and capillary
force involved in the liquid bridging between two solid
surfaces by means of solving the Laplace-Young Equa-
tion. They discussed the aspects of liquid mechanics,
including the volume of liquid, surface area, and mean
curvature of the meniscus, and the liquid-bridging forces
exerted on the solid surfaces. Recently, on the one hand,
instead of a rigid solid, some elastic deformations and
the coupling interaction between solid and liquid have
been considered and discussed by the well-known
Hertzian solution for the contact between a sphere and a
plane [4,13]. On the other hand, the effect of humidity on
the capillary has been studied by many researchers [14].
In the same time, of course, some computational simula-
tions have been made and developed based on the mod-
ern molecular theory [2,15], e.g. a density functional
theory (DFT), the molecular dynamics (MD), the Monte
Carlo (MC) method, the grand canonical MC (GCMC)
method, and so on. In addition to the equilibrium method
mentioned above, the energy method has also been used
to solve the pull-off force [16]. Although the equilibrium
method based on the Laplace-Young Equation is equiva-
lent to the energy method, there are also some differ-
ences in detail between them because many factors have
been neglected in the equilibrium method.
In the aspect of experiments, many studies have been
also made by earlier researchers [8,17-20]. The earliest
measurement was made by McFarlane and Tabor [8].
They measured the meniscus force of water in atmos-
pheres with different relative humidities by measuring
the pull-off force between a glass ball and a glass plane
surface in contact. According to the conventional simple
theory, the pull-off force is independent of the relative
humidity. However, McFarlane and Tabor found in their
experiments that the pull-off force decreased suddenly
when the relative humidity was less than 90% and the
decrease was dependent on the roughness of the glass
surfaces. They concluded that the decrease would occur
when the height of the surface roughness was compara-
ble with the thickness of the adsorbed liquid film. Later,
Fisher and Israelachvili [17] made a more precise meas-
urement of the meniscus force for water, benzene,
cyclohexane, n-hexane and 2-methylbutane in atmos-
pheres of their own vapors at a relative vapor pressure in
the range of 0% - 99%. They used molecularly smooth
mica in contact surfaces instead of glass to avoid the
effect of surface roughness on measurement. They found
that for organic liquids the surface tension theory based
on bulk thermodynamics was applicable even when the
adsorbed film was only a few molecules in thickness.
However, for water it was quite different. Their experi-
mental results for water showed that the meniscus force
due to the Laplace pressure reduced to 90% of that ex-
pected from bulk thermodynamics when the relative va-
por pressures is 0.9, corresponding to a Kelvin meniscus
radius of about 5 nm. They explained the results in terms
of the assumption that the long-range cooperative nature
of the hydrogen bonding interaction and electric double
layer forces in water film between solid surfaces may
play a role in reducing the effective surface tension of
water. Christenson [18] modified the surface force appa-
ratus by adopting a double cantilever spring. They ob-
tained very different experimental results from those of
Fisher and Israelachvili. They found that for organics
such as cyclohexane and n-hexane the measured pull-off
force increased with the decrease in the relative vapor
pressure, and for water, although the measured pull-off
force decreased as the relative vapor pressure decreased,
the decrease was much smaller than that obtained by

S. Q. GAO ET AL. 406
V
Fisher and Israelachvili. With th e inventions of the scan-
ning force microscope (SFM), scanning tunnel micro-
scope (STM) [21], the atomic force microscope (AFM),
scanning probe microscope (SPM), and the surface force
apparatus (SFA), many powerful tools have been made
and developed for observing surface morphology on an
nano-scale and atomic scale. They make a powerful
probe for a variety of surface studies available. They
enable us to investigate various sample properties such
as adhesion, surface charge, and magnetic properties on a
nanometer scale. But on the other hand , it is unavoidable
for them to face the liquid-bridge problems on nanometer
scale.
From the earlier research worksmentioned above,
whether the theoretical studies or the experimental stud-
ies, most of the investigated objects are the liquid-bridge
system composed of a spherical tip and a plane substrate.
Most of those studies were made with the constraint of
small separating distance. When the wetted area is much
larger than the gap between the two solids (i.e. large
deep-wide ratio), the shape of meniscus can be negligible
during calculating the volume of liquid. Even in the
modified model established by Mingyan He, et al. [1],
instead of the meniscus curve surface, a cylindrical sur-
face was still used for calculation of the liquid volume.
Nevertheless, when the gap becomes large, the shape of
profile has an apparent effect on the volume and other
geometrical parameters. From the theoretical analysis, it
can be also apparently seen that the capillary force de-
pends tightly on the geometric (shape) parameters of
meniscus profile, such as the principle radii, the contact
angles, the fulfilling angles, the volume, the interfacial
areas, the gap width, and so on. In order to model the
meniscus profile accurately, O. H. Pakarinen et al. [14]
presented a method to numerically calculate the exact
(non-circu lar) men iscus pr ofile fro m the Kelvin Equation.
But it is not analytical model. The co mputation based on
the difference Equations was also approximate. For a
micro scale problem, the conventional continuum model
is too simple to predict the capillary force. But the com-
putational simulation is too complicated to analyze. In
view of this micro scale, this current article attempts to
give a relatively accurate solution of the pull-off force of
micro liquid-bridge by means of an analytical method
based on the energy theory.
2. The Total Free Energy of the
Liquid-Bridge
The surface tension is always trying to make the area
contract. Therefore, with the increase of area, the poten-
tial energy will increase. On the contrary, the pressure is
always trying to make the volume expand. Therefore,
with the decrease of volume, the potential energy will
increase. The total free energy consists of two parts
which are free surface energy and free bulk energy re-
spectively. The free surface energy arises from the con-
tributions of the solid/liquid and liquid/vapor interfaces.
The free bulk energy arises from the contributions of
liquid and vapor volumes with corresponding pressures.
In order to calculate the free energy of the liquid-bridg-
ing system, the liquid volume and the surface areas of the
interfaces are need to be calculated. For a liquid bridge,
the total free energy can be written by
11
nm
ii jj
ij
EAp 



(1)
where the first sum term in right-hand side is the total
free su rface energy, th e second sum te rm is the total fr ee
bulk energy,
A
stands for interfacial area and

the
interfacial tension, stands for the phase volume and
the phase pressure, where the subscript stands for
the interface and the subscript stands for the phase.
Naturally there are usually three phases, which are vapor
phase, liquid phase and solid phase respectively. The
interface means the contact surface between every two
phases, e.g. the interface between vapor phase and liquid
phase, the interface between vapor phase and solid phase,
and the interface between liquid phase and the solid
phase. Liquid bridge is a system constructed by two solid
phase, one liquid phase and one vapor phase. Therefore
there are two vapor-solid interfaces, two liquid-solid
interfaces and one vapor-liquid interface shown in Fig-
ure 1.
V
p i
j
If the interface area between top solid and liquid is
lst
A
(top wetted area), the interface area between top
solid and vapor is vst
A
, the interface area between sub-
strate solid (bottom solid) and liquid is lsb
A
(bottom
wetted area), the interface area between substrate solid
and vapor is vsb
A
, whereas the interface area between
vapor and liquid (i.e. the profile of the liquid) is lvp
A
,
the volume of liquid is , and the volume of vapor is
l
V
Figure 1. A general liquid-bridge.

S. Q. GAO ET AL.407
v, the total free energy of the liquid bridge system de-
scribed by Equation (1) can be rewritten as
V
lstlstvstvstlsb lsbvsb vsb
lvplvpl lvv
EA AAA
ApVpV



  
 (2)
Because the interfacial tension between solid and va-
por is very small, the effect of solid-vapor interface in
Equation (2) can be neglected. Then, we have
lstlstlsblsblvplvpl lvv
EA AApVpV

   (3)
When we solve some forces by means of the energy
theory, it is needed to differentiate the total free energy.
At a constant temperature, the differentiation of total free
energy can be derived by
δδ δδ
δδ
lstlstlsb lsblvp lvp
ll vvv
EA AA
pV pV

  
 (4)
Because the total volume of liquid phase and vapor
phase is constant, i.e. , there is

δ0
lv
VV
δδ
v
V l V
V
(5)
Substituting Equation (5) into Equation (4), leads to

δδ δδδ
lstlstlsb lsblvp lvplvl
EA AApp     (6)
For rigid solids, there is no deformation on the inter-
faces of solid and liquid. The interfaces have the same
shapes as the solid surface. Nevertheless, the in terface of
liquid and vapor will keep meniscus shape with some
corresponding curvatures due to the capillary effect.
3. The Solution on the Interface of Liquid
and Vapor of the Liquid-Bridge
On the interface of liquid and vapor of the liquid bridge,
i.e. the meniscus profile, excepting the pressure of vapor
and the pressure of liquid, there is no other external force.
In terms of work-energy conservation theory, there is

δ
δδ δ
δδ δ
δ
0
δ
lvp
lst lsb
lvplst lsblvp
l
lv
δ
A
AA
E
frr r
V
pp r
   
 
r
(7)
where is the normal coordinate of the curve surface of
the meniscus profile. Considering
r0
lst lsb
AA

 , we
have

δδ0
δδ
lvp l
lvpl v
AV
pp
rr
   (8)
Supposing the two principal radii of the curve surface
of the meniscus profile are 1 and 2 respectively, by
means of the geometric relationships of the spatial curve
surface, we can obtain the following relationship
r r
12
11
δ
lvp l
δ
A
V
rr

 


(9)
Substituting Equation (9) into Equation (8), leads to

12
δ 11 0
δ
l
lvpl v
V
pp
rr r




 
 



(10)
That is
12
11
vl lvp
pp prr 






(11)
This equation is the so called Young-Lapl ace Equation.
4. The Pull-Off Force of the Top Solid in the
Liquid-Bridge System
4.1. The Solution for Constant Wetted Areas
To obtain the pull-off force of the top solid in the liquid
bridge, a classical derivative of the energy with respect
to the distance between the top and substrate solid ob-
jects (i.e. vertical coordinate ) can be used. This prin-
ciple of work-energy conservation can be explained as
follows. An increment displacement in direc-
tion will result in an in crement of total free energy of the
liquid bridge system . In terms of the principle of
work-energy conservation, this increment of en-
ergy should arise from the work done by pull-off force
a
z
δz z
E
δE
δ
f
in the distance of , that is , which
leads to
δzδEfδ
az
δ
δ
aE
fz  (12)
Substituting Equation (6) into Equation (12), leads to

δ
δδ δ
δδ δ
δ
δ
lvp
lst lsb
alstlsblvp
l
lv
δ
A
AA
E
fzz z
V
pp z
   

z
(13)
In the case of constant interfacial areas, there are
δδ 0
lst lsb
AA

. To take liquid with a small chip from a
cup of liquid belongs to this case shown in Figure 2. The
increment of the profile area is
δδsin
lvp tt
Alz


 (14)
where t

is the contact angle of the liquid with respect
to the top solid, and t is the perimeter of the interfacial
(wetted) area lst
l
A
. Whereas llst VA z

 . Substituting
them into Equation (13), leads to

δsin
δ
sin
alvpttlv
lvp ttlst
Elst
f
lpp
zlpA


A

 
 
(15)

S. Q. GAO ET AL. 408
Figure 2. Taking liquid with a piece of thin plate from a cup.
Taking lvp

  (the surface tension) and 2
m
pr


where is the mean radii of the meniscus profile
where m
r
1
211
m
rr
2
r, leads to
2
sin
att
mlst
f
l
rA

  (16)
4.2. An Approximate Solution for Constant
Liquid Volume
For a general liquid bridge, the liquid keeps a constant
volume, that is . Equation (13) can be rewritten
by
δ0
l
V
δ
δδ δ
δδ δ
lvp
lst lsb
alstlsblvp
δ
A
AA E
fzz z   z (17)
To obtain the solution of Eq uation (17), some geomet-
ric relationships need to be analyzed and discussed. We
define a deep-wide ratio as dw

 where is
thickness of liquid film or the minimum gap width be-
tween the two solid objects and is the length in
maximum wide direction of area
d
w
tls
A
. If the liquid bridge
has a small deep-wide ratio, i.e. 1

 and lst lsb
A
A

,
the volume of liquid can be approximately expressed as
llst
VdA dA 
lsb
(18)
Considering the volume as a constant (isovolume), we
have
δδδδδ0
llstlstlstlst
VdAdA dAzA   (19)
Therefore, there is
δ
δ
lst lst
A
A
zd
 (20)
Similarly there is
δ
δ
lsb lsb
A
A
zd
 (21)
From the geometric relationship of meniscus profile of
the liquid bridge shown in Figure 3, the relationship
between the thickness of liquid film (the distance be-
tween the two solid objects) and the curvature radius
can be written by
d
1
r


1cos cos t
dr b

  (22)
where b

is the contact angle of the liquid with respect
to the substrate solid.
Substituting Equ ations (1 4), (20 ) and (2 1) into Eq uation
(17) and noting that cos
lst t

  , cos
lsb b




and lvp



, leads to

δcos cossin
δ
lst
atb
A Ett
f
l
zd

   (23)
Substituting Equation (22) into Equation (23), lead s to
1
sin
lst
att
A
f
l
r

  (24)
4.3. An Accurate Solution for Large Gap Width
If the deep-wide ratio is not small, a more general model
should be built. If the top and substrate solids are all
planes shown in Figure 4, the increment of the vertical
distance can be also written as


1
δδcos cos
t
zr b

  (25)
Whereas the increment of volume should be written as
Figure 3. A circular liquid bridge.
Figure 4. A rectangular liquid bridge.

S. Q. GAO ET AL.409
δzδδ
l lvplst
VAxA  (26)
Because the volume keeps a constant, there is 0
l
V


.
Therefore we have
δ
lst
lvp
δ
A
x
z
A
 (27)
In this case, the area change of top interface can be
written as
δδ
tlst
lst tlvp
lA δ
A
lx z
A
  (28)
The area change of substrate interface can be written
as
δδ
blsb
lsb bδ
lA
lvp
A
lx z A
where t and b are perimeters of the top interface and
the substrate interface respectively.
(29)
l l
The change of profile area can be written as
δsinδ
lvp tt
A
lz

 (30)
Substituting Equation (28), (29) and (30) into Equa-
tion (17) and noting cos
lst t

  , cos
lsb b

 
and lvp

 , leads to

δcos cossin
δ
lst
attbb
lvp
A E
fll
zA
tt
l

    (31)
For a polygonal interface as shown in Figure 5, the
area of profile for one side can be written by means of
integral as
π
1
2
π
2
11
2tan tan
22 2
π
coscos d
2
t
b
iti i
i
t
l
A
rr



1
r













 
 
 (32)
where i

is the central angle of th side and ti is
the length of the side. Integrating Equation (32) and
summing all the sides, lead s to
th
i l
th
i

1
1
1
2
11 1
2tan tan
22 2
sin πcos cos
n
lvp i
i
nitii
i
ttb t
AA
l
rr r


b

 















 (33)
For a circular interface as shown in Figure 3, taking
the limit of 0
i

 and n, leads to
n
AA


 

0() 1
2
211
0
2
1
121
1
sin sinπ
cos cosd
2πsin π
cos cos
lim
i
lvp i
ni
tt t
tb
ttb
tb
rrr
r
rrr
r



b





 

 




  

 



 
(34)
For a rectangular interface shown in Figure 6, the pro-
file area is derived by




11
1
2
1
11
2
1
4sinπ
2
cos cos
sin π
2
cos cos
nb
AA
lvp itt b
i
tb
ttb
tb
a
rr
a
r
ab
rr
b
r

















 





 


(35)
where and are respectively length and width of
an




ab
the rectgle.
For a square interface, there is

8sin
n
lvpi t
AAlr


11
1
2
1
π
8coscos
tt b
i
tb
r
r




 






 (36)
It should be pointed out that, for a narrow-long rec-
tangular solid shown in Figure 6, the interface area will
Figure 5. A polygonal liquid bridge. Figure 6. A narrow-long rectangular liquid bridge.

S. Q. GAO ET AL. 410
first a
qua t i on ( 31), l ead s to *
Eq al of top solid is the same as that of sub-
st
vature radius. But the contact angles should keep con-
stant. Supposing the curvature center has a tiny displace-
ment in left-hand direction 0 δ
x
and a tiny upward dis-
placement 0, and the curvature radius has an incre-
ment , the wetted boundary on the spherical interface
will contract with a displacement
δy
δr
δt
x
in left-hand di-
rection, which can be written as
ly contract apart from the long side until to form
square shape, and then will contract apart from the short
side until to form a circler shape.
Substituting Equation (34) into E
uation (37)
If the materi
rate solid, there are tb

  and tb ll. Then th ere is


0
δδδsincos δ
ttt
xxr r

  

11 1
2cos
2sin π24πcos
sin
ttlst
atttt
tt
lA
frl rr
l

 (42)


 



(38)
For a liquid bridge with small deep-wide ratio,
where

is called the filling angle and δ

is defined
as positive in clockwise direction.
The vertical upward displacement can be written as
.
t
l
1cost
r2

. Equation (38) can be rewritten as


0
δδδcossin δ
ttt
yyr r

    (43)

1
2cos Asin
π2
tlst
att
t
l
r

From the geometric relationships shown in Figure 7, the
displacement of meniscus curve surface of profile (or the
displacement in left-hand direction of the horizontal apex
of the profile) can be written as
f




 (39)
Comparing Equation (24) with Equation (39), it is
found that these two Equations are not the same. It
should be said that Equation (39) is a more accurate
Equation in which the curve surface of profile has been
considered during the calculation of liquid volume. If we
use the straight line distance 1 2cost r

instead of the
curve arc distance

1π2rt

, E(39) will change
to Equation (24). are interface, substituting
Equation (36) into Equation (31) and considering .
t
l
1
2cost r
quation
For a squ

, the same Equation as (39) can be obtained
t be pointed out that, with the contracting
. of It mus
0
δδ δ
x
xr

 (44)
The wetted area on the substrate plane will contract
with a following decrement


δδ1sin δ
b
x
r    (45)
Because there are cos
t
xR




and 0cos b yr



,
we can obtain the following relationshi ps
δδ sin δ
t
zyR



 (46)
and
so
4.5. An Accurate Solution for the Sphere-Plane
When the top solid has the spherical shape and the sub-
(40)
Then th ere is
lid-liquid interface apart from every boundary side, the
shape of interface tends to a circle acted by the surface
tension force.


δcos cosδsin δ
tbt t
yrr







 
 (47)
Substituting Equation (47) into Equation (46), leads to


δcos cosδ
sin sinδ
bt
t
zr
Rr


 








(48)
Liquid Bridge System with a Large Gap
Width
Substituting Equation (42) into Equation (44), leads to



δ1sin δ
cos cosδ
t
t
xr
Rr




  


 


(49)
strate is plane shown in Figure 7(a), the problem becomes
relatively complicated. The conservation condition of
volume can be also written by
δδVAx From the Equations (41), (45), (47) and (48), the fol-
lowing solutions can be obtained
δ0
llvplst
Az
13
12 34
δ
δ
CC
r
z
CC CC


 (50)
δδ
lst
lvp
A
x
z
A
 (41)
When the sphere moves upward with a tiny displace-
man
and
24
12 34
δ
δ
CC
zCCCC



 (51)
en t δz, the meniscus interface of liquid-vapor will
also chge, including the curvature center and the cur-

 
11 1
cos cossin
2πsin π2πcoscos
ttbblst
att
tttb tb
llA
f
l
rl rr



 


 (37)*

S. Q. GAO ET AL.411
(a)
(b)
Figure 7. A sphere-plane liquid bridge system with a large
gap width.
and

51 3
δCC C
12 34
δzCC CC



   (52)
e wher

1coscos t
CR r

  ,


cos
bt2cosC

  ,

sinsin t CR r
3

  ,

41sint
C

  ,
51sinb
C

 and lst lvp
A
A

.

2
2π1cos
lst
AR

 (53)
The wetted area on the sub
as strate plane can be written
2
π
lsb
A

 (54)
The incremenniscus areaf profile can be de-
sc
t of me o
ribed as
δ2πsinδ
lvp
A
Rs


(55)
where
s

is the increment of the meridian of the pro-
file, which can be derived as


b
δδδπ
t
sr r



 (56)
By means of Equations (50), (51) and (52), deriving
Equations (53), (54) and (55) with respect to the vertical
coordinate , leads to z

224
1
2πsin
δ
lst RCC
A
zCCCC
 
  (57)
2 34
δ

The wetted area on the sphere can be written as
513
δlsb CC C A
12 34
2π
δzC C CC



 





 (58)
  
δlvp A
24 13
12 34
δ
π
2πsin t
z
rC CCC
RCC CC
b






Substituting Equations (57), (58) and (5
tion (17) and noting
  
(59)
9) into Equa-
cos
lst t

  , cos
lsb b




and lvp



, leads to



   
224
12 34
513
4 13
12 34
2πsin cos
πsin
at
tb
RCC
fCC CC
CC C
C C
RCC CC
 


12 34
2
2πcos
2
b
CC CC
rCC
 
 






 

(60)
As






goes to zero (i.e. 0



), the liquid-bridging
force a
f
also approachbut not to a constant
as poted out by Ref. 22. This is in consisten
with and not in conflict with the practical physical phe-
nomenon. Nevertheless, if a approximate cylindrical pro-
file instead of an accurate meniscus profile is used to
calculate the profile area or the volume of liquid, a
fli wr
es to zero
and 14 t
con-
in
ctionill occur. This can be addessed as follows.
When the thickness of liquid film is very small, the
curvature radius will be much smaller than the radius of
sphere, i.e. rR. In this case, instead of the practical
meniscus profile, an approximate cylindrical profile can
be used as in Ref. 1. The profile area described by (34)
(in which rr) may be approximately written as
12

S. Q. GAO ET AL. 412


2πsin
lvp
A
RDd   (61)
where D is the distance between the sphere and the
plane and d is the height of the sphere cap (the same as
in Ref. 1).
Substituting Equations (61) and (53) into Equation
(60), neglecting the surface tension (the third term of
Equation (6onsidering bt
0)), c

  andsinR



,
and taking and the limit of 0D 0

, leads to
4πcosfR
a

 
he
p
(62)
This is t conventional Equation. Because Equation
(62) is indeendent of the filling angle

, this expres-
sion shows that the liquid-bridging force approaches to a
constant as

goes to zero. Of course, this is in conflict
with the fact that there is no liquridginge-
tween two ctely dry surfaces.
In terms of Re1, the wetted area
id-b force b
omple
f.
approximately written as on the plane can be
22
πsin
lsb
AR

 (63)
Equation (49) can be appro ximately rewritten as
δcos δxR

  (64)
The conservation condition of volume results appro-
ximately in
δ
Aδ
lsb
lvp
x
z
A
 (65)
Substituting Equations (61), (63)
tio and (64) into Equa- n (65), leads to

δtan tan
δ221cos1 zDdRDd



uations (53), (61) and (63) with respect to
the vertical coordinate and subs
into them, leads to

(66)
 
Deriving Eqz titu ting Equ ation (66)

2
δ2πsin tan
δ
lst
AR
zR

21
c os 1Dd 
 (67)

2
δtan
π2sin cos
δ21cos1
lsb
A
R
zRDd

    (68)
δ2πsin AR
δ
lvp
z

 (69)
Substituting Equations (67), (68) and (6
tion (17) and noting 9) into Equa- cos
lst

  , cos
lsb

 
and lvp

 , leads to


2
1cos
πcos 2πsin
cos 1
a
fR R
Dd








(
If the surface tension is negligible
be rewritten as
70)
, Equation (70) can

2
(1cos )
πcos
a
fR



 )
cos1 Dd   (71
This is the same as that obtained by He, et al. in Ref. 1.
Although Equation (71) is not independent of th
angle e filling

, the same form as Equation (62) can be ob-
tained. This is because an approximate cylindrical profile
is also used for calculation of the liquid volume. As
0D

( as shown in Figure 7(b)) and 0

, Equation
(71) changes to
4πcos
a
fR



(72)
on
film a
This is the same as the conventional Equation (62).
It should be pointed out that, Equation (72) is appro-
priate ly for large sphere and thin liquid film. Al-
though Equation (71) has been partially modified relative
to Equation (72), it is appropriate only for a thin liquid
nd a small deep-wide ratio, i.e. 1

.
The model built in this article is appropriate not only
for the large sphere and thin liquid
sm
ive pressure
film, but also for the
all sphere and large separating distance.
4.6. The Edge-Effect Resulting From the
Profile of the Top Solid in the
Liquid-Bridge System
In a general liquid-bridge system, the liquid will not only
wet the major surface of top solid but also wet the profile
near the edge of it. In this case, the pull-off force will be
caused not only by the Laplace negat
2
pm
F
rA


 and the profile surface tension of li
sinFl quid




 (e.g. as shown in Equations (16)
but also by the surface tension of liquid
ear the edge of top solid. Th
and
on the pro-
file ne former as shown in
(24))
Figure 8 can be expressed by
Figure 8. The major surface is wetted.

S. Q. GAO ET AL.413
2sin
Tp m
FFFA l
r



  (73)
where
A
stands for the wetted area of top solid and

is thsion of liquid e surface ten

p is the contact angl the liquwith respect to the tosolid, and is th
rime wetted area
e of
e pe-
id
ter of the l
A
, m r is the m rad
the mes profile.
The latter as shown in Figure 9 can be expressed by
eanii of
niscu
cos
E
Fl

  (74)
The total pull-off force as shown in Figure 10 can be
expressed by
2sin cos
m
FAl l
r


    (75)
5. Exper
To validate the above model in which the
considered, a series of experiments are conducted. One
thn
.
re an
lates range from 200 mm to 400
me
iments and Comparisons
edge effect is
kind ofem is to take water from a water cup as show
in Figure 11. The other kind is to pull the water from a
silicon substrate plate as shown in Figure 12The shapes
of top silicon plate include ctgular and square. The
areas of top silicon p2
m2. When the amount of the water is enough, the sam
Figure 9. The edge is wetted.
Figure 11. Taking water from cup.
Figure 12. Taking water from the silicon substrate.
both kinds of experiments.
The relationship curves between the pull force and the
displacement of top silicon plate are shown in Figure 13.
The used top silicon plate is a rectangular plate which
has 20 mm length and 15.71 mm width. Figure 13 in-
cludes seven curves corresponding the different test
times. It is clear that they are very consistent and have
very little deviation. The peak value of the curve is con-
sidered as pull-off force of the liquid-bridge system. It is
found that the pull-off force depends strongly on the area
of the top silicon plate. The corresponding curves are
shown in Figure 14. In Figure 14 the calculated curves
results may be obtained for
Figure 10. The total pull-off force comes from the major
surface and the edge profile. Figure 13. The curves of taking force vs displacement.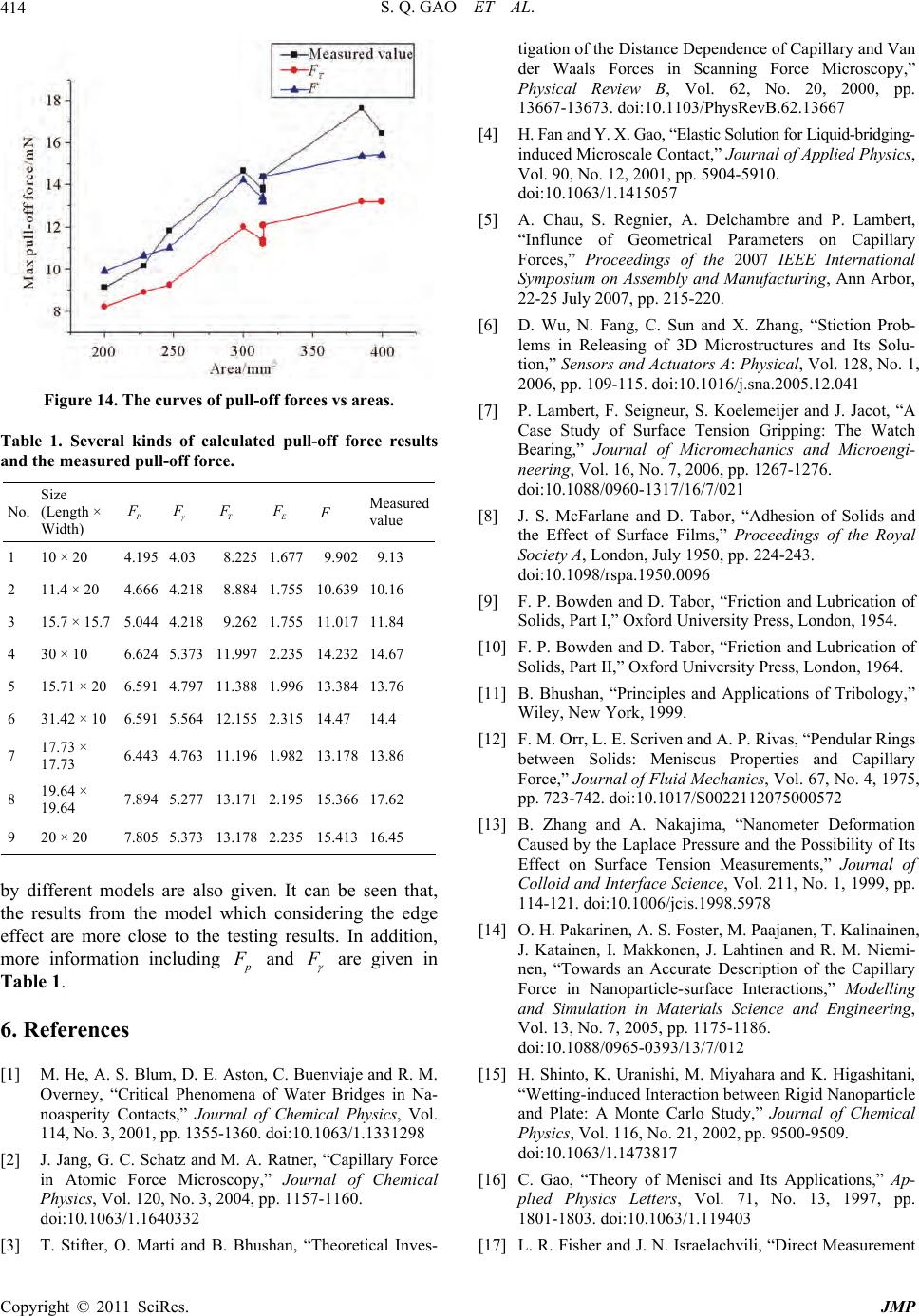

S. Q. GAO ET AL. 414
Figure 14. The curves of pull-off forces vs areas.
Table 1. Several kinds of calculated pull-off force results
and the measured pull-off force.
No. Size (Length ×
Width)
P
F
F

T
F
E
F
F
Measured
value
1 10 × 20 4.195 4.03 8.225 1.677 9.902 9.13
2 11.4 × 20 4.666 4.218 8.884 1.755 10.639 10.16
3 15.7 × 15.7 5.044 4.218 9.262 1.755 11.017 11.84
4
5 15.71 × 20 6.591 4.797 11.388 1.996 13.384 13.76
6 31.42 × 10 6.591 5.564 12.155 2.315 14.47 14.4
7 17.73 ×
17.73 6.443 4.763 11.196 1.982 13.178 13.86
8 19.64 ×
19.64 7.894 5.277 13.171 2.195 15.366 17.62
9 20 × 20 7.805 5.373 13.178 2.235 15.413 16.45
30 × 10 6.624 5.373 11.997 2.235 14.232 14.67
by different models are also given. It can be seen that,
the results from the model which considering the edge
effect are more close to the testing results. In add
more information including
ition,
p
F
and
F

are given
Table 1.
. R
a of Water Bridges in Na-
erity Contacts,” Journal of Chemical Phy
, 200, pp. 55-1doi:10.1063/1.
[2] G. C. Schatz and M. A. Ratner, “Capillary Force
ic n
63
[Bes-
of tran
aals Frceicroy,”
R Vpp.
R
[4] la ng-
il te ics,
0, No. 12, 2001, pp. 5904-5910.
63
[5] au, S. Regnier, A. Delchambre and P. Lambert,
e elary
Forces,” Proceedings of the 2007 IEEE International
Aal,
, pp. 109-115. doi:10.1016/j.sna.2005.12.041
[7] P. Lambert, F. Seigneur, S. Koelemeijer and J. Jacot, “A
f Surface Tension Gripping: The Watch
al of Micromechanics and Microengi-
l
ation of
niversity Press, London, 1954.
00572
eering,
oparticle
,” Journal of Chemical
ations,” Ap-
. 71, No. 13, 1997, pp.
t
in
[14] O. H. Pakarinen, A. S. Foster , M. Paaja nen, T. Kalina ine n,
J. Katainen, I. Makkonen, J. Lahtinen and R. M. Niemi-
nen, “Towards an Accurate Description of the Capillary
Force in Nanoparticle-surface Interactions,” Modelling
and Simulation in Materials Science and Engin
6eferences
[1] M. He, A. S. Blum, D. E. Aston, C. Buenviaje and R. M.
Overney, “Critical Phenomen
noasp sics, Vol.
1331298 114, No. 3
J. Jang,
113 360. Phy
in AtomForce Microscopy,” Joural of Chemical
Physics, Vol. 12
doi:10.10 0, No. 3, 2004, p /1.164 p. 1157-1160. 0332
3] T. Stifter, O. Marti and . Bhushan, “Theoretical Inv
tigation
der Whe Dis orces
tance D
in S
epende
cannin
nce of
g FoCapilla My and V scop
Physical eviewB, ol. 62, No. 20, 2000,
13667-13673.
d Y. X.
doi:10.1103
Ga
/Phys
stic Soluti
evB.62.13667
on for H. Fan an
induced M
Vol. 9
o, “ELiquid-bridgi
croscae Conact,” Journal of Applid Phys
doi:10.10
A. Ch
/1.1415057
“Influncof Gometrical Parameters on Capil
Symposium on Assembly and Manufacturing, Ann Arbor,
22-25 July 2007, pp. 215-220.
[6] D. Wu, N. Fang, C. Sun and X. Zhang, “Stiction Prob-
lems in Releasing of 3D Microstructures and Its Solu-
tion,” Sensors and Actuators: Physic Vol. 128, No. 1,
2006
Case Study o
Bearing,” Journ
neering, Vol. 16, No. 7, 2006, pp. 1267-1276.
doi:10.1088/0960-1317/16/7/021
[8] J. S. McFarlane and D. Tabor, “Adhesion of Solids and
the Effect of Surface Films,” Proceedings of the Roya
Society A, London, July 1950, pp. 224-243.
doi:10.1098/rspa.1950.0096
[9] F. P. Bowden and D. Tabor, “Friction and Lubric
Solids, Part I,” Oxford U
[10] F. P. Bowden and D. Tabor, “Friction and Lubrication of
Solids, Part II,” Oxford University Press, London, 1964.
[11] B. Bhushan, “Principles and Applications of Tribology,”
Wiley, New York, 1999.
[12] F. M. Orr, L. E. Scriven and A. P. Rivas, “Pendular Rings
between Solids: Meniscus Properties and Capillary
Force,” Journal of Fluid Mechanics, Vol. 67, No. 4, 1975,
pp. 723-742. doi:10.1017/S00221120750
[13] B. Zhang and A. Nakajima, “Nanometer Deformation
Caused by the Laplace Pressure and the Possibility of Its
Effect on Surface Tension Measurements,” Journal of
Colloid and Interface Science, Vol. 211, No. 1, 1999, pp.
114-121. doi:10.1006/jcis.1998.5978
Vol. 13, No. 7, 2005, pp. 1175-1186.
doi:10.1088/0965-0393/13/7/012
[15] H. Shinto, K. Uranishi, M. Miyahara and K. Higashitani,
“Wetting-induced Interaction between Rigid Nan
and Plate: A Monte Carlo Study
sics, Vol. 116, No. 21, 2002, pp. 9500-9509.
doi:10.1063/1.1473817
[16] C. Gao, “Theory of Menisci and Its Applic
plied Physics Letters, Vol
1801-1803. doi:10.1063/1.119403
[17] L. R. Fisher and J. N. Israelachvili, “Direct Measuremen

S. Q. GAO ET AL. 415
of the Effect of Meniscus Forces on Adhesion: A Study
of the Applicability of Macroscopic Thermodynamics to Meas
Microscopic Liquid Interfaces,” Colloids and Surfaces,
Vol. 3, No. 4, 1981, pp. 303-319.
doi:10.1016/0166-6622(81)80058-3
[18] H. K. Christenson, “Adhesion between Surfaces in Un-
saturated Vapors – A Reexamination of the Influence of
Meniscus Curvature and Surface Forces,” Journal of Col-
loid and Interface Science, Vol. 121, No. 1, 1988, pp.
170-178. doi:10.1016/0021-9797(88)90420-1
[19] H. K. Christenson and V. V. Yaminsky, “Adhesion and
Salvation Forces between Surfaces in Liquids Studied by
Vapor-Phase Experiments,” Langmuir, Vol. 9, No. 9,
1993, pp. 2448-2454. doi:10.1021/la00033a030
[20] J. P. Kirkness, H. K. Christenson, J. R. Wheatley and T.
C. Amis, “Application of the ‘Pull-Off’ Force Method for
urement of Surface Tension of Upper Airway Mu-
cosal Lining Liquid,” Physiological Measurement, Vol.
26, No. 5, 2005, pp. 677-688.
doi:10.1088/0967-3334/26/5/009
[21] J. Yuan, Z. Shao and C. Gao, “Alternative Method of
Imaging Surface Topologies of Nonconducting Bulk
Specimens by Scanning Tunneling Microscopy,” Physical
Review Letters, Vol. 67, No. 7, 1991, pp. 863-866.
doi:10.1103/PhysRevLett.67.863
[22] H. Fan and G. F. Wang, “Stability Analysis for Liquid-
bridging Induced Contact,” Journal of Applied Physics,
Vol. 93, No. 5, 2003, pp. 2554-2558.
doi:10.1063/1.1544652
[23] S. Gao and H. Liu, “Capillary Mechanics,” Science Press,
Beijing, 2010.