 J. Biomedical Science and Engineering, 2011, 4, 362-374 doi:10.4236/jbise.2011.45046 Published Online May 2011 (http://www.SciRP.org/journal/jbise/ JBiSE ). Published Online May 2011 in SciRes. http://www.scirp.org/journal/JBiSE A doublet mechanics model for the ultrasound characterization of malignant tissues Francesco Gentile1,2, Jason Sakamoto3, Raffaella Righetti4, Paolo Decuzzi1,3, Mauro Ferrari3,5 1Center of Bio-Nanotechnology and Engineering for Medicine, Magna Graecia University, Catanzaro, Italy; 2Italian Institute of Technology, Genova, Italy; 3Department of Nanomedicine and Biomedical Engineering, The Methodist Hospital Research Institute, Houston, USA; 4Department of Electrical and Computer Engineering, Texas A&M, 214 Zachry Engineering Center, College Station, USA; 5Anderson Cancer Center and Rice University, Houston, USA. Email: francesco.gentile@iit.it Received 30 October 2010; revised 4 November 2011; accepted 4 January 2011. ABSTRACT Non invasive ultrasound-based imaging systems are being more commonly used in clinical bio-microscopy applications for both ex vivo and in vivo analysis of tissue pathological and physiological states. These modalities usually employ high-frequency ultrasound systems to overcome spatial resolution limits of con- ventional clinical diagnostic approaches. Biological tissues are non continuous, non homogeneous and exhibit a multiscale organization from the sub-cellu- lar level (1 mm) to the organ level (1 cm). When the ultrasonic wavelength used to probe the tissues becomes comparable with the tissue’s microstructure scale, the propagation and reflection of ultrasound waves cannot be fully interpreted employing classical models developed within the continuum assumption. In this study, we present a multiscale model for ana- lyzing the mechanical response of a non-continuum double-layer system exposed to an ultrasound source. The model is developed within the framework of the Doublet Mechanics theory and can be applied to the non-invasive analysis of complex biological tissues. Keywords: Nanomechanics; Doublet Mechanics; Ultrasound; Spectroscopy; Biopsy; Microscopic Elastography; Ultrasound Biomicroscopy 1. INTRODUCTION In the last few years, there has been an increased interest to extend the limits of conventional clinical approaches to the level of microscopic resolution [1-5]. The goal here is to optimize the imaging of small tissue structures and, in general, to obtain information not available from the corresponding conventional macroscale applications. The ability to quantitatively and non invasively differen- tiate living tissues based upon their biological and physical properties would enable major breakthroughs in the early detection and diagnosis of diseases and in monitoring therapeutic effects. While surgical biopsy remains the ‘gold standard’ for the clinical screening of tissues and the assessment of pathologic conditions, there is a concerted effort to de- velop new imaging modalities that non-invasively visu- alize tissues providing information previously only available from biopsy [6-8]. Morphologic presentation of tissues together with the microbiologic, immunologic and molecular analysis are still critical for determining personalized medical treatments. However, the analysis of surgical biopsies suffers from being inherently opera- tor dependent and, ultimately, the quality of diagnoses is entrusted with the pathologist’s experience and knowl- edge [9-11]. Availability of quantitative imaging tech- niques capable of probing tissues at the microscale level may improve the accuracy of the diagnosis of biological samples and, most importantly, provide a new non-in- vasive means for the assessment of living tissues in situ. Recent developments in the fields of optics, nuclear medicine, computed tomography, magnetic resonance and ultrasound have suggested the feasibility of obtain- ing tissue information at the micrometer-scale level with high accuracy, sensitivity and contrast-to-noise ratios. For example, optical in vivo biopsy is a growing area in optical computed tomography applications, which promises the assessment of tissue morphology and cell function as well as the detection of early-stage tissue abnormalities associated with diseases [7,12]. Similarly, new magnetic resonance microscopy techniques now permit imaging tissue’s fine architecture in applications that range from assessing neural tissues [13] to imaging  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 363 angiogenesis and gene expression in cancers [14,15]. Among the various imaging techniques, ultrasound methods have always offered distinctive characteristics, which make them particularly suitable for clinical screening of tissues. These include: cost-effectiveness, portability, non-invasiveness, and the ability to provide in vivo tissue clinical information in real-time, at high resolutions and relatively large depths. Although the first acoustic microscope was proposed in the early 1930s [16], it was only in the late 1980s that the use of pulse-echo imaging systems operating at fre- quencies higher than the frequency range conventionally used in diagnostic imaging began to be experimented [17, 18]. Today, the ultrasonic visualization of tissues at mi- croscopic resolution is usually referred to in the litera- ture as ultrasound biomicroscopy or, more simply, high frequency ultrasound [4,6]. Important clinical applica- tions of high frequency ultrasound techniques include: ophthalmology [19], dermatology [20], intravascular ultrasound [18], cartilage imaging [21], and obstetrics [22]. While the imaging performance of the ultrasound system is ultimately determined by the frequency of the ultrasonic transducer, its geometry and the tissue acous- tic properties, the choice of the imaging system to be used in a given application is highly dependent on the nature of the application itself. For example, ophthalmic applications usually employ transducers with frequent- cies in the 40 to 60 MHz range [19]. These are used for imaging glaucoma, scleral and corneal diseases, and melanomas of the iris among the various clinical appli- cations. The typical frequency range for investigating skin and assess skin tumor markers is from 20 to 40 MHz [20], with possible extension up to 100 MHz [23]. For intravascular applications, ultrasound systems usu- ally operate in the range of 20 to 30 MHz, allowing high resolution imaging of vessel walls and coronary arteries [24]. Finally, a new and promising application of high frequency ultrasound systems relates to the development of microscopic elasticity imaging and intravascular elastography imaging techniques, which use pre- and post-excitation high frequency ultrasound data to recon- struct maps of the microscopic mechanical properties of tissues [25-28]. A common denominator for all the aforementioned ul- trasound applications is the use of high-frequency sys- tems to probe the tissues so that high spatial resolutions can be achieved. However, biological tissues are non continuous, non homogeneous and exhibit a multiscale organization from the sub-cellular level (1 mm) to the organ level (1 cm). When the ultrasonic wavelength becomes comparable with the tissue’s microstructure scale, the propagation and reflection of ultrasound waves cannot be fully interpreted employing classical models developed within the continuum assumption. In these regards, we have recently proposed the use of ultra- sound-based Non Destructive Evaluation (NDE) tech- niques in conjunction with multiscale mathematical models as an integrated tool to automatically screen tis- sue biopsy specimens with high accuracy and resolution [29-32]. Biopsy samples are exposed to an ultrasound source and the tissue response and physical properties can be interpreted employing multiscale mathematical models. Normal and malignant tissues are expected to provide different responses that could be readily de- tected. Several techniques have been proposed to model the mechanical behavior of materials at the nano/micro scale. This is the case for instance of the Lattice Dynamics (LD) and Molecular Dynamics [33], non-local Micromechan- ics theories of the differential (CGT) [34] and integral type (INT) [35-36]. In addition to these somehow clas- sical approaches, the theory of Doublet Mechanics (DM) has been developed over the last twenty years as a mul- tiscale field theory that allows to bridge the gap between Continuum Mechanics (CM) and discrete meso scale models without contradiction [37-39]. In this paper, we develop a mathematical model based on the DM approach to study the response of multilay- ered non continuum solids to ultrasounds. While the model is formulated for the analysis of biopsy samples, it may also be applied to the detection of malignant tu- mors developing in natural multi-layered systems such as the skin or the eye and might become an important tool for the further development of novel high frequency ultrasound elastography techniques. 2. A LINEAR ELASTICITY BOUNDARY VALUE PROBLEM WITHIN DM The theory of Doublet Mechanics is a multi-scale theory which recapitulates Lattice Dynamics at the nanoscale limit and is fully compatible with the continuum me- chanics framework at the macroscale limit. In the pre- sent paragraph, the governing equations for a linear elas- ticity problem are briefly recapitulated. A more detailed description can be found in [37-39]. Within the DM framework, a solid is considered as a spatial array of points (nodes) at finite distances. Any pair of adjacent nodes is termed a doublet comprising a reference node X and a node Yα located at a separation distance o and aligned along the doublet axis with unit vector o (Figure 1). A doublet is univocally identified by specifying its reference node (X), orientation (o ) and separation distance (o ). The superscript o means initial configuration. The node X is surrounded by other m adjacent nodes, which form a number m of doublets with corresponding Yα nodes. C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 364 o o Y α Figure 1. A doublet comprising a reference node X and a node Y, at a separation distance η aligned along the doublet axis indicated by the unit vector τ. Such a set of nodes constitutes a bundle for the reference node X. If the nodes are arranged as to form one of the fourteen Bravais lattices, m would coincide with the coordination number of the lattice and the internodal distances would coincide with the lattice constants. Under externally applied loads, the nodes of a doublet are displaced giving rise to microdisplacements and microstrains. In general, if the node are separated along o , the doublet undergoes an elongation , if the nodes are rotated about o or separated normally to o , the doublet undergoes a torsion μα or a shear γα, respectively. In the sequel, it is assumed that each doublet can only undergo elongations (central interac- tions) which would be associated with the build up of a microstress pα along o . An orthogonal Cartesian frame of reference is intro- duced with unit vectors ei(i = 1, 2, 3), and each node X is associated to a position vector x = x iei, where the clas- sical convention of the repeated Roman indices is used. A displacement vector uα(x; t) can be introduced and for each doublet; the increment displacement vector Δuα(x; t) can be defined as the difference between the displace- ment of the node γα and that of the node X at time t , oo aYX t uu uuxux ,t (1) As in linear elasticity, it is assumed that the relative displacement (;) atux is small compared to the dou- blet separation distance (;) oo at ux so that the initial and final configuration of the system can be as- sumed to coincide. Expanding a in a convergent Taylor series in a neighborhood of the reference point X, it follows, in scalar form u 1 1 1! oo i o M i akk kk u u x (2) where each of the subscript 1,,kk runs through 1 to 3. The order M at which the series is truncated defines the degree of approximation employed by the DM theory. For M = 1, the continuum theory of elasticity is recov- ered. The small elongation of the doublet can be de- fined as o u (3) and, using (2), Equation (3) can be rephrased as 1 1 1 1! oo o M oi ikk kk u x (4) which can be interpreted as the compatibility equation within the linear DM theory. The relationship between the doublet microstress pa and microstrain is given as pA (5) in the case of linear and homogeneous internodal central interactions. Equation (5) can be interpreted as the con- stitutive equation in the linear and homogeneous DM theory, and Aαβ is the matrix of the homogeneous micro modulii of the doublet. Finally, static equilibrium is im- posed as 1 1 1 /2 1 11 10 ! ... 1, 2, 3; i oo o mM kk i kk p F xx i ; (6) where Fi are the scalar components of the volume force F. The boundary conditions expressed in terms of stresses take the form 1 1 1 /2 1 1 1 1! 1, 2, 3; ... o rr i oo r r o mM kk r r kk ir kk n p Ti xx (7) where nkr are the scalar components of the unit vector n normal to the body surface, and the subscript r = 1, , M – 1 for M ≥ 2 and r = 1 for M = 1. Ti are the scalar components of the vector force T. The term dr1 is the Kronecker delta function. The Equations (4), (5) and (6) together with (7) give a boundary value problem within DM for a linear elastic body. Notice that Equations (6) and (7) are general to the extent that they are written as a function of the doublet unit vectors i . The relationship between the micro- and the macro- stresses has been derived in [37] as 12 1 2 11 21 11 1! ... ooo mM Mi kkk ki kk p x (8) at a generic level of approximation M. C opyright © 2011 SciRes. JBiSE 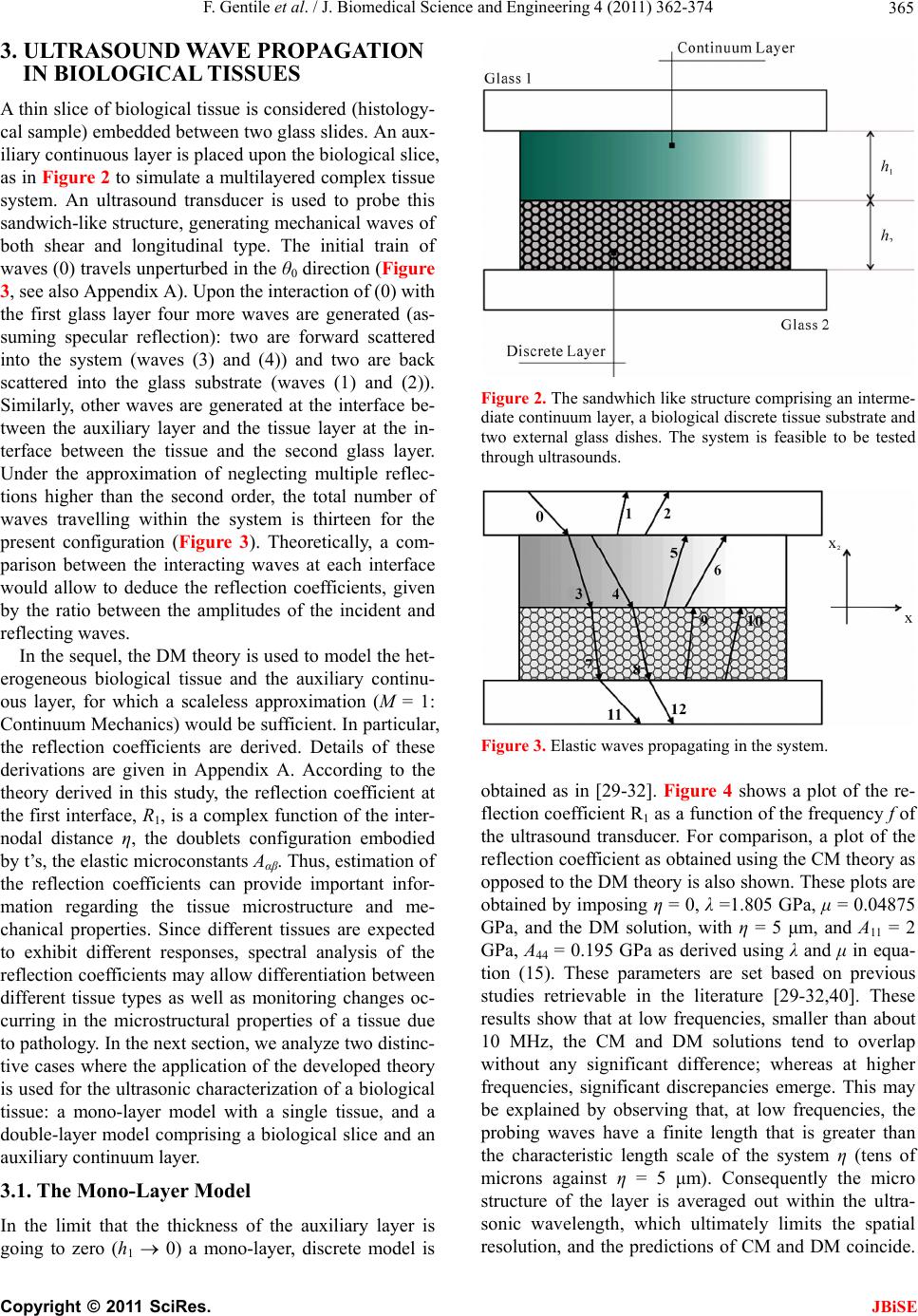 F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 365 3. ULTRASOUND WAVE PROPAGATION IN BIOLOGICAL TISSUES A thin slice of biological tissue is considered (histology- cal sample) embedded between two glass slides. An aux- iliary continuous layer is placed upon the biological slice, as in Figure 2 to simulate a multilayered complex tissue system. An ultrasound transducer is used to probe this sandwich-like structure, generating mechanical waves of both shear and longitudinal type. The initial train of waves (0) travels unperturbed in the θ0 direction (Figure 3, see also Appendix A). Upon the interaction of (0) with the first glass layer four more waves are generated (as- suming specular reflection): two are forward scattered into the system (waves (3) and (4)) and two are back scattered into the glass substrate (waves (1) and (2)). Similarly, other waves are generated at the interface be- tween the auxiliary layer and the tissue layer at the in- terface between the tissue and the second glass layer. Under the approximation of neglecting multiple reflec- tions higher than the second order, the total number of waves travelling within the system is thirteen for the present configuration (Figure 3). Theoretically, a com- parison between the interacting waves at each interface would allow to deduce the reflection coefficients, given by the ratio between the amplitudes of the incident and reflecting waves. In the sequel, the DM theory is used to model the het- erogeneous biological tissue and the auxiliary continu- ous layer, for which a scaleless approximation (M = 1: Continuum Mechanics) would be sufficient. In particular, the reflection coefficients are derived. Details of these derivations are given in Appendix A. According to the theory derived in this study, the reflection coefficient at the first interface, R1, is a complex function of the inter- nodal distance η, the doublets configuration embodied by t’s, the elastic microconstants Aαβ. Thus, estimation of the reflection coefficients can provide important infor- mation regarding the tissue microstructure and me- chanical properties. Since different tissues are expected to exhibit different responses, spectral analysis of the reflection coefficients may allow differentiation between different tissue types as well as monitoring changes oc- curring in the microstructural properties of a tissue due to pathology. In the next section, we analyze two distinc- tive cases where the application of the developed theory is used for the ultrasonic characterization of a biological tissue: a mono-layer model with a single tissue, and a double-layer model comprising a biological slice and an auxiliary continuum layer. 3.1. The Mono-Layer Model In the limit that the thickness of the auxiliary layer is going to zero (h1 0) a mono-layer, discrete model is Figure 2. The sandwhich like structure comprising an interme- diate continuum layer, a biological discrete tissue substrate and two external glass dishes. The system is feasible to be tested through ultrasounds. Figure 3. Elastic waves propagating in the system. obtained as in [29-32]. Figure 4 shows a plot of the re- flection coefficient R1 as a function of the frequency f of the ultrasound transducer. For comparison, a plot of the reflection coefficient as obtained using the CM theory as opposed to the DM theory is also shown. These plots are obtained by imposing η = 0, λ =1.805 GPa, μ = 0.04875 GPa, and the DM solution, with η = 5 μm, and A11 = 2 GPa, A44 = 0.195 GPa as derived using λ and μ in equa- tion (15). These parameters are set based on previous studies retrievable in the literature [29-32,40]. These results show that at low frequencies, smaller than about 10 MHz, the CM and DM solutions tend to overlap without any significant difference; whereas at higher frequencies, significant discrepancies emerge. This may be explained by observing that, at low frequencies, the probing waves have a finite length that is greater than the characteristic length scale of the system η (tens of microns against η = 5 μm). Consequently the micro structure of the layer is averaged out within the ultra- sonic wavelength, which ultimately limits the spatial resolution, and the predictions of CM and DM coincide. C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 366 Figure 4. The reflection coefficient R1 shown against the fre- quency f and comparison between the CM solution. Notice that η has the same order of magnitude of a cell size. Conversely, as f increases, and the ultrasonic wave- lengths become comparable to the scale length of the small components of the material (cells), the difference between the discrete and continuum approach becomes more and more evident. The relation between the angular frequency ω, the wave number ki and the phase velocity ci in the frame- work of DM is embodied by the quite complex equations (18) (Appendix A). Interestingly, these relations reduce to the non scale, classical dispersion ones (where simple relations ki = ω/ci, ci = (E/ρ)1/2 hold true) via two differ- ent assumptions: 1) the constituent granules of the bio- logical substrate are material points whose sizes are in- finitesimal η = 0 and all the waves may have arbitrary but finite length, 2) the constituent particles of the bio- logical substrate may have an arbitrary but finite size (η > 0) and all the waves have an infinite length (k 0). The diagrams of Figure 4 show the occurrence of a number of minima and maxima. These can be explained considering phenomena of interference occurring at each interface between the reflecting and transmitting waves. 3.2. The Double Layer Model Herein the results stemming out from the double layer model are presented, where both h1 and h2 are different from zero. For the analysis, it is assumed that the auxil- iary layer is made up of a polymeric material commonly used in biomedical applications (Ta b le 1 ). The biologi- cal tissue has the properties listed in Table 2. These pa- rameters are set based on previous studies retrievable in literature [29-32,40]. The CM and DM frameworks are used in describing the auxiliary and biological substrate, respectively. In Figures from 5 to 9, the reflection spec- tra of the system under study are shown for different auxiliary layer materials, with varying Young’s modulus E and for wave frequencies ranging from 4 to 12 MHz. It can be concluded that as E increases, the number of Table 1. The CM properties of the intermediate layer. Material ρ [103 kg/m3] E [GPa] ν h [mm] PDMS 0.97 4.8 10–4 0.49 0.133 Polyurethane 1.10 5.3 10–3 0.48 0.133 Polyethylene 0.955 0.70 0.41 0.133 Polypropylene0.91 1.30 0.42 0.133 Polycarbonate 1.23 2.40 0.41 0.133 Table 2. The CM properties of the glass substrates, and the DM parameters of the biological tissue. Material ρ [103 kg/m3] E [GPa] ν h [mm] CROWN glass2.50 71.8 0.23 0.133 Material ρ [103 kg/m3] A11 [GPa] A44 [GPa] h [mm] η [mm] Bio tissue 0.95 2.20 0.36 0.1335.6 minima decreases within the frequency range considered, as it does the difference in frequency between two suc- cessive minima. Most importantly, at high values of E, the minimum values of the reflection coefficient do not vary significantly. Since increased tissue stiffness is of- ten associated with changes in tissue pathology, spectral analysis of reflection coefficients as interpreted within the DM theory may contain important markers for the assessment of a tissue state and its changes due to the onset of diseases. These simulations also show that ma- terials with a high compliances, such as PDMS (Figure 5), generate a very complex response, with several min- ima. Such complexity would spoil the reflection signal, inducing more noise and making more difficult the ac- curate interpretation of the spectra. Stiffer intermediate layers would be more convenient. Additional simulation (Figure 10) shows the effects of varying the Young’s modulus (ΔE = 10%) about the mean value for the Polyethylene case. As E increases, the spectrum under- goes a rigid translation towards higher frequencies (see Table 3 for the complete list of values). The effect of thickness h1 of the continuum, interme- diate layer has been also investigated. Starting from a thickness of 134 μm, a 10% variation has been imposed (Polyethylene, Δh = 10%) and the reflection spectra evaluated. Results are shown in Figure 11 and Table 4. It is observed that as h1 increases, the spectra rigidly move towards lower frequencies, with no change in the number of minima. The thickness h1 also affects the damping of the system, the thicker is the intermediate layer and the stronger is the attenuation for the spectra. C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 367 Figure 5. The reflection spectrum of the system assuming that the intermediate layer is PDMS. Figure 6. The reflection spectrum of the system assuming that the intermediate layer is PU. Figure 7. The reflection spectrum of the system assuming that the intermediate layer is PE. Figure 8. The reflection spectrum of the system assuming that the intermediate layer is PP. Figure 9. The reflection spectrum of the system assuming that the intermediate layer is PC. Figure 10. The effect of the variation of the Young’s modulus upon the overall response of the system. E C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 Copyright © 2011 SciRes. 368 JBiSE Table 3. Characterist minima points for different plastic substrates. PDMS PU PE PP PC f [MHz] R f [MHz] R f [MHz] R f [MHz] R f [MHz] R 4.595 0.333 4.534 0.334 5.348 0.224 6.301 0.342 6.602 10.418 4.946 0.282 5.269 0.186 8.031 0.487 9.930 0.322 0.181 0.187 5.298 0.311 6.005 0.192 10.681 0.347 5.650 0.391 6.739 0.363 6.002 0.411 7.457 0.684 6.354 0.409 8.109 0.921 6.705 0.446 8.456 0.949 7.055 0.510 9.091 0.738 7.405 0.677 9.806 0.431 7.753 0.835 10.538 0.235 8.101 0.940 11.274 0.211 8.501 0.946 12.009 0.347 8.847 0.850 9.193 0.710 9.543 0.578 9.894 0.421 10.246 0.327 10.597 0.252 10.949 0.200 11.300 0.240 11.652 0.315 12.003 0.365 Table 4. Characterist minima points for different plastic substrates. Initial E +10% –10% min 1 2 3 1 2 3 1 2 3 f [MHz] 5.348 8.031 10.681 5.514 8.214 10.919 5.160 7.883 10.315 R 0.224 0.487 0.347 0.252 0.445 0.415 0.203 0.503 0.221 Notice that the thickness h1 and the stiffness E have op- posite effects. 4. DISCU SS IONS In this study, we have presented a multiscale model for analyzing the mechanical response of a non-continuum system exposed to an ultrasound source. The proposed model may be interpreted as a quantitative, non-invasive ultrasound spectroscopy method, which is based on the analysis of the reflection coefficients as a function of the ultrasonic wavelength (or conversely the frequency) for estimating changes in the tissue microstructure and me- chanical properties. The model was developed within the framework of the Doublet Mechanics theory, which led to the determination of the reflection coefficients as a function of the internodal distance, the doublets con- figuration and the elastic microconstants. In its present form, the model does not take into consideration scatter- ing effects at the various interfaces or within the tissue layer. Coupling this effect with the DM theory would  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 369 Figure 11. The effect of the variation of the intermediate layer thickness h1 upon the overall response of the system. require large mathematical efforts, which are considered outside the scope of the presented study and left for fu- ture investigations. In Appendix B, we provide a detailed analysis of the conditions under which this approxima- tion is valid. As a test platform, the DM model developed in this study was applied to the ultrasonic characterization of two tissue models: a mono-layer solid simulating a tissue specimen for histological analysis and a double-layer system simulating a more complex tissue. For the mono-layer case, the results obtained using the DM the- ory were statistically compared with the results obtained from the same tissue model using the classical CM the- ory. The results reported in this study demonstrate that at frequencies as high as 10 MHz and above, the CM re- sults significantly deviate from the DM results. This would suggest that the use of CM-based approaches to characterize the ultrasonic behavior of tissues exposed to high frequency (>10 MHz) insonications may lead to incorrect or incomplete interpretation of the ultrasonic parameters of interest with respect to the tissue micro- structural properties. In such experimental conditions, a more complicated model should be considered. The model described in this paper offers an attractive alterna- tive, which is based on the spectral analysis of the re- ceiving signals to differentiate between tissue types. In addition, the analysis of the single layer tissue model carried out in this paper may prove as a useful example on how to practically apply the proposed DM model to ultrasound-based histological applications. The present work with the development of a double layer mathematical model constitutes the first step to- wards a more realistic representation of natural multi- layered systems as the human skin and the growth and spread of malignancies such as melanoma. Human skin is a unique organ that permits life by regulating heat and water loss from the body while preventing the ingress of noxious chemicals or microorganisms [41]. Skin mem- branes may be examined at various levels of complexity. While the membrane is regarded sometimes as a simple physical barrier, more complexity may be introduced by considering skin as various layers in series, namely 1) the innermost subcutaneous fat layer (hypodermis); 2) the overlying dermis; 3) the viable epidermis; 4) the outermost layer of the tissue (the stratum corneum). All the cited layers posses, at different extents, a certain de- gree of heterogeneity due to sebaceous glands, hair folli- cles, fat lobules, blood vessels, nucleii and desmosomal junctions [41]. With such a scenario, a simple single- layer model would not be sufficient for interpreting the system response. In addition, skin cancer is associated with localized changes in the tissue microstructure and morphological modification at the interfaces between different skin layers making single-layer models poten- tially inaccurate in predicting the onset and spread of tumor masses. As a demonstration of the practical applicability of some of the concepts exposed in this paper, we have previously developed an ex vivo apparatus that uses ul- trasound technology and the Doublet Mechanics theory to obtain information about tissue pathological states [31,40]. For the purpose of illustration, a sketch of such apparatus and set-up is provided in Figure 12. The ul- trasonic wand delivers an acoustical wave of known frequency into the tissue, and then detects the reflected wave fractions with separate transducers. As described in this study, a characteristic reflection spectrum can be plotted depicting the reflection coefficient versus the Figure 12. A sketch of an ex vivo apparatus based on ultra- sound technology and the Doublet Mechanics theory for the determination of the malignancy potential of a cutaneous or mucousal growth such as melanoma. C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 370 excitation frequency. The spectrum can be related to tissue physical properties such as density, microelastic constants, attenuation, and internodal distance via the DM theory. Through comparative analysis of reflection spectra from normal and diseased tissue, it may be pos- sible to determine the malignancy potential of a cutane- ous or mucousal growth such as melanoma. This would allow physicians to screen patients on an annual or semi-annual basis for the presence of dysplastic nevi (pre-cancerous) or early stage cancerous skin lesions. In addition to dermatology applications, the proposed model may have significant potentials in several other clinical applications that employ high frequency ultra- sound systems for the assessment of tissue pathological and physiological states. It may be particularly useful in ophthalmology, where the anatomy of the eye resembles a multilayered system and where the use of high fre- quency ultrasound techniques has already shown sig- nificant potentials for the diagnosis and treatment of eye diseases [19]. Other possible applications may include cartilage assessment, intravascular applications, and high frequency elastography techniques, which ultimately long to the quantitative estimation of the tissue me- chanical behavior at the microscopic scale. 5. CONCLUSIONS The Doublet Mechanics theory has been employed to model the propagation of elastic waves within a biologi- cal tissue. The present case is characterized by hetero- geneous and not continuous materials that, consequently, may be conveniently analyzed within the multiscale DM framework. It has been observed that an operating frequency of the ultrasound generator increases, the difference be- tween the DM solution and the classical elasticity solu- tion becomes larger, as a consequence of the intimate interaction among waves and microscopic components of the biological tissue. It has been discussed that a DM multilayer model could be effective in describing the skin multi-layer structure. The design requirements for a characterization-mode ultrasound skin cancer detection system should provide primary care physicians with a rapid, noninvasive, screening tool for malignant mela- noma that would assign a quantitative malignancy po- tential for specific cutaneous lesions. REFERENCES [1] Rajadhyaksha, M., Grossman, M., Esterowitz, D. and Webb, R.H. (1995) In vivo confocal scanning laser mi- croscopy of human skin-melanin provides strong contrast. Journal of Investigative Dermatology, 104, 946-952. doi:10.1111/1523-1747.ep12606215 [2] Cross, S.E., Jin, Y.S., Rao, J. and Gimzewski, J.K. (2007) Nanomechanical analysis of cells from cancer patients. Nature Nanotechnology, 2, 780-783. doi:10.1038/nnano.2007.388 [3] Ellegala, D.B., Poi, H.L., Carpenter, J.E., Klibanov, A.L., Kaul, S., Shaffrey, M.E., Sklenar, J. and Lindner, J.R. (2003) Imaging tumor angiogenesis with contrast ultra- sound and microbubbles targeted to αvβ3. Circulation, 108, 336-341. doi:10.1161/01.CIR.0000080326.15367.0C [4] Foster, F.S., Pavlin, C.J., Lockwood, G.R., Ryan, L.K., Harasiewicz, K.A., Berube, L. and Rauth, A.M. (1993) Principles and applications of ultrasound backscatter mi- croscopy. IEEE Transactions on Ultrasonics Ferroelec- trics and Frequency Control, 40, 608-617. doi:10.1109/58.238115 [5] Othman, S.F., Xu, H.H., Royston, T.J. and Magin, R.L. (2005) Microscopic magnetic resonance elastography (μMRE). Magnetic Resonance in Medicine, 54, 605-615. doi:10.1002/mrm.20584 [6] Foster, F.S., Pavlin, C.J., Harasiewicz, K.A., Christopher, D.A. and Turnbull, D.H. (2000) Advances in ultrasound biomicroscopy. Ultrasound in Medicine and Biology, 26, 1-27. doi:10.1016/S0301-5629(99)00096-4 [7] Tearney, G.J., Brezinski, M.E., Bouma, B.E., Boppart, S.A., Pitris, C., Southern, J.F. and Fujimoto, J.G. (1997) In vivo endoscopic optical biopsy with optical coherence tomography. Science, 276, 2037-2039. doi:10.1126/science.276.5321.2037 [8] Sonn, G .A., Jones, S.N.E., Tarin, T.V., Du, C.B., Mach, K.E., Jensen, K.C. and Liao, J.C. (2009) Optical biopsy of human bladder neoplasia with in vivo confocal laser endomicroscopy. Journal of Urology, 182, 1299-1305. doi:10.1016/j.juro.2009.06.039 [9] Paradiso, A. et al. (2004) Interobserver reproducibility of immunohistochemical HER-2/neu evaluation in human breast cancer: The real-world experience. International Journal of Biological Markers, 19, 147-154. [10] Verkooijen, H. et al. (2003) Interobserver variability be- tween general and expert pathologists during the histo- pathological assessment of large-core needle and open biopsies of non-palpable breast lesions. European Jour- nal of Cancer, 39, 2187-2191. doi:10.1016/S0959-8049(03)00540-9 [11] Schlemper, R. et al. (2000) Differences in diagnostic cri- teria for esophageal squamous cell carcinoma between Japanese and Western pathologists. Cancer, 88, 996-1006. doi:10.1002/(SICI)1097-0142(20000301)88:5<996::AID -CNCR8>3.0.CO;2-Q [12] Fercher, A.F., Drexler, W., Hitzenberger, C.K. and Lasser, T. (2003) Optical coherence tomography-principles and applications. Reports on Progress in Physics, 66, 239- 303. doi:10.1088/0034-4885/66/2/204 [13] Benveniste, H., Hedlund, L.W. and Johnson, G.A. (1992) Mechanism of detection of acute crebral-ischemia in rats by diffusion-weighted magnetic-resonance microscopy. Stro ke, 23, 746-754. [14] McDonald, D.M. and Choyke, P.L. (2003) Imaging of angiogenesis: From microscope to clinic. Nature Medi- cine, 9, 713-725. doi:10.1038/nm0603-713 [15] Louie, A.Y., Huber, M.M., Ahrens, E.T., Rothbacher, U., Moats, R., Jacobs, R.E., Fraser, S.E. and Meade, T.J. (2000) In vivo visualization of gene expression using magnetic resonance imaging. Nature Biotechnology, 18, C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 Copyright © 2011 SciRes. 371 JBiSE 321-325. doi:10.1038/73780 [16] Sokolov, S.J. (1935) Ultrasonic oscillations and their applications. Technical Physics of the USSR, 2, 522-534. [17] Sherar, M.D., Noss, M.B. and Foster, F.S. (1987) Ultra- sound backscatter microscopy images the internal struc- ture of living tumour spheroids. Nature, 330, 493-495. doi:10.1038/330493a0 [18] Gussenhoven, E.J., Essed, C.E., Lancee, C.T., Mastik, F., Frietman, P., Vanegmond, F.C., Reiber, J., Bosch, H., Vanurk, H., Roelandt, J. and Bom, N. (1989) Arterial wall characteristics determined by intravascular ultra- sound imaging: An in vitro study. Journal of the Ameri- can College of Cardiology, 14, 947-952. doi:10.1016/0735-1097(89)90471-3 [19] Pavlin, C.J., Harasiewicz, K., Sherar, M.D. and Foster, E.S. (1991) Clinical use of ultrasound biomicroscopy. Ophthalmology, 98, 287-295. [20] Turnbull, D.H., Starkoski, B.G., Harasiewicz, K.A., Semple, J.L., From, L., Gupta, A.K., Sauder, D.N. and Foster, F.S. (1995) A 40-100 MHz B-scan ultrasound backscatter microscope for skin imaging. Ultrasound in Medicine and Biology, 21, 79-88. doi:10.1016/0301-5629(94)00083-2 [21] Viren, T., Saarakkala, S., Kaleva, E., Nieminen, H.J., Jurvelin, J.S. and Toyras, J. (2009) Minimally invasive ultrasound method for intra-articular diagnostics of Car- tilage degeneration. Ultrasound in Medicine and Biology, 35, 1546-1554. doi:10.1016/j.ultrasmedbio.2009.04.004 [22] Kurjak, A., Pooh, R.K., Merce, L.T., Carrera, J.M., Sali- hagic-Kadic, A. and Andonotopo, W. (2005) Structural and functional early human development assessed by three-dimensional and four-dimensional sonography. Fertility and Sterility, 84, 1285-1299. doi:10.1016/j.fertnstert.2005.03.084 [23] Passmann, C. and Ermert, H. (1996) A 100-MHz ultra- sound imaging system for dermatologic and ophthalmo- logic diagnostics. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 43, 545-552. doi:10.1109/58.503714 [24] Celermajer, D.S. et al. (1992) Noninvasive detection of endothelias dysfunction in children and adults at risk of atherosclerosis. Lancet, 340, 1111-1115. doi:10.1016/0140-6736(92)93147-F [25] Vogt, M. and Ermert, H. (2005) Development and evaluation of a high-frequency ultrasound-based system for in vivo strain imaging of the skin. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 52, 375-385. doi:10.1109/TUFFC.2005.1417260 [26] Cohn, N.A. et al. (1997) An elasticity microscope. 1. Methods. IEEE Transactions on Ultrasonics Ferroelec- trics and Frequency Control, 44, 1304-1319. doi:10.1109/58.656634 [27] Liu, D. and Ebbini, E.S. (2008) Viscoelastic property measurement in thin tissue constructs using ultrasound. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 55, 368-383. doi:10.1109/TUFFC.2008.655 [28] de Korte, C.L. et al. (2000) Characterization of plaque components with intravascular ultrasound elastography in human femoral and coronary arteries in vitro. Circula- tion, 102, 617-623. [29] Liu, J. and Ferrari, M. (2003) A discrete model for the high frequency elastic wave examination on biological tissue. Computer Modeling in Engineering and Sciences, 4, 421-430. [30] Liu, J. and Ferrari, M. (2002) Mechanical spectral signa- tures of malignant disease? A small-sample, comparative study of continuum vs nano-biomechanical data analysis. Disease Markers, 18, 175-183. [31] Sakamoto, J.H. (2005) Molecular analysis of breast can- cer utilizing tumor targeting ultrasound mechanical con- trast agents. Thesis presented in partial fulfillment of the requirements for the Degree Doctor of Philosophy in the Graduate School of the Ohio State University, The Ohio State University, Columbus. [32] Sakamoto, J.H., Gentile, F., Xie, B., Wang, L., Decuzzi, P., Rokhlin, S.I. and Ferrari, M. (2005) Nanomechanics and tissue pathology. In: Lee, A.P. and Lee, J.L., Eds., BioMEMS and Biomedical Nanotechnology, Vo l. I: Pro- spectus, Biological and Biomedical Nanotechnology. Springer, New York. [33] Böttger, H (1983) Principles of the theory of lattice dy- namics, Physik-Verlag, Weinheim. [34] Green, A.E. (1965) Micromaterials and multi-polar con- tinuum mechanics. International Journal of Engineering Science, 3, 533-537. doi:10.1016/0020-7225(65)90033-9 [35] Edelen, D.G .B. (1976) Non local field theories. Con- tinuum Physics, Academic Press, New York. [36] Kunin, I.A. (1982) Elastic media with microstructure. I. One-dimensional models. Springer Series in Solid-State Sciences, Springer-Verlag, Berlin. [37] Ferrari, M. (2000) Nanomechanics, and biomedical nanomechanics: Eshelby’s inclusion and inhomogeneity problems at the discrete/continuum interface. Biomedi- cal Microdevices, 2, 272-281. [38] Ferrari, M., Granik, V.T., Imam, A. and Nadeau, J. (1997) Advances in doublet mechanics. Springer, Heidelberg. [39] Granik, V.T. and Ferrari, M. (1993) Microstructural me- chanics of granular materials. Mechanics of Materials, 15, 301-322. doi:10.1016/0167-6636(93)90005-C [40] Sakamoto, J.H., Smith, B.R., Xie, B., Rokhlin, S.I., Lee, S.C. and Ferrari, M. (2005) The molecular analysis of breast cancer utilizing targeted nanoparticle based ultra- sound contrast agents. Technology in Cancer Research & Treatment, 4, 627-636. [41] Williams, A. (2003) Transdermal and topical drug de- livery: From theory to clinical practice. Pharmaceutical Press, London. [42] Zong, X.L., Laine, A.F. and Geiser, E.A. (1998) Speckle reduction and contrast enhancement of echocardiograms via multiscale nonlinear processing. IEEE Transactions on Medical Imaging, 17, 532-540. doi:10.1109/42.730398 [43] Lehmann, M. (1998) Statistical theory of two-wave speckle interferometry and its application to the optimi- zation of deformation measurements. Thèse Ecole Poly- technique Fédérale de Lausanne EPFL, No. 1797.  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 372 APPENDIX A The propagation of the waves in the media can be un- ambiguously identified specifying thirteen angles (Fig- ure 3) 01536497 108 110 122 ,,, ,, , (9) where the identities in (9) stem from the second law of optics of reflection. Given the mechanical properties of the media and θ0, Snell’s law may be used to derive six further independent equations having the form sin sin i ti c c t 2 i (10) where θi and θt are the incident and transmitted wave directions, and the ci the wave phase velocities. Using Equations (9) and (10) it is thus straightforward ex- pressing any characteristic parameter θi in terms of the sole incident angle θ0. The displacements u(n) can be expressed as exp ; nn n n n nn Ai kct ud xp (11) with (n) an index indicating the (n)th wave, An the am- plitude of the waves, x is the position vector, d(n) the particle motion unit vector, p is propagation unit vector and kn = 2π/λ the wave number. The most relevant coefficient in the system is the re- flection coefficient R1 = A1/A0 which can be determined imposing at each interface suitable boundary conditions for either the displacements and the stresses 1 11 22 12 11 ,, , mm ii ii mm i ii uu (12) here, m is the number of perturbations insisting upon the same boundary, u1, u2, σ22 and σ12 are the displacements and the stresses, of tangential and normal type respect- tively. Relations (12) generate a total of twelve equations meaning that the problem of solving for the twelve re- flection coefficients (four per interface) is completely determined. The reflection coefficients Ri depend upon the waves amplitude An and thus, through Equation (11), also upon the displacements u(n). On the other hand, displacements may be conveniently rephrased in terms of stresses, pro- vided that appropriate constitutive equations are used. The waves (0), (1), (2), (3), (4), (5), (6), (11) and (12) can be handled using the conventional theory of elastic- ity in that travel in continuum media. On the contrary DM is necessary in describing waves (7), (8), (9) and (10) which propagate in the biological, non continuum sub- strate. In this perspective, M has been chosen as M = 2, that is the smallest value of M that retains the scale fea- tures of DM. It is assumed that the dynamic process is isothermal and the volume forces vanish. The particle interactions are assumed to be longitudinal (central), so that the shear and torsion microstresses vanish every- where in the body. Recalling (4), for M = 2 the elonga- tion microstrains are derived as , 1 2 ijij ijkijk u , u (13) while, recalling (5), the micro moduli matrix Aαβ takes the form 1112 121515 11 121515 11 1515 44 44 44 0 0 0 00 0 AA AA AAA AAA AA A Sym A (14) 11 4444 1 ;4 A A (15) where solely the two constants A11 and A44 are inde- pendent. Under these conditions, relation (8) is simpli- fied into , 1 1 2 n ijijij kk pp (16) The unit vectors τ are chosen as follows 123 456 100 0,1, 0, 001 02 2 22,20,2 0 22 2 (17) and correspondingly the doublets distribute in space as in Figure 13. Notice that the problem is fully three-di- mensional. Substituting back within relations (12) the stresses and displacements written in terms of the amplitudes An ac- cording to Equation (11) and Equations from (13) to (16), a subset of 12 explicit equations is derived, which may be clothed in matrix form as to obtain M·R = B, where M is the [12 × 12] coefficients matrix, B the [12 × 1] vector comprising the known terms and R represents the [12 × 1] vector enclosing of the unknown reflection co- efficients Ri. Both M and B depend upon a number of C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 373 Figure 13. The doublets distributing in space as to form a 3D arrangement. parameters, namely: the micro mechanical properties of the biological substrate (density, nodal separation dis- tance ηα, micro moduli Aαβ); the classical continuum mechanics properties of the glass substrates and of the auxiliary layer (density, constants of Lamè λ and μ); the thickness of the layers (h1, h2); the initial set-up angle θ0; the phase velocities ci; the time harmonic waves’ angular frequency ω = 2πf. Noticeably, while conventionally the relation between ω and ki is represented by the cele- brated relation ki = ω/ci (ci = (E/ρ)1/2) in the framework of DM it assumes a far more elaborated form, for either pressure (P) or shear (S) waves 22 44 1144 24 1144 44 4 222 44 44 1 2 121 ,( ) 424 1,( ) 432 AA Ak AAk k Ak AS P (17) and we shall call the latter equations of dispersion in that demonstrate that propagation in discrete-media is dis- persive, and strongly influenced by the micro moduli and by the scale length. APPENDIX B In its present form, the model presented in the paper does not take into account diffraction or scattering. Cou- pling these effects with the DM theory would require considerable mathematical efforts which are considered outside the scope of this study and left for future invest- tigations. While there are several practical ways to re- duce speckle (such as the use of spatial and frequency compounding techniques [42], it is important to under- stand that, under certain circumstances a simple reflec- tion/refraction model is still sufficient for describing tissue/US interaction. A practical proof for this statement is the fact that ul- trasound reflection techniques are commonly employed to accurately measure the thickness of different tissues or tissue layers and for non destructive testing of materi- als. These circumstances are insonicating from different angles and averaging the results. This sentence is further substantiated in the following. A speckle field arises when a wave impinges on a rough surface, generating a scattered wave radiating in all directions. Each echo signal is the combination of the many signals coming from a group of scatterers within the resolution cell. At each point, the amplitude of the echo signal depends on whether constructive or destruct- tive interference predominates. Since the scattered wave emanates from numerous contributors, it is appropriate to characterize it in statistical terms. If this field is inte- grated over a finite detector area (that would be the US receiver) the probability distribution of the integrated intensity I is [43] 1 exp mm I mI m pI I Im I (18) where Γ(m) is the Gamma function, the operator <·> stands for spatial average and thus <I> would corre- spond to the “true” mean intensity in the limit of a per- fectly flat reflective surface, and m is, to a first approxi- mation, the number of correlation cells or speckles fal- ling onto the detection area. Figure 14 illustrates Equa- tion (18) for different m’s. Notice that for increasing m Figure 14. The probability distribution of the speckle inte- grated intensity I for different m’s. C opyright © 2011 SciRes. JBiSE  F. Gentile et al. / J. Biomedical Science and Engineering 4 (2011) 362-374 Copyright © 2011 SciRes. 374 the diagrams turn into quasi-Gaussian with most prob- able intensity <I>. Equivalently, in the limit of large de- tector area, the speckles would just represent a back- ground noise that would have negligible influence on the response of the sample. Founding on these considera- tions, scattering effects can be reasonably neglected. Note that by large detector area we simply mean an area containing a large number of scatterers compared to the resolution cell, which is equivalent to state that the tissue scatterer density satisfies the requirement for obtaining fully developed Raleigh backscatterers and thus m1. JBiSE
|