Paper Menu >>
Journal Menu >>
 Int. J. Communications, Network and System Sciences, 2011, 4, 345-350 doi:10.4236/ijcns.2011.45039 Published Online May 2011 (http://www.SciRP.org/journal/ijcns) Copyright © 2011 SciRes. IJCNS Permutation and Complementary Algorithm to Generate Random Sequences for Binary Logic Jie Wan, Jeffrey Z. J. Zheng School of Software, Yunnan University Kunming, Ku nming, China E-mail: {wanjiech, conjugatesys}@gmail.com Received December 15, 2010; revised March 23, 2011; accepted April 3, 2011 Abstract Randomness number generation plays a key role in network, information security and IT applications. In this paper, a permutation and complementary algorithm is proposed to use vector complementary and permuta- tion operations to extend n-variable Logic function space from functions to configurations 2 2n2 22 nn ! for variant logic framework. Each configuration contains functions can be shown in a 2 2n11 22 22 nn matrix. A set of visual results can be represented by their symmetric properties in W, F and C codes respec- tively to provide the essential support on the variant logic framework. Keywords: Logic Function, Permutation and Complementary, Variant Logic, Symmetric Distribution, Random Sequence 1. Introduction Random numbers play an important role in many net- work protocols and encryption schemas on various net- work security applications [1], for example: digital sig- natures, authentication protocols, key generation for PKI, RSA/AES [2], nonce frustrate, symmetric stream encryp- tion. A better random number algorithm will enhance encryption schemas, to do other applications. To satisfy different requirements, the NIST has published a series of statistical tests as standards [3] to determine whether a random number generator is suitable for a cryptographic application. After using the vector complementary and the permutation operations on binary logic, the variant logical framework extends the traditional Logic function space from functions to configurations [4]. Under the new extension conditions, it is possible to use simple transformation to generate huge numbers of random sequences for future app lications. 2 2n2 22 nn ! Permutation and complementary algorithm is de- scribed in the paper to express different random proper- ties through a series of binary image sequences under- taken typical recursive ope rations. 2. Method Cellular automata perform a natural way to generate random sequence. The principle of binary cellular auto- mata [5] [6] can be explained by an example as follow: First, a sequence 001100 and a func tion f: 000,01 1,101,110 are selected. Second, the sequence can be decomposed from left to right. The last bit is composed to th e first bit 001100 00,01,11,10,00,00 001100 010100 2 2n2 22! nn Third, according to the decomposed sequences and the generating function , a new sequence 010100 can be gen- erated. i.e.: f: Followed the algorithm, the space of the generation function can be extended further; large numbers of ran- dom sequences can be generated. This mechanism can increase the complexity of code-breaking. In variant logic framework, the logic function space has been extended from to by the per- mutation and the complementary operations. In 2 variable functions of cellular automata, there are 16 generated functions. And the 16 functions can be de- scribed in a truth table (Figure 1(a)) with 16 entries. 2.1. Permutation Operation The bit string of states 00,01,10,11 in generating function can be converted to decimal number 0,1,2,3 . An example in Figure 1(b) is shown to permute 3210 to  Int. J. Communications, Network and System Sciences, 2011, 4, 345-350 doi:10.4236/ijcns.2011.45039 Published Online May 2011 (http://www.SciRP.org/journal/ijcns) Copyright © 2011 SciRes. IJCNS (a) (b) Figure 1. Permutation example, (a) The Truth Table of 3210; (b) The Permutation Table of 1320. 1320 of the table. 2.2. Complementary Operation In the complementary operation, the complementary vector is applied operate to the truth table. It can be describe as ,1y ,0 yy In 2-variable variant logic, is a binary sequence of 4 bits in . In the example the original table is 0000, ,1111 1111 and shown in Figure 2(a) the given 1100 to Table 2 can be d esc ribed as . Under such operation, the sequence values of state 1 and 3 columns are invariant. But the values of columns whose index is 0 and values of the permutation sequence in state 2 and 0 are changed to their revised values respectively. 1100 11 0 0 13201 320 After the complementary operation, Figure 2(a) chan- ges to Figure 2(b). 2.3. Visualization For function f applies once applied again the sequence 001100 output 010100.then applied again the 010100 to output 111100.For such binary sequence, select black for 1 and white for 0 to generate the visual patterns as fol- lows (Figure 3). 2.4. Matrix Representation For example, (Figure 2(b)) the truth value of 3th func- tion is 1010. It can be converted to a binary coordinate 10 10 distinguished Left two and tight two bits re- spectively. So the decimal coordin ate is 22 . Then the (Figure 2(b)) can be converted to Table 1. Under such converting the 2D matrix can be repre- sented in Table 2. 3. Algorithm and Properties 3.1. Permutation and Complementary Algorithm Using permutation and complementary operations, an algorithm is extended to express the n-ary variant logic functional space.  J. WAN ET AL.347 Algorithm: Permutation and Complementary: Input: variable n Output: a set of truth table of P , 2n PS 2 2 n B , . (a) (b) Figure 2. Complementary Example, (a).The Permuatation Table of 1320(1111); (b).The Complementary Table of 1320(1100). Method: Step 1. Initial 1 0 000 0 T21 n Step 2. Generate a perm utation P for T Step 3. From 2 to 111 ··· 1 do vector complementary operation. Step 4. Any new permutation? Yes go to Step 2. Step 5. End where S(N) is a symmetry group with N member and M B 2 is a M variable Boolean structure with M members. 3.2. Representation Scheme Every truth table has a 2D matrix to arrange visual re- sults of random sequen ce. The , X Y is the coordinate to allocate each visual result. So for n-ary logic function space, the 2D matrix has a size of 2shown (Table 3). 11 22 2 nn 3.3. W, F and C Code Three coding schemes can be distinguished in the algo- rithm. W code [4] is a binary sequence of bits. It sepa- rates into two parts 2n 10 JJ 1 2n 1 . Each part has bits F code is a subset of W code. And it is a symmetry code. In F code, if the I-th Meta state in J is 1 or 0, the I-th meta state in 0 J is the negative state. 1 If a code is F code and the I-th meta state in J have the same value. Besides four corners of its matrix are included in 0, ,,1 x x, it is C code [4]. E.g. 3210111001 00 is an element of W code. In the sequence 1 isn’t the negative sequence of 3. And the 0 isn’t also the negative seque nce o f 2. Copyright © 2011 SciRes. IJCNS 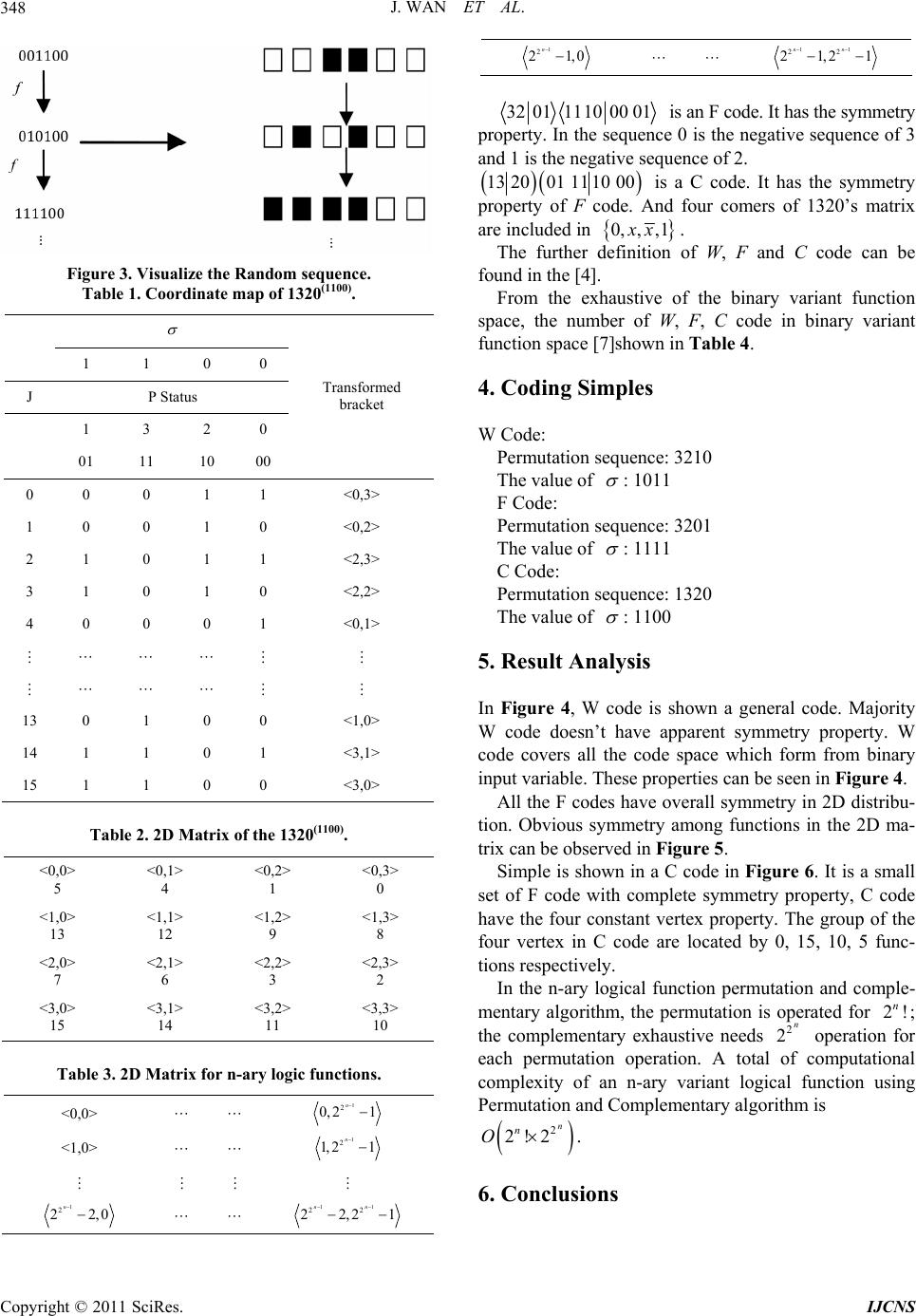 J. WAN ET AL. 348 Figure 3. Visualize the Random sequence. Table 1. Coordinate map of 1320(1100). 1 1 0 0 J P Status 1 3 2 0 01 11 10 00 Transformed bracket 0 0 0 1 1 <0,3> 1 0 0 1 0 <0,2> 2 1 0 1 1 <2,3> 3 1 0 1 0 <2,2> 4 0 0 0 1 <0,1> 13 0 1 0 0 <1,0> 14 1 1 0 1 <3,1> 15 1 1 0 0 <3,0> Table 2. 2D Matrix of the 1320(1100). <0,0> 5 <0,1> 4 <0,2> 1 <0,3> 0 <1,0> 13 <1,1> 12 <1,2> 9 <1,3> 8 <2,0> 7 <2,1> 6 <2,2> 3 <2,3> 2 <3,0> 15 <3,1> 14 <3,2> 11 <3,3> 10 Table 3. 2D Matrix for n-ary logic functions. <0,0> 1 2 0,2 1 n <1,0> 1 2 1, 21 n 1 2 22,0 n 11 22 22,21 nn 1 2 21,0 n 11 22 21,21 nn 32 011110 0001 is an F code. It has the symmetry property. In the sequence 0 is the negative sequence of 3 and 1 is the negative sequence of 2. 132001 1110 00 is a C code. It has the symmetry property of F code. And four comers of 1320’s matrix are included in 0, ,,1 x x. The further definition of W, F and C code can be found in the [4]. From the exhaustive of the binary variant function space, the number of W, F, C code in binary variant function space [7]shown in Table 4. 4. Coding Simples W Code: Permutation sequence: 3210 : 1011 The value of F Code: Permutation sequence: 3201 : 1111 The value of C Code: Permutation sequence: 1320 : 1100 The value of 5. Result Analysis In Figure 4, W code is shown a general code. Majority W code doesn’t have apparent symmetry property. W code covers all the code space which form from binary input variable. These properties can be seen in Figure 4. All the F codes have overall symmetry in 2D distribu- tion. Obvious symmetry among functions in the 2D ma- trix can be observed in Figure 5. Simple is shown in a C code in Figure 6. It is a small set of F code with complete symmetry property, C code have the four constant vertex property. The group of the four vertex in C code are located by 0, 15, 10, 5 func- tions respectively. In the n-ary logical function permutation and comple- mentary algorithm, the permutation is operated for ; the complementary exhaustive needs operation for each permutation operation. A total of computational complexity of an n-ary variant logical function using Permutation and Complementary algorithm is 2! n 2 2n 2 2!2n n O. 6. Conclusions Copyright © 2011 SciRes. IJCNS  J. WAN ET AL. Copyright © 2011 SciRes. IJCNS 349 A permutation and complementary algorithm has been proposed for n-ary logical function. And sample results are visualized. The visual results of W, F and C code in the variant and invariant properties support the variant Code System No W 384 F 128 C 16 Table 4. The number of W, F and C code in 2-ary variant functional space. Figure 4. The 2D matrix diagram and the visual result of 32101011. Figure 5. The 2D matrix diagram and the visual result of 32101111.  J. WAN ET AL. 350 Figure 6. The 2D matrix diagram and the visual result of 13201100. logic system through experimentation to use an algo- rithmic mechanism to generate a series of huge random number sequences. 7. References [1] W. Stallings, “Cryptography and Network Security: Prin- ciples and Practice,” Prentice Hall, 2005. [2] J. Soto and L. Bassham, “Randomness Testing of the Advanced Encryption Standard Finalist Candidates,” Na- tional Institute of Standards and Technology (NIST), 2000. [3] National Institute of Standards and Technology (NIST), “Random number generation,” 2008. Internet Avail- able: http://csrc.nist.gov/groups/ST/toolkit/rng/index.html [4] J. Zhi, J. Zheng and C. H. Zheng, “A framework to ex- press variant and invariant functional spaces for binary logic,” Frontiers of Electrical and Electronic Engineering in China, Vol. 5, No. 2, 2010, pp. 163-172. [5] S. Wolfram, “Theory and Applications of Cellular Auto- mata,” Singapore: Word Scientific, 1986. [6] S. Wolfram, “Cellular automata as models of complex- ity,” Nature, Vol. 311, 1984, pp. 419-424. [7] J. Wan and J. Zheng, “Showing Exhaustive Number Se- quences of Two Logic Variables for Variant Logic Func- tional Space,” Proceedings of Asia-Pacific Youth Con- ference on Communication (APYCC), October 2010, p. 4. Copyright © 2011 SciRes. IJCNS |

