Int. J. Communications, Network and System Sciences, 2011, 4, 323-334
doi:10.4236/ijcns.2011.45037 Published Online May 2011 (http://www.SciRP.org/journal/ijcns)
Hybrid Key Duplication Hashing Techniques for IP
Address Lookup
Rujiroj Tiengtavat, Wei-Ming Lin
Department of El ectri cal and C omput er Engineering, The Uni versi t y of Te xas at Sa n A ntonio San Ant o ni o, USA
Received February 9, 2011; revised March 26, 2011; accepted April 12, 2011
Abstract
In the past decade there has been an increasing need for designs to address the time and cost efficiency issues
from various computer network applications such as general IP address lookup and specific network intru-
sion detection. Hashing techniques have been widely adopted for this purpose, among which XOR-operation-
-based hashing is one of most popular techniques due to its relatively small hash process delay. In most cur-
rent commonly used XOR-hashing algorithms, each of the hash key bits is usually explicitly XORed only at
most once in the hash process, which may limit the amount of potential randomness that can be introduced
by the hashing process. In [1] a series of bit duplication techniques are proposed by systematically duplicat-
ing one row of key bits. This paper further looks into various ways in duplicating and re-using key bits to
maximize randomness needed in the hashing process so as to enhance the overall performance further. Our
simulation results show that, even with a slight increase in hardware requirement, a very significant reduc-
tion in the amount of hash collision can be obtained by the proposed technique.
Keywords: Hash Algorithm, IP Address Lookup, Intrusion Detection
1. Introduction
Fast address lookup or identification matching has be-
come critical to the feasibility of many modern appli-
cations. In a general form, this problem involves a search
process through a large database to find a record (or
records) associated with a given key. One modern exam-
ple is in that the routers in wide-area networks have to
look through a large database, a routing table, for a
forwarding link that matches the given destination
address [2]. Another example that calls for imminent
attention these days is in the area of internet security, in
which intrusion detection demands rapid evaluation of
client requests. In this, rules are established to allow the
intrusion detection system to check for wrong-doing.
There have been many designs developed for IP address
lookup problem using a hash function. Hashing provides
a way to search through a statistically smaller number of
steps than a simple sequential straightforward search.
Hashing in essence provides a process of mapping re-
cords (hash keys) between two regions, a domain space
(the database) and a hash space [3]. An algorithm, known
as a hashing function, issues a set of directives outlining
the mapping of a hash key (or record) from the domain
space into hash space by creating a corresponding hash
value.
A complete survey and complexity analysis on IP
address lookup algorithms has been provided in [4]. A
performance comparison of traditional XOR folding, bit
extraction, CRC-based hash functions is given in [5].
Although most of the hash functions, such as the simple
XOR folding and bit extraction, are relatively inex-
pensive to implement in software and hardware, their
performance tends to be far from desirable. CRC-based
hash functions are proved to be excellent means but are
more complex to compute. Some schemes are hardware
based that achieve an improvement in IP look-up by
maintaining a subset of routing table in a faster cache
memory [6,7], while others are software based which
improve their search performance mainly through effi-
cient data structures [8,9]. Waldvogel et al. [10] pro-
posed an address look-up scheme based on a binary
search of hash table, requiring an extra update process in
a look-up table. Other hashing algorithms have also been
widely adopted to provide for the address look-up
process [11-16]. All hashing algorithms inevitably suffer

R. TIENGTAVAT ET AL. 324
from unpredictable complexities involving conflicts among
the data with the same hash result (hash collision). A
search for matching a given query could end up with a
sequential search through the number of maximal con-
flicts in the database. This may result in a long search
process time that exceeds the time limitation imposed by
design specifications. The lower the number of hash
collisions is created by the hash algorithm the better the
performance becomes. Performance of a hashing algori-
thm is usually determined by two measurements: the
MSL (maximum search length) and ASL (average search
length) with the former one indicating the largest number
of hash collisions for any single hash value and the latter
denoting the average number of hash collisions for all
hash values.
Hashing techniques using simple XOR operations
have been very popular in applications where timely
response is critical due to its relatively small hash pro-
cess delay. In all the current commonly used XOR-
-hashing algorithms, when deriving the hash value, key
bits are partitioned into rows to be XORed, and each of
the hash key bits is usually explicitly XORed only at
most once in the hash process, which may limit the
amount of potential randomness that can be introduced
by the hash process. When a key bit is reused (duplicated)
for XORing in generating different hash value bits, there
exists a potential that the overall randomness of new
hash result may increase. In [1] a theory has been
developed in duplicating bits while avoiding induced bit
correlation which may easily offset any gained perfor-
mance through bit duplication. Very significant perfor-
mance improvement was obtained in this series of tech-
niques by employing a novel single-row bit duplica- tion
process to avoid bit nullification or downgrading pro-
blem. An extension from a recent publication in [17], this
paper aims to further extend the theory into duplicating
more than one rows of key bits. By relaxing the res-
triction in duplicating only one row of key bits, one is
able to XOR more duplicated bits to obtain each hash bit
without coming across the bit nullification or downg-
rading problem. Our simulation results show that a very
significant reduction in the amount of hash collision is
obtained by the proposed technique compared to the pre-
viously proposed duplication techniques.
2. XOR-Hashing Methodology
Throughout this paper, the database under discussion is
defined as consisting of =2
m
M
entries with each
entry having bits in length. It can also be viewed as
having M-bit vectors with each vector consisting of
each respective bit from all entries. An example of
and is shown in Figure 1(a). The target
n
=3m
n
=8n
(a) (b)
Figure 1. (a) Calculation of d values (b) sorted database by
d value.
hashing process is to hash each of the n-bit entries (an IP
address or part of it in this application) into an m-bit hash
value. These hash values need to be distributed as evenly
as possible so as to minimize the eventual search time.
XOR operator has been widely used for hashing and
known to be an excellent operator in enhancing rando-
mness in distribution. It also possesses a nice charac-
teristic allowing for analytical performance analysis and
thus better algorithm designing. A commonly used hash-
ing technique is to simply hash the n-bit key into m-bit
hash result through a simple process XORing every dis-
tinct n
m key bits into a final hash bit. Such a random
XORing process (so-called “Group-XOR” in this paper)
may not always lead to a desirable outcome. A much
more effective hashing approach is proposed in [18] by
preprocessing (and sorting) the database according to a
parameter, the value, that reveals a very useful
insight into the degree of uniformity of the database. The
value of a bit vector is the absolute difference
between the number of 0’s and 1’s in it (as shown in
Figure 1(a)). Translated to effect of hashing, in the final
-bit hash result, a bit of gives an even hashing
distribution (i.e. evenly divided) among the entire
address space allowing other bits to hash to it; while a bit
of will limit the hashing to only one half of the
hash space. Intuitively, using the bits with smaller
values for hashing would lead to a probabilistically better
hash distribution, i.e. less potential conflict in the final
mapping. Ideally, if one can identify (or through a
combination to obtain) bits with all their values
equal to 0, it should lead to the best potential performance,
assuming no correlation among the bit vectors. This
leads us to employing a simple pre-processing step in
re-arranging the n bit vectors according to their
values sorted into a non-decreasing order as shown in
Figure 1(b). This sorted sequence then gives us an “order
of significance” according to which each bit should be
utilized.
d
d
m=0d
=dM d
d
md
A XOR-hashing algorithm based on the principle of d
value is presented in [19]. This algorithm, the d-IOX (d
value in-order XOR folding), involves the aforemen-

R. TIENGTAVAT ET AL.325
tioned preprocessing/sorting step before applying the
simple in-order folding XOR hashing. Figure 2 shows
the folding process in the d-IOX algorithm, with each of
the i
H
’s referring to a hashing function in deriving a
hash value bit. The d-IOX proves to be much better than
the simple random Group-XOR approach by registering
an improvement in ASL and MSL up to 30% in
randomly generated database and up to 80% in real IP
database. Reasons behind such a significant improve-
ment have been clearly explained in [19], mainly due to
the nature in XORing bits with very different d values in
order to maximize the reduction in d values in XORing.
The new technique proposed in this paper will be
based on the result of preprocessing by exploiting the
“order of significance” among the key bits for bit reuse/
duplication, and the performance will be compared to the
d-IOX as the base non-duplication one due to its superior
performance over all other well-known XOR-hashing
techniques.
3. Bit-Duplication XOR Hashing
For the sake of completeness, a summary of the bit-
duplication theory presented in [1] is given here.
Note that when there is no bit duplication under
standard XOR hashing, no bits are shared in XORing to
lead to different hash value bits. That is, each hash value
bit comes from XORing a distinct set of hash key bits. If
one intends to reuse some key bits for XORing, then the
overall effectiveness may be compromised due to the
sharing. Here a notion is introduced to illustrate the
induced effect from bit duplication. In obtaining two
hash key bits, when there exist common bits between the
two sets of hash key bits for their XORing, an Induced
Duplication Correlation (IDC) arises between the two
hash value bits. The reason that this correlation is
regarded as “induced” because it is created through the
artificial bit-sharing from duplication, in contrast to the
inherent correlation that may already exist in the hash
key bits. Figure 3 gives a simple illustration for IDC,
where each of the letters (from A to F) denotes a distinct
hash key bit.
The figure on the left shows that a hash value bit is
obtained by XORing two distinct hash key bits, while the
figure on the right shows that through duplication IDC
occurs when every pair of hash value bits have some
common bits being XORed. When more bits are
duplicated for XORing, higher IDC tends to ensue. With
the introduction of IDC the d value obtained for each
hash value bit loses some of its meaning. That is, while
randomness in the bit-wise distribution (d value) for each
bit may be increased due to more bits being XORed, the
overall randomness across the m hash value bits may
Figure 2. In-order XOR (d-IOX) hash algorithm.
Figure 3. Induced duplication corr elation (IDC).
actually decrease due to the IDC. In order to reach the
best hash performance, one will need to duplicate effec-
tively while making an effort to reduce the effect of IDC.
In [1], a simple “cycle duplication” approach is
proposed to ensure minimal bit correlation through the
duplication process, in which key bits are shared between
two groups of source bits to be XORed. One typical
problem is the “nullification” problem where the same
bit is duplicated to be XORed with itself in producing a
hash bit, which results in a loss of one additional
potential bit for randomness. The other problem is, while
performing the cycle duplication process on the same
row as shown in Figure 4 where the first row is dupli-
cated twice in order to further increase the randomness.
With this, each pair of hash bits will have two key bits
shared in their XORing (e.g. bits 0 and 1 sharing A and
D), thus leading to a “downgrading” problem, or simply
a higher degree of IDC. Note that, in our discussion here,
the same segment (the one with the smallest d values) is
used for multiple duplication due to its low d values.
Using another different segment (a segment of bits with
larger d values) for the additional duplication has shown
a far less potential for performance improvement due to
an analysis result from [18] showing that XORing with
bits of larger d values may even degrade the performance.
Therefore, in order to avoid any kind of downgrading,
one has to first decide if there are sufficient number of
bits for further duplication. In order to duplicate X times
without the downgrading problem, [1] shows that the
minimal m required is


11mXX  (1)
or

R. TIENGTAVAT ET AL. 326
Figure 4. An example of downgrading from additional dup-
lication.
431
2
m
X




(2)
In the preceding example shown in Figure 4, where
and =4m=2
X
(two duplications are to be
attempted), obviously, the condition in Equation (1) is
violated - minimum value of m for two times of dup-
lication is 7.
The problem can be translated into a problem of
graphics for easier visualization and processing. Bor-
rowing from the notations used in [1], let the set of the m
bit position indices be denoted

=0,1,2, ,1S

m


1
,
and these bits are to be duplicated X times such that X
satisfies the condition in Equation (1). For the sake of
simplicity without losing generality, assume that each of
the X duplicated sequences of the m bits are to be rotated
starting from a particular bit position to avoid the two
problems. We can simply focus on the bit 0 position of
each of the strings to analyze the whole pattern. That is,
the bit 0 position of the original string is at position 0.
Let the position of bit 0 of each of the
X
 strings be
denoted as
j
s
where . Figure 5 shows an
illustration for a case with and , with 13
bit positions on a circle. In this case, the four starting
locations are 0, 1, 2 and 3. With
this notation, one can easily show that, in order to avoid
any nullification problem, the following condition has to
hold:
0jX
=3X
=1s s
=13m
=3 =9s=0s
, ,, 0,, and
ij
s
sij ijmi j
which guarantees that no bit position has two identical
bits to be XORed. In order to avoid any sharing of
multiple bits (i.e. the downgrading problem), the follow-
Figure 5. Three-time duplication with m = 13 using cycle
duplication with one bit in common.
ing condition has to be satisfied:



, ,,,, 0,,,, and ,,.
ij kl
DDijklijklmij kl (3)
where ij denotes the “shorter” distance from position D
i
s
to position
j
s
; that is,




=min mod , mod
ijijj i
Dssmssm
For example, between and , their dis-
tance is
1=1s3=9s








13 =19 13, 91 13=5,8=5.D minmodmodmin
Essentially, this condition guarantees that the no two
positions can share more than one bit in common. Note
that there are a total of such distance values
among the
1
2
X
C
1
X

starting positions (e.g. the six
different distance values,


4,5,61, 2,3,, in Figure 5),
and this number should be exactly the same as the
number of all possible “shorter” distance values available
from m positions along a circle, which is 2
m



, when m
is set to be the exact minimum that satisfies Equation (1).
Thus, one should be able to prove that
1
2=2
Xm
C


which can be easily derived from


1
2
11 1
==
22 2
X
XX XX
mC
=.

 
 

 
4. Multi-Row “Each-Row-Once” Duplication
All duplication techniques discussed so far have been the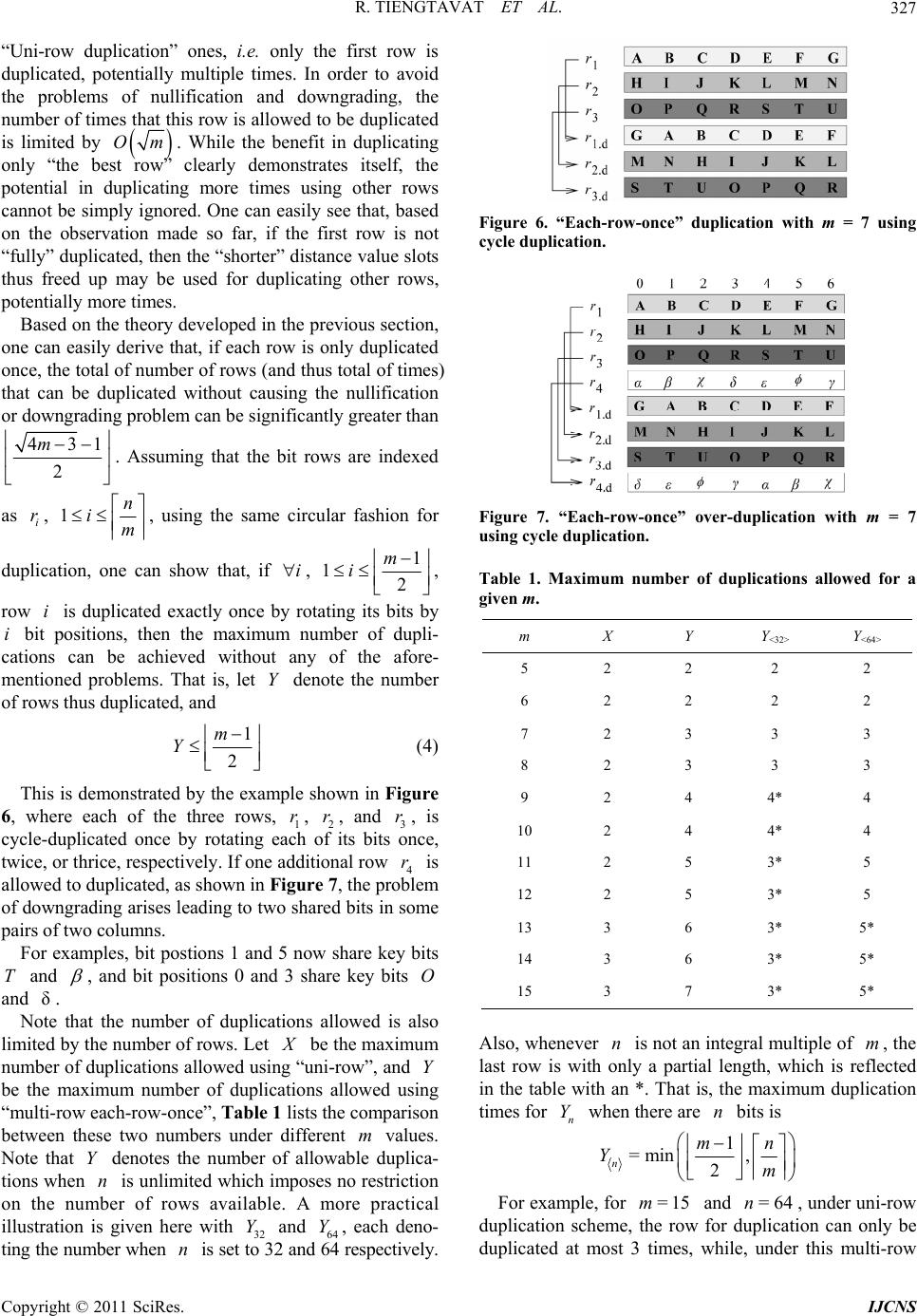

R. TIENGTAVAT ET AL.327
“Uni-row duplication” ones, i.e. only the first row is
duplicated, potentially multiple times. In order to avoid
the problems of nullification and downgrading, the
number of times that this row is allowed to be duplicated
is limited by

Om

. While the benefit in duplicating
only “the best row” clearly demonstrates itself, the
potential in duplicating more times using other rows
cannot be simply ignored. One can easily see that, based
on the observation made so far, if the first row is not
“fully” duplicated, then the “shorter” distance value slots
thus freed up may be used for duplicating other rows,
potentially more times.
Based on the theory developed in the previous section,
one can easily derive that, if each row is only duplicated
once, the total of number of rows (and thus total of times)
that can be duplicated without causing the nullification
or downgrading problem can be significantly greater than
431
2
m





. Assuming that the bit rows are indexed
as ,
i
r1n im




, using the same circular fashion for
duplication, one can show that, if , i1 12
m
i







,
row is duplicated exactly once by rotating its bits by
bit positions, then the maximum number of dupli-
cations can be achieved without any of the afore-
mentioned problems. That is, let denote the number
of rows thus duplicated, and
i
i
Y
1
2
m
Y






(4)
This is demonstrated by the example shown in Figure
6, where each of the three rows, 1, 2, and 3, is
cycle-duplicated once by rotating each of its bits once,
twice, or thrice, respectively. If one additional row 4 is
allowed to duplicated, as shown in Figure 7, the problem
of downgrading arises leading to two shared bits in some
pairs of two columns.
r rr
r
For examples, bit postions 1 and 5 now share key bits
and
T

, and bit positions 0 and 3 share key bits
and .
O
δ
Note that the number of duplications allowed is also
limited by the number of rows. Let
X
be the maximum
number of duplications allowed using “uni-row”, and
be the maximum number of duplications allowed using
“multi-row each-row-once”, Table 1 lists the comparison
between these two numbers under different values.
Note that denotes the number of allowable duplica-
tions when is unlimited which imposes no restriction
on the number of rows available. A more practical
illustration is given here with 32 and 64 Y, each deno-
ting the number when is set to 32 and 64 respectively.
Y
m
Yn
Y
n
Figure 6. “Each-row-once” duplication with m = 7 using
cycle duplication.


Figure 7. “Each-row-once” over-duplication with m = 7
using cycle duplication.
Table 1. Maximum number of duplications allowed for a
given m.
m X Y Y<32> Y<64>
5 2 2 2 2
6 2 2 2 2
7 2 3 3 3
8 2 3 3 3
9 2 4 4* 4
10 2 4 4* 4
11 2 5 3* 5
12 2 5 3* 5
13 3 6 3* 5*
14 3 6 3* 5*
15 3 7 3* 5*
Also, whenever is not an integral multiple of , the
last row is with only a partial length, which is reflected
in the table with an *. That is, the maximum duplication
times for when there are bits is
n m
n
Yn
1
=min ,
2
n
mn
Ym


 


 

 

For example, for and , under uni-row
duplication scheme, the row for duplication can only be
duplicated at most 3 times, while, under this multi-row
=15m=64n

R. TIENGTAVAT ET AL. 328
approach, all 5 rows can be duplicated, each row once.
Whether or not such a new approach brings additional
benefit remains to be decided. For the purpose of
discussion, let 12
=,,,
n
m
XXX X









represent the pat-
tern of duplication for all rows, where i
X
, 1n im







denotes the number of times row is duplicated. Thus,
under uni-row duplication, (3,0,0,0,0) is the most dup-
lication allowed; while under multi-row duplication just
discussed, (1,1,1,1,1) becomes the pattern for duplica-
tion.
i
5. Hybrid Duplication
Note that, as aforementioned, duplicating rows with
higher values tend to bring limited benefits and
sometimes can even be detrimental. In order to maximize
the benefit from duplication, one may have to use a
hybrid approach in duplicating several rows, by duplicating
different rows different number of times. Let i
d
X
den
the number of times row i is to be duplicated, in order
for no nullification or downgrading to happen, the fol-
lowing condition has to be satisfied.
ote

11
22
n
mii
i
XX m


 




where is the total number of rows under duplication.
Note that this is a necessary condition but not a sufficient
condition since a given pattern satisfying this condition
may not be feasible. A simple example is when ,
a satisfying pattern of (2,2) cannot be constructed. This
again follows the same reasoning in proving the uni-row
and multi-row duplication. Similarly, under and
, some of “maximally” allowed duplication
patterns are listed in the following:

,
, , and all permutations of each
of the patterns, such as and .
For example, in the case of
r
1,1
=14m
=15
1,0,0,0

2, 0,1, 2
m
3,
1,
=64n
2,1,1,
Figure 8. An example of hybrid duplication with (2,2,1,0,0)
on m = 15.
set of duplicated rows; that is, for the first row, the three
distance values between every pair of two starting
positions are 1 (between 0 and 1), 2 (between 1 and 3)
and 3 (between (0 and 3); for the second row the three
distance values are 4 (between 0 and 4), 5 (between 4
and 9) and 6 (between 9 and 0); for the third row the only
distance value is 7 (between 0 and 7). With this, all avai-
lable distance values (from 1 to 7) are taken, which re-
presents the maximally allowed duplication situation.
The complete duplication pattern is shown in Figure 9.1
6. Simulation Results



 
2, 2,1,0, 0

0,1,0,3,0


02, 2,1,0,, as shown in
Figure 8, first row is duplicated two times with each of
the three starting bit positions being 0, 1 and 3 (indicated
in circles), the second row is duplicated two times with
the starting positions being 0, 4 and 9 (indicated in
boxes), and the third row duplicated once with the two
starting positions being 0 and 7 (indicated in triangles).
Note that, the condition for avoiding nullification
problem still needs to be satisfied for each of the three
duplicated rows, independently; that is, all three rows
duplicated are allowed to share the starting bit position 0.
For the condition in avoiding downgrading problem
(Equation (3)), again, it has to be satisfied within each
Simulation runs are performed on randomly generated
data sets and real IP data sets to demonstrate the per-
formance improvement of the minimal IDC dupli- cation
XOR hash technique over other techniques with no dup-
lication. The Group-XOR algorithm which XORs groups
of random key bits is the general base of our comparison,
while the d-IOX [19] and the IDC technique from [1]
aforementioned will serve as the reference.
6.1. Randomly Generated Data Sets
We first use a data set randomly generated such that the
d value for each bit position is uniformly distributed.
Performance comparison among the three techniques are
in terms of MSL and ASL by taking an average of results
from 1000 runs. In order to disengage potential effect
1“Partial-row” duplication poses an additional relaxation on the cons-
traint from Equation (1) since the last partial row is not fully cycled
around the whole m-
b
it section thus leading to less restriction on the
downgrading. This issue will be disregarded in this paper due to its
minimal effect on the performance from duplicating the last row
which has the largest d values.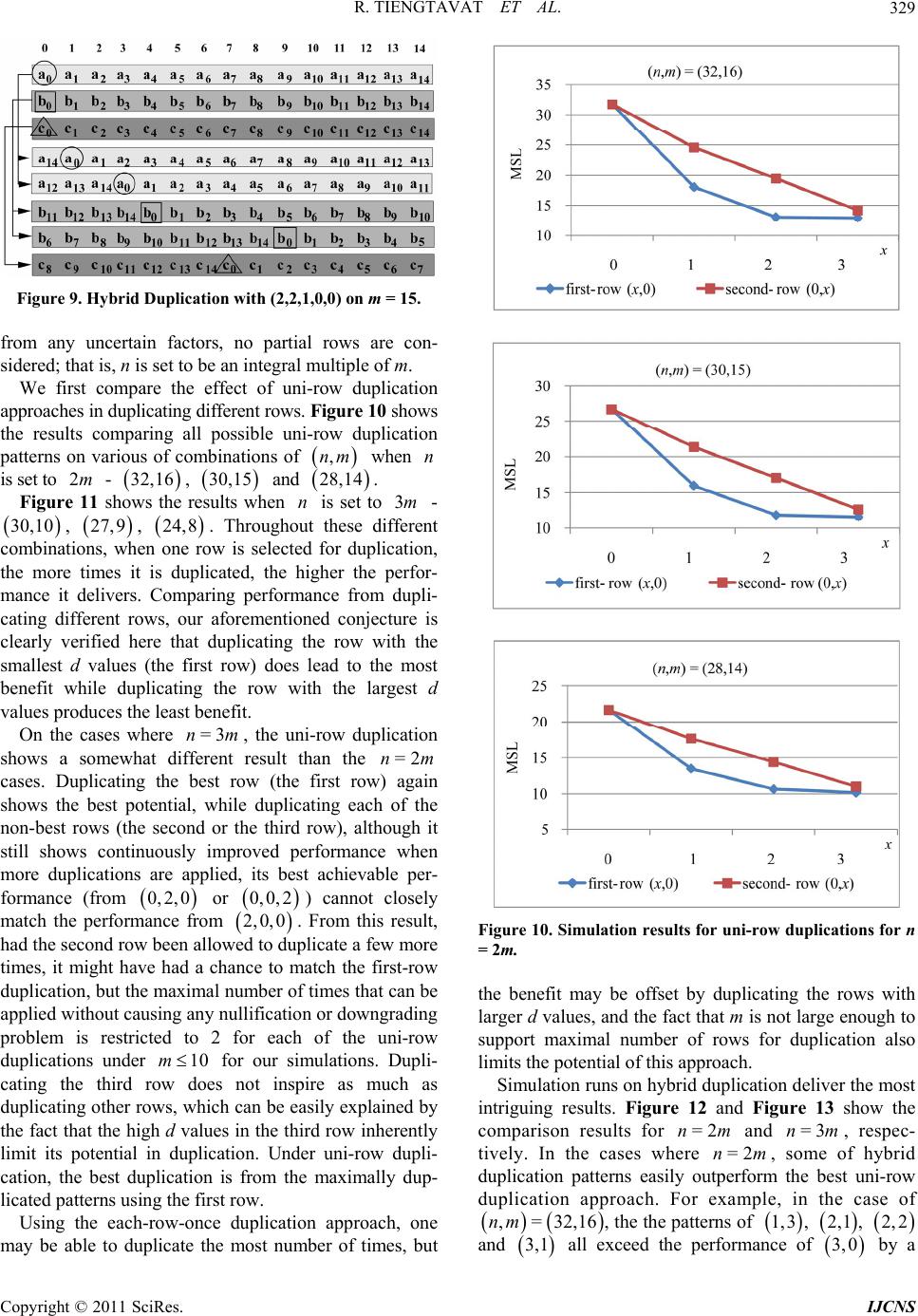

R. TIENGTAVAT ET AL.329
Figure 9. Hybrid Duplication with (2,2,1,0,0) on m = 15.
from any uncertain factors, no partial rows are con-
sidered; that is, n is set to be an integral multiple of m.
We first compare the effect of uni-row duplication
approaches in duplicating different rows. Figure 10 shows
the results comparing all possible uni-row duplication
patterns on various of combinations of when
is set to - , and

.

,nm
28,14
n



n
2m

32,16

30,15
Figure 11 shows the results when is set to -
, , . Throughout these different
combinations, when one row is selected for duplication,
the more times it is duplicated, the higher the perfor-
mance it delivers. Comparing performance from dupli-
cating different rows, our aforementioned conjecture is
clearly verified here that duplicating the row with the
smallest d values (the first row) does lead to the most
benefit while duplicating the row with the largest d
values produces the least benefit.
3m

30,10

27,9

24,8
On the cases where , the uni-row duplication
shows a somewhat different result than the
cases. Duplicating the best row (the first row) again
shows the best potential, while duplicating each of the
non-best rows (the second or the third row), although it
still shows continuously improved performance when
more duplications are applied, its best achievable per-
formance (from
=3nm
=2nm


0, 2,0 or


0,0, 2) cannot closely
match the performance from


2,0,0 . From this result,
had the second row been allowed to duplicate a few more
times, it might have had a chance to match the first-row
duplication, but the maximal number of times that can be
applied without causing any nullification or downgrading
problem is restricted to 2 for each of the uni-row
duplications under for our simulations. Dupli-
cating the third row does not inspire as much as
duplicating other rows, which can be easily explained by
the fact that the high d values in the third row inherently
limit its potential in duplication. Under uni-row dupli-
cation, the best duplication is from the maximally dup-
licated patterns using the first row.
10m
Using the each-row-once duplication approach, one
may be able to duplicate the most number of times, but
Figure 10. Simulation results for uni-row duplications for n
= 2m.
the benefit may be offset by duplicating the rows with
larger d values, and the fact that m is not large enough to
support maximal number of rows for duplication also
limits the potential of this approach.
Simulation runs on hybrid duplication deliver the most
intriguing results. Figure 12 and Figure 13 show the
comparison results for and , respec-
tively. In the cases where , some of hybrid
duplication patterns easily outperform the best uni-row
duplication approach. For example, in the case of
=2nm
n=3nm =2m




,= 32,16nm , the the patterns of ,

1,3


2,1 ,


2, 2
and


3,1 all exceed the performance of

by a

3,0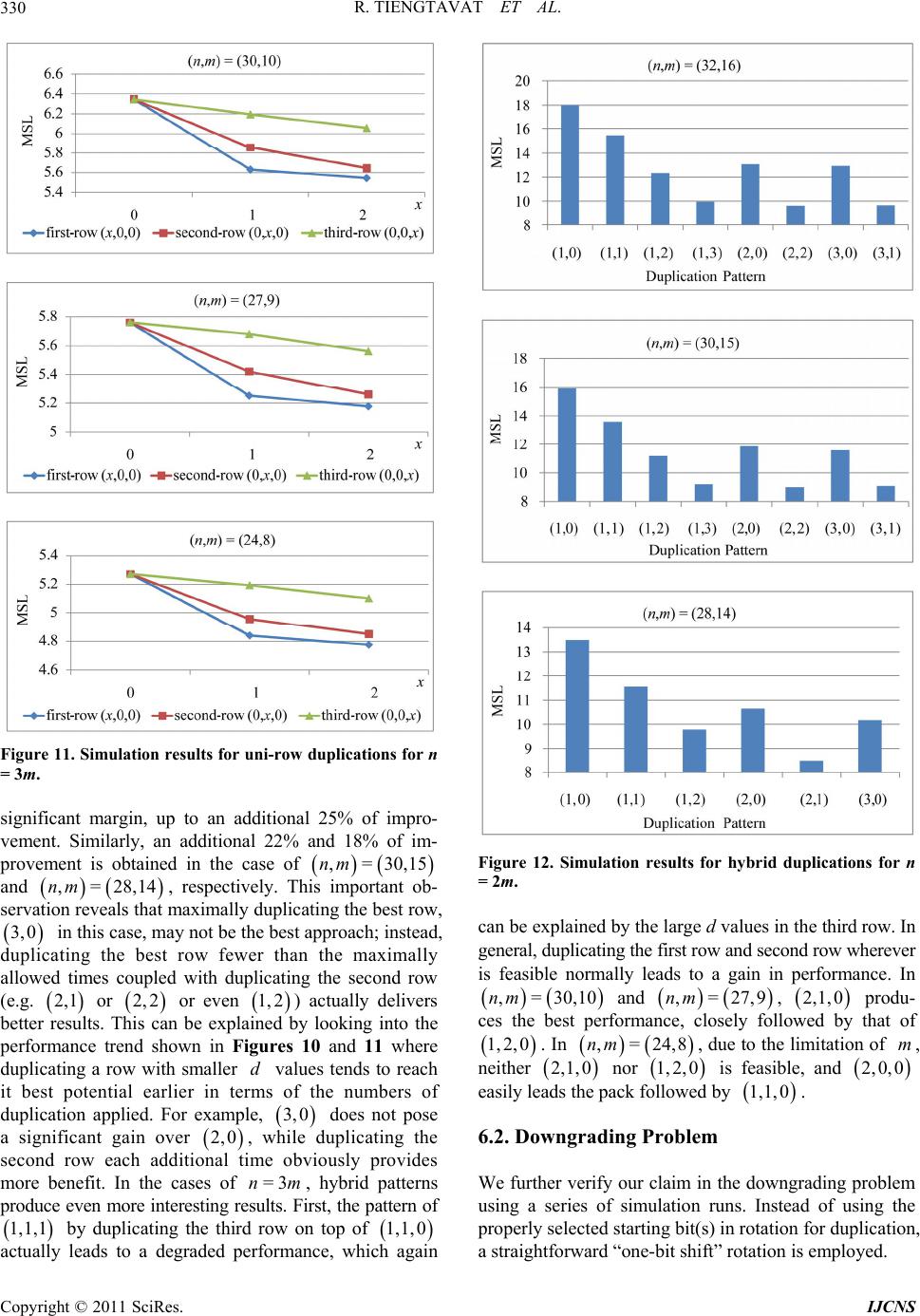

R. TIENGTAVAT ET AL. 330
Figure 11. Simulation results for uni-row duplications for n
= 3m.
significant margin, up to an additional 25% of impro-
vement. Similarly, an additional 22% and 18% of im-
provement is obtained in the case of



,=30,15nm

0
m
and , respectively. This important ob-
servation reveals that maximally duplicating the best row,
in this case, may not be the best approach; instead,
duplicating the best row fewer than the maximally
allowed times coupled with duplicating the second row
(e.g. or or even ) actually delivers
better results. This can be explained by looking into the
performance trend shown in Figures 10 and 11 where
duplicating a row with smaller values tends to reach
it best potential earlier in terms of the numbers of
duplication applied. For example, does not pose
a significant gain over , while duplicating the
second row each additional time obviously provides
more benefit. In the cases of , hybrid patterns
produce even more interesting results. First, the pattern of
by duplicating the third row on top of

,= 28,14nm


2,1

2, 2

1
Figure 12. Simulation results for hybrid duplications for n
= 2m.

 

3,0

1,1,

1, 2
d

3,

=3n

2,0


1,1,0
actually leads to a degraded performance, which again
can be explained by the large d values in the third row. In
general, duplicating the first row and second row wherever
is feasible normally leads to a gain in performance. In




,= 30,10nm and

 
,=27,9nm , produ-
ces the best performance, closely followed by that of

2,1,0



1, 2,0. In




24,8,=nm , due to the limitation of ,
neither
m


2,1,0 nor


1, 2,0 is feasible, and


,02,0
easily leads the pack followed by .

1,1,0
6.2. Downgrading Problem
We further verify our claim in the downgrading problem
using a series of simulation runs. Instead of using the
properly selected starting bit(s) in rotation for duplication,
a straightforward “one-bit shift” rotation is employed.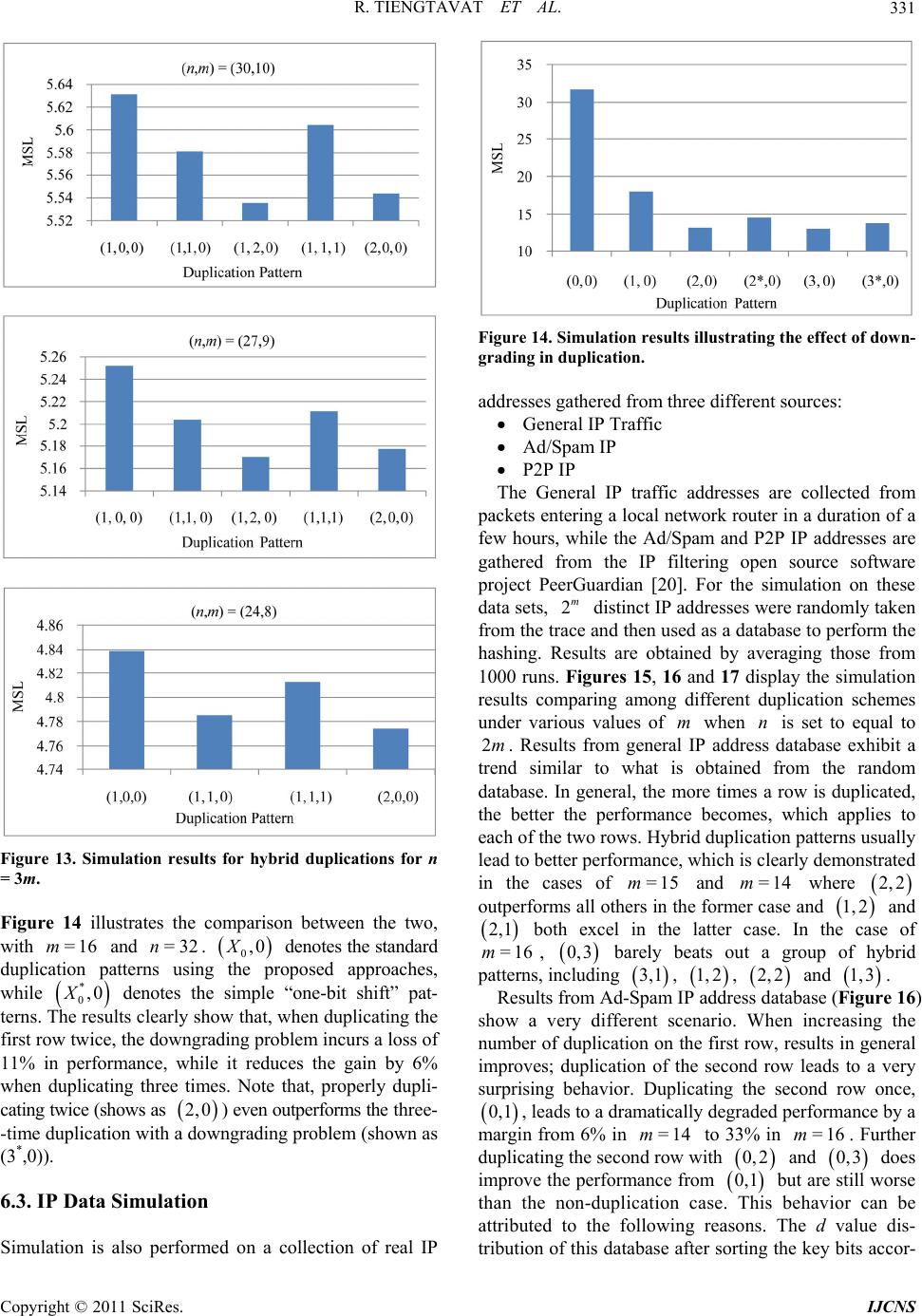

R. TIENGTAVAT ET AL.331
Figure 13. Simulation results for hybrid duplications for n
= 3m.
Figure 14 illustrates the comparison between the two,
with and . denotes the standard
duplication patterns using the proposed approaches,
while denotes the simple “one-bit shift” pat-
terns. The results clearly show that, when duplicating the
first row twice, the downgrading problem incurs a loss of
11% in performance, while it reduces the gain by 6%
when duplicating three times. Note that, properly dupli-
cating twice (shows as ) even outperforms the three-
-time duplication with a downgrading problem (shown as
(3*,0)).
=16m

*
0,0X
=32n

2,0

0,0X



6.3. IP Data Simulation
Simulation is also performed on a collection of real IP
Figure 14. Simulation results illustrating the effect of down-
grading in duplication.
addresses gathered from three different sources:
 General IP Traffic
 Ad/Spam IP
 P2P IP
The General IP traffic addresses are collected from
packets entering a local network router in a duration of a
few hours, while the Ad/Spam and P2P IP addresses are
gathered from the IP filtering open source software
project PeerGuardian [20]. For the simulation on these
data sets, distinct IP addresses were randomly taken
from the trace and then used as a database to perform the
hashing. Results are obtained by averaging those from
1000 runs. Figures 15, 16 and 17 display the simulation
results comparing among different duplication schemes
under various values of when is set to equal to
. Results from general IP address database exhibit a
trend similar to what is obtained from the random
database. In general, the more times a row is duplicated,
the better the performance becomes, which applies to
each of the two rows. Hybrid duplication patterns usually
lead to better performance, which is clearly demonstrated
in the cases of and where
2m
m
5
n
=1
2m
=1m4m


2, 2
outperforms all others in the former case and


21, and


2,1
=1m both excel in the latter case. In the case of , 6


0,3 barely beats out a group of hybrid
patterns, including


3,1 ,


1, 2, and

2,

2


31, .
Results from Ad-Spam IP address database (Figure 16)
show a very different scenario. When increasing the
number of duplication on the first row, results in general
improves; duplication of the second row leads to a very
surprising behavior. Duplicating the second row once,


0,1 , leads to a dramatically degraded performance by a
margin from 6% in to 33% in . Further
duplicating the second row with and
=14m=16m

0, 2


30, does
improve the performance from but are still worse
than the non-duplication case. This behavior can be
attributed to the following reasons. The d value dis-
tribution of this database after sorting the key bits accor-

0,1

R. TIENGTAVAT ET AL. 332
Figure 15. Simulation results for general IP addresses for (a)
n = 2m.
ding to the d value is very different from the general IP
one and especially from the randomly generated one. The
d values of most key bits of this database are already
small compared to the other databases, which leads to a
better result compared to other database when no dup-
lication is used (case ). According to our previous
theoretical analysis, it is harder to further reduce the d
value of a bit already with a small d value by XORing it
with another bit with a d value not significantly larger
[18]. When duplicating the second row which has d
values not significantly larger than the first row's, the
resulted d values after XORing tend to increase. Note
that the degree of performance degradation from dup-
licating the second row lessens as m becomes smaller.
For this database, the best duplication pattern is clearly
dominated by the duplication of only the first row -
usually outperforms all others.

0,0


0,3
Simulation from P2P IP address database shows
somewhat similar results (Figure 17) to those from
Ad-Spam IP database, but the degree of performance
degradation from duplicating the second row is not as
severe. In the case of , such a duplication ((0,1))
=14m
Figure 16. Simulation results for ad-spam IP addresses for
n = 2m.
actually leads to a 5% improvement in performance, and
it is furthered improved when duplicated more. The best
performance is usually achieved with a hybrid pattern,


2,1 for , =14m


2, 2 for , and =15m


3,0 for
.
=1m6
7. Conclusions
This paper further extends previously proposed hash
design methodology to allow for more performance
improvement. This new methodology provides an extra
degree of design flexibility and points out a direction for
future research, especially for cases with large number of
hash key bits. By duplicating and reusing hash key bits in
a more comprehensive manner, our technique further
enhances the randomness from the best known XOR-
hashing techniques. There still exist many potential
extensions along this line of research. This paper only
approaches bit duplication in a cyclic pattern, while a
mixture of different patterns may provide even more
benefit. In addition, this paper examined only induced
correlation from the duplication without considering the

R. TIENGTAVAT ET AL.333
Figure 17. Simulation results for P2P IP addresses for n =
2m.
inherent correlation already existing in the target data-
base, which may have a very significant impact on the
design of hash algorithms. By providing initial ground-
work for duplication in hashing, this paper has pointed
out the potential areas to improve hashing algorithms and
new ways to exploit specific characteristics of the target
database.
8. References
[1] C. Martinez and W.-M. Lin, “Advanced Hash Algorithms
with Key Bits Duplication for IP Address Lookup,” The
5th International Conference on Networking and Services,
Valencia, 20-25 April 2009, pp. 137-142.
[2] P. Newman, G. Minshall, T. Lyon and L. Hutson, “IP
Switching and Gigabit Routers,” IEEE Communications
Magazine, Vol. 35, No. 1, 1997, pp. 64-69.
doi:10.1109/35.568212
[3] O. Amble and D. E. Knuth, “Ordered Hash Tables,”
Computer Journal, Vol. 17, No. 2, 1974, pp. 135-142.
doi:10.1093/comjnl/17.2.135
[4] M. A. Ruiz-Sanchez, E. W. Biersack and W. Dabbous,
“Survey and Taxonomy of IP Address Lookup Algo-
rithms,” IEEE Network, Vol. 15, No. 2, 2001, pp. 8-23.
doi:10.1109/65.912716
[5] R. Jain, “A Comparison of Hashing Schemes for Address
Lookup in Computer Networks,” IEEE Transactions on
Communications, Vol. 40, No. 10, October 1992, pp. 1570-
1573. doi:10.1109/26.168785
[6] A. Moestedt and P. Sjodin, “IP Address Lookup in
Hardware for High-Speed Routing,” Proceedings of IEEE
Hot Interconnects 6 Symposium, Stanford, 13-15 August
1998, pp. 31-39.
[7] X. J. Nie, D. J. Wilson, J. Cornet, D. Damm and Y. Q.
Zhao, “IP Address Lookup Using A Dynamic Hash
Function,” Canadian Conference on Electrical and
Computer Engineering, Saskatoon, 1-4 May 2005, pp.
1642-1647.
[8] S. Nilsson and G. Karlsson, “IP Address Lookup Using
LC-Tries,” IEEE Journal on Selected Areas in Commu-
nications, Vol. 17, No. 6, June 1999, pp. 1083-1092.
doi:10.1109/49.772439
[9] V. Srinivasan and G. Varghese, “Faster IP Lookups Us-
ing Controlled Prefix Expansion,” Proceedings of the
1998 ACM SIGMETRICS Joint International Conference
on Measurement and Modeling of Computer Systems,
Madison, 22-26 June 1998, pp. 1-10.
[10] M. Waldvogel, G. Varghese, J. Turner and B. Plattner,
“Scalable High Speed IP Routing Lookups,” Proceedings
of the ACM SIGCOMM'97 Conference on Applications,
Technologies, Architectures, and Protocols for Computer
Communication, Cannes, 14-18 September 1999, pp. 25-
35.
[11] A. Broder and M. Mitzenmacher, “Using Multiple Hash
Functions to Improve IP Lookups,” 20th Annual Joint
Conference of the IEEE Computer and Communications
Societies, Anchorage, 22-26 April 2001, pp. 1454-1463.
[12] S.-H. Chung, S. Jean, H. Yoon and J.-W. Cho, “A Fast
and Updatable IP Address Lookup Scheme,” Interna-
tional Conference on Computer Networks and Mobile
Computing, Beijing, 16-19 October 2001, pp. 419-424.
[13] D. Yu, B. Smith and B. Wei, “Forwarding Engine for
Fast Routing Lookups and Updates,” Global Telecommu-
nications Conference, Rio de Janeireo, 5-9 December
1999, pp.1556-1564.
[14] C. Martinez, D. Pandya and W.-M. Lin, “On Designing
Fast Non-Uniformly Distributed IP Address Lookup Hash-
ing Algorithms,” IEEE/ACM Transactions on Networking,
Vol. 17, No. 6, December 2009, pp. 1916-1925.
doi:10.1109/TNET.2009.2014949
[15] D. Pao, C. Liu, L. Yeung and K. S. Chan, “Efficient
Hardware Architecture for Fast IP Address Lookup,”
IEEE Proceedings of Computers and Digital Techniques,
Vol. 150, No. 1, 2003, pp. 43-52.
doi:10.1049/ip-cdt:20030082
[16] P. A. Yilmaz, A. Belenkiy, N. Uzun, N. Gogate and M.
Toy, “A Trie-Based Algorithm for IP Lookup Problem,”
Global Telecommunications Conference, San Francisco,
27 November - 1 December 2000, pp. 593-598.
[17] R. Tiengtavat and W.-M. Lin, “Advanced Hashing with
Hybrid Key Duplication for IP Address Lookup,” The 9th

R. TIENGTAVAT ET AL. 334
IEEE International Symposium on Network Computing
and Applications, Cambridge, 15-17 July 2010, pp. 261-
264.
[18] C. Martinez and W.-M. Lin, “Adaptive Hashing Tech-
nique for IP Address Lookup in Computer Networks,”
14th IEEE International Conference on Networks, Sin-
gapore, 13-15 September 2006, pp. 198-203.
doi:10.1109/ICON.2006.302586
[19] D. Pandya, C. Martinez, W.-M. Lin and P. Patel, “Ad-
vanced Hashing Techniques for Non-Uniformly Distrib-
uted IP Address Lookup,” 3rd IASTED International
Conference on Communications and Computer Networks,
Lima, 4-6 October 2006, pp. 46-51.
[20] PeerGuaridan 2, 2007. http://phoenixlabs.org/pg2/