 Int. J. Communications, Network and System Sciences, 2011, 4, 297-303 doi:10.4236/ijcns.2011.45034 Published Online May 2011 (http://www.SciRP.org/journal/ijcns) Copyright © 2011 SciRes. IJCNS Fuzzy Digital Filtering: Signal Interpretation Juan Carlos García Infante1, José de Jesús Medel Juárez2, Juan Carlos Sánchez García1 1Professional School of Mechanical and Electrical Engineering, National Polytechnic Institute, Coyoacan, México 2Centre of Computing Research, National Polytechnic Institu te, Vallejo, México E-mail: jcnet21@yahoo.com, jjmedelj@yahoo.com.mx, jcsanchezgarcia@gmail.com Received February 15, 2011; r ev is e d March 2, 2011; accepted March 27, 2011 Abstract The paper makes a description of the fuzzy filter properties considering its operational principles. A digital filter interacts with a reference model signal into real process in order to get the best corresponding answer, having the minimum error at the filter output using the mean square criterion. Adding into this filter structure a fuzzy mechanism, to obtain an intelligent filtering because adaptively select and emit a decision answer according with the external reference signal changes, in order to actualize the best correct new conditions updating a process dynamically. The interpretation of the input signal level describes the operation of the reference model, to update the filter weights giving the answers approximation in accordance with the refer- ence signal in natural form. Finally the paper shows the simulations results of the fuzzy filter into the Kal- man structure using the Matlab© tool. Keywords: Digital Filters, Fuzzy Systems, Signal Processing, Estimation, Probability 1. Introduction To develop an intelligent system requires a deduction of its own natural external environment, using a fuzzy me- chanism that has the classification of its own set of an- swers in order to discover dynamically the changes of an external process. Interpreting the operation levels to de- duce and select the best response updating its answers weights, in order to follow the best approximation cond i- tion in accordance to the external process changes by taking a decision about the actual condition to correct or update a system [1]. Actually, one of the best tools used to solve this, is a recursive digital filter to adjust dynamically its parame- ters weights in order to give limited answers with respect to the mean square error criterion (1). A digital filter is a logic algorithm programmed into computer software or electronic chip in order to eliminate the noise of a system, takes specific data, identification system or predict a system [2]. The main problem in conventional filtering operation is that it can’t characterizes and infer its operation levels with respect with a reference system changes; inter- preting its external environment changes in order to se- lect its answers with the smallest error and considering different operation levels in dynamical sense, following the natural evolution of the reference system that inter- acts with the filter. In addition, a conventional filter has not a linguistic descriptio n as levels to display its answer conditions as human interface, expressing it as levels rank, making difficult to know the corresponding answer level as non-intelligent process, which have some prob- lems to develop capacities with high changing processes [2]. The systems related to artificial intelligent mecha- nisms should use into its architecture fuzzy tools (as fuzzy neural net and evolutive systems) in order to get its own perception giving the best decision answers, using this to solve complex problems, actualizing an d adapting its perceptions and answers in accordance with a refer- ence dynamical system in order to get knowledge [3,4]. The fuzzy intelligent tools into a digital filtering is an option for to obtain different decision answer levels, to interacts with a reference model dynamics, adapting its answers to the possible changes by selecting the best values in order to get the necessary convergence condi- tions, which should has the best operation each time [5] [6]. The goal of this kind of filter is the characterization of a system that has uncertainties in its operation, de- scribing the natural process, with a rule set. This requires a feedback law in order to follow the basic properties of a desired input signal, adjusting its parameters to give a  J. C. G. INFANTE ET AL. 298 correct solution dynamically to minimize the error crite- rion response [7]. According to this, the filter chooses the best decision answer to update the system. In accordance with this perspective, the paper de- scribes the FDF (Fuzzy Digital Filter) operation and the characterization of the Kalman filter internal structure to give answers with respect to the operation levels in order to follow the natural reference model [8]. 2. Fuzzy Digital Filtering The fuzzy filter is an intelligent filter that has two stages basically; the conventional adaptive filter structure con- sidering all its conditions, and the fuzzy stage integrated to the filter structure in order to characterize its op eration to get a best signal approximation by levels. This stages integration works together minimizing the error criterion difference having a natural signal description in accor- dance with the reference model changes [9]. In another hand, a digital filter structure without this fuzzy stage cannot have a characterization of an external process to have a normal operation without get an answer into levels, making difficult to select the best signal ap- proximation with the minimum error. Having this is dif- ficult to interpret the input signal of the external process and to get the best parameter value in order to update the process with the nearest value to have a better natural signal descri pt i on [10]. According with this a fuzzy digital filter is an adaptive filter adding a fuzzy stage that classifies the input signal k, into fuzzy grades to select the best filter parame- ter value ˆ ak from the knowledge base in order to update the filter weights dynamically trough time to get the best signal approximation respect to the operation level. A fuzzy filter classifies, search and associate in- formation giving the corresponding answer value ac- cording to the desired signal from the reference process at its input. This classifies a reference process in order to get a dynamical filter answers. The goal is to give a de- sired operation condition each time with stable op eration because this filter uses as limit answer value the mean square error criterion (1) as adaptive filtering, but the fuzzy stage minimize the error difference and gets the best signal approximation. The membership functions (parameters value set) are limited into the knowledge base [11]. 1 2 2 JkE ek (1) The criterion k to reduce the filter error de- scribes the mean square of the error between the desired signal k and the filter output k, allows finding the corresponding membership function that is the best signal approximation in order to minimize the filter cri- terion [12]. The Fuzzy filter with adaptive properties has an itera- tive searching methodology using the back-propagation (BP) learning algorithm, which updates its parameters per iteration dynamically by degrees classifying its membership functions into the knowledge base in accor- dance to the difference between the desired response k and the actual filter output ˆ k described as the error ek. The Figure 1 shows the fuzzy filter structure: The FDF interacts with an external reference model (real process) changes and the filter will selects the best answer to approximate the signal with minimum error. Then, the fuzzy filter has next stages [13]: The fuzzy filter previou sly has the classification of the reference process model conditions as opera- tion levels; having the knowledge of all the possi- ble levels. It interprets the desired signal k operation lev- els with the error value ek in prob abilistic form using the inference mechanism (with the logic connector if). It selects a corresponding membership function ˆ ak (parameter value) from the knowledge base (using the logic connector then) according to the error level ek. The parameter value ˆ ak selected, updates the filter operation, adapting automatically its weigh values to give a correct answer ˆ k, min imizing the least mean square criterion, with the best ap- proximation value of the desired signal k. Figure 1. Fuzzy filter operation description. Copyright © 2011 SciRes. IJCNS  J. C. G. INFANTE ET AL.299 The filter emits the best answer ˆ k, describing its responses as linguistic operational levels and continually repeats this cycle. This computational model described as intelligent process may interacts with natural processes as biologic signals, using processing elements making connections to constitute an automatic updating selection to follow the best condition of a process. The control area T is a set of answers that the filter has with respect to all set of desired signals that the ref- erence system emit; the control area (2) is into member- ship intervals inside the knowledge base; in accordance to a filtering criterion (mean square error). The set of membership function (parameters value) represents all the correct responses into the Knowledge Base (KB), according to an objective law, predefined by this natural reference process, the filter inference chooses the best correct response from the knowledge base to each refer- ence model change. ˆ , N Tykyk (2) The desired signal k at the filter input is chang- ing its operation conditions continuously, described in levels. The filter interprets the corresponding level inter- val and selects the best parameter value ˆ ak (mem- bership function) from the knowledge base. Updating the filter operation to give a correct response ˆ k, the goa l of the filtering process as predictor is to follow the de- sired signal k to describe the reference process into operation grades, and then the output filter ˆ k will be approximately the same signal [14]. The description of the signal into a fuzzy structure is using ranks limited by the reference system in order to characterize the sig- nal levels as: First using the logic connector if to get the member- ship grade of the input k, second using the logic connector then to get the corresponding parameter value , third the fuzzy mechanism updates the process to a new condition, and gets the output value described as ˆ ak ˆ k with the best approxi mation. This filtering process determines the best value to up- date de filter conditions and give a response with the smallest error. 3. Fuzzy Filtering Properties Considering the operational characteristics of a digital filtering, the fuzzy filter has the same principles as ex- ample: the mean square error criterion. Below there is a description of the main operation principles of the fuzzy filtering adding some other properties in order to give more intelligence to the answer selection with a classifi- cation into levels to minimize the error and get the best signal approximation. 3.1. Rule Mechanism The filtering process adding the fuzzy inference has a rules base in order to learn, recall, associate and compare the new information at its input in accordance with the reference model changes and the filter signal levels use its variance as operational limit in probabilistic form [15]. The fuzzy rules base has a set of logical connectors (if-then), to interpret the reference process conditions into grades and select the corresponding membership function fro m the knowledge ba se with its correspond ing level. All this rule mechanism has as operation limit the filter criterion, which has previously all th e possible data to process in accordance with the reference model (real process), that is interacting with the filter [16]. Using the logic connectors (if-then) in the fuzzy stage with respect to desired signals set k to deduce the signal level as indicator to select the corresponding membership function (parameter value) in order to update the filter weights dynamically. ˆ ak Each rule of the fuzzy filtering determines a specific membership function value with the connector then, in accordance with the input level deduced with the con- nector if. All this structure works inside the error crite- rion as limit, to maintain a correct operation, using the error distribution to define the intervals in order to de- scribe the filter operation into levels. The Figure 2, show the elements of the rule mechanism. First, the filtering process using the fuzzy connector if infer the input signal level (desire signal) k, from the reference model. The filter mechanism finds into its in- ternal database the corresponding new membership value ˆ ak with the fuzzy connector then to update the pa- rameter value having the operation level. Then the fuzzy rule selects the corresponding parameters from the know- ledge base in order to adjust the filter to give the correct answer ˆ k at th e filter output. 3.2. Error Criterion The fuzzy filter, works with the same basic concepts as a conventional filter using the error mean square (1) as its own criterion to delimit its answer levels. Additionally the fuzzy filter integrates the fuzzy stage that character- izes and interprets the input signal (desired signal), hav- ing all the information required to process the data into the knowledge base deducing the required membership function to update the filter to a new required condition. The fuzzy mechanism reduce the value of the filter error criterion to its minimum difference described as Copyright © 2011 SciRes. IJCNS  J. C. G. INFANTE ET AL. 300 Figure 2. The fuzzy rule base selection. min getting the n earest value answer to update the filter process, having the best signal approximati on at the filter output of the desired signal k, in this conditions the error must be closest to , that is a limit interval [0, 1]. Considering the response levels of the filter, the mem- bership functions have a rank representation by levels with minimum and maximum intervals limited with spe- cific metrics previously defined in order to describe the filter operation inside the error distribution func tion [17]. The previous classification represents the characteri- zation of the reference model (real process) that interacts with the filter. Using a fuzzy filter method avoids the initial instability because the use of supervised learning as artificial intelligence technique to reduce the process uncertainty [18]. The minimization of the filter error criterion reduce the distance between the desired signal k and the filter output ˆ k, this allows having the best signal approximation in accordance with the reference model, updating the filter operation getting the correct answer. Figure 3, shows the representation of the filter criterion described as the convergence. The filter convergence describes the error minimiza- tion dynamically using th e mean square criterion. This is a deduction of the error filter from its initial value (that is considerably high) to a desired error value (minimiza- tion), that accomplishes the filter requirements with re- spect to the reference process. Having this, the fuzzy filter gets the best answer value to update a process to a new best condition [19]. 3.3. Parameter Selection The membership function to select into the fuzzy stage is the corresponding parameter value respect to the input signal level, in order to update the filter weights. The goal of this parameter selection is to have a minimi- zation of the error difference between the input signal and the filter output, in order to get the best approxima- tion of the signal using the better weight value to update dynamically the filter process. ˆ ak The membership function set into the knowledge base bounds into the error criterion too, in order to get the filter response inside of the reference model require- ments [20]. The Figure 4, has th e me mb er sh ip f un ct ion ˆ ak es- timation in accordance with the input value k and the filter output ˆ k. This is the parameter dynamical selection using operation lev els by the fuzzy filtering. The figure above shows the fuzzy stage that makes a classification process describing the parameter values into levels and dynamically selects the best correspon- dence with the reference process changes having the best signal approximation considering the lowest error value. The parameter selection of the fuzzy filter allow to have the best signal approximation dynamically, chang- ing the parameter values to update the filter weights, having the desired signal values deduction at the filter input. The advantage of this metho d is that minimizes th e error criterion value; having a selection process in ac- cordance with the external changes, in other filter cases Figure 3. Filter convergence. Figure 4. Fuzzy parameter selection process. Copyright © 2011 SciRes. IJCNS  J. C. G. INFANTE ET AL.301 without the fuzzy stage co nsiders this parameter value as a constant [21]. The objectives of the knowledge base parameter selec- tion are: Has an automatic classification of the filter opera- tion: having previously all the information into le- vels. Generates knowledge about the parameter value about the reference model (in this case, th e desired signal k), and the fuzzy filter selects the logi- cal action, reflected in the filter out put k value. The adaptation rules modify dynamically the membership functions, renewing and updating its values in accordance with the reference model and the error criterion. Each membership value establishes the maximal correspondence between the desired signal and the filter output, minimizing the error of the filter. The fuzzy filtering process using the criterion of min lim kN kJ selects from a knowledge base (KB) the parameter ak to each value of k, this per- mits that ˆ lim kN kyN . The parameter selection pro- cess is realized in heuristic form, which establishes pa- rameters selection ranks in accordance with the error func- tional ranks; where 0,Jk , describing 1level Jk , 2level , 3level . For each level of Jk Jk k the filter finds a specific value of , describing the opera- tional filter levels and having as a goal to obtain * ak ˆ kyN. To make the selection of the parameter from the KB in accordance with k levels, it needs the next consid- erations: 1) the experimentation process needs to be fixed in accordance of its inputs and outputs, 2) To select a value parameter proposed into the KB, 3) Observe the error functional response, selecting parameters values into the stability region described for the system, probing it into the identification system described as ob- serving the error difference with respect to ˆ()yk k, se- lecting the value parameter that minimizes the error functional. For other new klevel, based on the first parameter value, we look for a new parameter near of the first parameter that minimizes the error functional in order to fix the KB of the filter [22]. 4. Simulation Results For the simulation of the fuzzy filter, we integrate the Kalman filter structure with the fuzzy stage in order to get a characterization of the filter operation, showing graphically the fuzzy filter operation [23]. The Kalman filter in this case uses the identification configuration, having a dynamical parameter selection in order to get the best-desired signal (from the reference model) ap- proximation. The filter has a set of membership function s describing all the filter changes limited by the error crite- rion (1). The reference model into the simulation is an ARMA model (Autoregressive Mobile Average), which interacts with the fuzzy filter in order to get the best answers. This has a description in discrete states space, expressed by the first order difference as: 1 kakxkw k (3) Its output has t he nex t description : : ,, kckxkvkxkwkvkR (4) where: k is the reference model interna l state, ak is the matrix parameters sequence, is the refer- ence model noise, wk k is the desired signal from the reference model to the filter input, ck is a system pa- rameters, and vk = is the output vector noises. With the fuzzy filter, the different operation levels proposed must match inside the filter erro r criterion , with respect with the desired signal k, the membership parameter selection ˆ ak into the filter structure, and the filter output ˆ k. In accordance with a mathe- matical and dynamical selection into th e fuzzy filter, this process has the next description: ˆ ˆˆ 1 kayk k (5) The Figure 5, shows the desired signal k approxi - mation with the fuzzy filter output described as . * ˆ yk In accordance with the desired signal levels, the fuzzy stage makes a selection process by the fuzzy rules to get dynamically the parameter value (membership value) changing its values through time, as you can see in the Figure 5. Desired signal approximation. Copyright © 2011 SciRes. IJCNS 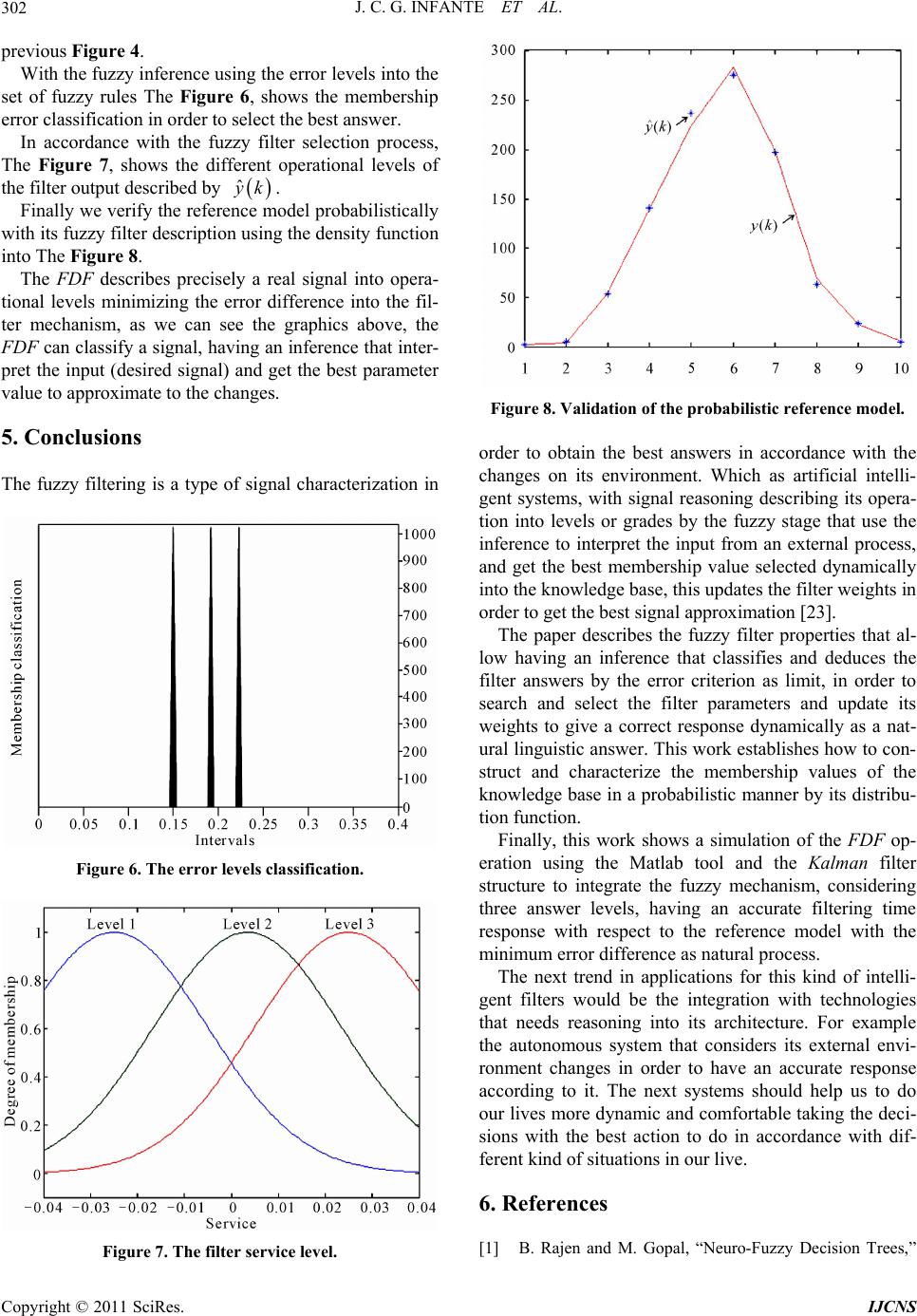 J. C. G. INFANTE ET AL. 302 previous Figure 4. With the fuzzy inference using the error levels into the set of fuzzy rules The Figure 6, shows the membership error classification in order to select the best answer. In accordance with the fuzzy filter selection process, The Figure 7, shows the different operational levels of the filter output described by ˆ k. Finally we verify the reference model probabilistically with its fuzzy filter description using the density function into The Figure 8. The FDF describes precisely a real signal into opera- tional levels minimizing the error difference into the fil- ter mechanism, as we can see the graphics above, the FDF can classify a signal, having an inference that inter- pret the input (desired signal) and get the best parameter value to approximate to the changes. 5. Conclusions The fuzzy filtering is a type of signal characterization in Figure 6. The error levels classification. Figure 7. The filter service level. Figure 8. Validation of the probabilistic reference model. order to obtain the best answers in accordance with the changes on its environment. Which as artificial intelli- gent systems, with signal reasoning describing its opera- tion into levels or grades by the fuzzy stage that use the inference to interpret the input from an external process, and get the best membership value selected dynamically into the knowledge base, this updates the filter weights in order to get the best signal approximation [23]. The paper describes the fuzzy filter properties that al- low having an inference that classifies and deduces the filter answers by the error criterion as limit, in order to search and select the filter parameters and update its weights to give a correct response dynamically as a nat- ural linguistic answer. This work establishes how to con- struct and characterize the membership values of the knowledge base in a probabilistic manner by its distribu- tion function. Finally, this work shows a simulation of the FDF op- eration using the Matlab tool and the Kalman filter structure to integrate the fuzzy mechanism, considering three answer levels, having an accurate filtering time response with respect to the reference model with the minimum error difference as natural process. The next trend in applications for this kind of intelli- gent filters would be the integration with technologies that needs reasoning into its architecture. For example the autonomous system that considers its external envi- ronment changes in order to have an accurate response according to it. The next systems should help us to do our lives more dynamic and comfortable taking the deci- sions with the best action to do in accordance with dif- ferent kind of situations in our live. 6. References [1] B. Rajen and M. Gopal, “Neuro-Fuzzy Decision Trees,” Copyright © 2011 SciRes. IJCNS  J. C. G. INFANTE ET AL. Copyright © 2011 SciRes. IJCNS 303 International Journal of Neural Filters, Vol. 16, No. 1, 2006, pp. 63-68. doi:10.1142/S0129065706000470 [2] K. M. Passino, “Fuzzy Control,” Addison Wesley, Bos- ton, 1998. [3] M. Margaliot and G. Langholz, “New Approaches to Fuzzy Modeling and Control Design and Analysis,” World Scientific, Singapore, 2000. doi:10.1142/9789812792716 [4] S. Haykin, “Adaptive Filtering,” Prentice Hall, Upper Saddle River, 2001. [5] T. Yamakawa, “A Survey on Fuzzy Information Proc- essing Hardware Systems,” 1995 IEEE International Symposium on Circuits and Systems, Seattle, 28 April - 5 March 1995, pp. 1310-1314. [6] J. J. Medel, J. C. García and J. C. Sánchez, “Real-Time Fuzzy Digital Filters Properties for SISO Systems,” Au- tomatic Control and Computer Sciences, Vol. 41, No. 1, 2008, pp. 26-34. [7] S. Mollov, R. Babuska, J. Abonyi, and H. Verbruggen, “Effective Optimization for Fuzzy Model Predictive Control,” IEEE Transactions on Fuzzy Systems, Vol. 12, No. 5, 2004, pp. 661-675. doi:10.1109/TFUZZ.2004.834812 [8] R. Ash, “Real Analysis and Probability,” Academic Press, Cambridge, 1970. [9] L. Zadeh, “Maximizing Sets and Fuzzy Markoff Algo- rithms,” IEEE Transactions on Systems, Man, and Cy- bernetics-Part C: Applications and Reviews, Vol. 28, No. 1, 1998, pp. 9-15. doi:10.1109/5326.661086 [10] G. Feng, “A Survey on Analysis and Desing of Model- Based Fuzzy Control Systems,” IEEE Transactions on Fuzzy Systems, Vol. 14, No. 5, 2006, pp. 676-697. doi:10.1109/TFUZZ.2006.883415 [11] J. García, J. Medel and L. Guevara, “Filtrado Difuso en Tiempo Real,” Computación y Sistemas, Vol. 11, No. 4, 2008, pp. 390-401. [12] J. García, J. Mede l and J. Sá nchez, “Evolutive Neural Net Fuzzy Filtering: Basic Description,” Journal of Intelligent Learning Systems and Applications, Vol. 2, No. 1, 2010, pp. 12-18. doi:10.4236/jilsa.2010.21002 [13] B. Kosko, “Fuzzy Engineering,” Prentice Hall, Upper Saddle River, 1997. [14] E. Mamdani, “Applications of Fuzzy Algorithms for Control of Simple Dynamic Plant,” Proceedings of IEEE, Vol. 121, No. 12, 1974, pp. 1585-1588. [15] T. Amble, “Logic Programming and Knowledge Engi- neering,” Addison Wesley, Boston, 1987. [16] T. Takagi and M. Sugeno, “Fuzzy Identification of Sys- tems and Its Applications to Modelling and Control,” IEEE Transactions and Systems, Man, and Cybernetics, Vol. 15, No. 1, 1985, pp. 116-132. [17] M. Shannon, “A Mathematical Theory of Communica- tion,” Bell Systems Technical Journal, Vol. 27, 1948, pp. 379-423 and pp. 623-656. [18] J. Smith and A. Eiben, “Introduction to Evolutionary Computing,” Springer, Cambridge, 2003. [19] L. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X [20] H. S. Ali, “Fundamentals of Adaptive Filters,” John Wi- ley & Sons, Hoboken, 2003. [21] E. Onieva, V. Milanés, J. Pérez and T. Pedro, “Estima- ción de un Control Lateral Difuso de Vehículos,” Inicio, Vol. 7, No. 2, 2010, pp. 91-98. [22] D. Marcek, “Stock Price Forecasting: Statistical, Classi- cal and Fuzzy Neural Networks,” The 8th International Conference on Modeling Decisions for Artificial Intelli- gence, Barcelona, 2-4 August 2004, pp. 41-48. [23] F. Gustafsson, “Adaptive Filtering and Change Detec- tion,”John Wiley and Sons, Ltd., Hoboken, 2000. doi:10.1002/0470841613
|