World Journal of Condensed Matter Physics, 2011, 1, 37-48
doi:10.4236/wjcmp.2011.12007 Published Online May 2011 (http://www.SciRP.org/journal/wjcmp)
37
Dielectric Relaxation in P ure Colu mbite Phase of
SrNb2O6 Ceramic Mater ial: Impedance Anal y sis
Karuna Nidhan Singh, Parmendra Kumar Bajpai*
Department of Pure & Applied Physics, Guru Ghasidas Vishwavidyalaya, Bilaspur, India.
Received January 5th, 2011; revised March 24th, 2011; accepted March 26th, 2011.
ABSTRACT
Controlling the heating rate during calcination and cooling rate during sintering, pure columbite like phase of SrNb2O6
is synthesized. By optimiz ing the sintering tempera ture, ceramic with density (> 92%) is achiev ed for material calcined
at 1125˚C and sintered at 1200˚C. The ceramic shows orthorhombic structure with lattice parameters a = 11.011 Å, b
= 7.7136 Å, c = 5.5969 Å having average grain size ≈ 1.03 μm. The temperature dependent dielectric response shows a
peak at temperature 300.9˚C, which shows significant dielectric dispersion towards high temperature side of the peak
with almost dispersion free low temperature side; an effect observed in relaxors. Dielectric dis persion in the material is
fitted with the Jonscher’s relation. Impedance analysis suggests strongly temperature dependent relaxation. The dielec-
tric relaxation is polydispersive and conduction is mainly through grains. The equivalent circuit model for the imped-
ance response is proposed and the temperature dependence of circuit elements deduced. The frequency dependent ac
conductivity at different temperatures indicated that the conduction is governed through thermally activated processes.
AC conduction activation energies are estimated from Arrhenius plots and conduction mechanism is discussed.
Keywords: Electro Ceramics, Dielectrics, Micro s tructure, Sintering Optimization, Dielectric Relaxation
1. Introduction
Alkaline earth and transition metal niobate with general
formula A2+ Nb2O6 (with A = Mg, Ca, Sr, Ba, Mn, Fe, Co,
Ni, Cu, Zn, Cd, and Pb) have been widely studied [1-8].
Most of these compounds stabilize in isomorphic or-
thorhombic phase [9,10]. Many of them in columbite
phase exhibit, excellent dielectric properties at micro-
wave frequencies [11-13]. Moreover, these compounds
are generally used as pr ecursor materials for the s ynthesis
of high-Q perovskite Ba(A1/3Nb2/3)O3 [14]. Microwave
dielectric properties of the columbite phases are, to a large
extent, s e nsitive to t he pre pa ration rout e [ 12,15]. However,
the synthesis of single phase columbite is often difficult
because of the formation of corundum-like (A4Nb2O9)
phases [15]. The properties of ceramics are greatly af-
fected by the characteristics of the powder such as particle
size, morphology, purity and chemical composition [16].
In normal solid state route, compositional homogeneity is
generally not achieved. By using chemical methods, e.g.
co-precipitation, sol-gel, hydrothermal and colloid emul-
sion techniques, one can efficiently control the morphol-
ogy and chemical composition of prepared powder [17].
However, the sinterability of the material remain s an issue
and often in the chemical synthesis routes, the densifica-
tion of materials is not reported that is important for using
the materials for device purposes. Further, the earlier st u-
dies have mainly concerned about the preparation routes
and detailed dielectric behavior; electrical conduction
mechanism and contribution of grains and grain bounda-
ries in dielectric relaxation are not studied. For any device
application, an understanding of these properties is very
much required. Therefore in this paper an attempt has
been made to control the processing parameter including
the oxidation of grain boundaries during cooling from
high temperature while sintering the materials. To the best
of our knowledge, no such detailed report exists in the
literature. We, therefore, report the optimization of pro-
cess parameters viz. calcination and sintering in order to
prepare the SrNb2O6 in pure columbite phase with good
siterability. Th e dielectric properties an d impedance anal-
ysis of SrNb2O6 of such phase pure are investigated and
reported in the pape r.
2. Experimental Procedure
2.1. Sample Preparation
SrNb2O6 is synthesized by taking stoichiometric amounts

38 Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
of SrCO3 (Loba 99.9%), Nb2O5 (Loba 99.5%) using sol-
id-state reaction route. The stoichiometric amounts of
precursors were wet mixed in acetone for 12 hours. The
mixed powders were calcined at 1125˚C for 6 hours in a
microprocessor controlled furnace (Superheat, India)
with controlled heating profile. Calcined powders were
analyzed using X-ray diffraction technique (X-ray dif-
fractometer, Rigaku-Miniflex). Fine calcined powders
were pressed into cylindrical pellets of 10 mm diameter
and 1-2 mm thickness under an isostatic pressure of 100
MPa. Polyvinyl alcohol (PVA) was used as a binder. The
pellets were sintered at different temperatures (1150˚C,
1175˚C, 1200˚C, 1225˚C) for 6 hours and cooled down to
room temperature with controlled cooling rate.
2.2. Characterization
The phase formation of the sintered pellet has been iden-
tified using x-ray diffraction analysis with CuKα
(λ = 1.54056 Å). For dielectric measurements, the sin-
tered samples were electroded with silver paste and
heated at 500˚C for 2 hours before measurements were
performed. The electrical impedance (Z), capacitance (C)
and loss angle (tan) were measured in the temperature
range (100 – 400˚C) and at the rate of 2˚C min-1 in the
frequency range (100 Hz-1MHz) using a computer con-
trolled LCR HI-TESTER (HIOKI-3532-50). Surface
morphology of the sample is investigated using surface
electron microscopy (SEM).
3. Result and Discussion
3.1. X-ray Diffraction Studies
Figure 1(a) depicts the XRD pattern of SrNb2O6 ceramic
calcined at 1125˚C. From the observed interplanar spac-
ing (dobs) of all XRD peaks, unit cell parameters were
obtained using a standard XRD interpretation software
POWD. The unit cell was selected for which d = (dobs-dcal)
is minimized. All major X-ray reflection peaks observed
could be fitted satisfactorily in orthorhombic columbite
phase with lattice constants a = 11.011 Å, b = 7.7136 Å,
c = 5.5969Å which matches well with reported JCPDS
data (JCPDS File No. 28-1243). The powders sintered at
different temperatures (1150˚C, 1175˚C, 1200˚C,
1225˚C,) were again subjected to X-ray diffraction anal-
ysis as shown in Figure 1(b). Phase pure material is ob-
tained for the sample calcined at 1125˚C and sintered at
1200˚C; the experimental density (> 92% of the theoret-
ical one) is obtained for sintered material. The estimated
density for different sintering temperatures is shown in
Table 1. The particle size determined using Scherer for-
mula, is estimated ≈ 413Å.
The microstructure of the s intered pellets and distrib u-
tion of grains over the sample surface were studied by
scanning electron micrographs. The typical SEM micro-
graph of SrNb2O6 is shown in Figure 2. Well developed
homogeneously distributed and elongated spherical
grains are observed. The average grain size (≈ 1.03m) is
calculated using linear intercept method.
3.2. Dielectric Study
The temperature dependence of both dielectric p ermittiv-
ity and tangent loss (in the inset) are depicted in F igure 3
at different frequencies ( 1 KHz, 5 KHz, 10 KHz, 50
KHz, 100 KHz, and 1 MHz); the values of dielectric
constant increases with increase in temperature and a
peak evolves at around 300˚C. The peak value of d ielec-
tric constant as well as that of tangent loss decreases
(Figure 3) and the peak shifts towards higher tempera-
ture with increase in frequency. The increase in dielectric
response with temperature may be due to interfacial po-
larization dominating over d ipolar po larization . Obs erved
peak also indicates the onset of some additional relaxa-
tion mechanism in the material around 300˚C. Dielectric
dispersion at higher temperature side of the peak is evi-
dent in both components of dielectric permittivity.
The frequency dependence of real (ε’) and imaginary
(ε”) part of dielectric constant on a log-log plot at differ-
ent temperatures are shown in Figure 4. Up to 200˚C,
real part of dielectric constant is higher than its imagi-
nary part, and both values decreases with frequency.
With further increase in temperature, there is a sudden
rise in ε” and it starts with higher value than ε’, inter-
secting at 3 kHz at 250˚C; intersecting frequency shift
towards higher frequency as temperature increased (4
kHz at 300˚C). Higher values of both the components of
dielectric constant, as temperature rises, reveal the effect
of space charge polarization and/or conducting ion mo-
tion. The relatively higher values of ε” at low frequency,
especially at higher temperature, suggests the free charge
motion that may be related to ac conductivity relaxation,
whereas the large values of ε’ at lower frequencies may
be associated with hopping conduction. Moreover, with
increase in frequency, the ε’ and ε” terms becomes al-
most parallel at higher temperatures. This type of beha-
vior is reported in other conducting ion dielectrics [18]
and is associated with ion hoping as the dominant me-
chanism of dielectric relaxation [19].
The frequency dependence of real (ε’) and imaginary
(ε”) part of dielectric constant in the 50-400˚C tempera-
ture range on a log-log scale is shown in f igures 5( a) and
(b), respectively. Both ε’ and ε” show dispersions at low
frequencies and gets almost saturated at higher frequen-
cies. The dispersions increase with increase in tempera-
ture. Such dispersions in both components of complex
dielectric constant are observed commonly in ferroelec-
trics with appreciable ionic conductivity and are r eferr ed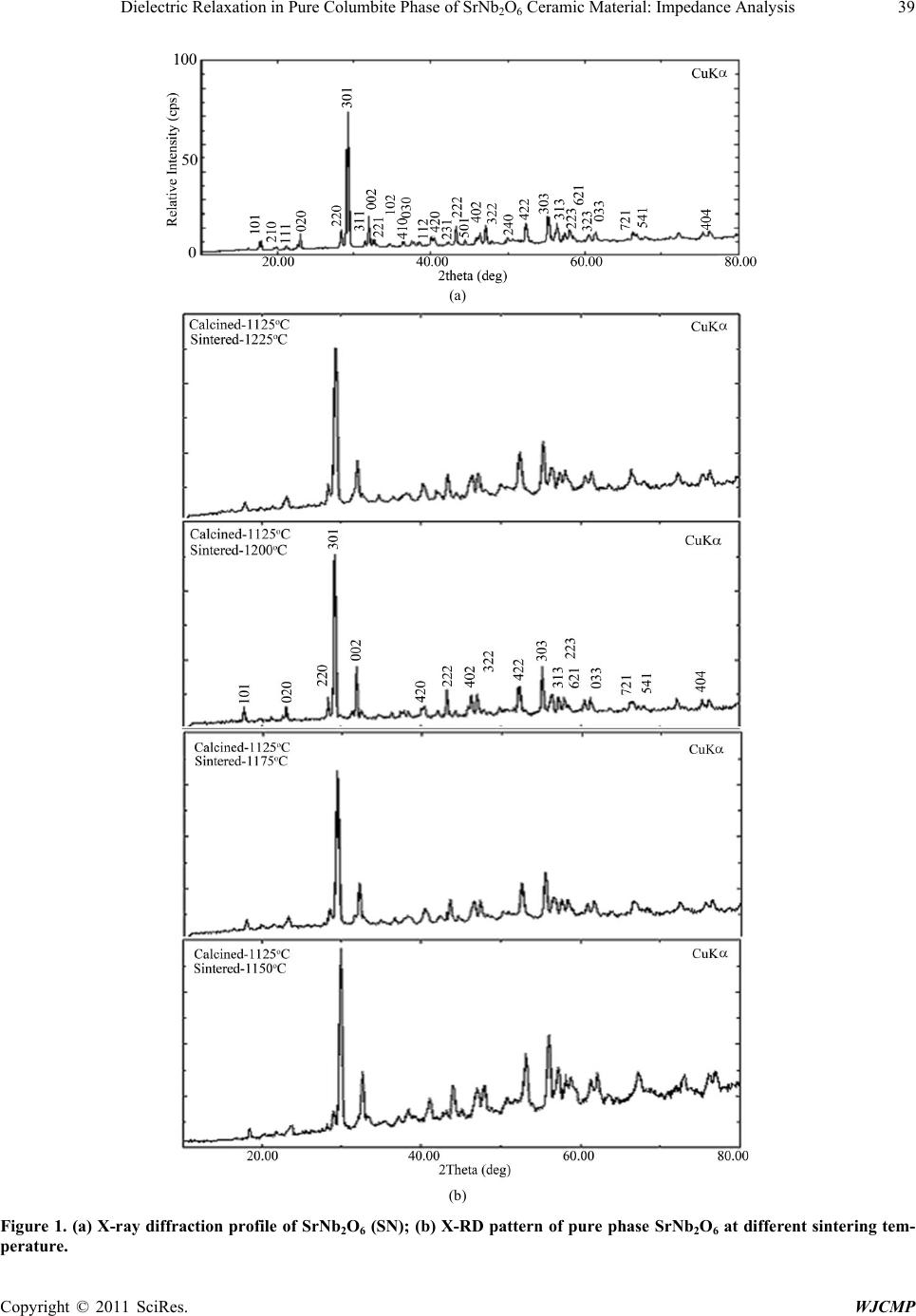

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
39
(a)
(b)
Figure 1. (a) X-ray diffraction profile of SrNb2O6 (SN); (b) X-RD pattern of pure phase SrNb2O6 at different sintering tem-
perature.

40 Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
Table 1. Structural parameters for various sintering conditions of SrNb2O6.
Figure 2. SEM micrograph of pure phas e SrNb2O6.
Figure 3. Temperature dependence of dielectric constant (ε’). Inset shows temperature dependence of dielectric loss.
Composition
Crystal Structure
Unit cell parameters in ( Å )
d
exptl
.gm/c.c
d
Theo
gm/c.c
% density
a
b
c
Sample-I Sintered
1150˚C Orthorhombic 11.210 7.6922 5.6254 4.329 5.523 78.38
Sample-II Sintered
1175˚C
Orthorhombic
11.124
7.7102
5.6204
4.5358
5.558
81.60
Sample-III Sintered
1200˚C
Orthorhombic
11.011
7.7136
5.5969
5.2489
5.638
92.60
Sample-IV Sintered
1225˚C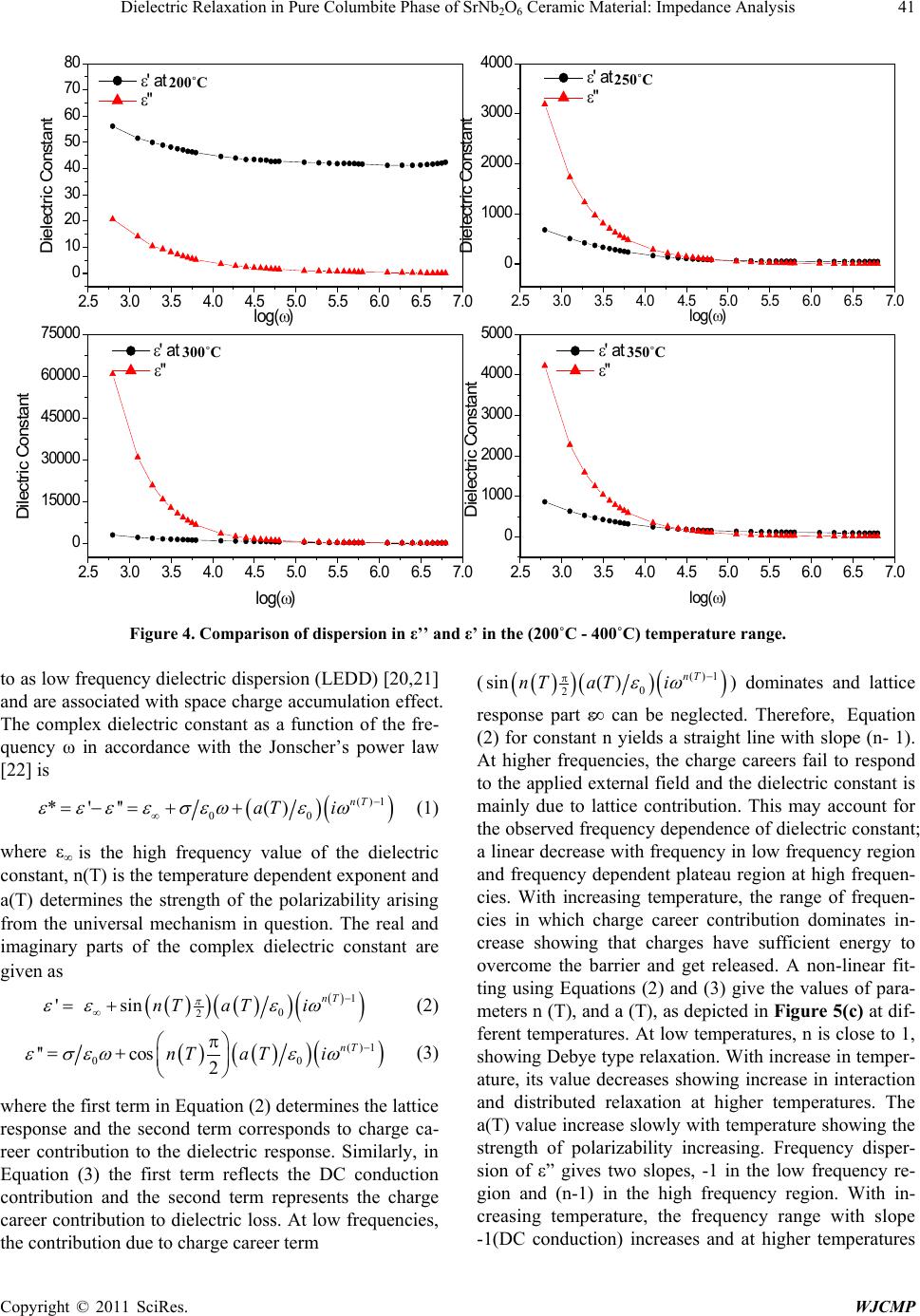
Orthorhombic
11.008
7.7198
5.6126
4.7786
5.619
85.04

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
41
Figure 4. Comparison of dispersion in ε’’ and ε’ in the (200˚C - 400˚C) temperature range.
to as low frequency dielectric dispersion (LEDD) [20,21]
and are associated with space charge accumulation effect.
The complex dielectric constant as a function of the fre-
quency ω in accordance with the Jonscher’s power law
[22] is
( )
( )
()1
00
*'''( )nT
aT i εεεεσεω εω
−
∞
=−=+ +
(1)
where ε∞ is the high frequency value of the dielectric
constant, n(T) is the temperature dependent exponent and
a(T) determines the strength of the polarizability arising
from the universal mechanism in question. The real and
imaginary parts of the complex dielectric constant are
given as
( )
( )
( )
( )
( )
( )
1
0
2
' sin
nT
nT aTi
π
εε εω
−
∞
= +
(2)
( )( )
( ) ( )
()1
00
''cos 2
nT
nT aTi ε σεωεω
−
π

=+ 

(3)
where the first ter m in Equation (2) determines the lattice
response and the second term corresponds to charge ca-
reer contribution to the dielectric response. Similarly, in
Equation (3) the first term reflects the DC conduction
contribution and the second term represents the charge
career contribution to dielectr ic loss. At low frequencies,
the contribution due to charge career term
(
( ) ( ) ( )
( )
()1
0
2
sin( )
nT
nT aTi εω
−
π
) dominates and lattice
response part ε∞ can be neglected. Therefore, Equation
(2) for constant n yields a straight line with slope (n- 1).
At higher frequencies, the charge careers fail to respond
to the applied external field and the dielectric constant is
mainly due to lattice contribution. This may account for
the observed frequency dependence of dielectric constant;
a linear decrease with frequency in low frequency region
and frequency dependent plateau region at high frequen-
cies. With increasing temperature, the range of frequen-
cies in which charge career contribution dominates in-
crease showing that charges have sufficient energy to
overcome the barrier and get released. A non-linear fit-
ting using Equations (2) and (3) give the values of para-
meters n (T), and a (T), as depicted in Figure 5(c) at dif-
ferent temperatures. At low temperatures, n is close to 1,
showing Debye type relaxation. With increase in temper-
ature, its value decreases showing increase in interaction
and distributed relaxation at higher temperatures. The
a(T) value increase slowly with temperature showing the
strength of polarizability increasing. Frequency disper-
sion of ε” gives two slopes, -1 in the low frequency re-
gion and (n-1) in the high frequency region. With in-
creasing temperature, the frequency range with slope
-1(DC conduction) increases and at higher temperatures
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
10
20
30
40
50
60
70
80
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
1000
2000
3000
4000
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
15000
30000
45000
60000
75000
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
0
1000
2000
3000
4000
5000
Dielectric Constant
l og(ω)
ε' at 200
0
C
ε"
Dielectric Constant
l og( ω)
ε' at 250
0
C
ε"
Dilectric Constant
l og(ω)
ε' at 300
0
C
ε"
Dielectric Constant
l og( ω)
ε' at 350
0
C
ε"
200˚C 250˚C
300˚C 350˚C

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
42
(b)
(c)
Figure 5. (a) Frequency dependence of real (ε’) part of dielectric constant in the (50-400˚C) temperature range on a log-log
scale. (b) Frequency dependence of imaginary (ε”) part of dielectric constant in the (50-400˚C) temperature range on a log-
log scale. (c) Temperature dependence of n(T) and a(T).
3 4 5 6 7
1. 6
2. 0
2. 4
2. 8
3. 2
3. 6
l og(
ε
')
l og( ω)
500C
1000C
1500C
2000C
2500C
3000C
3500C
4000C
2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
-1.5
0.0
1.5
3.0
4.5
6.0 50
0
C
100
0
C
150
0
C
200
0
C
250
0
C
300
0
C
350
0
C
400
0
C
log( ε")
log( ω)
100 150 200 250 300 350 400
0.0
0.2
0.4
0.6
0.8
1.0
n(T)
a(T)
Temperat ure( 0C)
n( T)
-5.0x10
-7
0.0
5.0x 10
-7
1.0x 10
-6
1.5x 10
-6
a( T)
(a)
(b)
(c)
50˚C
100˚C
150˚C
200˚C
250˚C
300˚C
350˚C
400˚C
50˚C
100˚C
150˚C
200˚C
250˚C
300˚C
350˚C
400˚C
Temperature (˚C)

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
43
dc conduction dominates the charge career conduction.
3.3. Impedance Studies
The nature of the material response to an applied a.c.
field and processes involved is explored by analyzing the
a.c. impedance behavior. Impedance spectroscopy may
be a better tool to understand the grain and grain boun-
dary relaxation process, especially when the contribution
of grains is separated from that of grain boundaries. The
frequency dependence of the electrical properties of a
material can be described in terms of complex impedance
Z*, complex admittance Y*, the complex permittivity *,
complex electric modulus M*, and the dielectric loss or
the dissipation factor tan. They are related to one another
[23] as follows;
tan"'M ''M 'Z'Z ''Y 'Y '' δ εε = ===
.
In case of single relaxation process, a semicircle is ob-
tained for each admittance function when plotted in the
complex plane. Spectroscopic techniques present various
possibilities insofar as the representation of data is con-
cerned. Each representation can be made use of to high-
light a particular aspect of the response of a sample. Thus
for instance, in as much as Z” vs. frequency plots high-
light phenomena with the largest resistance, the M” plots
pick out those of the smallest capacitances [23-29]. The
sample is sintered at higher temperature (1125˚C), oxy-
gen loss may occur. This may lead to the formation of
barrier layers at the grain-grain boundary interface thus
affecting the impedance of grains and grain boundaries
[30].
Figure 6 shows the variation of the imaginary part of
the impedance (
''Z
) as a function of frequency.
''Z
plots show broad peaks at different frequencies with
asymmetric broadening depending on the temperature of
measurement. This would imply that the relaxation is
temperature dependent, and there is apparently not a sin-
gle relaxation time, and thereby relaxation process in-
volved, but different relaxations with their own discrete
relaxation times depending on the temperature. As the
temperature is increased, in addition to the expected de-
crease in magnitude of
''Z
, there is a shifts in the peak
frequencies towards higher frequency side. Also it is
evident that with increasing temperature, there is a broa-
dening of the peaks and at temperatures where tempera-
ture dependent dielectric response shows peak, the
''Z
response is almost flat. As the temperature is increased
further,
''Z
response increases and then starts decreas-
ing associated with peak broadening at increased temper-
ature. This implies the spread of relaxation times on both
sides of dielectric peak temperatures and the existence of
temperature dependent electrical relaxation phenomena.
Probably, high temperature triggers grain boundary re-
laxation process as is also evident from the asymmetric
broadening of the peaks [30].The most probable relaxa-
tion time could be calculated from the loss peak in the
''Z
versus frequency plots using the relation τ = RbCb =
1/ωm. From these data, the τ at various temperatures is
calculated. Graph between ln(ωm) versus 1/T is shown in
inset of Figure 6. The τ value decreases with increasing
temperature, indicating that the behavior is typical semi-
conductor one. Calculated activation energy for the
process is 0.18 eV.
Figure 7 shows M" as a function of frequency at dif-
ferent temperatures (inset shows temperature dependence
of ωm obtained from M” curve). It is seen that M" exhi-
bits a symmetric maximum (M"max). The M"max shifts
toward higher frequencies as the temperature is increased.
At 300˚C, the electric modulus loss peak crosses the
measurement windows and beyond this temperature. At
further higher temperature, a more broadened peak ap-
pears that shifts towards higher frequencies with in-
creasing the temperature. This once again supports two
different relaxation processes dominating the response
above and below 300˚C. Thus the dielectric response
peak observed is associated with switching of relaxation
process. Frequency m corresponding to M"max gives the
most probable relaxation time τm (ωmτm = 1). Activation
energy estimated from modulus data is 0.59 eV below
300˚C and 0.32 eV above this temperature. As the mod-
ulus represents the response from the interior of grains,
the activation energies for charges (defects) in the bulk
are relatively more than for charges within interface re-
gion.
The complex impedance plots
'Z
vs.
''Z
for repre-
sentative temperatures is shown in Figure 8. The arc
crosses the
''Z
axis at lower values with increasing
temperatures, showing that the grain resistance decreases
with temperature. This could be fitted with series net-
work Rs-(R1Q)C1-R2C2, as shown in Figure 8, where Q
represents the constant phase element-a capacitor with
universal Jonscher’s type capacitance. The series resis-
tance Rs in the model is included as the
''Z
does not
intersect at origin. This may be due to electrode rough-
ness and porousness of the mate ri a l. Inclusi on of c onstant
phase element is due to the fact that value of exponent
n(T) in Jonscher’s equation decreases up to 0.5 from 1 in
dielectric response (Figure 5 (c)). The values of parame-
ters Rs, R1, C1, R2, C2, Q and n proposed are calculated
and plotted in Figures 9 (a) and (b) as a function of
temperature. The value of C1 increases slowly with in-
crease in temperature whereas the R1 decreases and
above the dielectric peak temperature both becomes al-
most constant. The behavior could be associated with the
grains dominating the conduction process below 300˚C.
The series resistance Rs also increases at high tempera-
ture and reached maximum at 250˚C, reflecting that the
charges trapped at the bulk electrode interface are mig-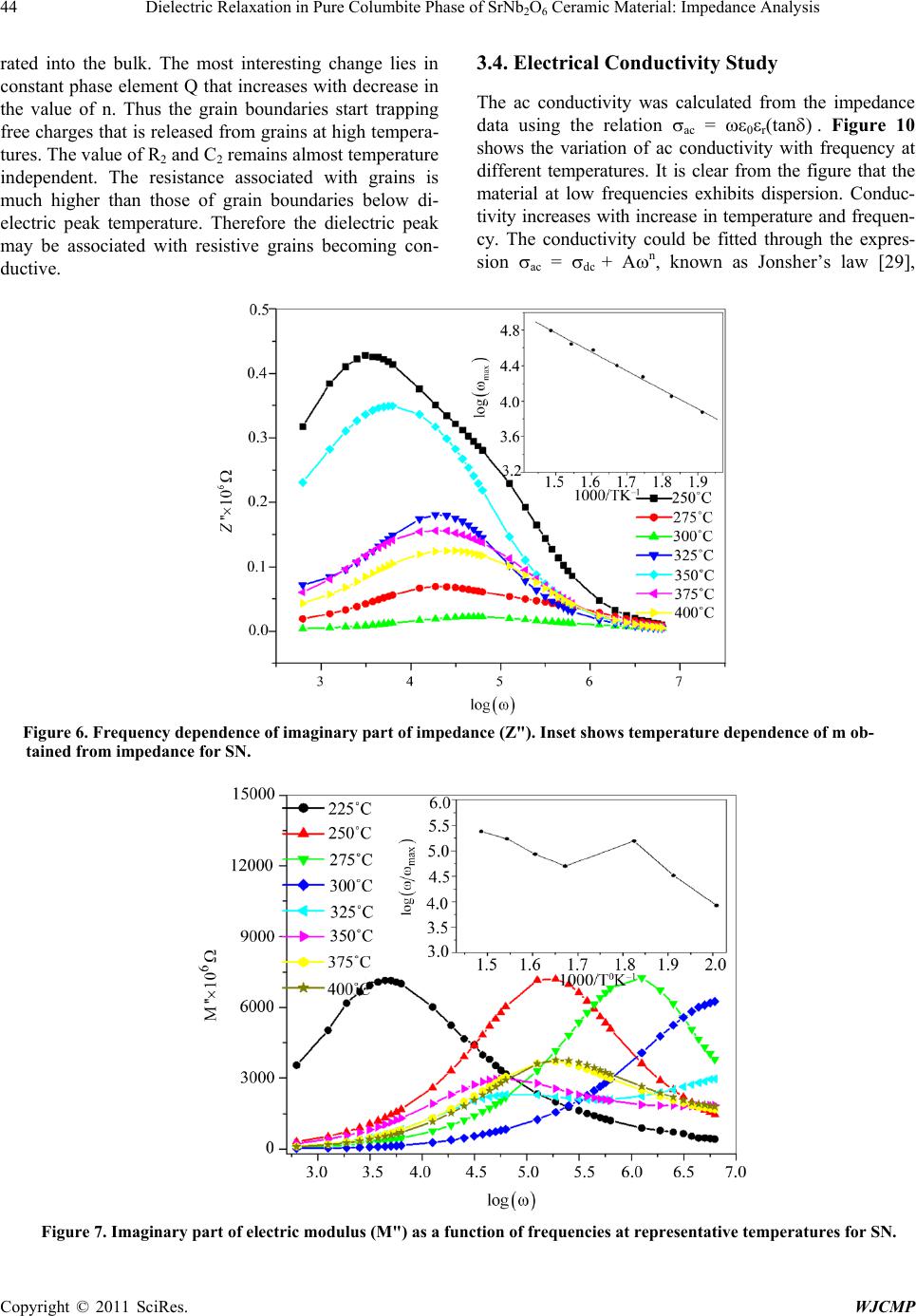

44 Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
rated into the bulk. The most interesting change lies in
constant phase element Q that increases with decrease in
the value of n. Thus the grain boundaries start trapping
free charges that is released from grains at high tempera-
tures. The value of R2 and C2 remains almost temperature
independent. The resistance associated with grains is
much higher than those of grain boundaries below di-
electric peak temperature. Therefore the dielectric peak
may be associated with resistive grains becoming con-
ductive.
3.4. Electrical Conductivity Study
The ac conductivity was calculated from the impedance
data using the relation σac = ωε0εr(tanδ) . Figure 10
shows the variation of ac conductivity with frequency at
different temperatures. It is clear from the figure that the
material at low frequencies exhibits dispersion. Conduc-
tivity increases with increase in temperature and frequen-
cy. The conductivity could be fitted through the expres-
sion σac = σdc + Aωn, known as Jonsher’s law [29],
Figure 6. Frequency dependence of imaginary part of impedance (Z"). Inset shows temperature dependence of m ob-
tained from impedance for SN.
Figure 7. Imaginary part of electric modulus (M") as a function of frequencies at representative temperatures for SN.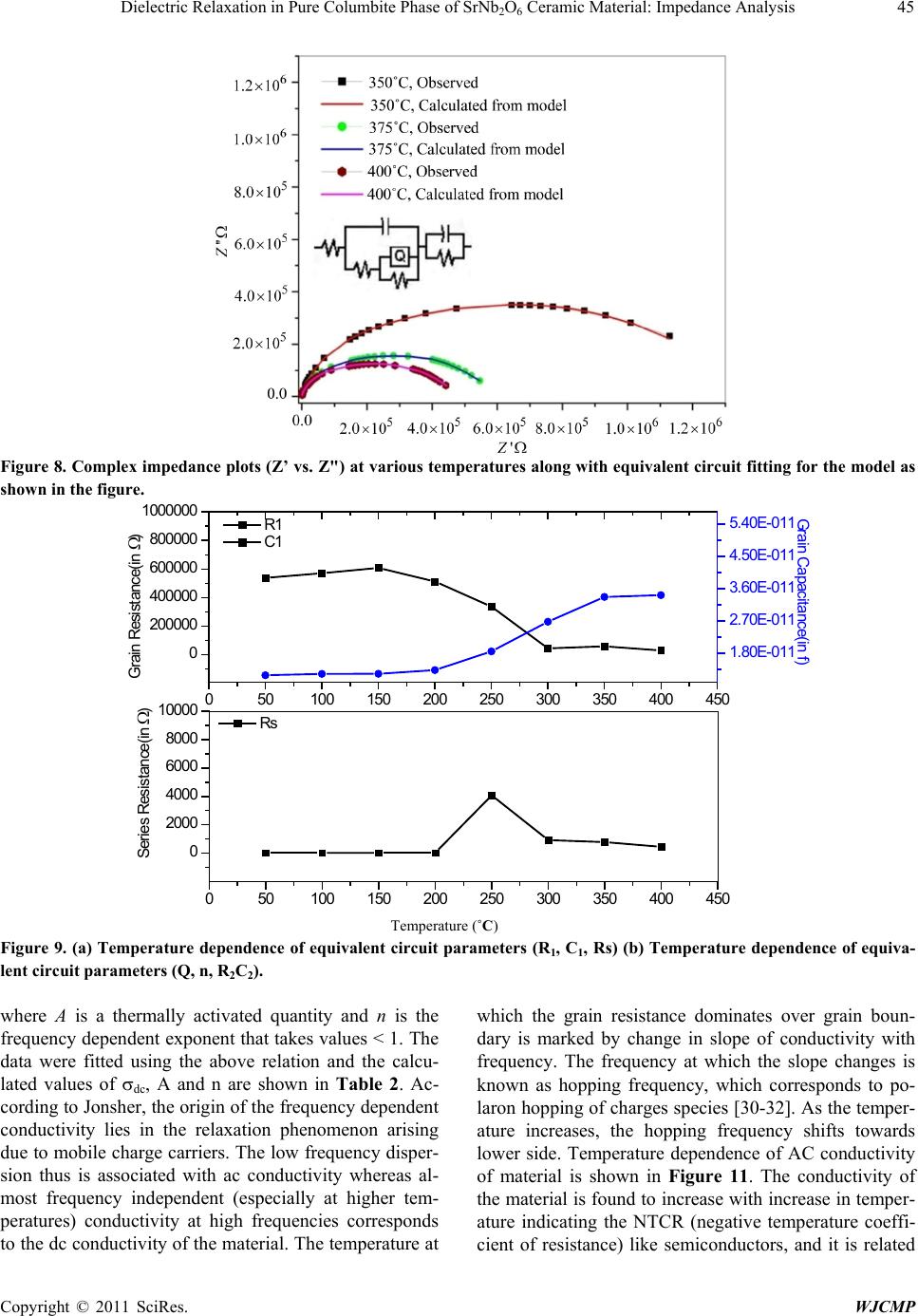

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
45
Figure 8. Complex impedance pl ots (Z’ vs. Z") at various temperatures along with equivalent circuit fitting for the model as
shown in the f i gur e.
Figure 9. (a) Temperature dependence of equivalent circuit parameters (R1, C1, Rs) (b) Temperature dependence of equiva-
lent circuit parameters (Q, n, R2C2).
where A is a thermally activated quantity and n is the
frequency dependent exponent that takes values < 1. The
data were fitted using the above relation and the calcu-
lated values of σdc, A and n are shown in Table 2. Ac-
cording to Jonsher, the origin of the frequency dependent
conductivity lies in the relaxation phenomenon arising
due to mobile charge carriers. The low frequency disper-
sion thus is associated with ac conductivity whereas al-
most frequency independent (especially at higher tem-
peratures) conductivity at high frequencies corresponds
to the dc conductivity of the material. The temperature at
which the grain resistance dominates over grain boun-
dary is marked by change in slope of conductivity with
frequency. The frequency at which the slope changes is
known as hopping frequency, which corresponds to po-
laron hopping of charges species [30-32]. As the temper-
ature increases, the hopping frequency shifts towards
lower side. Temperature dependence of AC conductivity
of material is shown in Figure 11. The conductivity of
the material is found to increase with increase in temper-
ature indicating the NTCR (negative temperature coeffi-
cient of resistance) like semiconductors, and it is related
050100 150 200 250 300 350 400 450
0
2000
4000
6000
8000
10000
Series Resistance(in
Ω
)
Temperatur e(
0
C)
Rs
050100 150 200 250 300 350 400 450
0
200000
400000
600000
800000
1000000 R1
C1
Grain Resistance(in
Ω
)
1.80E- 011
2.70E- 011
3.60E- 011
4.50E- 011
5.40E- 011
Grain Capacitance(in f)
Temperature (˚C)

46 Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
to the bound carriers trapped in the sample. The activa-
tion energy values at different frequencies have been
calculated assuming the Arrhenius behavior and summa-
rized in Table 3.
4. Conclusions
Phase pure columbite structure in SrNb2O6 is stabilized
through standard solid state reaction route by controlling
the processing parameters. The crystal structure is or-
thorhombic with unit cell parameter a = 11.011 Å, b =
7.7136 Å, c = 5.5969 Å. The experimental density is > 92%
and average grain size is 1.03 μm. Space charge accu-
mulation effect and free charge motion at low frequency
and higher temperature is established. The dielectric dis-
persion results fitted with Jonscher’s dielectric disp ersion
formalism gives coefficient a(T) and exponent n(T),
which show non-Debye type relaxation due to interaction
of charge careers at high temperatures. It also indicates
that conducting charges and free charges both contribute
to the dielectric relaxation in the material. Impedance
Figure 10. A.C conductivity as a function of (log) in SN.
Figure 11. Arrhenius plots of AC conductivity at different frequencies.

Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
47
Table 2. Calculated values of σdc, A and n by expression σac = σdc+ Aωn.
Temperature(˚C) σ dc A n
200
5.4203E-8
2.2404E-8
0.09656
225 2.6683E-9 1.7042E-10 0.50105
250
2.0532E-7
3.2756E-9
0.3982
275
2.7052E-7
1.7647E-7
0.23043
300 2.0637E-6 2.7393E-8 0.43341
325 6.3406E-7 1.1969E-11 0.90399
350
4.4132E-7
5.5385E-12
0.91078
375
7.4112E-7
7.7948E-11
0.72067
400 8.7604E-7 8.409E-11 0.71941
Table 3. Activation energy at different frequencies, calculated by linear fitting of temperature dependence of AC conductivity
data.
Frequency in (KHz) Temperature Range
Activation Energy (eV) 75˚C to 150˚C Activation Energy (eV) 175˚C to 325˚C
10
0.054
0.54
100
0.029
0.50
1000 0.14 0.46
spectroscopy is used to model the electrical properties of
the material showing the presence of porous material,
leakage capacitance and dominating grain response in the
material. AC conductivity exhibits dispersion at low fre-
quencies and follows Jonscher’s power law. The change
in the exponent n in ac conductivity dispersion term (Aωn)
reveals the nature of conductivity mechanics. The con-
duction mechanism changes from localized hopping to
free ion motion with increase in temperature and that the
conduction is a thermally activated process.
5. Acknowledgements
PKB would like to acknowledge Department of Science
& Technology, Government of India, New Delhi, for the
grants received under FIST program and University
Grants Commission, New Delhi for Major Research Pro-
ject Grant No. F-16/24-2004
REFERENCES
[1] K. Brandt and A. K emi, “X-Ray Studies on ABO4 Com-
pound Rutile Type and A B2O6 Columbite T ype,” Mineral.
Geol., Vol. 17A, No. 15, 1943.
[2] H. J. Goldschmidt, “An X-Ray Investigation of Systems
between Niobium Pentaoxide and Certain Additional
Oxides,” Metallurgia, Vol. 62, 1960, pp. 211-218.
[3] F. Laves, G. Bayer and A. Panagos, Schweiz Mineral
Petrogr. Mitt., Vol. 43, 1963, p. 217.
[4] H. Brusset, R. Mahe and U. Aung Kyi, “Etude de ni-
obates divalents binaires et ternaires a l'etat solide,” Ma-
terials Research Bulletin, Vol. 7, No. 10, 1972, pp. 1061-
1073. doi:10.1016/0025-5408(72)90158-4
[5] I. Yaeger, A. H. Morrish and B. M. Wanklyn, “Magneti-
zation Studies in Transition-Metal Niobates: I. NiNb2O6,”
Physical Review B, Vol. 15, No. 3, 1977, pp. 1465-1476.
doi:10.1103/PhysRevB.15.1465
[6] I. Yaeger, I. Maartense and B. M. Wanklyn, “Field-In-
duced Magnetic Transitions of CoNb2O6 in the Ordered
State,” Solid State Communications, Vol. 21, No. 1, 1977,
pp. 93-96. doi:10.1016/0038-1098(77)91485-5
[7] I. Yaeger, A. H. Morrish, B. M. Wanklyn and B. J. Gar-
rard, “Magnetization Studies in Transition-Metal Ni-
obates. II. FeNb_ {2} O_ {6},” Physical Revie w B, Vol.
16, 1977, p. 2289. doi:10.1103/PhysRevB.16.2289
[8] K. N. Singh and P. K. Bajpai, “Synthesis, Characteriza-
tion and Dielectric Relaxation of Phase Pure Columbite
MgNb2O6: Optimization of Calcination and Sinterin,”
Physica B, Vol. 405, No.1, January 2010, pp. 303-312.
[9] H. Brusset, M. Gillier-Pandraud and S. D. Voliotis,
“Etude de systemes binaires et pseudo-binaires definis
entre Nb2O5 et PbO, SrO, BaO,” Materials Research
Bulletin, Vol. 6, 1971, p. 5.
[10] R. Roth, “Unit-cell Data of the Lead Niobate,
PbNb2O6,”Acta Crystallographica, Vol. 10, No. 6, 1957,
p. 437. doi:10.1107/S0365110X57001437
[11] H. J. Lee, K. S. Hong, S. J. Kim and I. T. Kim, “Effect of
Vibro-Milling Time on Phase Formation and Particle Size
of ZnNbO6 Nano-Powders,” Materials Research Bulletin,
Vol. 32, No. 7, 1997, pp. 847-855.
doi:10.1016/S0025-5408(97)00034-2
[12] R. C. Pullar, J. D. Breeze and N. Alford, “Characteriza-
tion and Microwave Dielectric Properties of M2+ Nb2O6
Ceramics,” Journal of the American Cerami c Soc iety, Vol.
88, No. 9, 2005, pp. 2466-2471.
doi:10.1111/j.1551-2916.2005.00458.x

48 Dielectric Relaxation in Pure Columbite Phase of SrNb2O6 Ceramic Material: Impedance Analysis
[13] Y. C. Zhang, Z. X. Yue, Z. Gui and L. T. Li, Material
Letters, Vol. 57, 2003, pp. 4531-4534.
[14] T. Kolodiazhnyi, A. Petric, A. Belous, O. V’yunov and O.
Yanchevskij, “Synthesis and Dielectric Properties of Ba-
rium Tantalates and Niobates with Complex Perovskite
Structure,” Journal of Materials Research, Vol. 17, No,
12, 2002, pp. 3182-3189. doi:10.1557/JMR.2002.0460
[15] A. Ananta, R. Brydson and N. W. Thomas, “Synthesis,
Formation and Characterisation of MgNb2O6 Powde r in a
Columbite-Like Phase,” Journal of the European Ceram-
ic Society, Vol. 19, No. 3, 1999, pp. 355-362.
doi:10.1016/S0955-2219(98)00206-4
[16] N. Natarajan, V. Samuel, R. Pasricha, V. Ravi, “A Co-
precipitation Technique to Prepare BaNb2O6,” Material
Science & Engoneering B, Vol. 117, No. 2, March 2005,
pp. 169-171. doi:10.1016/j.mseb.2004.11.009
[17] V. Ravi, “A Coprecipitation Technique to Prepare
SrNb2O6,” Material Characterization, Vol. 55, No. 1, Ju-
ly 2005, pp. 92-95. doi:10.1016/j.matchar.2005.04.002
[18] K. S. Rao, P. M. Krishan, D. M. Prasad and J. H. Lee,
“Influence of Samarium Substitution on Impedance Di-
electric and El ectromechanical Properties of
Pb(1-x)K2xNb2O6,” International Journal of Modern Phys-
ics B, Vol. 21, No. 6, 2007, pp. 931-945.
doi:10.1142/S0217979207036795
[19] K. S. Rao, D. M. Prasad, P. M. Krishna, B. H. Bindu and
K. Suneetha, “Correlation between Low Frequency Di-
electric Dispersion (LFDD) and Impedance Relaxation in
Ferroelectric Ceramic Pb2KNb4TaO15,” The Journal of
Materials Science, Vol. 42, 2007, p. 7363.
[20] L. Zhigao, J. P. Bonnet, J. Ravez and P. Hagenmuller,
“Correlation between Low Frequency Dielectric Disper-
sion (LFDD) and Impedance Relaxation in Ferroelectric
Ceramic P b2KNb4TaO15,” Solid State Ionics, Vol. 57, No.
3-4, October 1992, pp. 235-244.
doi:10.1016/0167-2738(92)90153-G
[21] T. A. Nealon, “Low-Frequency Dielectric Responses in
PMN-Type Ceramics,” Ferroelectrics, Vol. 76, 1987, pp.
371-382. doi:10.1080/00150198708016958
[22] A. K. Janscher, “The 'universal'dielectric response,” Na-
ture, Vol. 267, 1977, pp. 673-679. doi:10.1038/267673a0
[23] F. A. Kroger and H. J. Vink, “Relations between the
Concentrations of Imperfections in Crystalline Solids,”
Solid State Physics, Vol. 3, 1956, pp. 307-435.
doi:10.1016/S0081-1947(08)60135-6
[24] D. R. Chen and Y. G. Yen, Electro. Elementary Math,
Vol. 1, 1982, p. 25.
[25] A. R. West, D. C. Sinclair, N. Hirose, “Characterization
of Electrical Materials, Especially Ferroelectrics, by Im-
pedance Spectroscopy,” The Journal of Electroceramics.
Vol. 1, No.1, 1975, pp. 65-71.
doi:10.1023/A:1009950415758
[26] J. Ross Macdonald, “Impedance Spectroscopy: Empha-
sizing Solid Materials and Systems,” Wiley Intersicence
Publications, 1987.
[27] J. Maier, “The Polarization of Mixed Conducting SOFC
Cathodes: Effects of Surface Reaction Coefficient, Ionic
Conductivity and Geometry,” The Journal of the Euro-
pean Ceramic Society, Vol. 24, No. 6, 2004, pp. 1343-
1347.
[28] J. Maier, Solid State Ionics, Vol. 157, 2003, p. 327.
[29] A. K. Jonscher, “The 'universal'dielectric response,” Na-
ture, Vol. 267, 1977, pp. 673-679.
[30] D. C. Sinclair and A. R. West, “Impedance and Modulus
Spectroscopy of Semiconducting BaTiO3 Showing Posi-
tive Temperature Coefficient of Resistance,” Journal of
Applied Physics, Vol. 66, No. 8, 1989, pp. 3850-3857.
doi:10.1063/1.344049
[31] I. M. Hodge, M. D. Ingram and Q. A. R. West, “Imped-
ance and Modulus Spectroscopy of Polycrystalline Solid
Electr olytes,” Journal of Electroanalytical Chemistry,
Vol. 74, No. 2, 1976, pp. 125-143.
doi:10.1016/S0022-0728(76)80229-X
[32] A.K. Jonscher, “A New Understanding of the Dielectric
Relaxation of Solids,” Journal of Materials Science, Vol.
16, No. 8, 1981, pp. 2037-2060.
doi:10.1007/BF00542364