Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 633-645 doi:10.4236/am.2011.25084 Published Online May 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Uses of the Buys-Ballot Table in Time Series Analysis Iheanyi S. Iwueze1, Eleazar C. Nwogu1, Ohakwe Johnson2, Jude C. Ajaraogu3 1Department of Statistics, Federal University of Technology, Owerri, Nigeria 2Department of Mathematics and Statistics, Anambra State University, Uli, Nigeria 3Department of Mathematics and Statistics, Federal Polytechnic, Owerri, Nigeria E-mail: isiwueze@yahoo.com Received December 14, 2010; revised March 30, 2011; accepted April 3, 2011 Abstract Uses of the Buys-Ballot table for choice of appropriate transformation (using the Bartlett technique), assess- ment of trend and seasonal components and choice of model for time series decomposition are discussed in this paper. Uses discussed are illustrated with numerical examples when trend curve is linear, quadratic and exponential. Keywords: Buys-Ballot Table, Trend Assessment, Assessment of Seasonality, Periodic Averages, Seasonal Averages, Data Transformation, Choice of Model 1. Introduction A time series is a collection of observations made se- quentially in time. Examples occur in a variety of fields, ranging from economics to engineering and methods of analyzing time series constitute an important area of sta- tistics [1]. Time series analysis comprises methods that attempt to understand such time series, often either to un- derstand the underlying context of the data points (Where did they come from? What generated them?), or to make forecasts. Time series forecasting is the use of a model to forecast or predict future events based on known past events. Methods for time series analyses are often divided into three classes: descriptive methods, time domain methods and frequency domain methods. Frequency domain me- thods centre on spectral analysis and recently wavelet analysis [2,3], and can be regarded as model-free ana- lyses. Time domain methods [4,5] have a distribution- free subset consisting of the examination of autocorrela- tion and cross-correlation analysis. Descriptive methods [1,6] invo lve the separation of an observed time series into components representing trend (long term direction), the seasonal (systematic, calendar related movements), cyclical (long term oscillations or swings about th e trend) and irregular (uns ystematic, s hor t term fluctuations) components. The descriptive method is known as time series decomposition. If short period of time are involved, the cyclical component is superim- posed into the trend [1] and the observed time series , t X can be decomposed into the trend-cycle component 1, 2,,tn t M , seasonal component and the ir- regular/residual component . t S t t e tt Decomposition models are typically additive or multi- plicative, but can also take other forms such as pseudo- additive/mixed (combining the elements of both the ad- ditive and multiplicative models). Additive Model: t X MSe (1) Multiplicative Model: tttt X MS e tt (2) Pseudo-Additive/Mixed Model; tt X MSe (3) The pseudo-additive model is used when the original time series contains very small or zero values. For this reason, this paper will discuss only th e additive and mul- tiplicative models. As far as the traditional method of decomposition is concerned (to be referred to as the Least Squares Method (LSE)), the first step will usually be to estimate and eli- minate t M for each time period from the actual data either by subtraction for Equation (1) or division for Equation (2). The de-trended series is obtained as t X ˆt M for Equation (1) or ˆ tt X M for Equation (2). In the second step, the seasonal effect is obtained by esti- mating the average of the de-trended series at each sea- son. The de-trended, de-seasonalized series is obtained as t ˆ ˆ tt X MS for Equation (1) or ˆ ˆ ttt X MS for Equa- tion (2). This gives the residual or irregular component. Having fitted a model to a time series, one often wants to see if the residuals are purely random. For detailed dis-  I. S. IWUEZE ET AL. 634 t s cussion of residual analysis, see [4,7]. It is always assumed that the seasonal effect, when it exists, has periods. That is, it repeats after s time per iods. ,forall ts t SS (4) For Equation (1), it is convenient to make the further assumption that the sum of the seasonal components over a complete period is zero. 10 s tj j S (5) Similarly, for Equations (2) and (3), the convenient variant assumption is that the sum of the seasonal com- ponents over a complete period is s. 1 s tj j S (6) It is also assumed that the irregular component t is the Gaussian e 2 1 0,N white noise for Equation (1), while for Equation (2), is the Gaussian t e 2 2 N1, white noise. This paper discusses the uses of the Buys-Ballot table for 1) choice of appropriate transformations (using the Bartlett technique) 2) assessment of trend and seasonal components and 3) choice of model for time series de- composition. We describe in great detail the Buys-Ballot table in Section 2 for better understanding of the methods used to achieve these objectives. When any of the assumptions underlying the time se- ries analysis is violated, one of the options available to an analyst is to transform the study series. The choice of appropriate transformation for a study series using Buys- Ballot table is described in Section 3. The presence and nature of trend and seasonal component of a study series can be inferred from the plot and values of the periodic /annual and seasonal averages. Assessment of trend and seasonal component of the actual series from the Buys- Ballot table was discussed in Sections 4 and 5 respec- tively. A major problem in the use of the descrip tiv e time series analysis is the choice of appropriate model for time series decomposition. This problem was addressed using Buys-Ballot table in Section 6. Numerical exam- ples are also given to illustrate these uses. 2. Buys-Ballot Table A Buys-Ballot table summarizes data to highlight sea- sonal variations (Table 1). Normally, each line is one pe- riod (usually a year) and each column is a season of the period/year (4 quarters, 12 months, etc), A cell, ,i j, of this table contains the mean value for all observations made during the period i at the season j. To analyse the data, it is helpful to includ e the period and seasonal to tals .. and i TT j , period and seasonal averages .i X and . j X , period and seasonal standard deviations . ˆi and . ˆ j , as part of the Buys-Ballot table. Also included for purposes of analysis are the grand total , grand mean .. T .. X and pooled standard deviation .. ˆ .[8] cred- its these arrangements of the table to [9], hence the table has been called the Buys-Ballot table in the literature. For easy understanding of Table 1, we define the row and column totals, averages and standard deviations as follows: .1 1 .1 1 ,1,2,, ,1,2,, s iisj j m jisj i TX i TX j , , m s Table 1. Buys-Ballot Table. Season (j) Period (i) 1 2 …j … s i. T i. X . ˆi 1 1 X 2 X …j X … s X 1. T 1. X 1. ˆ 2 1 s X 2s X … s j X … 2 s X 2. T 2. X 2. ˆ 3 21 s X 22s X …2 s j X … 3 s X 3. T 3. X 3. ˆ … … … …… … … … … … i 11is X 12is X … 1isj X … 1iss X .i T .i X . ˆi … … … …… … … … … … m 11ms X 12ms X … 1msj X … ms X .m T .m X . ˆm .j T .1 T .2 T ….j T … . s T .. T - - .j X .1 X .2 X ….j X … . s X - .. X - . ˆj .1 ˆ .2 ˆ …. ˆj … . ˆ s - - .. ˆ Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL.635 formation can be a complex issue and the usual statistical technique used is to estimate both the transformation and . .... . 11 ... .. ... 2 .. 1 1 2 .. 1 1 2 .. 1 11 ,,1,2,,, ,1,2,,, , 1 ˆ,1,2,, 1 1 ˆ,1,2,, 1 1 ˆ1 ms i iji ij j j s ii isj j m jj isj i ms isj ij T TTTX im s TTT , X jsX n mmsms XXi m s ms X Xj s m XX n where ,1,2,, t X tn m is the number ois the observed value of the se- ries, f periods/years, s is the perio- le d seasonal indices from the chosen de- sc dicity, he total number of observations /samp size. Finally, Buys-Ballot table is used to estimate the trend component an and nms is t riptive time series model. This method, called Buys- Ballot estimation procedure uses the periodic means ., i X i 1, 2,,m and the overall mean .. X to es- timate the trend component. Seasonal means ., j X the overall mean are usedstimate the seasonal indices. The advantages of the Buys-t cedure are that 1) it computes trend easily, 2) gets over the problem of de-trending a series before computing the estimates of the seasonal effects and 3) estimates the error variance without necessarily decom- posing the series. For further details on the Buys-Ballot estimation procedure, see [10-14]. 3. Choice of Appropriate Tr 2, ,jm and1, to eBallo estimation pro ansformation es e measurement scale of a variable. Reasons for trans- Transformation is a mathematical operation that chang th formation include stabilizing variance, normalizing, re- ducing the effect of outliers, making a measurement scale more meaningful, and to linearize a relationship. For further details on reasons for transformation, see [3,14]. Many time series analyst assume no rmality and it is well known that variance stabilization implies normal- ity of the series. The most popular and common are the powers of transformations such as log , et X log , et X 1, t X 1, t X 2, t X 2 1t X . Selecting the best trans- required model for the transformed t X at th e sa me t i me [15]. [16] have shown how to apply Bartlett transformation technique [17] to time series data using the Buys-Ballot ta hms of the group sta ble and without considering the time series model struc- ture. The relation between variance and mean over sev- eral groups is what is needed. If we take random sam- ples from a population, the means and standard devia- tions of these samples will be independent (and thus un- correlated) if the population has a normal distribution [18]. Furthermore, if the mean and standard deviation are independent, the distribution is normal. [16] showed that Bartlett’s transformation for time se- ries data is to regress the natural logarit ndard deviations . ˆ,1,2,, iim against the natu- ral logarithms of the group means .,1,2,, i X im and determine the slope, , of the relationship. .. ˆ loglog error eie i X ) (7 For non-seasonal data that require transf split the observed time series ormation, we ,,1,2, t X tn chrono- logically into m fairly equal different parts and compute .,1,2,, i X im and . ˆi for the parts. For seasonal data with the length of the periodic itions the observed data into m periods or rows for easy application. [16] showed that Bartlett’s transformation may also be regarded as the power transformation 1 log ,1 et t X Y m interval, s, the Buys-Ballot table naturally part ,1 ,2,,i ,1 t X (8) Summary of transformations for various values of is given in Table 2. However, [16] concluded that it is better to use the estimated value of the slope, , rectly in the power transformation (Equation (8)) than to approximate to the known and popular logarithmic, uare root, inverse, inverse of the square root, squares and in- verse of the squares transformations. An example that requires logarithmic transformation is the Nigerian Stock Exchange (NSE) All di- sq Shares Index (1985 – 2005) that is listed as Appendix A [19]. Sum- mary of the regression analysis of ˆ logeI on log , ei X 1, 2,, 21i is given in Table 3. mation for some values of β. S/No 1 Table 2. Bartlett’s transfor 2 3 4 5 6 7 β 0 1/2 1 3/2 2 3 –1 Transformation No transformation t X loget X 1t X 1t X 2 1t X 2 t X Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL. 636 Table 3. Ression analysis of on egr ˆ gei. σlo log , . X1,2,L, ei i for various transformations of the Nigerian Stock Ex- change (NSE) All Shares Index (1985-2005). 21 testtfor ˆ1.0 Transformations 2 Regression equation R df valuet :Original t X ˆ log2.5797 1.0260log eie i X 0.94 19 0.44 log te YX tˆ log2.8857 0.2490log ei ei Y 0.02 19 N/A ˆ 1ˆ , 1.0260 tt WX ˆ log6.2186 0.0794log eie i W 0.00 19 N/A It is clear from Table 3 that we can approximate the value ofand the suitable trans- rm . Regression an ˆˆ 1.0260 to1.0 ation using Table 2 is t fo logYX tet alysis summaries for loget YX and ˆ 1, tt WX ˆ1.0260 able 3. The transforma- tion ˆ 1ˆ , 1.0260 tt WX srela- tionships between the stanions an /yearlyroupings. 4. Assessment of Trend are also given in T u dard rely rem deviat oves the d the means for the row g he time plot of a time series, according to [1] reveals describe the pattern in es, the time plot of the pe- d additive model) ulation of 100 values from the ad- T the nature of the trend which can e series. Among other featurth riodic means follows the same pattern as the plot of the entire series with respect to the trend. Therefore, instead of looking at the plot of the entire series, one may look at only the plot of the period/annual means in order to choose the appropriate trend. We use the following ex- amples to illustrate this. 4.1. Linear Trend he data of Table 4 (linear trend anT and Figure 1 is a sim itive model d ttt X abtS e (9) with 5.0,a 0.2,b 11.5,S 22.5,S 33.5,S 44.5S an . The dat d t e b a of Tabl eing Gau e 4 (linear ssian tr 0,1N white end and multiplica-noise tive mulat from ultiplicative model ttt odel) and Figure 2 is a simion of 100 values the m X abtS e (10) with 5.0,a 0.2,b 10.6,S 21.1,S30.9,S S and 4 noise1.4 . Listed t e being in Table 4 Gaussian are the 1.0,0.01 white eriodic/row means N p ., i1,2,, X im of a plottted data, while the s of thectual series and perians are Figures 12 he simula timeodic/row me shown in and , respectively. It is clear that the tim plot ofe .i X for a with linear trend curve mimics the time plot of the etire series arow av- erages dat nnd the .i X can therefore, be used to estimate trend. tire series can be d n p The estimate of the parameters of the trend of the en- etermined from the estimate of the trend of the periodic means by recognizing that periodic averages are centred at the midpoints of the periodic in- tervals. Thus, whilesuccessive values in the actual series are one unit of time apart starting from 1t, successive values ieriodic average series .i X are s units of tim e apart starting from 12ts . Thus, periodic averages are derived from the original series by transla- tion of the original series by a factor 12s and dilation by a factor s. That is, periodic averages, .,1,2,, i X im may be looked at as th e values of the original series at times ,1,2,, i ti m.t is, Tha .i iti. X Xabt (11) where 211 13 15 1 ,,,, 22 2 i ms sss t 1, 2, 3,, im 2, for , Hence, .1) 1 i s X (2 1() 2 '' i t i Xab s ab bsi abi (12) where 2 1 '2 s aab , 'bbs or 'bbs , 1 '2 s aab . As an illustration, we observe from Figure 1 that 4,s 0.8003,b 4.6971.a Hence, '0.8003bbs 4 0.2001, 'aa 14.69711 4 1 2bs 2 0.200 4.9972 . The estimate of the parameters of the trend of the en- tire series can be determined from the estimate of the trend of the periodic means in quadratic [12] and expo- nential [13] trend curves as shown below. Copyright © 2011 SciRes. AM 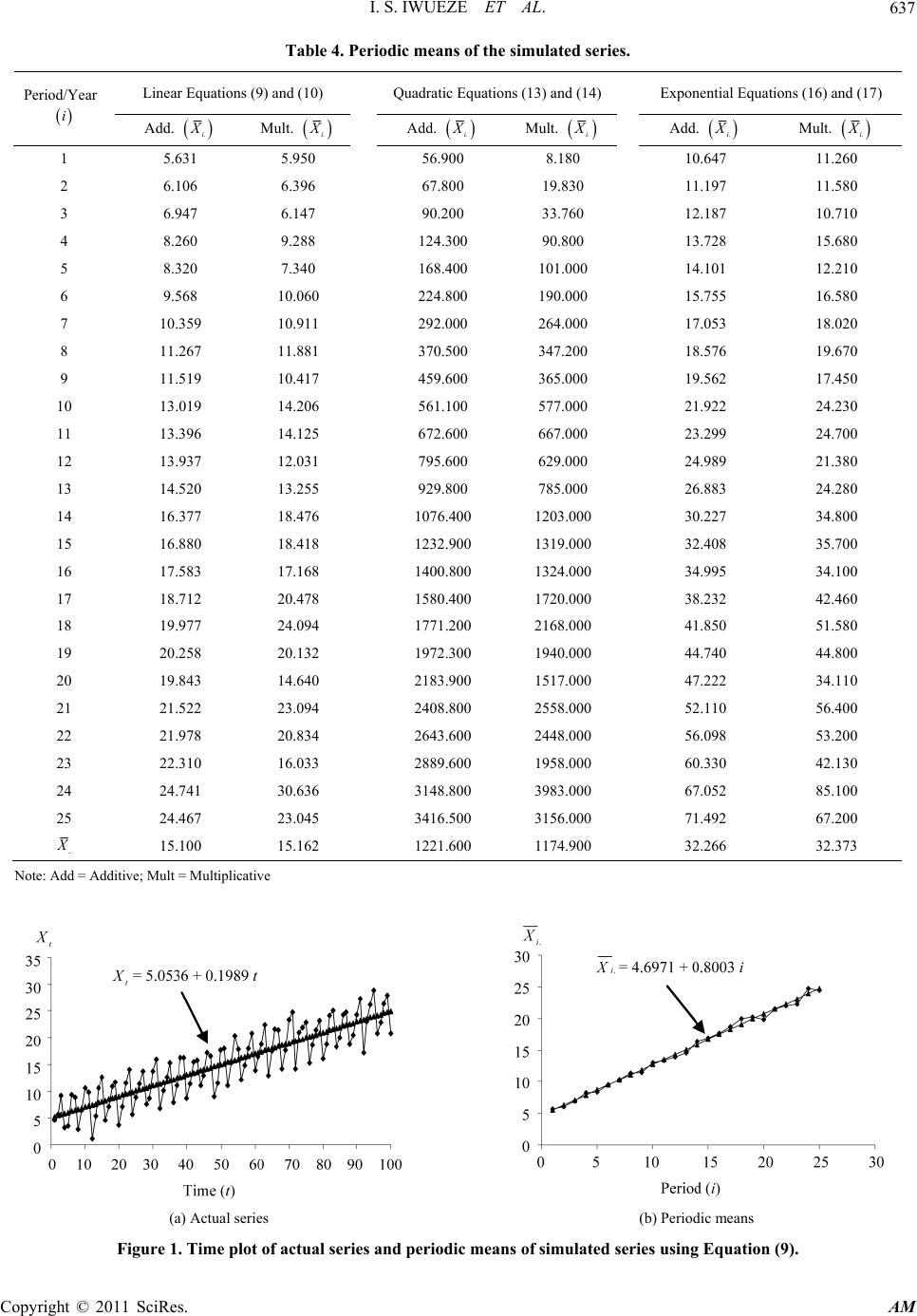 I. S. IWUEZE ET AL.637 able 4. Periodic means of Linear Equations (9) and (10) Quadraq(16) and ( 17) T tic E the simulated series. uations (13) and (14) Exponential Equations Period/Year i Add. i. X Mult. i. X Add. i. X Mult. i. X Add. i. X Mult. i. X 1 5.631 10.647 11.260 5.950 56.900 8.180 2 6.106 6.396 67.800 19.830 11.197 11.580 3 6.200 760 187 710 4 8.260 9.288 124.300 90.800 13.728 15.680 168. 101. 10.224. 190. 10.292. 264. 10. 11 13. 13 14. 1232. 1319. 1580. 1720. 947 6.147 90.33.12.10. 5 8.320 7.340 400 000 14.101 12.210 6 9.568 060 800 000 15.755 16.580 7 10.359 911 000 000 17.053 18.020 8 11.267 11.881 370.500 347.200 18.576 19.670 9 11.519 417 459.600 365.000 19.562 17.450 10 13.019 14.206 561.100 577.000 21.922 24.230 396 14.125 672.600 667.000 23.299 24.700 12 13.937 12.031 795.600 629.000 24.989 21.380 520 13.255 929.800 785.000 26.883 24.280 14 16.377 18.476 1076.400 1203.000 30.227 34.800 15 16.880 18.418 900 000 32.408 35.700 16 17.583 17.168 1400.800 1324.000 34.995 34.100 17 18.712 20.478 400 000 38.232 42.460 18 19.977 24.094 1771.200 2168.000 41.850 51.580 19 20.258 20.132 1972.300 1940.000 44.740 44.800 20 19.843 14.640 2183.900 1517.000 47.222 34.110 21 21.522 23.094 2408.800 2558.000 52.110 56.400 22 21.978 20.834 2643.600 2448.000 56.098 53.200 23 22.310 16.033 2889.600 1958.000 60.330 42.130 24 24.741 30.636 3148.800 3983.000 67.052 85.100 25 24.467 23.045 3416.500 3156.000 71.492 67.200 .. X 15.100 15.162 1221.600 1174.900 32.266 32.373 Note: Add = Additive; Mult =plicative Multi (a) Actual series (b) Periodic means Figure 1. Time plot of actual series and periodic means of simulated series using Equation (9). Copyright © 2011 SciRes. AM 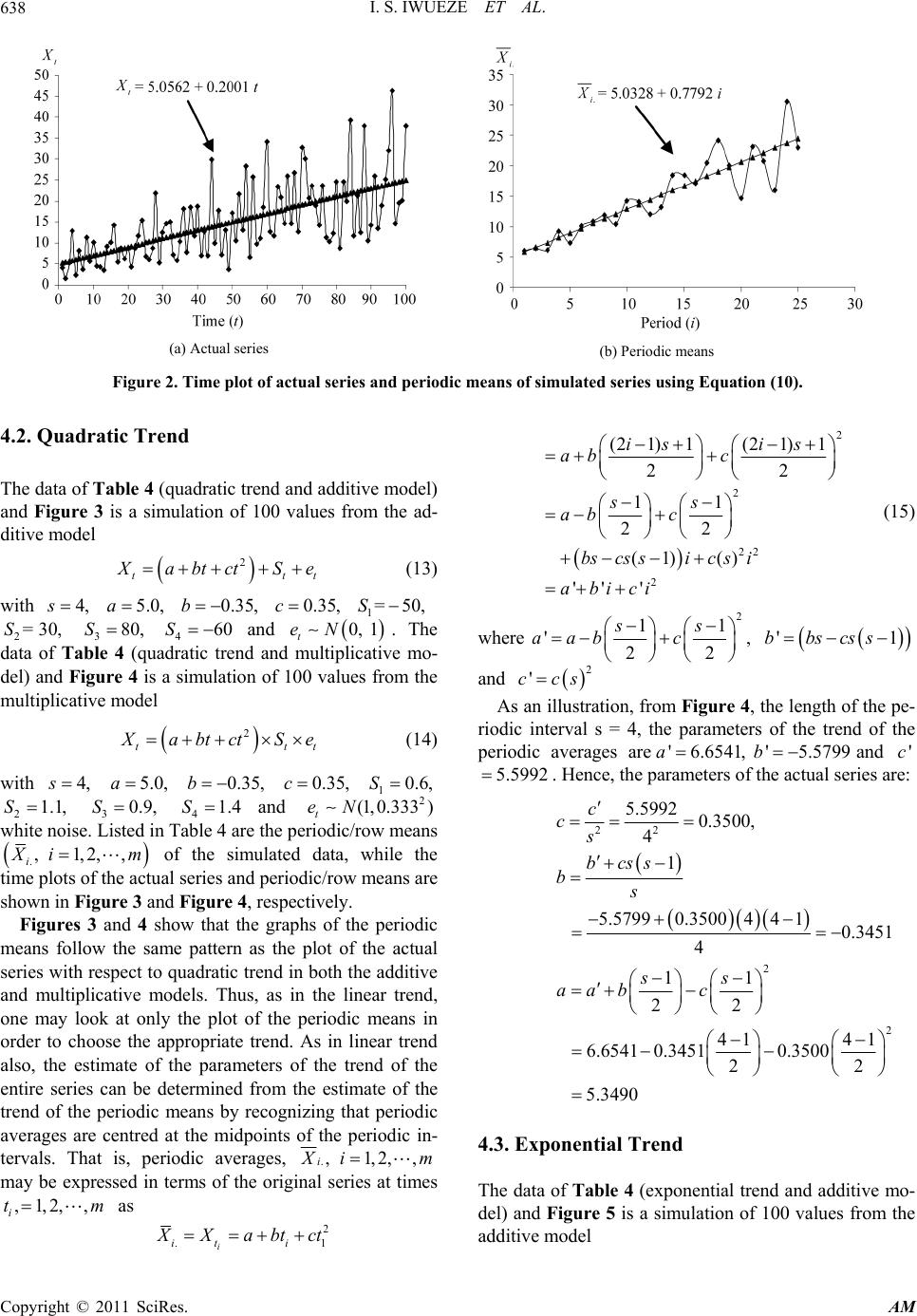 I. S. IWUEZE ET AL. 638 (a) Actual series (b) Periodic means Figure simulated seri (10). .2. Quadratic Trend The data of Table 4 (quadratic trend and additive model) and Figure 3 is a simulation of 100 values from the ad- ditive model t 2. Time plot of actual series and periodic means ofes using Equation 4 2 tt X abtctSe (13) with 4,s 5.0,a 0.35,b 0.35,c 1=50, S 2= 3S0, 3 S80, S460 and 0, 1. The plicative mo- t eN ultidata of Table 4 (quadratic trend and m del) and Figure 4 is a simulation of 100 values from the multiplicative model t 2 tt X abtct Se (1 ) 4 with 4, s 5.0,a 0.35,b 0.35,c 10.6,S 21.1, SS 30.9, 41.4S and le 4 are th 2 1,0.333) ow means ( t eN e periodic/rwhite noise. Listed in Tab .i,1,2,, X im of the simulated data, while the time plots of the actual series and periodic/row means are shown in Figure 3 and Figure 4, respectively. Figures 3 and 4 show that the graphs of the periodic means follow the same pattern as the plot of the actual series with respect to quadratic trend in b ultiplicative m, as in the ayook at only the plo periodic me means by recognizing that periodic averages are centred at the midpoints of tervals. That is, periodic averages, oth the additive and models. Thuslinear trend, one m lt of theans in order to choose the appropriate trend. As in linear trend also, the estimate of the parameters of the trend of the entire series can be determined from the estimate of the trend of the periodic the periodic in- .,1,2,, i X i m e expssed in terms of the original series at times as may bre ,1,2,, i tm 2 .1it i 2 2 22 2 (21) 1(21) 1 22 11 22 (1) () '' ' isis ab c ss ab c bscssic si abici (15) where 2 11 ', 22 ss aabc '1bbscss , the length of the pe- and Figure 4 riodic interval s = 4, the parameters of the trend of the periodic averag 2 'ccs As an illustration, from es are'6.65a i X Xabtct 41, '5.5799b and 'c 5.5992 . Hence, the parameters of the actual series are: 2 5.5992c cs 2 0.3500, 4 1bcss bs 2 2 5.57990.350044 10.3451 4 11 22 41 41 6.6541 0.34510.3500 22 5.3490 ss aab c The data of T (exponential trend and additive mo- del) and Figure 5 is a simulation of 100 v additive model 4.3. Exponential Trend able 4alues from the Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL.639 (a) Actual series ( Figure 3. Plot of actual series and periodic means of simulated series using Equation (13). b) Periodic means (a) Actual series (b) Periodic means eans of simulated series using Equation (14). Figure 4. Plot of actual series and periodic m (a) Actual series (b) Periodic means Figure 5. Actual series and periodic means of simulated series from Equation (16). Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL. 640 t ct tt X beS e (16) with 4,s 10,b 0.02,c 11.5,S 22.5,S e data of odel) and 3 S Ta 3.5, S ble 4 (expon 44.5 ential tr and t eN end and m 0, 1. Th ltiplicative mu Figure 6 is a simulation of 100 values from the multi- plicative model t ct tt X beSe (17) with 4, s 10,b 0.02,c 10.6,S 21.1,S 3 S noise. 0.9, 4 S Listed in Ta1.4 and ble 4 a 2 ,0.333 odic/row 1 t eN re the peri white means ., i X 1, of the act 2, ,im ual se of the sim ries and pe ulate riodic/row m d data, while the time eans are shown in plots Figures 5 and 6, respectively. The corresponding graphs of the actual series and th periodic means, sho 5 and 6, indicat clearly that the pattern in thehe periodic means is similar to that nd multiplicative models. As in linear and quadratic trend curves, the es timate of the parameters of the exponential trend of the entire se- ries can be determined from the estimate of the trend of the periodic means. That is, periodic averages, e e wn in Figures plot of t of the actual series in both the additive a ., i X i inal 1, 2,, m series at tim may be expressed in terms of the orig es as ,1,2,, i ti m (2 1)1 2 . 1() 2 i i is c ct it s ccsic i XXbebe beebe (18) where 1 2 ' s c bbe and 'ccs . As an illustration, from Figure 6 the length of the pe- riodic interval s = 4, the parameters of the trend of the periodic averages are and 0.0780c 9.9323,b . Hence, the parameters of the actual series are: 141 0.0195 22 0.0780 0.0195, 4 9.9323 10.2273 s c c cs bbe e 5. Assessment of Seasonal Component The seasonal component consists of effects that are rea- sonably stable with respect to timing, direction and mag- nitude. Seasonality in a time series can be identified from the time plot of the entire series by regularly spaced peaks and troughs which have a consistent direction and approximately the same magnitude every period/year, r lative to the trend. onal effect, the overall average e- For time series which contain a seas .. X and the seasonal average ., j X 1, 2,,js the effects either as a of the Buys-Ballot table are used to assess difference ...j X X or as a ratio ...j X X sonal averages a . That is, the deviations of the differences sea- nd the overall average (additive model) from zero or the ratios of the seasonal averages to the overall average from unity (multiplicative model) is used to assess the presence of seasonal effect. The wider the deviations, the greater the seasonal effect. This is illustrated below with stimulated time series data for the additive and multiplicative models when trend-cycle components are assumed 1) linear (Equations (9) and (10), respectively) 2) quadratic (Equations (13) and (14), respectively) and 3) exponential (Equation s (16) and (17), respectively). The assessed values of the se a- (a) Actual series (b) Periodic means ns of simulated series from Equation (17). Figure 6. Actual series and periodic mea Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL.641 sonal effects from these series are given in Table 5 while rresponding in Figures 7, 8 and their cographs enare giv respectively. As Table 5 and Figures 7, 8 and 9 show, 9 the patterns of the deviations ...j X X (additive model) of the seasonal averages (. j X ) from the overae (ll averag .. X ) and ratios ..j. X X (multiplicative model) mim- ics/follow those of the actual seasonal indices j S used in the simulation in all series. Thus, an analyst interested in studying the seasonal effect in any study series only eeds to look at either n..j. X X or ..j. X X to deter- ive test mine if there is seasonal effect or not. However, this should not be used as a conclus for the presence of or otherwise of seasonal effect in a study series. The use of seasonal averages to measure seasonal effect is most appropriate in a series with no trend. When trend dominates other components in any series, the true seasonal effect may be visible from ...j X X or ...j X X. Therefore, this assessment pro- cedure should be used with gr eat caution. 6. Choice of Appropriate Model te multiplicative ular varia change as hen the origi- na parameters of the Buys-Ballot table? The relationship between the seasonal means Traditionally, the ime plot of the entire series is usd to make the appropriate choice between the additive and models. In some time series, the amplitude of both the seasonal and irregtions do not the level of the trend rises or falls. In such cases, an additive model is appropriate. In many time series, the amplitude of both the seasonal and irregular variations increases as the level of the trend rises. In this situation, a multiplicative model is usually appropriate. The multiplicative model cannot be used w l time series contains very small or zero values. This is because it is not possible to divide a number by zero. In these cases, a pseudo-additive model combining the ele- ments of both the additive and multiplicative models is used. How can an appropriate model be obtained from the .,1,2,, j X js and the Table 5. Actual values of seasonal effects j S , deviations of seasonal averages from the overall averages . j.. X X and ratios of seasonal averages to the overall averages . j.. X X for the simulated series. Linear Quadratic Exponential Additive Equation (9) Multiplicative Equation (10) Additive Equation (13) Multiplicative Equation (14) Additive Equation (16) Multiplicative Equation (17) Season j j S ..j XX .j S ..j XX .j S..j XX.j S..j XX. j S ..j. X X j S ..j XX. 1 –1.5 –1.71 0.61 0.62 –50–103.0 0.60.60 –0.6–1.47 0.6 0.61 2 2.5 2.24 1.08 1.01 30 12.00 1.10.99 1.1 0.62 1.1 1.01 3 3.5 3.47 0.93 0.90 80 97.00 0.90.90 0.9 1.09 0.9 0.89 4 –4.5 –4.01 1.38 1.47 –60–7.00 1.41.51 –1.4–0.24 1.4 1.50 (b) Multiplicative model effects when trend is linear. (a) Additive model Figure 7. Assessment of seaso nal Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL. 642 (a) Ad ditidel ve mo( Mcatil re 8ssment oason wn tr qdratic. b)ultiplive mode Figu. Assef seal effectheend isua (a) Additive model (b) Multiplicative model Fi l. seasonal standard deviations gure 9. Assessment of seasonal effect when trend is exponentia . ˆ,1,2,, jjs odel. An additive m l standard deviations ase relative to any increase eans. On the other ha appropriate when th ow appreciable increa se/decrease in the seasonal strated in Table 6 for odels. Time plots of gives an indication of the desired model is appropriate when the seasona show no appreciable increase/decre or decrease in the seasonal mnd, a multiplicative model is usuallye sea- sonal standard deviations shse/de- crease relative to any increa means. This is vividly demonaddi- tive and multiplicative m. j X and . ˆ,(1,2, ,) jjs for values of Table 6 are given in Figures 10 th 12 . As Tab les 6 an d Figures 10 through 12 show, the o servations are true furves and for both additive and multiplicative models. For the multiplicative model, the plot of standard deviation, rough b- or all trending c (. ˆ j ) clearly show appreciable increase or decrease as the seasonal averages ) change. For the additive model, the plot of (. ˆ j ) of sea- (. j X show no appreciable change relative to the plot sonal ave rages (. j X ) in all the series. However, as earlier, when trend dominates other components, the sea sonal standard deviations may not follow the observed pattern and therefore, may not be used effectively for choice of appropriate model for decomposition. Therefore, the use of the plot of the seasonal averages and standard deviations as basis for the choice of appropriate model should be done wi noted - th great care. Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL.643 Tab ies. Linear Quadratic Exponential le 6. Seasonal means and standard deviations for the simulated ser Additive Equation (9) Multiplicative Equation (10) Additive Equation (13)Multiplicative Equation (14) Additive Equation (16) Multiplicative Equation (17) Season j .j X ˆj .j X ˆj .j Xˆj .j Xˆj .j X ˆj .j X ˆj 1 13.40 6.05 9.41 5.13 1119103470870730.8 17.95 19.61 13.28 2 17.34 5.94 15.25 7.89 123410541161106832.8818.14 32.56 20.08 3 18.57 6.07 13.7 7.83 1319107410581113c 18.72 28.68 21.11 4 11.09 5.84 22.29 10.55 121510941772174032.0318.88 48.64 31.8 (a) Additive model b) Multiplicative model ( Figure 10. Line plot of .j X and ˆ .j σ for simula ted data when trend is linear (Equations 9 and 10). (a) Additive m odel (b) Multiplicativeodel Figure 11. Seasonal means m .j X ˆ j σ and standarviations d deof simulated series from quadre 14). atic trnd (Equations 13 and Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL. 644 (a) Additive model (b) Multiplicative model Figure 12. Seasonal means .j X and standard deviations ˆ j σ of simulated series from exponential trend. 7. Conclusions This paper has examined four uses of the Buys-Ballot table. Uses examined in detail include 1) data transfor- mation 2) assessment of trend 3) assessment of seasonal- ity and 4) choice of model for decomposition. Use of Buys-Ballot table for the estimation of trend and compu- tation of seasonal indices was not discussed in details. For data transformation, the relationship between period /annual averages and standard deviations was used. As- sessment of trend is based on the period/annual averages while the assessment of the seasonal effect is based on the seasonal and overall averages. The choice of appro- priate model for decomposition is based on the seasonal averages and standard deviations. 8. References lysis o tion,” Chapman and Hall/CRC Press, Boca Raton, 2004. [2] D. B. Percival and A. T. Walden, “Wavelet Methods for Time Series Analysis,” Cambridge University Press, Cambridge, 2000. [3] M. B. Priestley, “Spectral Analysis and Time Series Analysis,” Academic Press, London, Vols. 1-2, 1981. [4] G. E. P. Box, G. M. Jenkins and G. C. Reinsel, “Time Series Analysis, Forecasting and Control,” 3rd Edition, Prentice-Hall, Englewood Cliffs, 1994. [5] W. W. S. Wei, “Time Series Analysis: Univariate and Multivariate Methods,” Addison-Wesley, Redwood City, 1989. [6] M. G. Kendal and J. K. Ord, “Time Series,” 3rd Edition, Charles Griffin, London, 1990. [7] G. M. Ljung and G. E. P. Box, “On a Measure of Lack of Fit in Time Series Models,” Biometrika, Vol. 65, No. 2, 1978, pp. 297-303. doi:10.1093/biomet/65.2.297 [8] H. Wold, “A Study in the Analysis of Stationary Time Series,” 2nd Edition, Almqrist and Witsett, Stockholm, 1938. [9] C. H. D. Buys-Ballot, “Leo Claemert Periodiques de Temperature,” Kemint et Fills, Utrecht, 1847. [10] I. S. Iwueze and A. C. Akpanta, “Effect of the Logarith- mic Transformation on the Trend-Cycle Component,” Journal of Applied Science, Vol. 7, No. 17, 2007, pp. 2414-2422. [11] I. S. Iwueze and E. C. Nwogu, “Buys-Ballot Estimates for Time Series Decomposition,” Global Journal of Mathematics, Vol. 3, No. 2, 2004, pp. 83-98. [12] I. S. Iwueze and J. Ohakwe, “Buys-Ballot Estimates When Stochastic Trend is Quadratic,” Journal of the Ni- gerian Association of Mathematical Physics, Vol. 8, 2004, pp. 311-318. [13] I. S. Iwueze and Journal of the Nigerian Association of Mathematical Physics, Vol. 9, 2005, pp 357-366. [14] I. S. Iwueze, E. C. Nwogu and J. C. Ajaraogu, “Properties of the Buys-Ballot Estimates When Trend-Cycle Com- ponent of a Time Series is Linear: Additive Case,” Inter- national Journal of Methematics and Computation, Vol. 8, No. S10, 2010, pp. 18-27. [15] G. E. P. Box and D. R. Cox, “An Analysis of Transfor- mations,” Journal of the Royal Statistical Society, Series B, Vol. 26, No. 2, 1964, pp. 211-243. [16] A. C. Akpanta and I. S. Iwueze, “On Applying the Bart- lett Transformation Method to Time Series Data,” Jour- nal of Mathematical Sciences, Vol. 20, No. 3, 2009, pp. 227-243. [17] M. S. Bartlett, “The Use of Transformations,” Biometrika, Vol. 3, 1947, pp. 39-52. [1] C. Chatfield, “The Anaf Time Series: An Introduc-Exponential and S-Shaped Curves, for Time Series,” E. C. Nwogu “Buys-Ballot Estimates for Copyright © 2011 SciRes. AM  I. S. IWUEZE ET AL.645 [18] R. V. Hogg and A. T. Craig, “Introduction to Mathe- matical Statistics,” 4th Edition, MacMillan Publishing Company, New York, 1978. [19] Central Bank of Nigeria, The Statistical Bulletin, Vol. 18, 2007. Appendix All Shares Index of the Nigerian Stock Exchange (1985-2005) Month .i X . ˆi Year Jan. Feb. Mar. Apr. May June July Aug. Sept. Oct. Nov. Dec. 1985 111.3 112.2 113.4 115.6 116.5 116.3117.2117.0116.9119.1124.6 127.3 117.34.7 1986 134.6 139.7 140.8 146.2 144.2 147.4150.9151.0155.0160.9163.3 163.8 149.89.5 1987 166.9 166.2 154.2 196.1193.4193.0194.9176.917.9 1988 .1 615.9 256.9 257.5 257.1 259.2269. 0 349.3 356.0 362.0 382.3 417.4445.63.1 6.2 6298.5 6113.9 6033.9 5892.15817. 5494.8 5376.5 5456.2 5315.7 5315.7 5977. 3 20128.9 15560.02502.0 161.7 157.5 154.8193.4 190.9 190.8 191.4 195.5 200199.2 206.0211.5217.224.1228.5231.4 233.6 210.8 1989 239.7 251.0 2281.0279.9298.4311.2 325.3 273.926.1 4463.6468.2480.3502.6 513.8 423.71990 343. 1991 528.7 557.0 601.0 625.0 649.0 651.868 1992 794.0 810.7 839.1 844.0 860.5 870.8879 1993 1113.4 1119.9 1130.5 1147.3 1186.9 1187.5118 1994 1666.3 1715.3 1792.8 1845.6 1875.5 1919.1192 1995 2285.3 2379.8 2551.1 2785.5 3100.8 3586.5431 1996 5135.1 5180.4 5266.2 5412.4 5704.1 5798.759 1997 7268.3 7699.3 8561.4 8729.8 8592.3 8459.38148. 8.0712.1737.3757.5769.0 783.0 671.683.7 .7969.31022.01076.51098.0 1107.6 931.0117.0 0.81195.51217.31310.91414.5 1543.8 1229.0131.1 6.31914.11956.02023.42119.3 2205.0 1913.2154.5 4.34664.64858.15068.05095.2 5092.2 3815.01149.0 19.46141.06501.96634.86775.6 6992.1 5955.0652.0 87682.07130.86554.86395.8 6440.5 7639.0876.0 05795.75697.75671.05688.2 5672.7 5961.9293.61998 6435.6 642 1999 94964.44946.24890.85032.55133.2 5266.4 5264.2304.3 77394.17298.97415.37164.4 8111.0 6701.0778.02000 5752.9 5955.7 5966.2 5892.8 6095.4 6466.76900. 2001 8794.2 9180.5 9159.8 9591.6 10153.8 10937.310576.410329.010274.211091.411169.6 10963.1 10185.0825.0 8.212327.911811.611451.511622.7 12137.7 11632.0637.0 62.0 15426.016500.518743.5 19319. 2002 10650.0 10581.9 11214.4 11399.1 11486.7 12440.71245 2003 13298.8 13668.8 13531.1 13488.0 14086.3 14565.5139 2004 22712.9 24797.4 22896.4 25793.0 27730.8 28887.427062.123774.322739.723354.823270.5 23844.5 24739.02131.0 2005 23078.3 21953.5 20682.4 21961.7 21482.1 21564.821911.022935.424635.925873.824635.9 24085.8 22877.01563.0 .j X 5533.1 5648.2 5579.6 5818.3 5981.3 6216.66099.86077.66129.16357.26329.4 6472.8 6020.3 . ˆj 6955.2 7116.6 6743.2 7281.1 7539.4 7782.97503.37246.97369.47761.47609.5 7723.7 7235.3 Source: Statistical Bulletin of the Central Bank of Nigeria (CBN, 2007) Copyright © 2011 SciRes. AM |

