Applied Mathematics, 2011, 2, 625-632
doi:10.4236/am.2011.25083 Published Online May 2011 (http://www.SciRP.org/journal/am)
Generalized Thermo Elasticity in an Infinite
Nonhomogeneous Solid Having a Spherical Cavity Using
DPL Model
Ahmed Elsayed Abouelrega
Department of Mat hematics, Fac ul t y of Sci ence, Mansoura Universit y , Mansoura, Egypt
Received January 2, 2011; revised March 39, 2011; accepted April 2, 2011
Abstract
The induced temperature, displacement, and stress fields in an infinite nonhomogeneous elastic medium
having a spherical cavity are obtained in the context dual-phase-lag model. The surface of the cavity is stress
free and is subjected to a thermal shock. The material is elastic and has an in homogeneity in the radial direc-
tion. The type of non homogeneity is such that the elastic constants, thermal conductivity and density are
proportional to the nth power of the radial distance. The solutions are obtained analytically employing the
Laplace transform technique. The numerical inversion of the transforms is carried out using Fourier series
expansions. The stresses, temperature and displacement are computed and presented graphically. A com-
parison of the results for different theories is presented.
Keywords: Generalized Thermo Elasticity, Nonhomogeneous, Functionally Graded Material (FGM),
Laplace Transform, Three-Phase-Lag Model
1. Introduction
The increasing use of anisotropic material in engineering
application has resulted in considerable research activity
in this area in recent years. An understanding of thermally
induced stresses in an isotropic bodies is essential for a
comprehensive study of their response due to an exposure
to a temperature field, which may in turn occurs in service
or during the manufacturing stages. For example, during
the curing stages of lament wound bodies, thermal str-
esses may be induced from the heat buildup and cooling
processes. The level of these stresses may be exceeding
the ultimate strength.
The generalized thermoelasticity theories have been
developed with the aim of removing the paradox of infi-
nite speed of heat propagation inherent in the classical
coupled dynamical thermo elasticity theory (C-D), see
Biot [1]. Many new theories have been proposed to take
care of this physical absurdity. Lord and Shulman [2] (L
-S) first modified Fourier's law by introducing the term
representing the thermal relaxation time. The heat equa-
tion associated this theory is a hyperbolic type and hence,
eliminates the paradox of infinite speed of propagation.
Following Green and Lindsay [3] (G-L) developed a more
general theory of thermoelasticity, in which Fourier's law
of heat conduction is unchanged, where as the classical
energy equation and Duhamel-Neumann's relations are
modified by introducing two constitutive constants having
the dimensions of time.
Recently, relevant theoretical developments on this su-
bject are due to Green and Naghdi [4] (G-N) to establish a
theory of thermoelasticity that permits propagation of the-
rmal waves at a finite speed, where its evolution equations
are hyperbolic. An important characteristic feature of this
theory, which is not present in other thermoelastic theo-
ries, is that this theory does not accommodate dissipation
of thermal energy.
Tzou [5,6] proposed the dual-phase-lag (DPL) model,
which describes the interactions between phonons and
electrons on the microscopic level as retarding sources
causing a delayed response on the macroscopic scale. For
macroscopic formulation, it would be convenient to use
the DPL mode for investigation of the micro-structural
effect on the behavior of heat transfer. The physical
meanings and the applicability of the DPL mode have
been supported by the experimental results [7]. The
dual-phase-lag (DPL) proposed by Tzou [7] is such a
modification of the classical thermoelastic model in

A. E. ABOUELREGA 626
which the Fourier law is replaced by an approximation to
a modified Fourier law with tow different time transla-
tions: a phase-lag of the heat flux q

and a phase-lag of
temperature gradient


. A Taylor series approximation
of the modified Fourier law, together with the remaining
field equations leads to a complete system of equations
describing a dual-phase-lag thermoelastic model. The
model transmits thermoelastic disturbance in a wave-like
manner if the approximation is linear with respect to q

and


, and 0 ≤


<q

; or quadratic in q

and li-
near in


, with q

>0 and


> 0. This theory is deve-
loped in a rational way to produce a fully consistent the-
ory which is able to incorporate thermal pulse transmis-
sion in a very logical manner.
Each of models has been introduced in the literature in
an attempt to eliminate shortcomings of the classical dy-
namical thermo elasticity such as: 1) infinite velocity of
thermoelastic disturbances, 2) unsatisfactory thermoelas-
tic response of a solid to short laser pulses, and 3) poor
description of thermoelastic behavior at low temperature
[17]. Attempts to present a theory of thermoelastic waves
that would be attractive to both the basic and applied re-
searchers have been continued in the literature to date.
Also, a stream of papers devoted to theoretical and ap-
plied aspects of the generalized thermoelasticity that
started with publications on the wave equation for a rigid
heat conductor in the 1940s has increased greatly to date.
Although the five theories are not the only ones that have
been proposed so far, they are, in the authors opinion, re-
presentative in discussing the subject [17].
Allam, et. al. [11] investigated the thermal stress dis-
tributions in a harmonic field for a homogeneous, iso-
tropic infinite body with a circular cylindrical hole based
on a Green and Naghdi theory. Sinha and Elsibai [10]
studied generalized thermoelastic interactions for an in-
finite body with a spherical cavity and for an isotropic
solid sphere. Mukhopadhyay [12] discussed the thermally
induced vibration in a homogeneous and isotropic un-
bounded body with a spherical cavity using the Green and
Naghdi model of thermo elasticity without energy dissi-
pation. Mukhopadhyay and Kumar [13] studied the
thermoelastic interactions in an unbounded elastic me-
dium with a spherical cavity in the context of four dif-
ferent theories of thermoelasticity, namely: the classical
coupled dynamical thermoelasticity, the extended ther-
moelasticity, the temperature-rate-dependent thermoelas-
ticity and the thermoelasticity without energy dissipation
in a unified way. Roychoudhuri [14] studied one-dimen-
sional thermoelastic wave propagation in an elastic half-
space in the context of dual-phase-lag mode.
Functionally graded materials (FGMs) are a type of
nonhomogeneous materials in which the composition
changes gradually with a corresponding change in the
properties. FGMs are usually designed to be used under
high temperature environments. Thermal shock loading
conditions may be involved with high thermal stresses
when a sudden heating or cooling happens. As a result,
thermal fracture problems may be usually met. Therefore,
it is significant to analyze the transient thermal fracture
behavior of FGMs.
Functionally graded material (FGM) as a new kind of
composites was initially designed as thermal barrier ma-
terials for aerospace structures, in which the volume fra-
ctions of different constituents of composites vary con-
tinuously from one side to another [15]. These novel non-
homogeneous materials have excellent thermo-mecha-
nical properties to withstand high temperature and have
extensive applications to important structures, such as
aerospace, nuclear reactors, pressure vessels and pipes,
chemicals plants, etc. The use of FGMs can eliminate or
control thermal stresses in structural components [16].
Laplace transform technique is used to solve the prob-
lem. The main difficulty encountered in solving problems
of coupled or generalized thermoelasticity theory is that
of inversion of the Laplace transforms used. This is
mainly due to the fact that the contour integral of Laplace
transforms complex inversion formula contains compli-
cated branch points in its integral. The inverse Laplace
transforms are obtained numerically using a method based
on Fourier expansion techniques.
The present paper is organized as follows. Section 2
describes the formulation of the problem and basic equa-
tions. Section 3 discusses the Laplace transform technique
and the solution in the transformed domain is obtained
using a potential function. Section 4 summarizes the in-
verse Laplace transforms using a numerical method based
on Fourier expansion techniques. The last section is de-
voted to the numerical example for finding the tempera-
ture, displacement and the stress. The numerical results
are presented graphically and compared it in the different
theories of thermoelasticity and discussed the differences
due to the presence of dual phase lags.
2. Mathematical Formulation of the Problem
and Basic Equations
We consider a nonhomogeneous thermal and mechanical
material properties in the radial direction infinite solid
having a spherical cavity of radius a. The surface of the
cavity is stress free and is suddenly heated and kept at
constant temperature. We also assume that neither the
body forces nor the heat sources are acting inside the
medium.
We use spherical polar coordinates 
,,r

 with the
origin at the center of the cavity and we consider those
thermoelastic interactions which are spherically symmet-
ric. It follows that all interactions considered depend on

A. E. ABOUELREGA627
the radial distance r and the time t then only the radial
component of the displacement and the nor-
mal stress components

,uurt
,
rr




''
12
C e

''
22
Ce


22
2,
will appear in the analysis.
The nonhomogeneous character of the material is dis-
cussed by considering that the elastic constants, density
and the thermal conductivity are given by some power law
of variation with radial distance r.
For a spherically orthotropic thermoelastic solid, the
constitutive equations will take the following forms:

1,ebT


'
23 2
Ce bT


'
'
11rr rr
Ce   (1)
12 rr
Ce

 (2)
where
'' '
1111 1
bC C

  '' '
212122
C'
223
C2 bC

 
in which ij Care elastic constants, Tis the temperature
excess over 0, and 1
T

,2

are the coefficients of linear
thermal expansion along the radial and tangential direc-
tions.
The equation of motion in absence of any body forces
becomes

2
2
2
rr u
rr t
 


rr 
  (3)
The non-zero components of strain are
,
u
ee


rr u
e
rr


 (4)
then the normal stresses are
''
1112 1
2,
rr uu
CCb
rr




'
T (5)
'''
122223 2
uuu
CCCb
rrr





'
T
0.
(6)
In an attempt to model ultrafast processes of thermoe-
lasticity Tzou (1997) proposed a dual-phase-lag model
(DPL) ofthermoelasticity in which the MaxwellCattaneo
equation is replaced by the relation
.
,
qq
qtqKTtTt t



 



 (7)
Equation (7) together with the energy balance equation
led to the heat conduction equation
2
'
10
2
2
2
2
1
1
qE
r
n
tCTbT
tr t
T
trK
tr r r



 


 

 







 


u
r



(8)
where q and tt

stand for the heat flux and temperature
gradient phase-lags, respectively, r
K
is the is coefficient
of thermal conductivity along radial direction,
E
C is
specific heat at constant strain,

is the density .
Clearly, a DPL model covers the hyperbolic L-S model
when 00
q
tt

, and 0t


.
We assume that the functionally graded spherical that
has nonhomogeneous thermal and mechanical properties
in the radial direction. In order to incorporate the non-
homogeneity of the material, we assumed to take the
following forms
'
0
nn n
ij ijr
CrCr KrK ,, 
0
, (9)
where 0

, 0
K
and ij are nonzero constants (they are
the values of in a homogeneous matter when
C
0n

).
Substituting from Equation (9) into Equations (5) and (6),
we obtain
11 12
2uu
C
rr
1
n
rr rC bT







(10)

12 22
u
23 2
nu
rCC CbT
rr








(11)
where
1111 122
2,bC C





212223 2
C C
12
bC

 
Using Equations (10) and (11), we have from Equation
(3) the displacement formulation of the equation of mo-
tion
 

2
1111122223
22
2
110
2
2
22
unu u
CC CCC
rr rr
TTu
bnbb
rr t

2
21 n






 





(12)
2
010
2
2
02
2
2
Tb
tr
1
qE n
tCTu
trr
t
TnT
Kt r
r




 


 








 









(13)
The problem is to solve Equations (12) and (13) subject
to the boundary conditions
1) Traction-free cavity surface


,0
rr at
 ,t0

 (14)
2) The surface of the cavity is considered to be main-
tained at a constant temperature To


0
,Tat T,t0

 (15)
The initial and regularity conditions may be put as
,0t,
Tu
Tu ar
rr



 

,




,0,,0,atTrt urtr

 (16)
The following non-dimensional quantities are intro-
duced as

A. E. ABOUELREGA 628

** *
,, ,
ii
r
rttt iq
aaa,,



  
** 2 11 11
001
,,
C T
Tuu
TaTb
 ,
C

  (17)
**
01 01
,.
rr
rr nn
rTbrTb


 


Using these non-dimensional variables, Equations (10)-
(13) take the form (dropping the asterisks for conven-
ience):
12
11
2
n
rr C
uu
r
rCr







T


(18)

22 232
12 1
nCC b
uu
rT
rCrb





 



 
(19)
22
222
2unuuuT T
mh
rrr r rrt
 

 
(20)
2
0
2
2
2
2
2
1
qn
tT
tr t
TnT
ttrr
r




 



 
 



 

 


 


u
r

(21)
where



12222312
11 1
21 22
,
nC CCnbb
mh
Cb
  

 

2
10 0
00
,
EE
bT K
CaC





3. Solution of the Problem
Applying the Laplace transform to Equations (18)-(21),
we get the field equations in the Laplace transform space
as
1112 1
d2
d
n
rr uu
rC CbT
rr





, (22)

22 232
12 1
d
d
nCC b
uu
rT
rCrb




 



(23)
2
2
2
d2d2
dd
d
ununuT
su
rr rrr
r


d
, (24)
2
22
2
d2d d2
dd d
nn
T
rrr r r





 

 u


(25)
where we assume and 0, 2hmn


21.
1
q
s
s
s





The boundary conditions in the Laplace transform
space read
 
1
1,,1, 0,
rr
Ts s
s


 (26)
while the regularity conditions are




,0,,0,atTrsursr .

 (27)
Taking d,
d
ur

 where

is the thermoelastic po-
tential function and introducing it in Equations (24) and
(25), we find


2
12
DD sT 

 (28)


22
12 12
DDT DD

   (29)
where
12
d2
,
dd
n
DD
rr

 
d
r
Eliminating from Equations (28) and (29), we get
T
 



22222
12 12
10DDs DDs  


 

(30)
Introducing


,1,2
i
mi into Equation (30) become




22
12 11220DD mDD m


 (31)
where


,1,2
i
mi are the positive solutions of the fol-
lowing characteristic equation




222 22
10msm   s

 
(32)
In order to transform Equation (31) into a normal
Bessell equation, a new dependant variable


r  is in-
troduced as


1/2n
rr 


Then, Equation (31) is rewritten as
22
2
22
d1d0,1, 2,
d di
mi
rr
rr
 

 

 (33)
where
1
2
n



The solution of

in will be the form


  
2
1/2
1
niiii
i
rr AKmrBImr





 (34)
where


i
K
mr

and


i
I
mr

are the modified Bessell
functions of order

of first and second kind respectively.
1
A
and 2
A
are independent of but depend on r
s
and
are to be determined from the boundary conditions. In the
case of spherical cavity the solution to be continuous
every where, we take equal to zero.
i
B

A. E. ABOUELREGA629
Using the relations between
 
,urTr and


r  ,
and using the recurrence relations of modified Bessell
functions, we obtain the solution for the displacement

ur and temperature

Tr as follows



 

1/2 2
1
1
12 2
2
n
iii
i
ur
r

i
A
nK mrmrKmr
r








(35)




2
1/2 22
1
nii i
i
TrrAms K mr






(36)
Substituting the above solutions for

ur and


Tr
in the relations (22) and (23), we obtain the following
solutions for rr

and



in the form

 

1/2 2
1
2
1
11
2
2
n
rr iii
i
r

1 i
A
LK mrmrKmr
rC






 (37)


 

1/2 22
56 21
2
1
11
4
4
n
iii ii
i
r
A
LmL KmrmrLKmr
rC









(38)
where

3


1
222
11 12
23422 242
L
Cnnnrs Cn  
 


211 1
22LCnC,
2
 
412222
22LCnCC,

 
22
312
22 23
43484
48 4
LC nnn
CC n




 
22
2
511 1
1
44
b
LrCCr
b
,
2
22
2
53 11
1
4b LL rCs
b
 .
In order to determine the parameters 1
A
and 2
A
, we
need to consider the boundary conditions (26), we t ge


21
22
1
ii i
i
Ams K m
s



, (39)

(40)
Solving (39) and (40), we obtain
 

2
11
1
20
iiii
i
ALK mmKm
 



1
A
and 2
A
as the
following
  
11221
12ALKmmKm
s
 



2
(41)
  
21111
12ALKmmKm
s
 












  
22
111221
22
2211111
2
2
msKmLKm mKm
msKmLKm mKm
 
 


 

2
Substituting the value of

1
A
and 2
A
from Equations
(4
deduced from
ou
1) and (42) yields the displacement, temperature and
thermal stresses in the transformed space.
The results for isotropic material can be
r problem by simply replacing 11 2,C

  12 ,C


22 23,CC





123bb 2t

  and r
K
K

win our calculation, here ,


are the Lame's constants,
t

is the coefficient of linear thermal expansion and
the thermal conductivity for the isotropic material.
Inversion of the Laplace Transforms
K
.
o obtain a solution of the problem in physical domain,
4
T
we adopt a numerical inversion method based on a Fourier
series expansion [9]. In this method, the inverse


gt of
the Laplace transform


gs is approximated by re-
lation
the
 
1
/
1
1
11
eRe e,0,
2
ct Nikt t
k
gc ik
g
tgc
tt




tt







 
(43)
where is a sufficiently large inte
o
N ger representing the
number f terms in the truncated infinite Fourier series.
N must chosen such that
1
/
1
1
eRee
ikt t ct ik
gc t



 







(44)
where 1

is a persecuted small positive number that
corresponds to the degree of accuracy to be achieved. The
parameter c is a positive free parameter that must be
greater than the real parts of all singularities of


g
s.
Two methods are used to reduce the total error. Firste
Korrecktur method is used to reduce the discretization
error. Next, the algorithm is used to reduce the truncation
error and therefore to accelerate convergence. The details
of these methods can be found in Honig and Hirdes [9].
The discretization error can be made arbitrarily small by
choosing the constant c large enough. The values of c
and 1 t are chosen according to the criteria outlined in [9].
Formla (43) was used to invert the Laplace transforms in
Equations (35)-(38), given the temperature, stress, and
displacement distribution numerically.
. Numerical Example and Dis
, th
cussion
tained in
u
5
ith the view of illustrating theoretical results obW

1
(42)
where
the preceding sections, we now present some numerical
results. The materials chosen for this purpose is single
crystal of magnesium, the physical data for which is given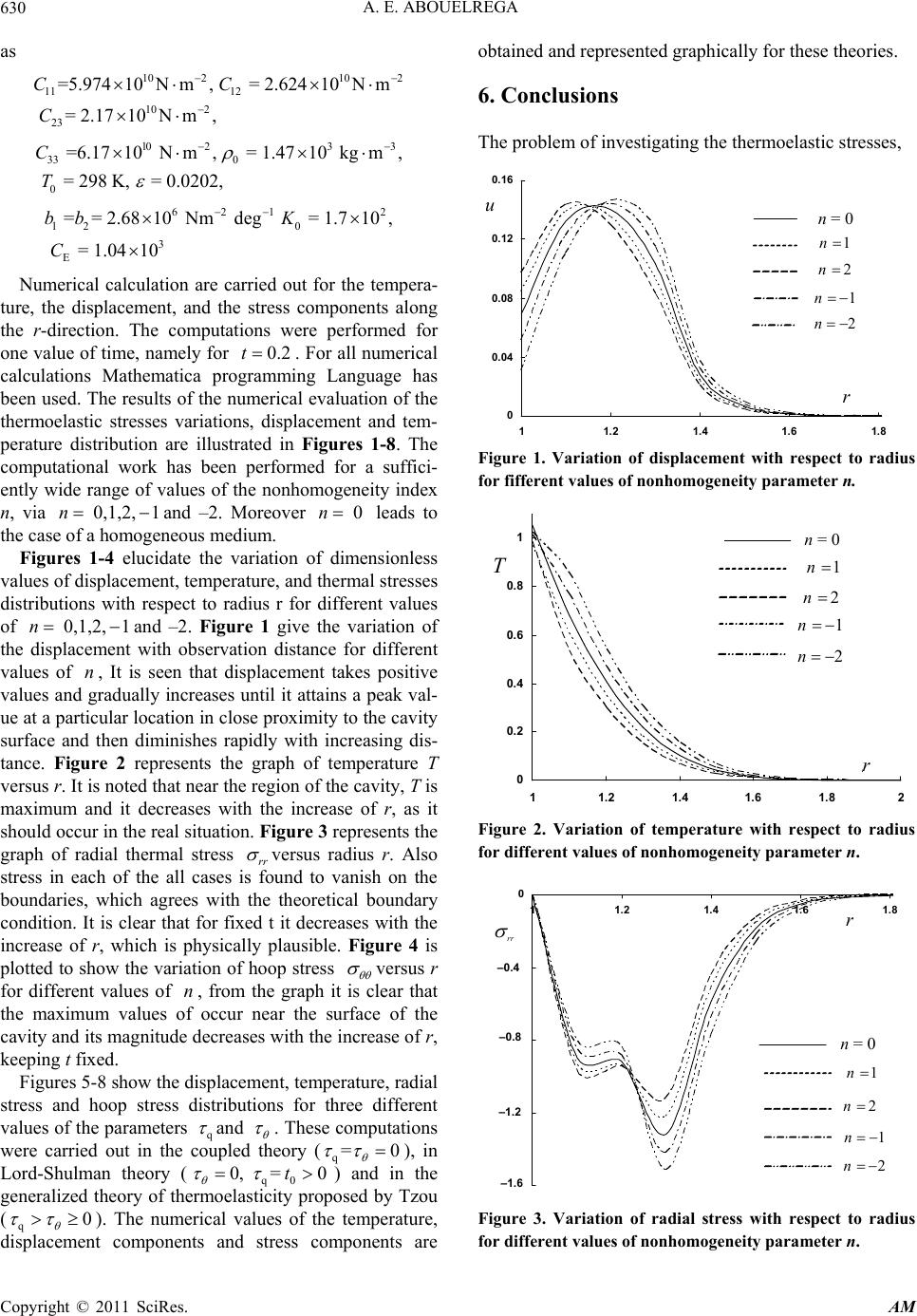

A. E. ABOUELREGA 630

2
Numerical calculation are carried out for the tempera-
tu
of a homoge
mensionless
va
as
10 2102
11 12
10 2
23
=5.97410Nm, = 2.62410Nm
= 2.1710Nm,
CC
C


 

l0 233
33 0
0
=6.1710Nm, = 1.4710kgm,
= 298 K, = 0.0202,
C
T



 
621
l2 0
3
E
== 2.6810Nm deg = 1.710,
= 1.0410
bb K
C



re, the displacement, and the stress components along
the r-direction. The computations were performed for
one value of time, namely for 0.2t. For all numerical
calculations Mathematica proing Language has
been used. The results of the numerical evaluation of the
thermoelastic stresses variations, displacement and tem-
perature distribution are illustrated in Figures 1-8. The
computational work has been performed for a suffici-
ently wide range of values of the nonhomogeneity index
n, via 0,1,2,1nand –2. Moreover 0n leads to
the caseneous medium.
Figures 1-4 elucidate the variation of di
gramm
lues of displacement, temperature, and thermal stresses
distributions with respect to radius r for different values
of 0,1,2,1nand –2. Figure 1 give the variation of
the with observation distance for different
values of n, It is seen that displacement takes positive
values andradually increases until it attains a peak val-
ue at a particular location in close proximity to the cavity
surface and then diminishes rapidly with increasing dis-
tance. Figure 2 represents the graph of temperature T
versus r. It is noted that near the region of the cavity, T is
maximum and it decreases with the increase of r, as it
should occur in the real situation. Figure 3 represents the
graph of radial thermal stress rr
displacement
g

versus radius r. Also
stress in each of the all cases is found to vanish on the
boundaries, which agrees with the theoretical boundary
condition. It is clear that for fixed t it decreases with the
increase of r, which is physically plausible. Figure 4 is
plotted to show the variation of hoop stress



versus r
for different values of n, from the graph it lear that
the maximum values o occur near the surface of the
cavity and its magnitude decreases with the increase of r,
keeping t fixed.
Figures 5-8 sh
is c
f
ow the displacement, temperature, radial
stress and hoop stress distributions for three different
values of the parameters q

and


. These computations
were carried out in the coupled theory (q=0




), in
Lord-Shulman theory (0,


q0 =0 t

 the
generalized theory of theosed by Tzou
(q0

) and in
prmoelasticity pro

 ). The numerical values of the temperature,
dit components and stress components are
obtained and represented graphically for these theories.
splacemen
6. Conclusions
he problem of investigating the thermoelastic stresses,
T
0.16
0
0.04
0.08
0.12
11.21.41.61.8
0n
2n
1n
2n
u
r
u
1n
n = 0
r
Figure 1. Variation of displacement with respect to radus i
for fifferent values of nonhomogeneity parameter n.
0
0.2
0.4
0.6
0.8
1
11.21.4 1.61.82
T
r
0n
n = 0
1n
2n
1n
2n
Figure 2. Variation of temperature with respect to radiu
r
s
for different values of nonhomogeneity parameter n.
-1. 6
-1. 2
-0. 8
-0. 4
0
11.2 1.41.6 1.8
rr

r
0n
r
–0.4
–0.8 n = 0
1n
2n
1n
–1.2


2n
Figure 3. Variation of radial stress with respect to radis
–1.6
u
for different values of nonhomogeneity parameter n.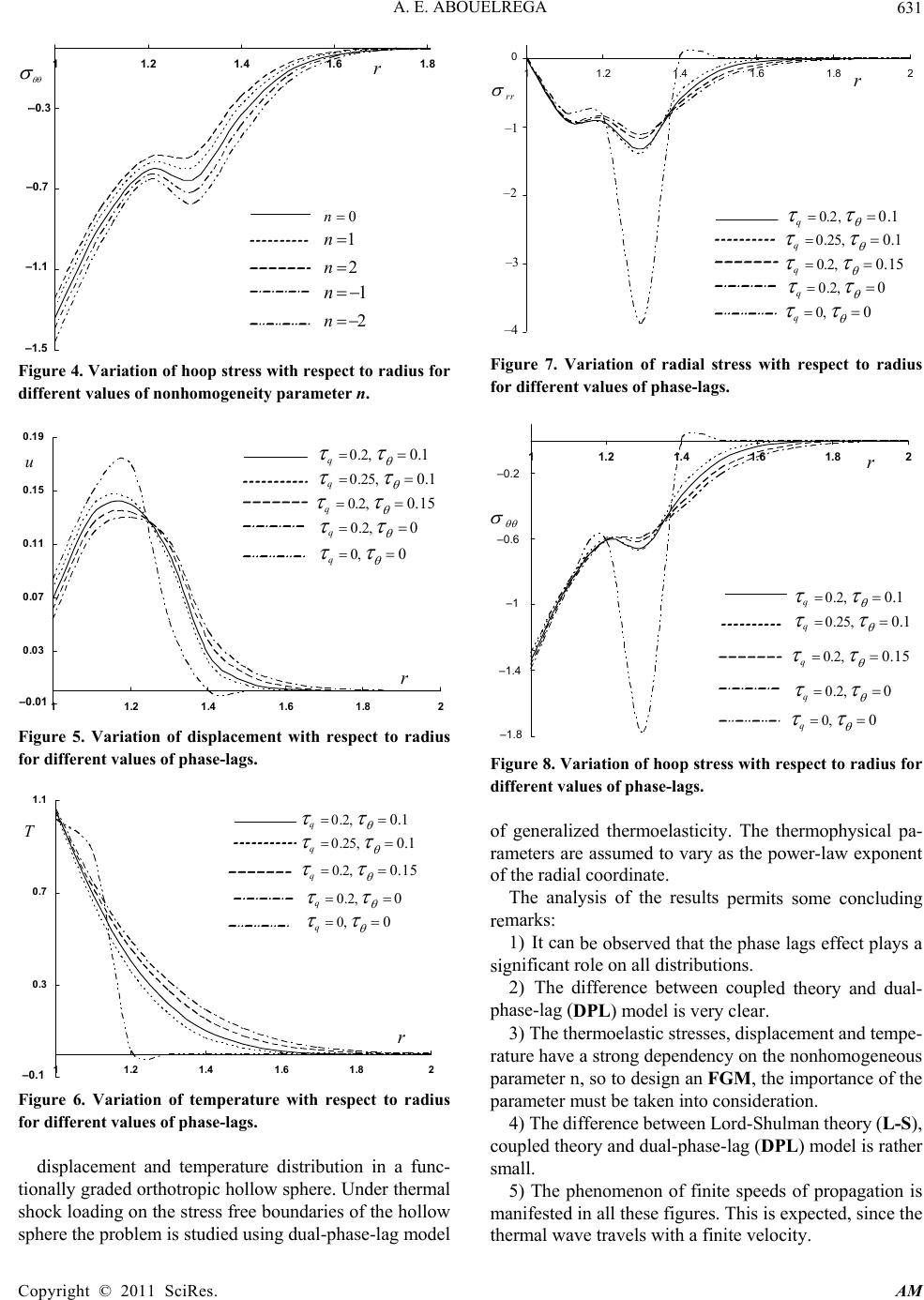

A. E. ABOUELREGA631
-1. 5
-1. 1
-0. 7
-0. 3
11.21.41.61.8


r
0n
1n
2n
1n
2n
Figure 4. Variation of hoop stress with respect to radius for
different values of nonhomogeneity parameter n.
-0.01
0.03
0.07
0.11
0.15
0.19
211.2 1.41.6 1.8
0.2, 0.15
q

 
0.2, 0.1
q

 
0.2, 0
q

 
0, 0
q

 
0.25, 0.1
q

 
u
r
Figure 5. Variation of displacement with respect to radius
for different values of phase-lags.
-0.1 11.2 1.41.6 1.82
0.3
0.7
1.1
0.2, 0.1
q

 
0.25,0.1
q

 
0.2,0.15
q

 
0.2, 0
q

 
0, 0
q

 
r
T
re 6. Variation of temperature with respect to radiu
displacement and temperature distribution in a func-
tio
Figus
for different values of phase-lags.
nally graded orthotropic hollow sphere. Under thermal
shock loading on the stress free boundaries of the hollow
sphere the problem is studied using dual-phase-lag model
-4
-3
-2
-1
0
11.2 1.4 1.6 1.82
0, 0
q

 
0.25, 0.1
q

 
0.2,0.1
q

 
0.2, 0
q

 
0.2, 0.15
q

 
r
rr

Figure 7. Variation of radial stress with respect to radius
for different values of phase-lags.
-1.
8
-1.4
-1
-0.6
-0.2 11.21.41.61.82
0.2, 0.1
q

 
0.25, 0.1
q

 
0.2, 0.15
q

 
0.2, 0
q

 
0, 0
q

 


r
F. Variation of hoop stress with respect to radius for
f generalized thermoelasticity. The thermophysical pa-
permits some concluding
re
be observed that the phase lags effect plays a
sig
d theory and dual-
ph
ement and tempe-
ra
eory (L-S),
co
phenomenon of finite speeds of propagation is
manifested in all these figures. This is expected, since the
thermal wave travels with a finite velocity.
igure 8
different values of phase-lags.
o
rameters are assumed to vary as the power-law exponent
of the radial coordinate.
The analysis of the results
marks:
1) It can
nificant role on all distributions.
2) The difference between couple
ase-lag (DPL) model is very clear.
3) The thermoelastic stresses, displac
ture have a strong dependency on the nonhomogeneous
parameter n, so to design an FGM, the importance of the
parameter must be taken into consideration.
4) The difference between Lord-Shulman th
upled theory and dual-phase-lag (DPL) model is rather
small.
5) The
r
r
–0.3
–
1
–0.7
–
2
–
3
–1.1
–
4
–1.5
r
u –0.2
–0.6
–1
–1.4
r
–0.01
–1.8
r
–0.1

A. E. ABOUELREGA 632
6.
rsible Thermo-
urnal of Applied Physics, Vol. 27, No. 3,
53. doi:10.1063/1.1722351
pp. 299-309.
ol. 31,
995, pp. 8-16. doi:10.1115/1.2822329
Mathematics, Vol. 10, No. 1, 1984,
[11] al, “Ther-
hout
Study of General-
l Thermoelastic
ction-
ang, “The Use of Function-
eneralized Thermoe-
References
[1] M. A. Biot, “Thermoelasticity and Irreve
dynamic s, ” Jo
1956, pp. 240-2
[2] H. Lord and Y. Shulman, “A Generalized Dynamical
Theory of Thermoelasticity,” Journal of the Mechanics
and Physics of Solids, Vol. 15, No. 5, 1967,
doi:10.1016/0022-5096(67)90024-5
[3] A. E. Green and K. A. Lindsay, “Thermoelasticity,”
Journal of Elasticity, Vol. 2, No. 1, 1972, pp. 1-7.
doi:10.1007/BF00045689
[4] A. E. Green and P. M. Naghdi, “Thermoelasticity With-
out Energy Dissipation,” Journal of Elasticity, V
No. 3, 1993, pp. 189-208. doi:10.1007/BF00044969
[5] D. Y. Tzou, “Macro- to Microscale Heat Transfer: The
Lagging Behavior,” 1st Edition, Taylor & Francis, Wa-
shington, 1996.
[6] D. Y. Tzou, “A Unified Approach for Heat Conduction
from Macro- to Microscales,” Journal of Heat Transfer,
Vol. 117, No. 1, 1
[7] D. Y. Tzou, “Experimental Support for the Lagging Be-
havior in Heat Propagation,” Journal of Thermophysics
and Heat Transfer, Vol. 9, No. 4, 1995, pp. 686-693.
doi:10.2514/3.725
[8] D. S. Chandrasekharaiah, “Thermoelasticity with Second
Sound,” Applied Mechanics Reviews, Vol. 39, No
1986, pp. 354-376.
. 3, ally Graded Materials to Eliminate or Control Thermal
Deformation,” Composites Science and Technology, Vol.
56, No. 9, 1996, pp. 1099-1104.
[9] G. Honig and V. Hirdes, “A Method for the Numerical
Inversion of the Laplace Transform,” Journal of Compu-
tational and Applied
pp. 113-132. doi:10.1016/0377-0427(84)90075-X
[10] S. B. Sinha and K. A. Elsibai, “Thermal Stresses for an
Infinite Body with Spherical Cavity with Tow Relaxation
Times,” Journal of Thermal Stresses, Vol. 19, No. 5, 1996,
pp. 745-759. doi:10.1080/01495739608946190
M. N. Allam, K. A. Elsibai and A. E. Abouelerg
mal Stresses in a Harmonic Field for an Infinite Body
with a Circular Cylindrical Hole Without Energy Dissi-
pation,” Journal of Thermal Stresses, Vol. 25, No. 1,
2002, pp. 57-68. doi:10.1080/014957302753305871
[12] S. Mukhopadhyay, “Thermoelastic Interactions wit
Energy Dissipation in an Unbounded Body with a Spher-
ical Cavity Subjected to Harmonically Varying Tem-
perature,” Mechanics Research Communications, Vol. 31,
No. 1, 2004, pp. 81-89.
doi:10.1016/S0093-6413(03)00082-X
[13] S. Mukhopadhyay and R. Kumar, “A
ized Thermoelastic Interactions in an Unbounded Me-
dium with a Spherical Cavity,” Computers and Mathe-
matics with Applications, Vol. 56, No. 9, 2008, pp. 2329-
2339.doi:10.1016/j.camwa.2008.05.031
[14] S. K. Roychoudhuri, “One-Dimensiona
Waves in Elastic Half-Space with Dual-Phase-Lag Ef-
fects,” Materials and Structures Journal, Vol. 2, No. 1,
2007, pp. 489-503. doi:10.2140/jomms.2007.2.489
[15] S. Suresh and A. Mortensen, “Fundamentals of Fun
ally Graded Materials,” Institute of Materials Communi-
cations Ltd., London, 1998.
[16] R. C. Wetherhold and S. S. W
doi:10.1016/0266-3538(96)00075-9
[17] R. B. Hetnarski and J. Ignaczak, “G
lasticity,” Journal of Thermal Stresses, Vol. 22, No. 4,
1999, pp. 451-476. doi:10.1080/014957399280832