Paper Menu >>
Journal Menu >>
 J. Electromagnetic Analysis & Applications, 2009, 1: 118-123 doi:10.4236/jemaa.2009.12019 Published Online June 2009 (www.SciRP.org/journal/jemaa) Copyright © 2009 SciRes JEMAA 1 ICI Performance Analysis for All Phase OFDM Systems Renhua Ge1, Shanlin Sun1,2 1Guilin College of Aerospace Technology, Guilin, 541004, China; 2Tianjin University, Tianjin, 300072, China. Email: grh1962@163.com Received January 26th, 2009; revised March 2nd, 2009; accepted March 10th, 2009. ABSTRACT Orthogonal frequency division multiplexing (OFDM) is a strong candidate for the next generation wireless communica- tion. But the frequency offset between the local oscillators at the transmitter and receiver causes a single frequency offset in the signal, while a time-varying channel can cause a spread of frequency offsets known as the Doppler spread. Frequency offsets ruin the orthogonal of OFDM sub-carriers and cause inter-carrier interference (ICI), therefore, quickly diminishing the performance of the system. A novel all phase OFDM (AP-OFDM) system is established. APFFT is introduced for the first time to overcome ICI aroused by carrier frequency offset (CFO) in OFDM systems. This scheme makes use of APFFT in time domain and zero inserting in frequency domain to reduce the amount of ICI gener- ated as a result of frequency offset, with little additional computational complexity. At the same time, the proposed sys- tem has zero phase error. It is proved to be correct and effective in mathematics. The simulation results indicate that AP-OFDM system has a better performance than conventional OFDM system. Keywords: All Phase Orthogonal Frequency-division Multiplexing (APOFDM), Carrier Frequency Offset (CFO), In- ter-carrier Interference (ICI) 1. Introduction Orthogonal frequency-division multiplexing (OFDM) communication systems require precise frequency syn- chronization [1-4], since otherwise inter-carrier interfer- ence (ICI) will occur. Currently, three different ap- proaches for reducing ICI have been developed in the literature. One is to estimate and remove the frequency offset [3-7]. While many methods exist that can estimate and remove the frequency offset quite accurately, they often have considerable computational complexity. An- other approach is to use signal processing and/or coding to reduce the sensitivity of the OFDM system to the fre- quency offset [8]. These methods can either be used as low complexity alternatives to fine frequency-offset es- timation techniques or they can be used together with a somewhat accurate oscillator. Windowing has been used in [9] and [10] to reduce the ICI created as a result of frequency offset. A simple and effective method known as ICI self-cancellation scheme [11,12] has been pro- posed by Zhao and Haggman. Other frequency-domain coding methods have been proposed in [13,14] that do not reduce the data rate. However, these methods produce less reduction in ICI. A new self-cancellation scheme has been proposed by Alireza, Seyedi and Saulnier [15]. This method has better performance with more computational complexity. This paper concentrates on the further development of the ICI cancellation method and APFFT is proposed for ICI cancellation. The advantages of APFFT are zero phase error and less ICI. It improves the OFDM system's ability to resist frequency offset with the cost of limited additional computational complexity. 2. The Model of APOFDM System In conventional FFT system, the spectrum of the receiver signal can expressed as [16]. 00 /)()1( /sin sin1 jNkNj ee Nk k N kX (1) where is the normalization frequency offset. Thus, the amplitude spectrum is: Nk k N kX /sin sin1 )( (2) And the phase spectrum is: 01 )( 1 k N N (3) Frequency offset can introduce ICI and phase noise and diminish the performance of the system Figure 1 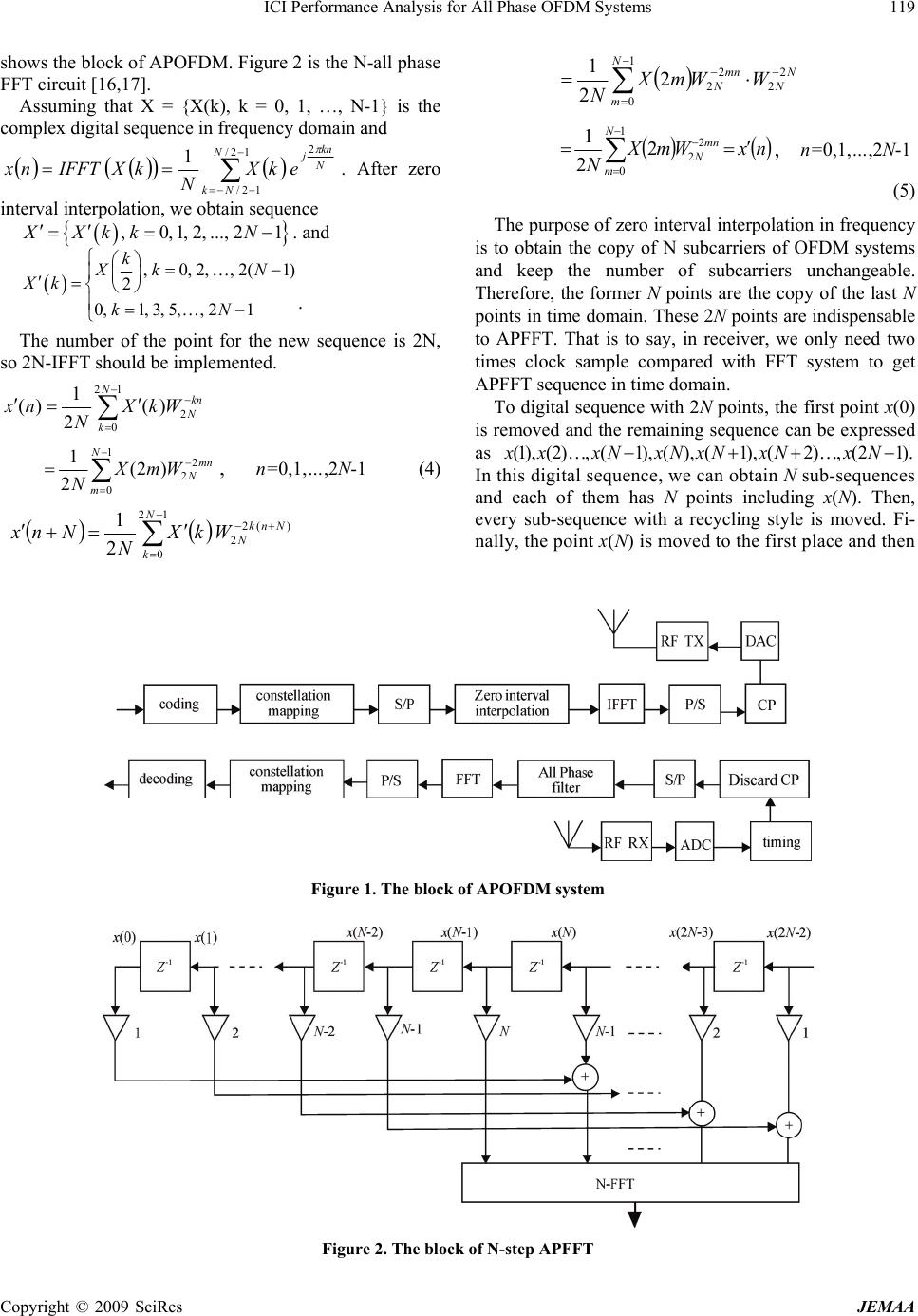 ICI Performance Analysis for All Phase OFDM Systems 119 Copyright © 2009 SciRes JEMAA shows the block of APOFDM. Figure 2 is the N-all phase FFT circuit [16,17]. Assuming that X = {X(k), k = 0, 1, …, N-1} is the complex digital sequence in frequency domain and N kn j N Nk ekX N kXIFFTnx 2 12/ 12/ 1 . After zero interval interpolation, we obtain sequence ,0,1,2,...,2 1XXkk N . and ,0,2,,2(1 2 0,1,3,5,, 21 k Xk N Xk kN ) . The number of the point for the new sequence is 2N, so 2N-IFFT should be implemented. 12 0 2 )( 2 1 )( N k kn N WkX N nx 1 0 2 2 )2( 2 1N m mn N WmX N, n=0,1,…,2N-1 (4) 12 0 )(2 2 2 1N k Nnk N WkX N Nnx N N N m mn NWWmX N 2 2 1 0 2 2 2 2 1 nxWmX N N m mn N 1 0 2 2 2 2 1, n=0,1,…,2N-1 (5) The purpose of zero interval interpolation in frequency is to obtain the copy of N subcarriers of OFDM systems and keep the number of subcarriers unchangeable. Therefore, the former N points are the copy of the last N points in time domain. These 2N points are indispensable to APFFT. That is to say, in receiver, we only need two times clock sample compared with FFT system to get APFFT sequence in time domain. To digital sequence with 2N points, the first point x(0) is removed and the remaining sequence can be expressed as ).12(,)2(),1(),(),1(,)2(),1( NxNxNxNxNxxx In this digital sequence, we can obtain N sub-sequences and each of them has N points including x(N). Then, every sub-sequence with a recycling style is moved. Fi- nally, the point x(N) is moved to the first place and then Figure 1. The block of APOFDM system Figure 2. The block of N-step APFFT 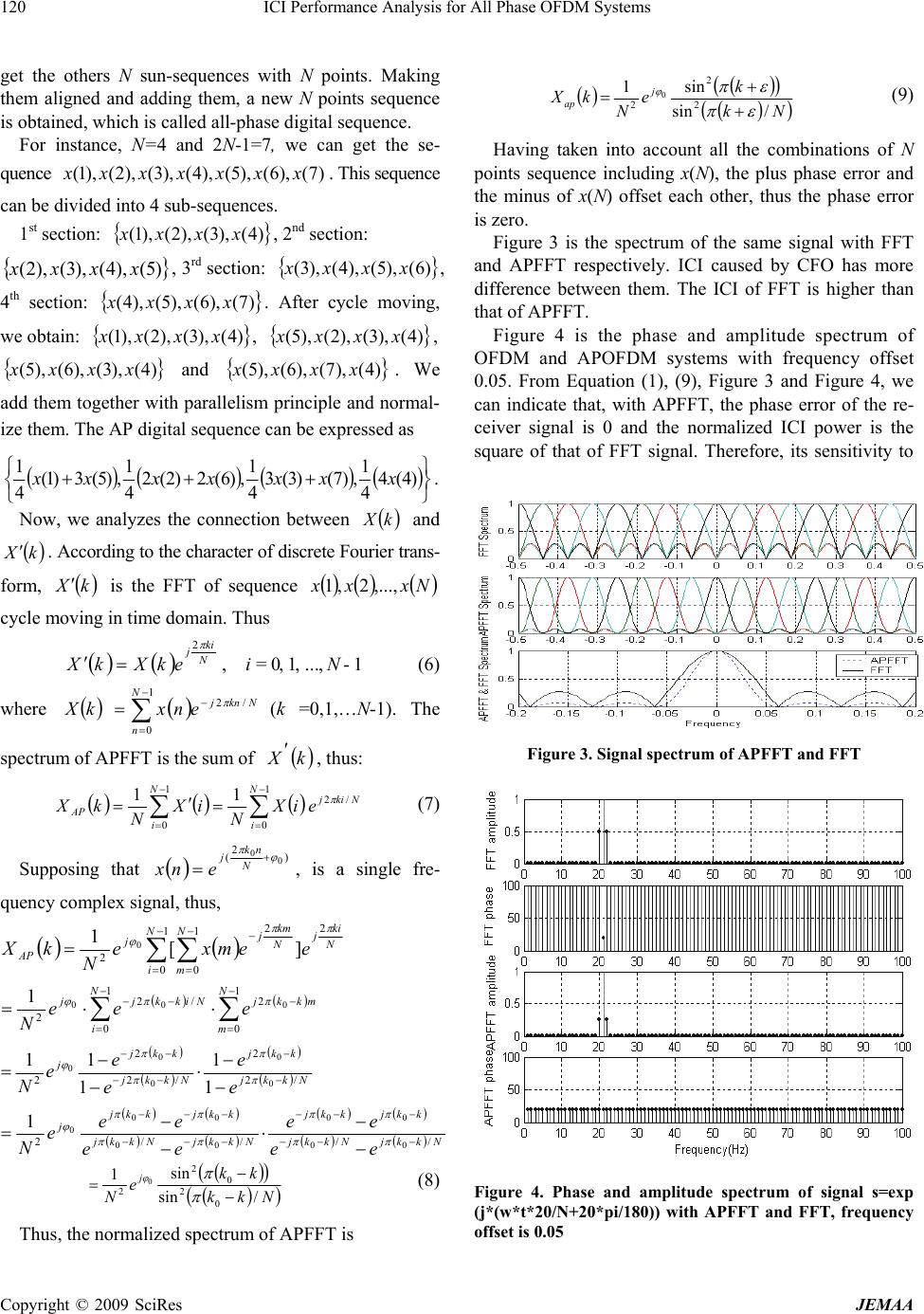 120 ICI Performance Analysis for All Phase OFDM Systems get the others N sun-sequences with N points. Making them aligned and adding them, a new N points sequence is obtained, which is called all-phase digital sequence. For instance, N=4 and 2N-1=7, we can get the se- quence . This sequence can be divided into 4 sub-sequences. )7(),6(),5(),4(),3(),2(),1( xxxxxxx 1st section: , 2nd section: )4(),3(),2(),1( xxxx )5(),4(),3(),2(xxxx ),5(),4(xx ),2(),1(xx , 3rd section: , 4th section: . After cycle moving, we obtain: , , )6(),5(),4(),3( xxxx )4(),3(),2(),5( xxxx )7(),6(xx )4(),3( xx )4(),3(),6(),5(xxxx and )4(),7(),6(),5( xxxx. We add them together with parallelism principle and normal- ize them. The AP digital sequence can be expressed as )4(4 4 1 ,)7()3(3 4 1 ,)6(2)2(2 4 1 ,)5(3)1( 4 1xxxxxxx . Now, we analyzes the connection between kX and . According to the character of discrete Fourier trans- form, is the FFT of sequence kX kX Nxx,1 x,...,2 cycle moving in time domain. Thus N ki j ekXkX 2 , i = 0, 1, …, N - 1 (6) where (k =0,1,…N-1). The spectrum of APFFT is the sum of , thus: kX 1 0 /2 N n Nknj enx kX 1 0 /2 1 0 11 N i Nkij N i AP eiX N iX N kX (7) Supposing that ) 2 (0 0 N nk j enx, is a single fre- quency complex signal, thus, N ki j N m N km j N i j AP eemxe N kX 2 1 0 2 1 0 2][ 10 1 0 2 1 0 /2 2 000 1N m mkkj N i Nikkjj eee N Nkkj kkj Nkkj kkj j e e e e e N/2 2 /2 2 20 0 0 0 0 1 1 1 11 NkkjNkkj kkjkkj NkkjNkkj kkjkkj j ee ee ee ee e N////2 00 00 00 00 0 1 Nkk kk e N j /sin sin 1 0 2 0 2 2 0 (8) Thus, the normalized spectrum of APFFT is Nk k e N kX j ap /sin sin1 2 2 2 0 (9) Having taken into account all the combinations of N points sequence including x(N), the plus phase error and the minus of x(N) offset each other, thus the phase error is zero. Figure 3 is the spectrum of the same signal with FFT and APFFT respectively. ICI caused by CFO has more difference between them. The ICI of FFT is higher than that of APFFT. Figure 4 is the phase and amplitude spectrum of OFDM and APOFDM systems with frequency offset 0.05. From Equation (1), (9), Figure 3 and Figure 4, we can indicate that, with APFFT, the phase error of the re- ceiver signal is 0 and the normalized ICI power is the square of that of FFT signal. Therefore, its sensitivity to Figure 3. Signal spectrum of APFFT and FFT Figure 4. Phase and amplitude spectrum of signal s=exp (j*(w*t*20/N+20*pi/180)) with APFFT and FFT, frequency offset is 0.05 Copyright © 2009 SciRes JEMAA  ICI Performance Analysis for All Phase OFDM Systems 121 Copyright © 2009 SciRes JEMAA 1 ICI caused by CFO is lower and APFFT is more suitable for OFDM system. 3. Performance Analysis for AP-OFDM Sys- tems with CFO The change of performance duo to CFO is more inter- ested in the research content. In this section we use a method similar to the one used in [16] to calculate the exact BER of the proposed system in the presence of a frequency shift. We assume that the system operates over an AWGN channel and that the data symbols are quater- nary phase-shift keying (QPSK) modulated. Similar analysis is possible if a 64-QAM modulation is used [16]. We assume an ideal additive white Gaussian noise (AWGN) channel. The CFO does not change during one OFDM symbol. The sampled signal for the kth sub-channel after the receiver fast Fourier transform processing can be written as: 1 0 0, ,0,1,, N kk lklk llk yXS SXnkN (10) where 1,13,15,17, 3,33,35,37, 5,53,55,57, 7,73,75,77 k j jjj j jj Xj j jjj j jj j denotes the transmitted symbol for the kth sub-carrier, nk is a complex Gaussian noise sample (with its real and imagi- nary components being independent and identically dis- tributed with variance ), and N is the number of sub-carriers. The second term in (12) is the ICI caused by the CFO. The sequence (ICI coefficients) depends on the CFO and is given by 2 k S 0 2 /sin sin1 j APk e Nk k N AkXS (11) If the ICI assumed to be a Gaussian- distributed ran- dom variables (RV) with a zero mean, both the BER and SER can readily be computed for carious modulation formats. The approximate error rates then can be ex- pressed in terms of the function and effective SNR for the kth sub-carrier as )(Q 2 2 0 1APICIS S eff S (12) where 2 2/ ks XE which is the SNR for the kth sub-carrier in the absence of a CFO. The variance of the signal constellation 2 k XE will be independent of if all sub-carriers use the same modulation format, which is the normal case. The variance of the ICI on the kth sub-car- rier can be given by 1 ,0 2 2 N kll klAPICI S (13) Compared with FFT-OFDM systems [16], the variance of the ICI of APFFT-OFDM systems can be expressed by 1 0 1 0 22 2 2ˆ var 1 ˆ N n N n ICI AP ICI AP N n N nN N nX N 1 0 22 3 2 2 ˆN n ICI nNnN N 2 1 2 6 121 ˆ3 3 2NN N NNN N N ICI 22 2 2 ˆ 3 1 ˆ 3 12 ICIICI N N (14) Equation (14) shows that, after APFFT, the ICI noise to every sub-carrier is the third of that in FFT system. Using the method in [16], the effect caused by CFO can be expressed with the losing of SNR. S D 2 3 1 10ln 10 (15) 4. APOFDM Performance Test with Simulation 4.1 The Design Based SIR According to the method of ICI cancellation in [15], we choose N=64, L=2, M=1 and SIRmin=25dB to design a system and compare its performance with FFT system, Zhao-Haggman (L=2) system and A-Seyedi system. Fig- ure 5 shows that the performance of APFFT is better than FFT and Zhao-Haggman (L=2) systems in low frequency offset, and poorer in high frequency offset. We will only be interested in frequency shifts in the range 5.0 . 4.2 The Design Based BER As SIR can not represent the system performance, and the result in Figure 6 obtained before frequency com- pensation, thus the APFFT-OFDM system SIR can not necessarily better than the other existing systems. The model method in [12] is used and all phase compensa- tion is adopted, BER performances are compared in Fig- ure 6. The parameters are same to the above. Assuming that channel is pilot and the pilot frequency account for 20% of the symbol. The CFO is 0.5. From Figure 6, when BER=10-4, APFFT is better than Zhao-Haggman system and A. Seyedi system 1.1 dB and 0.8 dB respec- tively. This is because of the zero phase error of APFFT with CFO. Equation (14), Figure 3 and Figure 4 can prove it to be correct. That is to say, the simulation and the theory are consistent. 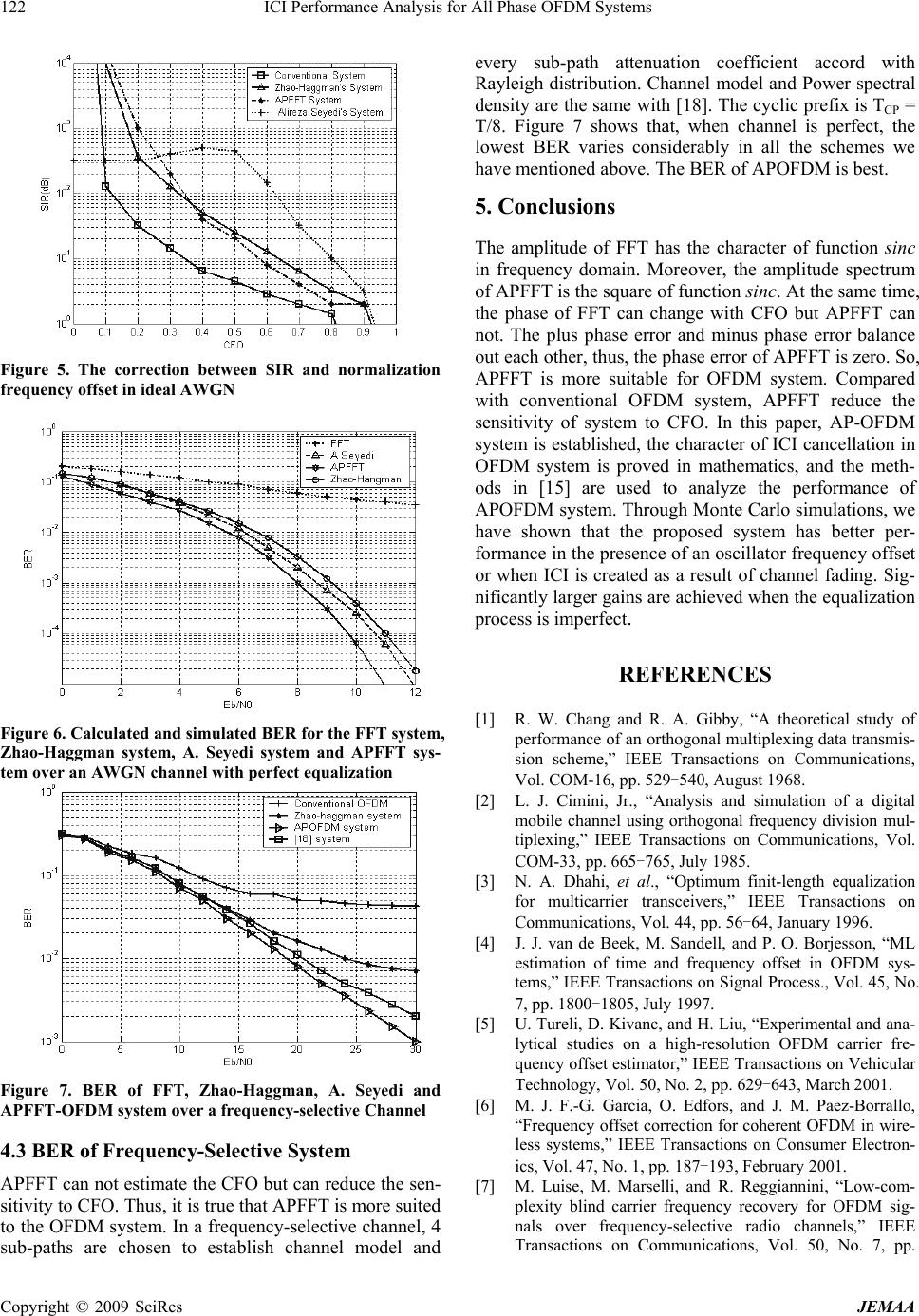 122 ICI Performance Analysis for All Phase OFDM Systems Figure 5. The correction between SIR and normalization frequency offset in ideal AWGN Figure 6. Calculated and simulated BER for the FFT system, Zhao-Haggman system, A. Seyedi system and APFFT sys- tem over an AWGN channel with perfect equalization Figure 7. BER of FFT, Zhao-Haggman, A. Seyedi and APFFT-OFDM system over a frequency-selective Channel 4.3 BER of Frequency-Selective System APFFT can not estimate the CFO but can reduce the sen- sitivity to CFO. Thus, it is true that APFFT is more suited to the OFDM system. In a frequency-selective channel, 4 sub-paths are chosen to establish channel model and every sub-path attenuation coefficient accord with Rayleigh distribution. Channel model and Power spectral density are the same with [18]. The cyclic prefix is TCP = T/8. Figure 7 shows that, when channel is perfect, the lowest BER varies considerably in all the schemes we have mentioned above. The BER of APOFDM is best. 5. Conclusions The amplitude of FFT has the character of function sinc in frequency domain. Moreover, the amplitude spectrum of APFFT is the square of function sinc. At the same time, the phase of FFT can change with CFO but APFFT can not. The plus phase error and minus phase error balance out each other, thus, the phase error of APFFT is zero. So, APFFT is more suitable for OFDM system. Compared with conventional OFDM system, APFFT reduce the sensitivity of system to CFO. In this paper, AP-OFDM system is established, the character of ICI cancellation in OFDM system is proved in mathematics, and the meth- ods in [15] are used to analyze the performance of APOFDM system. Through Monte Carlo simulations, we have shown that the proposed system has better per- formance in the presence of an oscillator frequency offset or when ICI is created as a result of channel fading. Sig- nificantly larger gains are achieved when the equalization process is imperfect. REFERENCES [1] R. W. Chang and R. A. Gibby, “A theoretical study of performance of an orthogonal multiplexing data transmis- sion scheme,” IEEE Transactions on Communications, Vol. COM-16, pp. 529-540, August 1968. [2] L. J. Cimini, Jr., “Analysis and simulation of a digital mobile channel using orthogonal frequency division mul- tiplexing,” IEEE Transactions on Communications, Vol. COM-33, pp. 665-765, July 1985. [3] N. A. Dhahi, et al., “Optimum finit-length equalization for multicarrier transceivers,” IEEE Transactions on Communications, Vol. 44, pp. 56-64, January 1996. [4] J. J. van de Beek, M. Sandell, and P. O. Borjesson, “ML estimation of time and frequency offset in OFDM sys- tems,” IEEE Transactions on Signal Process., Vol. 45, No. 7, pp. 1800-1805, July 1997. [5] U. Tureli, D. Kivanc, and H. Liu, “Experimental and ana- lytical studies on a high-resolution OFDM carrier fre- quency offset estimator,” IEEE Transactions on Vehicular Technology, Vol. 50, No. 2, pp. 629-643, March 2001. [6] M. J. F.-G. Garcia, O. Edfors, and J. M. Paez-Borrallo, “Frequency offset correction for coherent OFDM in wire- less systems,” IEEE Transactions on Consumer Electron- ics, Vol. 47, No. 1, pp. 187-193, February 2001. [7] M. Luise, M. Marselli, and R. Reggiannini, “Low-com- plexity blind carrier frequency recovery for OFDM sig- nals over frequency-selective radio channels,” IEEE Transactions on Communications, Vol. 50, No. 7, pp. Copyright © 2009 SciRes JEMAA  ICI Performance Analysis for All Phase OFDM Systems 123 Copyright © 2009 SciRes JEMAA 1182-1188, July 2002. [8] J. Armstrong, “Analysis of new and existing methods of reducing intercarrier interference due to carrier frequency offset in OFDM,” IEEE Transactions on Communications, Vol. 47, No. 3, pp. 365-369, March 1999. [9] M. Gudmundson and P. O. Anderson, “Adjacent channel interference in an OFDM system,” in Proceedings of 46th IEEE Vehicular Technology Conference, pp. 918-922, 1996. [10] C. Muschallik, “Improving an OFDM reception using an adaptive Nyquist windowing,” IEEE Transactions on Consumer Electronics, Vol. 42, No. 3, pp. 259-269, Au- gust 1996. [11] Y. Zhao and S. G. Haggman, “Sensitivity to Doppler shift and carrier frequency errors in OFDM systems - the con- sequences and solutions,” in Proceedings of 46th IEEE Ve- hicular Technology Conference, pp. 1564-1568, April 1996. [12] Y. Zhao and S. G. Haggman, “Intercarrier interference self-cancellation scheme for OFDM mobile communica- tion systems,” IEEE Transactions on Communications, Vol. 49, pp. 1185-1191, July 2001. [13] Y. Zhao and S. G. Haggman, “Intercarrier interference compression in OFDM communication systems by using correlative coding,” IEEE Communications Letters, Vol. 2, No. 8, pp. 214-216, August 1998. [14] K. Sathananthan and C. Tellambura, “Forward error correc- tion codes to reduce intercarrier interference in OFDM,” in Proceedings of IEEE International Symposium on Cir- cuits and Systems, Vol. 4, pp. 566-569, May 2001. [15] A. Seyedi and G. J. Saulnier, “General ICI self-cancel- lation scheme for OFDM systems,” IEEE Transactions on Vehicular Technology, Vol. 54, No. 1, pp. 198-210, January 2005. [16] K. Sathananthan and C. Terambulla, “Probability of error calculation of OFDM systems with frequency offset,” IEEE Transactions on Communications, Vol. 49, No. 11, pp. 1884-1888, November 2001. [17] Z. H. Wang, Z. X. Hou, and F. Su, “All phase FFT spec- trum analysis,” Journal of China Institute of Communications, Vol. 24, No.11A. pp. 16-20. [18] Y. Oda and K. Tsunekawa, “Advanced LOS path loss model in microwave mobile communications,” 10th In- ternational Conference on Antennas and Propagation, Conference Publication No. 436, IEE ’97, April 14-17, 1997. |

