Applied Mathematics, 2011, 2, 551-555
doi:10.4236/am.2011.25072 Published Online May 2011 (http://www.SciRP.org/journal/am)
Multi-Item EOQ Model with Both Demand-Dependent
Unit Cost and Varying Leading Time via Geometric
Programming
Kotb A. M. Kotb1, Hala A. Fergany2
1Department of Mathematics and Statistics, Faculty of Science, Taif University, Taif, Saudi Arabia
2Department of Mathematical Statistics, Faculty of Science, Tanta University, Tanta, Egypt
Received March 10, 2011; revised March 17, 2011; accepted March 21, 2011
Abstract
The objective of this paper is to derive the analytical solution of the EOQ model of multiple items with both
demand-dependent unit cost and leading time using geometric programming approach. The varying purchase
and leading time crashing costs are considered to be continuous functions of demand rate and leading time,
respectively. The researchers deduce th e optimal order quantity, the demand rate and the leading time as de-
cision variables then the optimal total cost is obtained.
Keywords: Inventory, Geometric Programming, Leading Time, Demand-Dependent, Economic Order
Quantity
1. Introduction
The problem of the EOQ model with demand-dependent
unit cost had been treated by some researchers. Cheng [1]
studied an EOQ model with demand-dependent unit cost
of single-item. The problem of inventory models involv-
ing lead time as a decision variable have been succinctly
described by Ben-Daya and Abdul Raouf [2]. Abou-
El-Ata and Kotb [3] developed a crisp inventory model
under two restrictions. Also, Teng and Yang [4] exam-
ined deterministic inventory lot-size models with
time-varying demand and cost under generalized holding
costs. Other related studies were written by Jung and
Klein [5], Das et al. [6] and Mandal et al. [7]. Recently,
Kotb and Fergany [8] discussed multi-item EOQ model
with varying holding cost: a geometric programming
approach.
The aim of this paper is to derive the optimal solution
of EOQ inventory model and minimize the total cost
function based on the values of demand rate, order quan-
tity and leading ti me using geometric programmin g tech-
nique. In the final a numerical example is solved to illus-
trate the model.
2. Notations and Assumptions
To construct the model of this problem, we define the
following variables:
r
D = Annual demand rat e (decision variabl e).
p
r
C
C = Unit pu rchase (pr oduction ) cost.
hr = Unit holding (inventory carrying) cost per item
per unit time.
or
C = Ordering cost.
SS = r
K
L  = Safety stock.
n = Number of different items carried in inventory.
r
L
Q = Leading rate time (decision variable).
r = Production (order) quantity batch (decision vari-
able).
TC


,,
rrr
DQL = Average annual total cost. For the
rth item.
The following basic assumptions about the model are
made:
1) Demand rate is uniform over time.
r
2) Time horizon is finite.
D
3) No shortages are allowed.
4) Unit production cost

,
b
pr rpr r
CD CD


1,2 3,,,1 r, nb


b is inversely related to the de- mand rate . W here is called the price elasticity.
5) Lead time crashing cost is related to the lead time
by a function of the form

,1,2,3,,,
rr
RLL rn




0,00 5.

 . where ,

 are real constants
selected to provide the best fit of the estimated cost func-

K. A. M. KOTB ET AL. 552
tion.
6) Our objective is to minimize th e annual relevant to-
tal cost.
3. Mathematical Formulation
The annual relevant total cost (sum of production, order,
inventory carrying and lead time crashing costs) which,
according to the basic assumptions of the EOQ model, is:
 

1
2
nr
rrrrpr ror
rr
rr
rhrr
r
D
TC D,Q,LDCDC
Q
QD
KLC RL
Q








 

 

(1)
Substituting

p
rr
CD and


r
RL into (1) yields:

1
1
2
nbr
rr rrpror
rr
rr
rhrr
r
D
TC D,Q,LDCC
Q
QD
KLC L
Q











 

 

(2)
To solve this primal objective function which is a
convex programming problem, we can write it in the
form:
1
1
min
2
nbr
pr ror
rr
rr
rhrr
r
D
TCC DC
Q
QD
KLC L
Q













 

(3)
Applying Duffin et al. [9] results of geometric pro-
gramming technique to (3), the enlarged predual function
could be written in the form:


13
2
45
2
13
5 4
1
1123
45
112 3
45
1
2
2
rr
r
rr
r
rr
r r
WW
W
b
nrpr ror rhr
rrrr r
WW
hr rrr
rrr
W
WW
npr or hr
rrr r
W W
hr
rr
bW
r
DC DC QC
GW WQWW
KC LDL
WQW
CCC
WW W
KC
WW
D








 

 


 








 


 
 


 



125 235
45
1
2
rrr rrr
rr
WW WWW
r
WW
r
Q
L

 


(4)
Since the dual variable vector
j
r,
is arbitrary and can
be chosen according to convenience subject to:
W
,1,2,3,4, 5,1,2,3,,jr n
0
12345
1
rrrrr jr
WWWWW ,W

 (5)
We choose
j
r such that the exponents of rr
are zero, thus making the right hand side of (4)
independent of the decision variables. To do this we re-
quire:
WD,Q
and r L

12 5
23 5
45
10
0
10
2
rrr
rr r
rr
bW WW
WW W
WW






 






(6)
These are called the orthogonality conditions which
together with (5) are sufficient to determine the v alues of
,12,3,4,5,
jr
Wj,

1,2, 3,,rn

.
Solving (5) and (6) for
j
r
W, we get:



15
25
35
45
112
21
21
11
21 21
112 and
21
2
rr
rr
rr
rr
WW
b
b
b
WW
bb
b
WW
b
WW





 






 

 



 


(7)
Substituting ,1,2,3,4, 1,2,3,,
jr
Wj rn



5r
gW in
(4), we get the dual function . To find 5r W
which maximize


5r
gW , the logarithm of both side of


5r
gW
5r
W, and the partial derivatives were taken relative
to . Setting it to equal zero and simplifying, we get:
  

2
3
2
5515 5
15
12 12
12 0
b
b
rrr r
b
r
fWW AbWW
Ab W


 
  (8)
where:
 
12 1
31
12
,,
21 2112
12 and
12
bb
bb
bb
bb
b











1
2
1
212
1
2
21 1
21
b
hr
or
b
bb
b
or hrpr
KC
AC
b
CC Cb

 




















  



It is clear that


00f

and which means
that there exists a root

10f


5r. The trial and error
method can be used to find this root. However, we shall
0,1W

K. A. M. KOTB ET AL.553

first verify the root 5 calculated from (8) to maxi-
mize . This is confirmed by the second deriva-
tive to with respect to , which is always
negative.
*
r
W
*
r

,r
*
jr
Wj
*
r
W

5r
gW

lngW
1,2,Wj

5r
W
gW
3,4,
5r
W
,n
2,3,4
**
DQ

Thus, the root calculated from (8) maximize the
dual function . Hence, the optimal solution is
, where 5 is the
solution of (8) and are evaluated by
substituting value of in (7).
5

5r
5, 1,2,3,
*
jr 
,1,
*
r
W
*
5
To find the optimal values rr
r
, we apply
Duffin et al. [9] of geometric programming as indicated
below:
,,L

15
25
*
r
**
r
W
g
1*b
r
*
r
*
r


*
r
r
Wg,
D
CWW,
Q

pr
or
CD


45
**
r
r
gW
gW
35
and
2
*
rr
***
r r
CW ,
L W



hr
hr
Q
CK
By solving these relations, the optimal demand rate is
given by:
1
12b
2
1
223
,
2
*
or hrr
**
prr r
CC W
D.
CWW





*
r (9)
The optimal order quantity is:
212
11
2
223
,
2
b
**b
*
r
Qor
pr
rorhrr
***
rprr r
CW CCW
CWC WW





(10)
The optimal lead time is:
2
2212
14 1
2
23 23
2
*
r
L2
b
*** b
or hr rr r
** **
pr rrpr rr
CCC WW W
WWCWW



 
 
 
or
KC 
(11)
By substituting the values of in
(3), we deduce the minimum total cost as: and
** *
rr r
D,Q L

1
2
1
123
2
22 1
11 2
2
12
2
11
2
223
min 2
1
22
b
*
n
*or hrr
r pr**
rpr rr
** *
rr r
hr
** *
rr r
b
rr
**
or hr
rr
***
rprrr
CC W
LC CWW
W
KC
W W
CC WW
WCWW






















 




23
1
2
**
rr
ro
**
pr
*
or hr r
or hr
pr
TC D ,Q ,
WW
WC
CWW
CC W
CC
C

 



12 4
3
1
b*
br
*
r
W
W












(12)
As a special case, we assume 0, 0
r
L

 and


0bRL , and
14
**
rr
WW
5
0,
*
r
W
23
1
2
**
rr
WW

. This is the classical EOQ inventory
model.
4. An Illustrative Example
We shall compute the decision variables (optimal order
quantity , optimal demand rate and optimal
lead time ) whose values are to be determined to
minimize the annual relev ant total cost for three items (n
= 3). The parameters of the model are shown in Table 1.
*
r
Q*
r
L
*
r
D
Assume that the standard deviation 6

 unit/year
and K = 2.
For some different values of

and b, we use equa-
tion (8) to determine 5, whose value is to be deter-
mined to obtain
*
r
W
*
j
r
W, j = 1, 2, 3, 4, r = 1, 2, 3 from (6).
It follows that the optimal values of the production
batch quantity Q demand rate *
r
Dad time *
r
L and
minimum annual total cost are given in Tables 2-7.
*
r,, le
Table 1. The parameters of the model.
r or
C
p
r
C hr
C r

1 $ 200 $ 10 $ 0.8 $ 1
2 $ 140 $ 08 $ 0.5 $ 2
3 $ 100 $ 05 $ 0.3 $ 3
Table 2. The optimal solution of and
*
r
Q*
r
D
as a func-
tion of b (forall

).
b 1
*
Q 2
*
Q 3
*
Q 1
*
D 2
*
D 3
*
D
2 28.21 31.17 33.10 1.450 1.5501.540
5 26.41 28.55 31.00 1.395 1.4551.440
8 25.65 27.49 29.90 1.316 1.3501.340
1025.25 26.99 29.40 1.280 1.3001.295
2024.20 25.72 28.03 1.170 1.1801.178
Table 3. The optimal solution of and as a
function of b ().
*
r
LminTC
=0.1 
b 1
*
L
2
*
L
3
*
L
min TC
2 8.4

10–9 8.9

10–8 1.310–6 59.6932
5 4.2

10–17 2.4

10–14 4.910–11 66.0704
8 2.1

10–23 2.4

10–17 1.010–12 71.6195
10 1.2

10–26 8.1

10–20 2.710–13 83.8121
20 3.4

10– 396.9

10–26 1.510–14 422.838
Table 4. The optimal solution of and as a
function of b (
*
r
LminTC
=0.2

).
b 1
*
L
2
*
L
3
*
L
min TC
2 2.7

10–9 5.1

10–8 6.510–7 77.539200
5 2.5

10–17 2.2

10–14 2.310–11 243.99000
8 2.2

10–24 4.3

10–19 3.710–14 2906.5400
10 7.1

10–28 1.4

10–21 1.710–15 15175.300
20 6.8

10–43 7.7

10–31 9.210–20 1.3203

107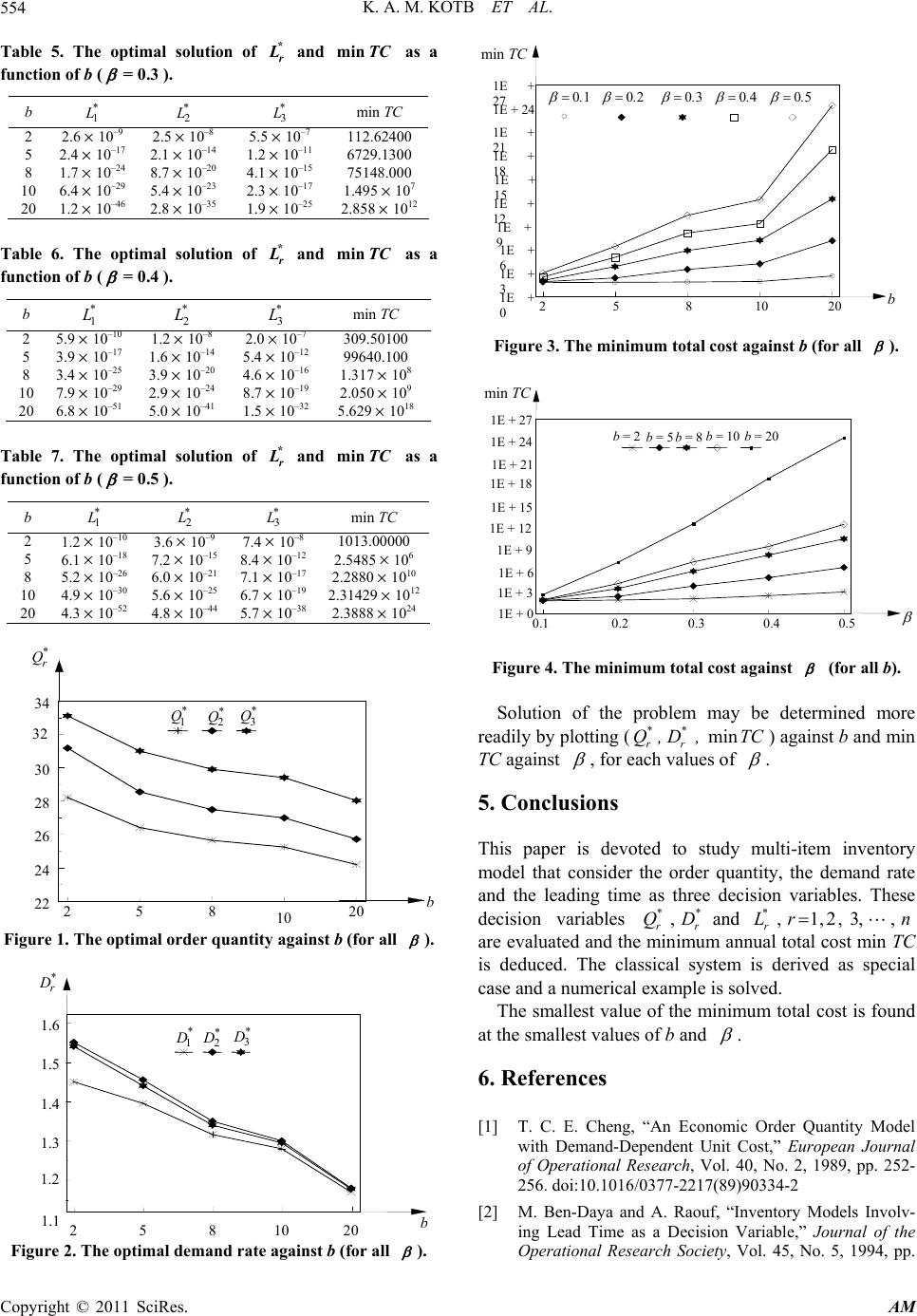

K. A. M. KOTB ET AL. 554
Table 5. The optimal solution of and as a
function of b ().
*
r
LminTC
=0.3 
b 1
*
L
2
*
L
3
*
L
min TC
2 2.6 10–9 2.510–8 5.510–7 112.62400
5 2.4 10–17 2.110–14 1.210–11 6729.1300
8 1.7 10–24 8.710–20 4.1 10–15 75148.000
10 6.4 10–29 5.410–23 2.310–17 1.495

107
20 1.2 10–46 2.810–35 1.9 10–25 2.858

1012
Table 6. The optimal solution of and as a
function of b (
*
r
LminTC
=0.4

).
b 1
*
L
2
*
L
3
*
L
min TC
2 5.9 10–10 1.210–8 2.010–7 309.50100
5 3.9 10–17 1.610–14 5.4 10–12 99640.100
8 3.4 10–25 3.910–20 4.6 10–16 1.317

108
10 7.9 10–29 2.910–24
8.7 10–19 2.050

109
20 6.8 10–51 5.010–41
1.5 10–32 5.629

1018
Table 7. The optimal solution of and as a
function of b (
*
r
LminTC
=0.5

).
b 1
*
L
2
*
L
3
*
L
min TC
2 1.2 10–10 3.610–9 7.410–8 1013.00000
5 6.1 10–18 7.210–15 8.410–12 2.5485

106
8 5.2 10–26 6.010–21 7.110–17 2.2880

1010
10 4.9 10–30 5.610–25 6.710–19 2.31429

1012
20 4.3 10–52 4.810–44 5.710–38 2.3888

1024
Figure 1. The optimal order quantity against b (for all

).
Figure 2. The optimal demand rate against b (for all

).
Figure 3. The minimum total cost against b (for all

).
Figure 4. The minimum total cost against

(for all b).
Solution of the problemmay be determined more
re adily by plotting (min
**
rr
Q,D ,TC) against b and min
TC against

, for each values of

.
5. Conclusions
his paper is devoted to study multi-item inventory
tal cost is found
at
T
model that consider the order quantity, the demand rate
and the leading time as three decision variables. These
decision variables ,and,1,2,3,,
** *
rr r
QD Lrn
are evaluated and the
is deduced. The classical system is derived as special
case and a numerical example is solved.
The smallest value of the minimum to
minimum annual total cost min TC
the smallest values of b and

.
6. References
] T. C. E. Cheng, “An Economic Order Quantity Model
Models Involv-
[1 with Demand-Dependent Unit Cost,” European Journal
of Operational Research, Vol. 40, No. 2, 1989, pp. 252-
256. doi:10.1016/0377-2217(89)90334-2
[2] M. Ben-Daya and A. Raouf, “Inventory
ing Lead Time as a Decision Variable,” Journal of the
Operational Research Society, Vol. 45, No. 5, 1994, pp.
10
2 5 8 10 20
1.1
1.2
1.3
1.4
1.5
1.6 *
1
D *
2
D*
3
D
b
*
r
D
58 10 202
1E +
3
0
1E +
6
1E +
9
1E +
12
1E +
15
1E +
18
1E +
21
1E +
1E + 24
27
1E +
b
min T
C
01 02030405.. ...
 


n TCmi
0.2
10.3 0.4 0.50.
1E + 0
1E + 3
1E + 6
1E + 9
1E + 12
1E + 15
1E + 18
1E + 21
1E + 24
1E + 27b = 2b = 5b = 8b = 10b = 20

*
r
Q
34
2 5 8 20
22
24
26
28
30
32
*
1
Q*
2
Q*
3
Q
b

K. A. M. KOTB ET AL. 555
Model with Varying Holding Cost under Two
mand and Cost
ulti-Item Inventory
osts and Demand-
Geometric
QO
Cost: A Geometric Pro-
n Wiley, New
579-582.
[3] M. O. Abou-El-Ata and K. A. M. Kotb, “Multi-Item EQO
Inventory
Restrictions: A Geometric Programming Approach,” Pro-
duction Planning & Control, Vol. 8, No. 6, 1997, pp.
608-611. doi:10.1080/095372897234948
[4] J. T. Teng and H. L. Yang, “Deterministic Inventory
Lot-Size Models with Time-Varying De
under Generalized Holding Costs,” Information and Man-
agement Sciences, Vol. 18, No. 2, 2007, pp. 113-125.
[5] H. Jung and C. M. Klein, “Optimal Inventory Policies
under Decreasing Cost Functions via Geometric Pro-
gramming,” European Journal of Operational Research,
Vol. 132, No. 3, 2001, pp. 628-642.
doi:10.1016/S0377-2217(00)00168-5
[6] K. Das, T. K. Roy and M. Maiti, “M
with Quantity-Dependent Inventory C Yor
Dependent Unit Cost under Imprecise Objective and Re-
strictions: A Geometric Programming Approach,” Pro-
duction Planning & Control, Vol. 11, No. 8, 2000, pp.
781-788. doi:10.1080/095372800750038382
[7] N. K. Mandal, T. K. Roy and M. Maiti, “Inventory Model
of Deteriorated Items with a Constraints: A
Programming Approach,” European Journal of Opera-
tional Research, Vol. 173, No. 1, 2006, pp. 199-210.
doi:10.1016/j.ejor.2004.12.002
[8] K. A. M. Kotb and H. A. Fergany, “Multi-Item E
Model with Varying Holding
gramming Approach,” International Mathematical Fo-
rum, Vol. 6, No. 23, 2011, pp. 1135-1144.
[9] R. J. Duffin, E. L. Peterson and C. Zener, “Geometric
Programming—Theory and Application,” Joh
k, 1967.