 Applied Mathematics, 2011, 2, 541-550 doi:10.4236/am.2011.25071 Published Online May 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Pressure/Saturation System for Immiscible Two-Phase Flow: Uniqueness Revisited Koffi B. Fadimba University of South Carolina Aiken, Aiken, USA E-mail: SCKoffiF@usca.edu Received December 31, 2010; revised March 18, 2011; accepted March 21, 2011 Abstract We give a sufficient condition for uniqueness for the pressure/saturation system. We establish this condition through analytic arguments, and then construct “mobilities” (or mobility-like functions) that satisfy the new condition (when the parameter is 2). For the constructed “mobilities”, we do graphical experiments that show, empirically, that this condition could be satisfied for other values of 1< <2 . These empirical experiments indicate that the usual smoothness condition on the fractional flow function (and on the total mobility), for uniqueness and convergence, might not be necessary. This condition is also sufficient for the convergence of a family of perturbed problems to the original pressure/saturation problem. Keywords: Porous Medium, Uniqueness of a Solution, Degenerate Equation, Immiscible Two-Phase Flow, Regularization, Phase Mobility. 1. Introduction Consider the coupled nonlinear problem (1), with , which arises from modeling incompre- ssible two-phase immiscible (water/oil, for example) flow through a porous medium (see [1,2], for instance). The problem considered, here, is in one of its simplified problem. 0 0Sx1 The conductivity of the medium is denoted by k while u is the total Darcy's velocity for the two-phase flow, f is the fractional flow fun ction, S the saturation of the invading fluid (or wetting phase), P is the global pressure, and the porosity of the medium. For the present analysis and for simplicity, we let 1 . The set is a sufficiently smooth bounded domain of , , 2 or 3, although this analysis focuses more on the case . n R=1n2n= Obviously, Problem 1 cannot, in general, be solved analytically: One needs to proceed through numerical approximations. Before attempting any solution method, one needs to investigate whether the problem has a solution and, if it does, whether the solution is unique. The main purpose of this paper is to revisit the uniqueness question of Problem 1, exhibit sufficient conditions for which the problem has a unique solution, and construct examples for which these conditions are satisfied. Those 1 0 =i div =in0, =0on[0, ] d=0forall [0,] =()0in (0,) =0on[0, ] ,0 =in uaSp T uQ T uT pxt T SfSu kSSQST tS kS T SxS x n0, (1)  K. B. FADIMBA 542 0 1 2 < conditions generalize the ones considered in [3] and in [4] for the uniqueness of the problem and for the conver- gence of a family of perturbed problems. This work con- stitutes, in some way, a complement to [3]. In addition, and on the applied side, the mobility-like functions that we construct can be used in testing codes for two-phase flow through porous media. The following conditions are usually imposed on the data (see [3], for instance). kk01 (2) 1 21 32 ,if0 ,if< 1,if 1 c c c k (3) where 12 1 0<< <<1 2 , and 0< 2 , for some 1 and 2 . The function f satisfies the following. 20,1fC in the variable (4) and 0= 1=0.ff (5) Conditions (2) thro ugh (5 ) imp ly the fo llowing (see [5, 6]). 2, bfa CKbKaba (6) for all 01ab where 0 = s Ksk d (7) Condition (6) h as been used (as a sufficient condition, among other conditions) for the proof of the wellposed- ness for the saturation equ ation , the con vergence for a re- gularization of that equation, and the convergence of numerical approximations of the same equation [7-9]. The rest of the paper is articulated as follows. In Sect- ion 2, we establish a new sufficient condition for (6) to hold, therefore for uniqueness of a solution of Problem 1. We also show that conditions (2) through (5) imply this new condition. In Section 3, we revisit the p ressure satu- ration problem, to show, indeed, that, under this new condition (defined in Section 2), there is uniqueness for Problem 1. In Section 4, we construct examples of rela- tive “mobilities” (mobility-like functions) and show that we have uniqueness under the special case =2 , with defined as in (3). We also explore experimentally, through graphs, the uniqueness problem for the pressure/ saturation problem, for these examples, for other values of , 1< <2 , though condition (4) is not satisfied for the corresponding total mobility , or fractional flow function a . In this work we use standard notations. In particular, we use 2 v for 2 L v, 22 L v for 22 0, ;LTL v, the norm of the function as an function in the variable t on ,vxt 2 L 0,T with values in 2 L . If 12 =,,vvv, n v is a vector, we denote by p v the norm p L v. 2. Sufficient Condition for Uniqueness for the Pressure/Saturation System Lemma 2.1 Let and be two functions defined on the interval 0g0h 0,1 . Assume that is conti- nuously differentiable on 0,1 , and that is continu- ous on h 0,1 . Define 0 =Hs h sd (8) and suppose that , 2 C xgxgahxxa Hx Ha (9) for all ,1 a and for all 0,1 ,a for some constant , then >0C 2, bgaCHbHaba (10) for all 01ab . Proof. We use a calculus argument. If , then the only value that =1a can assume is 1, and (10) is obvious. For 0<a1 , define the function 2 =. a GxgxgaCHx Ha xa (11) for a. Then, =0 a Ga , and =2 ' a Gxgxgx ga (12) Clearly, if (9) holds, then for all 0 ' a Gx a, i. e., a is decreasing on the interval G ,1a. Since a Ga=0, we must have 0 a Gx for all . This is true for any 1ax 0a1 . Hence the lemma is proved. In [9], for one space variable and the unilateral case ( 0=0k), and in [6] for several variables and the bilateral case ( 0= 1=0kk ), it is proved that if and satisfy conditions (2) through (5), then k and satisfy (6), for k 20,1fC. In the next lemma, we show that if (2) through (5) hold, then the couple , k satisfy (9), and therefore (6). Note: The above lemma is more general than what is known so far, since we do not require any of the con- ditions (2) through (5) to hold, nor do we require that be in 20,1C. However, if those conditions are satis- Copyright © 2011 SciRes. AM  K. B. FADIMBA543 fied, we have the following lemma. Lemma 2.2 Under conditions (2) through (5), and un- der the assumption that the function is twice conti- nuously differentiable on 0,1 , we have , xfxfaCkxxa Kx Ka (13) for all ,1 aand for all 0,1 ,a for some constant . >0C Thus, the combination of Lemma 2.1 and Lemma 2.2 gives an alternative way of proving that (6) holds, which in turns leads to uniqueness for Problem 1. Proof. We follow the lines of the proof of Proposition 3.2 of [6], with some modification. For the proof, it suf- fices to bound the quantity , fxfx fa kxx aKxKa independently of and a . Thanks to the symmetry implied by (3), we prove this for 1 0ax 1 only, without lost of generality; the rest of the prove can be obtained by the change of vari- able x , for 21ax 1 x, and by using the fact that for 2 kx c2 . Using (7) and (3), we obtain 1 11 1 =d . 1 xx aa d xKa ksscss cxa (14) Therefore, since ,0xakx, and is increa- sing, 11 1 11 1 1 1 xfxfafxfx fa kxxaKx KaKx Ka fxfx fa cxa fx fa fx xa cxa xa (15) By the Mean-Value Theorem, there exist such that <, <acdx = fx fa c xa and 11 =1 xa d xa Because the function s is increasing, its mean value occurs on the interval ,ax after the midpoint 2 ax , so >2 ax d . Hence >2 c d (16) and >. 2 d (17) Going back to (1 5 ) , w e get 1 122 11 22 1 2 1 |||| 1 2 , L xfcfxfx fa kxx aKxKacd fx fc cdd fx fc xc cxc Cf (18) where we have used (16), (17), and the fact that 0=0f. Therefore the lemma is proved. 3. Uniqueness of a Solution and Convergence of the Regularized Problem 3.1. Uniqueness We give an existence and uniqueness result for the case when and satisfy (9), i.e. ak asas acCksscKs Kc (19) for all , and for all 0c c. We also give a conver- gence result for a perturbation of Problem 1 to a nonde- generate case in the next subsection. Under condition (19) and the analogue for the fract- ional flow function , its is easy to see, through the proof of Theorem 6.1 of [3], that the following holds. Theorem 3.1 Suppose the data , a , and are Lip- schitz continuous in their argument k . Then Problem 1 has a solution ,pS , with * 21 0, ,, 0,1 ..0, SLTHand tSxtae T . (20) Furthermore, if the pairs , k and satisfy (9), respectively, and if we assume that ,ak . ,,aSpL L , then the solution is unique. Copyright © 2011 SciRes. AM  K. B. FADIMBA 544 3.2. Convergence of the Regularized Problem To get around the difficulties from the degeneracies of the problem, we perturb the diffusion coefficient, , to k k in such that a way that kk strongly as 0 . Define 0 = s Ks k d. (21) Then under the condition (19), the family of solutions ,pS converges to the unique solution ,pS of (1). More precisely. Theorem 3.2 Under the conditions of Theorem 3.1, let be the s olutio n to (1). For ,pS >0 small, say 1 0< <2 , let ,pS k be the solution of (1) when is replaced by k , with k as described above. Then 22 22 0, , 0, , ()()( )(), LTL LTL aSp pCaSaS (22) and 2 1* 0, ,() 0 0,1 , () () LTH T L SS KSKSS S CK K d (23) where 2 = , with and 0 defined by (7) and (21), respectively, and for some > . 4. Examples of Uniqueness In this Section, we describe the physical meanings of the parameters in Problem 1 and give an example that satis- fies conditions (2) through (3). These are purely mathe- matical examples that might not correspond exactly to models derived through physical experiments. Neverthe- less, the shapes of the graphs of the mobilities, the fract- ional flow function , and the conductivity, as functions of the saturation , resemble the ones obtained through experiments. See Figures 1-3, for S=32 . For more details on the physical meanings of these parameters, see [1,2,10-12], for instance. We retain the simplicity of the examples below for the mathematical analysis in this paper. For these examples, the diffusion coefficient (also called the total mobility) of the pre- ssure equation of (1), as well as the fractional flow funct- ion, a , satisfy (5). Physically 12 =asksks (24) where 1 is the mobility of the wetting phase, and the 2 the mobility of the nonwetting phase. The con- ductivity of the porous medium is defined by k k 12 12 d = dc ksks p ks ks kss, (25) where is the capillary pressure. Assuming c pdd c ps is bounded and bound ed away from 0, we will def ine, for this analysis, 12 12 = ksks ks ks ks, (26) dropping, in this manner, the factor dpds. The fract- ional flow func tio n is defined by 1 12 =ks fs ks ks (27) Figure 1. Fractional Flow. Figure 2. Mobilities. Copyright © 2011 SciRes. AM  K. B. FADIMBA545 Figure 3. Conductivity of the Medium. and , the total mobility, is given by (24). a For numerical modeling of immiscible two-ph ase flow through porous media, it has been used the following mobilities (see [13], for exam ple). 1=ks s (28) for the wetting, and 2=1ks s (29) for the nonwetting phase, up to multiplicative constants (or bounded functions). For a mathematical analysis purpose, and in order to get an example of uniqueness of a solution of Problem 1, we multiply both (28) and (29) by a bounded function of on the interval s 0,1 . 4.1. A case of Uniqueness We define our new mobilities (up to the same multipli- cative constant) by the following. For 1< 2 , let 2 1=e , ss ks s (30) for the wetting phase, and 2 2=1 e , ss ks s (31) for the non wetting phase. Then, the total mobility (up to a multiplicative constant , the absolute permeabi- lity, which we take here to be 1) is given by 2 =1e ss as ss , (32) while the conductivity of the medium (up to the same multiplicative constant ) is given by 2 1e =, 1 ss ss ks ss (33) and the fractional flow function is given by = 1 s fs . s (34) It is clearly seen that , defined by (26), satisfies (2) and (3), and that k and satisfy (5) for 1< a2 . One also checks that if =2 , then 22 0,10,1 . LL af C (35) Therefore, for defined by (33), k defined by (34), and defined by (32), we have that the couple a ,ak and , k satisfy (6), by Lemma 2.1 and Lem- ma 2.2. Hence the following. Corolla ry 4.1 Under the conditions (26) through (34), if =2 , Problem 1 has a unique solution . Fur- thermore, the family of regularized solutions ,pS pS, , as defined by Theorem 3.2, converges to the unique solution ,ps of (1). Conditions (32) through (35) and Corollary 4.1 show that condition (9) is not empty, neither is condition (6), which is often used in the proof of the well-posedness of problem 1 or the like and for the convergence of the re- gularization of the same type of problems ([3,4,6,7,14]. 4.2. Graphical Experiments for Uniqueness One can check, through computations, that and a , as defined by (32) and (34), respectively, are not twice continuously differentiable, for 1< <2 . They fail to be twice differentiable at and . For some =0s=1s values of ,1< <2 , namely for the values =32 and =43 , we show graphically, experimenting with several values of , that condition (19) seems to hold for and c a defined by (32) and (34). So this is an indication that Corollary 4.1 could hold for these values of (and, maybe, for 1< <2 ). We emphasize that this does not constitute a rigorous mathematical proof that Corollary 4.1 holds for these values of , but it does point to the conjecture that this could be the case. For our graphical illustrations, we define the functions Gs and s on the interval 0,1, for a given 1< <2 by, * 1 : = Gs asasaccksscKsKc (36) and, in the same way, * 2 : =, Fs sfsfccksscKsKc (37) for a parameter 0c1 . Here and are fixed positive constants that are independent of , but could depend on * 1 c* 2 c c . Copyright © 2011 SciRes. AM 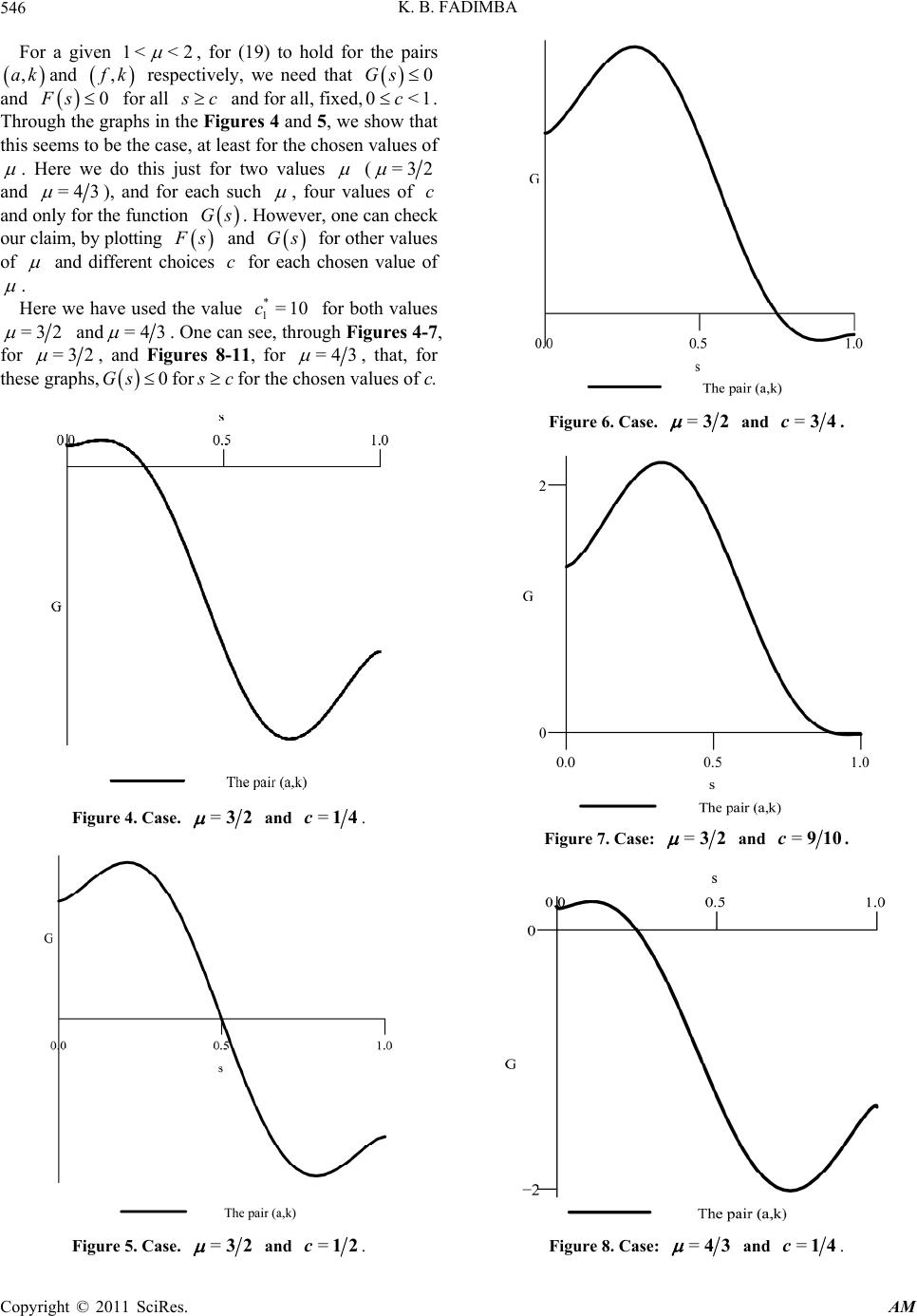 K. B. FADIMBA 546 For a given 1< <2 , for (19) to hold for the pairs and ,ak , k respectively, we need that 0Gs and for all Fs 0 c and for all, fixed,0<1c . Through the graphs in the Figures 4 and 5, we show that this seems to be the case, at least for the chosen va lues of . Here we do this just for two values (=32 and =43 ), and for each such , four values of and only for the function . Ho we ver, one can check our claim, by plotting c Gs s and for other values of Gs and different choices for each chosen value of c . Here we have used the value 1 for both values *=10c =32 and=43 . One can see, thro ugh Figures 4-7, for =32 , and Figures 8-11, for =43 , that, for these graphs, 0Gsfor cfor the chosen values of c. Figure 4. Case. =32 and =14c. Figure 5. Case. =32 and =12c. Figure 6. Case. =32 and =34c. Figure 7. Case: =32 and =910c. Figure 8. Case: =43 and =14c. Copyright © 2011 SciRes. AM  K. B. FADIMBA547 Figure 9. Case: =43 and =12c. Figure 10. Case: =43 and =34c. Figure 11. Case: =43 and =910c. 4.3. Other Graphical Experiments for Uniqueness for <<12 In this subsection, we use other arguments to show that the hypotheses of Lemma 2.1 seem to hold for the fun- ctions and a , respectively, for 1< <2 . We con- sider the following functions . ,:= , fxfx fy Fxy kx x yKxKy (38) and ,:= . (39) axax ay Gxy kxx yKxKy Clearly, conditio n (9) hold s for and a, if the fun- ctions and , defined resp ectively by (38) an d (39) are bounded above independently of G and on the region enclosed by the triangle with vertices (0,0), (1,0), and (1,1) i.e. the region y 2,:=>xy,Rx 0,1y R . Notice that the common denominator of both functions is positive in the interior of the region . See Figure 12 below. Functions and Gare very complex by their defi- nition, especially for non integer values of . They in- volve the integral-defined function . They e diffi- cult to handle algebraically. For the present work, we sketch the surfaces representing the two functions, above the region R, for some valu of ar es , using Maple So- ware, in order to analyze their boundedness. This is illu- strated through the Figures 13 through 18. We notice ft the smoothness of the surfaces correspond- ing to the case =2 . This suggests that the two funct- ions are definitended in this case. For =2 ly bou , we show directly that this is indeed the casethat Corollary 4.1 holds. W e prove this through the following lemma. Lemm , i.e. a 4.2 For =2 , functions and , defined by tiv G (38) and (39), resely, are bounded indepen- dently of pec , y over the region R. Proof of Lemma From (32) and (34), i 4.2.t is easily se en that 1 1 2 1 =1 xx fx xx (40) and 2 2 2 = 112123 xx xx xxxx e . (41) s ax Copyright © 2011 SciRes. AM  K. B. FADIMBA 548 Figure 12. Region R. Figure 13. Surface =,zFx , over region R, for =32 . Figure 14. Surface =, Gxy x Figure 15. Surface =, Fxy, over region R, for=43 . =, Gxy over region R, for =32 . Figure 16. Surface, over region R, for=43 . =,zFx =2 . Figure 17. Surface, over region R, for Copyright © 2011 SciRes. AM 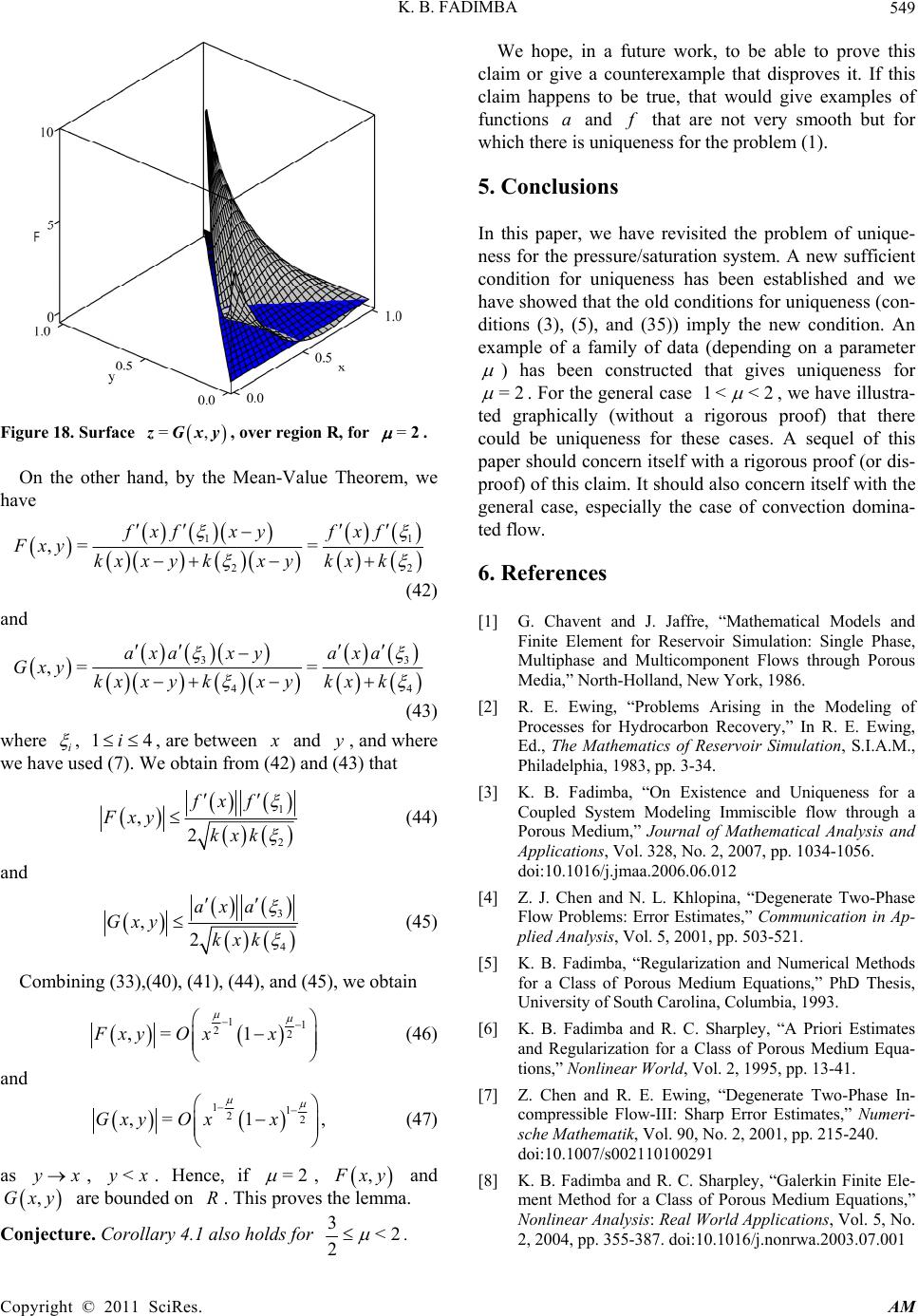 K. B. FADIMBA549 Figure 18. Surface =,zGx , over region R, for =2 . On the other hand, by the Mean-Value Theorem, we have 1 2 ,= = fxf xyfxf Fxykxx ykx ykxk 1 2 (42) and 3 4 ,= = axax yaxa Gxy kxx ykx ykxk 3 4 (43) where i , 14i , are between and and wh ere we haveobtain from an) that y, d (43 used (7). We (42) 1 2 2 fxf yk ,Fx xk (4 an 4) d 3 4 ,2 axa Gxy kxk (45 Combining (33),(40 ), (41), (44), and (45), we obta ) in 11 22 ,= 1Fxy Oxx (4) and 6 11 22 =1 ,Ox (47) ,Gxy x as , . Hence, if yx<yx=2 , , xy and ,Gxy are bounded on. Th Conjecture. Corollary 4.1 also holds f or Ris proves the lemma. 3<2 2 . hope, in a future work, to be able to prove this claim or give a counterexample that disproves it. If this claim happens to be true, that would functions and We give examples of a que that are not very smooth but for which thes uniness for the problem (1). 5. Conclusions In this paper, we have revisited the problem of unique- r the pressure/saturation system. A new sufficient condition for uniqueness has been established and we have showed that the old conditions for un ditions (3), (5), and (35)) imply the new condition. An mple of familndingn a param re i ness fo iqueness (con- exa ay of data (depe oeter ) has been constructedthat gives uniqueness for =2 . For the general case 1< <2 , we have illustra- ted graphically (without a rigorous prothere of) that co e [3] K stence an ysis, Vol. 5, 2001, pp. 503-521. “Regularization and Numerical Methods Porous Medium Equations,” PhD Thesis, University of South Carolina, Columbia, 1993. uld be uniqueness for these cases. A sequel of this paper should concern itself with a rigorous proof (or dis- proof) of this claim. It should also concern itself with the general cas, especially the case of convection domina- ted flow. 6. References [1] G. Chavent and J. Jaffre, “Mathematical Models and Finite Element for Reservoir Simulation: Single Phase, Multiphase and Multicomponent Flows through Porous Media,” North-Holland, New York, 1986. [2] R. E. Ewing, “Problems Arising in the Modeling of Processes for Hydrocarbon Recovery,” In R. E. Ewing, Ed., The Mathematics of Reservoir Simulation, S.I.A.M., Philadelphia, 1983, pp. 3-34. . B. Fadimba, “On Exid Uniqueness for a Coupled System Modeling Immiscible flow through a Porous Medium,” Journal of Mathematical Analysis and Applications, Vol. 328, No. 2, 2007, pp. 1034-1056. doi:10.1016/j.jmaa.2006.06.012 [4] Z. J. Chen and N. L. Khlopina, “Degenerate Two-Phase Flow Problems: Error Estimates,” Communication in Ap- plied Anal [5] K. B. Fadimba, for a Class of [6] K. B. Fadimba and R. C. Sharpley, “A Priori Estimates and Regularization for a Class of Porous Medium Equa- tions,” Nonlinear World, Vol. 2, 1995, pp. 13-41. [7] Z. Chen and R. E. Ewing, “Degenerate Two-Phase In- compressible Flow-III: Sharp Error Estimates,” Numeri- sche Mathematik, Vol. 90, No. 2, 2001, pp. 215-240. doi:10.1007/s002110100291 [8] K. B. Fadimba and R. C. Sharpley, “Galerkin Finite Ele- ment Method for a Class of Porous Medium Equations,” Nonlinear Analysis: Real Wo rld Appl icati ons, Vol. 5, No. 2, 2004, pp. 355-387. doi:10.1016/j.nonrwa.2003.07.001 Copyright © 2011 SciRes. AM  K. B. FADIMBA Copyright © 2011 SciRes. AM 550 s for Flows through Po- ater Flow and umerical a, “Computational Methods mylie, “A near Optimal Order Approximation to a eak Solu- [9] M. E. Rose, “Numerical Method rous Media-I,” Mathematics of Computations, Vol. 40, No. 162, 1983, pp. 437-467. [10] J. Bear and A. Verruijt, “Modeling Groundw Pollution,” D. Reidel Publication Company, Dodreich, 1987. [11] R. E. Ewing and H. Wang, “A Summary of N Methods for Time-Dependent Advection Dominated Par- tial Differential Equations,” Journal of Computational and Applied Mathematics, Vol. 128, No. 1-2, 2001, pp. tion 423-445. doi:10.1016/S0377-0427(00)00522-7 [12] Z. Chen, G. Huan, and Y M for Multiphase Flows in Porous Media,” SIAM Computa- tional Science and Engineering, Philadelph ia , 2006. [13] D. L. S Class of Two-Sided Nonlinear Parabolic Partial differen- tial Equations,” PhD Thesis, University of Wyoming, Laramie, 1989. [14] Z. Chen, “Degenerate Two-Phase Incompressible Flow-I: Existence, Uniqueness, and Regularity of a W ,” Journal of Differential Equations, Vol. 171, 2001, pp. 203-232. doi:10.1006/jdeq.2000.3848
|