Journal of Environmental Protection, 2011, 2, 287-297
doi:10.4236/jep.2011.23032 Published Online May 2011 (http://www.scirp.org/journal/jep)
287
Landfill Liner Failure: An Open Question for
Landfill Risk Analysis
Alberto Pivato
IMAGE, Department of Hydraulic, Maritime, Geotechnical and Environmental Engineering, University of Padua, Padova, Italy.
Received December 29th, 2010; revised February 1st, 2011; accepted March 10th, 2011.
ABSTRACT
The European Union Landfill regulations (1999 /31/EC) are based on the premise that technological barrier systems
can fully contain all landfill leachate produced during waste degradation, and thus provide complete protection to
groundwater. The long-term durability of containment systems are to da te unproven as landfill liner systems have only
been used for about 30 years. Many recent studies have drawn attention to some of the deficiencies associated with ar-
tificial lining systems, particularly synthetic membrane systems. Consequently, failure modes of landfill liners need to
be quantified and analysed. A probabilistic approach, which is usually performed for complex technological systems
such as nuclear reactors, chemical plants and spacecrafts, can be applied usefully to the evaluation of landfill liner
integrity and to cla rify the failure issue (reliability) of liners currently applied. This approach can be suitably included
into risk analysis to manage the landfill aftercare period.
Keywords: Landfill Liners, System Reliability, Risk Analysis, Landfill Aftercare Period
1. Introduction
In the last decades the contained landfill has been deve-
loped, installing liners (mineral and synthetic) and col-
lecting gas and leachate emissions.
However, many researches have found that the lining
system has limited (10 - 30 years) duration. When liners
fail, a variety of compounds whose concentration may be
above the acceptable level (table values) spread into the
environment.
The uncontrolled emissions depend on the long term
behaviour of chemicals in the landfill and on the typo-
logy of liner failure. Figure 1 shows a potential scenario
of contamination constituted by a biodegradable organic
chemical leakage. The uncontrolled emissions to the en-
vironment over the time is the sum of two opposite pro-
cesses: a long-time degradation of chemicals in the land-
fill and a short-time increase of leachate leakage due to
liner failure.
The first process is generally modelled by a first order
kinetic such as:
0
() kt
l
CtC e


where: Cl(t) is the concentration of the contaminant in
the leachate (mg/m3); C0 is the initial peak concentration
of the contaminant in the leachate (mg/m3); t is the simu-
lation time; k is a kinetic constant describing the rate of
decrease of the chemical. This value can be expressed also
by the half time (T1/2 ): 1/2
ln 2kT

.
The second process depends on many variables such
as the leachate head, the liner layer and the liner per-
formance. Many analytical models have been proposed
and all show an initial period in which the leakage is
very low because the the containment system is ex-
pected to function adequately. The results are in term
of leachate quantity by time (m3/day) that emigrates
from the landfill to the environment.
The problem consists in the fact that the potential
emissions from landfills (biogas and leachate) can last
for a very long time (centuries), more than the barriers
(liners).
In order to control long term environmental impact
and guarantee landfill sustainability an approach based
on the risk evaluation of long term emissions should be
assessed; this is mainly correlated to the chemical degra-
dation into the landfill and to the barrier (e.g. liner) per-
formance. However, the Landfill regulations in Europe
state that aftercare must continue for almost 30 years
after the site has been closed independently to the landfill
risk at that time. This is a bureaucratic term and after 30
years the landfill will be a contaminated soil, no longer
financially supported by a waste fee. The operations
lanned for this phase consist only in monitoring and p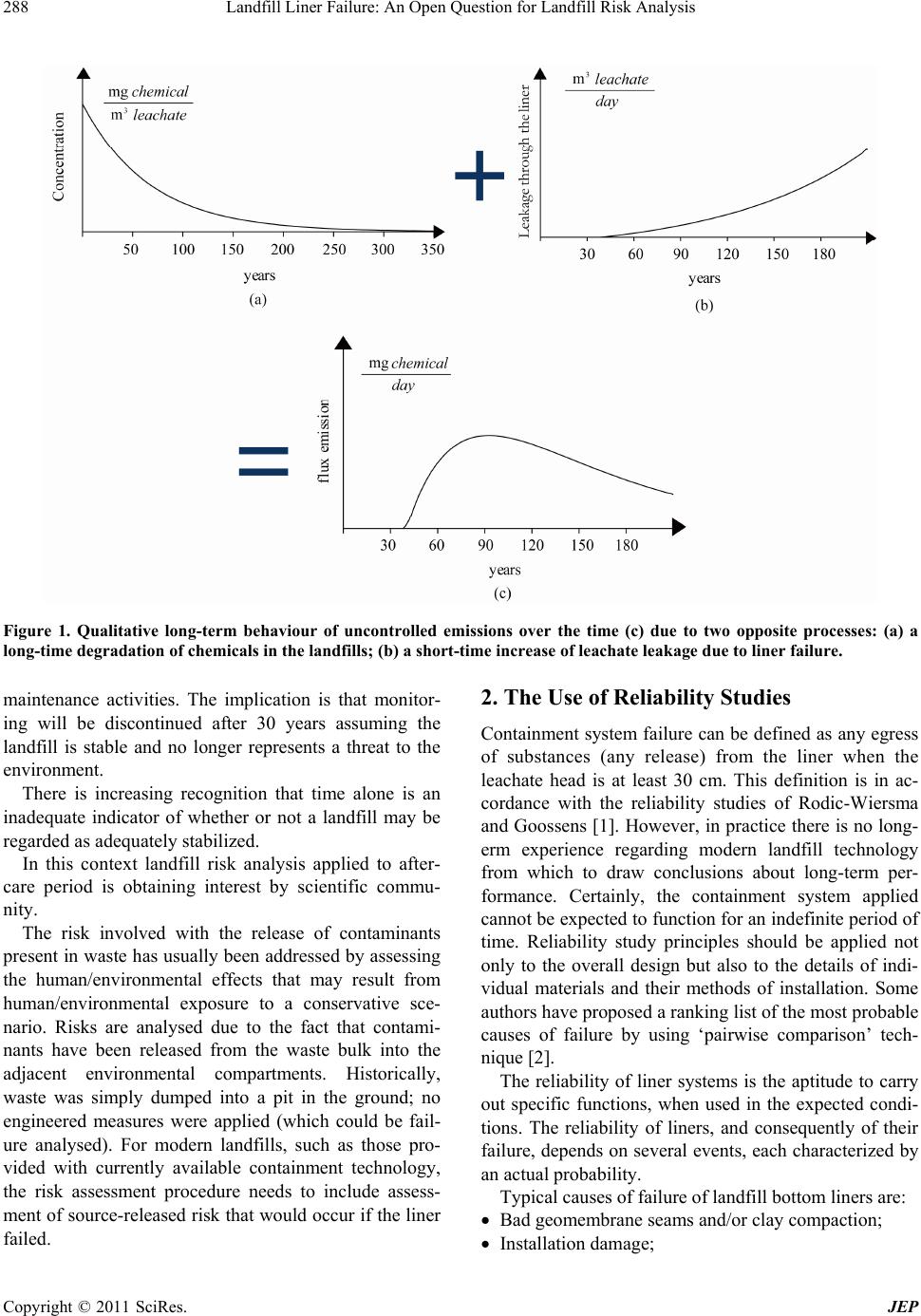

Landfill Liner Failure: An Open Question for Landfill Risk Analysis
288
Figure 1. Qualitative long-term behaviour of uncontrolled emissions over the time (c) due to two opposite processes: (a) a
long-time degradation of chemicals in the landfills; (b) a short-time increase of leachate leakage due to liner failure.
maintenance activities. The implication is that monitor-
ing will be discontinued after 30 years assuming the
landfill is stable and no longer represents a threat to the
environment.
There is increasing recognition that time alone is an
inadequate indicator of whether or not a landfill may be
regarded as adequately stabilized.
In this context landfill risk analysis applied to after-
care period is obtaining interest by scientific commu-
nity.
The risk involved with the release of contaminants
present in waste has usually been addressed by assessing
the human/environmental effects that may result from
human/environmental exposure to a conservative sce-
nario. Risks are analysed due to the fact that contami-
nants have been released from the waste bulk into the
adjacent environmental compartments. Historically,
waste was simply dumped into a pit in the ground; no
engineered measures were applied (which could be fail-
ure analysed). For modern landfills, such as those pro-
vided with currently available containment technology,
the risk assessment procedure needs to include assess-
ment of source-released risk that would occur if the liner
failed.
2. The Use of Reliability Studies
Containment system failure can be defined as any egress
of substances (any release) from the liner when the
leachate head is at least 30 cm. This definition is in ac-
cordance with the reliability studies of Rodic-Wiersma
and Goossens [1]. However, in practice there is no long-
erm experience regarding modern landfill technology
from which to draw conclusions about long-term per-
formance. Certainly, the containment system applied
cannot be expected to function for an indefinite period of
time. Reliability study principles should be applied not
only to the overall design but also to the details of indi-
vidual materials and their methods of installation. Some
authors have proposed a ranking list of the most probable
causes of failure by using ‘pairwise comparison’ tech-
nique [2].
The reliability of liner systems is the aptitude to carry
out specific functions, when used in the expected condi-
tions. The reliability of liners, and consequently of their
failure, depends on several events, each characterized by
an actual probability.
Typical causes of failure of landfill bottom liners are:
 Bad geomembrane seams and/or clay compaction;
 Installation damage;

Landfill Liner Failure: An Open Question for Landfill Risk Analysis289
 Not safeguarding liner in operation;
 Pipes penetrating liner;
 Clogging of the leachate collection and removal sys-
tem;
 Geotechnical failure;
 Unanticipated chemical attack;
 Breach by vertical pipes.
The reliability evaluation can be carried out with two
different approaches.
The first is deductive analysis, which analyses a series
of similar historical failure events. A considerable
amount of information on different installations should
be collected and divided into the better comparable
categories according to the characteristic elements. For
example, a landfill with only a clay liner on the bottom
should be included in the group that contains the same
containment system. Once the reliability for a set of
landfills with similar features has been estimated, a sta-
tistical estimator can be defined and extended to the
whole group.
The comparison is always subject to approximation,
due to the diversification of the boundary conditions: the
geology of the sites, the environmental conditions, the
design and the materials, etc. In a comprehensive evalua-
tion, it is also important to consider the analogies in the
different working conditions. These precautions are
needed in order to develop a statistical study that pro-
duces results consistent with the aforementioned reliabi-
lity definition as well as reduce the inevitable approxi-
mations and uncertainties in this type of comparison.
A more adaptable and reliable method is predictive
analysis. This analysis entails knowledge of failure
probability of the individual elements (subsystems) and
combines them with an appropriate probabilistic analysis
to define the reliability of a more complex system. A
standardized procedure is “Fault Free” analysis, which is
used in the Netherlands and in other countries to predict
the aftercare period cost [3].
Aftercare period costs are the ones connected to the
operations planned for this phases and consist only in
monitoring and maintenance activities:
 Cap maintenance and monitoring;
 Leachate recirculation operation and maintenance
(where permitted!);
 Leachate collection system operation and mainte-
nance;
 Landfill gas collection
80 03
。
'
system maintenance and
monitoring;
 Landfill gas migration control and monitoring;
 Groundwater and surface water monitoring;
 Security and grounds maintenance.
 The leakage of a bottom liner, i.e. the failure of the
barrier, is caused by one or a set of system compo-
nents generating failure events. The environment,
plant personnel, aging of materials etc. can influence
the system only through its components. As proposed
by Henley and Kumamaoto [4] we distinguish dif-
ferent component failures:
 A primary failure is defined as the component being
in the non-working state for which the component is
held accountable. A primary failure occurs under in-
puts within the design envelope, and component
natural aging is responsible for such failure. Among
other aspects, the aging of the components in the liner
depends on the chemical composition of the leachate
and on the high temperature due to the exothermic
reactions inside the landfill.
 A secondary failure is the same as a primary failure
except that the component is not held accountable for
the failure. Past or present excessive stresses placed
on the component are responsible for secondary fail-
ure. Examples are environmental stresses (geological
assessment, uncontrolled groundwater infiltration,
high leachate head, etc.), human error such as if per-
sonals break the components (installation damage,
bad compaction of clay liner, etc.).
 A command fault is defined as the component being
in the non-working state due to improper control sig-
nal or noise (failure of pump signal to extract leachate,
etc).
This subdivision is essential in order to properly collect
failure data for reliability studies.
In the present work, basic events related to system com-
ponents with binary states, i.e., normal state and failed state
will be quantified first. The quantification is then extended
to components having plural failure modes.
3. Single Failure Mode Analysis
We assume that at any given time a liner system is ei-
ther functioning normally or failed, and that the com-
ponent state changes as time evolves (Figure 2). It is
assumed that the component changes its state instanta-
neously when the normal to failed transition takes place.
The transition to the failed state is failure and the failed
state continues forever if the component is non-repair-
able (as generally is the case of a landfill liner).
The time failure is defined as the interval of time be-
tween the moment the barrier system is put into opera-
tion (including all the elements composing it) and its
failure. This interval is generally a stochastic variable (x
 0). The distribution

()

F
tP tx is the probability
that the system fails prior to time t, assuming that the
system has been in function since t = 0. The system reli-
ability is expressed by:

Landfill Liner Failure: An Open Question for Landfill Risk Analysis
290
NORMAL
STATE
FAILED
STATE
COMPONENT FAILS
The failure rate is the probability that the component
experiences a failure per unit time at time t, given that the
component is in normal state at time zero and is normal at
time t. A suitable model is the one proposed by Herz [6]
developed for water mains. He proposed a failure prob-
ability distribution density function based on the principles
that had originally been applied to population age classes
or cohorts. The probability density
 
Figure 2. Transition diagram of component state.

f
t, failure rate




t  and failure probability


F
t

functions are:
 
1RtFtPt x
The mean time of failure is the mean of the variable x
[5]. Since for , we conclude that:

0Fx0x
 

2
1btc
btc
abe
ft ae










0
d
M
TTFRtt




btc
btc
be
tae





Probability that the system functioning at time t fails
prior to time
x
t t equals:







,
/1
PxtFxFt
Fx tPt Ft
 
 

xx
xx
 


1
1
btc
btc
abe
Ft ae



 
differentiating with respect to x:
where a is the aging factor (year-1); b is the failure factor
(year-1); and c is the resistance time (years).



/1
f
x
fxt
F
t


x
4. System Reliability Analysis
The product

/

f
xxt dx equals probability that the
system fails in a time interval


,d
x
x+x, assuming that
it functions at time t. The conditional density


/
f
xtx
is a function of x and t. Its value at x = t is a function of t
only. This function is denoted as and is called the
failure rate:

t 
The problem considered above strictly involves a single
failure mode, defined by a single failure state. Many
physical systems that are composed of multiple compo-
nents can be classified as series connected systems or par-
allel-connected systems, or a combination of both. More
specifically, the failure events (eg. in the case of multiple
failure modes) may also be represented as events in series
(union) or in parallel (intersection) (Figure 3).
 

/1
f
t
tftt
F
t
 

x
Figure 3. Interconnection of systems: (a) parallel; (b) series. The figures on the right show the regions in the x,y space that
atisfy the probability conditions. s

Landfill Liner Failure: An Open Question for Landfill Risk Analysis291
We can assume that a landfill is constituted by several
cells (system in series) and each cell is provided with a
liner with more elements (system in parallel). Each cell
will function as long as at least one liner functions and
the complete landfill system will function as long as all
the cells function.
Two systems S1 and S2, with failure times respect-
tively x and y, can be connected in parallel or series,
making a new system with failure time z (Figure 3). In
the case of system in parallel, the system S fails when all
the subsystem fails and the following expression is used:
z


max ,xy
If the two systems are independent, then:
 
,
zxy
F
zPzzFzFz xy
In the case of system in series, the system S fails when
at least one subsystem fails and the following expression
is used:
z


max ,xy
If the two systems are independent, then:
 
 
1,
z
xyxy
FzPz z
F
zFzFzFz
 

xy
We can assume that a landfill is constituted by sev-
eral cells (system in series, Figure 4) and each cell is
provided with a liner with more elements (system in
parallel, Figure 5). Each cell will function as long as at
least one liner is functioning and the complete landfill
system will function so long as all the cells are func-
tioning.
Complex liner systems involve multiple failure modes,
in which the occurrence of any one of the potential fail-
ure modes will constitute failure or non-performance of
the system or component. A systematic scheme, such as
a Fault Tree for identifying all potential failure modes,
may be required.
4.1. Fault Tree Analysis
A Fault Tree is widely used to assess the failure of a
“Technological System”. Firstly, the Technological Sys-
tem for which the analysis to be performed is defined.
Then, a system failure event is specified (this is called
Top Event) and a “backwards” analysis is conducted to
identify all possible chains of events that could lead to
the given end point. In doing so, individual basic events
are identified which may lead to the top event alone or in
combination with others. It makes use of a codified
symbology for the events and for those decision-making
structures (Logical Gate). A summary of such symbol-
logy is collected in Table 1.
The fundamental logic gates are AND and OR. The
logic functions and indicates that an event occurs only if
all of the sub-events take place simultaneously. The logic
functions or indicates that an event occurs only if at least
one of the sub-events is verified, independently from
others.
Figure 4. Example of a landfill with several cells (system in series).

Landfill Liner Failure: An Open Question for Landfill Risk Analysis
292
Figure 5. Example of a liner with more elements (system in parallel).
Table 1. Symbology used in the fault tree analysis.
EVENTS
LOGIC ELEMENT SYMBOLS MEANING
EVENT
Primary system
EVENT
Intermediate event
EVENT
Top Event or Final Event
LOGIC GATE
LOGIC ELEMENT SYMBOLS MEANING
The event happens if E1
and E 2
simultaneous take place
The event happens if E1 or
E2
takes place
For generic event Ei, the probability P(Ei) is the exis-
tence probability of the event A at time t. Given two ge-
neric events A and B, each characterized by an actual
probability, the following relations are verified:





 

12121
212 121
||
PEPEandEPEEPEE
PEPE EPEPEE

 

2









  
12 121
1212
PEPEOrEPEEPEE
PEPEPEE



2

where


12
|PE E is the conditional probability of E1,
given E2 and it is equal to:



12
12
2
|PEE
PE EPE 
If E1 and E2 are independent the above expressions
become easier, because


12 1
|PE EPE

. In the case
of more events (E1, E2, E3 and E4) the probability of the
top event is:




 
1234
1312412
||
PEPEEE E
PEPEEEPEE EE



3





 
  
12341 2
341234
PEPEEE EPEPE
PEPEPE EEE
 
 
Knowing the probabilities of the individual basic
events that constitute the system’s Fault Tree, you can
estimate the probability of failure of the entire system by
means of these fundamental algebra rules.

Landfill Liner Failure: An Open Question for Landfill Risk Analysis293
A detailed Fault Free can be developed for the bottom
liner of a Sanitary Landfill. The diagram structure should
contain a mineral liner, a collection system and a syn-
thetic liner. The failure of the whole liner system occurs
in the case of simultaneous failure of the mineral liner
(clay, bentonite), synthetic liner (geomembrane, GCL)
and leachate collection system. The probability (P(E)) of
liner failure can be determined as follows:
 
123
PEPEEE
The events are dependent. In fact, a failure of one
component increases the load supported by the other
components. Consequently, the remaining components
are more likely to fail, and we can not assume statistical
independence of components.
The functionality loss of each of these three compo-
nents is due to different causes that international litera-
ture has studied for a long time. Although each failure is
an individual event related to site-specific ground condi-
tions, climate conditions and design details, general be-
haviour trends can be deduced by considering these three
elements. A summary of the findings is presented in Ta-
ble 2. However, for each component a main failure state
can be defined as shown in Table 3. The failure of the
component at time t occurs if the physical variable (pi)
that describes the failure state is higher than a safety or
project value (si).
4.2. Conditional Events
The calculation of safety or failure probability of a sys-
tem through the above equations is generally difficult
due to the dependence of variables; approximation is
almost always necessary. With regard to the latter, upper
bounds of the corresponding probabilities are useful un-
der the conservative principle assumption.
For the selected fault tree, an estimation of the failure
upper bound (P(E)) is [26]:


3
1
11 i
i
PE PE

  


This expression indicates that the containment system
will survive until all the components (mineral liner, syn-
thetic liner and collection system) will work. This is a
strong simplification of the study, but at the moment, if
there are not sufficient data to support the conditional
statistics of the compartments, it is the only solution.
Table 2. Causes of the basic failure events.
COMPONENT CAUSES
COLLECTION SYSTEM Settlement, bad design and/or choice of materials, clogging due to particulate transport/chemical precipitation,
Clogging due to biological material buildup, Pipe breakage/slope change
MINERAL LINER
Waste movement, settlement, bad compaction, bad design and/or choice of materials, pipes penetrating liner, geo-
technical failure, uncontrolled groundwater infiltration, instability of the sub-grade both slope and basal heave,
exhaustion adsorption capacity, increase in hydraulic conductivity due to interaction with leachate and to cracking
SYNTHETIC LINER
Installation damage, bad design and/or choice of materials, aging, pipes penetrating liner, geotechnical failure,
unanticipated chemical attack, tension of the materials, uncontrolled groundwater infiltration, instability of the
sub-grade both slope and basal heave
Table 3. Failure state for single component.
COMPONENT DESRIPTION OF FAILURE PHYSICAL
VARIABLE (pi) THE FAILURE STATE (si) REFERENCE
Leachate
collection system
Clogging of drainage layer due to
chemical precipitation and to bio-
film growth
Ks
(Hydraulic conductivity) 10−5 - 10−7 m/s [7,8]
Exhaustion adsorption capacity EC (Exchangeable
Cations)
CEC
(Cation Exchange Capacity) [9]
Mineral liner Increase in hydraulic conductivity
due to interaction with leachate and
to cracking
Ks
(Hydraulic conductivity) 10−9
m/s [10-12]
Aging of matrix structure due to
the corrosive effects of leachate
and to elevated temperatures gen-
erated by the exothermic processes
occurring in landfills
Concentration of
antioxidant
Allowable number/type of
defects as reported in the
Construction Quality
Assurance
[13-19]
Synthetic liner
Damage due to poor dumping
practices
Number of defects by unit
area
Allowable number/type of
defects as reported in the
Construction Quality
Assurance
[20-25]

Landfill Liner Failure: An Open Question for Landfill Risk Analysis
294
5. Liner Failure Data Base Procedure
When N items being considered fail respectively at times
t1, t2,.., tn, then the failure probability at time t1 can be
approximated by


11/
F
tN, at time t2 by

22/
F
tN,
and, in general by

r/
F
trN.
Given sufficient data, a failure distribution can be de-
termined by a piecewise polynomial approximation.
When only fragmentary data are available we cannot
construct the complete curve. In such case, an appropri-
ate distribution (such as Exponential, Normal, Log-
Normal, Weibull, Poisson, etc.) must be assumed and its
parameters evaluated from data.
This approach can be conducted in two different ways.
First, the failure data are related to many landfills
where the failure has been ascertained by means of
monitoring data (inductive analysis). The failure of the
system has been indirectly estimated as chemical con-
centration (for example in a monitoring well outside the
landfill) exceeding a table value. The problem of this
approach consists in 1) the selection of a group of land-
fills with similar liner design and operating conditions; 2)
scarce data available on groundwater contamination be-
fore the establishment of Law 471/99 in Italy; 3) unsuit-
able location of monitoring wells; 4) ambiguous data that
does not permit locating the contaminant source; and, 5)
underestimated failure curves, because it considers deg-
radation of contaminants in the landfill, natural attenua-
tion in liner and in the environment.
Second, the failure data are related to single compo-
nent performance (mineral layer, drainage system, syn-
thetic liner) according to Table 3. Probability re-mposi-
tion of the components results in failure of the entire
system (predictive system). For these reliability problems,
the ‘average’ failure data from several lab tests may best
describe the system behaviour. In this case, measure-
ments of a parameter at one scale (eg. laboratory meas-
urements) can be used to define the parameter at a larger
scale. This approach of using sample measurements to
define the ‘average’ system behaviour is described as
upscaling. Where the system is believed to be heteroge-
neous, then upscaling should be used with care.
However, literature studies reveal that field and lab
data on landfill failures are not enough for establishing
probability distributions. In the future, a more accurate
measure of liner failure could be done by a monitoring
approach based on a Leak Detection Sump [27]. There-
fore, subjective data needed to be included. In these
cases it has become fairly customary for experts in re-
lated fields to be asked to give their best subjective esti-
mate, i.e. their expert opinion on the subject.
Direct estimates about the mean life of liner barrier
components can be obtained by the Delphi technique the
contribution of each factor to the failure of the subsystem.
The purpose of the Delphi technique is to elicit informa-
tion and judgments from participants to facilitate the reso-
lution of reliability problems when there are no field data.
It does so without physically assembling the contributors.
Instead, information is exchanged via mail, FAX, or email.
This technique is designed to take advantage of partici-
pants’ creativity as well as facilitating effects of group
involvement and interaction. It is structured to capitalize
on the merits of group problem-solving and minimize the
liabilities of group problem-solving.
According to the first approach, a failure distribution
has been determined for a size sample of almost 30 sites
in the North of Italy that are designed as contained land-
fills respecting the following principles ( details on land-
fills are collected in Table 4):
 Minimize rainfall infiltrations;
 Maintain anaerobic conditions;
 Isolate the waste from the environment with natural
and artificial materials;
 Collect biogas and leachate by means of extraction
systems, such as vertical and horizontal materials
(when collection systems are present).
Figure 6 shows the failure of landfills in the first 30
years and the Herz model fitting curve [6]. The applica-
tion shows that in the North of Italy landfills can con-
taminate with high probability (more than 60%) the
groundwater in the first 30 years.
6. Conclusions
This paper illustrates a suitable methodology for evalu-
ating landfill liner failure during aftercare. There are two
different approaches: a deductive and a predictive analy-
sis. The former can be used only for landfills with similar
design and operating conditions, the latter (more flexible)
requires information regarding correlation of variables.
For successful application, both approaches require more
accurate liner failure data.
Currently, the analysis of failure data shows a lack
of information to assess the approach of system reli-
ability. A simplification can be obtained considering
the worst case (P(E) = 1) for the containment system.
This assumption is routinely included in traditional
hydrological risk assessments and it is reliable if the
failure time is lower than the simulation time in which
the risk is evaluated; otherwise the approach is too
conservative and the results do not represent what
really could occur.
In this “precautionary” approach, average defect val-
ues for synthetic liner are assumed; performance of min-
eral liner remains constant over time and is the same as
measured in the liner test; performance of drainage sys-
tem is indirectly considered in the leachate head estima-

Landfill Liner Failure: An Open Question for Landfill Risk Analysis295
Table 4. Characteristics of landfills used for the definition of the failure curve. All the landfills are sited in the North of Italy.
For each landfill the failure time has been estimated as the number of years after the beginning in which the chemical con-
centration exceeding a table value. Municipal Solid Waste = MSW; Inert Waste = IW.
LANDFILL
VOLUME
ESTIMATED FAILURE
TIME
LANDFILL
CODE
WASTE
TYPE CONTAINMENT SYSTEM DESIGN
(m3) (years)
RSA MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 1,450,000 12
BCA MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 700,000 43
NBA MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 600,000 22
CAN MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 350,000 19
URB MSW Clay liner (>1 m) 200,000 1
GRI MSW and
IW
Clay liner (>2 m), geomembrane, drainage layer, leachate col-
lection system 420,000 59
DEN MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 135,000 28
AUS MSW Clay liner (>1 m), drainage layer, leachate collection system 900,000 36
GER MSW Clay liner (>1 m), geomembrane 850,000 17
NOD MSW Clay liner (>1 m), geomembrane, drainage layer 930,000 34
USA MSW Clay liner (>1 m) , drainage layer, leachate collection system 1,300,000 5
AMC MSW Clay liner (>1 m), drainage layer, leachate collection system 1,100,000 20
BBL IW Clay liner (>1 m), geomembrane 970,000 25
BST MSW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 780,000 26
BRT MSW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 670,000 25
ILP MSW Clay liner (>1 m), geomembrane 440,000 13
RIF MSW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 820,000 7
MCH MSW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 600,000 28
RNO MSW and
IW Clay liner (>1 m), geomembrane 760,000 30
SHC MSW and
IW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 300,000 23
UNM MSW Clay liner (>1 m), geomembrane 470,000 40
CPD MSW
Clay liner (>1 m) geomembrane, drainage layer, leachate
collection system 292,500 27
AQO MSW Clay liner (>1 m), geomembrane 300,000 35
MDA MSW
Clay liner (> 1 m), geomembrane, drainage layer, leachate
collection system 1,000,000 36
LGO IW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 1,600,000 38
TRO MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 3,200,000 39
CRA MSW
Clay liner (>1 m), geomembrane, drainage layer, leachate col-
lection system 1,101,000 40
TRV1 MSW and
IW Clay liner (>1 m) 250,000 41
TRV2 MSW and
IW Clay liner (>1 m) geomembrane 450,000 21
TRV3 MSW and
IW Clay liner (>1 m), geomembrane 650,000 33

Landfill Liner Failure: An Open Question for Landfill Risk Analysis
296
Figure 6. Cumulative curve of failure of contained landfills in the north of Italy.
tion used for assessing leachate leakage.
A simplification can be assumed considering the worst-
case approach as is generally used in traditional hydro-
logical risk assessments. This implies calculating the
effects of contamination given that leachate has been
released from the landfill liner. However, the results are
often too conservative and do not represent what could
actually occur.
7. Current & Future Developments
The approach described in the paper should be included
in a standardized methodology in order to manage after-
care period. Three should be the possible outcomes from
this methodology:
Continue Aftercare. If leachate emissions still require
significant levels of care within the regulatory frame-
work for environmental protection, the outcome of the
evaluation will direct continuation of aftercare under the
currently approved plan. Some care activities may be
optimized according to outcome of the study.
Optimize Aftercare. In many cases, the evaluation may
reveal that the intensity or scope of some care activities
can be reduced while still providing the necessary level
of environmental protection. In these cases, the relevant
aftercare activities may be optimized. Optimization may
involve, for example, eliminating non-detected constitu-
ents from further monitoring, reducing maintenance fre-
quencies, or changing the design of a system.
End Regulated Aftercare. If the study reveals that
leachate emissions don’t represent a risk for the envi-
ronment, then regulated aftercare would be ended, al-
though a minimum level of care (herewith, custodial care)
will invariably still be required (generally for the cap and
general site upkeep). A custodial care program would
involve property management activities that are typical
of any property, such as paying property taxes, control-
ling access, complying with local zoning ordinances, and
complying with the property-use restrictions identified in
the deed to the property.
8. Acknowledgements
The Author wish to thank Prof. Raffaello Cossu from
Padua University for his fundamental help in this study.
REFERENCES
[1] L. J. Rodic-Wiersma and L. H. J. Goossens, “Assessment
of Landfill Technology Failure,” In: T. H. Christensen, R.
Cossu and R. Stegmann, Eds., Proceedings Sardinia 2001,
8th International Waste Management and Landfill Sym-
posium, Environmental Sanitary Engineering, CISA,
Cagliari, Vol. 1, 2001, pp. 695-704.
[2] T. H. Saaty, “The Analytic Hierarchy Process,” RWS
Publications, Pittsburgh, 1990.
[3] A. A. M. Boerboom, E. Foppen and O. Van Leeuwen,
“Risk Assessment Methodology for Aftercare of Land-
fills Based on Probabilistic Approach,” In: T. H. Chris-
tensen, R. Cossu and R. Stegmann, Eds., Proceedings
Sardinia 2003, 9th International Waste Management and
Landfill Symposium, Published by CISA, Environmental
Sanitary Engineering, Cagliari, 2003.
[4] E. J. Henley and H. Kumamoto, “Reliability Engineering
and Risk Assessment,” Englewood Cliffs, Prentice-Hall,

Landfill Liner Failure: An Open Question for Landfill Risk Analysis297
New Jersey, 1981.
[5] A. Papoulis, “Probability, Random Variables and Sto-
chastic Processes,” McGraw-Hill, New York, 1993.
[6] R. K. Herz, “Ageing Process and Rehabilitation Needs of
Drinking Water Distribution Networks,” Journal of Wa-
ter SRT-Acqua, Vol. 47, No. 6, 1996, pp. 275-283.
[7] D. Cazzuffi, R. Cossu and M. C. Lavagnolo, “Efficiency
of Geotextiles and Geocomposites in Landfill Drainage
Systems,” In: T. H. Christensen and R. Cossu, Eds.,
Landfilling of Waste: Barriers, London, 1994.
[8] H. August, “Leachate Drainage Systems,” Advanced
Landfill Liner Systems, Thomas Telford Publishing,
Thomas Telford Services Ltd., London, 1997, pp. 84-93.
[9] C. A. J. Appelo and D. Postma, “Geochemistry, Ground-
water and Pollution,” 2th Edition, Taylor & Francis,
Rotterdam, 1994, p. 536.
[10] R. M. Quigley and F. Fernandez, “Effect of Organic Liq-
uids on the Hydraulic Conductivity of Natural Clays,” In:
T. H. Christensen, R. Cossu and R. Stegmann, Eds.,
Landfilling of Waste: Barriers, E & FN Spon, London,
1994, pp. 203-218.
[11] A. Cancelli, R. Cossu, F. Malpei and A. Offredi, “Effects
of Leachate on the Permeability of Sand-Bentonite Mix-
tures,” In: T. H. Christensen, R. Cossu and R. Stegmann,
Eds., Effect of Organic Liquids on the Hydraulic Conduc-
tivity of Natural Clays, in Landfilling of Waste: Barriers,
E & FN Spon, London, 1994, pp. 259-293.
[12] J. L. Daniels, H. I. Inyang and I. K. Iskandar, “Durability
of Boston Blue Clay in Waste Containment Applica-
tions,” Journal of Materials in Civil Engineering, Vol. 15,
No. 2, 2003, pp. 144-152.
doi:10.1061/(ASCE)0899-1561(2003)15:2(144)
[13] H. E. Haxo and P. D. Haxo. “Basic Composition and
Properties of synthetic Materials in Lining Systems,” In:
T. H. Christensen, R. Cossu and R. Stegmann, Eds.,
Landfilling of Waste: Barriers, E & FN Spon, London,
1994, pp. 317-343.
[14] A. L. Rollin, J. Mlynarek, J. Lafleur and A. Zanescu,
“Performance Changes in Aged In-Situ HDPE Geomem-
brane,” In: T. H. Christensen, R. Cossu and R. Stegmann,
Eds., Landfilling of Waste: Barriers, E & FN Spon, Lon-
don, 1994, pp. 431-443.
[15] C. Duquennoi, C. Bernhard and S. Gaumet, “Laboratory
Ageing of Geomembranes in Landfill Leachates,” In: T.
H. Christensen, R. Cossu and R. Stegmann, Eds., Pro-
ceedings Sardinia 95, Fourth International Waste Man-
agement and Landfill Symposium, CISA, Environmental
Sanitary Engineering, Inc, Cagliari, Vol. 2, 1993, pp.
397-404.
[16] R. Surmann, P. Pierson and P. Cottour, “Geomembrane
Liner Performance and Long Term Durability,” In: T. H.
Christensen, R. Cossu and R. Stegmann, Eds., Proceed-
ings Sardinia 95, Fourth International Waste Manage-
ment and Landfill Symposium, CISA, Environmental
Sanitary Engineering, Inc., Cagliari, Vol. 2, 1994, pp.
405-414.
[17] H. P. Sangam and R. K. Rowe, “Migration of Dilute
Aqueous Organic Pollutants through HDPE Geomem-
branes,” Geotextiles and Geomembranes, Vol. 19, No. 6,
2001, pp. 329-357.
doi:10.1016/S0266-1144(01)00013-9
[18] R. M. Koerner and Y. G. Hsuan, “Lifetime Prediction of
Polymeric Geomembranes Used in New Dam Cons- truc-
tion and Dam Rehabilitation,” Proceedings Associate of
State Dam Safety Officials Conference, Lake Harmony,
2003.
[19] W. Mueller and I. Jakob, “Oxidative Resistance of
High-Density Polyethylene Geomembranes,” Polymer
Degradation and Stability, Elsevier Science Ltd., Oxford,
Vol. 79, No. 1, 2003, pp. 161-172.
[20] J. P. Giroud and R. Bonaparte, “Leakage through Liners
Constructed with Geomembranes-Part I. Geomembrane
Liners,” Geotextiles and Geomembranes, Vol. 8, No. 1,
1989, P. 27. doi:10.1016/0266-1144(89)90009-5
[21] G. T. Darilek, D. Laine and J. O. Parra. “The Electrical
Leak Location Method for Geomembrane Liners: Devel-
opment and Applications,” Proceedings of the Geosyn-
thetics’89 Conference, San Diego, 1989, pp. 456-466.
[22] D. L. Laine and M. P. Miklas, “Detection and Location of
Leaks in Geomembrane Liners Using an Electrical
Method Case Histories,” Superfund’89 Proceedings of
the 10th National Conference, Washington DC, 1989, pp.
35-40.
[23] P. Colucci and M. C. Lavagnolo, “Three Years Field
Experience in Electrical Control of Synthetic Landfill
Liners,” In: T. H. Christensen, R. Cossu and R. Stegmann,
Eds., Proceedings Sardinia 2001, 5th International Waste
Management and Landfill Symposium, CISA, Environ-
mental Sanitary Engineering, Cagliari, Vol. 2, 1995, pp.
437-452.
[24] S. J. McQuade and A. D. Needham, “Geomembrane
Liner Defect-Causes, Frequency and Avoidance,” Pro-
ceeding Instituion, Civil Engeers Geotechnical Engi-
neering, Vol. 137, No. 4, 1999, pp. 203-213.
[25] A. L. Rollin, M. Marcotte, T. Jacqueline and L. Chaput,
“Leak Location in Exposed Geomembrane Liners Using
an Electrical Leak Detection Techniques,” Proceedings
Geosynthetic 99, Industrial Fabrics Association Interna-
tional, Minneapolis, 1999, pp. 27-102.
[26] J. D. Esary and F. Proschan, “Coherent Structures with
Non-Identical Components,” Technometric, Vol. 5, No. 2,
1981, p. 191. doi:10.2307/1266063
[27] K. H. Johnson and J. L. Panders, “How do Modern Land-
fills Leak?” In: T. H. Christensen, R. Cossu and R. Steg-
mann, Eds., Proceedings Sardinia 2003, 9th International
Waste Management and Landfill Symposium, CISA, En-
vironmental Sanitary Engineering, Inc., Cagliari, 2003.