Materials Sciences and Applications, 2011, 2, 404-410
doi:10.4236/msa.2011.25052 Published Online May 2011 (http://www.SciRP.org/journal/msa)
Some Mechanical and Thermal Properties of
PC/ABS Blends
Rachida Krache, Ismahane Debbah
LMPMP, Département de Génie des Procédés, Faculté de Technologie, Université Ferhat Abbas, Sétif, Algérie.
Received March 9th, 2011; revised March 16th, 2011; accepted March 30th, 2011.
ABSTRACT
A series of blends of Acrylonitrile-Butadiene-Styrene (ABS) and Polycarbonate (PC) were prepared and some of their
thermal and mechanical properties were de termined. The Young’s modulus chang ed gradually and monoton ically with
the polycarbonate con tent. This effect was tentatively explain ed as the antiplasticization of the PC wh ich is ascribed to
the chain mobility, which permits the PC chains to pack more tightly, to the secondary cross-linking between the PC
chains, or to the secondary attachment of bulky side-chains to the PC, thus producing steric hindrance to the rotation of
the PC main chains. Th e experimental values found fo r the impa ct s tr eng th w ere int erme dia te bet wee n th ose of th e n eat
polymers, depending upon the dispersed rubber particles of butadiene in the matrix of SAN (Styrene-Acrylonitrile), and
the dispersed PC particles which gen erally make the ABS more brittle. A maximum value of about 88 KJ/m2 for th e im-
pact strength was observed for the blend with 90% PC. This may be attributed to the strong polymer-polymer interac-
tions for this particular composition. The variations in the heat deflection temperature HDT and the Vicat softening
point with the blend compos ition were very similar, and allowed us to assume that the phase inversion between the ma-
trices of the two polymers takes place at 50% PC. The morphology of the blends revealed by SEM observation, show a
co-continuous structure.
Keywords: PC, ABS, Blends, Impact Strength, Tensile and Flexural Properties, HDT, Vicat Point, Hardness, FTIR,
Morphology
1. Introduction
The mixing or blending of polymers can be an efficient
way of developing materials with novel or selectively
enhanced properties. It is possible to modify some cha-
racteristics of polymer blends by varying the composition.
Incompatible blends present phase separation as dis-
persed nodules in the matrix phase, the consequent low
adhesion leading to undesirable properties. By control-
ling the fraction of each component, a resulting polymer
with the desired properties can be obtained. Usually, the
final objective is to reach a balance between maximum
temperature resistance, toughness, etc, and ease of fabri-
cation. The behavior of polymer blends can be discussed
according to the variation of their properties with the
blend composition. The blending of two or more poly-
mers always affects the properties of the resulting ma-
terial. Three different effects on those properties can be
distinguished: synergistic, antagonistic and additive ef-
fect.
Polycarbonate PC is characterized for its high modulus,
high toughness, high impact strength and difficult proce-
ssability, due to its high melt viscosity. Acrylonitrile-
Butadiene-Styrene (ABS) is a rubber toughened ther-
moplastic, characterized by its notch insensitivity and
low cost. On the other hand, the ABS limitations are:
poor flame and chemical resistance, and low thermal
stability [1].
The commercialization of PC began in 1958; the pro-
duction of the PC/ABS blends started on 1977. The addi-
tion of ABS to PC minimizes its drawbacks without af-
fecting its superior mechanical properties, and also ge-
nerates other useful characteristics, such as glossiness
and low temperature toughness [2]. A number of patents
concerning these blends have been issued in the past, but
the scientific knowledge about their behavior is still li-
mited owing to the complexity of the system. The blends
consist, in fact, of four polymeric species and three
phases, their morphology depending on a variety of fac-
tors: molecular characteristics of the components, ABS

Some Mechanical and Thermal Properties of PC/ABS Blends 405
composition, blend composition, rheological properties,
processing conditions, thermal treatments, etc.
PC and ABS are fairly similar in polarity, and might
be compatible with each other; the ABS grafted rubber
(butadiene) particles chains would remain insoluble, but
firmly bonded by their styrene-acrylonitrile side-chains,
producing good physical properties [3]. Assuming this
fundamental basis for semi-compatibility, it is interesting
to determine simultaneously the behavior of the modulus
and the impact strength of the blends versus the PC con-
tent. The objective of the current study is to investigate
the optimal composition of PC/ABS blend showing the
highest value in different properties without adding any
comptabilizer to this blend.
In the present paper we report the results obtained in
the mechanical and thermal characterization of the
PC/ABS blends. Thus, the bending, tensile, hardness and
impact strength tests, as well as the heat deflection and
distortion temperature tests were performed in the PC/
ABS blends, and the results obtained were correlated
with the blends composition.
2. Experimental
2.1. Materials and Blend Preparation
The materials used in this investigation were the follow-
ing:
Polycarbonate PC Makrolon 3100, supplied by Bayer.
Acrylonitrile-Butadiene-Styrene (ABS) terpolymer Ter-
luran, supplied by BASF.
Both polymers were dried in vacuum at 100˚C (PC)
and 70˚C (ABS) for a period of 24 h before processing.
Dry PC/ABS mixtures with 100/0, 90/10, 80/20, 70/30,
60/40, 50/50, 40/60, 30/70, 20/80, 10/90 and 0/100
weight compositions were prepared in a two roller mixer
Polymix 80 T (Schwabenthan) at 220˚C for 10 minutes
Thereafter, the pelletized blends were mould compressed
for 3 min in a hydraulic press at 250˚C and 200 kg/cm2.
2.2. Techniques
Tensile test on PC/ABS blends (ISO-R-527 standard)
were carried out at room temperature using an Adamel-
Lhomargy DY25 testing machine, assisted with a com-
puter. The force sensor was 2000 Newton and a cross-
head speed of 20 mm/min was used.
Flexural test was carried out in three-point bending on
the same machine of the tensile test at a cross head speed
of 5 mm/min. The specimen dimensions were 4 mm in
thickness and 10 mm in width. The distance between the
supports was 100 mm.
Izod impact test was performed on notched specimens
(method A, ASTM.D 256-73 standard) using a CEAST
pendulum, equipped with a 7.5 Joule hammer.
The hardness shore D test (ASTM D2240 standard)
was performed using a conventional testing machine ap-
paratus and a load of 5 kg.
Vicat softening temperatures were determined accord-
ing to ASTMD 648-72 method A, using a Heraeus Ha-
nalt apparatus.
The heat deflection temperature (HDT) was calculated
according to ISO-R-75 method A, using a DAVENPORT
equipment.
Fourier transform infrared (FTIR) spectra, of com-
pression molded thin films were recorded on a Perkin
Elmer Infrared spectroscopy.
The fractured surface of compression molded speci-
mens (of Notched Impact testing) were coated, and
etched (to have a phase contrast) with an aqueous sodium
hydroxide solution (35 wt% soda) at 110˚C for about 20
minutes to dissolve the PC phase. The specimens were
examined in a LEO 435 VP Scanning Electron Micro-
scopy (SEM).
3. Results and Discussion
3.1. Tensile Test
The variation of Young's modulus in PC/ABS blends as a
function of composition is illustrated in Figure 1. It can
be observed that the experimental values follow the addi-
tivity law, as expected from the general composite theo-
ries. Thus, the modulus of the PC/ABS blends appears to
vary gradually and monotonically from the value of the
ABS to that of the PC. As it is commonly found, the
modulus progressively decreases as the ABS content is
increased, due to the influence of the ABS rubber com-
ponent. The decrease has been postulated to be the tigh-
ter molecular packing revealed by the lowering in the
density data as mentioned in [4] and was tentatively ex-
plained as the anti plasticization of the PC which is as-
cribed to the chain mobility, which permits the PC chains
to pack more tightly, to the secondary cross-linking be-
tween the PC chains, or to the secondary attachment of
bulky side-chains to the PC, thus producing steric hin-
drance to the rotation of the PC main chains [5].
In Figure 2, it can be observed that the stress-at-break
composition curves show negative deviation, (blend pro-
perties lie below the additives line up to 100% PC con-
tent), except for the blend containing 90% PC were a
maximum is again obtained. The observed negative dev-
iation is due to the poor interfacial adhesion between the
homopolymers phases, which causes poor stress transfer
between the matrix and the dispersed phase. A little de-
crease in the slope of the stress properties composition
curve is seen between the composition range (0 - 30%
PC), and then an increase is observed with PC which is
due to the higher proportion of the hard plastic phase.

Some Mechanical and Thermal Properties of PC/ABS Blends 406
Figure 1. Young Modulus of P C/ABS ble nds as a function of
the PC content.
Figure 2. Stress at break of PC/ABS blends as a function of
the PC content.
The effect of the mixing on the break strain of the
blends is even more important than that observed in the
break stress, and it is illustrated in Figure 3. A dramatic
reduction of this property is observed in the mixtures
with respect to linearity until the PC content reaches
30%. Then, the break strain remains constant for the
blends with 30% to 60% PC. Thereafter, a speedy rise in
the values of the break strain is observed, with a maxi-
mum appearing again for the sample with 90% PC. The
extreme influence of the incompatibility in the deforma-
tion at break of polymer blends is well known. Incompa-
tibility gives rise to deformations at break on the order
of 1%. Thus, the ductility level of the PC/ABS blends
can be a consequence of the combined effect of the rub-
bery behavior of the butadiene chains in the ABS and
the partial compatibility between the two polymers at
90% PC.
Figure 3. Strain at break of PC/ABS blends as a function of
the PC content.
3.2. Flexural Properties
Both the flexural modulus and the strength of the blends
have been measured. In Figure 4, the values of the flex-
ural elastic modulus measured in three-point bending
exhibit a clear positive deviation from linearity, that is, a
synergistic behavior. Thus, all the E values obtained for
the blends with 60%, 70%, 80% and 90% PC are higher
than those obtained for the pure components of the
blends. It can be supposed that the component of highest
modulus contributes to the resulting value in a greater
extent than the corresponding to the composition. The
stress or strain concentrations in the matrix may give rise
to increased local contributions to the overall stress with
respect to that which corresponds to the composition of
the blend [6]. Synergistic behavior in the modulus of
polymer blends in relation with composition has been
explained in some cases as a consequence of the blend
densification, due to interactions between the compo-
nents [6]. In Figure 5, the flexural break stress appears to
vary gradually and monotonically with the PC content,
while a significant decrease in the strain is observed in
Figure 6. However, a maximum strain value is again
obtained for the blend with 90% PC.
3.3. Impact Strength
The level of the notched impact strength for both neat
polymers was rather poor (see Figure 7). Due to their in-
compatibility, the blends exhibited impact strength even
lower to the ones showed by pure components. The result
of the Izod impact testing shows the same features as
shown by elongation-at-break (Figure 3). While blends
with lower ABS content (10%) exhibit high impact
strength value (88 kJ/m2), ABS rich blends have much
smaller impact strength values than, both, pure PC and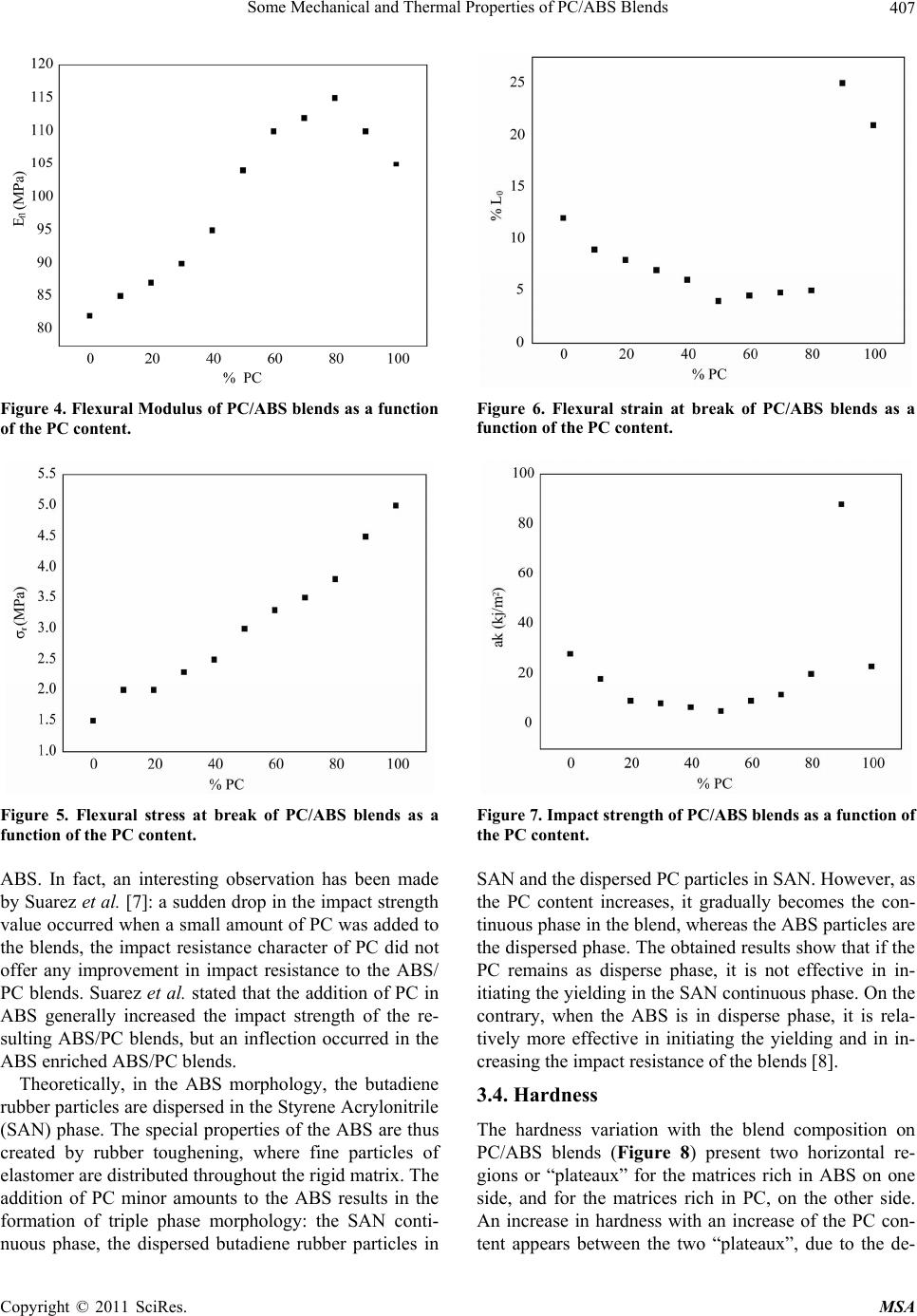

Some Mechanical and Thermal Properties of PC/ABS Blends 407
Figure 4. Flexural Modulus of P C/ABS blends as a function
of the PC content.
Figure 5. Flexural stress at break of PC/ABS blends as a
function of the PC content.
ABS. In fact, an interesting observation has been made
by Suarez et al. [7]: a sudden drop in the impact strength
value occurred when a small amount of PC was added to
the blends, the impact resistance character of PC did not
offer any improvement in impact resistance to the ABS/
PC blends. Suarez et al. stated that the addition of PC in
ABS generally increased the impact strength of the re-
sulting ABS/PC blends, but an inflection occurred in the
ABS enriched ABS/PC blends.
Theoretically, in the ABS morphology, the butadiene
rubber particles are dispersed in the Styrene Acrylonitrile
(SAN) phase. The special properties of the ABS are thus
created by rubber toughening, where fine particles of
elastomer are distributed throughout the rigid matrix. The
addition of PC minor amounts to the ABS results in the
formation of triple phase morphology: the SAN conti-
nuous phase, the dispersed butadiene rubber particles in
Figure 6. Flexural strain at break of PC/ABS blends as a
function of the PC content.
Figure 7. Impact strength of PC/ABS blends as a function of
the PC content.
SAN and the dispersed PC particles in SAN. However, as
the PC content increases, it gradually becomes the con-
tinuous phase in the blend, whereas the ABS particles are
the dispersed phase. The obtained results show that if the
PC remains as disperse phase, it is not effective in in-
itiating the yielding in the SAN continuous phase. On the
contrary, when the ABS is in disperse phase, it is rela-
tively more effective in initiating the yielding and in in-
creasing the impact resistance of the blends [8].
3.4. Hardness
The hardness variation with the blend composition on
PC/ABS blends (Figure 8) present two horizontal re-
gions or “plateaux” for the matrices rich in ABS on one
side, and for the matrices rich in PC, on the other side.
An increase in hardness with an increase of the PC con-
tent appears between the two “plateaux”, due to the de-

Some Mechanical and Thermal Properties of PC/ABS Blends 408
Figure 8. Hardness Shore D of PC/ABS blends as a function
of the PC content.
crease in flexibility of the ABS chains. The hardness
values found are lower than those cited in the literature
because the phenomenon of surface degradation that
takes place in the samples tested. The increase in hard-
ness and the abrupt increase at higher proportion of PC
can be explained by the phase inversion of PC from dis-
persed to continuous phase when its concentration in the
blend was increased from 40% to 70%.
3.5. Heat Deflection and Vicat Temperature
The HDT can be considered as a measure of the temper-
ature at which certain creep compliance is reached after
the polymer has been subjected to a standard temperature
program. Measurements of the HDT of blends as a func-
tion of their composition can then be expected to give
information on their phase topology. This possibility
requires, of course, that the transition temperatures of the
two components are sufficiently separated [9].
Figure 9 shows the HDT’s measured for all the sam-
ples investigated. The curve of the binary PC/ABS sys-
tem shows two different paces, indicating the occurrence
of a phase inversion between PC and ABS at 50% of
blend composition.
The PC/ABS polymer blends have found commercial
utility. However, it is obvious that only a precise balance
of polymer types and blend ratios can produce blends of
high impact strength with a minimal sacrifice of the heat
deflection temperature.
On the other hand, the values of the Vicat softening
temperature drop steadily from that of pure PC to that of
pure ABS (see Figure 9), forming a small plateau at 0 -
10% PC. The complex shapes of these curves suggest
some of the complexity of this system, which may in-
volve partial solubility, coexistence of three or more pha-
ses, changing domain sizes, and other critical variables.
Figure 9. Heat deflection temperature HDT and Vicat sof-
tening temperature of PC/ABS blends as a function of the
PC content.
Generally, gradual increases of the HDT and Vicat is
observed as the PC content is increased.
4. Morphology and FTIR Characterization
The morphology of ABS/PC blends is complex and de-
pends on the composition, the type of ABS and PC, the
conditions of implementation and on the interfacial inte-
raction. Thus, for ABS or PC content between 0 and 40%
by weight, the minority phase is dispersed as nodules or
fibrils in the matrix. For compositions near 50%, the
structure is co-continuous, that the ABS and PC phases
are interconnected. Experimental results indicate that the
impact strength of the ABS/PC blends is higher when the
morphology is fibrillar or co-continuous [10-12].
In order to verify the above hypothesis, the morphol-
ogy of the ABS/PC blends was examined with the help
of a scanning electron microscope. Figure 10 shows mi-
crographs of the fractured surfaces with respect to com-
position of the PC-rich blend and ABS-rich blend.
For the blends containing 90% PC, we can see that the
ABS phase appears as spherical inclusions in the PC
phase matrix and the blend look more uniform. For the
blend containing 40% PC, the PC phase is dispersed as
nodules in the ABS matrix and the dispersion is irregu-
lar.
The IR spectrums (see Figure 11) reveal the absence
of oxidized species around 3200 - 3300 cm−1 in the ho-
mopolymers, this means that the polymers do not under-
go significant degradation during the implementation.
This reveals also the very good heat resistance of PC. For
the blend of (90/10) PC/ABS, the spectrum show no sig-
nificant difference compared to the spectra of pure PC
and pure ABS, that means that there is no chemical reac-
tion between PC and ABS. Thus the optimum properties

Some Mechanical and Thermal Properties of PC/ABS Blends 409
(a)
(b)
Figure 10. Scanning electron micrographs of fractured sur-
faces of: (a) (90/10) PC/ABS blend and (b) etched surface of
(40/60) PC/ABS blend.
obtained with a rate of 90% PC can be attributed to par-
tial miscibility between PC and ABS.
5. Conclusions
In this work we have systematically studied a number of
properties of PC/ABS blends as a function of composi-
tion. Ultimate properties, such as impact strength and
toughness, present attractive enhancement for a 90% PC
composition. Indeed, despite contradictory trends cited in
several research studies, all authors always get an impact
strength of blends with high rates of PC. The addition of
a few PC to the ABS leads in general, to a resilience of
(a)
(b)
(c)
Figure 11. FTIR Spectrum of (a) pure ABS, (b) (90/10) PC/
ABS Blend and (c) pure PC.
blends less than that of ABS. The rate of PC for which
the resilience of the mixture is maximum varies accord-
ing to the authors. The elastic modulus, the heat deflec-
tion temperature and the Vicat softening temperature are
intermediate between those of the components for any
blend composition. These two last properties show the
occurrence of an inversion phase for the 50/50 composi-
tion. The morphology of the PC/ABS blend was found to
be co-continuous. The results obtained in this study show

Some Mechanical and Thermal Properties of PC/ABS Blends 410
some interesting aspects that may be of practical applica-
tion in case of blends with high PC content, the mixtures
typically have a partial miscibility (or intermixing misci-
bility window) at 90% PC and the properties are optimal.
In case of blends with low PC content, the decrease in
properties is an important disadvantage for the practical
application of these blends.
REFERENCES
[1] L. A. Utracki, “Polymer Blends Handbook,” Kluwer
Academic Publisher, Amsterdam, 2002.
[2] F. Nordgren and M. Nyquist, “FE-Modelling of PC/
ABS—Experimental Tests and Simulations,” Master’s
Dissertation, Division of Solid Mechanics, Lund Univer-
sity, Lund, 2006.
[3] L. A. Utracki and B. D. Favis, “Polymer Alloys and
Blends,” In: P. N. Cheremisinoff, Ed., Handbook of Po-
lymer Science and Technology, Marcel Dekker, Inc., New
York, 1989, pp. 121-201.
[4] A. Pavan, T. Riccò and M. Rink, “High Performance
Polymer Blend,” Materials Science and Engineering, Vol.
48, No. 9, 1981, pp. 9-15.
doi:10.1016/0025-5416(81)90060-4
[5] R. D. Deanin and R. R. Geoffroy, “Major Thermoplastic
Polyblends: Compatibility and Practical Properties,” Or-
ganic Coating and Plastics Chemistry, Vol. 37, No. 1,
1977, pp. 257-262.
[6] J. M. Martínez, J. I. Eguiazábal and J. Nazábal, “Phase
Behavior of Mechanical Properties of Injection Molded
PET/Par Blends,” Journal of Applied Polymer Science,
Vol. 45, No. 7, July 1992, pp. 1135-1143.
doi:10.1002/app.1992.070450702
[7] H. Suarez, J. W. Barlow and D. R. Paul, “Mechanical
properties of ABS/polycarbonate blends,” Journal of Ap-
plied Polymer Science, Vol. 29, No. 11, November 1984,
pp. 3253-3259. doi:10.1002/app.1984.070291104
[8] A. Hassan and W. Y. Jwu, “Mechanical Properties of
High Impact ABS/PC Blends—Effect of Blend Ratio,”
Polymer Symposium, Kebangsaan Ke-V Hotel Residence,
August 2005, pp. 23-24.
[9] J. Bastida, I. Eguiazábal and J. Nazábal, “The Vicat Sof-
tening Temperature as a Method to Assess the Phase Be-
haviour of Amorphous Polymer Blends,” Polymer Testing,
Vol. 12, No. 3, 1993, pp. 233-242.
doi:10.1016/0142-9418(93)90005-A
[10] M. L. Barthes, “Régénération d’ABS et de PC Issus de
DEEE sous Forme d’Alliages de Polymères Techniques
ou de Nanocomposites,” Ph.D. Dissertation, Mechanic
and Engineering, Doctoral School of Physical Sciences
for Engineering, Bourdeaux, 2010.
[11] M. M. K. Khan, R. F. Liang, R. K. Gupta and S. Agarwal,
“Rheological and Mechanical Properties of ABS/PC
Blends,” Korea-Australia Rheology Journal, Vol. 17, No.
1, 2005, pp. 1-7.
[12] T. Matchimapiro, P. Sornthummalee, T. Pothisiri and S.
Rimdisit, “Impact Behaviors and Thermomechanical Pro-
perties of TPP-Filled Polycarbonate/Acrylonitrile-Buta-
diene-Styrene Blends,” Journal of Metals, Materials and
Minerals, Vol. 18, No. 2, 2008, pp. 187-190.