 Journal of Computer and Communications, 2014, 2, 103-111 Published Online July 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.29014 How to cite this paper: Stenane, N.M. and Folly , K.A. (2014) Application of Evolutionary Algorithm for Optimal Directional Overcurrent Relay Coordination. Journal of Computer and Communications, 2, 103-111. http://dx.doi.org/10.4236/jcc.2014.29014 Application of Evolutionary Algorithm for Optimal Directional Overcurrent Relay Coordination N. M. Stenane, K. A. Folly Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa Email: Komla.Folly@uct.ac.za Received May 2014 Abstract In this paper, two Evolutionary Algorithms (EAs) i.e., an improved Genetic Algorithms (GAs) and Population Based Incremental Learning (PBIL) algorithm are applied for optimal coordination of directi onal overcurrent relays in an interconnected power system network. The problem of coor- dinating directional overcurrent relays is formulated as an optimization problem that is solved via the improved GAs and PBIL. The simulation results obtained using the improved GAs are com- pared with those obtained using PBIL. The results show that the improved GA proposed in this paper performs better than PBIL. Keywords Evolutionary Algorithms, GA, Learning Rate, Optimal Relay Coordination, PBIL 1. Introduction Power system protection equipment is used to protect the power system and swiftly isolate abnormal conditions from the system [1] [2]. In order for the protection system to perform its function optimally, it must operate se- lectively, reliably and dependably. To achieve these requirements, relay coordination study should be carried out [1] [2]. Coordination of protection is defined as the process of choosing settings or time delay characteristics of protective devices such that the operation of the devices will occur in a specified order to minimize customer service interruption, reduce equipment damage, or personal injury [2]. Overcurrent relays are the most widely used protection system relays to detect and isolate faults in power systems. There are two types of overcurrent relays: 1) the instantaneous overcurrent relays, operate instantane- ously when the current reaches a predetermined value and 2) time delay relays which require that both the cur- rent and the time to exceed the setting values before the relay can operate. For time delay overcurrent relays, re- lay coordination involves setting the pickup current and time multiplier parameters. The most important pa- rameter for the overcurrent relay coordination is the time multiplier which has a direct influence on the operating time of the relay. The pick-up current is set to be stable for maximum load current that the equipment can carry continuously but should also be sensitive enough to detect minimum fault at the end of intended reach [3]. For  N. M. Stenane, K. A. Folly many years, power system engineers have relied on conventional methods for overcurrent relay coordination. These methods are based on trial and error approach that can be laborious and time consuming depending on the size and the complexity of the network. As a result, it has been proposed to automate the relay coordination pro- cedure using computer programs [3] [4]. However, these automated methods do not provide optimal solutions but rather the best of the tried solutions [5]. Consequently, new methods that can provide optimal overcurrent relay coordination have been proposed. A comprehensive review of different optimal coordination methods to overcome this problem is given in [6] [7]. Recently, the applications of Evolutionary Algorithms (EAs) such as genetic algorithms (GAs) have received increasing attention [8]-[14]. In general, the operating time of the main relays for primary zone fault has been used as the objective function for the optimization problem. Researchers have handled constraints in different ways. In [10], the preferred time multiplier setting, current pick-up setting and coordination time interval were added as part of the objective function. In [12], the coordination time interval is also part of the objective func- tion. Other authors have incorporated additional terms, besides the constraints in the objective function [13] [14] evolutionary programming (EP) [15] [16] and differential evolution (DE) [17]-[20], have been proposed for op- timal relay coordination. In general, researchers have used the operating time of the main relays for primary zone fault as the objective function for the optimization problem. Other authors have incorporated additional terms, besides the constraints, in the objective function. The different ways researchers handle constraints are discussed in the subsequent sections. In [10], the preferred time multiplier setting, current pick up setting and coordination time interval were added as part of the objective function. In [11] [12], the coordination time inter- val is also part of the objective function. Other authors have incorporated additional terms, besides the con- straints in the objective function [13] [14]. Several authors have discussed the limitations of simple GAs such as premature convergence, the long time required to solve difficult problems, etc. To cope with these limitations, several variant of GAs have been pro- posed in recent years. Some of these variants include hybrid GA [15], continuous GA [16], Evolutionary Pro- gramming (EP) [17], Mo d ified, Evolutionary Programming (EP) [18], Differential Evolution (DE) and its vari- ants [19]-[22]. In this paper, an improved GAs is used for optimal coordination of overcurrent relays. The simulation results are compared with the results obtained using a relatively new algorithm called Population-Based Incremental learning (PBIL). This algorithm has been first introduced by Baluja in [23]. PBIL has been successfully applied to solve power system small signal stability problems [24]-[29]. However, this algorithm has not been applied to relay coordination before. It is shown in this paper that PBIL is able to provide relay coordination for the net- work studied. However, the performance of PBIL used in this paper is not as good as that of the improved GAs. Thi s could be due to several reasons. T he performance of the improved Gas used in this paper has been en- hanced by using a combination of single point crossover and extrapolation. In addition, a more unbiased selec- tion method based on ranking method coupled with truncation method (only the best 50% of the population are used for reproduction) was used instead of the traditional roulette wheel selection method. Another reason could be attributed to thepremature convergence of PBIL [28] and the fact that the version of PBIL used in this paper is based on binary coding and not real coding like GAs used in this paper. This creates some problems in han- dling the constraints. 2. Power System Model The power system considered in this research is the IEEE 24 Bus system as shown in Figur e 1. This system consists of two voltage levels, the 138 kV and the 230 kV. In this paper, the coordination of overcurrent relays is performed on the 230 kV voltage level. The 230 kV voltage level consists of 6 sets of machines, 14 buses and 20 lines. The data used for this power system model can be found in [30]. 3. Background to Genetic Algorithms Genetic Algorithms (GAs) are random search algorithm based on the mechanisms of natural selection and natural genetics [8] [9]. This algorithm applies the principles of survival of the fittest to search for optimal solutions [8]. Solutions from one population are used to create a new population through genetic operators such as selection, crossover and mutation. Initially, the trial solutions are generated randomly. In every generation, a new set of trial solutions is created through the evolutionary process of selection, crossover and mutation. A new popula- tion is created by combining the information of the two parent solutions. Selection determines which i ndividuals 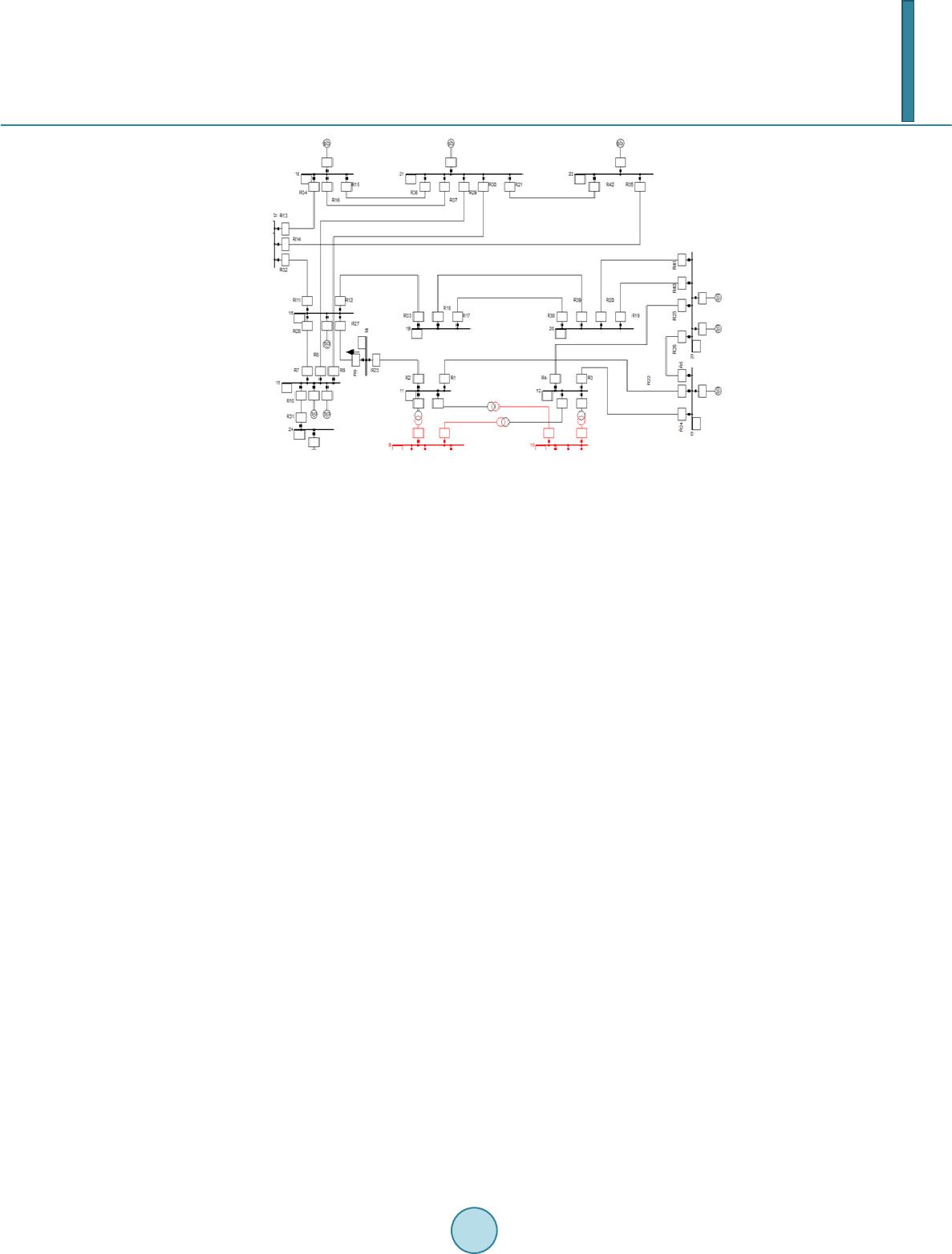 N. M. Stenane, K. A. Folly Figure 1. IEEE 24-bus system (230 kV side). will survive and continue on to the next generation. Selection is done through various selection methods [9]. In this paper, a selection method based on ranking coupled with truncation method (the best 50% of the population are used for reproduction) was used. In the ranking method, a probability of selecting an individual solution is assigned based on the rank of the individual solution when all the solutions are sorted according to their fitness values [9]. This method has an advantage in that the fittest individuals will not dominate the population [8] [9]. The aim of crossover function is to produce new solutions from two parent solutions in order for the algo- rithm to search through the solution space [8]-[10]. In this paper, a combination of single point crossover and extrapolation was used. To prevent premature convergence, diversity is introduced into the population by using mutation operator [8], [9]. There are various methods of implementing mutation, these include uniform mutation, non-uniform mutation, multi-non-uniform mutation, etc. In this paper, uniform mutation was used. A summary of the GAs used in this paper is given below [9]: Step 1: Create an initial population. Step 2: Evaluate all of the individuals. Step 3: Select a new population from the old population based on the fitness of the individuals as given by the evaluation function. Step 4: Apply some genetic operators (crossover and mutation) to members of the population to create new solutions. Step 5: Evaluate these newly created individuals, and check whether termination criteria is met. Step 6: Repeat steps 3-5 (one generation) until the termination criteria has been satisfied (usually perform for a certain fixed number of generations). 4. Overview of Population-Based Incremental Learning Population Based Incremental Learning (PBIL) combines aspects of Genetic Algorithms with competitive learning [23]. In PBIL, there is no crossover operator [23] [24]. Instead a probability vector is used to create new trial solutions through learning [25] [26]. This probability vector is initially set to 0.5 to ensure that the probabil- ity vector is unbiased and the initial trial solutions created from the probability vector are completely random [23] [27]. In every generation, the probability vector is updated towards the current best solution through learn- ing [24] [25]. The best solution is used to update the probability vector. The probability vector is updated using the following expression [23]: . (1) where P is the probability vector, l is the learning rate and is the current best solution. The learning rate provides a compromise between exploration and exploitation. The higher the value of the  N. M. Stenane, K. A. Folly learning rate the faster the algorithm will converge towards an optimal solution (i.e., more exploitation). The lower the value of the learning rate the more exploration of the search space the algorithm will perform [26]. After the vector is updated, new trial solutions are created using the updated probability vector. The cycle is repeated until termination criteria is met [23]-[28]. To avoid premature convergence of the algorithm, mutation is introduced to increase the diversity in the population. Mutation is implemented on the probability vector by using a forgetting factor to relax the updated probability vector towards the neutral value of 0.5 as given in equation below [24]-[29] . (2) where f is the forgetting factor. A summary of the PBIL used in this paper is given below [24]-[29]. Step 1: Initialize the elements of the probability vector to a neural value (of 0.5) to ensure completely random initial population. Step2: Generate a population of uniformly-random bitstring and compare it element-by-element with the probability vector. Whenever and element of the probability vector is greater than the corresponding element of the random vector, a “1” is generated, otherwise a “0” is generated. Step 3: Evaluate the fitness of the bitstring using the objective function in order to identify current best solution Step 4: Update the probability vector through the learning rate towards the current best solution Step 5: Apply mutation on the updated probability vector and generate the new population based on the new probability vector. Step 6: Check if termination criteria is met. Step 7: Stop if criteria are met and satisfactory solution is found. Otherwise go to step 3. 5. Problem Formulation 5.1. Overcurrent Relay Operating Characteristics The purpose of this study is to optimize the parameters of the overcurrent relay (TMS and ) such that oper- ating time of primary relays is minimized while sufficient coordination is provided between main relays and back-up relays. The most widely used operating characteristic for standard inverse relays is given by: () () 0.02 0.14 1 F PU t TMSII =×− . (3) where t is the relay operating time; is the time multiplier setting; is the fault current through the re- lay; is the pick-up current. and are the two most important parameters that must be set for relay coordination. For evolutionary algorithms, the relay coordination problem can be cast into the following categories of optimization problems: linear problem, non-linear problem, or mixed Integer non-linear problem. In this paper, for simplicity, the pickup current setting is pre-determined based on the conductor rating and the fault current. Thus, the problem is treated as a linear and the time multiplier is considered to be a discrete variable. 5.2. Objective Function Researchers have in general used the operating time of the main relays for primary zone fault as the objective function for the optimization problem. Other authors have incorporated in the objective function additional terms, besides the constraints. Different methods have been used by researchers to handle constraints as dis- cussed in the introduction. In this paper, the objective function is chosen in such a way that the operating time of the main relays is minimized while ensuring appropriate coordination between the relays. It should also be noted that the objective function is minimized within the parameter bounds. The following objective function is used . (4) where the i-th is relay operating time for a fault close to the relay; is used to control the weighting of the relay operating time. The optimization problem can be formulated as the following: Minimize subject to the following constraints  N. M. Stenane, K. A. Folly . (5) . (6) . (7) where . (8) where and are the operating times of the main and backup relays, respectively, for a fault close to the i-th relay; CTI is the coordination time interval (grading margin). The grading margin between the main and the back-up relays is very important as it allows the main relay sufficient time to trip for a primary fault before the backup relay can trip. This is done in order to preserve selec- tivity and coordination between relays. The bounds on the parameters are as given in [10]. The relay coordina- tion time takes into consideration the following factors, relay detection time, relay pickup time, and a safety margin [2]. In this paper the standard value for CT I = 0.3 s has been used. 5.3. Constraints Handling To handle the constraints, penalty functions are introduced [14]. A penalty function penalizes the infeasible so- lutions by adding a penalty factor to the objective function based on the amount of constraint violation. In using penalty functions the common method is to convert all the constraints into inequality constraints of the follow- ing form. . (9) where p is the penalty function and is a small tolerance value. For relay coordination, the following penalty functions are identified based on the constraints . (10) . (11) . (12) is used to control the weighting of “miscoordination” penalty; is used to control the weighting of upper bound penalty and is used to control the weighting of lower bound penalty. Therefore the following objective function Equation (13) including the penalty functions Equatio ns (10)-(12) is used: 11 23 1 0.01 i mb J ttTMSTMS αβ ββ =+−∆+−+− ∑∑ ∑∑ (13) The penalty function is added to the objective function only if there’s a constraint violation. In this paper, to ensure that the discrete nature of TMS parameter is considered, the determined trial solutions from the algorithm are rounded off to the next upper available value before fitness evaluation [13]. 6. Relay Coordination Optimization There are in total 42 relays that must be set for the power system under study. In addition, there are 100 relay pairs that should be coordinated. In this study, for simplicity the parameter is predetermined based on the following criteria [2]: • To ensure that the overcurrent relay is sensitive, the minimum operating current is set less than the minimum end-of line phase-phase fault current. • To ensure the stability of the overcurrent relay, the minimum operating current is also chosen to be more than the maximum load current. To ensure optimal performance, the parameter of GA and PBIL were configured as follows: Parameters of GA: • Population size: 100 • Generation: 1500 • Selection: Ranking based coupled with truncation method (the best 50% of the population are used for re-  N. M. Stenane, K. A. Folly production) • Crossover: Single Point and extrapolation • Mutation: Uniform • Mutation rate: 0.01 Parameters of PBIL: • Population size: 100 • Generation: 1500 • Mutation/Forgetting Factor: 0.005 • Learning Rate: 0.1 The main objective of the relay coordination is to find an optimal trade-off between speed of operation of the relays and the proper coordination of main and back up relays. This task becomes more difficult when the power system is large and more relays have to be set, especially when one relay takes part in many main and back-up relay pairs that have to be coordinated. 7. Simulation Results Figure 2 and Figure 3 show the convergence rate of PBIL and GAs, respectively. It can be seen that the sum of Figure 2. Convergence rate of PBIL (LR = 0.1). Figure 3. C onvergence rate of GAs. 0100 200 300 400 500600 0 50 100 150 200 250 300 350 400 450 500 550 600 GA Generation Fitness Value (s)  N. M. Stenane, K. A. Folly the operating time of the main overcurrent relays that is provided by GAs is smaller than that provided by PBIL. From the results, it can be seen that there are larger variations in the fitness value for PBIL algorithm when the number of generation is less than 100 as compared to GAs algorithm. This means diversity is better for PBIL than for GAs for generations less than 100. However, at the end, PBIL settles at a higher fitness value of 48.02 seconds compared to GA, which settles at the fitness value of 19.84 seconds. This means after 100 generations PBIL loses diversity and converges prematurely. Therefore, TMS parameters for overcurrent relays determined by PBIL results in longer operating time for the main and backup relays. The results of the final fitness values attained by the algorithms are compared in Table 1. From this Table, it can be seen that the relay coordination using GAs gives a total operating time of 19.83 sec. for the main relay, whereas, PBIL gives a total of operating time of 48.02 sec. The same is true for the backup relays, where GAs provide a better result. From these results, it can be concluded that GAs gives a better performance than PBIL. To investigate the effect of the learning rate of the performance of the PBIL, the learning rate is varied from 0.01 to 1 as shown in Table 2. Table 2 also shows the average of the fitness value and the success rate for each learning rate. The success rate refers to the number of trials for which all the constraints were met over the total number of trials. It can be seen from Table 2 that LR = 0.4 provides the best average fitness value with a success rate of 90%, the second best is LR = 0.2 followed by LR = 0.6, both with success rates of 80%.The results for learning rates LR = 0.8 and LR = 1.0 yield relatively higher average fitness values compared to the learning rates LR = 0.2, 0.4, and 0.6. The worst average fitness value is provided by LR = 0.01 with 0% success rate, followed by LR = 0.05 with a success rate of 60%. The poor performances of LR = 0.01 and LR = 0.05 can be explained by the fact that at lower learning rates there is less exploitation of the best solution and therefore the algorithm tends to require more time to converge. At higher learning rates (i.e., LR = 0.8 and LR = 1), there is less exploration of the search space and therefore the algorithm tends to converge prematurely. Although for LR = 0.1, the average fit- ness value is slightly higher than those of LR = 0.2 - 0.8, it is the only learning rate that has a 100% success rate. This means this learning rate is more stable. The simulation results show that the learning rate has an impact on the performance of the PBIL. Therefore, a trade-off between exploration and exploitation is required for a good performance of PBIL. Table 1. Average fitness values for GA and PBIL. GA PBIL Fitness value(s) 1 9. 83 4 8. 02 Main operating time(s) 19.83 4 8. 02 Backup operating time(s) 9 3. 46 2 16 .47 Table 2. Average fitness for PBIL with varying learning rate. LR Ave. J Success Rate (%) 0.01 210.85 0 0.05 66.79 60 0.1 5 1. 68 1 00 0.2 4 5. 62 80 0.4 4 3. 81 90 0.6 4 5. 67 80 0.8 4 9. 03 60 1.0 4 9. 24 60  N. M. Stenane, K. A. Folly 8. Conclusions The application of an improved GAs algorithm for the optimal directional overcurrent relay coordination has been investigated. Results show that although PBIL has the ability to solve the relay coordination problem, the improved performance GAs proposed in this paper performs better than PBIL. To assess the extent to which the learning rate has impact on PBIL, further investigations have been done with varying learning rates. The simula - tion results show that the learning rate has some effect on the performance of the PBIL. At lower learning rates the algorithm explore the search space for a very long time and does not converge for a number of generations tested in the research. At high learning rates, the algorithm loses the ability to explore the search space effec- tively and may converge prematurely to non optimal values. More investigation into the application of PBIL for optimal directional overcurrent relay coordination needs to be done. This research studied only the effects of learning rate on the performance of the PBIL algorithm. Further research into the effects of other parameters such as population size, mutation scheme and the manner in which the probability vector is updated can be done to improve the performance of PBIL. Another area of fur- ther investigation is to consider the effects of formulating the relay coordination problem as non-linear problem where both the pickup current and time multiplier settings are determined by the algorithm. Acknowledgem ents This work is based on research supported in part by the National Research Foundation of South Africa UID 83977 and UID 85503. References [1] (2001) IEEE Recommended Practice for Protection and Coordination of Industrial and Commercial Power Systems. IEEE Standard 242. [2] Anderson, P.M. (1999) Po we r System Protection. McGraw-Hill, New York. [3] Tsien, H.Y. (1964) An Automatic Digital Computer Program for Setting Transmission Line Directional Overcurrent Re lays . IEEE Transactions on Power Apparatus and Systems, 83, 1048-1053. http://dx.doi.org/10.1109/TPAS.1964.4765939 [4] Albrecht, R.E., et al. (1964) Digital Computer Protective Device Co-Ordination Program I-General Program Descrip- tion. IEEE Transactions on Power Apparatus and Systems, 83, 402-410. http://dx.doi.org/10.1109/TPAS.1964.4766018 [5] Urdanet a, A.J. et al., (1988) Optimal Coordination of Directional Overcurrent Relays in Interconnected Power Systems. IEEE Transactions on Power Delivery, 3, 903-911. http://dx.doi.org/10.1109/61.193867 [6] Birla, D., et al., (20 05) Ti me -Overcurrent Relay Coordination: A Review. International Journal of Emerging Electric Power Systems, 2. [7] Hussain, M.H., et al. (2013) Optimal Overcurrent Relay Coordination: A Review. Procedia Engineering, 53, 332-336. http://dx.doi.org/10.1016/j.proeng.2013.02.043 [8] Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley Pub. Co., Readin g. [9] Haupt, R.L. and Haupt, S.E. (2004) Practical Genetic Algorithms. Wiley-Interscience, Hoboken. [10] So, C.W., et al., (1997) Application of Genetic Algorithm to Overcurrent Relay Grading Coordination. In: Pro ceedings of the 4th In t ernational Conference on Advances Power System Control, Operation and Management, Hong Kong, 283-287. http://dx.doi.org/10.1049/cp:19971845 [11] Kavehni a, F., et al (20 06 ) Optimal Coordination of Directional Overcurrent Relays in Power System Using Genetic Algorithm. In: Proceedings of the 41st International Universities Power Engineering Conference, 824-82 7 . http://dx.doi.org/10.1109/UPEC.2006.367595 [12] Uthitsunthorn, D. and Kulworawanichpong, T. (2010) Opt imal Overcurrent Relays Coordination Using Genetic Algo- rithm. Advances in Energy Engineering (ICAEE) Conference, 162-165. [13] Razavi, F., et al., (2008 ) A New Comprehensive Genetic Algorithm Method for Optimal Overcurrent Relays Coordi- nation. Electric Power Systems Research, 78, 713-720. http://dx.doi.org/10.1016/j.epsr.2007.05.013 [14] Coello Coello, C.A. (2002) Theoretical and Numerical Constraint-Handling Techniques used with Evolutionary Algo- rithms: A Survey of the State of the Art. Computer Methods in Applied Mechanics and Engineering, 191, 1245-1287 . http://dx.doi.org/10.1016/S0045-7825(01)00323-1  N. M. Stenane, K. A. Folly [15] Noghabi, A.S., et al., (2009) Considering Different Network Topologies in Optimal Overcurrent Relay Coordination Using a Hybrid GA. IEEE Transactions on Power Delivery, 24, 1857-1863. http://dx.doi.org/10.1109/TPWRD.2009.2029057 [16] Bedekar, P.P. and Bhide, S.R. (2011) Optimum Coordination of Overcurrent Relay Timing Using Continuous Genetic Algorithm. Expert Systems with Applications, 38, 11286-11292. http://dx.doi.org/10.1016/j.eswa.2011.02.177 [17] So, C.W. and Li, K.K. (2000) Overcurrent Relay Coordination by Evolutionary Programming. Electric Power Systems Research , 53, 83-90. http://dx.doi.org/10.1016/S0378-7796(99)00052-8 [18] So, C. W. an d Li , K.K. (2004 ) Intelligent Method for Protection Coordination. In: Proceedings of the 2004 IEEE In t e r- national on Electric Utility Deregulation, Restructuring and Power Technologies, 378-382. http://dx.doi.org/10.1109/DRPT.2004.1338525 [19] Thangaraj , R., et al. (20 12) Overcurrent Relay Coordination by Differential Evolution Algorithm. In: IEEE Interna- tional Conference on Power Electronics, Drives and Energy Systems. [20] Thangaraj, R., Pant, M. and Abraham, A. (2010) New Mutation Schemes for Differential Evolution Algorithm and Their Application to the Optimization of Directional Over-Current Relay Settings. Applied Mathematics and Computa- tion, 216, 532-544. http://dx.doi.org/10.1016/j.amc.2010.01.071 [21] Thangaraj, R., Pant, M. and Deep , K. (2010) Optimal Coordination of Over-Current Relays Using Modified Differ en- tial Evolution Al- gorithms. Engineering Applications of Artificial Intelligence, 23, 820-829. http://dx.doi.org/10.1016/j.engappai.2010.01.024 [22] Moirangthem, J., Krishnanand, K.R., Dash, S.S. and Ramaswam, R. (2013) Adaptive Differential Evolution Algorithm for Solving Non-Linear Coordination Problem of Directional Overcurrent Relays. IET Generation, Transmission and Distribution, 7, 329-336. http://dx.doi.org/10.1049/iet-gtd.2012. 01 10 [23] Baluj a, S. (1994) Population-Based Incremental Learning: A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning. Carnigie Mellon University, Technical report CMU-CS-94-163. [24] Folly, K.A. (2011) Performance Evaluation of Power System Stabilizers Based on Population-Based Incremental Learning. International Journal of Electrical Power Energy Systems, 33, 1279-1287. [25] Folly, K.A. and Ven ayagamoorthy, G.K. (2009) A Real-Time Implementation of a PBIL Based Stabilizing Controller for Synchronous Generator. Proceedings of the IEEE Industry Applications Society Annual Conference. [26] Folly, K.A. and Venayagamoorthy, G.K. (2009) Effects of Learning Rate on the Performance of the Population Based Incremental Learning Algorithm. International Joint Conference on Neural Networks, 861-868. [27] Folly, K.A. (2012) Population Based Incremental Learning Algorithm with Adaptive Learning Rate Strategy. Pro- ceedings of the 3rd International Conference on Advanced Neural Networks, International Joint Conference on Neural Nin Swarm Intelligence (ICSI’12), Vol. 1, 11-20. [28] Folly, K.A. (2007) Robust Controller Based on a Combination of Genetic Algorithms and Competitive Learning. Pro- ceedings of the 2007 International Joint Conference on Neural Network (IJCNN). [29] Folly, K.A. (2006) Design of Power System Stabilizer: A Comparison between Genetic Algorithms (GAs) and Popula- tion-Based Incremental Learning (PBIL). Proceedings of the 20 06 IEEE Power and Energy Society, General Meeting. [30] Power system Test Case Archive. http://www.ee.washington.edu/research/pstca/rts/pg_tcarts.htm
|