 Journal of Computer and Communications, 2014, 2, 87-92 Published Online July 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.29012 How to cite this paper: Xu, G.L., Wang, X.T., Xu, X.G. and Shao, L.M. (2014) Amplitude and Phase Analysis Based on Signed Demodulation for AM-FM Signal. Journal of Computer and Communications, 2, 87-92. http://dx.doi.org/10.4236/jcc.2014.29012 Amplitude and Phase Analysis Based on Signed Demodulation for AM-FM Signal Guanlei Xu1*, Xiaotong Wang2, Xiaogang Xu2, Limin Shao1 1Ocean Department, Dalian Navy Academy, Dalian, China 2Navigation Dep art men t, Dalian Navy Academy, Dalian, China Email: *xgl_86 @163.com Received May 2014 Abstract This paper proposes a new amplitude and phase demodulation schem e different from the tradi- tional method for AM-FM signals. The traditional amplitude demodulation assumes that the am- plitude should be non-negative, and the phase is obtained under the case of non-negative ampli- tude, which approximates the true amplitude and phase but dis tor ts the true amplitude and phase in some cases. In this paper we assume that the amplitude is signed (zero, positive or negative), and the phase is obtained under the case of signed amplitude by optim iza ti on, as is called signed demodulation. The main merit of the signed demodulation lies in the revelat ion of senseful p hysi- cal meaning on phase and frequency. Experiments on the real-world data show the effici ency of the me th od. Keywords Amplitude Demodulation, Phase, Hilbert Transform, Signed Demodulation 1. Introduction In many signal processing fields such as communication, wireless navigation and machine systems, the modula- tion and demodulation are often used to process the amplitude component and the phase component [1]-[10]. In fact, the basic problem in processing AM-FM signals is d emodulation, i.e., estimation of the information stored in the amplitude and phase signals while given the composite signal. For monocomponent AM-FM signals many successful demodulation approaches have existed, ranging from standard methods such as Hilbert transform demodulation [1] or phase-locked loops (PLL’s) to the recent energy separation algorithm (ESA) that tracks and demodulates the energy of the source producing the AM-FM signal using instantaneous nonlinear differential operators [2]-[18]. While each of these monocomponent algorithms may have its advantages and disadvantages, they more or less offer a solution to the monocomponent AM-FM demodulation problem. However, these me- thods shown in above only process the positive amplitudes, i.e., they think that the amplitudes should be the ab- solute values (or non-negative). In other words, they fail to demodulate the signed amplitudes (or non-positive AM component). *  G. L. Xu et al. In this paper, we derive a new scheme, different from the traditional method for AM-FM signals that can ob- tain the signed amplitude and accordingly senseful physical meaning phase and frequency by optimization. 2. Signed Demodulation 2.1. Traditional Demodulation of Amplitude and Phase For a real function, a direct and simple way to obtain the complex signal is via Hilbert transform [????]. A real function and its Hilbert transform are related to each other in such a way that they together create a so called strong analytic signal . The strong analytic signal can be written with the am- plitude and the phase where the derivative of the phase can be identified as the instantaneous frequency. The Hilbert transform defined in the time domain is a convolution between the Hilbert transformer and the real function : ( )( ) ( ) ( )( ) 11 *d x xtH xtxtP tt ττ ππ τ ∞ −∞ ===− ∫ , (1) where the P in front of the integral denotes the Cauchy principal value which expanding the class of functions for which the integral in (1) exist and “*” denotes the convolution operator and “ ” denotes the Hilbert transform operator. In frequency domain, we have the following relation: ( )( )( )( ) sgn H X uXuuXu= + , (2) where ( ) 10 sgn 00 10 for u ufor u for u > = = −< and is the Fourier transform of the real function . We also see that is the inverse Fourier transform of . The biggest advantage of Hilbert transform is that one can directly obtain the amplitude and phase for AM-FM components, e.g., a real signal , one can obtain the follows via Hilbert transform Amplitude: , (3) Phase: ( )( )( ) ( ) ( ) ( ) Im lntxtjH xt φ = + , (4) where “ ” denotes the imaginary part operator and “ ” is the natural logarithm operator. After Hilbert transform, turns to a complex signal , which is typical AM-FM signal with the AM component and the FM component . In fact, the FM component is a special AM-FM signal with the amplitude being 1. This process is called demodulation. However, there is one question: 1) why the Hilbert transform of is but not ? 2) why cannot we obtain the amplitude function rather than that nearly all the demodulation methods obtain? For the first question, Bedrosian’s theorem [15] has yielded the answer. Now let us review the Bedrosian’s theorem. Bedro sian’s theorem [15]: For two real functions and , if then , and if then , , then ( )( ) { } ( )( ) { } 12 12 Hxtx txtHx t= ⋅ , (5) where and are the Fourier transform of and respectively. Bedrosian’s theorem tells us that for two functio ns, and , of which is with low frequency and the other com- ponent is with high frequency, then through Hilbert transform we have ( )( ) { } ( )( ) { } ( )( ) coscos sinHatt atHt att φ φφ = = . For the second question, we will answer it in the following few sections via the signed demodulation and some optimizations.  G. L. Xu et al. 2.2. The Proposed Signed Demodulation Method The first work is to o b tain the signed amplitude function out of the positive amplitude function via taking abso- lute value of the complex signal . However, it is not hard to see that a function and its Hil- bert transform are not absolutely orthogonal (even though they are orthogona l in principle) because of trunca- tions in numerical calculations and the boundary effects. Therefore, for a real function with its complex function after Hilbert transform has no more than the following relations: and . (6) Therefore, taking absolute value of the complex signal , we have . Thus, we only can obtain an approximation (i.e. ) of even if we know the exact si gns of . Hence, we have the following method. The process of signed demodulation: 1) For the signal with low-frequency component and high-frequency component , obtain the complex signal ( )( )( ) { } 12h x tHxtx t= via Hilbert transform, then find all the zero positions (indeed these positions make be the local minima) in , and M is the total num- ber of zero positions; 2) Obtain the high-frequency signal by ; 3) Estimate the amplitud e function by ( )( )( ) ( )( ) 1 ifis evenodd ifis oddeven h h xt m xt xt m =− , where and ; 4) Reconstruct the high-frequency signal by ( )( )( ) ( ) ( ) 2 12 sgn h xtxt xtxt= ⋅⋅ where ( ) 10 sgn 00 10 s ss s > = −< . 3. Experiment and Discussion Here we have , , , . Now we use the traditional demodulation method and our signed demodulation to demodulate signal and give the comparison (see Figure 1). The first row ((a) (b) (c)) is the composed two signals with low-frequency and high-frequency respectively. The second row ((d) (e) (f)) is the demodulated amplitude, the high-frequency signal and the phase respectively by traditional method. The third row ((g) (h) (i)) is the demodulated amplitude, the high-fr equency signal and the phase respectively by our method. (a) (b) 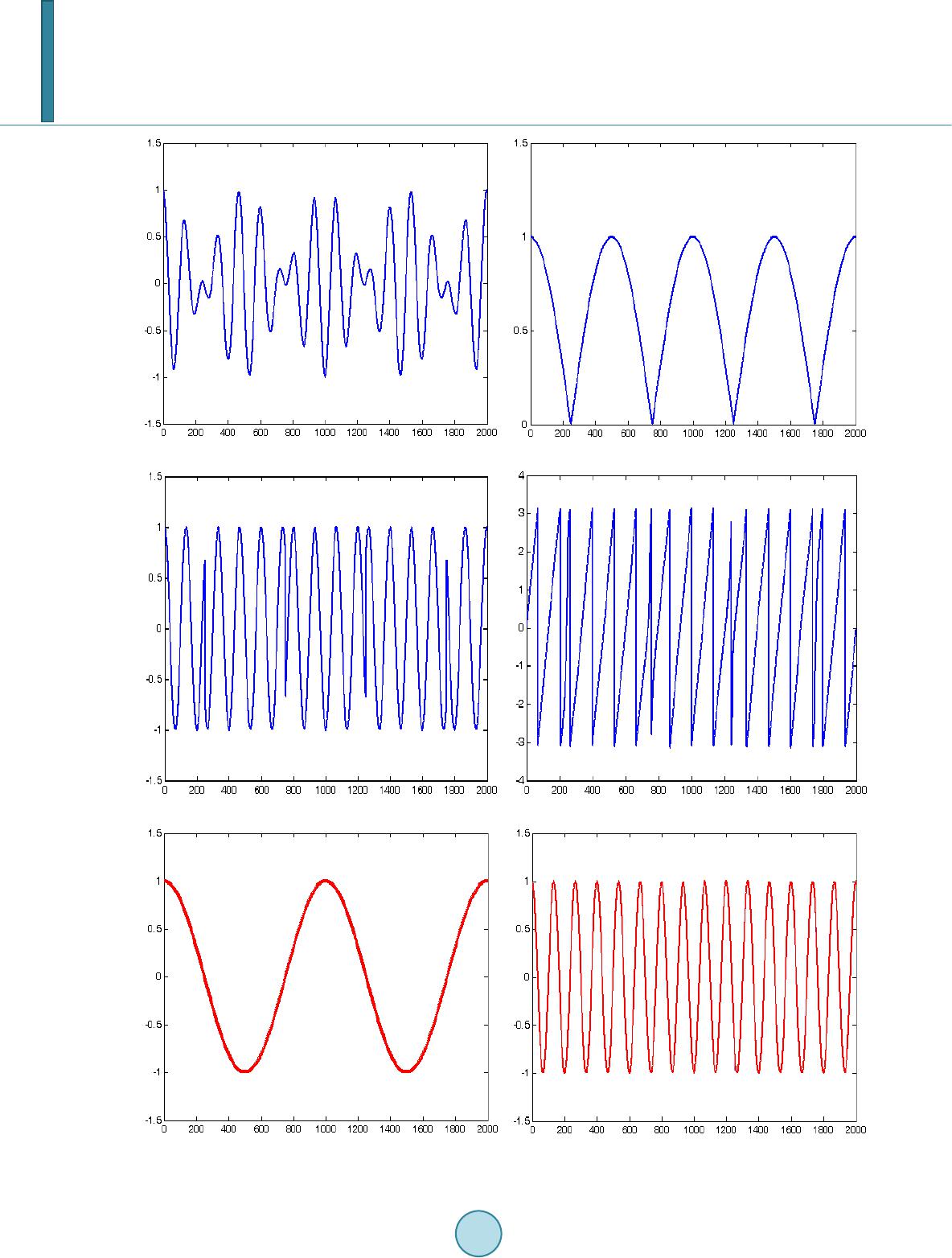 G. L. Xu et al. (c) (d) (e) (f) (g) (h)  G. L. Xu et al. (i) Figure 1. The comparison of two methods for demodulation of amplitude and phase. (a) The low-frequency signal; (b) The high -frequency signal; (c) The composed signal by (a) × (b); (d) Demodulated amplitude by traditional method; (e) Demo- dulated high-frequency signal by traditional method; (f) The phase of (e); (g) Demodulated amplitude by our method; (h) Demodulated high -frequency signal by our method; (i) The phase of (h). Clearly, our demodulation method gives more rational physical sense. We allow our amplitude to be negative, under such case we obtain the rational phase in (i) (compared with (f)). 4. Conclusion This paper proposes a new amplitude and phase demodulation scheme different from the traditional method for AM-FM signals. We assume that the amplitude is signed (zero, positive or negative), and the phase is obtained under the case of signed amplitude by optimizatio n, as is called signed demodulation. The main merit of the signed demodulation lies in the revelation of senseful physical meani ng on phase and frequency. Experiments on the real-world data show the ef ficienc y of the method. Acknowledgem ents This work is sponsored by NSFCs (Grant No. 61002052, 61273262, 61250006). References [1] Potamianos, A. and Maragos, P. (1994) A Comparison of the Energy Operator and Hilbert Transform Approaches for Signal and Speech Demodulation. Signal Processing, 37, 95-120. http://dx.doi.org/10.1016/0165-1684(94 )90 16 9-4 [2] Marago s, P., Kaiser, J.F. and Quatieri, T.F. (1993) On Amplitude and Frequency Demodulation Using Energy Opera- tors. IEEE Transactions on Signal Processing, 41, 1532-1550. http://dx.doi.org/10.1109/78.212729 [3] Marago s, P., K aiser, J.F. and Quatieri, T.F. (1993) Energy Separations in Signal Modulations with Application to Speech An alys is. IEEE Transactions on Signal Processing, 41, 3024-3051 . http://dx.doi.org/10.1109/78.277799 [4] Gupta, S.C. (1975) Phase-Locked Loops. Proceedings of the IEEE, 63, 291-306. http://dx.doi.org/10.1109/PROC.1975.9735 [5] Lindsey, W.C. and Chie, C.M. (1981) A Survey of Digital Phase-Locked Loops. Proceedings of the IEEE, 410-43 1. [6] Hawkes, H.W. (1991) Study of Adjacent and Co-Channel FM Interference. IEE Proceedings I (Communications, Speech and Vision), 138 , 319-32 6. [7] Xu, G.L., Wang, X.T. and Xu, X.G. (20 09 ) Time-Varying Frequency-Shifting Signal Assisted Empirical Mode De- composition Method for AM-FM Signals. Mechanical Systems and Signal Processing, 23, 2458-2469. http://dx.doi.org/10.1016/j.ymssp.2009.06.006 [8] Brad ley, J.N. and Kirlin, R.L. (1993) Phase-Locked Loop Cancellation of Interfering Tones. IEEE Transactions on Signal Processing, 41 , 391-394. http://dx.doi.org/10.1109/TSP.1993.193161  G. L. Xu et al. [9] Bar-Ness, Y. , Cassara, F.A., Schachter, H. and Difazio, R. (1982 ) Cross-Coupled Phase-Locked Loop with Closed Loop Amplitude Control. IEEE Transactions on Communications, 32, 195-198. [10] Sundresh, T.S., Cassara, F.A. and Schachter, H. (19 77 ) Maximum a Posteriori Estimator for Suppression of Interch an- nel Interference in FM Receiver . IEEE Transactions on Communications, 25, 1480-1485. http://dx.doi.org/10.1109/TCOM.1977.1093782 [11] Lu, S. and Doerschuk, P.C. (19 96) Nonlinear Modeling and Processing of Speech Based on Sums of AM-FM Formant Models. IEEE Transactions on Signal Processing, 44, 773-782. http://dx.doi.org/10.1109/78.492530 [12] Kumaresan , R., Sadasiv, A. G. , R ama li ng am, C.S. and Kaiser, J.F. (1992 ) Instantaneous Nonlinear Operators for Tracking Multicomponent Signal Parameters. In: P roceedings of 6th SP Workshop on Statistical Signal and Array Processing , 404-407. http://dx.doi.org/10.1109/SSAP.1992.246870 [13] Dimonte, C.L. and Arun, K.S. (1990) Tracking the Frequencies of Superimposed Time-Varying Harmonics. Pro ceed- ings of ICASSP, 2, 2539-2542. [14] Xu, G.L., Wang, X.T., Xu, X.G. and Zho u , L.J. (20 12 ) Improved EMD for the Analysis of FM Signals. Mechanical Systems and Signal Processing, 33, 181-196. http://dx.doi.org/10.1016/j.ymssp.2012.07.003 [15] Xu, G.L., Wang, X.T., Zh ou, L.J., Shao, L.M. and Xu, X.G. (2013) Time -Varying Bandpass Filter Based on Assisted Signals for AM-FM Signal Separation: A Revisit. Journal of Signal and Information Processing, 4, 229-242. http://dx.doi.org/10.4236/jsip.2013.43031 [16] Sant han am, B. and Maragos, P. (1996) Energy Demodulation of Two-Co mponent AM-FM Signal Mixtu res. IEEE Signal Processing Letters, 3, 294-298. http://dx.doi.org/10.1109/97.542159 [17] Fried land er, B. and Francos, J.M. (1995) Estimation of Amplitude and Phase Parameters of Multicomponent Signals. IEEE Transactions on Signal Processing, 43, 917-926. http://dx.doi.org/10.1109/78.376844 [18] Xu, G.L., Wang, X.T. and Xu, X.G. (2014) Generalized Uncertainty Principles associated with Hilbert Transform. Signal, Image and Video Processin g, 8, 279-28 5. http://dx.doi.org/10.1007/s11760-013-0547 -x
|