 Journal of Computer and Communications, 2014, 2, 46-53 Published Online July 2014 in SciRes. http://www.scirp.org/journal/jcc http://dx.doi.org/10.4236/jcc.2014.29007 How to cite this paper: Folly, K.A. and Mulumba, T. (2014) Self-Adaptive DE Applied to Controller Design. Journal of Computer and Communications, 2, 46-53. http://dx.doi.org/10.4236/jcc.2014.29007 Self-Adaptive DE Applied to Controller Design K. A. Folly, T. Mulumba Department of Electrical Engineering, University of Cape Town, Cape Town, South Africa Email: Komla. Folly@uct.a c.za Received May 2014 Abstract Adequate damping is necessary to maintain the security and the reliability of power systems. The most-cost effective way to enhance the small-signal of a power system is to use power system con- trollers known as power system stabilizers (PSSs). In general, the parameters of these controllers are tuned using conventional control techniques such as root locus, phase compensation techni- ques, etc. However, with these methods, it is difficult to ensure adequate stability of the system over a wide range of operating conditions. Recently, there have been some attempts by research- ers to use Evolutionary Algorithms (EAs) such as Genetic Algorithms (GAs), Particle Swarm Opti- mization, Differential Evolution (DE), etc., to optimally tune the parameters of the PSSs over a wide range of operating conditions. In this paper, a self-adaptive Differential Evolution (DE) is used to design a power system stabilizer for small-signal stability enhancement of a power system. By us- ing self-adaptive DE, the control parameters of DE such as the mutation scale factor F and cross- over rate CR are made adaptive as the population evolves. Simulation results are presented to show the effectiveness of the proposed approach. Keywords DE, Power System Stabilizer, Self-Adaptive DE, Small-Signal Stability 1. Introduction In the last three decades, there has been a growing interest in applying Evolutionary Algorithms (EAs) to solve optimization problems. Until now, Genetic Algorithms (GAs) are by far the most used EAs [1]-[6]. Although GAs provide robust and powerful adaptive search mechanism, they have several drawbacks such as “genetic drift” which prevents GAs from maintaining diversity in the population [3]. In the last few years, several other variant of GA such as Breeder Genetic Algorithms [7], Population-Based Incremental Learning [8]-[15], Particle Swarm Optimization [16]-[18], Differential Evolution (DE) [19]-[21], etc., have been proposed. Among these algorithms, DE algorithm has started to emerge as one of the most powerful stochastic and parameter optimizers due to its simplicity and a straightforward strategy [19]. It was first proposed by Price and Storm [19] as a float- ing point of EA for global optimization over continuous spaces. It is a stochastic population-based optimization that uses differential mutation technique as the main operator to arrive at the desired solutions. Although in the  K. A. Folly, T. Mulumba last decades researchers have proposed many variants of DE to improve its performance, there are still many open problems that need to be tacked for DE to be successfully applied to emerging new application areas [20], [21]. For example, it is known that the performance of DE is sensitive to the choice of the mutation and cross- over strategies and their associated control parameters such as the scale factor F and the crossover constant CR [22]-[26]. Choosing suitable parameter values is often a problem dependent task and requires previous expe- rience of the user [22]-[24]. In general, the optimal selection of the parameters is done using trial-and-error ap- proach, which in many cases is time consuming and inadequate. In addition, the optimal parameters for one op- timization problem might not be adequate for another problem [24]. In order to improve the performance of DE, several research efforts have been devoted to the tuning and adaptation of the DE control parameters F and CR [22]-[28]. One of the most attractive approach is to use self-adaptive DE where DE control parameters such as the amplification factor F and the crossover rate CR are encoded into the chromosome (individuals) so that they undergo the actions of genetic operators and evolve with the individuals [24] [26]. This not only will save the precious time of the users but also will make the performance of DE more robust. In this paper, we explored the idea of using self-adaptive DE similar to the one proposed in [19] to optimally tune the parameters of a power system stabilizer for the enhancement of small-signal stability in a simple power system network [29] [30]. Simulation results show that the controller designed based on the self-adaptive DE (denoted here by jDE-PSS) is more effective in improving the small-signal stability of the system than the PSS designed using the classical DE (CE-PSS). 2. Selected Operating Conditions The system considered in this paper is a single machine infinite bus (SMIB) system [29]. The generator is con- nected to the infinite bus through a double transmission line. The non-linear differential equations of the system are linearized around the nominal operating condition to form a set of linear equations [10]-[13]. The generator is modeled using a 6th order machine model, whereas the Automatic Voltage Regulator (AVR) was represented by a simple exciter of first order differential equation [14]-[15]. The dynamics of the system are described by a set of nonlinear differential equations. However, for the pur- pose of controller design, these equations are linearized around the nominal operating conditions [12] [29] [30]. For the design, several operating conditions were considered. These operating conditions were obtained by va- rying the active power output and the reactive power of the generator as well as the line reactances. However, for simplicity only four operating conditions are presented in this paper as listed in the Table 1. The Table shows the operating conditions with the open loop eigenvalues and their respective damping ratios in % in brackets. 3. Background to DE 3.1. Overview Define DE is a parallel direct search method that uses a population of points to search for a global minimum/ maximum of a function over wide search space [19] [20]. Like GAs, DE is a population-based algorithm that uses operators such as crossover, mutation and selection to generate successive solutions from the population of individuals with the hope that the solutions will improve over time [19]. However DE search methods differ from GAs in many aspects. The main differences between the two search methods are: Table 1. Selected operating conditions. Case Active Power Pe (p.u.) Line Reactance Xe (p.u) Eigenvalues (ζ%) 1 1.000 0.3000 −0.268 ± 4.457i (6.00) 2 1.000 0.5000 −0.118 ± 3.781i (4.83) 3 0.700 1.1000 −0.133 ± 3.311i (4.02) 4 0.900 0.9000 −0.0997 + 2.947 (3.38)  K. A. Folly, T. Mulumba • GAs rely on the crossover to escape from local optima and search in different zones of the search space; whereas DE relies on the mutation and selection operation as a search mechanism to direct the search toward the prospective regions in the search space [19]-[24]. • Unlike GA which uses fitness-based selection for parents, in DE, all solutions have the same chance of being selected as parents regardless of their fitness values. This increases the exploration of the search space. Some of the other features of DE are: ease of use, efficient memory utilization, lower computational complex- ity. 3.2. DE Operators In DE, the population is constituted of Np candidates solutions. Each candidate is a D dimensional real-valued vector where D is the number of parameters. The summary of DE’s operation is as follows [17] [18] • Step 1 (Initialization): DE generates Np vectors candidates xi,g, where “i” represents the vector and “g” the generation. The ith trial solution can be written as xi,g = [zj,I,g] where j = 1, 2, …, D. The vector’s parameters are initialized within the specified upper and lower bounds of each parameter ZjL ≤ Zj,i,g ≤ ZjU. • Step 2 (Mutation): There are several strategies to perform mutation in DE. The most popular strategy is called DE/rand/1/. In this process, four vectors from the initial population are randomly sampled where one is chosen as the target vector and another as the base vector. The difference of the remaining two vectors, scaled by a factor F, is added to the base vector to form the mutant vector. The equation below shows how mutant vectors are created. ( ) 12 , 0,,,igrgr grg v xFxx= +⋅− (1) The mutation scale factor F is a positive real number between 0 and 2 that controls the rate at which the pop- ulation evolves [20]. The base vector, denoted by r0, is randomly chosen, in such a way that r0 ≠ r1 ≠ r2 where r1 and r2 are also randomly chosen. is the trial vector. • Step 3 (Recombination or crossover): In this stage DE crosses each vector with a mutant vector, as in (2), to form a trial population. , ,rand ,, ,, if [(0,1) ] otherwise jig j jig jig vrandCRj j Ux ≤= = (2) where CR [0, 1] is the crossover probability defined by the user within the specified range. • Step 4 (Selection): The selection of vectors to populate the next generation is accomplished by comparing each vector Ui,g of the trial population Ug to its target vector xi,g from which it inherits parameters. The val- ues of the vectors are obtained using the function in (3) , ,1 , if () () otherwise i gi,gi,g ig ig UfU fx xx + ≤ = (3) In the above, we assume the minimization of a function. As soon as the new population is obtained, the cycle from step 2 to step 4 is repeated until the optimum is located or the termination criterion is satisfied. The values of DE control parameters F, CR have a significant impact on the performance of the algorithm. In general, the selection of the parameters is done using trial-and-error method, which in many cases is time con- suming. The best way to deal with this problem would be to make the control parameters of DE adaptive (i.e., the values of the parameters are changed during the run) [24]-[26]. One the most attractive approaches is to make the parameters self-adaptive by encoding them into the chromosome (individuals) so that they to undergo the actions of genetic operators and evolve with the individuals [24]. The best of these parameters will lead to better individuals which in turn are more likely to survive and produce better offspring 4. Self-Adaptive DE DE’s ability to find the global maximum is mainly dependent on the mutation and crossover process. The differ- ential mutation allows DE to explore the search space for the global maximum or minimum. This process is controlled by the mutation scale factor F ∈ ]0 2]. “F” controls the rate at which the population evolves. On the  K. A. Folly, T. Mulumba other hand, the crossover ensures that the diversity of population is maintained so as to avoid premature conver- gence. Hence this process is directly dependent on the crossover constant “CR”. The self-adaptive DE (jDE) proposed by Brest et al., in [24] uses a strategy based on DE/rand/1/bin. It fixes the population size during the optimization whilst adapting the control parameters Fi and CRi associated with each individual. Each individual in the population is extended with parameter values as shown in Figure 1. In other words, the control parameters that will be adjusted by means of evolution are F and CR. The initialization process sets Fi = 0.5 and CRi = 0.9 for each individual. jDE regenerates (with probabilities at each generation) new values for Fi and CRi according to uniform distributions on [0.1,1] and [0,1], according to the following Equations (4) and (5): 1u 21 ,1 , rand*F if otherwise l ig ig F rand FF τ + +< = (4) 3 42 ,1 , rand if otherwise ig ig rand CR CR τ + < = (5) where randj, j = 1, 2, 3, 4, are uniform random values on [0,1], and τ 1 = τ 2 = 0.1 represent the probabilities to adjust the control parameters. The newly generated parameter values are used in the mutation and crossover op- erations to create the corresponding offspring vectors and will replace the previous parameter values if the offspring survive in the selection. It is believed that better parameter values tend to generate individuals which are more likely to survive, and thus the newly generated better values are able to go into the next generation. The self-adaptive DE used in this paper is similar to the one proposed in [24] except that the mutation strategy adopted is DE/rand/2 as given below ( ) ( ) 12 3 ,0,,,, 4,ig rgrgrgrgrg v xFxxFxx= +⋅−+⋅− (6) 5. Controller Structure and Objective Function The objective in this paper is to optimize the parameters of the PSSs such that the controllers designed using conventional DE and self-adaptive DE can simultaneously stabilize a family of system models and provide ade- quate damping to the system over a wide range of operating conditions. In order words, the PSSs should be ro- bust with respect to changes in the operating conditions. In this paper, the rotor speed is used as input to the PSS. It was found that a PSS of the form of Equation (7) made of double stage lead-lag networks with time constants T1-T4, Tw and gain Kp is adequate to damp the low-frequency oscillations [12]. 3 1 24 1 1 () 111 w pw TsTs Ts Ks KTs Ts Ts + + = +++ (7) where, Kp is the gain, T1-T4 represent suitable time constants. Tw is the washout time constant needed to prevent steady-state offset of the voltage. Since the electromechanical modes are generally poorly damped and dominate the time response of the sys- tem, it is expected that by maximizing the minimum damping ratio, we could simultaneously stabilize the family of the system models over the given range of operating conditions and ensure that the closed-loop system is sta- ble [10]-[15]. To design the PSS using conventional DE (CDE) and self-adaptive DE (jDE), we need to select an objective or fitness function. The following objective function is used: Figure 1. Self-adaptive DE.  K. A. Folly, T. Mulumba (8) i = 1, 2, … n, and j = 1, 2, … m where, ζ i,j is the damping ratio of the i-th eigenvalue in the j-th operating condition. σ ij is the real part of the ei- genvalue and the ω ij is the frequency. N denotes the total number of eigenvalues and m denotes the number of operating conditions. 6. Controller Des ig n 6.1. Design of Self-Adaptive DE-PSS The parameter’s configuration that was used for jDE-PSS is as follows Population: 30 Generation: 100 Mutation scale factor F: Adaptive Crossover CR: Adaptive 6.2. Design of Conventional DE-PSS The parameter’s configuration that was used for CDE is as follows Population: 30 Generation: 100 Mutation scale factor F: 0.9 Crossover CR: 0.9 The parameter domain for both CDE and jDE are set as: 0 ≤ Kp ≤ 20 0 ≤ T1, T3 ≤ 1 0.010 ≤ T2, T4 ≤ 0.5 7. Simulation Results 7.1. Eigenvalue Analysis Table 2 shows the closed-loop eigenvalues and damping ratios for CDE-PSS and jDE-PSS. Also included in Table 2 is the case where there is no PSS (No PSS). It can be seen that jDE-PSS gives the best damping under all operating conditions considered. As the system becomes weaker (i.e., line reactance becomes bigger), the performance of CDE-PSS is seen to be deteriorating. On the other hand, jDE-PSS is providing better perfor- mance as the system becomes weaker. Therefore, jDE-PSS can be considered to be more robust than CDE. 7.2. Small Disturbance A small disturbance was simulated by applying a 10% step change in the reference voltage. The step responses for the speed deviations of the generator are presented in Figures 2-5. Table 2. Clo sed-loop eigenvalues and damping factors. Case CDE-PSS jDE -PSS No PSS 1 −1.52 ± j3.41 (0.410) −1.92 ± j3.98 (0.430) −0.268 ± 4.457i (0.06) 2 −1.13 ± j2.74 (0.380) −1.57 ± j3.23 (0.440) −0.118 ± 3.781i (0.048) 3 −0.83 ± j2.32 (0.330) −1.34 ± j2.69 (0.450) −0.133 ± 3.311i (0.040) 4 −0.49 ± j1.69 (0.280) −1.16 ± j2.25 (0.460) −0.0997 + 2.947 (0.034) 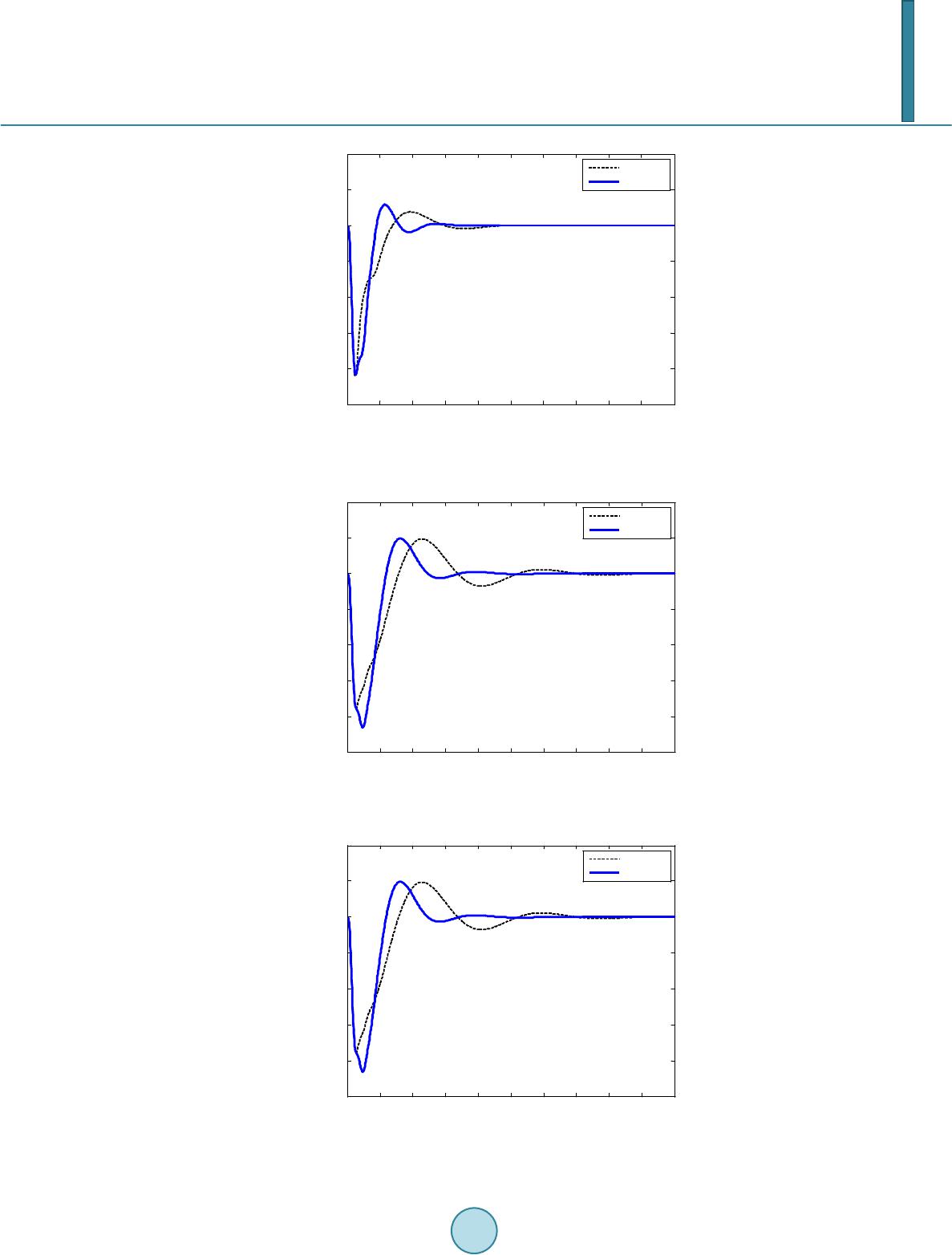 K. A. Folly, T. Mulumba Figure 2. Speed deviations for a step response (case 1). Figure 3. Speed deviations for a step response (case 2). Figure 4. Speed deviations for a step response (case 3). 012345678910 -5 -4 -3 -2 -1 0 1 2x 10-4 Step response for Case study:1 time(s) speed deviation CDE-PSS jDE-PSS 012345678910 -5 -4 -3 -2 -1 0 1 2x 10 -4 Step response for Case study:3 time(s) speed deviation CDE-PSS jDE-PSS 0 1 23 45 6 78 910 -5 -4 -3 -2 -1 0 1 2x 10 -4 Step response for Case study:3 time(s) speed deviation CDE-PSS jDE-PSS  K. A. Folly, T. Mulumba Figure 5. Speed deviations for a step response (case 4). Figure 2 shows the responses of the rotor speed deviations for case 1. It can be seen that all the controllers are able to damp the oscillations and improve the stability of the system. However, jDE-PSS has a slightly higher overshoot and undershoot but settles within 2.5 sec. as compared to CDE-PSS which settled in about 3 sec. Figure 3 shows the responses for case 2. The performances of the controllers are similar to the ones observed in case 1. Figure 4 and Figure 5 show the speed responses of the system for cases 3 to 4, respectively. jDE-PSS pro- vides the best performance in terms of settling time. In particular in case 4, where the system is weaker than the previous cases, jDE -PSS settled quicker (in about 5.5 sec) compared to CDE which settled in about 10 sec. The relatively large undershoots of j DE -PSS is probably due the the relatively higher PSS gain of jDE-PSS (Kp = 18.9) compared to CDE-PSS (Kp = 17.2). 8. Conclusion In this paper, self-adaptive DE is used to optimally tune the parameters of a power system controller for small- signal stability improvement. It is shown that there are clear advantages in using self-adaptive DE as compared to the conventional DE. Firstly, the time consuming trial-and-error approach is removed and secondly, there is a high possibility that the algorithm will converge to optimal values. Results based on eigenvalue analysis and time domain simulations show that under small disturbance, the self-adaptive DE performs better than the clas- sical DE in terms of settling time. Work is in progress to extend the self-adaptive DE approach to controller de- sign in a multi-machine power system in the future. Acknowledgem ents This work is based on research supported in part by the National Research Foundation of South Africa UID 83977 and UID 85503. References [1] Mitchell, M. (1996) An Introduction to Genetic Algorithms. The MIT Press. [2] Goldberg, D.E. (1989) Genetic Algorithms in Search, Optimization & Machine Learning. Addison-Wesley. [3] Abdel, Y.L., Abido, M.A. and Mantawy, H. (1999) Simultaneous Stabilization of Multimachine Power Systems via Genetic Algorithms. IEEE Transactions on Power Systems, 14, 1428-1438. http://dx.doi.org/10.1109/59.801907 [4] Man , K.F., Tang, K . S. and Kwong, S. (1996 ) Genetic Algorithms: Concepts and Applications. IEEE Transactions on Industrial Electronics, 43, 519-534. http://dx.doi.org/10.1109/41.538609 [5] Kaveshg ar, N. and Huynh, N. (2012) An Efficient Genetic Algorithm for Solving the Quay Crane Scheduling Problem. Expert Systems with Applications, 39, 13108-13117. [6] Li , D., Das, S., P a hwa, A. and Deb, K. (2013) A Multi-Objective Evolutionary Approach for Generation. Expert Sys- 012345678910 -5 -4 -3 -2 -1 0 1 2 3x 10-4 Step response for Case study:4 ti me (s) speed deviation CDE-PSS jDE-PSS  K. A. Folly, T. Mulumba tems with Applications, 40, 7647-7655. [7] Mühlenbein, H. and Schlierkamp-Voosen, D. (1994) The Science of Breeding and its Application to the Breeder Ge- netic Algorithm-BGA. IEEE Transactions on Evolutionary Computation, 1, 335-360. [8] Balu ja, S. (1994) Population-Based Incremental Learning: A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning. Carnigie Mellon University, Technical Report CMU-CS-94-163. [9] Ho, S.L. and Yang, S. (2010) A Population-Based Incremental Learning Method for Robust Optimal Solutions. IEEE Transactions on Magnetics, 46 , 3189-3192. http://dx.doi.org/10.1109/TMAG.2010.2043650 [10] Folly, K.A. (2013) An Improved Population-Based Incremental Learning Algorithm. International Journal of Swarm Intelligence Research (IJSIR), 4, 35-61. http://dx.doi.org/10.4018/jsir.2013010102 [11] Folly, K.A. and Venayagamoorthy, G.K. (2009) Effects of Learning Rate on the Performance of the Population Based Incremental Learning Algorithm. In: Neural Networks, Int ernational Joint Conference on Neural Networks, 861 -868. [12] Folly, K.A. (2011) Performance Evaluation of Power System Stabilizers Based on Population-Based Incremental Learning. International Journal of Electrical Power & Energy Systems, 33, 1279-1287. http://dx.doi.org/10.1016/j.ijepes.2011.05.004 [13] Folly, K.A. and Venayagamoorthy, G.K. (2009) A Real-Time Implementation of a PBIL Based Stabilizing Controller for Synchronous Generator. IEEE Industry Applications Society Annual Conference. [14] Folly, K.A. (2012) Population Based Incremental Learning Algorithm with Adaptive Learning Rate Strategy. In The Proceedings of the 3rd International Conference on advanced Neural Networks, International Joint Conference on Neural Nin Swarm Intelligence (ICS I’ 12 ), 1, 11-20. [15] Folly, K.A. (2007) Robust Controller Based on a Combination of Genetic Algorithms and Competitive Learning. In: Proceedings of the 2007 International Joint Conference on Neural Network (IJCNN), Orlando, Florida. http://dx.doi.org/10.1109/IJCNN.2007.4371446 [16] He, N., Xu , D. and Huang, L. (2009) The Application of Particle Swarm Optimizer to Passive and Hybrid Active Pow- er Filter. IEEE Transactions on Industrial Electronics, 56, 2841-2851. http://dx.doi.org/10.1109/IJCNN.2007.4371446 [17] Shayeghi, H., Safari, A. and Sh ayanfar, H.A. (2008) Multimachine Power System Stabilizers Design Using PSO Algo- rithm. International Journal of Electrical Power & Energy Systems, 1, 226-233. [18] Chan, K.Y. , Dillon, T.S. and Chang, E. (2013) Intelligent Particle Swarm Optimization for Short-Term Traffic Flow Forecasting Using on Road Sensor Systems. IEEE Transactions on Industrial Electronics, 60, 4714-47 2 5. [19] Price, K., Storn, R. and Lampinem, J. (2005) Differential Evolution: A Practical Approach to Global Optimization. Springer-Verlag, Berlin, Heidelber g. [20] Mulumba, T., Folly, K.A. and Malik, O.P. (2011) Tuning of PSS Parameters Using Differential Evolution. Proceedings of the 20th Southern African Universities’ Power Engineering Conference (SAUPEC 2011), Cape Town, 13-15 July 2011. [21] Fan, Z., Li u , J., Søren sen, T. and Wang, P. (2009) Improved Differential Evolution Based on Stochastic Ranking for Robust Layout Synthesis of MEMS Components. IEEE Transactions on Industrial Electronics, 56, 937-948. http://dx.doi.org/10.1109/TIE.2008.2006935 [22] Zhang, J. and Sanderson, A.C . (2009) Adaptive Differential Evolution: A Robust Approach to Multimodal Problem Optimization. Springer, Berlin. Heidelb erg. http://dx.doi.org/10.1007/978-3-642-0152 7 -4 [23] Islam, S.K.M., Das, S., Ghosh, S., Roy, S. and Suganthan, P.N. (2012) An Adaptive Differential Evolution Algorithm with Novel Mutation and Crossover Strategies for Global Numerical Optimization. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 42 , 482-500. [24] Brest, J., Greiner, S. , Bo ško vié , B. , Me rn i k , M. and Žumer, V. (2006) Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Transactions on Evolutionary Computa- tion, 10, 646-65 7. http://dx.doi.org/10.1109/TEVC.2006.872133 [25] Lui, J. and Lampinen, J. (2005) A Fuzzy Adaptive Differential Evolution Algorithm. Soft Computing, 9, 448-462. http://dx.doi.org/10.1007/s00500-004-0363-x [26] Suganthan, P. N. and Quin, A.K. (2005) Self-Adaptive Differential Evolution Algorithm for Numerical Optimization. In: Congress on Evolutionary Computation, 1785-1791 [27] Tvrdik, J. (2009) Adaptation in Differential Evolution: A Numerical Compari so n. Applied Soft Computing, 9, 1149- 1155. http://dx.doi.org/10.1016/j.asoc.2009.02.010 [28] Qin, A.K., Huang, V. L. and Suganthan, P.N. (20 09 ) Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Transactions on Evolutionary Computation, 13, 398-417 . http://dx.doi.org/10.1109/TEVC.2008.927706 [29] Kundur, P. (1994) Power System Stability and Control. McGraw-Hill, Inc. [30] Rogers, G. (1999) Power System Oscillations. Kluwer Academic, Boston.
|