Paper Menu >>
Journal Menu >>
 Materials Sciences and Applications, 2011, 2, 314-318 doi:10.4236/msa.2011.25041 Published Online May 2011 (http://www.SciRP.org/journal/msa) Copyright © 2011 SciRes. MSA Vibrations of a One-Dimensional Host-Guest System Amelia Carolina Sparavigna Dipartimento di Fisica, Politecnico di Torino C.so Duca degli Abruzzi 24, Torino, Italy. Email: amelia.sparavigna@polito.it Received January 14th, 2011; revised March 17th, 2011; accepted March 24th, 2011. ABSTRACT A simple model shows how it is possible to create a gap in the vibrational spectrum of a one-dimensional lattice. The proposed model is a host-guest chain having, instead of point-like masses connected by spring, massive cages hosting particles inside. We imagine the cage as a rigid box containing a mass linked by a spring to the box inner wall. The presence of guests creates an energy gap in the dispersion of vibrational frequencies. The gap is about the internal resonance of the mass hidden in the cage. The model is proposed to help understanding the macroscopic behaviour of some phononic materials and the properties of materials with microscopic rattling modes. Keywords: Metamaterials, Phonons, Band Gap, Thermal Properties 1. Introduction In spite of their simplicity, the study of models with masses or rods connected by springs can be quite helpful in understanding the properties of metamaterials as of other nano-engineered structures. The term “metamate- rial”, credited to Rodger Walser, indicates a material, which gains its properties from its structure, rather than from the properties of components [1,2]. In fact, the term “metamaterial” is commonly used for composites, which are distinguishing themselves for unusual properties. There are several examples regarding electromagnetism and elastic properties. We have, for instance, the left- handed materials possessing negative refractive index, able to affect in an uncommon way the passage of elec- tromagnetic waves near them [3-6]. In the case of elastic materials, a property considered as unusual is a negative Poisson’s ratio. Materials with negative Poisson coeffi- cient are named auxetics [7-12]. Among them, natural auxetics occur in biological systems too. Metamaterials usually share similar behaviours with photonic and phononic crystals [13,14]. For instance, some metamaterials have been prepared, which are able to act as total wave reflector within certain sonic fre- quency ranges. These sonic materials, which are then behaving as phononic crystals, are mainly fabricated in- cluding in a hosting component some localized resonant structures [15]. As in the case of electromagnetic metamaterials, we can prepare some composites displaying an effective “ne- gative” elastic constant, analogous to the negative refrac- tive index [16,17]. In [16], the author is discussing the case of metamaterials, which are guest-host systems, having units possessing hidden resonant masses inside. Figures in Reference [16] are quite stimulating to study and discuss the vibrational properties of such structures. Among the many models composed of rigid cages with moving particles inside, let us use the simplest one we can imagine, that is a one-dimensional chain composed of rigid host-guest units. 2. A Host-Guest Model Figure 1 shows the model. It is a simple spring model describing an interacting system of host cages of mass M interconnected by springs having constant K and guest atoms of mass m attached to the cage inner walls by means of springs with constant K . The one-dimen- sional model we consider has then rigid units and spring connections, with distance L between cages. The unit cell of the lattice has a position given by the lattice indi- ces 1, , 1, 2,iiii . If the cage is imagined as a closed box, a mass can be hidden in it. Its presence is revealed by the frequencies of the system. Let us define o K M , K m which are the natural angular frequencies of cage and hidden masses. In the following we will use the dimensionless ratios:  Vibrations of a One-Dimensional Host-Guest System Copyright © 2011 SciRes. MSA 315 Figure 1. The unit of the chain is composed by a cage with a hidden mass inside. kKK , mmM , o and o . Let us investigate the harmonic vibrations of the chain supposed to be infinite with displacements of masses in longitudinal direction. ,bi x is the displacement from equilibrium of one of two masses, that are the cage and the hidden mass: b can have two possible determina- tions M and m for the reticular position i of equi- librium. In the case of small displacements, equations are: ,,,1,1,, ,,, 20 0 MiMiMiMimi Mi mimiM i MxKxKxKxK xx mxK xx (1) that is, using .,, , iMiiMimi x xx , we have: 11 20 0 iiii i ii i MKKKK mmK (2) If we are looking for Bloch waves with wavevector q, it is possible to write for each lattice site: exp; exp iiii A itiqxBit iqx (3) and then the dispersion relations for frequency ω can be easily obtained from the dynamical Equations (2); in the following way. We defined L the distance between cages; then 1ii Lx x , is the distance between the sites of the chain. Inserting (3) in (1) we have: 2 22 2e eee0 ee 0 i i iqx iqLiqLit iqx it MA KAKAKAKB mBmAKB (4) and then: 2 22 2e e0 0 iqL iqL MA KAKAKAKB mBmAKB (5) These equations have a non-trivial solution when: 2 22 0 MC K mmK (6) In Equation (6), 21cosCK qL . This equation gives the dispersion relation q of the angular frequency as a function of a given wavenumber q. Let us consider for plotting, the reduced frequencies o , o . Dispersion relations of the chain as a function of the wavenumber q are shown in Figure 2. Let us remember that the dispersion relation is showing the angular frequency (in our case the reduced an- gular frequency ), as a function of the wavenumber q. Note the existence of a phononic gap between the two branches. This gap is about the natural frequency of the mass inside the cage. The figure is obtained assuming 14, 14mk . The horizontal line represents Ω , the reduced natural frequency of the hidden oscillator. At the edge of the Brillouin Zone, we have a frequency of the system almost corresponding to that of the natural oscillation Ω . This is an important result for the engi- neering of phononic materials, because it means that the propagation of waves with a frequency equal to that of the internal resonance is not allowed. Using specific val- ues of , mk , it is possible tailoring the phononic prop- erties of the metamaterial. Figure 3 shows the dispersion of vibrational frequent- cies in several conditions. In the upper part of the figure, Figure 2. Dispersion of vibrational frequencies for model in Figure 1 Ω' is the reduced natural frequency of the hidden oscillator. Note that at the edge of the Brillouin Zone (en- circled) we have a frequency almost corresponding to that of the natural oscillation of the hidden mass. This means that the propagation of waves with a frequency equal to that of the internal resonance is not allowed. 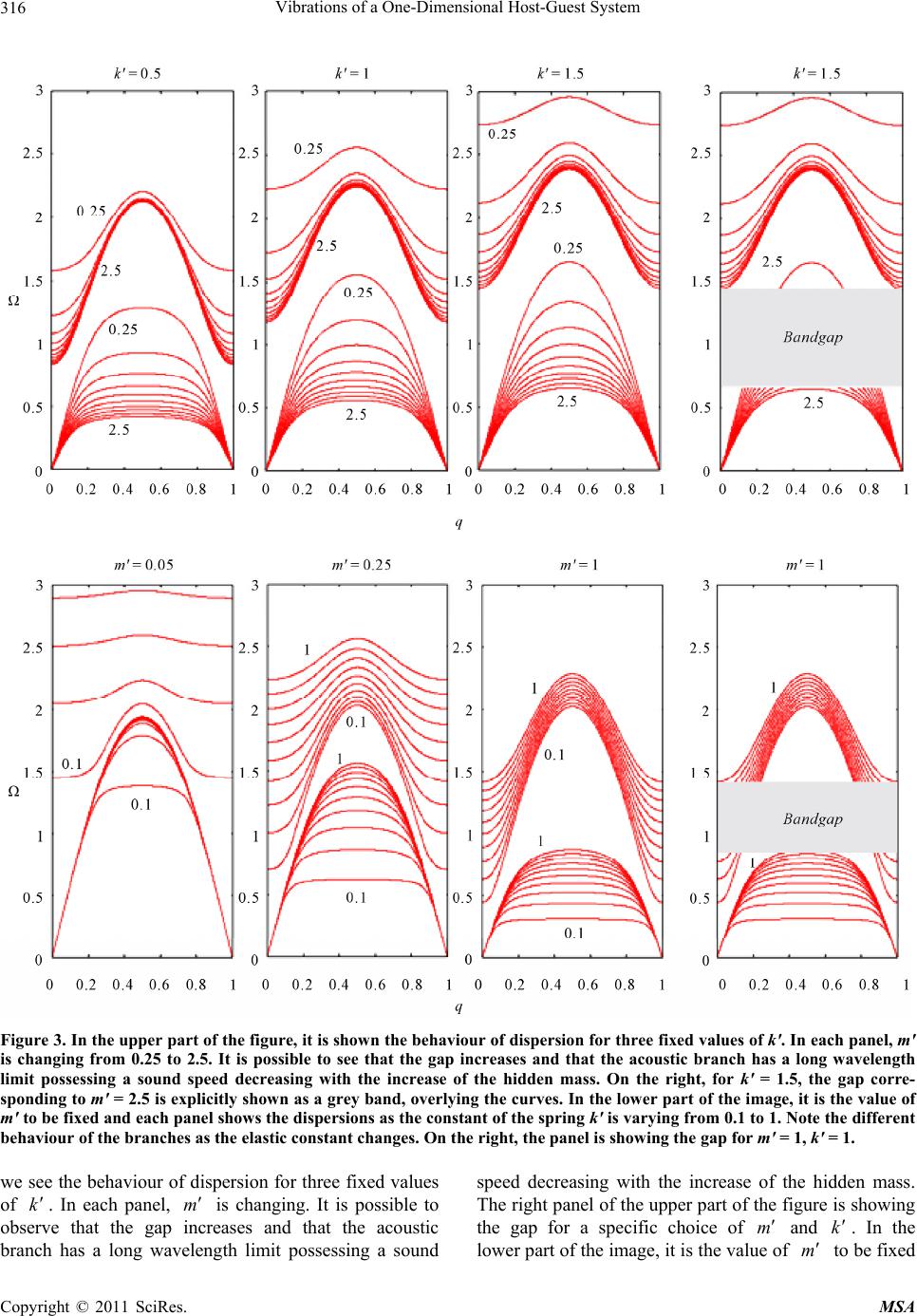 Vibrations of a One-Dimensional Host-Guest System Copyright © 2011 SciRes. MSA 316 Figure 3. In the upper part of the figure, it is shown the behaviour of dispersion for three fixed values of k'. In each panel, m' is changing from 0.25 to 2.5. It is possible to see that the gap increases and that the acoustic branch has a long wavelength limit possessing a sound speed decreasing with the increase of the hidden mass. On the right, for k' = 1.5, the gap corre- sponding to m' = 2.5 is explicitly shown as a grey band, overlying the curves. In the lower part of the image, it is the value of m' to be fixed and each panel shows the dispersions as the constant of the spring k' is varying from 0.1 to 1. Note the different behaviour of the branches as the elastic constant changes. On the right, the panel is showing the gap for m' = 1, k' = 1. we see the behaviour of dispersion for three fixed values of k. In each panel, m is changing. It is possible to observe that the gap increases and that the acoustic branch has a long wavelength limit possessing a sound speed decreasing with the increase of the hidden mass. The right panel of the upper part of the figure is showing the gap for a specific choice of m and k . In the lower part of the image, it is the value of m to be fixed  Vibrations of a One-Dimensional Host-Guest System Copyright © 2011 SciRes. MSA 317 and each panel shows the dispersions as the constant of the spring k is varying. Again, the right panel is showing the gap. As we can see from the figure, adjust- ing the ratios of masses or of spring constants or both it is possible to tailor the gap. We have then a band of fre- quencies where the propagation of the waves in the ma- terial is not allowed. It means that the material is not transmitting these frequencies: the waves are reflected by the composite material. 3. Discussion The model shows, from a macroscopic point of view, that a structure with a cage hosting a mass displays a gap in the allowed frequencies. It is therefore illustrating how some phononic crystals could be created by means of host-guest systems. Moreover, we have seen that an in- crease of the hidden mass reduces the speed of the acous- tic long wavelengths, an interesting result for engineering materials with very low thermal conductivity and for the development of more efficient thermoelectric devices. In fact, a low thermal conductivity is required for the thermoelectric conversion in solid-state heat engines. In these devices, the electron gas serves as the working fluid, converting the heat flow in electric power [18]. For thermoelectric applications, materials must have a high figure-of-merit, which is a goodness factor including the Seebeck coefficient and the electrical and thermal con- ductivities. A decrease of thermal conductivity means an increase of the figure-of-merit. In the case of crystalline materials, it is enough to disturb the phonon paths by disorder or lattice defects [19-21] to have a low conduc- tivity. Unfortunately, defects decreased the charge trans- port too. Therefore, the figure-of-merit can only be moderately improved by reducing the lattice thermal conductivity: to have a significantly larger goodness parameter it is nec- essary to improve the electrical properties [22]. The aim of recent researches is to employ the Phonon Glasses - Electronic Crystals, PGECs, where the lattice is disor- dered and then phonons are strongly scattered, but the electrons remain free to move. To create such structures, a possibility is the use of materials containing weakly bound atoms, “rattling” within an atomic cage. These materials have a low thermal conductivity, as that dis- played by glasses, but have an electric conductivity as high as in crystals [23]. Typical of these materials are the filled skutterudites [24] and the clathrates [25], which are host-guest systems at the atomic, microscopic scale. In host-guest lattices, the guest entities are supposed to have oscillations, so-called rattler modes, which scatter the acoustic phonons and reduce the thermal conductivity. In a resonant scattering model [26], it was hypothesized an “avoided crossing” between acoustic phonons and localized guest modes, that coming from a mixing of guest and host modes with an energy exchange as a con- sequence. Avoided crossing was found in hydrates [27,28] and recently in a PGEC material. In Reference [29], the phonon dispersion relations of Ba8Ga16Ge30 are showing unambiguously the theoretically predicted avoided cross- ing of the rattler modes and the acoustic-phonon bran- ches. Ba8Ga16Ge30 is a clathrate type-I structure with a host cage framework of Ga and Ge atoms holding Ba guest atoms inside the cages. The phenomenon referred as the “avoided crossing”, is the same as that we show in Figures 2 and 3, that is, the presence of a gap separating the two branches of frequency dispersion. This gap is created about the natural frequency of the guest. As a conclusion, we can tell that the use of host-guest systems, from macroscopic to microscopic scales, can be an interesting method for engineering new materials. The host-guest model we proposed is showing that the struc- ture is able to create some phononic band-gaps. It is also changing the sound speed in the material. The proposed model can hopefully stimulate new engineering methods for metamaterials with improved vibrational properties or reduced thermal conductivity. Applied to microscopic materials, it helps understanding the microscopic proper- ties of those materials with rattling modes. REFERENCES [1] R. M. Walser, “Metamaterials: An Introduction,” In: W. S. Weiglhofer and A. Lakhtakia, Eds. Introduction to Com- plex Mediums for Optics and Electromagnetics, SPIE Press, Bellingham, 2003, pp. 295-316. doi:10.1117/3.504610.ch13 [2] R. M. Walser, “Electromagnetic Metamaterials,” Pro- ceeding SPIE Complex Mediums II beyond Linear Iso- tropic Dielectrics, San Diego, Vol. 4467, 2001, pp. 1-15. [3] V. G. Veselago, “The Electrodynamics of Substance with Simultaneously Negative Values of and μ,” Soviet Phy- sics Uspekhi, Vol. 10, No. 4, 1968, pp. 509-514. doi:10.1070/PU1968v010n04ABEH003699 [4] J. B. Pendry, A. J. Holden, D. J. Robbins and W. J. Stew- art, “Magnetism from Conductors and Enhanced Nonlin- ear Phenomena,” IEEE Transactions on Microwave The- ory and Techniques, Vol. 47, No. 11, 1999, pp. 2075- 2084. doi:10.1109/22.798002 [5] A. Grbic and G. V. Eleftheriades, “Overcoming the Dif- fraction Limit with a Planar Left-Handed Transmis- sion-Line Lens,” Physical Review Letters, Vol. 92, No. 11, 2004, pp. 117403-1-117403-4. [6] E. Yablonovitch, “How to be Truly Photonic,” Science, Vol. 289, No. 5479, 2000, pp. 557-559. doi:10.1126/science.289.5479.557 [7] A. Sparavigna, “Phonons in Conventional and Auxetic Honeycomb Lattices,” Physical Review B, Vol. 76, No. 13, 2007, pp. 1343021-1343021-6.  Vibrations of a One-Dimensional Host-Guest System Copyright © 2011 SciRes. MSA 318 [8] K. E. Evans, M. A. Nkansah, I. J. Hutchinson and S. C. Rogers, “Molecular Network Design,” Nature, Vol. 353, No. 6340, 1991, pp. 124-125. doi:10.1038/353124a0 [9] A. Alderson, “A Triumph of Lateral Thought,” Chemistry & Industry, Vol. 17, May 1999, pp. 384-391. [10] R. S. Lakes, “Foam Structures with a Negative Poisson’s Ratio,” Science, Vol. 235, No. 4792, 1987, pp. 1038-1040. doi:10.1126/science.235.4792.1038 [11] C. P. Chen and R. S. Lakes, “Dynamic Wave Dispersion and Loss Properties of Conventional and Negative Pois- son’s Ratio Polymeric Cellular Materials,” Cellular Polymers, Vol. 8, No. 5, 1989, pp. 343-359. [12] C. W. Smith, J. N. Grima and K. E. Evans, “A Novel Mechanism for Generating Auxetic Behaviour in Reticu- lated Foams: Missing Rib Model,” Acta Materialia, Vol. 48, No. 17, 2000, pp. 4349-4356. doi:10.1016/S1359-6454(00)00269-X [13] T. Suzuki and P. K. L. Yu, “Complex Elastic Wave Band Structures in Three-Dimensional Periodic Elastic Media,” Journal of the Mechanics and Physics of Solids, Vol. 46, No. 1, 1998, pp. 115-138. doi:10.1016/S0022-5096(97)00023-9 [14] M. Kafesaki, M. M. Sigalas and N. Garcìa, “Frequency Modulation in the Transmittivity of Wave Guides in Elas- tic-Wave Band-Gap Materials,” Physical Review Letters, Vol. 85, No. 19, 2000, pp. 4044-4047. doi:10.1103/PhysRevLett.85.4044 [15] Z. Liu, X. Zhang, Y. Mao, Y. Y. Zhu, Z. Yang, C. T. Chang and P. Sheng, “Locally Resonant Sonic Materi- als,” Science, Vol. 289, No. 5485, 2000, pp. 1734-1736. doi:10.1126/science.289.5485.1734 [16] G. W. Milton, “New Metamaterials with Macroscopic Behavior outside that of Continuum Elastodynamics,” New Journal of Physics, Vol. 9, No. 10, 2007, pp. 359-1- 359-13. [17] G. W. Milton and J. R. Willis, “On Modifications of Newton’s Second Law and Linear Continuum Elastody- namics,” Proceedings of the Royal Society A, Vol. 463, No. 2079, 2007, pp. 855-880. [18] D. M. Rowe, “Review, Thermoelectric Waste Heat Reco- very as a Renewable Energy Source,” International Journal of Innovations in Energy Systems and Power, Vol. 1, No. 1, November 2006, pp. 13-23. [19] A. Sparavigna, “Influence of Isotope Scattering on the Thermal Conductivity of Diamond,” Physical Review B, Vol. 65, No. 6, 2002, pp. 064305-1-064305-5. doi:10.1103/PhysRevB.65.064305 [20] A. Sparavigna, “Lattice Thermal Conductivity in Cubic Silicon Carbide,” Physical Review B, Vol. 66, No. 17, 2002, pp. 174301-1-174301-5. doi:10.1103/PhysRevB.66.174301 [21] M. Omini and A. Sparavigna, “Role of Grain Boundaries as Phonon Diffraction Gratings in the Theory of Thermal Conductivity,” Physical Review B, Vol. 61, No. 10, 2000, pp. 6677-6688. doi:10.1103/PhysRevB.61.6677 [22] M. Gao and D. M. Rowe, “A serious Limitation to the Phonon Glass Electron Crystal (PGEC) Approach to Improved Thermoelectric Materials,” Journal of Materi- als Science Letters, Vol. 18, No. 16, 1999, pp. 1305-1306. [23] G. A. Slack, “Design Concepts for Improved Thermoe- lectric Materials,” Materials Research Society Symposium Proceedings, Vol. 478, 1997, pp. 47-54. [24] J. P. Fleurial, T. Caillat and A. Borshchevsky, “Skutteru- dites: An Update,” Proceedings ICT '97 XVI International Conference on Thermoelectrics, Dresden, 1997, pp. 1-11. [25] G. S. Nolas, “Semiconductor Clathrates: A PGEC System with Potential for Thermoelectric Applications,” Materi- als Research Symposium Proceedings, Vol. 545, 1999, pp. 435-442. [26] J. S. Tse and M. A. White, “Origin of Glassy Crystalline Behavior in the Thermal Properties of Clathrate Hydrates: A Thermal Conductivity Study of Tetrahydrofuran Hy- drate,” Journal of Physical Chemistry, Vol. 92, No. 17, 1988, pp. 5006-5011. doi:10.1021/j100328a036 [27] J. S. Tse, V. P. Shpakov, V. V. Murashov and V. R. Be- losludov, “The Low Frequency Vibrations in Clathrate Hydrates,” Journal of Chemical Physics, Vol. 107, No. 21, 1997, pp. 9271-9275. doi:10.1063/1.475218 [28] J. Baumert, C. Gutt, V. P. Shpakov, J. S. Tse, M. Krisch, M. Müller, H. Requardt, D. D. Klug, S. Janssen and W. Press, “Lattice Dynamics of Methane and Xenon Hydrate: Observation of Symmetry-Avoided Crossing by Experi- ment and Theory,” Physical Review B, Vol. 68, No. 17, 2003, pp. 174301-1-174301-4. doi:10.1103/PhysRevB.68.174301 [29] M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, “Avoided Crossing of Rat- tler Modes in Thermoelectric Materials,” Nature Materi- als, Vol. 7, No. 10, 2008, pp. 811-815. doi:10.1038/nmat2273 |

