Paper Menu >>
Journal Menu >>
 J. Electromagnetic Analysis & Applications, 2009, 2: 73-83 doi:10.4236/jemaa.2009.12012 Published Online June 2009 (www.SciRP.org/journal/jemaa) Copyright © 2009 SciRes JEMAA 1 Design of Axial-Flux Motor for Traction Application Nadia Chaker, Ibrahim Ben Salah, Souhir Tounsi, Rafik Neji Ecole Nationale d’Ingénieurs de Sfax (ENIS), BP. 1173, 3038 Sfax Tunisie, Laboratoire d’Electronique et des Technologies de l’Information (LETI), Equipe Véhicule Electrique et Electronique de Puissance (VEEP), Tunisia. Email: nadia.chaker@enis.rnu.tn, rafik.neji@enis.rnu.tn Received February 9th, 2009; revised March 26th, 2009; accepted April 2nd, 2009. ABSTRACT This paper deals with the design of high power – low dimensions axial-flux permanent-magnet motor intended for trac- tion application. First, two motor configurations are analytically designed and compared using finite element calcula- tion. Then, the configuration yielding the best performances is integrated and modelled with the whole traction chain under MATLAB/SIMULINK environment in order to demonstrate the motor operation on a large speed band. Keywords: Axial-Flux Permanent-Magnet Motor, Design Criteria, Finite Elements, Traction Chain, Circulation Mission 1. Introduction Nowadays, the use of internal combustion engines in vehicles is one of the principal causes of several pollution problems as air and sound ones. Therefore, the electrical vehicles constitute an excellent candidate to avoid these problems. However, since their appearance, the major problems of this type of vehicles remain in high cost, weak autonomy and over speed problems. For that, it becomes essential to give a particular care when choosing the principal element of the electric traction chain which is the electric motor. For electric traction applications, synchronous or asyn- chronous motors [1] with radial or axial fluxes [2,3], can be used. In order to increase the torque generation capabil- ity, these motors can be modulated. Moreover, the conse- quent progress of the permanent-magnet technology makes permanent magnets synchronous motors more and more utilized for variable speed and high performance systems. In [4], an effectiveness and mass comparison study between radial and axial structures of a perma- nent-magnet synchronous motor was presented. For a constant power, it was demonstrated that the axial con- figuration with 4 pole pairs in rotor and 6 teeth in stator has the best compromise effectiveness-mass. Thus, this motor appears particularly interesting for electric vehicle applications. In fact, the axial-flux permanent-magnet motor has many advantages [5] as: 1): high effectiveness and high power factor, 2) high specific power, 3) no ring-brushes and 4) possibility of modularity. As an industrial application we can mention that JEUMONT industry used the technology of axial flux structures to develop high power machines intended to boats and Aeolian alternators driving [6]. This paper presents the design of a high power – low dimensions axial-flux permanent-magnet motor for a traction application. First, the design criteria of electrical parameters are highlighted for trapezoidal and sinusoidal motor configurations. Then, considering the vehicle specification, the motor geometric parameters are ana- lytically determined for a comparison based on finite element calculation between both configurations per- formances. Finally, a traction chain integrating best con- figuration is modelled under MATLAB/SIMULINK en- vironment in order to demonstrate the motor operation on a large speed band without weakening flux method. 2. Generalities about Axial-Flux Permanent- Magnet Motor Several axial-flux machine configurations exist depending on the stator(s) position(s) with respect to the rotor(s) ones, as shown in Figure 1. We can find: ● A structure with one rotor and one stator, Figure 1 (a). ● A structure, in which the rotor is located between the stators, Figure 1(b). ● A structure, in which the stator is located between the rotors, Figure 1(c). ● A multistage structure including several rotors and stators Figure 1(d). In traction applications, more the motor has higher torque generation capabilities more it is interesting. As  Design of Axial-Flux Motor for Traction Application 74 (b) (c) (d) (a) Figure 1. Permanent-magnet axial-flux machines configurations. Legend: (a): Single-rotor - single-stator structure; (b): Sin- gle-rotor - two-stators structure; (c): Two-rotors - single-stator structure, called hereafter also as AFIPM machine (Ax- ial-Flux Interior rotor Permanent-Magnet machine); (d): Multistage structure including two stator blocks and three rotor blocks [2] radial-flux motors, the axial-flux ones can be modulated which leads to the increase of their torque generation capabilities [1,2,4]. In fact, the four configurations shown in Figure 1 are used for traction applications. The torque generated with the fourth configuration, composed of four modules (Figure 1(d)), is twice times greater than the torque of the third and the second configurations which contain two modules, Figure 1(c) and Figure 1(b), and four times than the first configuration developed torque (one module), Figure 1(a). It is to be signalled that configurations illustrated in Figure 1(b) and Figure 1(c) have the same torque genera- tion capabilities and the choice between both depends if the application needs an outer or inner rotor. In the present paper, we have been interested in the in- tegration of the axial-flux technology for automotive traction application as shown in Figure 2. 3. Analytical Design of the Unit Motor – Inverter In the present section, the single-rotor – single-stator structure which is the simplest axial-flux permanent- magnet motor configuration [7] is considered, Figure 1(a). At the beginning and in order to satisfy the design criteria of the motor associated to its inverter, the electrical pa- rameters are calculated for two configurations: the three-phase motor with trapezoidal back e.m.f wave form and the three-phase motor with sinusoidal back e.m.f wave form. Then, in order to define the structure of the considered motor configurations, the geometrical pa- rameters are analytically calculated, using the vehicle specifications recapitulated in Table 1 (Appendix). During the design process it is required that: when the vehicle reaches the maximum specified speed, the motor is controlled with full wave form and develops the needed torque. At this operation point: ● The electromagnetic torque Tem, via the mechanical transmission system (reducer and differential), is ex- pressed as the following: maxemdm b TTVV (1) where Tdm is the starting torque expressed as: sin( ) w dmv bdv d R TMVtMg r . ● The maximum value of the motor back e.m.f is: 22 maxmaxint 4 CsphsphCsphexte ENddtN ddENDDB (2) Taking in account the vehicle specification mentioned in Table 1, the motor must develop a torque of Tem = 40.625Nm with a maximum value of back e.m.f equal to Ec=138.462V. It is to be signaled that, in coming EF study the last men- tioned values of Tem and Ec will be used to verify the calculated geometrical parameters of the obtained con- cept. (e) (a) (b) (c) (d) Figure 2. Integration of axial-flux motor in automotive traction chain. Legend: (a): a battery providing the input direct volt- age of the inverter; (b): a conventional six-switch three-phase inverter insuring the generation of the three-phase voltage sup- plying the motor armature; (c): a permanent-magnet axial-flux motor with sinusoidal back e.m.f used for the vehicle driving; (d): a reducing system insuring the transmission of the motor mechanical energy to the vehicle wheels; (e): vehicle wheel Copyright © 2009 SciRes JEMAA 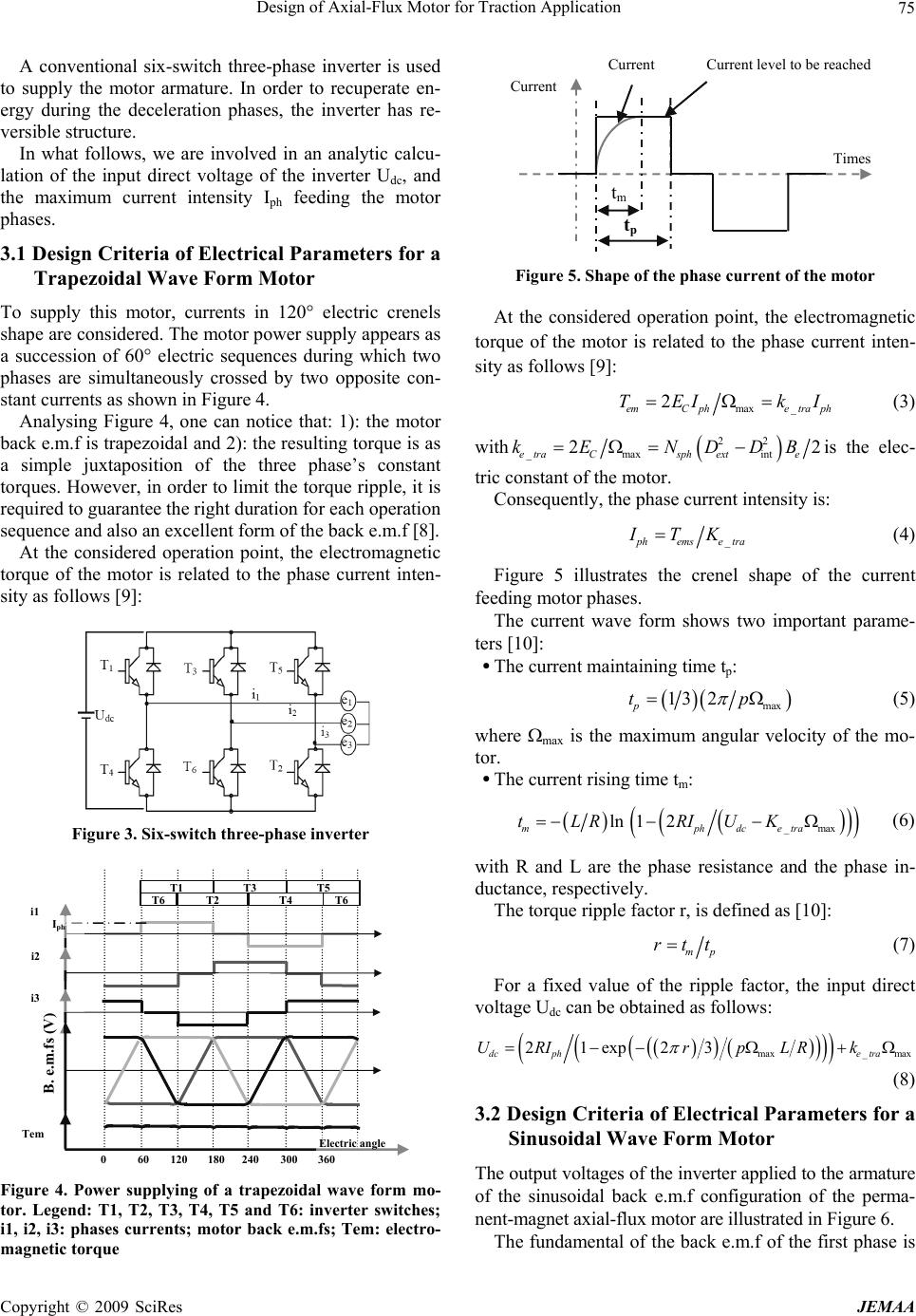 Design of Axial-Flux Motor for Traction Application 75 A conventional six-switch three-phase inverter is used to supply the motor armature. In order to recuperate en- ergy during the deceleration phases, the inverter has re- versible structure. In what follows, we are involved in an analytic calcu- lation of the input direct voltage of the inverter Udc, and the maximum current intensity Iph feeding the motor phases. 3.1 Design Criteria of Electrical Parameters for a Trapezoidal Wave Form Motor To supply this motor, currents in 120° electric crenels shape are considered. The motor power supply appears as a succession of 60° electric sequences during which two phases are simultaneously crossed by two opposite con- stant currents as shown in Figure 4. Analysing Figure 4, one can notice that: 1): the motor back e.m.f is trapezoidal and 2): the resulting torque is as a simple juxtaposition of the three phase’s constant torques. However, in order to limit the torque ripple, it is required to guarantee the right duration for each operation sequence and also an excellent form of the back e.m.f [8]. At the considered operation point, the electromagnetic torque of the motor is related to the phase current inten- sity as follows [9]: Figure 3. Six-switch three-phase inverter Figure 4. Power supplying of a trapezoidal wave form mo- tor. Legend: T1, T2, T3, T4, T5 and T6: inverter switches; i1, i2, i3: phases currents; motor back e.m.fs; Tem: electro- magnetic torque Current Current level to be reached Current Figure 5. Shape of the phase current of the motor At the considered operation point, the electromagnetic torque of the motor is related to the phase current inten- sity as follows [9]: max _ 2 emC phe tra ph TEI kI (3) with 22 _max int 22 etraCsph exte kE NDDBis the elec- tric constant of the motor. Consequently, the phase current intensity is: _ p hemsetra ITK (4) Figure 5 illustrates the crenel shape of the current feeding motor phases. The current wave form shows two important parame- ters [10]: ● The current maintaining time tp: max 13 2 p tp (5) where max is the maximum angular velocity of the mo- tor. ● The current rising time tm: _max ln 12 mphdce tLR RIUK tra (6) with R and L are the phase resistance and the phase in- ductance, respectively. The torque ripple factor r, is defined as [10]: mp rtt (7) For a fixed value of the ripple factor, the input direct voltage Udc can be obtained as follows: max_ max 21exp23 dcphe tra URIr pLRk (8) 3.2 Design Criteria of Electrical Parameters for a Sinusoidal Wave Form Motor The output voltages of the inverter applied to the armature of the sinusoidal back e.m.f configuration of the perma- nent-magnet axial-flux motor are illustrated in Figure 6. The fundamental of the back e.m.f of the first phase is Tem 0 60 120 180240 300 360 i1 i2 i3 Iph B. e.m.fs (V) Electric angle T1 T3 T5 T2 T4 T6 T6 tm tp Times Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application 76 Figure 6. Phases voltages shapes noted Uph11. It is expressed as the following [11]: 11 ()2sin 2 ph dc Ut UTt (9) To guarantee operation regime under maximum torque, the motor piloting angle between the back e.m.f EC and the phase current Iph is fixed equal to zero in the control system. At the maximum speed, the maximum value of the fundamental can be simply obtained from the Fresnel diagram as: 2 11 maxphph Cph URIELI 2 (10) where max is the maximum pulsation of motor voltage. The input direct voltage Udc can so be calculated using the following expression: 2 max 2 dcph Cph URIEL 2 I (11) At the considered operation point, the electromagnetic torque developed by the considered configuration of the motor is related to the phase current intensity as follows [9]: max_ sin 32 emC pheph TEI kI (12) with 22 _ sinint 32 38 esphext kE NDDB e is the elec- tric constant of the motor. Consequently, the phase current intensity is: _sinphems e ITK (13) Furthermore and for both configurations of the motor: the permanent-magnet axial-flux motor with trapezoidal back e.m.f wave form and the permanent-magnet axial-flux motor with sinusoidal back e.m.f wave form, the armature parameters R and L are expressed as the following [12]: ● Phase resistance: 6 p hbtcsp RTNLI with b T is copper resistivity at the temperature Tb, Ntc is the total number of conductors, is the current density and Lsp is the mean length of one turn. U p h 2Udc/3 Udc/3 t ● Phase inductance: T/6 ph (14) p hepf LLL p (15) with is the air-gap inductance and is the phase leakage inductance through one slot. ep Lfp L 3.3 Geometrical Parameters of the Motor The considered permanent-magnet axial-flux motor is composed of only one module containing two parts: one stator and one rotor, as illustrated in Figure 1(a). The stator yoke is laminated and made up of iron-silicium, Figure 1(a). It contains 12 identical slots where the three phase winding is inserted. Totally, 6 coils are used and each phase is obtained by putting in series two appropriate coils, as shown in Figure 8. The stator teeth are of two kinds: 1) 6 large teeth called principal teeth, around which coils are winded, and 2) 6 small teeth located in between adjacent principal teeth, called in- serted teeth. The width of the inserted tooth is variable depending on wished back e.m.f form. The rotor is an iron massive disc where eight samar- ium-cobalt permanent magnets, with a remanent polariza- tion of 1.175T, are mounted on its surface and four pole pairs are so obtained as shown in Figure 7(a) and (b). Figure 9 shows the geometrical parameters necessary to define the structures of both configurations of the sur- face-mounted axial-flux permanent-magnet motor. Be- fore calculating these geometrical parameters, specific coefficients have to be defined: ● p Lp : pitch in between poles. ● aP LL : rotor occupancy rate by permanent mag- nets. This coefficient is equal to 1 when the mounted permanent magnets cover the whole surface of the rotor, and is equal to 0.5 when permanent magnet surface is equal to the air one in rotor. ● ldlaptm a RAL : report between angular width of a principal tooth Aptm by the angular width of a magnet La, Figure 7. ● ndnp te RNp : report of the teeth number (Nte) by the number of pole pairs. ● diditm ptm RAA : report between the angular width of an inserted tooth Aitm by the angular width of a principal tooth Aptm, Figure 7. In coming finite elements study, the last defined coeffi- cients are taken same as ones used in [9] and [10]. These coefficients are resumed in Table 2 (Appendix). In the mentioned works, [9,10], it has been demonstrated that the considered values guarantee the best wave forms of gene- 0 T/3 T/2 t t Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application 77 (a) Trapezoidal back e.m.f configuration (b) Sinusoidal back e.m.f configuration Figure 7. Structures of both configurations of the perma- nent-magnet axial-flux motor Figure 8. Cylindrical cut plan of the stator of the axial-flux motor Figure 9. Geometrical parameters of the permanent-magnet axial-flux motor. Legend: Hr: rotor disc thickness; Hpm: permanent magnet height; Hth: slot height; Hy: stator yoke thickness; e: air-gap thickness; Ls: slot width rated fluxes and discard leakage fluxes between perma- nent magnets, for trapezoidal and sinusoidal motors. Referring to [12], the motor geometrical parameters are calculated by integrating the mentioned coefficient in trigonometric formulas. The obtained geometrical pa- rameters for both motor configurations are recapitulated in Table 2 (Appendix). 4. Finite Elements Study In axial-flux motor, the magnetic phenomena are sym- metrical according to the motor radial direction. Thus, the finite elements study of the two motor configurations can be simplified from 3D to 2D finite elements study which is simpler and more speed from the point of view of cal- culation time. The used software is MAXWELL 2D [13]. Figure 10 illustrates the finite elements study domain of the trapezoidal configuration of the axial-flux motor. In order to validate the analytical calculated parameters, this study is intended to the computation of the generated fluxes in the motor air-gap which yields the back e.m.fs and the developed torque at load operation point. In the first step, the geometrical parameters analytically calcu- lated in Subsection 2.3 are used to define the geometry used in the finite elements program. Then, in a second step and for different values of the rotor position, two different finite elements calculations are processed: ● An investigation of the effect of only the permanent magnets: the machine is working as a generator at no-load operation regime. The fluxes wave forms due to the permanent magnets effect are so carried out. Conse- quently, motor back e.m.fs wave forms and amplitudes are deduced which characterise the electric/mechanic power transfer. 1’ ● A computation under load operation point: the cur- rent feeding the motor armature is in phase with the back e.m.f obtained through the previous study. The so gener- ated flux is used to find out the machine torque. Figure 11 shows the flux lines through the magnetic circuit of the sinusoidal wave form configuration of the axial-flux motor due to the effect of only the permanent magnets and Figure 12 shows the flux lines through the magnetic circuit of the sinusoidal wave form configura- tion of the axial-flux motor under load operation. Analyzing these figures, one can notice that leakage fluxes between permanent magnets do not exist and all generated fluxes are useful. 4.1 Finite Elements Study at Generation Mode For both configurations of the axial-flux motor, the con- sidered operation point corresponds to the maximum speed of the vehicle (80km/h) which means an angular velocity equal to 341.88rad/s. For trapezoidal configura- 2 2 3’ 3’ 1 1 2’ 2’ 3 31’ North magnet Stator yoke Rotor disc South magnet Principal tooth Hr Inserted tooth Slot Hy Hth e Hpm Ls Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application Copyright © 2009 SciRes JEMAA 78 Figure 10. Cylindrical cut plan of the trapezoidal wave form motor Figure 11. Flux lines through the magnetic circuit of the sinusoidal wave form configuration of the axial-flux motor due to the effect of only the permanent magnets Figure 12. Flux lines through the magnetic circuit of the sinusoidal wave form configuration of the axial-flux motor under load operation -0,010 -0,008 -0,006 -0,004 -0,002 0,000 0,002 0,004 0,006 0,008 0,010 0 10203040506070809 Angle (°) Flux (Wb) 0 Flux1_no-load Flux2_no-load Flux3_no-load -0,008 -0,006 -0,004 -0,002 0,000 0,002 0,004 0,006 0,008 0 10203040506070809 Angle (°) Flux (Wb) 0 Flux1_no-load Flux2_no-load Flux3_no-load (a) Trapeze case (b) Sine case Figure 13. Fluxes generated in the air-gap of the machine for a generation regime at no-load operation and for a vehicle speed of 80km/h tion and sinusoidal one, the wave form of generated fluxes in the air-gap are illustrated respectively in Figure For each motor phase, the back e.m.f can be obtained considering a perfect magnetic circuit and using the fol- lowing expression: 13(a) and (b) where rotor position is varied from 0° to 90°. Csph phsphphsphph etNd dtNddtd dNd d (16) with is the rotor position and p h is the flux of the considered phase. The differential ph dd can be obtained by a lin- earization between two consecutive positions and the back e.m.f is so expressed as: 112 () () Csph phph eN 12 (17) Figure 14 shows the wave form of the obtained back e.m.fs for both axial-flux motor configurations. Analyzing those figures one can remark that in the case of the trapezoidal configuration of the motor the gener- ated back e.m.fs are perfectly trapezoidal and in the case of the sinusoidal motor configuration the generated back e.m.fs are also perfectly sinusoidal. 4.2 Finite Elements Study under Load Operation In this section, the motor is considered under load opera- tion regime. The motor armature is supplied by three currents in phase with the back e.m.fs obtained at the no-load operation of the generation regime. As illustrated in Figure 15(a) and (b), crenel shape currents with a maxi- mum intensity Iph_trapeze = 50.154A are used for the trape- zoidal configuration, and sinusoidal shape currents with a  Design of Axial-Flux Motor for Traction Application 79 -200 -150 -100 -50 0 50 100 150 200 0 10203040506070809 Angle (°) Back e.m.f (V) 0 Back e.m.f 1_no-loadBack e.m.f 2_no-loadBack e.m.f 3_no-load -200 -150 -100 -50 0 50 100 150 200 0 10203040506070809 Angle (°) Back e.m.f (V) 0 Back e.m.f 1_no-loadBack e.m.f 2_no-loadBack e.m.f 3_no-load (a) Trapeze case (b) Sine case Figure 14. Wave form of the generated back e.m.f for a generation regime at no-load operation and for a vehicle speed of 80km/h maximum intensity Iph_sine = 66.872A are used for the sinusoidal configuration. Figure 15(c) and Figure 15(d) illustrate the wave form of obtained fluxes in the motor air-gap for the maximum vehicle speed (80 km/h), and different rotor positions varying from 0° to 90°, respectively for trapezoidal and sinusoidal motors. Analysing these figures, one can notice the appearance of flux distortion at the load operation re- gime in respect with the no-load operation one. This dis- tortion is essentially due to the magnetic armature reaction. Considering Equation (16) and for a perfect magnet circuit, the back e.m.f of the motor can be calculated and illustrated as shown in Figure 15(e) and (f) for trapezoi- dal and sinusoidal configurations, respectively. Referring to the aforementioned figures, one can remark the fol- lowing: 1): for both configurations the analytical maxi- mum value of the back e.m.f Ec = 138.462V is reached, 2): the sinusoidal configuration generates a sinusoidal back e.m.f without peaks which yields a torque wave form with no peaks, Figure 15(h). However, the trape- zoidal configuration generates a trapezoidal distorted back e.m.f containing several peaks giving a torque wave form with several peaks too, Figure 15(g). Referring to Figure 15(g) and (h), both motors are able to develop the requested torque. The ripple figuring in the torques wave forms is due essentially to the motors cog- ged structures which cause the appearance of a cogging torque. Considering the obtained torques wave forms, vibration problems due to the torque ripple are sharper in the case of trapezoidal motor than in the case of the si- nusoidal one. For that, in coming study, only the features of the permanent-magnet axial-flux sinusoidal motor are investigated. 5. Traction Chain Modelling The present section is devoted to the modelling of an axial-flux motor with sinusoidal back e.m.f wave form associated to a six-switch three-phase inverter for traction application. The whole traction chain is modelled in order to investigate the motor behaviour vis-à-vis of a desired speed sequence and of the circulation mission of the Na- tional Institute of Research on Transports and their Secu- rity (INRETS). Figure 16 shows the block diagram of the adopted control vector strategy of the motor implemented under MATLAB/SIMULINK environment. The synchronous permanent magnet machine can be described in the d-q referential as follows [14]: ddddeqq qqqqedde VRiLdidt Li VRiLdidtLiK m (18) with e is the electric pulsation, Ld and Lq are respec- tively direct in squaring inductances. The direct and in squaring components of the current can be deduced using: ddeqqd qqeddemq IV LiLSR I VLiK LS R (19) with S is Laplace operator. The developed electromagnetic torque is so expressed [15]: 32 12 eme qdqdq TKIpLLII (20) Considering the fundamental dynamic law describing the vehicle motion, the torque needed on wheels is: wbraerog vwrvw TTTTMRdVdtTMRdVdt (21) with Tbr is the torque due to bearing resistance force, Taero is the torque due to aerodynamic load, Tg is the torque due to gravity forces, a coefficient related to the inertia Copyright © 2009 SciRes JEMAA 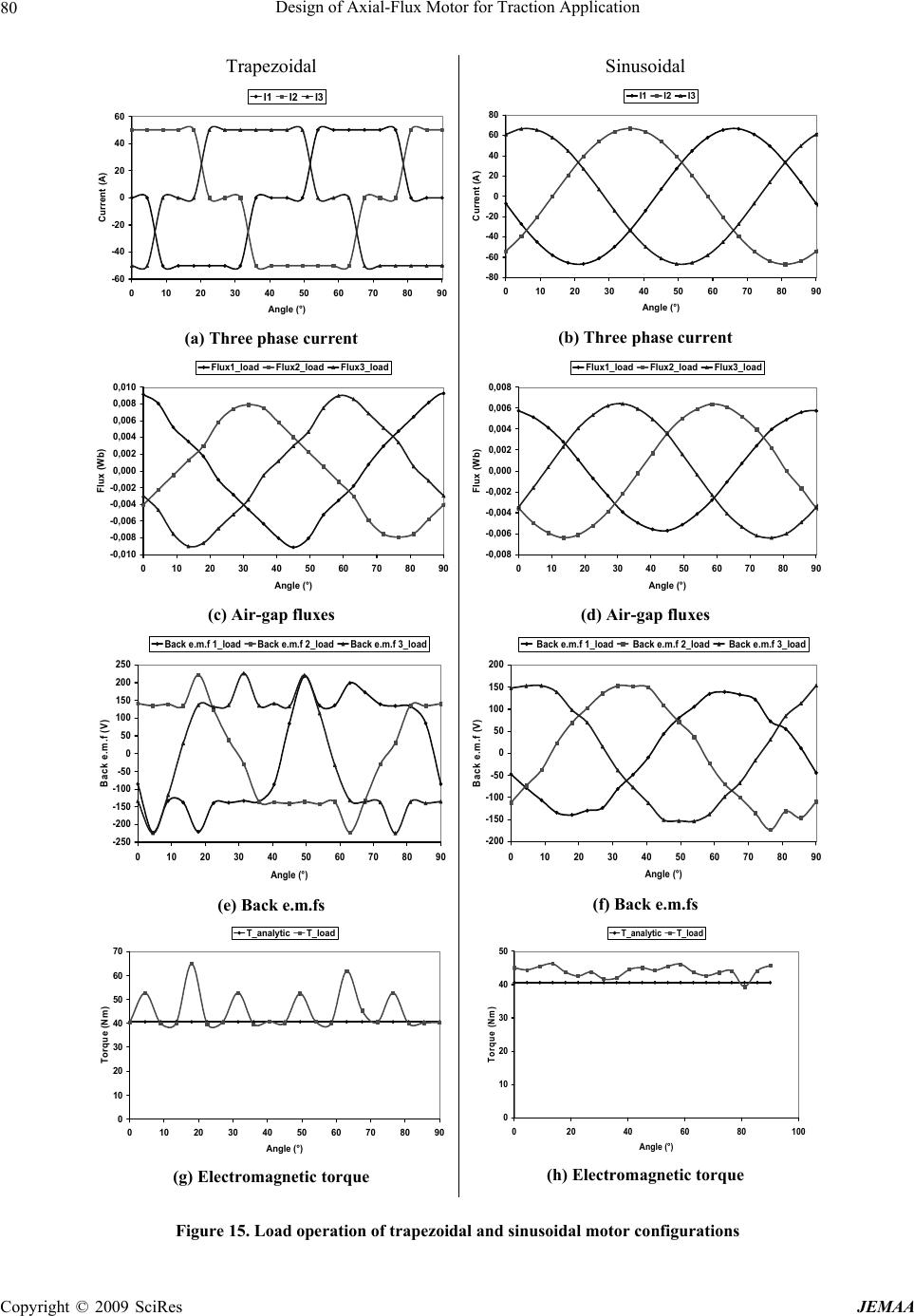 Design of Axial-Flux Motor for Traction Application 80 Trapezoidal Sinusoidal -60 -40 -20 0 20 40 60 0 10203040506070809 Angle (°) Current (A) 0 I1 I2 I3 (a) Three phase current -80 -60 -40 -20 0 20 40 60 80 0 10203040506070809 Angle (°) Current (A) 0 I1 I2I3 (b) Three phase current -0,010 -0,008 -0,006 -0,004 -0,002 0,000 0,002 0,004 0,006 0,008 0,010 0 10203040506070809 Angle (°) Flux (Wb) 0 Flux1_load Flux2_loadFlux3_load (c) Air-gap fluxes -0,008 -0,006 -0,004 -0,002 0,000 0,002 0,004 0,006 0,008 0 10203040506070809 Angle (°) Flux (Wb) 0 Flux1_load Flux2_loadFlux3_load (d) Air-gap fluxes -250 -200 -150 -100 -50 0 50 100 150 200 250 0 10203040506070809 Angle (°) Back e.m.f (V) 0 Back e.m.f 1_loadBack e.m.f 2_loadBack e.m.f 3_load (e) Back e.m.fs -200 -150 -100 -50 0 50 100 150 200 0 10203040506070809 Angle (°) Back e.m.f (V) 0 Back e.m.f 1_load Back e.m.f 2_load Back e.m.f 3_load (f) Back e.m.fs 0 10 20 30 40 50 60 70 0 10203040506070809 Angle (°) Torque (Nm) 0 T_analytic T_load (g) Electromagnetic torque 0 10 20 30 40 50 0 20406080 Angle (°) Torque (Nm) 100 T_analytic T_load (h) Electromagnetic torque Figure 15. Load operation of trapezoidal and sinusoidal motor configurations Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application 81 3 C3 2 C2 1 C1 triangular signal Sine Wave2 Sine Wave1 Sine Wave Re lay 2 Re lay 1 Relay C1 C2 C3 Figure 16. Block diagram of the vector control strategy of the axial-flux motor Figure 16. Block diagram of the vector control strategy of the axial-flux motor of turning parts (wheels, driving shaft and gearing system) and Tr is the resistive torque. of turning parts (wheels, driving shaft and gearing system) and Tr is the resistive torque. The control strategy block diagram, shown in Figure 16, presents two regulation loops: the first loop is used for speed regulation and the second one for current regu- lation. The control vector strategy operates with only the in squaring component of the current. For that the direct current is cancelled and its reference value is fixed to zero. Consequently, referring to Equation (20), the de- veloped electromagnetic torque is expressed as: The control strategy block diagram, shown in Figure 16, presents two regulation loops: the first loop is used for speed regulation and the second one for current regu- lation. The control vector strategy operates with only the in squaring component of the current. For that the direct current is cancelled and its reference value is fixed to zero. Consequently, referring to Equation (20), the de- veloped electromagnetic torque is expressed as: 32 eme q TKI (22) The Inverter switches are driven using PWM control signals and the three voltages provided to supply the mo- tor armature are: 112 221 332 32 32 32 ph dc ph dc ph dc UU CCC UU CCC UU CCC 3 3 1 (23) with Uph1, Uph2, Uph3 are the three phase voltage provided by the inverter, and C1, C2, C3 are the command constants for the inverter high transistors T1, T3 and T5, respectively. The constants C1, C2 and C3 are generated using a PWM generation block, Figure 17, based on the com- parison between a triangular signal which frequency is equal to the desired commutation frequency of the in- verter switches and a sinusoidal one which pulsation gives the desired motor speed. A transistor switched on corresponds to C = 1, and a transistor switched off corre- sponds to C = 0. At vehicle maximum speed (80km) and for the geo- metrical parameters analytically calculated and validated by the finite elements study, the direct voltage applied to the inverter Udc, the motor resistance R, the direct induc- tance of the motor Ld, the in squaring inductance of the motor Lq and the electric constant of the motor Ke are analytically determined, Table 3 (Appendix). For the ob- tained values and for a switching frequency fc = 3.3kHz, the inverter provides three chopped and equilibrated voltages to supply motor armature, Figure 18. 5.1 Simulation Results 5.1.1 Speed Sequence The desired speed sequence, Figure 19, requires three speed levels. Considering the parameters given by Table 3, Figure 17. Generation of the inverter command constants PI 0 PI PI dq 2 abc PWM generation Inverter Iq ref C1 VqVa + PMSM abc 2 dq - + - + - - - m IdVd C2 Vb C3 Vc Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application 82 00.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01 -200 -150 -100 -50 0 50 100 150 200 Time (s) Chopped voltage (V) Figure 18. Motor phase chopped voltage provided at the output of the inverter the motor speed carried out using the traction elaborated traction chain model is illustrated in Figure 19. Analyzing this figure, one can notice that the vehicle speed reaches the wanted value in a relatively weak time. 5.1.2 Circulation Mission To validate the use of a motor for traction application, the INRETS tests the behaviour of such motor using the speed instruction illustrated in Figure 20(a). Such speed instruction is called circulation mission. It consists of a normalised trial for vehicle motor tested for long dis- tances and variable speed under hard constraints. In the last section, the designed motor was able to fol- low a desired speed instruction. For the present study, let us consider the INRETS circulation mission and investi- gate the motor behaviour. Figure 20(b) shows that the electric vehicle speed fol- lows to the required circulation mission with a little delay as found in Subsection 5.1.1. 6. Conclusions The present paper was devoted to the design of high power – low dimensions axial-flux permanent-magnet motor for electric vehicles. In a first step, the electrical and the geometrical parameters of the motor integrated in the whole traction chain was analytically calculated con- sidering the vehicle specifications. Then in a second step, we have been interested in a finite elements study in or- der to validate and complete the analytical obtained re- sults. It has been found, that the built analytical model provides accurate values of electrical and geometrical motor parameters. Furthermore, a comparison between the electromagnetic torque obtained by the trapezoidal configuration and one developed by the sinusoidal con- figuration was made using the finite elements study. The high ripple noticed in the wave form of trapezoidal mo- tor’s torque leads to discard this configuration and em- phasize the choice of sinusoidal configuration for traction applications. Finally, the designed sinusoidal motor be- haviour was investigated considering firstly a desired 0 2 46 81012 14 16 18 20 0 10 20 30 40 50 60 70 80 Time (s) Vehicle speed (Km/h) Desired speed sequence Electric vehicle response Figure 19. Desired speed sequence and motor speed carried out using the developed traction chain model Copyright © 2009 SciRes JEMAA 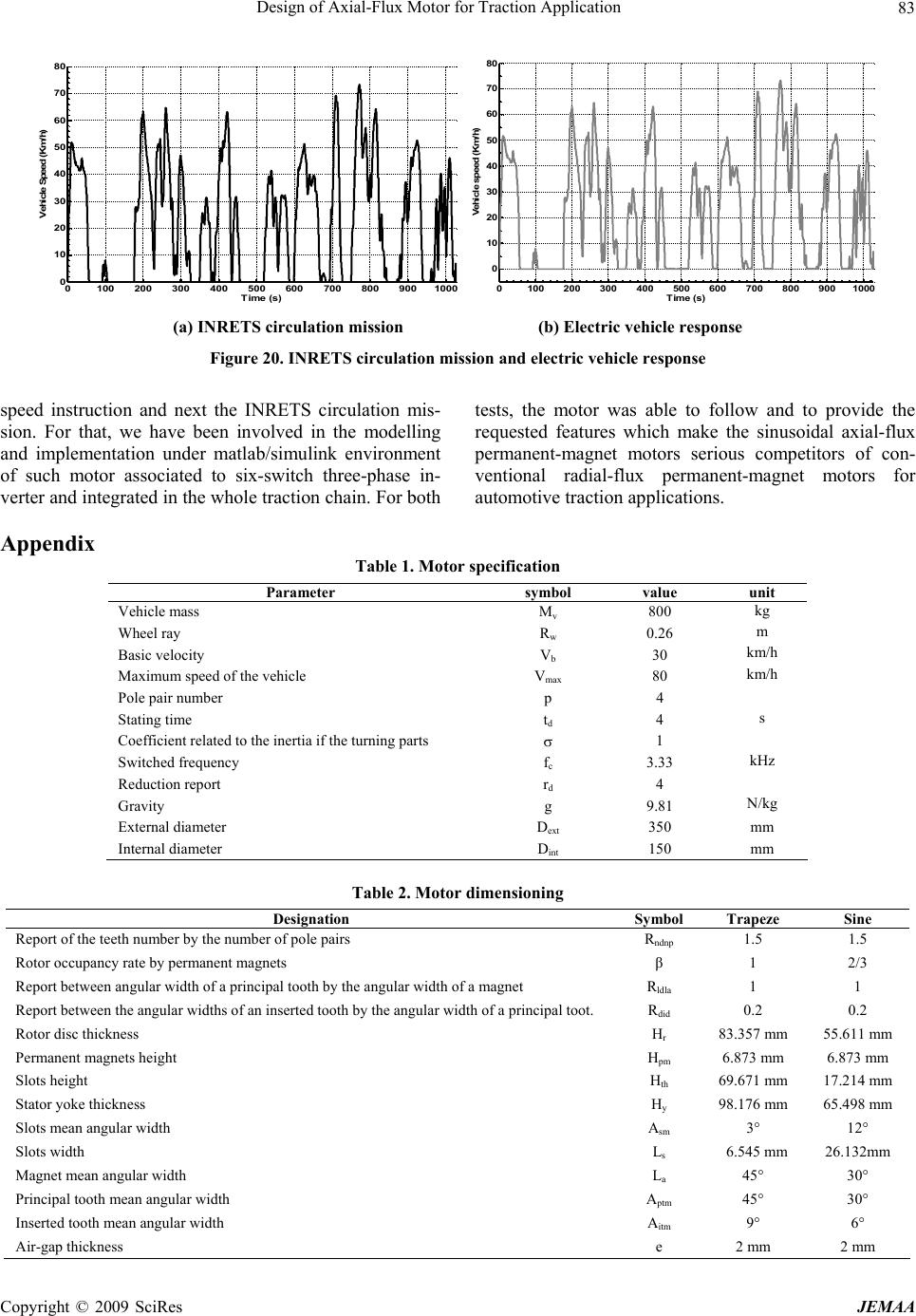 Design of Axial-Flux Motor for Traction Application 83 0100 200 300 400 500 600700 800 900 1000 0 10 20 30 40 50 60 70 80 Time (s) Vehicle Speed (Km/h) 0100 200 300 400 500 600 700 800 900 1000 0 10 20 30 40 50 60 70 80 Time (s) Vehicle speed (Km/h) (a) INRETS circulation mission (b) Electric vehicle response Figure 20. INRETS circulation mission and electric vehicle response speed instruction and next the INRETS circulation mis- sion. For that, we have been involved in the modelling and implementation under matlab/simulink environment of such motor associated to six-switch three-phase in- verter and integrated in the whole traction chain. For both tests, the motor was able to follow and to provide the requested features which make the sinusoidal axial-flux permanent-magnet motors serious competitors of con- ventional radial-flux permanent-magnet motors for automotive traction applications. Appendix Table 1. Motor specification Parameter symbol value unit Vehicle mass Mv 800 kg Wheel ray Rw 0.26 m Basic velocity Vb 30 km/h Maximum speed of the vehicle Vmax 80 km/h Pole pair number p 4 Stating time td 4 s Coefficient related to the inertia if the turning parts 1 Switched frequency fc 3.33 kHz Reduction report rd 4 Gravity g 9.81 N/kg External diameter Dext 350 mm Internal diameter Dint 150 mm Table 2. Motor dimensioning Designation Symbol Trapeze Sine Report of the teeth number by the number of pole pairs Rndnp 1.5 1.5 Rotor occupancy rate by permanent magnets β 1 2/3 Report between angular width of a principal tooth by the angular width of a magnet Rldla 1 1 Report between the angular widths of an inserted tooth by the angular width of a principal toot. Rdid 0.2 0.2 Rotor disc thickness Hr 83.357 mm 55.611 mm Permanent magnets height Hpm 6.873 mm 6.873 mm Slots height Hth 69.671 mm 17.214 mm Stator yoke thickness Hy 98.176 mm 65.498 mm Slots mean angular width Asm 3° 12° Slots width Ls 6.545 mm 26.132mm Magnet mean angular width La 45° 30° Principal tooth mean angular width Aptm 45° 30° Inserted tooth mean angular width Aitm 9° 6° Air-gap thickness e 2 mm 2 mm Copyright © 2009 SciRes JEMAA  Design of Axial-Flux Motor for Traction Application 84 Table 3. Electric parameters used for the simulation of the traction chain model Parameter symbol value unit Direct voltage Udc 291 V Drag coefficient Cx 0.55 Frontal surface Sf 1.8 m² Coefficient to bearing pneumatic resistance fr 0.01 Electric constant Ke 0.3 Phase resistance Rph 0.007 Ω Direct inductance Ld 0.157 mH In squaring inductance Lq 0.157 mH REFERENCES [1] Y. Amara, “Contribution à la conception et à la commande des machines synchrones à double excitation, Application au véhicule hybride,” Thèse de doctorat, université, PARIS VI, 2001. [2] A. Parviainen, “Design of axial-flux permanent-magnet low-speed machines and performance comparison be- tween radial-flux and axial-flux machines,” thesis of doc- torate, Lappeeranta University of Technology, Lappeer- anta, Finland, 2005. [3] A. Parviainen, M. Niemelä, J. Pyrhönen, J. Mantere, “Performance comparison between low-speed axial-flux and radial flux permanent-magnet machines including mechanical constraints,” Electric Machines and Drives, IEEE International Conference, pp. 1695–1702, 2005. [4] S. Tounsi, “Modélisation et optimisation de la motori- sation et de l’autonomie d’un véhicule électrique,” Thèse de doctorat en Génie Electrique, Ecole Nationale d’Ingénieurs de Sfax-Tunisie, 2006. [5] B. Multon and J. Bonal, “Les entraînements électro- magnétiques directs: Diversité, contraintes et solutions, La conversion électromécanique directe,” - ENS Cachan – SEE, 1999. [6] P. Kurronen, “Torque vibration model of axial-flux sur- face-mounted permanent magnet synchronous machine,” Dissertation, Lappeenranta University of Technology, Finland, 2003. [7] B. Tounsi, “Etude comparative de groupes électrogènes embarqués à large gamme de vitesse variable associant machines à aimants permanents et conversion statique,” Thèse de Doctorat, INP Toulouse, 2006. [8] S. Tounsi, R. Neji, and F. Sellami, “Contribution à la conception d’un Actionneur à Aimants Permanents pour Véhicules Electriques en vue d’Optimiser l’Autonomie,” Revue Internationale de Génie Electrique, RIGE, Vol. 9/6, pp. 693-718, Edition Lavoisier, 2006. [9] C. Cavallaro, A. O. Di Tommaso, R. Miceli, A. Raciti, G. R. Galluzzo, and M. Trapanese, “Efficiency enhancement of permanent-magnet synchronous motor drives by online loss minimization approaches,” IEEE Transactions on Industrial Electronics, Vol. 52, No. 4, pp. 1153-1160, 2005. [10] R. Neji, S. Tounsi, and F. Sellami, “Contribution to the definition of a permanent magnet motor with reduced production cost for the electrical vehicle propulsion,” European Transactions on Electrical Power, ETEP, Vol. 16, No. 4, pp. 437-460, 2006. [11] R. Neji, S. Tounsi, and F. Sellami, “Optimization and design for a radial flux permanent magnet motor for elec- tric vehicle,” Journal of Electrical Systems, JES, Vol. 1, No. 4, 2005. [12] N. Chaker, “Conception et commande d’un moteur à aimant permanent à flux axial pour véhicule électrique,” Mémoire de Mastère en génie électrique, Ecole Nationale d’Ingénieurs de Sfax, Tunisie, 2006. [13] MAXWELL® 2D (2002) Student Version; A 2D Magne- tostatic Problem. [14] F. Khatounian, S. Moreau, J. P. Louis, E. Monmasson, F. Louveau, and J. M. Alexandre, “Modeling and simulation of a hybrid dynamic system used in haptic interfaces,” Electrimacs, Hammamet, Tunisie, 2005. [15] G. Kayhan, A. A. Ahmed, and P. Halit, “Improving the performance of hysteresis direct torque control of IPMSM using active filter topology,” S¯adhan¯a, Vol. 31, Part 3, pp. 245–258, 2006. Copyright © 2009 SciRes JEMAA |

