Journal of Modern Physics, 2011, 2, 284-288
doi:10.4236/jmp.2011.24037 Published Online April 2011 (http://www.SciRP.org/journal/jmp)
Unbiased Diffusion to Escape through Small Windows:
Assessing the Applicability of the Reduction to Effective
One-Dimension Description in a Spherical Cavity
Marco-Vinicio Vázquez1, Leonardo Dagdug1,2
1Departamento de Física, Universidad Autónoma Metropolitana-Iztapalapa, México
2Mathematical and Statistical Computing Laboratory, Division of Computational Bioscience,
Center for Information Technology, National Institutes of Health, Bethesda, USA.
Received January 21, 2011; revised March 1, 2011; accepted March 6, 2011
Abstract
This study is devoted to unbiased motion of a point Brownian particle that escapes from a spherical cavity
through a round hole. Effective one-dimensional description in terms of the generalized Fick-Jacobs equation
is used to derive a formula which gives the mean first-passage time as a function of the geometric parameters
for any value of a, where a is the hole’s radius. This is our main result and is given in Equation (19). This
result is a generalization of the Hill’s formula, which is restricted to small values of a.
Keywords: Diffusion, Brownian Particle, Fick-Jacobs Equation, Narrow-Escape Time
1. Introduction
The first-passage time, namely, the probability that a
diffusing particle or a random-walk first reaches a speci-
fied site (or set of sites) at a specified time, is known to
underlie a wide range of stochastic processes of practical
interest [1]. Indeed, chemical and bio-chemical reactions
[2,3], animals searching for food [4], the spread of sexu-
ally transmitted diseases in a human social network or of
viruses through the world wide web [5], and trafficking
receptors on biological membranes [6], are often con-
trolled by first encounter events [7]. Studying the narrow
scape time (NET), the mean time which a Brownian par-
ticle spends before to be trapped in an opening window
to exit a cavity for the first time, has particular impor-
tance. The applications goes from cellular biology to
biochemical reactions in cellular micro-domains as den-
dritic spines, synapses and micro-vesicles, among others
[6,8]. For those cases where the particles first must exit
the domain in order to live up to their biological function,
the narrow scape time is the limiting quantity and the
first step in the modeling of such processes [7].
Experimentally, high-resolution crystallography of
bacterial porins and other large channels demonstrates
that their pores can be envisaged as tunnels whose cross
sections change signiÞcantly along the channel axis. For
some of them, variation in cross-section area exceeds an
order of magnitude [9,10]. This leads to the so-called
entropic walls and barriers in theoretical description of
transport through such structures. In addition to biologi-
cal systems, diffusion in confined geometries are also
important for understanding transport in synthetic
nanopores [11-13], transport in zeolites [14], controlled
drugs release [15], and nanostructures of complex ge-
ometries [16], among others.
Theoretically, the transport in systems of varying ge-
ometry has been deeply studied in recent years since
these systems are ubiquitous in nature and technology
[18-23]. Diffusion in two and three dimension, has been
formulated as a one dimension problem in terms of the
effective one-dimensional concentration of diffusing
molecules. If one assumes that the distribution of the
solute in any cross section of the tube is uniform as it is
at equilibrium, directing the x-axis along the center line
of a tube, one can write an approximate one-dimensional
effective diffusion equation as
  

,,
=,
,
cxt cxt
DxAx
tx xAxt









 





(1)
where


Dx

=
is a position-dependent diffusion coeffi-
cient,

2
π
A
xrx



 is the cross section area of the
tube of radius


rx , and is the effective

,cxt

M.-V. VÁZQUEZ ET AL.
285
one-dimensional concentration of the diffusing particles
at a given x. This equation was derived by Jacobs in
1967 [17]. is related to the three-dimensional
concentration by

,cxt
Cx

cxt

Ux

,,,yzt

,=
Ax
C



,,,dd.xyzt yz (2)
As Zwanzig pointed out [18], (1) can be considered as
the Smoluchowski equation for diffusion in the entropy
potential defined as,


=ln
B
C
,
A
x
Ux kT (3)
A
x

where
B
k is the Boltzmann constant and T the absolute
temperature, and at

Ux =C
x
x is taken to be zero,
.

Ux =0
C
Equation (1) with position-independent diffusion coef-
ficient, , is known as the Fick-Jacobs (FJ)
equation [17]. To improve FJ’s reduction, Zwanzig (Zw)
derived one-dimension diffusion equation assuming that
the tube radius is a slowly varying function,

=Dx D

rx

1rx


[18]. He showed that satisfies the
probability conservation equation

,cxt
 
,,
=
cxt jxt
tx



(4)
where the flux, , is given by,

jx
 

,t
 

,=jxt cx AxDx
x
Ax





(5)
The expression for derived by Zwanzing is as
follows [18],

Dx
 
2
=
12
.
D
Dx
rx


Zw

Dx

(6)
Later, in the same spirit of amending the FJ's reduc-
tion, Reguera and Rub (RR) proposed the following ex-
pression for [19],
 
2
2
1
=1
21
RR
D.D rx
rx





 
Dx (7)
In order to determine what the explicit form of


Dx
should be used in a given geometry (and its associated
boundary conditions), we can exploit that the Mean
First-Passage Time (MFPT),

, is a quantity often ob-
tained by means of computer simulations. Then the
MFPT, defined as the time a random walker spends to
reach a specified place for the first time, averaged over
all the trajectories or realizations of a random walk, is
found to satisfy a backwards equation [20],
 

00
0
00
dd
ee =
dd
1,
Ux Dx
xx







Ux (8)
where


=1 B kT  (
B
k and retain their usual
meaning), and the potential , defined in (3), is
due to the change in the cross-sectional area along the
axial length of the tubes. Then (8) is solved for the ap-
propriate boundary conditions to obtain an algebraic ex-
pression that relates
T

0
Ux


with and geometrical
parameters of the system.

Dx

In the present paper we derive a formula which gives
the mean first-passage time as function of the geometri-
cal parameters using the effective one-dimension de-
scription for a sphere with absorbing spots. This formula
will be proved to reproduce the data obtained by Monte-
carlo simulations for any value of the hole radius, a,
when (7) is used.
2. Results and Discussion
Back to the narrow escape problem, in 2002 I. V. Grigo-
riev et al. studied the time dependence of the survival
probability of a Brownian particle that escapes from a
cavity through a round hole [24]. Two main results were
reported: 1) an algebraic proof that for small holes the
decay is exponential, based on the spectral representation
of the survival probability, and 2) the expression for the
rate constant in terms of the problem parameters (the
diffusion constant D of the particles, the hole radius a,
and the cavity volume V) is given by,
4
==
Da
kV
1

(9)
In their work they also ran Brownian dynamics simu-
lations to calculate the survival probability in spherical
and cubic cavities for different values of the absorb-
ing-window’s radius. They also founded that when the
spot radius is small enough (0.1aR for a spherical
cavity, R is the radius of the sphere), the decay is expo-
nential and the rate constants found in simulations are in
a good agreement with those predicted by (9). For the
means first-passage time predicted by Hill’s formula for
a sphere with two absorbent holes, the following volume
has to be introduced in (9), see Figure 1,




32
22 22
sph
4π2π
=2
33
R
VRRaRRa (10)
obtaining,




Hill32 222 2
sph=2)(2
12 RRRaRRa Da

 
(11)
Equation (11) is just applicable when >0.1aR . In
the following lines we will obtain an expression for any
value of a.
To solve (8) for a sphere with two absorbing windows
(see Figure 1), we have to take the potential


0
Ux

286 M.-V. VÁZQUEZ ET AL.
Figure 1. Sphere of radius R with two absorbing windows
of radii a (shaded inthe picture, while the remaining surface
is reflective). Its height is given by

=22 rxR x. The
enclosed volume is changed as one varies a because of
22
2=LRa.
defined as,





2 122
22
π
e= ==
0π0
Ux Ax rx Rx
AR
r

 (12)
where

0
A
x is the cross-sectional area, and

2
0
R x2
0
=rx is the height of the sphere. In these
calculations 0
x
denotes the initial position of each tra-
jectory of a Brownian particle. Then, using


RR 0
Dx
as
given by
 
22
0
0RR0 2
0
== =
1
Rx
D
DxD xD
R
rx



(13)
we replace and in （8） to yield,

0
Dx

0
Ux
e
 
22
22 22
0
00
2
00
dd
=
dd
Rx
Rx Rx
D
xRx
R








2
R
(14)
which happens to be a separable ordinary differential
equation. Integrating twice we obtain,

3
022
0
2
22
022
0
3
0
12
222
0
1
=
3
R
xDRx
R
Rx
DRx
x RCC
DRR x
 









R




(15)
The equation above have two integration constants,
namely, and , which can be fixed by using ap-
propriate boundary conditions. Since we have absorbing
windows in the positions
1
C2 C
0=2
x
L, and 0=2
x
L, we
can state this type of boundary conditions as follows,


2= 2=0LL   (16)
with these conditions in (15), we found, and
1=0C
3
2
2
=33
RaR
CDa D . Thus we have an expression of

as a
function of the initial position 0
x
,

33
22
00
22
0
21 2
=333
RRR
xRx
DDDa
Rx
 
3
aR
D

(17)
If we also want the solution when the initial positions
of the particles are distributed uniformly in the cavity,
we have to consider the average over all the accessible
initial positions in the interval 0 22LxL given
by

2
00
2
1
=d
L
L.
x
x
L


 (18)
Substituting


0
x
 from (17), in the above definition
allows one to obtain an expression for

,

2
32
RR
22
3
=4 arcsin
6
sph
Ra aRa
aDa RR
Ra


2
.

 




 



(19)
Equation (19) along with (17) are the main results of
this work. Equation (19) depends only on the geometrical
parameters R and a, and the bulk diffusion constant D.
The comparison of this expression with the data obtained
by Montecarlo simulations shows and excellent agree-
ment for any value of a, see Figure 2. Additionally, in
the limit , the ratio
0a
R
RHill

 goes to the con-
stant value 4

.
The results obtained here can be extended to any num-
ber of spots—provided these spots are far enough to not
interact with each other, dividing Equation (19) by two,
times the number of holes. The procedure outlined in this
work can be used to obtain the mean first-passage time
for any geometry when is applicable.

RR
Dx
3. Computational Details
The problem is to find the survival time of a Brownian
particle escaping from a domain of size V, whose bound-
ary is reflective, except for a small absorbing window of
circular shape and radius a. In simulations we obtain the
mean time to absorption

, a mean first-passage time.
When running simulations we take and the
0=1D

M.-V. VÁZQUEZ ET AL.
287
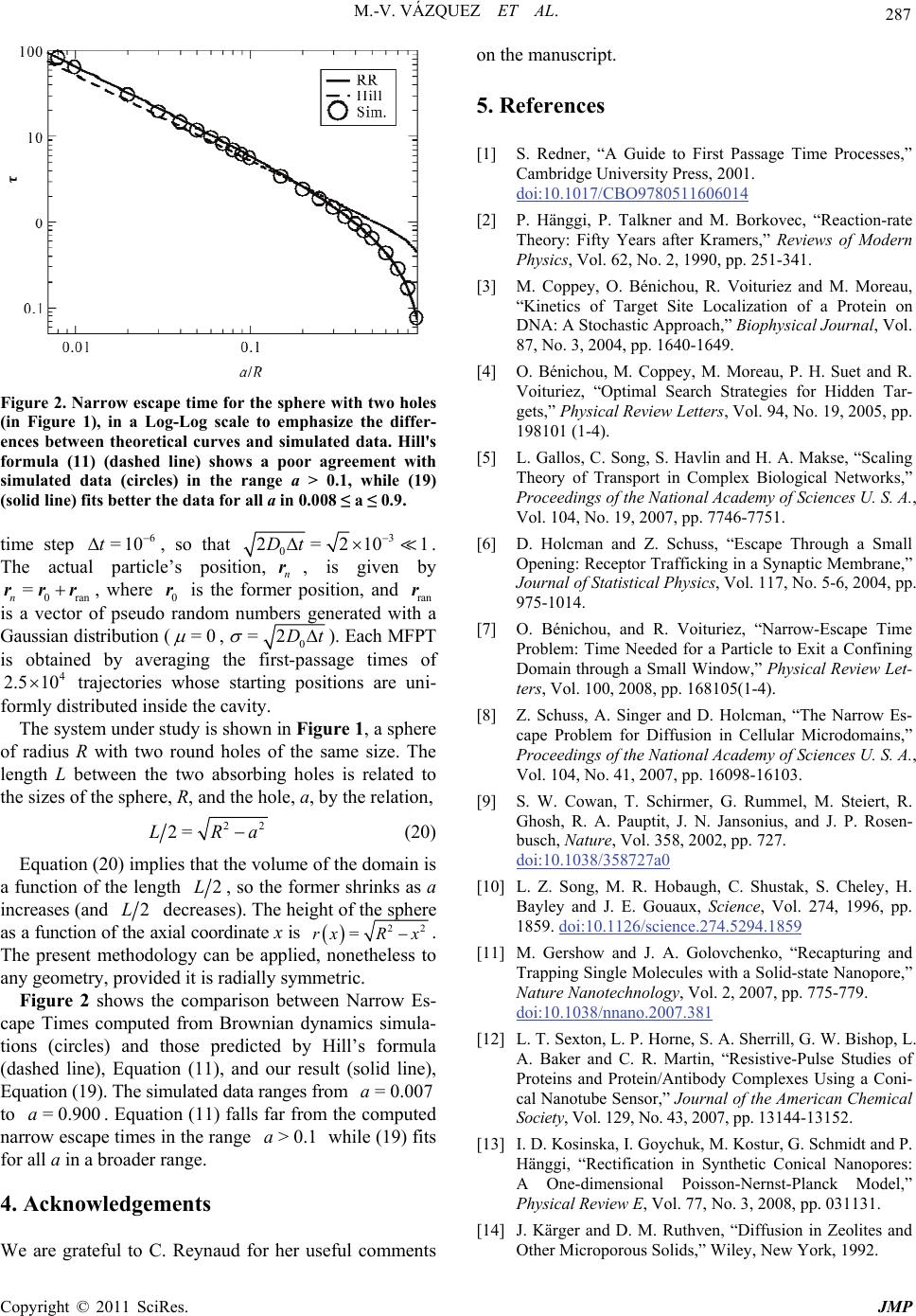
Figure 2. Narrow escape time for the sphere with two holes
(in Figure 1), in a Log-Log scale to emphasize the differ-
ences between theoretical curves and simulated data. Hill's
formula (11) (dashed line) shows a poor agreement with
simulated data (circles) in the range a > 0.1, while (19)
(solid line) fits better the data for all a in 0.008 ≤ a ≤ 0.9.
time step , so that
6
=10t 3
0
2=210Dt  1.
The actual particle’s position, n, is given by
0ran
, where 0 is the former position, and ran
is a vector of pseudo random numbers generated with a
Gaussian distribution (
r
=
nrrr r r
=0

,0
=2Dt  ). Each MFPT
is obtained by averaging the first-passage times of
trajectories whose starting positions are uni-
formly distributed inside the cavity.
4
2.5 10
The system under study is shown in Figure 1, a sphere
of radius R with two round holes of the same size. The
length L between the two absorbing holes is related to
the sizes of the sphere, R, and the hole, a, by the relation,
22
2=LRa

(20)
Equation (20) implies that the volume of the domain is
a function of the length 2L, so the former shrinks as a
increases (and 2L decreases). The height of the sphere
as a function of the axial coordinate x is

22
=rxR x

.
The present methodology can be applied, nonetheless to
any geometry, provided it is radially symmetric.
Figure 2 shows the comparison between Narrow Es-
cape Times computed from Brownian dynamics simula-
tions (circles) and those predicted by Hill’s formula
(dashed line), Equation (11), and our result (solid line),
Equation (19). The simulated data ranges from
to . Equation (11) falls far from the computed
narrow escape times in the range while (19) fits
for all a in a broader range.
=0.007a
=0.900a
>0.1a
4. Acknowledgements
We are grateful to C. Reynaud for her useful comments
on the manuscript.
5. References
[1] S. Redner, “A Guide to First Passage Time Processes,”
Cambridge University Press, 2001.
doi:10.1017/CBO9780511606014
[2] P. Hänggi, P. Talkner and M. Borkovec, “Reaction-rate
Theory: Fifty Years after Kramers,” Reviews of Modern
Physics, Vol. 62, No. 2, 1990, pp. 251-341.
[3] M. Coppey, O. Bénichou, R. Voituriez and M. Moreau,
“Kinetics of Target Site Localization of a Protein on
DNA: A Stochastic Approach,” Biophysical Journal, Vol.
87, No. 3, 2004, pp. 1640-1649.
[4] O. Bénichou, M. Coppey, M. Moreau, P. H. Suet and R.
Voituriez, “Optimal Search Strategies for Hidden Tar-
gets,” Physical Review Letters, Vol. 94, No. 19, 2005, pp.
198101 (1-4).
[5] L. Gallos, C. Song, S. Havlin and H. A. Makse, “Scaling
Theory of Transport in Complex Biological Networks,”
Proceedings of the National Academy of Sciences U. S. A.,
Vol. 104, No. 19, 2007, pp. 7746-7751.
[6] D. Holcman and Z. Schuss, “Escape Through a Small
Opening: Receptor Trafficking in a Synaptic Membrane,”
Journal of Statistical Physics, Vol. 117, No. 5-6, 2004, pp.
975-1014.
[7] O. Bénichou, and R. Voituriez, “Narrow-Escape Time
Problem: Time Needed for a Particle to Exit a Confining
Domain through a Small Window,” Physical Review Let-
ters, Vol. 100, 2008, pp. 168105(1-4).
[8] Z. Schuss, A. Singer and D. Holcman, “The Narrow Es-
cape Problem for Diffusion in Cellular Microdomains,”
Proceedings of the National Academy of Sciences U. S. A.,
Vol. 104, No. 41, 2007, pp. 16098-16103.
[9] S. W. Cowan, T. Schirmer, G. Rummel, M. Steiert, R.
Ghosh, R. A. Pauptit, J. N. Jansonius, and J. P. Rosen-
busch, Nature, Vol. 358, 2002, pp. 727.
doi:10.1038/358727a0
[10] L. Z. Song, M. R. Hobaugh, C. Shustak, S. Cheley, H.
Bayley and J. E. Gouaux, Science, Vol. 274, 1996, pp.
1859. doi:10.1126/science.274.5294.1859
[11] M. Gershow and J. A. Golovchenko, “Recapturing and
Trapping Single Molecules with a Solid-state Nanopore,”
Nature Nanotechnology, Vol. 2, 2007, pp. 775-779.
doi:10.1038/nnano.2007.381
[12] L. T. Sexton, L. P. Horne, S. A. Sherrill, G. W. Bishop, L.
A. Baker and C. R. Martin, “Resistive-Pulse Studies of
Proteins and Protein/Antibody Complexes Using a Coni-
cal Nanotube Sensor,” Journal of the American Chemical
Society, Vol. 129, No. 43, 2007, pp. 13144-13152.
[13] I. D. Kosinska, I. Goychuk, M. Kostur, G. Schmidt and P.
Hänggi, “Rectification in Synthetic Conical Nanopores:
A One-dimensional Poisson-Nernst-Planck Model,”
Physical Review E, Vol. 77, No. 3, 2008, pp. 031131.
[14] J. Kärger and D. M. Ruthven, “Diffusion in Zeolites and
Other Microporous Solids,” Wiley, New York, 1992.

M.-V. VÁZQUEZ ET AL.
288
[15] R. A. Siegel, “Theoretical Analysis of Inward Hemi-
spheric Release above and below Drug Solubility,” Jour-
nal of Controlled Release, Vol. 69, No. 1, 1992, pp. 109-
126.
[16] N. F. Sheppard, D. J. Mears, and S. W. Straka, “Micro-
machined Silicon Structures for Modelling Polymer Ma-
trix Controlled Release Systems ,” Journal of Controlled
Release, Vol. 42, No. 1, 1996, pp. 15-24.
[17] M. H. Jacobs, “Diffusion Processes,” Springer, New
York, 1967.
[18] R. Zwanzig, “Diffusion past an Entropy Barrier,” Journal
of Physical Chemistry, Vol. 96, No. 10, 1992, pp. 3926-
3930.
[19] D. Reguera and J. M. Rubí, “Kinetic Equations for Diffu-
sion in the Presence of Entropic Barriers,” Physical Re-
view E, Vol. 64, No. 6, 2001, pp. 061106(1-8).
[20] A. M. Berezhkovskii, M. A. Pustovoit and S. M. Bezru-
kov, “Diffusion in a Tube of Varying Cross Section: Nu-
merical Study of Reduction to Effective One-Dimensional
Description,” Journal of Chemical Physics, Vol. 126, No.
13, 2007, pp. 134706(1-5).
[21] P. Kalinay, “Mapping of Forced Diffusion in Quasi-One-
Dimensional Systems,” Physical Review E, Vol. 80, No.
3, 2001, pp. 031106(1-10).
[22] R. M. Bradley, “Diffusion in a Two-Dimensional Chan-
nel with Curved Midline and Varying Width: Reduction
to an Effective One-Dimensional Description,” Physical
Review E, Vol. 80, No. 6, 2009, pp. 061142(1-7).
[23] P. S. Burada and G. Schmid, “Steering the Potential Bar-
riers: Entropic to Energetic,” Physical Review E, Vol. 82,
No. 5, 2010, pp. 051128(1-6).
[24] I. V. Grigoriev, Yu. A. Makhnovskii, A. M. Berezhkovskii
and V. Yu. Zitserman, “Kinetics of Escape through a
Small Hole,” Journal of Chemical Physics, Vol. 116, No.
22, 2002, pp. 9574-9577.