Journal of Modern Physics, 2011, 2, 256-273
doi:10.4236/jmp.2011.24035 Published Online April 2011 (http://www.SciRP.org/journal/jmp)
Quantum Supercurrent Transistors in Silicon Quantum
Wells Confined by Superconductor Barriers
Nikolay T. Bagraev1, Edward Yu. Danilovsky1, Leonid E. Klyachkin1, Andrei A. Kudryavtsev1,
Roman V. Kuzmin1, Anna M. Malyarenko1, Wolfgang Gehlhoff2, Vladimir V. Romanov3
1Ioffe Physical Technical Institute, St.Petersburg, Russia
2Institut für Festkörp erphysik, TU Berlin, Berlin, Germany
3State Polytechnical University, St.Petersburg, Russia
Received January 18, 2011; revised March 2, 2011; accepted March 3, 2011
Abstract
We present the findings of spin-dependent single-hole and pair-hole transport in plane and across the p-type
high mobility silicon quantum wells (Si-QW), 2 nm, confined by the superconductor δ-barriers on the n-type
Si (100) surface. The oscillations of the conductance in normal state and the zero-resistance supercurrent in
superconductor state as a function of the top gate voltage are found to be correlated by on- and off-resonance
tuning the two-dimensional levels of holes in Si-QW with the Fermi energy in the superconductor δ-barriers.
The SIMS and STM studies have shown that the δ-barriers heavily doped with boron, 5 × 1021 cm–3, repre-
sent really alternating arrays of silicon empty and doped dots, with dimensions restricted to 2 nm. This con-
centration of boron seems to indicate that each doped dot located between empty dots contains two impurity
atoms of boron. The EPR studies show that these boron pairs are the trigonal dipole centres, B+ - B–, that
contain the pairs of holes, which result from the negative -U reconstruction of the shallow boron acceptors,
2B0 => B+ - B–. The electrical resistivity, magnetic susceptibility and specific heat measurements demon-
strate that the high density of holes in the Si-QW (> 1011 cm–2) gives rise to the high temperature supercon-
ductor properties for the δ-barriers. The value of the superconductor energy gap obtained is in a good agree-
ment with the data derived from the oscillations of the conductance in normal state and of the zero-resistance
supercurrent in superconductor state as a function of the bias voltage. These oscillations appear to be corre-
lated by on- and off-resonance tuning the two-dimensional subbands of holes with the Fermi energy in the
superconductor δ-barriers. Finally, the proximity effect in the S-Si-QW-S structure is revealed by the find-
ings of the quantization of the supercurrent and the multiple Andreev reflection (MAR) observed both across
and along the Si-QW plane thereby identifying the spin transistor effect.
Keywords: Silicon Quantum Well, Superconductor δ-barrier, ESR, Dipole Boron Center, Multiple Andreev
Reflection, Supercurrent Conductance, EDESR, Silicon Microcavity
1. Introduction
Semiconductor silicon is well known to be the principal
material for micro- and nanoelectronics. Specifically, the
developments of the silicon planar technology are a basis
of the metal-oxygen-silicon (MOS) structures and sili-
con-germanium (Si-Ge) heterojunctions that are suc-
cessfully used as elements of modern processors [1]. Just
the same goals of future high frequency processors esp e-
cially to resolve the problem of quantum computing are
proposed to need the application of the superconductor
nanostructures that represent the Josephson junction se-
ries [2]. Therefore the manufacture of superconductor
device structures within frameworks of the silico n planar
technology seems to give rise to new generations in
nanoelectronics. Furthermore, one of the best candidate
on the role of the superconductor silicon nanostructure
appears to be the high mobility silicon quantum wells
(Si-QW) of the p-type confined by the δ-barriers heavily
doped with boron on the n-type Si (100) surface which
exhibit the properties of high temperature superconduc-
tors [3]. Besides, the heavily boron doping has been

N. T. BAGRAEV ET AL.
257
found to assist also the superconductivity in diamond [4].
Here we present the findings of the electrical resistance,
specific heat and magnetic susceptibility measurements
that are actually evidence of the superconductor proper-
ties for the δ-barriers heavily doped with boron which
appear to result from the transfer of the small hole bipo-
larons through the negative-U dipole centres of boron at
the Si-QW – δ-barrier interfaces. These ‘sandwich’
structures, S-Si-QW-S, are shown to be type II high
temperature superconductors (HTS) with characteristics
dependent on the sheet density of holes in the p-type
Si-QW. The transfer of the small hole bipolarons appears
to be revealed also in the studies of the proximity effect
that is caused by the interplay of the multiple Andreev
reflection (MAR) and the quantization of the supercur-
rent. Both phenomena appear to be a basis of the quan-
tum supercurrent.
2. Sample Preparation and Analysis
The preparation of oxide overlayers on silicon monocrys-
talline surfaces is known to be favourable to the genera-
tion of the excess fluxes of self-interstitials and vacan-
cies that exhibit the predominant crystallographic orien-
tation along a <111> and <100> axis, respectively (Fig-
ure 1(a)) [5-8]. In the initial stage of the oxidation, thin
oxide overlayer produces excess self-interstitials that are
able to create small microdefects, whereas oppositely
directed fluxes of vacancies give rise to their annihilation
(Figures 1(a) and 1(b)). Since the points of outgoing
self-interstitials and incoming vacancies appear to be
defined by the positive and negative charge states of the
reconstructed silicon d anglin g bond [6,9], the dimensions
of small microdefects of the self-interstitials type near
the Si (100) surface have to be restricted to 2 nm. There-
fore, the distribution of the microdefects created at the
initial stage of the oxidation seems to represent the frac-
tal of the Sierpinski Gasket type with the built-in
self-assembled Si-QW (Figure 1(b)) [6-8]. Then, the
fractal distribution has to be reproduced by increasing
the time of the oxidation process, with the Pb centers as
the germs for the next generation of the microdefects
(Figure 1(c)) [9,10]. The formation of thick oxide over-
layer under prolonged oxidation results in however the
predominant generation of vacancies by the oxidized
surface, and thus, in increased decay of these microde-
fects, which is accompanied by the self-assembly of the
lateral silicon quantum wells (Figure 1(d)).
Although Si-QWs embedded in the fractal system of
self-assembled microdefects are of interest to be used as
a basis of optically and electrically active microcavities
in optoelectronics and nanoelectronics, the presence of
dangling bonds at the interfaces prevents such an appli-
cation. Therefore, subsequent short-time diffusion of
boron would be approp riate for the passivation o f silicon
vacancies that create the dangling bonds during previous
oxidation of the Si (100) surface thereby assisting the
transformation of the arrays of microdefects in the neu-
tral -barriers confining the ultra-narrow, 2 nm, Si-QW
(Figures 1(e), (f ) and (g)).
We have prepared the p-type self-assembled Si-QWs
with different density of holes (109 - 1012 cm–2) on the Si
(100) wafers of the n-type within frameworks of the
conception discussed above and identified the properties
of the two-dimensional high mobility gas of holes by the
cyclotron resonance (CR), electron spin resonance (ESR),
scanning tunneling spectroscopy (STM) and infrared
Fourier spectroscopy techniques.
Firstly, the 0.35 mm thick n-type Si (100) wafers with
resistivity 20 Ohmcm were previously oxidized at
1150˚C in dry oxygen containing CCl4 vapors. The
thickness of the oxide overlayer is dependent on the du-
ration of the oxidation process that was varied from 20
min up to 24 hours. Then, the Hall geometry windows
were cut in the oxide overlayer after preparing a mask
and performing the subsequent photolithography. Sec-
ondly, the short-time diffusion of boron was done into
windows from gas phase during five minutes at the dif-
fusion temperature of 900˚C. Additional replenishment
with dry oxygen and the Cl levels into the gas phase
during the diffusion process provided the fine surface
injection of self-interstitials and vacancies to result in
parity of the kick-out and vacancy-related diffusion me-
chanism. The variable parameters of the diffusion ex-
periment were the oxide overlayer thickness and the Cl
levels in the gas phase during the diffusion process [6].
The SIMS measurements were performed to define the
concentration of boron, 5 × 1021 cm–3, inside the boron
doped diffusion profile and its depth that was equal to 8
nm in the presence of thin oxide overlayer [6]. The
Si-QWs confined by the δ-barriers heavily doped with
boron inside the B doped diffusion profile were identi-
fied by the four-point probe method using layer-by-layer
etching and by the cyclotron resonance (CR) angular
dependencies (Figures 2(a) and (b)).
These CR measurements were performed at 3.8 K with
a standard Brucker-Physik AG ESR spectrometer at
X-band (9.1 - 9.5 GHz) [11,12]. The rotation of the mag-
netic field in a plane normal to the diffusion profile plane
has revealed the anisotropy of both the electron and hole
effective masses in silicon bulk and Landau levels
scheme in Si-QWs. This CR quenching and the line
shifts for which a characteristic 180˚ symmetry was ob-
served can be explained with the effect of the electrical
field created b y the confinin g potential insid e p+-diffusion
profile and its different arranement in longitudinal and g

N. T. BAGRAEV ET AL.
258
Figure 1. A scheme of self-assembled silicon quantum wells (Si-QWs) obtained by varying the thickness of the oxide overlayer
prepared on the Si (100) wafer. The white and black balls label the self-interstitials and vacancies forming the excess fluxes
oriented crystallographically along a <111> and <100> axis that are transformed to small microdefects (a, b). The longitudi-
nal Si-QWs between the alloys of microdef ects are produced by performing thin oxide overlayer (b), whereas growing thick
oxide overlayer results in the formation of additional lateral Si-QWs (d). Besides, medium and thick oxide overlayers give
rise to the self-assembled microdefects of the fractal type (c). The atoms of boron replace the positions of vacancies in the
process of subsequent short-time diffusion after making a mask and etching thereby passivating the alloys of microdefects
and forming the neutral  barriers that confine both the longitudinal (e, f) and lateral (g) Si-QWs.
lateral Si-QWs formed naturally between the -barriers
heavily doped with boron (Figures 2(a) and (b)). The
observed different behavior of the heavy and light holes
may be explained by lifting the degeneracy between the
Jz = ± 3/2 and Jz = ± 1/2 valence bands for k = 0 due to
the confining potential.
The energy positions of two-dimensional subbands for
the light and heavy holes in the Si-QW studied were de-
termined by studying the far-infrared electrolumines-
cence spectra obtained with the infrared Fourier spec-
trometer IFS-115 Brucker Physik AG (Figure 3(a)) [3,
13]. The results obtained are in a good agreement with
corresponding calculations following by Ref [14] if the
width of the Si-QW, 2nm, is taken into account (Figure
3(b)).
The STM technique was usd to control the formation e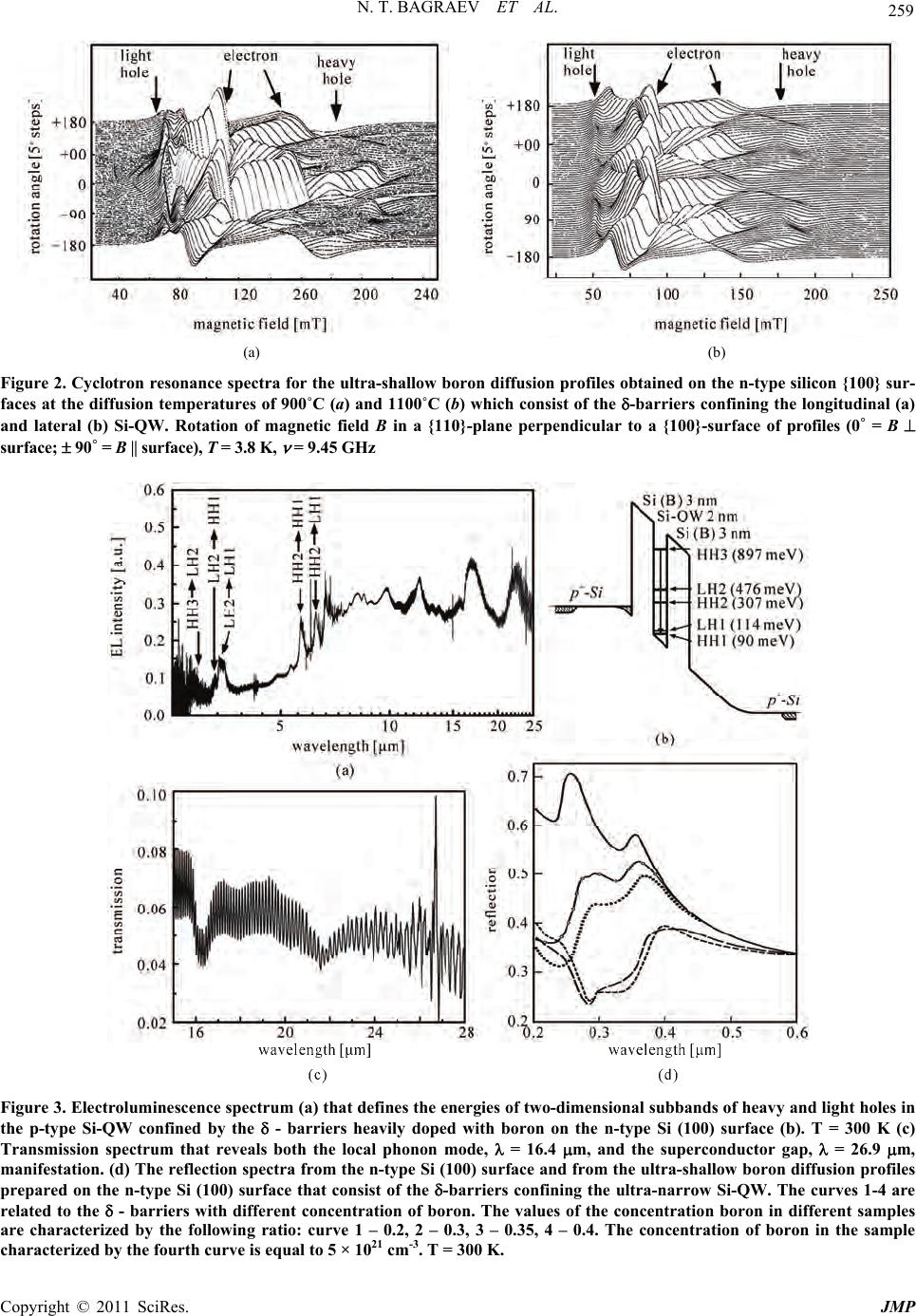

N. T. BAGRAEV ET AL.
259
(a) (b)
Figure 2. Cyclotron resonance spectra for the ultra-shallow boron diffusion profiles obtained on the n-type silicon {100} sur-
faces at the diffusion temperatures of 900˚C (a) and 1100˚C (b) which consist of the -barriers confining the longitudinal (a)
and lateral (b) Si-QW. Rotation of magnetic field B in a {110}-plane perpendicular to a {100}-surface of profiles (0˚ = B 
surface;  90˚ = B  su rface), T = 3.8 K,  = 9.45 GHz
Figure 3. Electroluminescence spectrum (a) that defines the energies of two-dimensional subbands of heavy and light holes in
the p-type Si-QW confined by the  - barriers heavily doped with boron on the n-type Si (100) surface (b). T = 300 K (c)
Transmission spectrum that reveals both the local phonon mode,  = 16.4 m, and the superconductor gap,  = 26.9 m,
manifestation. (d) The reflection spectra from the n-type Si (100) surface and from the ultra-shallow boron diffusion profiles
prepared on the n-type Si (100) surface that consist of the -barriers confining the ultra-narrow Si-QW. The curves 1-4 are
related to the  - barriers with different concentration of boron. The values of the concentration boron in different samples
are characterized by the following ratio: curve 1 – 0.2, 2 – 0.3, 3 – 0.35, 4 – 0.4. The concentration of boron in the sample
haracterized by the fourth curve is equal to 5 × 1021 cm-3. T = 300 K. c

N. T. BAGRAEV ET AL.
260
of the fractal distribution of the self-interstitials micro-
defects in the windows before and after diffusion of bo-
ron (Figure 4(a)). The self-assembled layers of mi-
crodefects inside the -barriers that confine the Si-QW
appear to be revealed by the STM method as the de-
formed potential fluctuations (DPF) after etching the
oxide overlayer an d after subsequen t short-time diffu sion
of boron. The DPF effect induced by the microdefects of
the self-interstitials type that are displayed as light poles
in Figure 4(a) is found to be brought about by the pre-
vious oxidation and to be enhanced by subsequent boron
diffusion [6,15]. The STM images demonstrate that the
ratio between the dimensions of the microdefects pro-
duced during the different stages of the oxidation process
is supported to be equal to 3.3 thereby defining the
self-assembly of microdefects as the self-organization of
the fractal type (Figures 4(b) and 1(f)). The analysis of
the STM image in detail has sh own that th e dimension of
the smallest microdefect observed in fractal series, ~2
nm, is consistent with the parameters expected from the
tetrahedral model of the Si60 cluster (Figure 4(c)) [16].
Thus, the -barriers, 3 nm, heavily doped with boron,
5 × 1021 cm–3, represent really alternating arrays of the
smallest undoped microdefects and doped dots with di-
mensions restricted to 2 nm (Figure 4(c)). The value of
the boron concentration determined by the SIMS method
seems to indicate that each doped dot located between
undoped microdefects contains two impurity atoms of
boron. Since the boron dopants form shallow acceptor
centers in the silicon lattice, such high concentration has
to cause a metallic-like conductivity. Nevertheless, the
angular dependencies of the cyclotron resonance spectra
demonstrate that the p-type Si-QW confined by the  -
barriers heavily doped with boron contains the high mo-
bility 2D hole gas which is characterized by long mo-
mentum relaxation time of heavy and light holes at 3.8 K,
τ ≥ 5 × 10–10 s (Figures 2(a) and (b)) [8,11,12 ]. Thus, th e
momentum relaxation time of holes in the ultra-narrow
Si-QW appeared to be longer than in the best MOS
structures contrary to what might be expected from
strong scattering by the heavily doped -barriers. This
passive role of the  - barriers between which the Si-QW
is formed was quite surprising, when one takes into ac-
count the high level of their boron doping. To eliminate
this contradiction, the ESR technique has been applied
for the studies of the boron centers packed up in dots [5,
8].
The angular dependences of the ESR spectra at dif-
ferent temperatures in the range 3.8 - 27 K that reveal the
trigonal symmetry of the boron dipole centers have been
obtained with the same ESR spectrometer, the
Brucker-Physik AG ESR spectrometer at X-band (9.1 -
9.5 GHz), with the rotation of the magnetic field in the
(a)
(b)
(c)
Figure 4. (a) STM image of the ultra-shallow boron diffu-
sion profile prepared at the diffusion temperature of 800 ˚C
into the Si (100) wafer covered previously by medium oxide
overlayer X[001], Y[010], Z[100]. Solid triangle and ar-
rows that are labeled as 1 and 2 exhibit the microdefects
with dimensions 740 nm, 225 nm and 68 nm, respectively,
which are evidence of their fractal self-assembly; (b) The
model of the self-assembled microcavity system formed by
the microdefects of the fractal type on the Si (100) surface;
(c) STM image of the ultra-shallow boron diffusion profile
prepared at diffusion temperature of 900˚C into the Si (100)
wafer covered previously by medium oxide overlayer.
X[001], Y[010], Z[100].

N. T. BAGRAEV ET AL.
261
{110}-plane perpendicular to a {100}-interface (Bext = 0˚,
180˚ parallel to the Si-QW plane, Bext = 90˚ perpendicu-
lar to the Si-QW plane) (Figures 5(a), (b), (c) and (d)).
No ESR signals in the X-band are observed, if the
Si-QW confined by the -barriers is cooled down in the
external magnetic field (Bext) weaker than 0.22 T, with
the persistence of the amplitude and the resonance field
of the trigonal ESR spectrum as function of the crystal-
lographic orientation and the magnetic field value during
cooling down process at Bext ≥ 0.22 T (Figures 5(a), (b)
and (c)). With increasing temperature, the ESR line ob-
served changes its magnetic resonance field position and
disappears at 27 K (Figure 5(d)).
The observation of the ESR spectrum is evidence of
the fall in the electrical activity of shallow boron accep-
tors contrary to high level of boron doping. Therefore,
the trigonal ESR spectrum observed seems to be evi-
dence of the dynamic magnetic moment that is induced
by the exchange interaction between the small hole bi-
polarons which are formed by the negative-U reconstruc-
tion of the shallow boron acceptors, 2B0  B
+ + B–,
along the <111> crystallographic axis (Figure 6(a)) [5,
12,17]. These small hole bipolarons localized at the di-
pole boron centers, B+ - B–, seem to undergo the singlet-
triplet transition in the process of the exchange interac-
tion through the holes in the Si-QW thereby leading to
the trigonal ESR spectrum (Figures 5(a), (b), (c) and
(d)). Besides, the sublattice of the hole bipolarons lo-
cated between the undoped microdefects appears to de-
fine the one-electron band scheme of the  - barriers as
well as the transport properties for the 2D gas of holes in
the Si-QW (Figures 6(b) and 3(b)) [5].
In order to determine the one-electron band scheme of
the  - barriers that confine the Si-QW, the reflection
spectra R() were studied using a UV-VIS Specord M-40
spectrophotometer with an Ulbricht sphere for the reflec-
tivity measurements [15]. Figure 3d shows the spectra of
the reflection from the -barriers with different concen-
tration of boron. The decrease in R() compared with the
data of the silicon single crystal and the drops in the po-
sition of the peaks at the wavelengths of  = 354 and 275
nm are observed. The above peaks are related to the
transitions between Γ-L valleys and in th e vicinity of the
point X in the Brillouin zone, with the former of the
above peaks being assigned to the direct transition Γ’25 -
Γ’2, whereas the latter peak is attributed to the transition
X4 – X1 [17]. An analysis of the spectral dependence of
the reflection coefficient shows that the presence of the
microcavities formed by the self-assembled microdefects
with medium size reduces R() most profoundly in the
Figure 5. The trigonal ESR spectrum observed in field cooled ultra-shallow boron diffusion profile that seems to be evidence
of the dynamic magnetic moment due to the trigonal dipole centers of boron inside the  - barriers confining the Si-QW
which is persisted by varying both the temperature and magnetic field values. Bext  <110> (a),  <112> (b),  <111> (c, d).
Rotation of the magnetic field in the {110}-plane perpendicular to a {100}-interface (Bext = 0o, 180o  interface, Bext = 90o 
interface), ν = 9.45 GHz, T = 14 K (a, b, c) and T = 21 K (d).

N. T. BAGRAEV ET AL.
262
(a)
(b)
Figure 6. (a) Model for the elastic reconstruction of a shal-
low boron acceptor which is accompanied by the formation
of the trigonal dipole (B+ - B–) centers as a result of the neg-
ative-U reaction: 2B0  B+ + B–. (b) A series of the dipole
negative-U centers of boron located between the undoped
microdefects that seem to be a basis of nanostructured
-barriers confining the Si-QW.
short-waveleng th region of the spectrum (200 - 300 nm).
It follows from the comparison of R() with the STM
data that the position of the minima in the reflection co-
efficient in the spectral dependence R() and the micro-
cavity size are interrelated and satisfy the Bragg condi-
tion, x = /2n, where x is the cavity size,  is the wave-
length, and n is the refractive index of silicon, n = 3.4
(see Figure 4(a)). The R() drop in the position of the
Γ’25 - Γ’2 and X4 – X1 transitions appears to be due to the
formation of the wide-gap semiconductor layer with in-
creasing the concentration of boron. These data substan-
tiate the assumption no ticed ab ove th at the role of th e dot
containing the small hole bipolaron is to establish the
band structure of the -barrier with the energy confine-
ment more than 1.25 eV in both the conduction and the
valence band of the Si-QW (Figure 3(d) ).
3. Superconductor Properties for -Barriers
Heavily Doped with Boron
In common with the other solid s th at con tain small onsite
localized small bipolarons [18-24], the  - barriers con-
taining the dipole bo ron centres have b een found to be in
an excitonic insulator regime at the sheet density of holes
in the Si-QW lower than 1015 m–2. The conductance of
these silicon nanostructures appeared to be determined
by the parameters of the 2D gas of holes in the Si-QW [5,
7,25]. However, here we demonstrate using the electrical
resistance, specific heat magnetic suscep tibility and local
tunnelling spectroscopy techniques that the high sheet
density of holes in the Si-QW (> 1015 m–2) gives rise to
the superconductor properties for the -barriers which
result from the transfer of the small hole bipolarons
through the negative-U centers [26-30] in the interplay
with the multiple Andreev reflections inside the Si-QW
[31-35].
The resistance, thermo-emf and Hall measurements of
the device with high density of 2D holes, 6 × 1015 m–2,
performed within Hall geometry were made in Special
Design Electric and Magnetic Measurement System with
high precision bridge (Figure 7(a)). The identical device
was used in the studies of the local tunneling spectros-
copy with the STM spectro meter to register th e tunn eling
current as a function of the voltage applied between the
STM tip and the Hall contacts (Figure 7(b)). The meas-
urements in the range 0.4-4 K and 1.2-300 K were car-
ried out respectively in a He3 and He4 cryostat.
The current-voltage characteristics (CV) measured at
different temperatures exhibited an ohmic character,
whereas the temperature dependence of the resistance of
the device is related to two -dimen sio nal metal o n ly in th e
range 220 - 300 K (Figure 8). Below 220 K the resis-
tance increases up to the value of 6.453 kOhm and then
drops reaching the negligible value at the temperature of
145 K. The creation of the additional peak when the re-
sistance begins to fall down seems to be evidence of the
superconductor properties caused by the transfer of the
small hole bipolarons. This peak shows the logarithmic
temperature dependence that appears to be due to the

N. T. BAGRAEV ET AL.
263
(a)
(b)
Figure 7. (a) Schematic diagram of the devices that demon-
strates a perspective view of the p-type Si-QW confined by
the  - barriers heavily doped with boron on the n-type Si
(100) surface. The top gate is able to control the sheet den-
sity of holes and the Rashba SOI value. The depletion re-
gions indicate the Hall geometry of leads; (b) Planar field-
effect silicon transistor structure with the STM tip, which is
based on an ultra-shallow p+-diffusion profile prepared in
the Hall geometry. The circle dashed line exhibits the point
STM contact region.
Figure 8. The resistance temperature dependences that were
observed in the ultra-shallow p+-diffusion profile which
contains the p-type Si-QW confined by the δ - barriers
heavily doped with boro n on the n-type Si (100) surface.
Kondo-liked scattering of the single 2D holes tunneling
through the negative-U boron dipole centres of boron at
the Si-QW –  - barrier interfaces.
As was to be expected, the application of external
magnetic field results in the shift of the resistance drop to
lower temperatures, which is accompanied by the weak
broadening of the transition and the conservation of the
peak values of the resistance (Figure 8). Similar peaks
followed by the drops of the resistance revealed in its
temperature dependences are evidence of the Kondo-liked
scattering that seems to be the precursor of the optimal
tunneling of single holes into the negative-U boron cen-
ters of boron [36]. This process is related to the conduc-
tion electron tunneling into the negativ e-U centers that is
favourable to the increase of the superconducting transi-
tion temperature, Tc, in metal-silicon eutectic alloys [26,
27]. The effect of single-hole tunneling is also possible
to resolve some bottlenecks in the bipolaronic mecha-
nism of the high temperature superconductivity, which
results from the distance between the negative-U centers
lesser than the coherence length [28,30]. Besides, two
experimental facts are needed to be noticed. Firstly, the
maximum value of th e resistan ce, 6.45 3 kOhm  h/4e2, is
independent of the external magnetic field. Secondly,
applying a magnetic field is surprised to stabilize the  -
barrier in the state of the two-dimensional metal u p to th e
temperature value corresponding to the shift of a transi-
tion to lower temperatures (Figure 8). Thus, the -barri-
ers confining Si-QW seem to be self-organized as gra-
phene [37] owing to heavily doping with boron which
gives rise to the formation of the negative-U dipole cen-
ters.
The value of the critical temperature, Tc = 145 K, the
estimations of the superconductor gap, 2 = 0.044 eV,

264 N. T. BAGRAEV ET AL.
and the T = 0 upper critical field, HC2 = 0.22 T, that were
derived from the resistance and thermo-emf measure-
ments using well-known relationships 2 = 3.52kBTc and
Hc2(0) = –0.69(dHc2/dT|Tc)Tc [38] appear to be revealed
also in the temperature and magnetic field dependencies
of the static magnetic susceptibility obtained by the Fa-
raday balan ce metho d (Figures 9(a), (b) and (c)).
These dependences w ere measured in the range 3.5 - 300
K with the magnetic balance spectrometer MGD312FG.
High sensitivity, 10–9 - 10–10 CGS, should be no ted to be
provided by the ddBB x stability us ing th is installation .
Pure InP samples with the shape and size similar to the
silicon samples studied here that are characterized by
temperature stable magnetic susceptibility,  = 313 ×
10–9 cm3/g, were used to calibrate the ddBB x values.
The value of temperatures corresponding to the drops
of the diamagnetic response on cooling is of importance
to coincide with the drops of the resistance thereby con-
firming the role of the charge correlations localized at the
negative-U dipole centers in the Kondo-liked scattering
and the enhancement of the critical temperature (Figures
9(a), (b) and (c)). Just the same temperature dependence
of the paramagnetic response observed after the field-in
procedure exhibits the effect of the arrays of the Joseph-
son transitions revealed by the STM image ( Figure 4(c))
on the flux pinning processes in the superconductor
-barriers heavily doped with boron [3]. The plots of the
magnetic susceptibility vs temperature and magnetic field
shown in Figure 9(a) result in the value of HC2, HC2 =
0.22 T, that corresponds to the data obtained by the
measurements of the resistance and allow the estimation
of the coherence length, ξ = 39 nm, where ξ = (0/
2HC2)1/2, 0 = h/2e. This value of the coherence length
appears to be in a good agreement with the estimations
of the superconductor gap, 2 = 0.044 eV, made if the
value of the critical temperature, TC = 145 K, is taken
into account, 0.18
F
Bc
vkT

, where vF is the Fermi
velocity, and with the first critical magnetic field, HC1 =
215 Oe, defi ned visuall y fr om Figure 9(a).
The oscillations of the magnetic susceptibility value
revealed by varying both the temperature and magnetic
field value seem to be due to the vortex manipulation in
nanostructured  - barriers (Figures 9(b) and (c)). Since
the fractal series of silicon microdefects identified b y the
STM images is embedded in the superconductor  - bar-
rier, the multi-quanta vortex lattices are able to be self-
organized [39]. These self-assembled pinning arrays that
can be simulated as a series of alternating silicon empty
dots and dots doped with boron appear to capture in
consecutive order several vortices and thus to enhance
critical current [39,40]. Furthermore, the upper critical
field, HC2, is evidently dependent step-like on both tem
perature and magnetic field, because the critical current
(a)
(b)
(c)
Figure 9. Plots of static magnetic susceptibility vs tempera-
ture and magnetic field that was observed in field-cooled
ultra-shallow p+ -diffusion profile which contains the p-type
Si-QW confined by δ - barriers heavily doped with boron
on the n-type Si (100) surface. Diamagnetic response (a)
revealed by field-out procedure demonstrates also the os-
cillations that seem to be related to the ratchet effect (b)
and the quantization of the critical current (c).

N. T. BAGRAEV ET AL.
265
increase jump-like each time when the regular vortex is
captured at such silico n empty dot that is revealed by the
corresponding oscillations of the diamagnetic response
(Figure 9(c)). The period of these oscillations that is
derived from the plots in Figure 9(c) appears to be due
to the distance between the small microdefects in the
fractal series identified by the STM image,  120 nm,
with average dimensions equal to 68 nm (Figure 4(a)):
ΔBS = Φ0, where ΔB is the period oscillations, S = πd2/4,
d is the distance between silicon microdefects that seem
to be modulated as empty dots ( 120 nm). The depend-
ence HC2(T) is of importance to be in a good agreement
with the value of this period, because each maximum of
the diamagnetic response as a function of magnetic field
is accompanied by the temperature satellite shifted by
approximately 140 K (~TC) to higher temperatures. In
addition to the oscillatio ns of the magnetic susceptib ility,
the B-T diagram shown in Figure 9(b) exhibits also the
quantization of the critical current which seems to be
caused by the vortex ratchet effect [40].
The enhancement of the critical current due to the N
Φ0 vortex capture at the anti-dots seems to result also
from the studies of a specific heat anomaly at TC (Fig-
ures 10(a) and (b)). This anomaly arises at the tempera-
ture of 152 K (H = 0) that is close to the value of the
critical temperature derived from the measurements of
the resistance and the magnetic susceptibility. With in-
creasing external magnetic field, the position of the jump
in specific heat is shifted to the range of low tempera-
tures (Figure 10(a)). The jump values in specific heat,
ΔC, appear to be large if the abnormal small effective
mass of heavy holes in these ‘sandwich’ structures,
S-Si-QW-S, is taken into account to be analyzed within
frameworks of a weak coupled BCS superconductor [3,
41]. The oscillations of a specific heat anomaly as a
function of external magnetic field are seen to be in a
good agreement with the corresponding behavior of the
diamagnetic response that corroborates additionally the
important role of vortices in the superconductor proper-
ties of the nanostructured  - barriers (Figure 10(b)).
The values of the superconductor energy gap derived
from the measurements of the critical temperature using
the different techniques appear to be practically identical,
0.044 eV. Nevertheless, the direct methods based on the
principles of the tunneling spectroscopy are necessary to
be applied for the identification of the superconductor
gap in the -barriers confining the Si-QW (Figures 7(a)
and (b)). Since the nanostructured -barriers are self-
assembled as the dots containing a single dipole boron
center that alternate with silicon empty dots shown in
Figure 4(c), the tunneling current can be recorded by
applying the voltage to the contacts prepared in the Hall
geometry (Figure 7(a)). The tunneling current-voltage
(a)
(b)
Figure 10. (a) Specific heat anomaly as C/T vs T that seems
to reveal the superconducting transition in field-cooled ul-
tra-shallow p+-diffusion profile which contains the p-type
Si-QW confined by δ - barriers heavily doped with boron
on the n-type Si (100) surface. Magnetic field value: 1 – 0
mT; 2 – 5 mT, 3 – 10 mT; 4 – 21.5 mT; 5 – 50 mT; 6 – 300
mT. (b) The oscillations of a specific heat anomaly as a
function of external magnetic field that seem to be due to
the quantization of the critical current.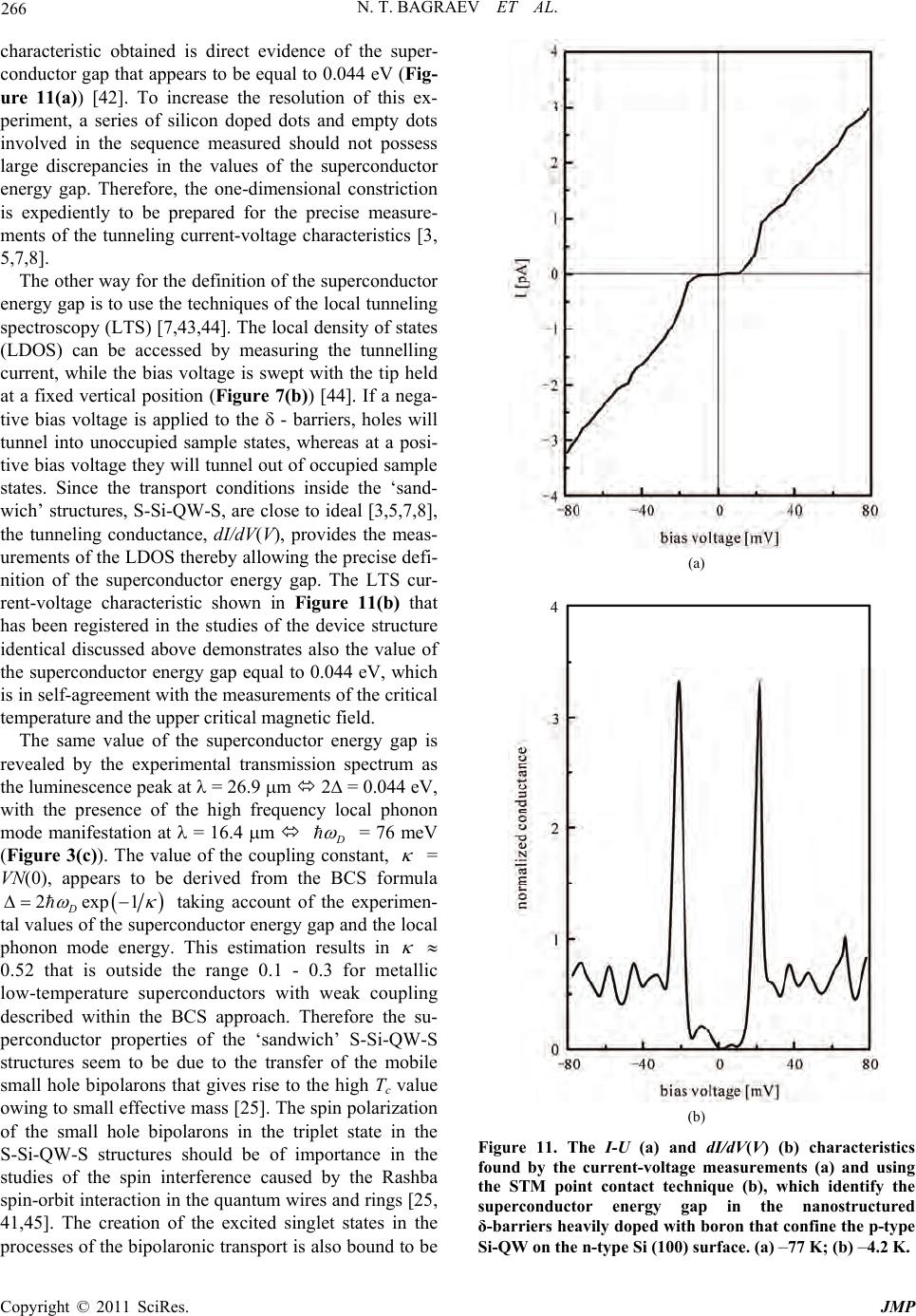

266 N. T. BAGRAEV ET AL.
characteristic obtained is direct evidence of the super-
conductor gap that appears to be equal to 0.044 eV (Fig-
ure 11(a)) [42]. To increase the resolution of this ex-
periment, a series of silicon doped dots and empty dots
involved in the sequence measured should not possess
large discrepancies in the values of the superconductor
energy gap. Therefore, the one-dimensional constriction
is expediently to be prepared for the precise measure-
ments of the tunneling current-voltage characteristics [3,
5,7,8].
The other way for the definition of the superconductor
energy gap is to use the techniques of the local tunneling
spectroscopy (LTS) [7,43,44]. The local density of states
(LDOS) can be accessed by measuring the tunnelling
current, while the bias voltage is swept with the tip held
at a fixed vertical position (Figure 7(b)) [44]. If a nega-
tive bias voltage is applied to the  - barriers, holes will
tunnel into unoccupied sample states, whereas at a posi-
tive bias voltage th ey will tunnel out of occupied sample
states. Since the transport conditions inside the ‘sand-
wich’ structures, S-Si-QW-S, are close to ideal [3,5,7,8],
the tunneling conductance, dI/dV(V), provides the meas-
urements of the LDOS thereby allowing the precise defi-
nition of the superconductor energy gap. The LTS cur-
rent-voltage characteristic shown in Figure 11(b) that
has been registered in the studies of the device structure
identical discussed above demonstrates also the value of
the superconductor energy gap equal to 0.044 eV, which
is in self-agreement with the measurements of the critical
temperature and the upper critical magnetic field.
The same value of the superconductor energy gap is
revealed by the experimental transmission spectrum as
the luminescence peak at  = 26.9 m  2 = 0.044 eV,
with the presence of the high frequency local phonon
mode manifestation at  = 16.4 m 
D

 = 76 meV
(Figure 3(c)). The value of the coupling constant,

=
VN(0), appears to be derived from the BCS formula

2exp1
D
(a)


   taking account of the experimen-
tal values of the superconductor energy gap and the local
phonon mode energy. This estimation results in


0.52 that is outside the range 0.1 - 0.3 for metallic
low-temperature superconductors with weak coupling
described within the BCS approach. Therefore the su-
perconductor properties of the ‘sandwich’ S-Si-QW-S
structures seem to be due to the transfer of the mobile
small hole bipolarons that gives rise to the high Tc value
owing to small effective mass [25]. The spin polarization
of the small hole bipolarons in the triplet state in the
S-Si-QW-S structures should be of importance in the
studies of the spin interference caused by the Rashba
spin-orbit interaction in the quantum wires and rings [25,
41,45]. The creation of the excited singlet states in the
processes of the bipolaronic transport is also bound to be
(b)
Figure 11. The I-U (a) and dI/dV(V) (b) characteristics
found by the current-voltage measurements (a) and using
the STM point contact technique (b), which identify the
superconductor energy gap in the nanostructured
δ-barriers heavily dope d with boron that confine the p-type
Si-QW on the n-type Si (100) surface. (a) –77 K; (b) –4.2 K.

N. T. BAGRAEV ET AL.
267
noticed, because owing to the transitions from the ex-
cited to the ground singlet state of the small hole bipola-
rons these ‘sandwich’ structures seem to be perspective
as the sources and recorders of the THz and GHz emis-
sion that is revealed specifically in the electrolumines-
cence and transmission spectra as a low frequency mod-
ulation (see Figures 3(a) and 3( c)). The optical detection
of magnetic resonance of the single impurity centers in
the Si-QW confined b y the -barriers heavily doped with
boron was especially performed by the direct measure-
ments of the transmission spectra under such an internal
GHz emission in the absence of the external cavity reso-
nator [46,47].
Thus, the extremely low value of the hole effective
mass in the ‘sandwich’ S-Si-QW-S structures seems to
be the principal argument for the bipolaronic mechanis m
of high temperature superconductor properties that is
based on the coherent tunneling of bipolarons [28,30].
The results obtained have a bearing on the versions of
the high temperature superconductivity that are based on
the promising application of the sandwiches which con-
sist of the alternating sup erconductor and insulato r layers
[48-51]. In the latter case, a series of the silicon dots
doped with boron and silicon empty dots that forms the
Josephson junction area in nanostructured -barriers is of
advantage to achieve the high Tc value,
  
exp 0
cDB
TkN  

V, because of the presence
of the local high frequency phonon mode which com-
pensates for relatively low density of states, N(0).
Nevertheless, the mechanism of the bipolaronic trans-
fer is still far from completely clear. This raises the ques-
tion of whether the Josephson tran sitions dominate in the
transfer of the pair of 2D holes in the plane of the nanos-
tructured -barriers and in the proximity effect due to the
tunneling through the Si-QW or the Andreev reflection
plays a part in the bipolaronic transfer similar to the suc-
cessive two-electron (hole) capture at the negative-U
centers [23,24].
4. Superconducting Proximity Effect
Since the devices studied consist of a series of alternating
semiconductor and superconductor nanostructures with
dimensions comparable to both the Fermi wavelength
and the superconductor coherence length, the periodic
modulation of the critical current can be observed in
consequence with quantum dimensional effects [32-35].
Here the S-Si-QW-S structures performed in the Hall
geometry are used to analyse the interplay between the
phase-coherent tunneling in the normal state and the
quantization of supercurrent in the superconducting state.
Firstly, the two-dimensional subbands of holes in the
Si-QW identified by studying the far-infrared electrolu-
minescence (EL) spectrum (Figures 3(a) and (b) ) appear
to be revealed also by the I-V characteristic measured
below the superconducting critical temperature of the  -
barriers which exhibits the modulation of the supercur-
rent flowing across the junction defined as the Josephson
critical current (Figure 12). The modulation of super-
current seems to be caused by the tuning of on- and
off-resonance with the subbands of 2D holes relatively to
the Fermi energy in superconductor  - barriers [34,35]
(see Figures 13(a) and (b)). The two-dimensional sub-
bands of 2D holes are revealed by varying the forward
bias voltage (Figures 12 and 13(a)), whereas the reverse
bias voltage invo lves the levels that result fro m the Cou-
lomb charging effects in the Si-QW filled with holes
(Figures 12 and 13(b)). The spectrum of supercurrent in
the superconducting state appears to correlate with the
conductance oscillation s of the 2e2/h value in the normal
state of the S-Si-QW-S structure (Figures 14(a) and (b)).
This highest amplitude of the con ductance oscillations is
evidence of strong coupling in the superconductor
-barriers (Figure 14(b)). The data obtained demonstrate
also that the amplitude of the quantum supercurrent is
within frameworks of the well-known relationship IcRn =
/e [32,35]; where Rn = 1/Gn is the normal resistance
state, 2 is superconducting gap, 0.044 eV. Besides, the
strong coupling of on-resonance with the subbands of 2D
holes which results from the 2e2/h value of the conduc-
tance amplitude in the normal state is not related to the
Kondo enhancement that is off-resonance [52].
Secondly, the spectrum of the supercurrent at low bias
voltages appears to exhibit a series of peaks that are
caused by multiple Andreev reflection s (MARs) from the
-barriers confining the Si-QW (Figures 15(a) and (b)).
The MAR process at the Si-QW--barrier interface is
due to the transformation of the 2D holes in a Cooper
pair inside the superconducting  - barrier which results
Figure 12. I-V characteristic that demonstrates the modula-
tion of the critical current with the forward and reverse
bias applied to the p-type Si-QW confined by the δ - barri-
ers on the n-type Si (100) surface.

268 N. T. BAGRAEV ET AL.
(a) (b)
Figure 13. The one-electron band scheme of the p-type
Si-QW confined by the δ - barriers on the n-type Si (100)
surface under forward (a) and reverse (b) bias, which de-
picts the superconducting gap, 2, as well as the two-di-
mensional subbands of holes and the levels that result from
the hole interference between the δ-barriers (a) and the
Coulomb charging effects in the Si-QW filled with holes (b).
(a)
(b)
Figure 14. Correlation between critical current (a) and
normal state conductance (b) revealed by varying the re-
verse bias voltage applied to the sandwich structure, δ-
barrier-p-type Si-QW-δ-barrier, on the n-type Si (100) sur-
face.
(a)
(b)
Figure 15. Multiple Andreev reflections (MAR) with the
forward (a) and reverse (b) bias applied to the sandwich
structure, δ-barrier-p-type Si-QW-δ-barrier on the n-type
Si (100) surface. The MAR peak positions are marked at Vn =
2/ne with values n indicated. The superconducting gap
peak, 2Δ, is also present. The difference in the values of
critical current under forward and reverse bias voltage is
due to non-symmetry of the sandwich struct ur e.
in an electron being coherently reflected into the Si-QW,
and vice versa, thereby providing the superconducting
proximity effect (Figures 16(a) and (b)) [32]. The single
hole crossing the Si-QW increases its energy by eV.
Therefore, when the sum of these gains becomes to be
equal to the superconducting energy gap, 2, the reso-
nant enhancement in the supercurrent is observed (Fig-
ures 15(a) and (b)). The MAR peak positions occur at
the voltages Vn = 2/ne, where n is integer number, with
the value n = 1 related to the supercondu cting energ y gap.
It should be noted that the value of 2, 0.033 eV, derived
from the MAR oscillations does no t agree with the mag-
netic susceptibility data because of heating of the device
by bias voltage at finite temperatures. The mechanism of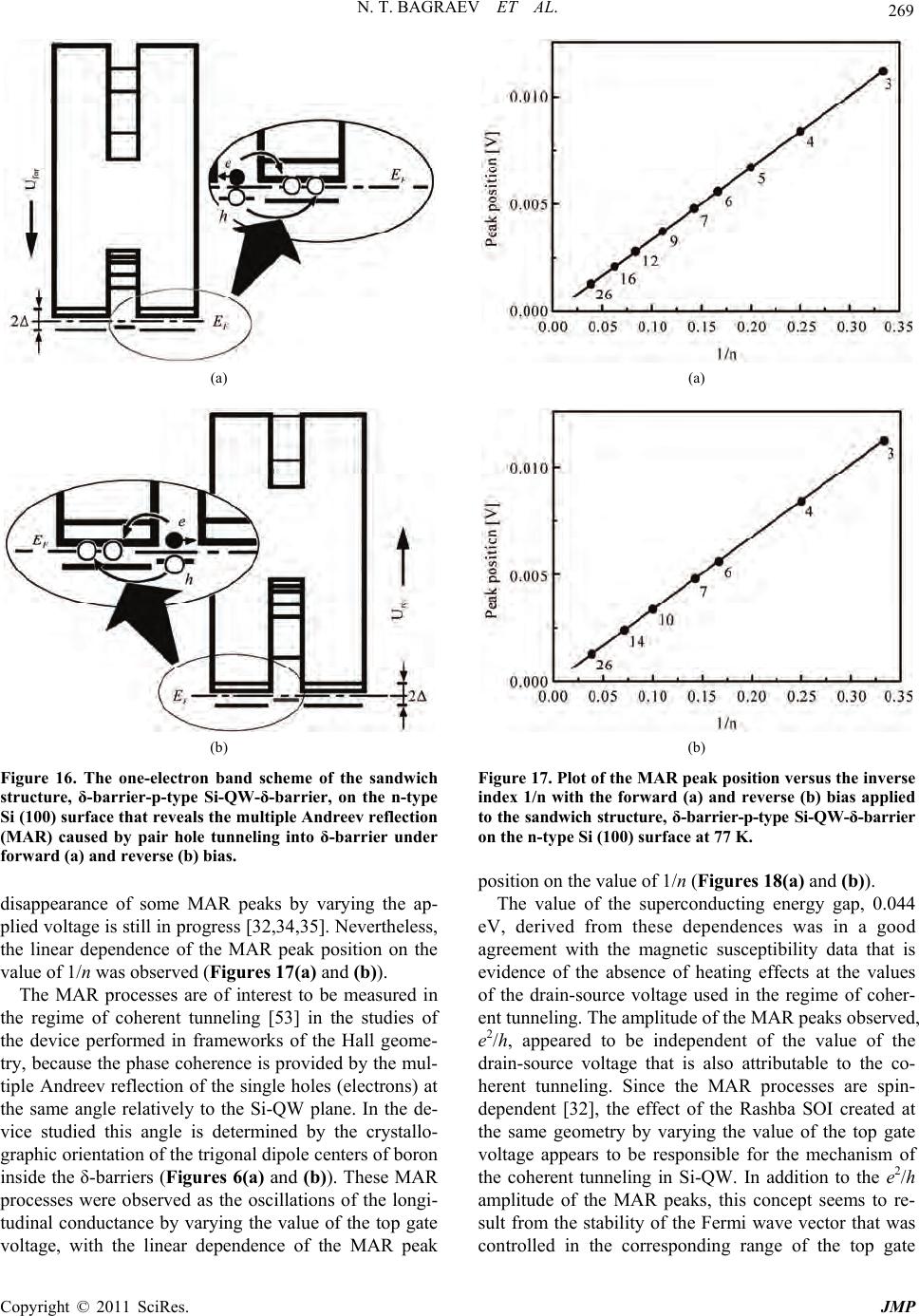

N. T. BAGRAEV ET AL.
269
(a)
(b)
Figure 16. The one-electron band scheme of the sandwich
structure, δ-barrier-p-type Si-QW-δ-barrier, on the n-type
Si (100) surface that reveals the multiple Andreev reflection
(MAR) caused by pair hole tunneling into δ-barrier under
forward (a) and reverse (b) bias.
disappearance of some MAR peaks by varying the ap-
plied voltage is still in progress [32,34 ,35]. Nevertheless,
the linear dependence of the MAR peak position on the
value of 1/n was observed (Figures 17(a) and (b)).
The MAR processes are of interest to be measured in
the regime of coherent tunneling [53] in the studies of
the device performed in frameworks of the Hall geome-
try, because the phase coherence is provided by the mul-
tiple Andreev reflection of the single holes (electrons) at
the same angle relatively to the Si-QW plane. In the de-
vice studied this angle is determined by the crystallo-
graphic orientation of the trigonal dipole centers of boron
inside the δ-barriers (Figures 6(a) and (b)). These MAR
processes were observed as the oscillations of the longi-
tudinal conductance by varying the value of the top gate
voltage, with the linear dependence of the MAR peak
(a)
(b)
Figure 17. Plot of the MAR peak position versus the inverse
index 1/n with the forward (a) and reverse (b) bias applied
to the sandwich structure, δ-barrier-p-type Si-QW-δ-barrier
on the n-type Si (100) surface at 77 K.
position on the value of 1/n (Figures 18(a) and (b)).
The value of the superconducting energy gap, 0.044
eV, derived from these dependences was in a good
agreement with the magnetic susceptibility data that is
evidence of the absence of heating effects at the values
of the drain-source voltage used in the regime of coher-
ent tunneling. The amplitude of the MAR peaks observed,
e2/h, appeared to be independent of the value of the
drain-source voltage that is also attributable to the co-
herent tunneling. Since the MAR processes are spin-
dependent [32], the effect of the Rashba SOI created at
the same geometry by varying the value of the top gate
voltage appears to be responsible for the mechanism of
the coherent tunneling in Si-QW. In addition to the e2/h
amplitude of the MAR peaks, this concept seems to re-
sult from the stability of the Fermi wave vector that was
controlled in the corresponding range of the top gate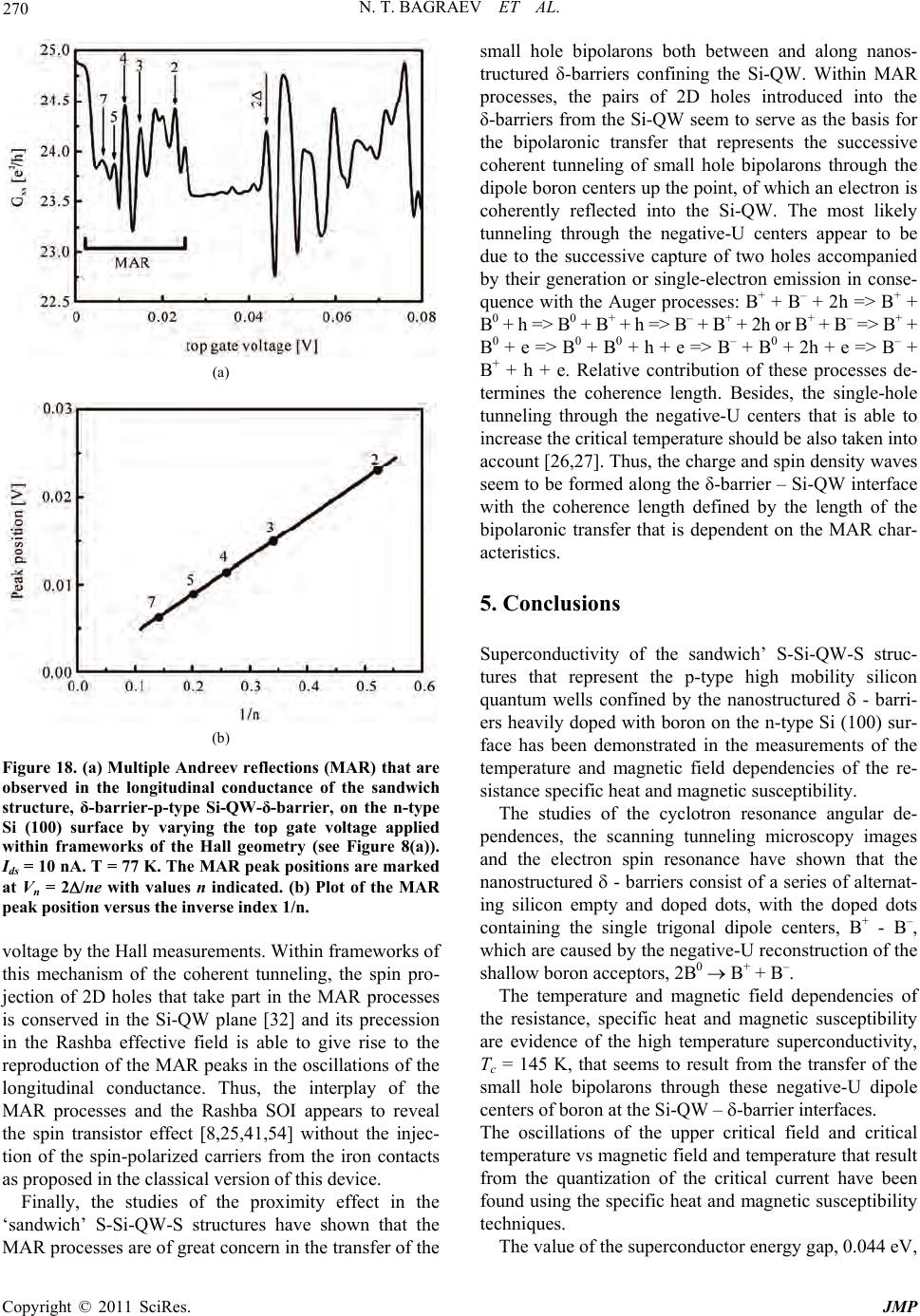

270 N. T. BAGRAEV ET AL.
(a)
(b)
Figure 18. (a) Multiple Andreev reflections (MAR) that are
observed in the longitudinal conductance of the sandwich
structure, δ-barrier-p-type Si-QW-δ-barrier, on the n-type
Si (100) surface by varying the top gate voltage applied
within frameworks of the Hall geometry (see Figure 8(a)).
Ids = 10 nA. T = 77 K. The MAR peak positions are marked
at Vn = 2/ne with values n indicated. (b) Plot of the MAR
peak position versus the inverse index 1/n.
voltage by the Hall measurements. Within frameworks of
this mechanism of the coherent tunneling, the spin pro-
jection of 2D holes that take part in the MAR processes
is conserved in the Si-QW plane [32] and its precession
in the Rashba effective field is able to give rise to the
reproduction of the MAR peaks in the oscillations of the
longitudinal conductance. Thus, the interplay of the
MAR processes and the Rashba SOI appears to reveal
the spin transistor effect [8,25,41,54] without the injec-
tion of the spin-polarized carriers from the iron contacts
as proposed in the classical version of this device.
Finally, the studies of the proximity effect in the
‘sandwich’ S-Si-QW-S structures have shown that the
MAR processes are of great concern in the transfer of the
small hole bipolarons both between and along nanos-
tructured δ-barriers confining the Si-QW. Within MAR
processes, the pairs of 2D holes introduced into the
δ-barriers from the Si-QW seem to serve as the basis for
the bipolaronic transfer that represents the successive
coherent tunneling of small hole bipolarons through the
dipole boron centers up the point, of which an electron is
coherently reflected into the Si-QW. The most likely
tunneling through the negative-U centers appear to be
due to the successive capture of two holes accompanied
by their generation or single-electron emission in conse-
quence with the Auger processes: B+ + B– + 2h => B+ +
B0 + h => B0 + B+ + h => B– + B+ + 2h or B+ + B– => B+ +
B0 + e => B0 + B0 + h + e => B– + B0 + 2h + e => B– +
B+ + h + e. Relative contribution of these processes de-
termines the coherence length. Besides, the single-hole
tunneling through the negative-U centers that is able to
increase the critical temperature should be also taken into
account [26,27]. Thus, the charge and spin density waves
seem to be formed along the δ-barrier – Si-QW interface
with the coherence length defined by the length of the
bipolaronic transfer that is dependent on the MAR char-
acteristics.
5. Conclusions
Superconductivity of the sandwich’ S-Si-QW-S struc-
tures that represent the p-type high mobility silicon
quantum wells confined by the nanostructured  - barri-
ers heavily doped with boron on the n-type Si (100) sur-
face has been demonstrated in the measurements of the
temperature and magnetic field dependencies of the re-
sistance specific heat and magnetic suscep tibility.
The studies of the cyclotron resonance angular de-
pendences, the scanning tunneling microscopy images
and the electron spin resonance have shown that the
nanostructured  - barriers consist of a series o f alternat-
ing silicon empty and doped dots, with the doped dots
containing the single trigonal dipole centers, B+ - B–,
which are caused by the negative-U reconstruction of the
shallow boron acceptors, 2B 0  B+ + B–.
The temperature and magnetic field dependencies of
the resistance, specific heat and magnetic susceptibility
are evidence of the high temperature superconductivity,
Tc = 145 K, that seems to result from the transfer of the
small hole bipolarons through these negative-U dipole
centers of boron at the Si-QW – -barrier interfaces.
The oscillations of the upper critical field and critical
temperature vs magnetic field and temperature that result
from the quantization of the critical current have been
found using the specific heat and magnetic su sceptibility
techniques.
The value of the superconductor energy gap, 0.044 eV,

N. T. BAGRAEV ET AL.
271
derived from the measurements of the critical tempera-
ture using the different techniques appeared to be practi-
cally identical to the data of the current-voltage charac-
teristics and the local tunneling spectroscopy.
The extremely low value of the hole effective mass in
the ‘sandwich’ S-Si-QW-S structures seems to be the
principal argument for the bipolaronic mechanism of
high temperature superconductor properties that is based
on the coherent tunneling of bipolarons. The high fre-
quency local phonon mode that is revealed with the su-
perconductor energy gap in the infrared transmission
spectra seems also to be responsible for the formation
and the transfer of small hole bipolarons.
The proximity effect in the S-Si-QW-S structure has
been identified by the findings of the MAR processes
and the quantization of the supercurrent. The value of the
superconductor energy gap, 0.044 eV, appeared to be in
a good agreement with th e data derived from the oscilla-
tions of the conductance in normal state and of the
zero-resistance supercurrent in superconductor state as a
function of the bias vo ltage. These oscillation s have b een
found to be correlated by on- and off-resonance tuning
the two-dimensional subbands of holes with the Fermi
energy in the superconductor -barriers.
Finally, the studies of the proximity effect in the
‘sandwich’ S-Si-QW-S structures have shown that the
multiple Andreev reflection (MAR) processes are of
great concern in the coherent transfer of the small hole
bipolarons both between and along nanostructured
δ-barriers confining the Si-QW. The interplay of the
MAR processes and the Rashba SOI appears to reveal
the spin transisto r effect.
6. Acknowledgements
The work was supported by the programme of funda-
mental studies of the Presidium of the Russian Academy
of Sciences “Quantum Physics of Condensed Matter”
(grant 9.12); programme of the Swiss National Science
Foundation (grant IZ73Z0_127945/1); the Federal Tar-
geted Programme on Research and Development in Pri-
ority Areas for the Russian Science and Technology Com-
plex in 2007–2012 (contract No. 02.514.11.4074), the
SEVENTH FRAMEWORK PROGRAMME Marie Cu-
rie Actions PIRSES-GA-2009-246784 p roject SPINM ET.
7. References
[1] C. Macilwain, “Computer Hardware: Silicon Down to the
Wire,” Nature, Vol. 436, No. 22-23, 2005, pp. 22-23.
[2] L. Ozyuzer, A. E. Koshelev, C. Kurter, N. Gopalsami, Q.
Li, M. Tachiki, K. Kadowaki, T. Yamamoto, H. Minami,
H. Yamaguchi, T. Tachiki, K. E. Gray, W.-K. Kwok and
U. Welp, “Emission of Coherent THz Radiation from
Superconductors,” Science, Vol. 318, No. 5854, 2007, pp.
1291-1293. doi:10.1126/science.1149802
[3] N. T. Bagraev, W. Gehlhoff, L. E. Klyachkin, A. M.
Malyarenko, V. V. Romanov and S. A. Rykov, “Super-
conductivity in Silicon Nanostructures,” Physica C, Vol.
437-438, 2006, pp. 21-24.
doi:10.1016/j.physc.2005.12.011
[4] E. A. Ekimov, V. A. Sidorov, E. D. Bauer, N. N. Mel’nik,
N. J. Curro, J. D. Thompson and S. M. Stishov,
“Superconductivity in Diamond,” Nature, Vol. 428, 2004,
pp. 542-545. doi:10.1038/nature02449
[5] N. T. Bagraev, A. D. Bouravleuv, L. E. Klyachkin, A. M.
Malyarenko, W. Gehlhoff, V. K. Ivanov and I. A. She-
lykh, “Quantized Conductance in Silicon Quantum
Wires,” Semiconductors, Vol. 36, No. 4, 2002, pp. 439-
460. doi:10.1134/1.1469195
[6] N. T. Bagraev, A. D. Bouravleuv, W. Gehlhoff, L. E.
Klyachkin, A. M. Malyarenko, V. V. Romanov and S. A.
Rykov, “Fractal Self-Assembled Nanostructures on
Monocrystalline Silicon Surface,” Proceedings of the 6th
International Conference on Diffusion in Materials, Cra-
cow, 2005; pp. 1049-1054.
[7] N. T. Bagraev, V. K. Ivanov, L. E. Klyachkin and I. A.
Shelykh, “Spin Depolarization in Quantum Wires Polar-
ized Spontaneously in a Zero Magnetic Field,” Physical
Revive B, Vol. 70, No. 15, 2004, pp. 155315-1-9.
[8] N. T. Bagraev, A. D. Bouravleuv, L. E. Klyachkin, A. M.
Malyarenko, W. Gehlhoff, Y. I. Romanov and S.A.
Rykov, “Local Tunneling Spectroscopy of Silicon
Nanostructures,” Semiconductors, Vol. 39, No. 6, 2005,
pp. 716-728.
[9] J. Robertson, “Electronic Structure of Amorphous Semi-
conductors,” Advances in Physics, Vol. 32, No. 3, 1983,
pp. 361-452. doi:10.1080/00018738300101571
[10] G. J. Gerardi, E. H. Poindexter, P. J. Caplan and N. M.
Johnson, “Interface Traps and Pb Centers in Oxidized
Silicon Wafers,” Applied Physics Letterrs, Vol. 49, No. 6,
1986, pp. 348-351. doi:10.1063/1.97611
[11] N. T. Bagraev, W. Gehlhoff and L. E. Klyachkin, “Cy-
clotron Resonance in Heavily Doped Silicon Quantum
Wells,” Solid State Phenomena, Vol. 47-48, 1995, pp.
589-594.
[12] W. Gehlhoff, N. T. Bagraev and L. E. Klyachkin, “Shal-
low and Deep Centres in Heavily Doped Silicon Quan-
tum Wells,” Materials Science Forum, Vol. 196-201,
1995, pp. 467-472.
[13] N. T. Bagraev, N. G. Galkin, W. Gehlhoff, L. E. Klyach-
kin, A. M. Malyarenko and I. A. Shelykh, “Spin Interfer-
ence in Silicon One-Dimensional Rings,” Journal of
Physics: Conference Series, Vol. 61, 2007, pp. 56-60.
doi:10.1088/1742-6596/61/1/012
[14] J. P. Kotthaus and R. Ranvaud, “Cyclotron Resonance of
Holes in Surface Space Charge Layers on Si,” Physical
Review. B, Vol. 15, No. 12, 1977, pp. 5758-5761.
doi:10.1103/PhysRevB.15.5758
[15] N. T. Bagraev, A. D. Bouravleuv, L. E. Klyachkin, A. M.
Malyarenko, S. A. Rykov, “Self-Ordered Microcavities

272 N. T. BAGRAEV ET AL.
Embedded in Ultra-shallow Silicon p-n Junctions,”
Semiconductors, Vol. 34, No. 6, 2000, pp. 700-711.
doi:10.1134/1.1188058
[16] B. X. Li, P. L. Cao and D. L. Que, “Distorted Icosahedral
Cage Structure of Si60 Clusters,” Physical Review B, Vol.
61, No. 3, 2000, pp.1685-1687.
doi:10.1103/PhysRevB.61.1685
[17] A. Slaoui, E. Fogarassy, J. C. Muller and P. Siffert,
“Study of Some Optical and Electrical Properties of
Heavily Doped Silicon Layers,” J. de Physique Colloq.,
Vol. 44, No. C5 44, 1983, pp. 65-71.
[18] P. W. Anderson, “Model for the Electronic Structure of
Amorphous Semiconductors,” Physical Review Letters,
Vol. 34, No. 15, 1975, pp. 953-955.
doi:10.1103/PhysRevLett.34.953
[19] G. D. Watkins, “Negative-U Properties for Defects in
Solids,” Festkoerperprobleme, Vol. 24, 1984, pp. 163-
184.
[20] R. A. Street and N. F. Mott, “States in the Gap in Glassy
Semiconductors,” Physical Review Letters, Vol. 35, No.
19, 1975, pp. 1293-1296.
doi:10.1103/PhysRevLett.35.1293
[21] M. Kastner, D. Adler and H. Fritzsche, “Va-
lence-Alternation Model for Localized Gap States in
Lone-Pair Semiconductors,” Physical Review Letters, Vol.
37, No. 22, 1976, pp. 1504-1507.
doi:10.1103/PhysRevLett.37.1504
[22] G. A. Baraff, E. O. Kane and M. Schlüter, “Theory of the
Silicon Vacancy: an Anderson Negative-U System,”
Physical Review B, Vol. 21, No. 12, 1980, pp. 5662- 5686.
doi:10.1103/PhysRevB.21.5662
[23] N. T. Bagraev and V. A. Mashkov, “Tunneling Nega-
tive-U Centers and Photo-Induced Reactions in Solids,”
Solid State Communications, Vol. 51, No 7, 1984, pp.
515-521. doi:10.1016/0038-1098(84)91024-X
[24] N. T. Bagraev, V. A. Mashkov, “A Mechanism for
Two-Electron Capture at Deep Level Defects in Semi-
conductors, Solid State Communications,” Solid State
Communications, Vol. 65, No. 12, 1988, pp. 1111-1117.
doi:10.1016/0038-1098(88)90904-0
[25] N. T. Bagraev, N. G. Galkin, W. Gehlhoff, L. E. Klyach-
kin and A. M. Malyarenko, “Phase and Amplitude Re-
sponse of the ‘0.7 Feature’ Caused by Holes in Silicon
One-Dimensional Wires and Rings,” J. Phys.:Condens.
Matter, Vol. 20, 2008, pp. 164202-1-12.
doi:10.1088/0953-8984/20/16/164202
[26] E. Šimánek, “Superconductivity at Disordered Inter-
faces,” Solid State Communications, Vol. 32, No 9, 1979,
pp. 731-734.
[27] C. S. Ting, D. N. Talwar, K. L. Ngai, “Possible Mecha-
nism of Superconductivity in Metal-Semiconductor
Eutectic Alloys,” Physical Review Letters, Vol. 45, No
14, 1980, pp. 1213-1216.
doi:10.1103/PhysRevLett.45.1213
[28] A. Alexandrov, J. Ranninger, “Bipolaronic supercond-
uctivity,” Phys. Rev. B 24 , No. 3, 1981, pp. 1164-1169.
doi:10.1103/PhysRevB.24.1164
[29] B. K. Chakraverty, “Bipolarons and Superconductivity,”
Journal de Physique, Vol. 42, No. 9, 1981, pp. 1351-
1356.
[30] A. S. Alexandrov and N. F. Mott, “Bipolarons,” Rep.
Prog. Phys., Vol. 57, No. 12, 1994, pp. 1197-1288.
doi:10.1088/0034-4885/57/12/001
[31] A. F. Andreev, “The Thermal Conductivity of the Inter-
mediate State in Superconductors,” Soviet Physics-JETP,
Vol. 19, No. 6, 1964, pp. 1228-1232.
[32] T. M. Klapwijk, “Proximity Effect from an Andreev Per-
spective,” Journal of Superconductivity: Incorporating
Novel Magnetism, Vol. 17, No. 5, 2004, pp. 593- 611.
[33] J. A. van Dam, Y. V. Nazarov, E. P.A. M. Bakkers, S. De
Franceschi and P. Kouwenhoven, “Supercurrent Reversal
in Quantum Dots,” Nature, Vol. 442, No. 7103, 2006, pp.
667-670. doi:10.1038/nature05018
[34] P. Jarillo-Herrero, J. A. van Dam and L. P. Kouwenhoven,
“Quantum Supercurrent Transistors in Carbon Nano-
tubes,” Nature, Vol. 439, 2006, pp. 953-956.
doi:10.1038/nature04550
[35] X. Jie, A. Vidan, M. Tinkham, R. M. Westervelt and Ch.
Lieber, “Ge/Si Nanowire Mesoscopic Josephson
Junctions,” Nature Nanotechnology, Vol. 1, No. 3, De-
cember 2006, pp. 208-213.
[36] O. Trovarelli, M. Weiden, R. Müller-Reisener, M.
Gómez-Berisso, P. Gegenwart, M. Deppe, C. Geibel, J. G.
Sereni and F. Steglich, “Evolution of Magnetism and Su-
perconductivity In CeCu2(Si1-xGe x)2, ” Physical Review B,
Vol. 56, No. 2, 1997, pp. 678-685.
doi:10.1103/PhysRevB.56.678
[37] A. K. Geim, K. S. Novoselov, “The rise of Graphene,”
Nature Materials, Vol. 6, No. 3, 2007, pp. 183-191.
doi:10.1038/nmat1849
[38] N. R. Werthamer, E. Helfand, P. C. Hohenberg, “Tem-
perature and Purity Dependence of the Superconducting
Critical Field, Hc2. III. Electron Spin and Spin-Orbit Ef-
fects,” Physical Review, Vol. 147, No. 1, 1966, pp.
295-302. doi:10.1103/PhysRev.147.295
[39] D. Y. Vodolazov, D. S. Golubović, F. M. Peeters and V.
V. Moshchalkov, “Enhancement and Decrease of Critical
Current Due to Suppression of Superconductivity by a
Magnetic Field,” Physical Review B, Vol. 76, No. 13,
2007, pp. 134505-1-7. doi:10.1103/PhysRevB.76.134505
[40] C. C. de Souza Silva, J. van de Vondel, M. Morelle and V.
V. Moshchalkov, “Controlled Multiple Reversals of a
Ratchet Effect,” Nature, Vol. 440, No. 7084, 2006, pp.
651-654. doi:10.1038/nature04595
[41] N. T. Bagraev, N. G. Galkin, W. Gehlhoff, L. E. Klyach-
kin, A. M. Malyarenko and I.A. Shelykh, “Spin Interfer-
ence in Silicon One-Dimensional Rings,” Physica E, Vol.
40, 2008, pp. 1338-1340.
doi:10.1016/j.physe.2007.08.079
[42] N. T. Bagraev, L. E. Klyachkin, A. M. Malyarenko and
W. Gehlhoff, “High Temperature Single-Hole Silicon
Transistors,” Superlattices and Microstructures, Vol. 23,
No. 6, 1998, pp. 1333-1338.
doi:10.1006/spmi.1996.0360

N. T. BAGRAEV ET AL.
273
[43] H. Suderow, E. Bascones, A. Izquierdo, F. Guinea and S.
Vieira, “Proximity Effect and Strong-Coupling Super-
conductivity in Nanostructures Built with an STM,”
Physical Review B, Vol. 65, No. 10, 2002, pp. 100519R-
1-4.
[44] Ø. Fischer, M. Kugler, I. Maggio-Aprile, Ch. Berthod and
Ch. Renner, “Scanning Tunneling Spectroscopy of
High-Temperature Superconductors,” Reviews of Modern
Physics, Vol. 79, No. 1, 2007, pp. 353-419.
doi:10.1103/RevModPhys.79.353
[45] R. Laiho, M. M. Afanasjev, M. P. Vlasenko and L. S.
Vlasenko, “Electron Exchange Interaction in S = 1 De-
fects Observed by Level Crossing Spin Dependent Mi-
crowave Photoconductivity in Irradiated Silicon,” Physi-
cal Review Letters, Vol. 80, No. 7, 1998, pp. 1489-1492.
doi:10.1103/PhysRevLett.80.1489
[46] N. T. Bagraev, A. D. Bouravleuv, W. Gehlhoff, L. E.
Klyachkin, A. M. Malyarenko and V. V. Romanov,
“Electron- Dipole Resonance of Impurity Centres Em-
bedded in Silicon Microcavities,” Physica B, Vol.
340-342, 2003, pp. 1078- 1081.
doi:10.1016/j.physb.2003.09.184
[47] N. T. Bagraev, A. D. Bouravleuv, W. Gehlhoff, L. E.
Klyachkin, A. M. Malyarenko and V. V. Romanov, “Er-
bium- Related Centres Embedded in Silicon Microcavi-
ties,” Physica B, Vol. 340-342, 2003, pp. 1074-1077.
doi:10.1016/j.physb.2003.09.239
[48] V. L. Ginzburg, “On Surface Superconductivity,” Physi-
cal Letters, Vol. 13, No. 2, 1964, pp. 101-104.
[49] A. I. Larkin and Y. N. Ovchinnikov, “Nonuniform State
of Superc onductors,” Soviet Physics-JETP, Vol. 20, No. 3,
1965, pp. 762-770.
[50] P. Fulde and R. A. Ferrell, “Superconductivity in a Strong
Spin-Exchange Field,” Physical Review, Vol. 135, No.
3A, 1964, pp. A550-A563.
doi:10.1103/PhysRev.135.A550
[51] W. A. Little, “Higher Temperatures: Theoretical Mod-
els,” Physica, Vol. 55, 1971, pp. 50-54.
doi:10.1016/0031-8914(71)90240-0
[52] S. M. Cronenwett, H. J. Lynch, D. Goldhaber-Gordon, L.
P. Kouwenhoven, C. M. Marcus, K. Hirose, N. S. Win-
green and V. Umansky, “Low-Temperature Fate of the
0.7 Structure in a Point Contact: A Kondo-Like Corre-
lated State in an Open System,” Physical Review Letters,
Vol. 88, No. 22, 2002, pp. 226805-1-4.
doi:10.1103/PhysRevLett.88.226805
[53] J. P. Eisenstein, T. J. Gramila, L. N. Pfeiffer and K. W.
West, “Probing a Two-Dimensional Fermi Surface by
Tunneling,” Physical Review B, Vol. 44, No. 12, 1991, pp.
6511-6514. doi:10.1103/PhysRevB.44.6511
[54] N. T. Bagraev, W. Gehlhoff, L. E. Klyachkin, A. A.
Kudryavtsev, A. M. Malyarenko, G. A. Oganesyan, D. S.
Poloskin and V. V. Romanov, “Spin-Dependent Trans-
port of Holes in Silicon Quantum Wells Confined by Su-
perconductor Barriers,” Physica C, Vol. 468, No. 7-10,
2008, pp. 840-843.doi:10.1016/j.physc.2007.11.060