Journal of Modern Physics, 2011, 2, 200-209
doi:10.4236/jmp.2011.24028 Published Online April 2011 (http://www.SciRP.org/journal/jmp)
Designing and Modeling of Efficient Resonant Photo
Acoustic Sensors for Spectroscopic Applications
Fahem Yehya, Anil K. Chaudhary
Advanced Centre of Research in High Energy Materials,
University of Hyderabad, India
Received October 2, 2010; revised November 22, 2010; accepted November 25, 2010
Abstract
We report the modeling and designing aspects of different types of photo-acoustic (PA) cell based on the
excitation of longitudinal, radial and azimuthal mode using CW and pulse lasers. The results are obtained by
employing fluid dynamics equations along with Bessel’s function. The obtained results based on stimulation
of longitudinal, radial and azimuthally resonance modes of the Photo acoustic signals in the suitable cavity.
This is utilized to design highly efficient low volume PA detector for the spectroscopic studies of different
types of atmospheric pollutants. We have also studied the dependence of the excited photo acoustic signals
on various parameters such as cell radius, laser power, absorption coefficient, quality factor ‘Q’ along with
the first longitudinal, radial, azimuthal mode and the pressure. The simulated results show the linearity of the
PA signal with different concentration of the gas sample.
Keywords: Photo Acoustic, Resonance, Cavity, Spectroscopy, Modes
1. Introduction
The photo acoustic effect was first reported by A. Bell
(1880), he found th at thin disc emit sound when exposed
to a rapidly interrupted beam of sunlight [1], in the fol-
lowing years several renowned scientists studied this
new phenomena in detail Tyndall [2], Rontgen [3].
But the first application of the effect of trace g as mon-
itoring were reported in the late 1960s because of the two
important steps leading to this techniqu e were the inven-
tion of the laser as an intense light source and the devel-
opment of the highly sensitive sound detector such as
microphone and lock-in-amplifier for amplification. Kerr
and Atwood were the first to apply the laser in photo
acoustic signal (PAS) where they used CW (CO2) laser
and they achieved the minimum detectable absorption
coefficient αmin the order of 10-7cm-1 for CO2 buffered in
N2, Kreuzer (1971) who reported on the sensitive detec-
tion of (CH4) in N2with lowest detection order of 10-8
(ppb) using He Ne laser operating at 3.39 nm [4].
Typically non resonant photo acoustic cell of cylin-
drical shape has been investigated by Sigrist et al. [5].
Resonant cell based on excitation of radial, azimuthal
and longitudinal modes by different types of lasers are
reported by different groups [6-10]. A special feature of
PAS is the fact that the ultimate detection sensitivity de-
pends on several factors such as the amount of energy
stored in the absorption sample in the form of heat, size
of absorbing sample, cell constant, in put laser power and
the sensitivity of the microphone [11].
In the PA effect the molecular absorption of photons
result in the excitation of molecular energy level, the
excited state can released its energy either by radiative
process or by non-radiative process (collisional relaxa-
tion). As the radiative lifetime of vibrational level are
long compared to the time required for collisional deac-
tivation and the photon energy is too small to induce
chemical reaction [6]. Thus, the absorbed energy is com-
pletely released as heat in the sample as shown in Figure
1. In fact this process is generated by two distinct meth-
ods [10].
1.1. Modulated Excitation
In modulated excitation scheme, the intensity of the ra-
diation sources periodically modulated in the form of a
square or a sine wave using mechanical chopper. The
range of modulation frequencies usually lies between few
Hz up to several kHz. The resulted pressure fluctuations
generate sound waves in the audible range, which can be

F. YEHYA ET AL.
201
Figure 1. Schematic of generation and detection of photo
acoustic signal
detected by microphones. As data analysis is performed
in the frequency domain with the help of lock-in ampli-
fiers which enables the simultaneous recording of both
amplitude and phase of the sound signal. If the modu-
lated frequency matches with one of the eigen frequency
of the cavity, then the cavity cell works as an amplifier.
1.2. Pulse Excitation
However, In case of pulsed PAS, Nano seconds laser
pulses are employed to excite the cavity mode. Since the
repetition rate is in the range of a few Hz, provid es short
illumination followed by a longer dark period. Data
analysis in this case is performed in the time domain
using boxcar average/integrator systems couples with
oscilloscope.
Transformation of the signal pulse into the frequency
domain generates a wide spectrum range of acoustic fre-
quencies which extended up to the ultrasonic range. Thus,
laser beams modulated in the form of a sine wave excite
only single acoustic frequency, whereas short laser
pulses generate broadband of acoustic signals.
In this work, we have thoroughly studied three differ-
ent sized cavities and simulated the dependence of photo
acoustic signal on several factors such Q-factor, cavity
radius, pressure, absorption coefficients, pulse duration
of laser along with modulation frequency. The work is
divided into three main sections. The first section de-
scribes the typical experimental set up for photo acoustic
measurement along with calculation details of first four
values of resonance frequency of all modes for the three
types of cavities.
The second section deals with the estimation of
Q-factor of all acoustic cavities correspond to first reso-
nance mode. This help to understand the dependence of
photo acoustic signal on Q-factor .In addition, depend-
ence of photo acoustic signal on the cavity radius, laser
power and gas concentration are also being studied.
In the last section, we have studied the dependence of
photo acoustic signal on pressure and the absorption co-
efficient along with the first three longitudinal and radial
modes of three acoustic cavities.
2. Theory
The inhomogeneous wave equation of the sound pressure
in the lossless cylindrical resonator is well explained by
different groups [4,12-14].

 
222
2
d, d,
,1
d
d
Prt Hrt
cPrt t
t
   (1)
where c, γ and H are the sound velocity, the adiabatic
coefficient of the gas and the heat density deposited in
the gas by light absorption , respectively.
Because the sound velocity which is proportional to
the gradient of P(r) vanishes at the cell wall, the P(r)
must satisfy the boundary conditions of the vanishing
gradient of p(r) normal to the wall [11].
The solution of Equation (1) is given by:
 
00
,nn
n
PrtCtCtPr



 (2)
where C0(t), Cn(i) are the eigen mode amplitude of cor-
responding sound wave, Cn(t)is given by the Fourier se-
ries as :

0
,
,
e
nimwt
nnm
nm
Ct A (3)
The dimensionless eigen modes distribution of cylin-
drical resonator is the so lution of the homogeneous wave
equation and we can be expressed as:


,imnt
nn
Prt Pre (4)
where Wn is the resonance frequency of the cavity reso-
nator, Pn(r) is:
 



cos
,,,cos sin
nmnq mz
m
PrPrzJ KrKzm



 



(5)
And amplitude as:


0
22
00
i1
i
n
n
n
wfn
Aw
ww w
Q
 




(6)
where fn is the overlap integral which describes the effect
of overlapping between the pressure distribution of the
nth acoustic resonance frequency and the propagating
laser beam divided by the normalized value of the nth
eigen mode as:

F. YEHYA ET AL.
202




2
d
d
n
n
H
rP rv
fPn rv 
 (7) min
min S
CP
 (11)
where Smin is the minimum detectable signal:
min det
mic
S
SS  (12)
2.1. The Photo Acoustic Signal (PAS)
where Sdet is the minimum detectable microphone signal
and Smic is the microphone responsivity.
The photo acoustic signal (s) is given by:
SCP (8) The contribution of noise comes from the microphone,
background noise, preamplifier, gas flow, and environ-
ment …etc. effect on the value of Smin., [17] cell constant
(c) = 175 pa·cm/w, the beam laser power p = 10 mw,
microphone responsivity Smic = 100 mv/pa and the level
of the PA detector Sdet = 100 nv - 1 µv, so from (12) the
minimum absorption b e in the range (5 × 10–7 - 5 × 10–9)
cm–1. We can also estimate the minimum detectable
concentration of the sample by us ing this expression [4]:
where C is the cell constant which can expressed as:
 
1nmic n flQ
CR
wV
 
Pr (9)
where Rmic is the microphone sensitivity (mv/pa), Q is
the quality factor which physically means the accumu-
lated energy in one period divided by the energy lost
over one period, the quality factor can be defined as:
min
min
N
tot
C


 (13)
0
w
Qw (10)
For,

min = 10–8 cm–1, Ntot = 1019 cm-3, σ = 10–8 cm–1
the minimum detectable concentration is Cmin = 10–9 this
means in the ppb range.
w0 and ∆w are the resonance frequency and the half
width of the resonance profile (FWHM).
Therefore the minimum detectable absorption coeffi-
cient αmin is given by: The PAS for longitudinal and radial for different value
of n and α can be written as [16,17]:










2
00
1e
21longitudnal mode14A
π
1
,12π
11eradial mode14B
xl
n
x
jM jjnj
l
n
n
PL
PAS r vvfvV
Jx








 

 

 









3. Results and Discussion
It is divided into three parts, the first part deals with the
experimental layout whereas second part deals with ef-
fect of quality factor on PAS and third parts comprises
the effect of pressure on PAS.
3.1. Typical Photo Acoustic Set Up for PA
Measurement
Figure 2 shows the typical experiment set up for re-
cording the PAS exited by lasers. Where we are using a
chopper for modulating the incident laser beam if CW
laser is employed in place of pulsed laser, the different
types of acoustic filter which can used to reduce the ex-
ternal noise, the resonance cavity which is made of
stainless steel and its first resonance frequencies in the
range of the chopper values, a microphone coupled with
lock-in-amplifier for CW laser or with boxcar average
and oscilloscope in the case of pulsed laser.
3.2. Resonance Frequencies
When the laser beam directed along the lossless cylin-
drical resonator axis, the eigen frequencies fmnq of the
Figure 2. The typical set up for PA measurement.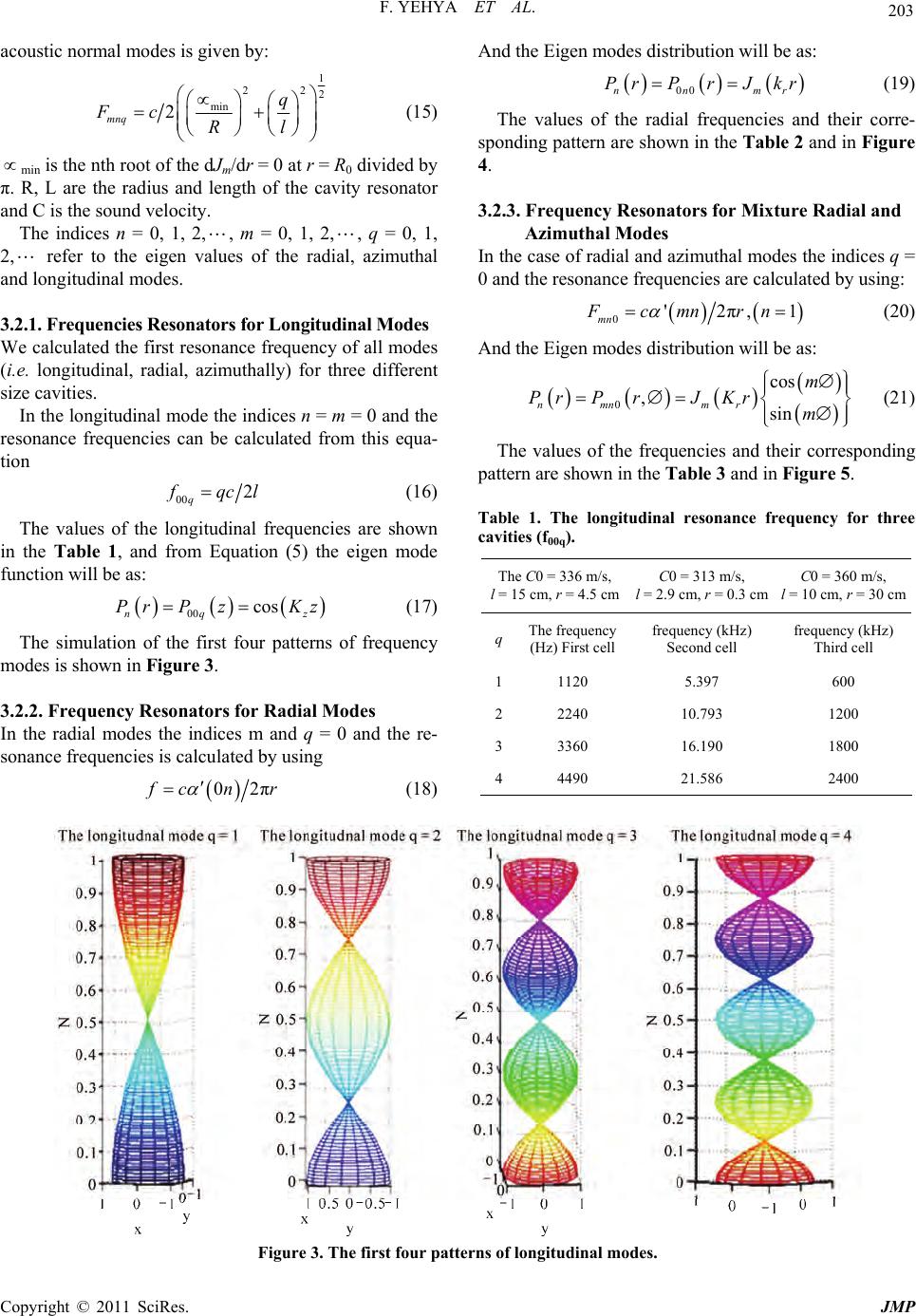

F. YEHYA ET AL.
203
acoustic normal modes is given by:
1
222
min
2
mnq q
Fc Rl


 


 

 



(15)
min is the nth root of the dJm/dr = 0 at r = R0 divided by
π. R, L are the radius and length of the cavity resonator
and C is the sound velocity.
The indices n = 0, 1, 2,, m = 0, 1, 2,, q = 0, 1,
2, refer to the eigen values of the radial, azimuthal
and longitudinal modes.
3.2.1. Frequencies Resonators for Longitudinal Modes
We calculated the first resonance frequency of all modes
(i.e. longitudinal, radial, azimuthally) for three different
size cavities.
In the longitudinal mode the ind ices n = m = 0 and the
resonance frequencies can be calculated from this equa-
tion
00 2 q
f
qc l (16)
The values of the longitudinal frequencies are shown
in the Table 1, and from Equation (5) the eigen mode
function will be as:
 
00 cos nq
PrP zKz
z
(17)
The simulation of the first four patterns of frequency
modes is shown in Figure 3.
3.2.2. Frequency Resonators for Radial Modes
In the radial modes the indices m and q = 0 and the re-
sonance frequencies is calculated by using

02π
f
cn 
 
And the Eigen modes distribution will be as:


00nnm
PrPrJ kr

r
(19)
The values of the radial frequencies and their corre-
sponding pattern are shown in the Tab le 2 and in Figure
4.
3.2.3. Frequen c y Res ona t ors for Mi xt ure Ra di al and
Azimuthal Modes
In the case of radial and azimuthal modes the indices q =
0 and the resonance frequencies are calculated by using:


0'2π,1 mn
Fcmnrn 


 (20)
And the Eigen modes distribution will be as:
 

0
cos
,sin
nmn mr
m
PrPrJKrm


 





(21)
The values of the frequencies and their corresponding
pattern are shown in the Table 3 and in Figure 5.
Table 1. The longitudinal resonance frequency for three
cavities (f00q).
The C0 = 336 m/s,
l = 15 cm, r = 4.5 cmC0 = 313 m/s, l = 2.9 cm, r = 0.3 cm C0 = 360 m/s, l = 10 cm, r = 30 cm
qThe frequency
(Hz) First cellfrequency (kHz) Second cell frequency (kHz) Third cell
11120 5.397 600
22240 10.793 1200
33360 16.190 1800
44490 21.586 2400
r (18)
Figure 3. The first four patterns of longitudinal modes.

F. YEHYA ET AL.
204
Table 2. The radial resonance frequencies for three cells.
The C0 = 336 m/s,
l = 15 cm, r = 4.5 cm C0 = 313 m/s, l = 2.9 cm, r = 0.3 cm C0 = 360 m/s, l = 30 cm, r = 10 cm
n The frequency
(Hz) (First cell) frequency (kHz) (Second cell) freq ue n cy (kHz) (Third cell)
1 4553 68.3 2.05
2 8337 125.1 3.75
3 12090 181.3 5.44
4 15833 237.5 7.125
Figure 4. The first three patterns of radial modes.
Table 3. The resonance frequencies of both radial and azi-
muthal.
The C0 = 336 m/s,
l = 15 cm, r = 4.5 cm C0 = 313 m/s, l = 2.9 cm, r = 0.3 cm C0 = 36 0 m/s, l = 30 cm, r = 10 cm
m The frequency
(Hz) (First cell) frequency (kHz) (Second cell) frequency (kHz) (Third cell)
1 6335 95.02 2.850
2 7969 119.5 3.586
3 9525 142.87 4.286
Figure 5. The radial and azimuthally patterns.
In case of radial and azimuthal modes the excited fre-
quency of the smallest cavity resonator are much higher
than that for other cavities.
3.3. The Effect of the Quality Factor “Q” on the
Profile of Eigen Frequency and PAS
The cavity resonance having cross section in the range of
centimeters usually has high-Q for cavity eigen modes
[12]. In general, the typical quality factor is determined
from the profile of the Eigen mode of the resonance cav-
ity by using Equation (11). But this can also be estimated
by considering different type of losses of the cavity [13,
15].
From equation [6], it is very much clear that the am-
plitude of the resonance frequency can be enhanced by
increasing the Q-factor which can only be achieved by
decreasing the losses of the cavity. P. Hess et al. reported
that the smoothness of the internal surface of cavity plays
very important role to stabilize the profile of the excited
mode along with position of maxima and minima.
Therefore, it can easily be achieved by polishing the in-
ternal surfaces and attaching acoustic filters as an exter-
nal buffers at the end of the cavity along with selection
of high acoustic impedance microphone.
Figures 6(a), (b) and (c) show the effect of the Q-
factor on the photo acoustic signals at first resonance
frequency for three different modes i.e. longitudinal,
azimuthal and radial, respectively for first cell of (R =
4.5 cm., L = 15 cm.). The corresponding frequency is
also mentioned in Table 3 It is very much clear that the
longitudinal modes with high Q provides the highest
photo acoustic signal.
Figures 7(a), (b) and (c) describe the effect of Q-factor
on the photo acoustic signal of the second cell (R = 3.0
mm, L = 2.9 cm.). It is very much clear that the strength
of the PAS related to high Q longitudinal mode shows
superiority over the corresponding PAS of radial and
azimuthal modes.
For the third cell (R = 10.0 cm, L = 30.0 cm.), the
graphs between Q-factor Vs. PAS are shown in Figures
8(a), (b) and (c) respectively. We find that the strength
of photo acoustic signal is much higher than the signal
from other two cavities. But it also to be noted that the
effect of different types of losses are being neglected (the
detailed study is communicated in another paper). These
losses are directly proportional to the cavity size. There-
fore, large sized cavity will always have more losses than
the small sized cavity. In addition, the cell constant in-
versely proportional to the cavity volume which is de-
scribed in Figure 10. This shows th e superiority of small
sized cavity over the large sized cavity.

F. YEHYA ET AL.
205
(a) (b) (c)
Figure 6. Photo acoustic signal at first resonance frequency for all modes for different Q-factor (a), (b), (c) are the first longi-
tudinal, radial and azimuthal resonance frequenc y for a fir st.
(a) (b) (c)
Figure 7. Photo acoustic signal at first resonance frequency for all modes for different Q-factor (a), (b), (c) are the first longi-
tudinal, radial and azimuthal resonance frequenc y for a se cond cell.
(a) (b) (c)
Figure 8. Photo acoustic signal at first resonance frequency for all modes for different Q-factor (a), (b), (c) are the first longi-
tudinal, radial and azimuthal resonance frequenc y for a third c e ll.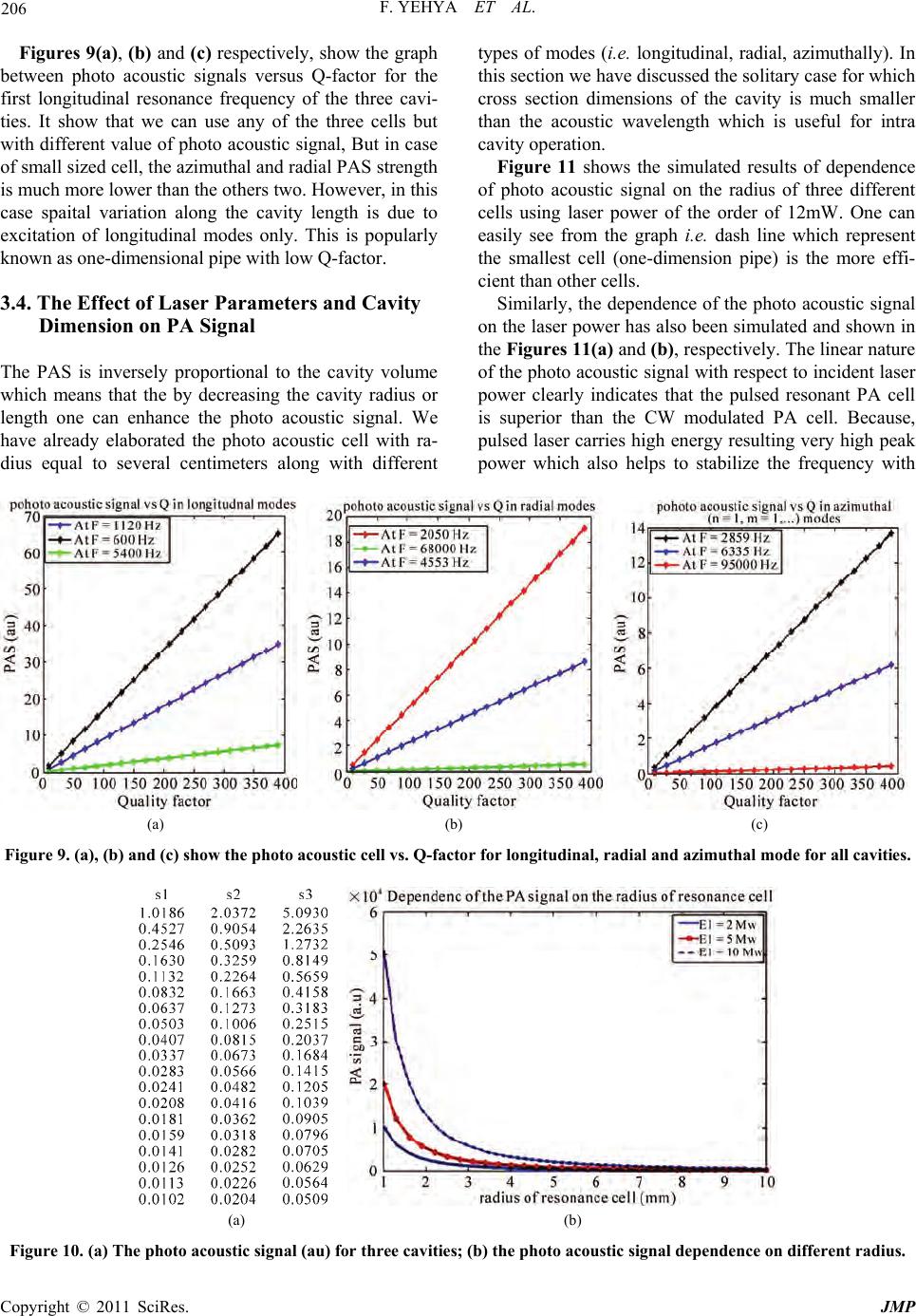

F. YEHYA ET AL.
206
be
.4. The Effect of Laser Parameters and Cavity
he PAS is inversely proportional to the cavity volume
pes of modes (i.e. longitudinal, radial, azimuthally). In
the simulated results of dependence
of
of the photo acoustic signal
on
Figures 9(a), (b) and (c) respectively, show the graph ty
tween photo acoustic signals versus Q-factor for the
first longitudinal resonance frequency of the three cavi-
ties. It show that we can use any of the three cells but
with different value of photo acoustic signal, But in case
of small sized cell, the azimuthal and radial PAS strength
is mu ch mo re lower t han the others two. However, in this
case spaital variation along the cavity length is due to
excitation of longitudinal modes only. This is popularly
known as one-dimensional pipe with low Q-factor.
3Dimension on PA Signal
T
which means that the by decreasing the cavity radius or
length one can enhance the photo acoustic signal. We
have already elaborated the photo acoustic cell with ra-
dius equal to several centimeters along with different
this section we have discussed the solitary case for which
cross section dimensions of the cavity is much smaller
than the acoustic wavelength which is useful for intra
cavity operation.
Figure 11 shows
photo acoustic signal on the radius of three different
cells using laser power of the order of 12mW. One can
easily see from the graph i.e. dash line which represent
the smallest cell (one-dimension pipe) is the more effi-
cient than other cells.
Similarly, the dependence
the laser power has also been simulated and shown in
the Figures 11(a) and (b), respectively. The linear nature
of the photo acoustic signal with respect to incident laser
power clearly indicates that the pulsed resonant PA cell
is superior than the CW modulated PA cell. Because,
pulsed laser carries high energy resulting very high peak
power which also helps to stabilize the frequency with
(a) (b) (c)
Figure 9. (a), (b) ande for all cavities. d (c) show the photo acoustic cell vs. Q-factor for longitudinal, radial and azimuthal mo
(a) (b)
Figure 10. (a) The photo acoustic signal dependence on different radius. stic signal (au) for three cavities; (b) the photo acou

F. YEHYA ET AL.
207
(a)
(b)
(c)
Figure 11. (a) The photo acic signal(au)for three cavi-
odes at a time.
ear in nature and
PA
Average Modulated Laser Power
uaor of the PA
gnal with respect to the incident input laser power
ak
igu hows the linear behavior of the PA signal
ith respect to the incident pulse laser E, The strength of
pendence of Photo Acoustic Signal on the
igu l is increasing
nearly with increase of the gas concentration. However,
rst Three Longitudinal
igu ow the Pressure dependence
f the PAS which is plotted after optimizing the over-
oust
ties and the photo acoustic signal dependence on average
laser power; (b) The photo acoustic signal(au) for three
cavities and the photo acoustic signal dependence on pulse
peak power; (c) The effect of the concentration of gas on the
photo acoustic signal.
excite all the exiting m
negligible effect of “Q” value. Pulsed laser also help to
Figure 11(c) shows the graph between PA signal Vs.
Concentration of the gas which is lin
S strength increases with the concentration of gas.
3.5. Dependence of the PA Signal on the
tion (8) clearly shows the linear behaviEq
si
which is shown in Figure 11(a) for CW laser source.
3.6. Dependence of the PA Signal on Pulsed Pe
Power
re 11(b) sF
w
the PA signal gets enhanced with enhanced input laser
power.
3.7. De
Concentration of a Sample Gas
re 11(c) clearly shows that the signaF
li
for some gases this linearity can be maintained up to
certain limit as a factor of increasing the concentration of
the sample gas which ultimately reduces the signal be-
yond certain concentration due to adsorption of sample
gas on the walls of cell.
3.8. Third Part: The Fi
Modes vs. Pressure
res 12(a), (b) and (c) shF
o
lapped integral factor Ft which also represent the interac-
tion between laser beam and frequency modes .The value
of Ft has been optimized to the unity by considering each
specific location of eigen modes and suitable laser beam
intensity at specific resonance frequency for the given
photo acoustic detector. From Equation (15) it is very
much clear that photo acoustic signal explicitly depends
on the absorption coefficient α which means that the PA
signal depends on the amount of optical power absorbed
by the gas which is linear in nature with change of pres-
sure of buffer gas. Figures 12(a), (b) and (c) show the
photo acoustic dependency on the pressure at first three
longitudinal modes for three different cavities. There are
two distinguish pressure regions, out of which the in the
first pressure region PA signal increases drastically with
ascending value of pressure which is due to the change

208
F. YEHYA ET AL.
(a) (b)
(c) (d)
Figure 12. The simulation of photo a) L = 10 cm, R = 5 cm (b) L =
f concentration and fast relaxation from excitation states.
sure is
no
shows the dependence of PAS on the
ab
. Conclusions
e have successfully simulated the designing aspects of
nance frequencies for longitudinal, radial and azimuth-
coustic signal Vs pressure for the first three longitudinal modes (a
2.9 cm, R = 3 mm (c) L = 15 cm, R = 4.5 cm (d) the dependence of PAS on the absorption coefficient with R = 10 cm, L = 30 cm.
o
While the second pressure region appears just after first
region, where photo acoustic signal almost get saturated
due to dominating effect of collision broadening.
The dependence of PA signal on varying pres
t similar for all resonance frequency because each re-
sonance frequency has its own pressure which is respon-
sible for getting saturation point for each one of them
independently.
Figure 12(d)
sorption coefficient for the first longitudinal and radial
modes for the third cell (R = 10.0 cm, L= 30.0 cm).
4
W
different types of resonant photo acoustic systems/cells
for trace gas monitoring. The calculated values of reso-
ally modes for three different types of cavity resonators
show that the reduced volumes of the resonator enhances
the efficiency of the sensor. In addition, simulation re-
sults also show that at radial and azimuthal modes related
to the smallest cavity resonators are much higher than
that for other cavities. In present work, we have success-
fully demonstrated the feasibility aspects based on the
dimension of the resonant cavity along with their limita-
tions. For small sized cavity to it is difficult to detect
PAS produced by excited radial and azimutal modes. In
addition, the small sized PA cell has the cross section of
the cavity resonator smaller than the acoustic wavelength
as a result the excited field appears as a spaital variation
along the cavity and treated as one dimensional pipe.
Also the variation of pressure a, cavity radius, laser
power and absorption coefficients along with the detec-
tion concentration ha ve been studied.

F. YEHYA ET AL.
209
the DST, SERC Project
OP-13 Govt, of India and DRDO, Ministry of Defe
eferences
On the Production and Reproduction of
American Journal of Science, Vol. 5,
Proceedings of the Royal
ual R
, 1994.
ec-
5. Acknowledgements
Authors gratefully acknowledge
Lnse
Govt, of India for financial support. We also acknowl-
edge the fruitful advice from Prof. S. P. Tewari, ACR-
HEM, University of Hyderabad, Hyderabad (A.P.), In-
dia.
6. R
[1] A. G. Bell, “
Sound by Light,”
No. 118, 1880, pp. 305-324.
[2] J. Tyndall, “Action of an Intermittent Beam of Radiant
Heat upon Gaseous Matter,”
Society, Vol. 31, No. 307, 1881. pp. 307-317.
[3] W. C. Rontgen, “U¨berTo¨ne, Welchedurchintermittier-
ende Bestrahlungeines Gases Entstehen,” Anneview
of Physical Chemistry, Vol. 1, No. 155, 1881.
[4] W. M. Sigrist, “In Air Monitoring by Spectroscopic
Techniques,” John Wiley and Sons, New York
[5] I. G. Calasso, V. Funtov and M. W. Sigrist, “Analysis of
Isotopic CO2 Mixtures by Laser Photo Acoustic Sp
troscopy,” Applied Optics, Vol. 36, 1997, pp. 3212-3216.
doi:10.1364/AO.36.003212
[6] A. Thöny and M. W. Sigrist, “New Developments in
CO2-Laser Photo acoustic Monitoring of Trace Gases,”
rosols,” Applied Physics Letters, Vol. 66
Infrared Physics & Technology, Vol. 36, No. 2, 1995, pp.
585-615.
[7] A. Petzold and R. Niessner, “Photo Acoustic Sensor for
Carbon Ae, No.
10, 1995, pp. 1285-1297. doi:10.1063/1.113271
[8] Z. Bozóki, A. Mohácsi, V. Szabó, Z. Bor, M. Erdélyi, W.
Chen and F. K. Tittel, “Near-Infrared Diode Laser Based
Spectroscopic Detection of Ammonia: A Comparative
Study of Photo acoustic and Direct Optical Absorption
Methods,” Application Spectrosc, Vol. 56, No. 6, 2002,
pp. 715-719.
[9] A. Boschetti, D. Bassi, E. Iacob, S. Ionnatta, L. Ricci and
M. Scotoni, “Resonant Photo Acoustic Simultaneous De-
tection of Methane and Ethylene by Means of a 1.63-μm
Diode Laser,” Applied Physics B, Vol. 74, No. 3, 2002,
pp. 273-278. doi:10.1007/s003400200790
[10] S. Thomas, “Photo Acoustic Spectroscopy for Process
Analysis” Analytical and Bioanalytical Chemistry, Vol.
384, No. 5, 2006, pp. 1071-1086.
[11] S. Tapio, M. Albert, T. Juha, S. Jaakko and H. Rolf,
“Resonant Photo Acoustic Cell for Pulsed Laser Analysis
of Gases at High Temperature” Review scientific Instru-
ments, Vol. 80, No. 12, 2009, p. 123103.
[12] A. Miklos, P. Hess, “Application of Acoustic Resonators
in Photo Acoustic Trace Gas Analysis and Metrology”
Review scientific Instruments, Vol. 72, No. 4, 2001, pp.
1937-1955. doi:10.1063/1.1353198
[13] A. Rosenzwaig, “Photo Acoustic and Photo Acoustic
Spectroscopy,” John Wiley and Sons, New York, 1980.
[14] C. Brand, A. Winkler, P. Hess, A. Miklos, Z. Bozoki and
J. Sneider, “Pulsed-laser Excitation of Acoustic Modes in
Open High-Q Photo Acoustic Resonators for Trace Gas
Monitoring: Results for C2H4,” Applied Optics, Vol. 34,
No. 18, 1995, pp. 3257-3266. doi:10.1364/AO.34.003257
[15] P. M. Morse and K. U. Ingard, “Theoretical Acoustics,”
Princeton University Press, Princeton, New Jersey, 1986.
[16] A. Karbach and P. Hess, “Photo Acoustic Signal in a
Cylindrical Resonator: Theory and Laser Experiments for
CH4 and C2H4,” Journal of chemistry Physics, Vol. 84,
1986, p. 2945. doi:10.1063/1.450809
[17] A. Miklos, P. Hess, A. Mohacsi, J. Sneider, S. Kamm and
S. Schafer, “Photo Acoustic and Photo Theraml Phe-
nomena,” 10th International Conference, edited by I. F.
Scudier and M. Bertolotti, AIP, Woodbury, New Jersey,
1999.