Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2011, 4, 272-281 JBiSE doi:10.4236/jbise.2011.44037 Published Online April 2011 (http://www.SciRP.org/journal/jbise/). Published Online April 2011 in SciRes. http://www.scirp.org/journal/JBiSE Fuzzy splicing in precursor-mRNA sequences: prediction of aberrant splice-junctions in viral DNA context Perambur S. Neelakanta, Sharmistha Chatterjee, Mirjana Pavlovic, Abijit Pandya, Dolores de Groff Department of Computer and Electrical Engineering & Computer Science, Florida Atlantic University, Boca Raton, Florida, USA. Email: neelakan@fau.edu Received 31 January 2011; revised 25 March 2011; accepted 28 March 2011. ABSTRACT RNA splicing normally generates stable splice-junc- tion sequences in viruses that are important in the context of virus mimicry. Potential variability in envelop proteins may occur with point-mutations inducing cryptic splice-junctions, which would re- main unrecognized by T-memory cells of higher organisms in vaccine trials. Such aberrant splice- junctions result from evolution-specific non-conser- vation of actual splice-junction sites due to muta- tions; as such, locations of splice-junctions in a test DNA sequence could only be imprecisely specified. Such impreciseness of splice-junction locations (or cryptic sites) in a sequence is eva luated in this study via “noisy” attributes (with associated stochastics) to the mutated subspace; and, relevant fuzzy con- siderations are invoked with membership attributes expressed in terms of a spatial signal-to-noise ratio (SSNR). That is, SSNR adopted as a membership function expresses the belongingness of a site-region to exon/intron subspaces. An illustrative example with actual (Dengue 1 viral) DNA data is furnished demonstrating the pursuit developed in predicting aberrant splice-junctions at cryptic sites in the test sequence. Keywords: DNA; Exon/Intron; Aberrant/Cryptic Splice-Junction; MRNA Sequence; Fuzzy Subspace; Spatial SNR 1. INTRODUCTION Eukaryotic genomic data encoded via spatial statistical occurrence of the nucleotide set {A, T, C, G} eventually translates into a protein complex through transcription and translation processes. The effort of such correct translation is, however, subject to the effects of muta- tions on the evolutionary conservation. The underlying corruptions may manifest at the so-called splice junc- tions that separate/delineate two subsequences in a DNA sequence, namely, the (genetic) information-bearing codon segment (called an exon) and the non-informative “junk” codon, also known as non-codo n or int ron. (Exons bear necessary information towards protein-making, whereas non-codons are non-informative and their genetic role has not been fully elucidated. Exons and introns appear randomly along the DNA sequence. Codons tend to be typically no more than 200 characters long, while non- codons could be tens of thousands of characters in length. Thus in majority, introns prevail mostly in a typical eu- karyotic gene). Towards the process of protein-making, introns are first scissored out (in the transcription stage) from the sequence and the remaining exons are spliced together constituting the so-called messenger RNA (mRNA), which is rendered ready for translation into a protein complex (at the cell interior). Should any errors have occurred (due to mutations), they would give room to the possi- bility of evolving wrong or cryptic splice-junctions and lead to (imperfect) translations. That is, aberrant splice- junctions may result from mutational spectrum [1] and would hamper the making of correct proteins. Illustrated in Figure 1 is the formation of mRNA via transcription through translation steps. Further, in Figure 1, the locations of splice-junction shown may not so reliably be distinct. In a canonical sense, the splice-junction consensus (Figure 1(a)) may follow certain rules as regard to introns and exons [2]. For example, the introns almost always begin with the residue set {gt} at 5’-end and ends with an {ag} at the 3’-end. But, inasmuch as the nucleotide sequence corre- sponds to a set of statistically permutated elements, {A, T, C, G}, numerous putatively occurring {gt} and {ag} locations (other than in the introns as indicated) may prevail and resemble such canonical patterns. The putatively occurring {gt} and {ag} locations im- ply that relying on such canonical details alone may not reasonably and robustly indicate the presence of true splice-junctions. Further, in the event of point mutations,  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 273 Folded protein 5’ 3’ Intron gt Pyrimidine tract ag Exon Intron IntronIntron ExonExon Exon 5’ Splice site3’ Splice site mRNA (Post-splicing) 5’ 3’ UTR P r otein Precu r so r -mRNA Transcription 3’ Exon Intron Intron IntronExon Exon Exon 3’ UTR Translation DNA 5’ UTR 3’ UTR .. (a/c)ag gt(a/g) a gt……………............(c/t)6 x (c/t) ag g(g/t) (a) (b) 5’ UTR Figure 1. Transcription through translation steps: (a) Typical splice-junction consensus. (b) Illus- tration of splice-junctions delineating exons and introns in the context of transcription through translation phases of central dogma dictating the use of genetic information in the DNA to make the eventual protein complex. (UTR: Untranslated region). stemming of aberrant splice-sites is inevitable [1]. As such, should a junction be recognized and prevailing of possible cryptic junction sites elucidated, it is necessary to analyze statistically, the prevailing long-range genetic information so as to determine the extent to which sub- sequences surrounding the splice-junctions differ from sequence segments of adjoining spurious analogs; hence, true versus aberrant (cryptic) splice junctions can be distinguishably identified. Among feasible techniques developed in ascertaining the delineation of codon/noncodon parts, (that is, in lo- cating the splice-junctions), indicated in [3] is an entropy estimator method that extracts “meaningful signal” from the exon/intron segments of a test DNA; and hence, an entropy technique is applied to detect the underlying splice-junctions between the segments. This is, an in- formation-theoretic (or entropy-based) tool envisaged in a classical setting. It demarcates introns/ exon boundary with a fair efficacy of performance. With the advent of newly sequenced genomes, recog- nition of genes has, however become a challenge and detecting relevant splice-junctions with a system (that does not require prior training) implies inherent difficul- ties in this endeavor warranting more novel approaches; for example, the so-called entropic segmentation method of [4], has shown promising results in using an algorithm based on the so-called Jensen-Shannon (JS) contrast measure to distinguish coding versus non-coding regions in a DNA sequence. This JS-measure is based on condi- tional entropy aspects of statistical divergence (SD) specified in terms of the well-known Kullback-Liebler measure [5]. The main driver behind the success of this method is due to distinguishable statistical characteris- tics of exon and intron segments. That is, a non-uniform codon usage prevails in the exon part meaning that, spe- cific to coding regions not all bases of {A, T, C, G} oc- cur with the same probability; but, there are subtle dif- ferences between the statistics of their appearance exist depending on the position of each base in the codon triplets. In contrast, in non-informative intron segments, the occurrence probabilities of A, T, C and G are the same (equal to 1/4). Developed in [6] is another strategy that identifies the splice-junctions between codon and non-codon regions present in a massive stretch of a DNA chain, especially when the delineating boundary in question is submerged  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 274 in a subspace where codon and non-codon parts exist as overlapping and ambiguous/fuzzy entities. A fuzzy in- ference engine (FIE) developed thereof uses again in- formation-theoretic based metrics (with relevant algo- rithms applied to symbolic as well as binary sequence data representing the DNA) so as to score differentiating extents of codon/non-codon populations at a given site in the DNA sequence. The information-theoretic metrics adopted in [6] refer to various statistical divergence (such as KL and JS measures) as well as distance and discriminant concepts. Further, the algorithms indicated in [6] yield consistent results on the delineation bound- ary sought on test subspaces that are fuzzy; and simu- lated studies using human as well as bacteria codon- statistics confirm the efficacy of the approach pursued. Another approach due to Neelakanta et al. [7] uses the concept of information redundancy in complex systems and defines a complexity metric that is adopted to dif- ferentiate codon/non-codon segments and specify there- of, the intermediate splice-junction. Notwithstanding the existence of pursuits as above in locating splice-junctions, the computed statistical diver- gence (SD) is extended in the present study in getting mapped into a novel membership function that specifies the fuzzy subspace of overlapping exon and intron seg- ments. Relevant membership function is defined on the basis of “error’’ feature prevailing in the overlapping (“noisy”) segment with mutational aberrations. The un- derlying heuristics are described below. As indicated before, the evolutionary conservation of splice-junctions could be hampered with inevitable phy- logenetic-specific mutations. If such mutations are (as- sumed) independent, any “noisy” change in the spatial DNA pattern of the sequence (at the splice- junctions) can be marked as a “spatial jitter” with a characteristic parameter called spatial signal-to-noise ratio (SSNR). Splice-junctions with a spatial jitter as above corres- pond to fuzzy offsets of exons and introns at their junc- tions. That is, the spatially-jittered junction corres ponds to an overlapping mix of codon and non-codon entities and hence constitutes a (fuzzy) universe. In other words, the splice-junction information has a fuzzy structure that can only be identified/specified in norms of linguistic descriptions. Such descriptions can be characterized by a membership (function) [5,8] of belongingness to the attributes of exon or introns. The thematics of the present study refers to develop- ing an appropriate FIE that delineates fuzzy overlaps of codon/non-codon parts so as to elucidate the underlying cryptic (or aberrant) splice-junctions. This is done on the basis of SSNR defined with reference to the spatial-jitter. The SSNR is also adopted to represent the relevant membership function. Remainder of the paper describes the underlying considerations. 2. SPATIAL JITTER ACROSS SPLICE JUNCTIONS Consider a small window(-length) accommodating a fi- nite-number (say, 100) of putatively occurring base re- sidues along a DNA sequence. Suppose this window traverses a splice-junction. With no a priori information available on the accurate disposition of the splice- junc- tion, it can be initially assumed that the reading gathered thereof is a “blurred” information implying an overlap of exon/intron region with a fuzzy codon /non-codon transi- tion. That is, a spreading function is assumed to prevail across the finite window-length. The resulting spa- tially-varying 1-D signal so gathered from the scan of the entire DNA sequence would resemble a set of ran- dom telegraphic waveform train constituted by changing statistical profiles of exons and introns (being scanned). The task in hand is then to detect the spatial transition sites, each delineating adjoining exon/intron (or intron/ exon) segments despite of the noisy, blurred spatial in- formation of the transition site. Suppose (x) represents an uncorrupted DNA se- quence pattern metric computed along the variable x denoting the 1-D space of the sequence length. Relevant signal component will assumed to be corrupted in the event of mutational changes in {A, C, T, G} had oc- curred along the sequence are encountered. Such muta- tion- specific effects can be modeled as a contrbution of “noise”, m(x) on the signal part, (x). Hence, the signal output of the window-reader can be modeled by either a spatial-domain convolution description, namely, s(x) = (x) × m(x) or, equivalently by a corresponding fre- quency-domain description, S(f) = (f)M(f), where S(f), (f) and M(f) are the Fourier transforms of s(x),(x) and m(x) respectively. Consider an intron-exon splice junction illustrated in Figure 2. The upper figure (marked as (a)) is a crisp noise-free (uncorrupted) site with a splice-junction at xo along the DNA sequence constituted by {A, C, T, G} residues. Should mutational corruptions have taken place, this crisp transition-boundary xo becomes (xo x), where x denotes spatial jitter. Further in Figure 2, the y-axis depicts the measure/metric of (relative) statistical divergence of exon versus intron (or vice versa) prevail- ing at any point, x on the sequence. (This statistical di- vergence prevails due to the reason that exon has a dis- tinct distribution of {A, C, T, G} constituents vis-à-vis the corresponding distribution in the intron segment). The effect of (mutation-specific) corruption would make the splice-junction to become unclear or fuzzy, as shown in Figure 2(b). In essence, x is a jitter variable superimposed on s(x) corresponding to crisp disposition  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 275 x o x Exon Intron (a) (b) y Nucleotide sequence y Figure 2. “Spatially-jittered” splice-junction mani- festing as fuzzy exon/intron (or vice versa) tran- sitional residues along the sequence. (a) Unal- tered (crisp) splice-junction; (b) Fuzzy splice- junction with a graded variation of divergence (distance) between the statistical features of exon/ intron (or intro/exon) along the transition region (specified as a measure on the ordinate, (y) The abscissa (x) depicts a scale of residues along the DNA sequence. of the splice junction xo. The expected root-mean- squared (RMS) jitter Jr at any splice-junction xo can be expressed by the “noise power” imposed by the mutation errors. In traditional communication theory, the term sig- nal-to-noise ratio (SNR) is defined to specify the quality of an uncorrupted “signal (power) level” to the corrupt- ing “noise power”. Translating this concept, suppose the average length of intron-plus-exon is X , corresponding “spatial SNR” (SSNR) with reference to the DNA se- quence space (of Figure 2) can be defined as follows: SSNR = 22 r X J. 2.1. Error Probability of Splice-Junction Prediction Relevant to a “noisy” intron/exon (or exon/intron) tran- sitions, the accuracy of locating the transition site, xo is constrained by the probability of error associated with the estimation of xo. In this context, within the specified blurring limits of jitter, the SSNR implicitly would pre- dict the error probability of estimating the splice-junc- tion. Suppose a sequence of exon/intron (or vice versa) transitions (0 i x ,s) prevail at locations indexed by i = 0, 1, 2, , m. From these data, one can extract exon or intron widths (χ) as follows: +11E or I = () iii xx for all values of i = 0, 1, 2,, m, where the suffix (E or I) denotes the measurement done on an exon or an intron respectively. In terms of the average length of consequent intron plus exon X subspaces, the transition (split-junction) locations in the presence of mutation error-induced jitter can be expressed as follows: Noisy = 0 = + i iji j xkXδ X where kj is an integer with ko being zero; and, i = 0, 1, 2, , m; further, is a dimensionless random variable, which in a simple case, has zero-mean Gaussian distri- bution with variance 2 = (1/SSNR). (This variance is invariant along the sequence length if the sequence sta- tistics is assumed to be stationary). Now defining a nor- malized variable, ii X , it can be estimated as: 1 = + iiii kδδ with (i = 0, 1, 2,, m); hence one can specify the probability of correct decoding of the splice-junction, Pc(m) as the probability that κ0.5. ii k Inasmuch as, 1 = + iiii kδδ , the aforesaid probability can be restated as follows: 10 10 1 Prob 0.5, , 0.5 c mm Pm (1) With the assumed Gaussian statistics for , the cumula- tive probability of correct decoding of the splice-junc- tion, namely Pc(m) can be deduced as follows: o 2 11 exp d 22 11 22 2 x cx x Px, x x erf (2) where x with respect to an ith junction is given by ix = 1 ii δδ x ; and, 2 0 2exp d u erf uuu . Fur- ther, the fuzzy-space in question enclaves the universe mdepicting an m-dimensional hypercube across the unit interval, I [0.5, +0.5]. Eq.2 implies that the probability of correct detection (and hence error probability) of the splice-junction disposition is implicitly dependent on SSNR parameter. The plot of Eq.2 is shown in Figure 3 where Pc is plotted as a function of 0 x xx with respect to a presumed, crisp splice-junction at xo posing a transi- tional error-prone width x. This error-prone region depicts a subspace of overlapping exon/intron sub- spaces that smear the exact location of xo. This unspe- cific (error-prone) subspace x is therefore, fuzzy impos- ing an imprecision on xo. Relevantly, the generic descrip- tion of Pc in this fuzzy subspace takes a membership at- tribute of vagueness vis-à-vis the position vari-  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 276 (x o + x)/x o (x o x)/x o 1.0 0.5 0.90 1.0 P c 0.85 1.10 1.15 0 Increasing SSNR Increasing SSNR Location of crisp exon/intron crisp transition (x o ) Exon subspace I ntron subspace Figure 3. Probability (Pc) of correct estimation of a splice- junction versus (xo x)/xo. able, x. The membership here depicts the belongingness to exon subspace or intron subspace. Hence described in the next section are the underlying aspects of the fuzzy subspace in question with the object of ascertaining the splice-junction in the fuzzy subspace. 3. FUZZY SPLICE-JUNCTION PREDICTION Suppose a set of input values xi are taken from the se- quence and considered as non-specific or fuzzy. By de- noting those segment values by {ix}f, corresponding {(Pc)i}f can be written in terms of uncertain limit- ing-values of all the vectors in the bounding (lower and upper) interval, x [xL, xH]. Hence it follows that [5]: ΔΔ ΔΔ f cc L ii ff α-1 j-1 j cL if j = 1 PxPx +ρPxx /j! (3) where f (.) depicts the slope equal to d(Pc)i/dxi and is the number of interval-valued parameter for the range within [xL, xH]. Further, Equation (3) denotes an alge- braic sum of addenda computed via interval arithmetic, which denotes the “width of the results”. In other words, for the specified vector bounding-limits of {(Pc)i}f, namely, x [xL, xH], an -set of interval-valued pa- rameters namely, {Q}, Q = Q1, Q2, …, Q , prevails at or around xo with no fuzzy attributes. Then relevant crisp- domain relation of {x} versus {Pc} can be written by a differential equation given by [5]: d2Pc/dx2 + (dPc/ dx)2 = g(x) where g(.) is some arbitrary function of x. In the event of overlapping fuzzy attributes existing at xo, then the corresponding (fuzzy)-domain relation between {x} versus {Pc} can be generalized by a stochastical discourse of Pc versus x expressed in terms of a fuzzy stochastical differential Equation [5]. Further, in such exon-to-intron transition subspace (denoted as F) having fuzzy attributes, corresponding demarcation of exon/intron transition can be assumed to be at a centroid location (XC) with a line-of-delineation through the centroid. This lo- cation refers to a defuzzified elucidation based on mem- bership-of-belongingness of the site-of-interest in the fuzzy space. The procedure to find XC is described be- low. 3.1. Centroid of the Fuzzy Subspace The SSNR and Pc considerations versus (xo x)/xo indicated before imply inherent statistical attributes of {A, C, T, G} population in the exon and intron regions across the splice-junction. As said earlier, the exon-side statistics encodes for genetic information (so as to make necessary protein) and the intron-side statistics is non-informative. In other words, suppose the probabili- ties of occurrence of the elements {A, C, T, G} in the exon are denoted by the set: {QA, QC, QT, QG} with (QA + QC + QT + QG = 1). Then, the associated errors for the elements of {A, C, T, G) are decided by the inequalities, QA QC QT QG. Now, suppose the corresponding probabilities of occurrence in the intron are: {A, C, T, G} with (A + C + T + G = 1); then, the associated errors for the elements of {A, C, T, G} on intron-side are set by the condition that, A = C = T = G = 0.25. This is because the intron-side being non-informative, Laplacian hypothesis applies in presuming that all (four) elements are equally-likely to occur. Hence, by virtue of the distinction between {Q}A, C, T, G and {} A, C, T, G, rele- vant entropy/information-theoretic (IT) distances (that is, statistical divergence or SD values) can be computed (for the exon and intron regions). The results would show distinction in the profiles of SD (in exon and intron regions) as illustrated in Figure 4. (This SD can be any one on the divergence measure such as KL or JS men- tioned before. Illustrative measures are presented later in the results with reference to a real DNA structure). Following the considerations presented in [9,10], the expression for Pc is 12 122erf x and it can be approximately written as: 0 qq Lz L where q Lz denotes the Bernoulli-Langevin function and the prime sign depicts the differentiation with respect to the argument 2zx . Explicitly, 112coth 112 12coth 12 q Lz qqz qqz where q represents an disorder entity associated with the statistics of the population concerned [11]. Described in 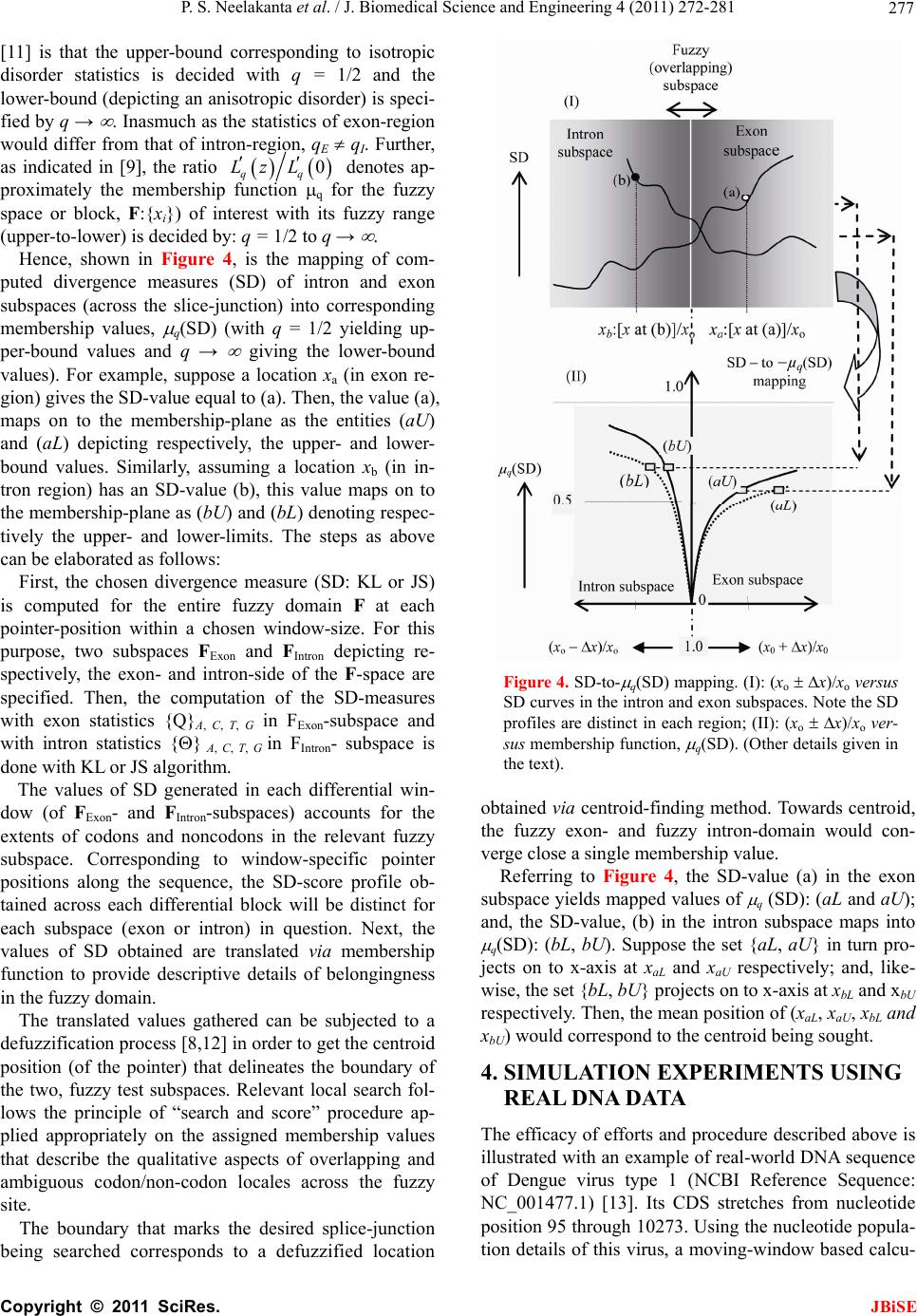 P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 277 [11] is that the upper-bound corresponding to isotropic disorder statistics is decided with q = 1/2 and the lower-bound (depicting an anisotropic disorder) is speci- fied by q → . Inasmuch as the statistics of exon-region would differ from that of intron-region, qE qI. Further, as indicated in [9], the ratio 0 qq Lz L denotes ap- proximately the membership function q for the fuzzy space or block, F:{xi}) of interest with its fuzzy range (upper-to-lower) is decided by: q = 1/2 to q → . Hence, shown in Figure 4, is the mapping of com- puted divergence measures (SD) of intron and exon subspaces (across the slice-junction) into corresponding membership values, q(SD) (with q = 1/2 yielding up- per-bound values and q → giving the lower-bound values). For example, suppose a location xa (in exon re- gion) gives the SD-value equal to (a). Then, the value (a), maps on to the membership-plane as the entities (aU) and (aL) depicting respectively, the upper- and lower- bound values. Similarly, assuming a location xb (in in- tron region) has an SD-value (b), this value maps on to the membership-plane as (bU) and (bL) denoting respec- tively the upper- and lower-limits. The steps as above can be elaborated as follows: First, the chosen divergence measure (SD: KL or JS) is computed for the entire fuzzy domain F at each pointer-position within a chosen window-size. For this purpose, two subspaces FExon and FIntron depicting re- spectively, the exon- and intron-side of the F-space are specified. Then, the computation of the SD-measures with exon statistics {Q}A, C, T, G in FExon-subspace and with intron statistics {} A, C, T, G in FIntron- subspace is done with KL or JS algorithm. The values of SD generated in each differential win- dow (of FExon- and FIntron-subspaces) accounts for the extents of codons and noncodons in the relevant fuzzy subspace. Corresponding to window-specific pointer positions along the sequence, the SD-score profile ob- tained across each differential block will be distinct for each subspace (exon or intron) in question. Next, the values of SD obtained are translated via membership function to provide descriptive details of belongingness in the fuzzy domain. The translated values gathered can be subjected to a defuzzification process [8,12] in order to get the centroid position (of the pointer) that delineates the boundary of the two, fuzzy test subspaces. Relevant local search fol- lows the principle of “search and score” procedure ap- plied appropriately on the assigned membership values that describe the qualitative aspects of overlapping and ambiguous codon/non-codon locales across the fuzzy site. The boundary that marks the desired splice-junction being searched corresponds to a defuzzified location Figure 4. SD-to- q(SD) mapping. (I): (xo x)/xo versus SD curves in the intron and exon subspaces. Note the SD profiles are distinct in each region; (II): (xo x)/xo ver- sus membership function, q(SD). (Other details given in the text). obtained via centroid-finding method. Towards centroid, the fuzzy exon- and fuzzy intron-domain would con- verge close a single membership value. Referring to Figure 4, the SD-value (a) in the exon subspace yields mapped values of q (SD): (aL and aU); and, the SD-value, (b) in the intron subspace maps into q(SD): (bL, bU). Suppose the set {aL, aU } in turn pro- jects on to x-axis at xaL and xaU respectively; and, like- wise, the set {bL, bU} projects on to x-axis at xbL and xbU respectively. Then, the mean position of (xaL, xaU, xbL and xbU) would correspond to the centroid being sought. 4. SIMULATION EXPERIMENTS USING REAL DNA DATA The efficacy of efforts and procedure described above is illustrated with an example of real-world DNA sequence of Dengue virus type 1 (NCBI Reference Sequence: NC_001477.1) [13]. Its CDS stretches from nucleotide position 95 through 10273. Using the nucleotide popula- tion details of this virus, a moving-window based calcu-  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 278 lation of KL-measure is plotted in Figure 5 across the entire sequence length. The data available in [13] for example, shows a CDS stretch from position 7574 through 10270 with an indi- cation of a transition at 7574. Presented in Figure 6 is an exclusive plot of KL-measure across this selected CDS regime at the transition locale around 7574. While the codon (exon)/non-codon (intron) transition is markedly seen (via KL value change), there is however a subspace of fuzziness, wherein an overlap of exon and intron re- gimes prevails indistinguishably (viewed in terms of simple KL-measure). Therefore, by assigning member- ship attribute, the FIE algorithm (described earlier) can be invoked to decide on the location of the splice-junc- tion in the fuzzy region. Hence, drawn in Figure 7 is the profile of membership values ( q) mapped from the computed KL-measures (of Figure 6) across the transi- tion region of interest. There are two profiles: (A) de- picts q-values with q = 1/2 (meaning the upper-bound on the membership); and, (B) denotes q-values with q = (meaning the lower-bound on the membership). From Figure 7, the location of the splice-junction buried in the fuzzy domain can be ascertained. This lo- cation corresponds to the centroid coordinate (xC). This centroid position is featured by the upper- and lower- bound profiles of the -value. As discussed earlier, xC corresponds to the mean position of xaL, xaU, xbL and xbU; and, for the data presented in Figure 7, the computed results show that this centroid (xC) is at 7401 as against the crisp value indicated in [13] as 7574. (The centroid (7401) is the mean of: [(xbL + xbU)/2 = 7401] and [(xaL + xaU)/2 = 7401]). 5. DISCUSSIONS AND CLOSURE Depicted in Figure 8, are base residues reported around, for example splice-junction site, namely 7574 of [13]. The present method predicts in addition, a cryptic set of 7370 and 7419 in the vicinity of the centroid 7401 de- termined. The selection of this set {7370, 7401} is based on the considerations of [2] suggesting the intron’s 3’-side preferential ending being ag. That is, the values 7370 and 7401 are picked around the centroid deter- mined such that they are in conformance with the abut- ting of ag-residues. Further, in Figures 8(a)-8(b), the intron-subspace ends with residue set {ag} at 7574 and is consistent with the canonical splice-junction consen- sus (as mentioned earlier) of [2]. Notwithstanding this canonical pattern, the mutational influences could have possibly induced aberrant splice-junctions. A scan through the test DNA indicates a cluster of sites between 7500 through 7700 exist at which the residues a and g occur together making it ambiguous on 02000 40006000 8000 10000 N ucleotide p ositions ( DEN1 virus ) 5 3 0 0.2 0.4 KL Figure 5. Nucleotide position versus computed KL-mea- sure of the DNA sequence of Dengue virus type 1 (NCBI Reference Sequence: NC_001477.1) [13]. KL 5 3 Nucleotide positions Fuzzy subspace DEN1 virus 60008000 0.2 0.4 ( a ) (b) Intron subspace Exon subspace Figure 6. Nucleotide position in the limited range of 5000 to 9000 versus computed KL-measure of the DNA sequence of Dengue virus type 1 (NCBI Refe- rence Sequence: NC_001477.1) [13]. the decision that splice-junction (such 7574 of [13]) alone can be the splice-junction of interest. However, following the fuzzy pursuit presented here, it enables pointing out that other cryptic splice-junctions such as 7370 and 7419 could reasonably be alternative splice- junction sites having adjacent ag residues as illustrated, for example in Figures 8(a)-8(b) with 7419 site. The complete list of aberrant splice junctions evalu- ated for the test viral DNA in the present study is pre- sented in Table 1 and illustrated in Figure 9. Table 1 indicates the centroid values determined as well as cryp- tic transition sites predicted on the basis of the details in [2]. It may be noted that the data available in [13] por- trays overlaps of CDS domains that eventually facilitate various protein structures as listed. The purpose of knowing correct and aberrant splice-junctions in the context of viral DNA (such as DEN 1 virus) is pertinent to and implicates vaccine de- signs [14]. In general, a gene is first transcribed into pre-mRNA, which is a copy of genomic DNA containing  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 279 0.8 0.9 1.0 with q = 1/2 (Upper- bound ) ( a ) 0.9 0.9 1.0 6000 6400 6800 7200 7600 800 0 with q = (Lower-bound) ( b ) 5 3 Nucleotide p ositions Exon subspace Exon subspace Fuzzy centroid location of intron/exon transition at: 7401 Intron subspace Intron subspace Fuzzy subspace Figure 7. Membership profiles ( q) across the fuzzy transition region of interest. (a) q-values with q = 1/2 (meaning the upper-bound on the membership) versus nucleotide positions of the test DNA; (b) q-values with q = (meaning the lower-bound on the membership) versus nucleotide positions of the test DNA. (a) g c a c g c g g… …g g a g a g 7574 Exon subspace Intron subspace CDS 5 3 Nucleotide positions … a g 7419 Exon subspace Intron subspace CDS 5 3 Nucleotide positions (b) Figure 8. Details on nucleotides adjacent to the predicted splice-junctions: (a) As per [13]; and (b) as per present method. (In both cases, the intron-subspace ends with a residue pair ag bases consistent with the canonical splice- junction consensus. (See text). Figure 9. Summary of results on the locations of splice junctions. Downward arrows indicate values available in [13] for DEN 1 virus. Upward arrows indicated computed values that include details of cryptic sites in the fuzzy subspace. exon and intron regions. Gene-splicing is an important form of protein diversity and has also regulatory funtions and RNA-splicing is essential so as to regulate precisely the process that occurs after gene transcription and be- fore mRNA translation (in which introns are removed and exons are retained). The sequences between the boundaries of introns (denoting regions of DNA or pre- cursor RNA that are not represented in mature RNA, but  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 280 Table 1. Transition sites indicated in [13] and the predicted sites as per the present method. Bounds of membership value CDS range data from [ ] Description Transition site [ ] Upper-bound (UB)* Lower-bound (LB)* Centroid of UB and LB Cryptic transition sites predicted** 95 394 Capsid protein 394 1, 401 301 352 350 354 394 94 436 Anchored capsid protein 436 301, 701 301, 701 501 515 710 934 Membrane glycoprotein 710 701 701 701 437 934 Membrane glycoprotein precursor 934/935 701, 1101 701, 1101 901 954 935 2419 Envelope protein 2419/2420 1801, 2501 2801 2151 2160 2420 3475 Nonstructural protein 1 3475/3476 3301, 3801 3301, 3801 3551 3553 3476 4129 Nonstructural protein 2a 4129/4130 4001, 4301 4001, 4301 4151 4149, 4170 4130 4519 Nonstructural protein 2b 4519/4520 4301, 4701 4301, 4701 4501 4326, 4356 4452, 4505 4520 6376 Nonstructural protein 3 6376 6201, 6701 6201, 6701 6451 6447, 6462 6377 6757 Nonstructural protein 4a 6757 6701, 7001 6701, 7001 6851 6758 6826 2k protein 6826 6701, 7001 6701, 7001 6850 6833, 6857 6827 7573 Nonstructural protein 4b 7573/74 7201, 7601 7201, 7601 7401 7370, 7419 7574 10270 Nonstructural protein 5 10270 10001, 10401 10001, 10401 10201 10202, 10211 ** The UB and LB values indicated correspond to the sites where minima of q-plot (map) in the fuzzy domain of interest are observed, (for example, see Figure 7). * The predicted site is based on locating a site in the vicinity of the centroid where the introns almost always begin with the residue set {GT} at 5’-end and ends with an {AG} at the 3-end as illustrated in Figure 8. reside between regions) and exons (depicting regions of DNA or precursor RNA represented in mature RNA) are not random. There are several splicing events that are possible eventually resulting in: Exon-skipping, intron- retention, cryptic splice-site usage and alternative 3- and 5’-side splice-sites [1]. Further, in RNA splicing, the so-called splicing-variants may be formed prior to mRNA translation due to differential inclusion or exclu- sion of regions in the pre-mRNA structure. Also, a sys- tematic analysis of splice-junction sequences in eu- karyotic protein coding genes using GenBank databank has revealed a striking similarity among the rare splice- junctions [2] that do not contain ag at the 3’ splice site, or gt at the 5’ splice site. As mentioned before, indistinct splice-junctions would result from deleterious effects of mutations that target the splice-sites causing variability in splicing patterns. Such deleterious effects eventually form a major source of protein diversity leading to a considerable ex- tent of diverse proteomic functions that stem from a relatively small number of genes. Thus, changes in splice-site (alternative splicing) can induce different ef- fects on the encoded proteins, not only in humans but also in viruses. As regard to the viral leader sequences, there may be a splice donor site for generation of subgenomic messages,  P. S. Neelakanta et al. / J. Biomedical Science and Engineering 4 (2011) 272-281 Copyright © 2011 SciRes. JBiSE 281 usually the Env (viral envelope) transcript. In general, the role of RNA splicing is to generate a set of stable splice-junctions across viral sequences so that virus mimicry is enabled as a mechanism for potential vari- ability in envelope proteins, (which are prone to changes due to point-mutation and thus, avoid to be recognized by T-memory cells of higher organisms in vaccine trials). The present study offers a systematic way of elucidating cryptic splice-junction sites in viral DNA structures, the knowledge of which can be profitably used in vaccine design efforts. The study is being extended to a variety of viruses in order to elucidate the underlying cryptic aspects of splice-junctions. Pertinent analytical frame- work and computational aspects are augmented with the details available in [15-17]. REFERENCES [1] Krawczak, M., Reiss, J. and Cooper, D.N. (1992) The mutational spectrum of single base-pair substitutions in mRNA splice junctions of human genes: Causes and con- sequences. Human Genetics, 90, 41-54. [2] Shapiro, M.B. and Senapathy, P. (1987) RNA splice junc- tions of different classes of eukaryotes: Sequence statis- tics and functional implications in gene expression. Nu- cleic Acid Research, 15, 7155-7174. doi:10.1093/nar/15.17.7155 [3] Farach, M., Noordewier, M., Savari, S., Shepp, L., Wyner A. and Ziv, J. (1995) On the entropy of DNA: Algorithms and measurements based on memory and rapid conver- gence. Proceedings of the Sixth Annual ACM-SIAM Sym- posium on Discrete Algorithms (SODA’95), San Fran- cisco, January 1995, 48-57. [4] Bernaola-Galván, P., Grosse, I., Carpena, P., Oliver, J.L., Román-Roldán, R. and Stanley, H.E. (2000) Finding borders between coding and noncoding DNA regions by entropic segmentation method. Physical Review Letters, 85, 1342-1345. doi:10.1103/PhysRevLett.85.1342 [5] Neelakanta, P.S. (1999) Information-theoretic aspects of neural networks. CRC Press, Boca Raton. [6] Arredondo, T.V., Neelakanta, P.S. and Groff, D.D. (2005) Fuzzy attributes of a DNA complex: Development of a fuzzy interference engine for codon-“junk” codon de- lineation. Artificial Intelligence in Medicine, 35, 87-105. doi:10.1016/j.artmed.2005.02.008 [7] Neelakanta, P.S., Arredondo, T.V. and Groff, D.D. (2003) Redundancy attributes of a complex system: Application to bioinformatics. Complex Systems, 14, 215-233. [8] Jang, J.S.R., Sun, C.T. and Mizutani, E. (1997) Neuro- fuzzy and soft computing. Prentice Hall, New Jersey. [9] Neelakanta, P.S., Abusalah, S.T., Groff, D.F.D. and Park, J.C. (1998) Fuzzy nonlinear activity and dynamics of fuzzy uncertainty in the neural complex. Neurocomputing, 20, 123-153. doi:10.1016/S0925-2312(98)00006-X [10] Neelakanta, P.S., Park, J.C. and Degroff, D. (1997) Com- plexity parameter vis-à-vis interaction systems: Applica- tion to neurocybernetics. Cybernetica, XL, 243-253. [11] Neelakanta, P.S. and Groff, D.D. (1994) Neural network modeling: Statistical mechanics and cybernetic perspec- tives. CRC Press, Boca Raton. [12] Neelakanta, P.S. and Deecharoenkul, W. (2000) A com- plex system characterization of modern telecommunica- tion services. Complex Systems, 12, 31-69. [13] GenBank, Dengue virus type 1: Complete genome. NCBS reference Sequence NC_001477.1. Available at: http://www.ncbi.nlm.nih.gov/nuccore/NC_001477 (Ac- cessed on January 28, 2011). [14] Pavlovic, M., Cavallo, M., Kats, A., Kotlarchyk, A., Zhuang, H. and Shoenfels, Y. (2011) From Pauling’s Abzyme concept to the new era of hydrolytic anti-DNA autoantobodies: A link to rational vaccine desin? A re- view. International Journal of Bioinformatics Research and Applications (accepted for publication). [15] Krishnamachari, A., Mandal, V.M. and Karmeshu, B. (2004) Study of binding sites using Renyi parametric en- tropy measure. Journal of Theoretical Biology, 227, 429-436. doi:10.1016/j.jtbi.2003.11.026 [16] Florea, L. (2006) Bioinformatics of alternative splicing and its regulation. Briefing in Bioinformatics, 7, 55-69. doi:10.1093/bib/bbk005 [17] Stephens, R.M. and Schneider, T.D. (1992) Features of spliceosome evolution and function inferred from an analysis of the information at human splice sites. Journal of Molecular Biology, 228, 1124-1136. doi:10.1016/0022-2836(92)90320-J |

