Impact of Depolarization Phenomena on Polarized MIMO Channel Performances

doi:10.4236/ijcns.2008.12016

Paper Menu >>

Journal Menu >>

I. J. Communications, Network and System Sciences, 2008, 2, 105-206

Published Online May 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/).

Impact of Depolarization Phenomena on Polarized MIMO

Channel Performances

Nuttapol PRAYONGPUN, Kosai RAOOF

Laboratoire Grenoble Images Paroles Signal Automatique (GIPSA-LAB), UMR CNRS 5216

961, Rue de la Houille Blanche - BP 46 - 38402 Saint Martin d'Hères, France

E-mail: {nuttapol.prayongpun, kosai.raoof}@gipsa-lab.inpg.fr

Abstract

The performance and capacity of multiple-input multiple-output (MIMO) wireless channels are limited by

the spatial fading correlation between antenna elements. This limitation is due to the use of mono polarized

antennas at receiver and transmitter sides. In this paper, in order to reduce the antenna correlation, the

polarization diversity technique is employed. Although the spatial antenna correlation is attenuated for multi-

polarization configurations, the cross-polar components appear. This paper highlights the impact of

depolarization effect on the MIMO channel capacity for a 4×4 uniform linear antenna array. We assume that

the channel is unknown at the transmitter and perfectly known at the receiver so that equal power is

distributed to each of the transmit antennas. The numerical results illustrate that for low depolarization and

spatial correlation, the capacity of single-polarization configuration behaves better than that of multi-

polarization configuration.

Keywords: Multiple-input Multiple-output (MIMO), Channel Capacity, Spatial Fading Correlation, Multi-

polarized Antenna Arrays, Depolarization Effects.

1. Introduction

For the next-generation of wireless communication

systems, multiple antennas at both transmitter and

receiver could be engaged to achieve higher capacity

and reliability of wireless communication channels,

under rich scattering environments, in comparisons with

traditional single antennas. Due to the potential use of

MIMO systems on a limited bandwidth and transmission

power, the initial researches demonstrate that the

uncorrelated channel capacity can be proportionally

increased according to the number of antennas [4,5].

Unfortunately, in practice, the performances of

MIMO communication channel are affected by spatial

correlation and channel environments [6]. The spatial

correlation depends on the array configuration such as

radiation pattern, antenna spacing and array geometry.

The channel environments are dependent on the

environment characteristics such as number of channel

paths, distribution and properties of scatterers, angle

spread and cross-polarization discrimination [8–10].

Thus, the antenna arrays at transmitter and receiver

should be properly designed to reduce the spatial

correlation effects and to improve the communication

performances [11].

However, it is possible to reduce this effect

traditionally by increasing antenna array spacing, but it

is not often suitable to apply in some wireless

applications where the array size is limitted. Therefore,

to eliminate spatial correlation effects with high

transmission performances, there are essentially two

diversity techniques; pattern and polarization diversity

techniques [12,16]. For pattern diversity technique, the

radiation of antennas should be generated in a manner to

isolate the radiation pattern. For polarization diversity

technique, the antennas are designed to radiate with

orthogonal radiation polarizations to create uncorrelated

channels. In general, there are more than two diversity

techniques employed in MIMO wireless systems.

However, there are also other techniques such as

multimode diversity that exploits the difference of

higher order modes to obtain low correlated channel [14].

Polarization diversity technique can be used with pattern

IMPACT OF DEPOLARIZATION PHENOMENA ON POLARIZED MIMO 125

CHANNEL PERFORMANCES

diversity technique in order to boost channel capacity.

Numerous MIMO channel models have already been

proposed in literature. In this paper we focus on

geometry-based stochastic channel models (GSCM)

[15,16]. This calculates the channel response by taking

into account the characteristics of wave propagation, Tx-

Rx environments, and the scattering mechanisms. All

parameters are statistically set to closely match the

measured channel observation.

In this paper, we define a geometric scattering model

based on a three-dimensional double bouncing model

that takes into account the antenna configuration [17–19].

All antennas are provided as a uniform linear array with

isotropic or dipole antennas at transmitter and receiver

sides. However, all scatterers are uniformly distributed

on scattering areas and take into account the cross-polar

discrimination (XPD). This parameter indicates the ratio

of the co-polarized average power to the cross-polarized

average power. Therefore, scattering matrix is used to

describe the depolarization of incident wave for each

scatterer. Afterward, to simplify the simulated

environment configuration, we assume that the angle of

arrival and that of departure are uniformly distributed.

Figure 1. Geometries of MIMO channel

We present a simulation study of the spatial

correlation and moreover the channel capacity of single-

and dual-polarized antenna arrays applied to 4×4 MIMO

system. All antenna elements are separated by a half

wavelength even in the case of the dual polarization

configuration. In addition, we examine the cross-polar

discrimination effects on MIMO polarized channel

capacity for different antenna configurations.

In Section 2, we provide electromagnetic patterns

regarding different electric dipoles. These patterns are

then used in Section 3 to create a channel model

combining the effect of space separation, polarization

antenna gains and depolarization mechanisms. In

Section 4, we apply the information theory in order to

examine the MIMO channel capacity. Finally, in Section

5, we analyze the numerical results of single- and dual-

polarization configurations.

2. Antennas

In practice, not only the propagation environment has an

important role but the proper implementation of the

antennas plays also another dominant role for

determining the multiple antenna transmission

performances. The receiving signals on one element

antenna can be correlated to that of another element

antenna. Therefore, the systems, which can achieve the

best performances, should properly reconfigure the

transmitting or/and receiving antenna element arrays

with the channel state information derived from the

propagation channels.

Table 1. Patterns for different electric dipoles

(

)

cos cos

−

cos sin

− sin

(

)

sin

cos

− 0

Here we are interested in one array configuration.

Orthogonally oriented antennas can offer orthogonal

polarization, which corresponds to a complete separation

between individual channels, although the antennas are

co-located. Thus, using multiple polarization technique

helps to guarantee an effective antenna deployment

space. However, the receiving energy can be reduced

due to the imbalance of depolarization mechanisms.

Three dipole antennas are concerned in this paper; x-,

y- and z-oriented dipole antennas. Their patterns of

electromagnetic radiations can be simplified by

neglecting path loss and distance phase because the

electromagnetic radiations are homogenously and

identically diffused in the far field case. Their simple

expressions of radiation patterns are given by [1]

(

)()

,,GG G

θφ

φθ θφφ

(1)

where

(

)

and

(

)

are the antenna gains at

elevation and azimuth directions. These gains also

depend on the propagation direction. The radiation

patterns of differently oriented dipoles are shown in

Table 1.

In this paper, the propagation patterns of these

antennas are normalized with the isotropic antenna

which is specified as the reference antenna.

3. Geometric Scattering Modelling

We focus on a useful model called “geometric scattering

model” which is based on the assumption that scatterers

around the transmitter and receiver organize the AOD

and AOA respectively within transmit and receive

scattering areas [15,16,18]. The scatterers are randomly

located with according to a certain probability

distribution. In particular, the scatterers are additionally

used to represent the depolarization and attenuation

mechanism of incident waves. To reduce the

computational time, we consider that only one

126 N. PRAYONGPUN ET AL.

propagation path channel occurs when one of transmit

and one of receive scatterers are randomly linked. Then

the actual channel impulse response is established by a

simplified ray-tracing route.

By using our simulated double bounce geometric

scattering model as seen in Figure 1, we employ a

uniform linear array at both transmitter and receiver. The

height of transmitter and receiver has the same level.

Moreover, transmit and receive scatterers are uniformly

distributed within an angular region characterized by

πφ

+≤∆

in elevation area and 22

πθ

+≤∆

in azimuth area at transmitter and 22

πφ

−≤∆ in

elevation area and 22

πθ

−≤∆ in azimuth area at

receiver.

Subsequently transmit and receive scatterers are

randomly paired as previously mentioned. From one

transmit scatterer to one receive scatterer, there is a

double depolarization mechanism which is replaced by

one scattering matrix. We also assume that the channel

coherence bandwidth is larger than the transmitted

bandwidth of the signal. This channel is usually called

frequency non-selective or flat fading channel.

In the case of far field transmission without line-of-

sight channel, the narrowband (flat fading) transmission

channel between the antenna p at the transmitter and the

antenna m at the receiver can be expressed as [20]

(2)

where Ns is the number of scatterers at the receiver and

the transmitter; Tx

rand Rx

rare the velocity vector of the

transmitter and the receiver; ()i

′

and ()i

are the vectors

of wave number in the direction of the ith transmit

scatterer and the ith receive scatterer where

()() 2

′

;

()

and

()

θφ

are the

gain in the direction of

and

of the pth transmit

antenna in the direction of the ith transmit scatterer.

()

and

()

are the gain in the direction

and

of the mth receive antenna in the direction of

the ith receive scatterer; t is time; ()i

a is the mth element

of the local vector of the receive antenna, so that the

local receive vector can be expressed as

() ()

()

Rx 1

ijk rjk r

−

−⋅ −⋅

⎡⎤

=⎢⎥

⎣⎦

L, ()i

a is the pth

element of the local vector of the transmit antenna,

where a local transmit vector is expressed as

()

Tx 1 i

jk rijk r

−

′′

′′ −⋅

−⋅

⎡⎤

=⎢⎥

⎣⎦

L; ()i

S are the

scattering matrix for the pth transmit scatterer and the

mth receive scatterer and is also defined as

() ()

()

() ()

mp ii

θφθ

φφφ

⎡

⎤

⎢

⎥

⎢

⎥

⎣

⎦

S (3)

The cross polarization discrimination (XPD) is

defined as the average power ratio of the co-polarization

component and the cross-polarization component.

{

}

{

}

{}{}

XPD ESES

θθθ θφ

φφφ φθ

(4)

In some conditions such as the imbalance of

depolarization and the use of different antenna patterns,

PD XPD

≠

. We assume that the sum of the co-

polarized power and the cross-polarized power is

constant. Therefore the scattering matrix can be written

(5)

where ()i

denotes phase offset of ith incident wave

which changes from

direction to

direction and

superposing on mp channel.

4. MIMO Capacity

In this section, we assume that the noise has a Gaussian

distribution. Therefore, the optimal distribution of input

signal is Gaussian for maximizing the mutual

information (MI). The mutual information is given by

[4,5]

()

(

)

†

log detR

−

=+Φ

IHHKI (6)

where

(

)

†

EΦ= xx is the spatial covariance matrix of the

input vector x under the total transmitting power

constraint

(

)

tr P

Φ and Kn is the covariance matrix of

the noise vector n.

()

†

⋅

denotes the conjugate transpose

operator,

(

)

⋅

is the expected value and

(

)

⋅

is the

trace operator.

When the MIMO channel state information (CSI) is

known at the receiver but unknown to the transmitter

and n is complex additive white Gaussian noise (AWGN)

vector with zero mean, the covariance is equal to

KI. When CSI is not available at the

transmitter, the transmitter splits equally the total power

to each transmitting antenna. Then the input covariance

matrix is a diagonal matrix T

tTN

PNΦ= ⋅I.

IMPACT OF DEPOLARIZATION PHENOMENA ON POLARIZED MIMO 127

CHANNEL PERFORMANCES

(a)

(b)

Figure 2. 4×4 MIMO channel capacity of isotropic

antennas: (a) single-polarization system and (b) dual-

polarization system

Therefore, the average MI, E(I), called the ergodic

channel capacity, with equal-power allocation at

transmitter can be written as

()

log detR

noCSI N

CEE N

⎡⎤

⎛⎞

== +

⎢⎥

⎜⎟

⎝⎠

⎣⎦

IHHI (7)

By applying an eigenvalue decomposition, (7) can be

rewritten as

log 1

noCSI i

CE N

⎡⎤

⎛⎞

⎢⎥

⎜⎟

⎝⎠

⎣⎦

∑

(8)

where M = min(NT,NR) that corresponds to the rank of

channel matrix and 2

H is the ith eigenvalue of H.

5. Simulation Results Based on Geometric

Scattering Modelling

5.1. Capacity Versus Angle Spread

The antenna correlation effect is an important indicator

for transmission performance since lower correlation

will tend to produce higher mean channel capacity for

single polarization system as seen in Figure 2. Thus

employing polarization and angular diversity techniques

is an attractive way to improve MIMO systems. The 4×4

MIMO systems employ isotropic antennas for λ/2

antenna spacing as shown in Figure 1. In order to

estimate the channel capacity of different antenna

configuration, the simulated environments must be

identical. Hence the channel capacities are studied in

terms of different antenna configurations. The radiation

patterns of each antenna are normalized by the radiation

pattern of an isotropic antenna.

As mentioned in previous section, the distribution of

angles of departure is assumed to have a uniform

elevation distribution 22

πφ

+≤∆

and a uniform

arrival azimuth distribution 22

πθ

+≤∆ and the

distribution of angles of arrival is assumed to have a

uniform elevation distribution 22

πφ

−≤∆ and a

uniform arrival azimuth distribution 22

πθ

−≤∆

where AS

∆

=∆ = and XPDθ=XPDØ=XPD=0dB with

20 scatterers at both transmitter and receiver and 15 dB

of SNR. The aim of this section is to study the effects of

angle spreads and antenna radiation patterns in terms of

ergodic capacity.

Figure 2 demonstrates 4×4 MIMO channel capacity

of single and dual polarized configuration. For single-

polarization case, only azimuth isotropic antennas are

employed and for dual-polarization case, we put

successively azimuth and elevation isotropic antennas in

order with λ/2 antenna spacing. From Figure 2a, the

MIMO channel capacity increases as the angle spread

increases at transmitter and receiver for the same

polarization antennas. In contrast, the dual polarization

achieves better channel capacity due to the lower

antenna correlation. It founds that the MIMO channel

capacity is significantly dependent on the antenna

correlation. The polarization diversity technique can

diminish the spatial correlation effect and improve the

system performances as shown in Figure 2b.

Figure 3. Difference between dual-polarized and single-

polarized channel capacity of 4×4 MIMO systems in

functions of XPD and AS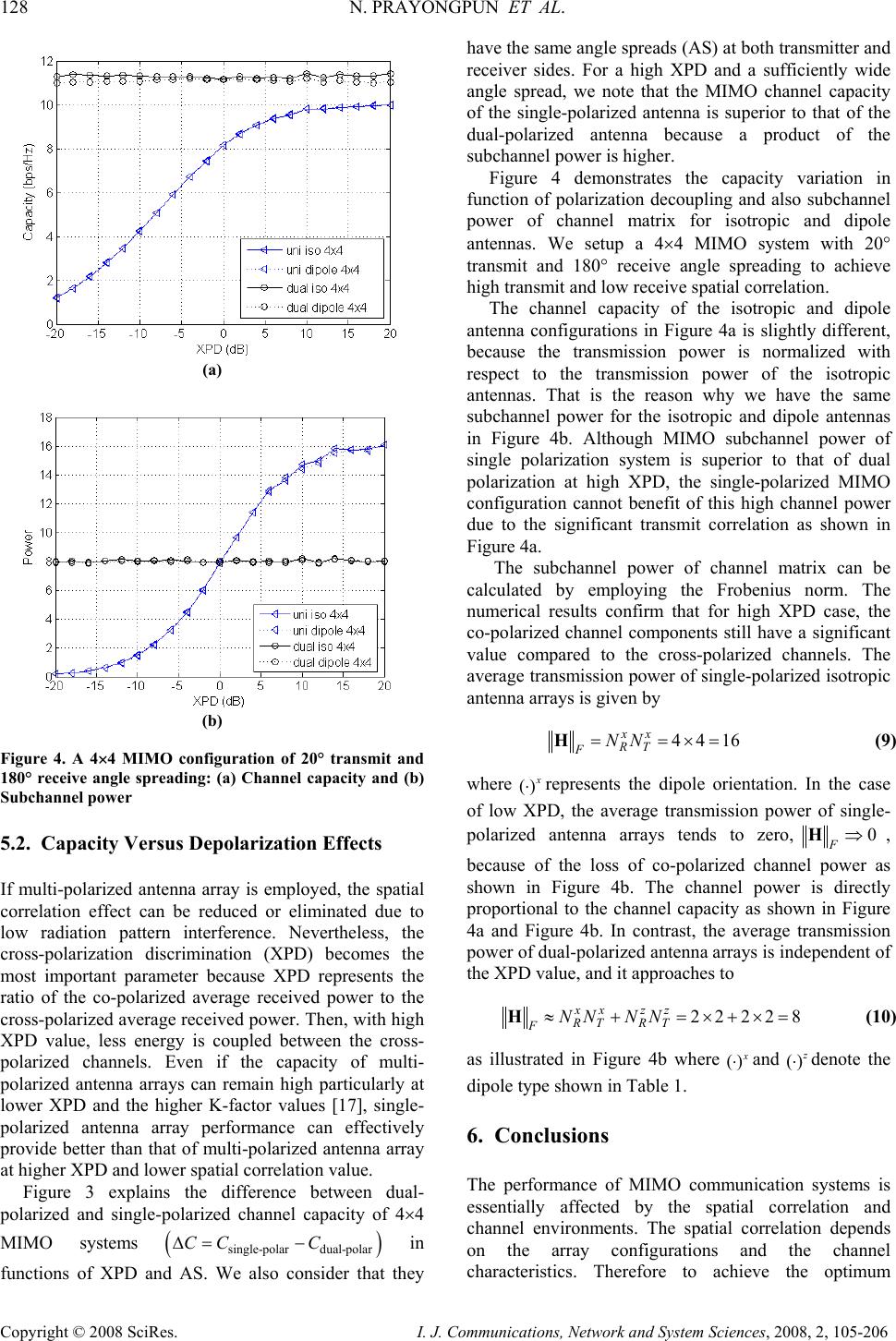

128 N. PRAYONGPUN ET AL.

(a)

(b)

Figure 4. A 4×4 MIMO configuration of 20° transmit and

180° receive angle spreading: (a) Channel capacity and (b)

Subchannel power

5.2. Capacity Versus Depolarization Effects

If multi-polarized antenna array is employed, the spatial

correlation effect can be reduced or eliminated due to

low radiation pattern interference. Nevertheless, the

cross-polarization discrimination (XPD) becomes the

most important parameter because XPD represents the

ratio of the co-polarized average received power to the

cross-polarized average received power. Then, with high

XPD value, less energy is coupled between the cross-

polarized channels. Even if the capacity of multi-

polarized antenna arrays can remain high particularly at

lower XPD and the higher K-factor values [17], single-

polarized antenna array performance can effectively

provide better than that of multi-polarized antenna array

at higher XPD and lower spatial correlation value.

Figure 3 explains the difference between dual-

polarized and single-polarized channel capacity of 4×4

MIMO systems

()

single-polar dual-polar

CC C∆= − in

functions of XPD and AS. We also consider that they

have the same angle spreads (AS) at both transmitter and

receiver sides. For a high XPD and a sufficiently wide

angle spread, we note that the MIMO channel capacity

of the single-polarized antenna is superior to that of the

dual-polarized antenna because a product of the

subchannel power is higher.

Figure 4 demonstrates the capacity variation in

function of polarization decoupling and also subchannel

power of channel matrix for isotropic and dipole

antennas. We setup a 4×4 MIMO system with 20°

transmit and 180° receive angle spreading to achieve

high transmit and low receive spatial correlation.

The channel capacity of the isotropic and dipole

antenna configurations in Figure 4a is slightly different,

because the transmission power is normalized with

respect to the transmission power of the isotropic

antennas. That is the reason why we have the same

subchannel power for the isotropic and dipole antennas

in Figure 4b. Although MIMO subchannel power of

single polarization system is superior to that of dual

polarization at high XPD, the single-polarized MIMO

configuration cannot benefit of this high channel power

due to the significant transmit correlation as shown in

Figure 4a.

The subchannel power of channel matrix can be

calculated by employing the Frobenius norm. The

numerical results confirm that for high XPD case, the

co-polarized channel components still have a significant

value compared to the cross-polarized channels. The

average transmission power of single-polarized isotropic

antenna arrays is given by

4416

FNN

=×=H (9)

where ()

⋅

represents the dipole orientation. In the case

of low XPD, the average transmission power of single-

polarized antenna arrays tends to zero,0

F⇒H,

because of the loss of co-polarized channel power as

shown in Figure 4b. The channel power is directly

proportional to the channel capacity as shown in Figure

4a and Figure 4b. In contrast, the average transmission

power of dual-polarized antenna arrays is independent of

the XPD value, and it approaches to

2222 8

≈

+=×+×=Hxx zz

RT RT

FNN NN (10)

as illustrated in Figure 4b where ()

⋅and ()

⋅denote the

dipole type shown in Table 1.

6. Conclusions

The performance of MIMO communication systems is

essentially affected by the spatial correlation and

channel environments. The spatial correlation depends

on the array configurations and the channel

characteristics. Therefore to achieve the optimum

IMPACT OF DEPOLARIZATION PHENOMENA ON POLARIZED MIMO 129

CHANNEL PERFORMANCES

performances with MIMO systems, the proper selection

of array configuration is required. In this paper, we

studied the MIMO wireless channel capacity of single-

and multi-polarized antenna arrays applied to a uniform

linear array with two isotropic antenna configurations.

The simulation results demonstrate that for the non-

line-of-sight (NLOS) case, the use of multi-polarization

antennas can provide capacity improvement over

conventional single-polarization antennas for narrow

angle spread. However, when the cross-polarization

discrimination is superior than 0dB corresponding to

high co-polarized channel power and low cross-

polarized channel power, the subchannel power of

single-polarization system can be higher by employing

the same polarization as that of the co-polarized channel.

Thus, with high XPD and low spatial correlation values,

single-polarized antenna array performance can

effectively provide better capacity than that of multi-

polarized antenna array. Finally, the cross-polarization

discrimination should be also investigated before

employing the polarization diversity technique.

7. References

[1] C.A. Balanis, “Antenna Theory,” Second Edition, John

Wiley & Sons, New York, 1997.

[2] L.M. Correia, Ed., Wireless Flexible Personalised

Communication (COST 259 Final Report), Wiley, 2001

[3] Mobile Broadband Multimedia Networks (COST 273

Final Report), Elsevier, 2006.

[4] E. Telatar, “Capacity of multi-antenna Gaussian

channels,” European Trans. Telecommun., vol. 10, no. 6,

pp. 585–595, November–December 1999.

[5] G.J. Foschini and M.J. Gans,“On the limits of wireless

communications in a fading environment when using

multiple antennas,” Wireless Personal communication,

vol. 6, pp. 311–335, March 1998.

[6] D.S. Shiu, G.J. Foschini, and M.J. Gans, “Fading

Correlation and Its Effect on the Capacity of

Multielement Antenna Systems,” IEEE Trans.

Comm.,vol. 48, no. 3, pp. 502–513, March 2000.

[7] M. Ali Khalighi, K. Raoof, and G. Jourdain, “Capacity of

Wireless Communication Systems Employing Antenna

Arrays, a Tutorial Study,” Kluwer Academic Publishers,

vol. 23, no. 23, pp. 321–352, 2002.

[8] P.Kyritsi et al., “Effect of antenna polarization on the

capacity of a multiple element system in an in-door

environment,” IEEE J. Sel. Areas Commun., vol. 20, pp.

1227–1239, August 2002.

[9] “Correlation analysis based on MIMO channel

measurements in an indoor environment,” IEEE J. Sel.

Areas Commun., vol. 21, pp. 713–720, June 2003.

[10] J. Lempiainen, J. K. Laiho-Steffens, and A. F. Wacker,

“Experimental results of cross polarization

discrimination and signal correlation values for a

polarization diversity scheme,” in Proceeding VTC, pp.

1498–1502, May 1997.

[11] M.A. Jensen and J.W. Wallace, “A Review of Antennas

and Propagation for MIMO Wireless Communication,”

IEEE Trans. Antennas Propagat., vol.52 no. 11,

November 2004.

[12] M.R. Andrews, P.P. Mitra, and R. deCarvalho, “Tripling

the capacity of wireless communication using

electromagnetic polarization,” Nature, vol. 409, pp. 316–

318, January 2001.

[13] T. Svantesson, M.A. Jensen, and J.W. Wallace,

“Analysis of electromagnetic field polarizations in multi

antenna systems,” IEEE on Wireless Commun., vol. 3,

no.2, pp. 641–646, March 2004.

[14] T. Svantesson., “On the potential of multimode antenna

diversity,” in Proceeding VTC, pp. 2368–2372,

September 2000.

[15] 3GPP–3GPP2 Spatial Channel Model Ad-hoc

Group3GPP TR 25.996, “Spatial Channel Model for

Multiple Input Multiple Output (MIMO) Simulations,”

v6.1.0 (2003–09).

[16] C. Oestges, V. Erceg, and A.J. Paulraj, “Propagation

Modeling of MIMO Multipolarized Fiwed Wireless

Channels,” IEEE Trans. Veh. Technol., vol. 53, no. 3,

May 2004.

[17] N. Prayongpun and K. Raoof, “MIMO Channel

Capacities in Presence of Polarization Diversity with and

without Line-of-Sight Path,” Journal WSEAS Trans. on

Commun., vol. 5, no. 9, pp. 1744–1750, September 2006.

[18] K. Raoof and N. Prayongpun, “Channel Capacity

Performance for MIMO polarized diversity systems,”

IEEE/WCNM2005, pp. 1–4, September 23–26, 2005.

[19] N. Prayongpun and K. Raoof, “Impact of Depolarization

Effects on Polarized MIMO Channel Performances,”

IEEE/WiCOM2007, pp. 1–4, September 21–23, 2007.

[20] K.Raoof, A.Khalighi, and N.Prayongpun, “MIMO

Systems: Principles, advanced polarization and iterative

techniques,” Adaptive Signal Processing inWireless

Communications, Editor: M. Ibnkahla, CRC, pp.95–134,

New York, 2008, ISBN–10: 1420046012.