 Vol.3, No.4, 307-318 (2011) doi:10.4236/ns.2011.34040 C opyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ Nat ural Scie nce A new constitutive theory for extrusion-extensional flow of anisotropic liquid crystalline polymer fluid Shifang Han Chengdu Institute of Computer Application, Academia Sinica, Chengdu, P. R. China; sfh5578@yahoo.com.cn Received 29 January 2011; revised 22 February 2011; accepted 20 March 2011. ABSTRACT A new continuum theory of the constitutive equation of co-rotational derivative type was developed by the author for anisotropic viscoe- lastic fluid-liquid crystalline (LC) polymers (S.F. Han, 2008, 2010). This paper is a continuation of the recent publication [1] to study extru- sion-exten- sional flow of the fluid. A new con- cept of simple anisotropic fluid is introduced. On the basis of anisotropic simple fluid, stress behavior is described by velocity gradient ten- sor F and spin tensor W instead of the velocity gradient tensor D in the classic Leslie-Ericksen continuum theory. A special form of the consti- tutive equation of the co-rotational type is es- tablished for the fluid. Using the special form of the constitutive equation in components a com- putational analytical theory of the extru- sion-extensional flow is developed for the LC polymer liquids-anisotropic viscoelastic fluid. Application of t h e con stitutive theory to th e flow is successful in predicting bifurcation of elon- gational viscosity and contraction of extrudate for LC polymer liquids- anisotropic viscoelastic fluid. The contraction of extrudate of LC poly- mer liquids may be associated with the stored elastic energy conversion into that necessary for bifurcation of elongational viscosity in ex- trusion ex tensional flow of the fluid. Keywords: Constitutive Equation of Co-Rotational Derivative Type; Simple Anisotropic Fluid; Liquid Crystalline Polymer; Extrusion-Extensional Flow; Bifurcation of Elongational Viscosity; Contraction of Extrudate of LC Polymer Liquids 1. INTRODUCTION The liquid crystalline (LC) is a fundamental material in the hi-tech industries. The rheological behavior of LC polymer melt and solutions is considerably different from that of the common Polymers [1-3]. The extrusion of thermotropic LC polymer melts has been shown to be very effective in producing a high degree of macroscopic orientation material, as Keclar (p-phenylence terephtha- lamide). The PE melt extruded with the same slit die shows substantial extrudate swell. However LC polymer shows different contraction of the extrudate and a slight decrease with increasing shear rate, which is consistent with the PE melt results [4-6]. Special behavior of the first and second normal stresses is observed by Baek, Larson, Hudson, Huang by experimental investigation with HPC and PBLG [7-9]. The experimental results show regions of both positive and negative of the first and second normal stress differences, that is the normal stresses 1 and 2 change sign two times with variation of shear rates. The especial behavior of LC polymer is due to the anisotropy of the material. The classic continuum theory for LC material was developed by Ericksen and Leslie [10-15] which de- scribes the main features of flow of nematic liquid crys- tal of low molecular weight or the flow at low shear rates. In research on continuum theory of anisotropic fluids, Green has given attempts to extend basic concept of simple fluid for anisotropic fluid case [16-17]. Ac- cording to Green a simple anisotropic fluid is defined as one for which the stress tensor at a particular particle at time is dependent on the whole history of the deforma- tion gradients F and the whole history of rotation tensor R at the same time. The constitutive equation can be reduced to that which contains only the whole history of the deformation gradients F, with no history of rotation tensor R in it. The convected constitutive equation of Oldroyd type is well used for the isotropic polymer solu- tions or melts in Non-Newtonian fluid mechanics, but rarely for the case of anisotropic LC polymer fluid. The first attempts were given by Volkov and Kulichikhin for LC polymer fluid [18,19]. Using the Maxwell linear equation (1867) for anisotropic liquid crystals and in- troducing a convected Maxwell model with relaxation and viscosity tensor Vokov and Kulichikhin developed a  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ 308 more simple constitutive equation with non-symmetric shear viscosity. As pointed out by the authors that the constitutive equation is available for the case of small recoverable strains in comparison with the total strains [19]. As pointed out by Larson [20], the nematic LC poly- mer shows director tumbling in shear flow. The experi- ments have confirmed the tumbling for nematic polymer solutions, but relatively rare in small-molecular nematics. The research of Vokov and Kulichikhin have also con- firmed that it needs further study the non-symmetry of the shear stress components in shear flow [19] which may lead to director tumbling in it. The anisotropic behaviour of LC polymer liquids can be studied by the continuum theory. Using convected co-rotational time derivative, we developed a new con- cept continuum theory of the constitutive equation for LC polymer [1-3,21-24]. In the constitutive equation theory a new concept of simple anisotropic fluid was introduced. Extending co-rotational Oldroyd fluid B [1,2] the components of the stress tensor ij and its co-rota- tional derivative in it are assumed to be a tensor function of i n,i,ij S N and ij Winstead of velocity gradient tensor D in the classic Leslie-Ericksen continuum theory. Using the tensor analysis approach [10-15] and analyzing the physical nature of the fluid, a general form of constitu- tive equation is constructed for the fluid. The developed theory is successful in predicting special behavior of the first and second normal stress differences which are in agreement with the experiments [7-9]. This paper uses the new concept constitutive equation [1] extrusion-extensional flows of the anisotropic vis- coelastic fluids are studied, which is an important appli- cation of the developed constitutive theory. A new con- cept of extrusion-extensional flow is introduced to de- scribe the flow near the die exit of LC polymer melts in extrusion process. This concept is more general than pure extensional flow, which could not exist near the die exit. Application of the constitutive theory to the extru- sion-extensional flow is successful in predicting bifurca- tion of elongational viscosity and contraction of extru- date for LC polymer liquids–anisotropic viscoelastic fluid. 2. PRINCIPLES OF NEW CONCEPT CONSTITUTIVE THEORY 2.1. New Concept of Anisotropic Simple Fluid To start research on extrusion-extensional flow it is necessary to discuss the main principles of new contin- uum theory of the constitutive equation of co-rotational derivative type for anisotropic viscoelastic fluid [1]. The constitutive equation will be rewritten in an available form for research on the flow. The “Simple fluid” is a fundamental concept which is based on the theory for modern non-Newtonian fluid mechanics; it is generally valid for isotropic fluid. The “principle of objectivity of material properties” introduced by Noll (1958) is well used to construct constitutive equation in non-Newtonian fluid mechanics and rheology. The simple fluid in sense of Noll is a great significance in construction of consti- tutive equation theory for isotropic non-Newtonian flu- ids. But as pointed by out Tanner, it is easy to construct physical systems where this principle does not hold [25]. For example it does not hold for a dilute suspension of spheres when the microscale Reynolds number is not negligible. Zahorski noted [26] that the requirement of invariance with respect to the reference frame in consid- erations involving some fields may prove to be too re- strictive. The principle may also be too restrictive for anisotropic fluids! Therefore, the concept of simple fluid should be improved further for the special case-anisot- ropic viscoelastic fluid. A concept of superposed rigid body rotations was in- troduced by Green [16,17] which leads to the following conclusion that the rotation tensor does not affect stress, apart from orientation, i.e. invariance of the equations with respect to superposed rigid rotations. The conclu- sions of Green are only valid for the nematic liquid crystal of low molecular weight or the flow at low shear rates with any orientation. The nematic liquid crystalline polymer shows director tumbling in shear flow which is confirmed by experiments for nematic polymer solutions [20]. Using the Maxwell linear equation (1867) for ani- sotropic liquid crystals, non-symmetric shear stresses in shear flow were founded by Vokov and Kulichikhin for LC polymer liquids [18,19] which may be a cause of rotation motion in the flow. The new concept of simple anisotropic fluid was defined for the liquid crystalline polymers [1], which is a basic point of investigation. Let the observer is attached to the rotating particle of fluid, i.e. in co-rotational coordinate system. The simple ani- sotropic fluid is understood as one for which the stress behavior is assumed to be a functional of the whole his- tory of the deformation gradients F and the whole his- tory of spin tensor W instead of rotation tensor R in the Green theory.The relationship between the spin tensor stWmeasured with respect to the fixed reference frame and the spin tensor measured with respect to the co-rotational reference frame is given as ctW TT sc ttttWWQ Q t (1) It was easily proved that the spin tensor ctW is also anti-symmetric T0 c c tt WW (2)  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openl y accessible at http://www.scirp.org/journal/NS/ 309 t It was proved T cc ttt WQWQ (3) The new spin tensor measured with respect to the co-rotational reference frame is objective. Instead of rotation tensor in the Green Theory, a spin tensor ctW tR W W in constitutive equation measured with respect to fixed coordinates is expressed by a sum of spin tensor c measured with respect to co-rotational coordinates and co-rotational tensor term as given by (1). The simple anisotropic fluid is defined as one for which the stress tensor at a particular particle is a functional of the whole history of the deformation gradient F and the whole his- tory of spin tensor W measured with respect to the co- rotational coordinates. 0 £,Ts FWs A (4) where W is defined by (3). 2.2. General Constitutive Theory In construction of continuum theory of constitutive equation for the LC polymer-anisotropic viscoelastic fluids, the following principal concepts are introduced [1,3]: 1) A concept of anisotropic simple fluid is introduced. According the new definition the stress is dependent on the whole history of deformation gradient and the whole history of spin tensor measured with respect to co-rota- tional coordinates. 2) The constitutive equation contains both contribu- tions due to the orientational motion of director and hy- drodynamic motions of fluid, to describe anisotropic effects of LC polymer [1,3,21-24]. The stress tensor is considered as a functional of the deformation tensors and tensors composed of the director vector and its deriva- tive. According to the statistic physics, the macroscopic magnitudes are considered as an average of the micro- scopic values. 3) Because the nematic LC polymer solution is also viscoelastic fluid, the constitutive equation of co-rota- tional Oldroyd fluid B is a basic point in constructing the equation theory for anisotropic viscoelastic fluid. Con- stitutive equation for anisotropic viscoelastic fluid can be constructed by generalizing co-rotational Oldroyd fluid B. The Oldroyd fluid B of upper-convected derivative type is well used for isotropic non-Newtonian fluid me- chanics. The Oldroyd fluid B with upper-convected de- rivative is extended to the case of co-rotational time de- rivative developed by S.F. Han [21-24] 000 oo ij ij ij ij SSA (5) where: 0 - isotropic relaxation time ;0 - isotropic limit- ing viscosity;ij - components of the extra-stress ten- sor; ij S - components of the first Rivlin-Ericksen tensor; the top circle “o” denotes the contravariant components of co-rotational time derivative defined as , ij ijm ijikjj ki mk k S SvSS t S (6) For anisotropic fluid, a generalized Maxwell equation is given as [19] d d kl ijklijijkl kl SS t (7) where the relashinship between the viscosity tensor ijkl and the relaxation time tensorijkl is defined by ijklijkl ijkl G (8) Eq.7 describes the linear anisotropic viscoelastic fluid behavior. In the Leslie-Ericksen continuum theory [10- 14], the hydrodynamic components of the stress tensor are assumed to be a tensor function of i,i and ij , the full deformation history is described only by the symmetric part of the velocity gradient , i.e. the rate tensor ij are symmetric. This is a limitation of the Leslie-Ericksen theory. According to new definition of anisotropic simple fluid instead of velocity gradient ten- sor in the classic theory, the stress tensor is de- scribed by 1st Rivlin-Ericksen tensor ij S Dn N D D D and spin tensor for the solutions and the liquids. Extending the gen- eral principle in constructing constitutive equation by Truesdell [27] and Ericksen [11] and generalizing con- stitutive equation of co-rotational Oldroyd fluid B (5) and generalized Maxwell equation, the stress compo- nents and those co-rotational derivative are assumed to be of functional of i,i, ij W n N and ij , a general form of the constitutive equation of the fluid is given as W 0,,,, oo ijijkl ijijijijijiij SSA AnN (9) where ij is tensor functional, the , j are mate- rial constants, ij - components of the first Rivlin- Ericksen tensor, ij - components of spin tensor , W iikk Nn n . For anisotropic viscoelastic fluid-LC polymer melt and solution the stress tensor is un-symmetric. The anisotropy in elasticity of LC polymers leads to an un-symmetry of the stress tensor. The rotation of the director vector is a source of dissipation in the nematic liquid even in the absence of flow [20]. The stress relationship derived from the Ossen integral equation shows that for nematic fluid the orientational motion of the director vector cha- racterized by the director surface body stress and intrin- sic director body force, leads to un-symmetry in stress tensor.  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ 310 2.3. Symmetric and Un-Symmetric Stress The first Rivlin-Ericksen tensor ij expresses de- formation history due to the normal-symmetric part of the deformation velocity gradient in the fluid, the spin tensor ij expresses deformation history due to the un-symmetric part of deformation velocity gradient in the fluid. However the un-symmetry of the stress tensor is determined by the un-symmetry of the shear stress components. It does not have principal influence on the normal stress differences which is of completely sym- metric. The stress tensor can be split into two parts: symmetric and un-symmetric W n ijij ij SSS s (10) where “n” denotes normal-symmetric part, “s” denotes shear un-symmetric part. The tensor functionalij in Eq.9 is split into symmetric and un-symmetric too. For the normal-symmetric part of the stress tensor a general form of the constitutive equation is proposed as 0 12 ,,,, ooo nn ijijkl klijijijijiij oo jk kiik kj SSAAAnN AA oo (11) The special term 12 kki ikkj A of high order in Eq.11 is introduced to describe the special change of the normal stress differences which is considered as a result of director tumbling effect by Larson et al. [20]. For the shear un-symmetric part of the stress tensor the general form of the constitutive equation is proposed as ,, ,, , 1,2,3 o sss ijkl ijkijijiij SS nN ijk (12) In Eqs.11 and 12 the relaxation time tensor compo- nents n ijkl and kl are introduced for normal-symmetric and shear un-symmetric stresses respectively. 2.3.1. Normal Symmetric Part The constitutive Eq.11 can be reduced to the follow- ing form [1] 01 2 123 ooo o n ijijklklijijjk kiik kj ij ksksi kkjjkik SSAA AA nnnnAnn Ann A (13) 2.3.2. Shear Un-Symmetric Part For the shear un-symmetric part, the partial Eq.12 can be reduced to the following form [1,2] 12 34 o sss ijklijkj sisi sjs ijij k sks SSnn nn nnnn (14) where 17 48291031341 , , , . In Eqs.13-1 4 ijkl - anisotropic relaxation times, di- mension of which is [s]; ,12 3 ,, - anisotropic vis- cosities being influence of the orientational motion on the viscosity; 0 - anisotropic retardation time; , , 1 , 23 3 , ,12 , , 4 , - [Pas] , - [Pas2]. 2.4. Constitutive Equation for Axial-Symmetric Case Now axial-symmetric flow is studied. This is two di- mensional problems. The cylindrical coordinate system ,,zr is used. For the 2D problem the velocity field and the director field are given as ,0,, ,0, rz Vuwnnn (15) For the velocity field Eq.15 co-rotational time deriva- tive components of extra stress components are calcu- lated. For velocity field Eq.15 and the normal- symmet- ric part of the stress the constitutive Eq.13 can be re- duced to equations in stress components, where the property of symmetry for the relaxation time tensor ijlm Eq.8 was used. The stress process is assumed to be time-independent. Using the definition of co-rotational derivative, the constitutive equations in components can be reduced. The constitutive Eq.13 in components is finally reduced to the following type: 11 2 012 222 1 23 2 22 2 rrrz rzkrz rz rzrzrrzz rrrr zzzrzrz rrrrzrz SS u AA r nnA nAnnA nnA nA (16) 11 2 012 222 1 23 2 22 2 zzrz rzkrz rz rzrzrrzz zrrr zzzrzrz zrrzzzz SS w AA r nnA nAnnA nnA nA (17) 36 2 0 22 1 22 1 2 4 2 2 rzrz rzrz rzrrzzrz rz rzr rrz zzrzrz rzr rrz zzrzrz SS uw AA zr nnnAnAnnA nnnAnAnnA (18) For the constitutive equation the following eight in- dependent material functions are introduced 13600 212 1 , , , , , , , 2 k Eqs.16-18 are generally available for the axial-sym-  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openl y accessible at http://www.scirp.org/journal/NS/ 311 metric (2D) problem of anisotropic viscoelastic fluid flow. 3. BIFURCATION IN EXTRUSION-EXTENSIONAL FLOW 3.1. Kinematics of Exrusion-Extensional Flow The process of production of high degree of macro- scopic orientation fiber by LC polymer melt, as Keclar (p-phenylence terephthalamide) is an anisotropic-vis- coelastic fluid flow [Figure 1]. The polymer melt mo- tion in extrusion process near the die exit of fiber spin- ning is a viscometric or extrusion-extensional flow, i.e. a shear flow dominating extension, or an extensional flow with an additional shear flow element. The axial-sym- metric case is considered. The cylindrical coordinate system ,,rz is used. For symmetric case the veloc- ity and director vector field are given as ,, ,, 0uurz wwrz v (19) ,,0, 0. (20) rz nnn As a first approximation the velocity field is assumed to be of d d, dd Vz wkz k zz where the u, w are the velocity components in radial and axial directions, V(z) denotes the velocity field which is uniform across the fiber section. According to the equa- tion of continuity the velocity component u can be ob- tained from 11 , 22 uu kz kz rr Thus 1, d 2 ukzrwkz z 0 0 (21) The first Rivlin-Ericksen tensor A and spin tensor W are reduced to 00 00, 00 02 00 rz rz rz rz kA k Ak AW where dd , 2d4d 2 rz rz kz kz rr Azz Neglecting gravity, surface tension and air resistance at the surface of the filament. The boudary condition and Figure 1. Sketch of fiber spinning process of polymer melt. the stress condition at the surface are given as ,, ,, ra a uUaxt wazt tz a , (22) coscos0, coscos0 rr rzrz zz PP PP , (23) where 22 1 cos, cos 11 a z aa zz . (24) 3.2. Bifurcation of Elongational Viscocity The elongational viscosity is specially interested. The elongational viscosity of extrusion-extensional flow of the LC polymer fluid will be studied. For axial-symmetric problem Eq.19 the equation of motion is reduced to rr rrrz SS SS uuu p uw trzrrz r (25)  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ 312 1rz z rS S www p uw trz zrr z (26) For extrusion process of LC polymer melt a condition of no director tumbling can be proposed, 12 0 . The constitutive Eqs.16-18 can be reduced to the fol- lowing form 11 222 00 1 2 23 23 2 31 2 rrrz rzkrz rz rz rrz SS knnkn nk nn n (27) 11 222 00 1 2 23 2 231 2 zzrz rzkrz zz rz zr z SS knnkn nn kn 2n (28) 36 2 001 2 23 2 331 2 2 2 rzrz rzrz rzzrz rrzrzz SS knnnknn nnnk nnkn 2 (29) Solving Eqs.27-29 by the computational symbolic manipulation, such as Maple, general analytical expres- sions are obtained by the constitutive equation for the shear stresses and the normal stress. Three special cases will be interested. Case 1: Director vector is parallel to stretching direc- tion sin0, cos1 The analytical expressions of shear stress and normal stress differences are calculated by Maple. The elongational viscosity is difined as 2 0310123 3 2 1631 3 2 030 103 2 1631 3 312 1 1 22 1 zz rr E kk kk SS k k k (30) Replacing extension rate in axial direction k in Eq.30 by that in radial direction r k , Eq.30 is reduced to 2 0310123 3 2 1631 3 2 030103 2 1631 3 312 1 1 22 1 E kk r kk k (31) It can be seen from Figures 2-6, that all curves of elongational viscocity vs radial extension rate have a same point of intersection with curve 0 3 e . Figure 2. Elongational viscosity vs radial extension rate with variation of shear rate k (no orientation case) 0 3 e — Co-rotational Maxwell model [2,21]. For simplicity it is asummed 6103 , 0 k The Eq.30 is reduced to 2 0101 23 22 1 01 0 3 22 1 32 1 2 1 zz rr E r SS k k (32) Let at point of intersection ic ee , one can obtain from (31) 22 2 001230 2 0103 132 3 22 ic e r k 0 (33) For all curves of elongational viscocity vs extension rate the sufficient and necessary condition of intersection at a same point is that the coordinates of the point are independent on shear rate. Let the constants and the co- effcients of 2 at both sides of Eq.33 are equal each other one can obtain the coordinates of intersection point 0123 3 ic e (34) and 2 01230 000003 3 1 32 2 r k thus  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openl y accessible at http://www.scirp.org/journal/NS/ 313 0000 3 2 000 01 2 30 2 3 r k (35) Case 2: Director is vertical to stretching direction 0cos,1sin . For this case the analytical expres- sions of shear stress and normal stresses diffeence are cal- culated by Maple. The elongational viscosity is given as 2 0310123 3 2 1631 3 2 03010 2 2 1631 3 31 1 1 222 1 zz rr E kk kk SS k k (36) Case 3: The angle between director and stretching di- rection is π4, 2 1 cos, 2 1 sin . The elongational viscosity is given as 2 1631 3 2 0310 1231 233 2 0301 01123 2 1631 3 1 1 31 13 42 22 22 1 zz rr E kk kk SS k k k (37) Case 4: No orientational motion 123 613 0, , 0 The elongational viscosity is given as 2 0310 2 1631 3 2 0301 0 22 1 31 1 2 1 zz rr E kk SS k k (38) For Figure 2 00 1 2 3 42, 0.2, 0.0, 0.0, 0.0, 136 0.42, 0.0, 0.42, 0.05 k For Figures 3 to 6 00123 42, 0.2, 1.5, 4.0, 10, 136 0.42, 0.05, 0.4, 0.05 k The first Rivlin-Ericksen tensor for the extrusion- extensional may be split into two parts, the first part in it Figure 3. Elongational viscosity vs radial extension rate with variation of shear rate k (Director parallel to stretching direction) 0 3 e — Co-rotational Maxwell model [2,21]. Figure 4. Elongational viscosity vs radial extension rate with variation of shear rate k (Director vertical to stretching direction) 0 3 e — Co-rotational Maxwell model [2,21]. represents pure extensional flow, and the second part- shear flow. According to the previous investigation [1] the additional normal stress differences are caused by shear-unsymmetric part of the constitutive Eq.14. The additional normal stress differences do not contain elon- gational parameters and for the extrusion extensional flow no principle influence on behavior of total normal stress differences will be given. 4. COMPUTATIONAL ANALYTICAL APPROACH TO EXTRUSION-EXTENSIONAL FLOW The computational analytical apprach is used to study  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ 314 Figure 5. Elongational viscosity vs radial extension rate with variation of shear rate k (Angle between director and stretching direction —π4). Figure 6. Elongational viscosity vs radial extension rate with variation of director vector and shear rate k , 0 3 e — Co-rotational Maxwell model. the extrusion extensional flow [2]. In research the com- putater software such as Maple is used for symbolic calculation. The extrusion process is assumed to be iso- thermal. The velocity field of the extrusion-extensional flow is assumed to be of ,, , 0 rz vurzvwzv (39) For the velocity field Eq.39 the equation of motion Eq.25 and 26 are reduced to 1rz zz rS P ww w tzzrr (40) where: zr PpS z Multiplying obe sides of Eq. 40 by and inte- grating it with respect to from 0 to radius of filament one can obtain 2πrdr r 000 2πd2πdd aaa rz zz rS P w wrrrrr rzr (41) Using the parameter integrating formular from ma- thematics 00 d dd, dd aa d a xfxfau ux u (42) the first integral at right side of Eq.41 can be splitted into two terms , first one of which can be reduced to 000 dd ddd dd aa a zz zz zz zz rP Pa rrrrP r aPa zzz z Using boundary condition the second term at right side in Eq.41 can be integrated which is given as 0 0 d aa rz rz rz rS rrS aSa r Eq.41 is finally reduced to 2 0 0 1d 2πd2π 2d d 2πd d a rz zz a zz wa rraSaP a rz Prr z (43) In the process of extruding on molten polymer, the ra- dius of filament is most less than its length, aL , an approximate condition is satisfied at boundary of fila- ment 2 1, 1 aa zz Eq.24 is reduced to cos1, cos1 According to above geometric analysis the boundary condition Eq.23 is approximately simplified to d0 d rzzz a Sa Pa z (44) Using Eq.44 the Eq.43 is reduced to 2 00 1d 2πd2πd 2d aa zz wrr Prr rz Introducing an averaging filament section, the above equation is then reduced as 2 dd dd 2 z w waa P zz (45)  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openl y accessible at http://www.scirp.org/journal/NS/ 315 where the averaging filament section is given as 22 _ 2 00 d1d1 d, d dd ππ aa zz zz ww rr PPrr zz aa 2 , (46) Neglecting inetia in Eq.45, Eq.41 is finally simplified to 2 πconstant zz aP C (47) The continuity equation may be written as 2 πQa w (48) where w - average filement cross section velocity, Q - mass flux, - melt dencity. Solving Eq.47 and Eq.48 yields 1zz Cw P Q C w , (49) where 1 C CQ . (50) Due to condition of stress equilibrium, the normal strss at surface of filament is zero 0 rr rr PpS It yields , the normal stress rr pS z P is given as zzzzz PpSSS rr (51) The extrusion extensional flow with orientation of di- rector will be studied. Case 1: Direcor vector is parallel to stretching direc- tion: sin0, cos1 . Assuming 30 k , the normal stress difference may be rewritten as 2 2 163 2 2 010 123 2 2 01 0 3 1 d 4d d (123)8 d d 2d zz rr k SS kz rz kz rk z kz rz z (52) Substitution of Eq.52 into Eq. 49 yields an ordinary differential equation, then multiplying it by and integrating it with respect to 2πr from to 0rra yields 2 163 1100103 2 0123 1 32 2 d12 840 d k aCwk z kz kz Cw z (53) The motion is assumed to be time independent. Using velocity profile Eq.21 , the boundary condition Eq.22 can be simplified as 1d 2d a kaw z Because of d d w kz , the above equation is reduced to the form 1d d 2d d w aw zz a (54) Integrating Eq.54 yields 22 C aw (55) Substitution of Eq.55 into Eq.53 yields 2 163 1100103 2 01231 32 2 d12840 d k CCwk z w kz kzCw z (56) Assuming the following dimensionless variables 11 00 , , , , wRz wCC a VR a R 000 1 1 00 , , , V R kkWeFa VR 00 , 36 2 2363 001 , , , , 3 1 and considering the following character 2 02 1202 2 0 , , 1. C CCRVC RVR Eq.56 can be reduced to the following dimensionless equation 6313 123 `1 321 2 d12 84 d k We WeCwFaWekFa w kkCw .(57) Finally, it is derived from Eq.57 `1123 363`1 d d 832 321 k k wCw k WeFaWekFaWeCw (58) 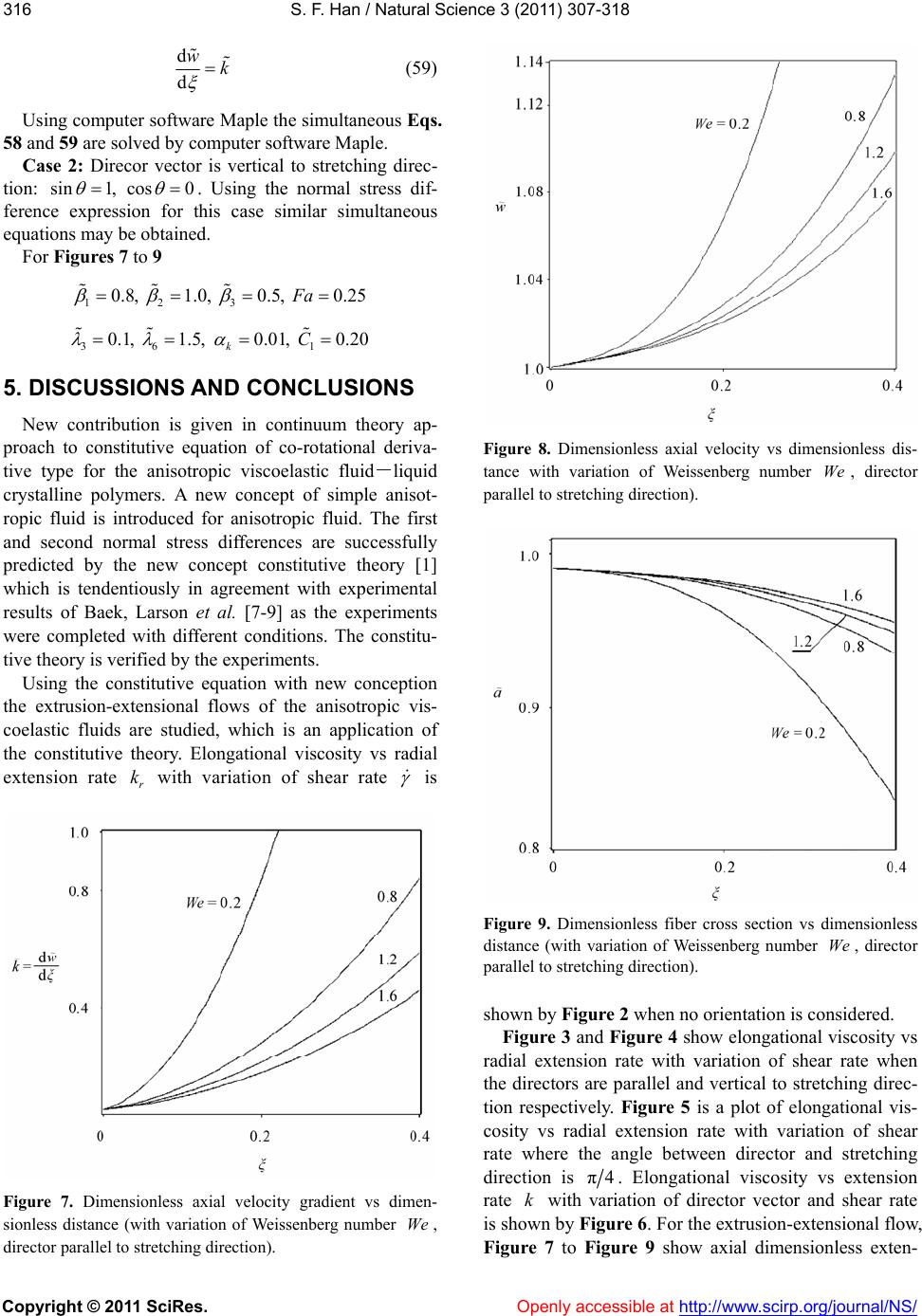 S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openly accessible at http://www.scirp.org/journal/NS/ 316 d d wk (59) Using computer software Maple the simultaneous Eqs. 58 and 59 are solved by computer software Maple. Case 2: Direcor vector is vertical to stretching direc- tion: sin1, cos0 . Using the normal stress dif- ference expression for this case similar simultaneous equations may be obtained. For Figures 7 to 9 123 0.8, 1.0, 0.5, 0.25Fa 36 1 0.1, 1.5, 0.01, 0.20 kC 5. DISCUSSIONS AND CONCLUSIONS New contribution is given in continuum theory ap- proach to constitutive equation of co-rotational deriva- tive type for the anisotropic viscoelastic fluid-liquid crystalline polymers. A new concept of simple anisot- ropic fluid is introduced for anisotropic fluid. The first and second normal stress differences are successfully predicted by the new concept constitutive theory [1] which is tendentiously in agreement with experimental results of Baek, Larson et al. [7-9] as the experiments were completed with different conditions. The constitu- tive theory is verified by the experiments. Using the constitutive equation with new conception the extrusion-extensional flows of the anisotropic vis- coelastic fluids are studied, which is an application of the constitutive theory. Elongational viscosity vs radial extension rate with variation of shear rate r k is Figure 7. Dimensionless axial velocity gradient vs dimen- sionless distance (with variation of Weissenberg number , director parallel to stretching direction). We Figure 8. Dimensionless axial velocity vs dimensionless dis- tance with variation of Weissenberg number We , director parallel to stretching direction). Figure 9. Dimensionless fiber cross section vs dimensionless distance (with variation of Weissenberg number , director parallel to stretching direction). We shown by Figure 2 when no orientation is considered. Figure 3 and Figure 4 show elongational viscosity vs radial extension rate with variation of shear rate when the directors are parallel and vertical to stretching direc- tion respectively. Figure 5 is a plot of elongational vis- cosity vs radial extension rate with variation of shear rate where the angle between director and stretching direction is π4. Elongational viscosity vs extension rate with variation of director vector and shear rate is shown by Figure 6. For the extrusion-extensional flow, Figure 7 to Figure 9 show axial dimensionless exten- k  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. Openl y accessible at http://www.scirp.org/journal/NS/ 317 sion velocity gradient d d w , extension velocity and w fiber diameter vs dimensionless distance a respec- tively with variation of Weissenberg number . We First conclusion can be drawn by Figure 2 to Figure 6. According to bifurcation theory a system has bifurca- tion at parameter when the system with parameters is changed suddenly and its structure become unstable. The Figures 2 to 5 show the curves of elongational vis- cosity e vs radial extension rate with variation of shear rate k intersect at the same point on the phase plane , e k. As shown by Figure 2 to Figure 6, the intersection point or bifurcation point is located at line 0e3 for no orientation case, above the line for di- rectors parallel and vertical to stretching direction, and below the line for angle between director and stretching direction π4. This phenomenon is so called the bifur- cation in elogational viscosity of LC polymer liquids which is most interesting for modern non-linear science. Shear rate and director angle are the bifurcation parameters. Second conclusion can be drawn by Figure 7 to Fig- ure 9. Present theory is further verified by the following comparison with the experiments of Mantia et al. [4,5]. In general case die swell is observed in many plastics processes involving extrusion of polymer melt through die into surroundings. On the contrary a contraction of extrudate of LC polymer melt is observed by the ex- perimental results of Mantia et al., which is a special character of the anisotropic material. As shown by Fig- ure 9, a contraction of the extrudate and a slight de- crease with increasing the dimensionless distance are predicted by the present continuum theory, which is ten- dentiously in agreement with the experiments. This phenomenon is called the contraction of extrudate, anti-die swell. In comparison with the results of co-rotational Maxwell model a remarkable change in elongational viscosity of LC polymer liquids is observed in Figures 3-6, when the orientation of director vector is considered. The contraction of extrudate of LC polymer melt may be associated with the stored elastic energy conversion into that necessary for bifurcation of elonga- tional viscosity in extrusion process. The next conclusion is verified by the present investi- gation. As pointed by Tanner and Zahorski [25,26], the principle of material objectivity should be considered as relative one. Generally, the co-rotational process of LC polymer liquids is a slow one. For the anisotropic vis- coelastic liquids we introduce a new concept of quasi or pseudo-objectivity. When the co-rotational process of LC polymer liquids is relatively slow, the spin tensor measured with respect to a fixed coordinate sys- tem can be considered as a quasi-objective, or pseudo- objective. Consequentially for the the anisotropic fluid the constitutive Eq.4 can be considered as quasi-objec- tive, or pseudo-objective if the spin tensor W meas- ured with respect to a fixed coordinate system is used in the investigation. The constitutive equation can be ap- plied to address a series of new anisotropic non-New- tonian fluid problems. s Wt Application of the constitutive theory to the extru- sion-extensional flow is successful in predicting bifurca- tion and contraction of extrudate of LC polymer liquids. The present continuum theory of the constitutive equa- tion is reasonable and available to predict macroscopic rheological behaviour for this kind of fluids. 6. ACKNOWLEDGEMENTS This project is supported by National Natural Science Foundation in China: No. 10772177, 19832050. REFERENCES [1] Han, S.F. (2010) New conception in continuum theory of constitutive equation for anisotropic crystalline polymer liquids. Natural Science, 2, 948-958. doi:10.4236/ns.2009.29116 [2] Han, S.F. (2000) Constitutive equation and computa- tional analytical theory of Non-Newtonian fluids. Sci- ence Press, Beijing, (in Chinese). [3] Han, S.F. (2008) Continuum mechanics of anisotropic non-Newtonian fluids —rheology of liquid crystalline polymer. Science Press, Beijing, (in Chinese). [4] Wagner, M.H., Ixner, T. and Geiger, K. (1997) A note on the melt strength of liquid crystalline polymer. Journal of Rheology, 41, 1087-1093. doi:10.1122/1.550826 [5] Mantia, F.P. and Valenza, A. (1989) Shear and noniso- thermal elongational characterization of a liquid crystal- line polymer. Polymer Engineering and Science, 29, 625-631. doi:10.1002/pen.760291003 [6] Gotsis, A.D. and Odriozola, M.A. (2000) Extensional viscosity of a thermotropic liquid crystalline polymer. Journal of Rheology, 44, 1205-1225. doi:10.1122/1.1289276 [7] Baek, S.-G., Magda, J.J. and Larson, R.G. (1993) Rheo-logical differences among liquid-crystalline poly- mers I. The first and second normal stress differences of PBG solutions. Journal of Rheology, 37, 1201-1224. [8] Baek, S.-G., Magda J.J., Larson R.G. and Hudson S.D (1994) Rheological differences among liquid-crystalline polymers II. T Disappearance of negative N1 in densely packed lyotropic and thermotropes. Journal of Rheology, 38, 1473-1503. doi:10.1122/1.550555 [9] Huang, C.M., Magda, J.J. and Larson, R.G. (1999) The effect of temperature and concentration on N1 and tum- bling in a liquid crystal polymer. Journal of Rheology, 43, 31-50. doi:10.1122/1.551037 [10] Ericksen, J.L (1962) Hydrostatic theory of liquid crystals. Archive for Rational Mechanics and Analysis, 9, 371-378. [11] Ericksen J.L. (1960) Anisotropic fluids. Archive for Ra-  S. F. Han / Natural Science 3 (2011) 307-318 Copyright © 2011 SciRes. http://www.scirp.org/journal/NS/Openly accessible at 318 tional Mechan ic s and Analysis, 4, 231-237. doi:10.1007/BF00281389 [12] Ericksen, J.L. (1961) Conversation laws for liquid crys- talls. Transaction of Society of Rheology, 5, 23-34. doi:10.1122/1.548883 [13] Leslie, F.M. (1979) Theory of flow phenomena in liquid crystals. In Brown, G..H., ed., Advances in Liquid Crys- tals, Academic, New York, p. 1. [14] Chandrasekhar, S. (1977) Liquid Crystals, Cambridge University Press, London. [15] Smith, G.F. and Rivlin, R.S. (1957) The anisotropic ten- sors. Quarterly of Applied Mathematics, 15, 308-314. [16] Green, A.E. (1964) Anisotropic simple fluid. Proceedings of the Royal Society of London, Series A, 279, 437-445. doi:10.1098/rspa.1964.0115 [17] Green, A.E. (1964) A continuum theory of anisotropic fluids. Proceedings of the Cambridge Philosophical So- ciety, 60, 123-128. doi:10.1017/S0305004100037531 [18] Volkov, V.S. and Kulichikhin, V.G., (1990) Anisotropic viscoelasticity of liquid crystalline polymers. Journal of Rheology, 34, 281-293. doi:10.1122/1.550129 [19] Volkov, V.S.and Kulichikhin, V.G. (2000) Non-symmetric viscoelasticity of anisotropic polymer liquids, Journal of Rheology, 39, 360-370. [20] Larson R.G. (1993) Roll-cell instability in shearing flows of nematic polymers, Journal of Rheology, 39, 175-197. doi:10.1122/1.550440 [21] Han, S.F. (2001) Constitutive equation of liquid crystal- line polymer-anisotropic viscoelastic fluid. Acta Mechani- ca Sinica, 5, 588-600, in Chinese. [22] Han, S.F. (2004) Constitutive equation of co-rotational derivative type for anisotropic viscoelastic fluid. Acta Mechanica Sinica, 2, 46-53. [23] Han, S.F. (2007) An unsymmetric constitutive equation for anisotropic viscoelastic fluid. Acta Mechanica Sinica, 2, 46-53. [24] Han, S.F. (2008) Research advances of un-symmetric constitutive theory of anisotropic viscoelastic liquids and its hydrodynamic behavior. Journal of Central South University of Technology, 15, 1-4. [25] Tanner, R.L. (1985) Engineering Rheology, Clarendon Press, Oxford. [26] Zahorski, S. (1982) Mechanics of viscoelastic fluids. Martinus Nijhoff Publishers, London. [27] Truesdell, C. (1951) A new definition of a fluid II. The Maxwell fluid. International Journal of Pure and Ap- plied Mathematics, 9, 115-158.
|