 Journal of Geoscience and Environment Protection, 2014, 2, 159-169 Published Online June 2014 in SciRes. http://www.scirp.org/journal/gep http://dx.doi.org/10.4236/gep.2014.23021 How to cite this paper: Das, S. K., & Maity, R. (2014). On the Application of Probabilistic Hydrometeorological Simulation of Soil Moisture across Different Stations in India. Journal of Geoscience and Environment Protection, 2, 159-169. http://dx.doi.org/10.4236/gep.2014.23021 On the Application of Probabilistic Hydrometeorological Simulation of Soil Moisture across Different Stations in India Sarit Kumar Das, Rajib Maity Department of Civil Engineering, Indian Institute of Technology, Kharagpur, India Email: saritkdas@iitkgp.ac.in Received March 2014 Abstract An application of a proposed hydrometeorological approach for probabilistic simulation of soil moisture is carried out. The time series of in-situ soil moisture and meteorological variables at monthly scale from a few monitoring stations having different soil-hydrologic properties across India are utilized. Preliminary investigation with both precipitation and near-surface air-tempe ra- ture as meteorological variables to establish that the strength of association between soil mois- ture and precipitation is more significant as compared to that between soil moisture and tem- perature. Precipitation-based probabilistic estimation of soil moisture using the proposed hy- drometeorological approach is tested with in-situ observed soil moisture, CPC model output and with soil moisture data of the Climate Change Initiative (CCI) project. The parameter of the devel- oped model is linked to the soil-hydrologic characteristics through Hydrologic Soil Group (HSG) classification. Higher values of model parameter (dependence parameter (θ) for the selected cop- ula) correspond to HSG A and B having higher soil porosity, whereas, lower values correspond to HSG B and C having lower soil porosity. Keywords Soil Moisture, Probabilistic Modelling, Copula, Hydro m ete orol ogy , Hyd r oclim at ology 1. Introduction Soil moisture has significant impact on temperature-evaporation-precipitation feedback loop (Seneviratne et al., 2010) and plays a significant role in numerical weather prediction using climate variables at regional scale (Ek & Hostslag, 2004; Drusch, 2007; Panareda et al., 2010). Soil moisture also controls the terrestrial water balance through partitioning precipitation among infiltration, runoff and evapotranspiration. The capillary action that determines the evaporative demand and withdrawal of water through plant roots is driven by soil moisture con- tent (Entekhabi et al., 1996). Thus, soil moisture is also critical for drought, flood prediction, erosion caused by surface runoff, ground water recharge etc. (Dripps & Bradbury, 2007; Seneviratne et al., 2010). Amount of moisture content in the root zone is also significant, especially during the critical growth period of the crops (Narasimhan & Srinivasan, 2005). The temporal distribution of soil moisture over a catchment is useful for  S. K. Das, R. Maity forecasting irrigation requirements (Pandey & Pandey, 2010). Recently, United Nations Framework Convention on Climate Change (UNFCCC) has declared soil moisture as Essential Climate Variable (ECV) in the terrestrial domain and taken steps for monitoring soil moisture during 2010-15 (GCOS, 2010). Climate variables, espe- cially, precipitation and temperature, have strong association with spatio-temporal distribution of soil moisture. It has been revealed that the temporal variation in the relationship between soil moisture and precipitation is non-linear and stochastic (Rodriguez-Iturbe et al., 2001). The factors behind the spatio-temporal variability of soil moisture, especially for topsoil, can be of two types—static and dynamic. Static factors include properties of soil, topography, land use etc. and dynamic factors include hydroclimatic parameters, such as precipitation, evapotranspiration, vegetation growth etc. (Rosenbaum et al., 2012). Sensitivity of soil moisture over changing frequency of precipitation and rise in temperature due to climate change scenarios is found to vary with soil tex- ture (Bormann, 2012). At point locatio ns, spatial variation of soil moisture primarily depends on soil structure defined by soil texture (Gaur & Mohanty, 2013), plant characteristics (Porporato et al., 2004), whereas the temporal variability depends on hydrometeorological variables, like precipitation (Oyedele & Tijani, 2010). The classification of various soil types based on these soil-hydrologic factors is defined in the US National Engineering Handbook as Hydrologi- cal Soil Groups (HSG) as four major groups, viz., A, B, C and D. The rate of infiltration, i.e. the porosity of soil varies high to low from HSG A to HSG D (USDA, 2009). Hydrometeorological approaches for modelling the variation of different hydrologic variables are gaining popularity (Maity & Ka shi d, 2011). With the availability of extensive hydroclimatic database, there is a scope for developing such a probabilistic model for soil moisture simulation prompted by the established physical in- teractions among available soil moisture and hydrometeorological variables responsible for its spatio-temporal variability. Such a model would cater the stochastic behaviour of these relationships and may yield better esti- mation with quantification of associated uncertainty. Moreover, developed approach can also be used to estimate the future soil moisture using the climate variables, simulated by different climate models. Joint probability distribution between soil moisture series and influencing hydroclimatic variable is adopted for probabilistic model development. Copulas are found to be the best choice to develop the joint distribution by joining the individual marginal distribution of any two or more variables (Nelsen, 2006). These functions are recently used in several studies to obtain joint distribution among hydrological or climatological variables (Kao & Govindaraju, 2008; Maity & Nagesh Kumar, 2008; Das & Maity, 2013). This applies a hydrometeorological approach, which can be considered as an alternative method for estimat- ing soil moisture using hydrometeorological variables. The scope of this paper is to investigate the association between surface soil moisture and two hydrometeoro logical variables—precipitation and temperature. A cop- ula-based bivariate probabilistic modelling approach for simulation of soil moisture is adopted. The modelled soil moisture data are compared with in-situ data to check the accuracy of proposed simulation approach during both model development and testing periods. The performance of the proposed approach is also tested with the surface soil moisture data set for depth 0 - 5 cm developed under the Climate Change Initiative (CCI) project funded by ESA (ESA CCI). The Climate Prediction Centre’s (CPC’s) leaky bucket model (Huang et al., 1996) based soil moisture estimates (Fan & Dool, 2004) are also considered to check the accuracy of the model output. Finally, an attempt is also made to check the relationship of the model properties (in terms of model parameter) with the soil hydrologic characteristics in terms of HSGs at the monitoring locations. 2. Data Used and Preliminary Analysis 2.1. Data Thirteen locations across different HSGs in India, as shown in the HSG map for India (F igure 1) are selected. The weekly in-situ surface (for depth 0 - 7.5 cm) soil moisture data for bare soil during the years 1991 to 2006 is procured from National Data Centre (NDC) of Indian Meteorological Department (IMD), Pune, India. The daily precipitation and mean daily temperature data are also obtained from IMD. Precipitation data are converted into the cumulative monthly values, and soil moisture as well as temperature data into monthly average values. There exist some missing data periods for some of the variables considered. These time instances are excluded from the analysis. ESA CCI data, as mentioned before, is obtained from 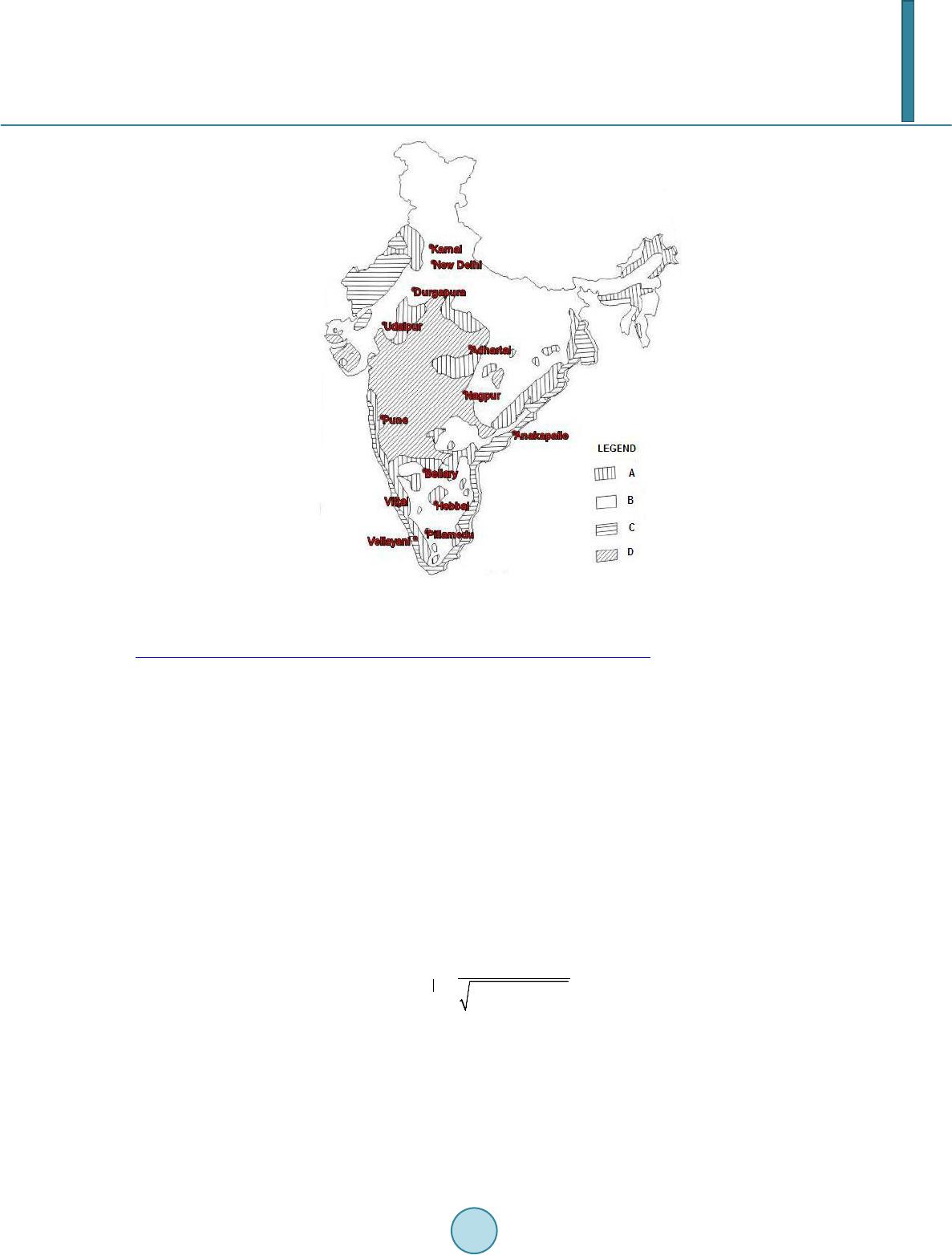 S. K. Das, R. Maity Figure 1. Location of soil moisture monitoring stations on HSG map of India (Source: CGWB, 2007). http://www.ip f.tuwie n.ac.at/rad ar/dv_ne w/ipfdv/inde x.php? datavie wer=wacmo s (accessed on March 15, 2014). The ESA CCI soil moisture data is available at 0.25˚ by 0.25˚ geo-spatial grid (Albergel et al., 2013a). and so the Inverse Distance Weighting (IDW) method is adopted to estimate the values at the station locations. Finally, the information on HSG classification is obtained from Central Ground Water Board of India (CGWB, 2007). 2.2. Preliminary Analysis A preliminary analysis is carried out to investigate the association of surface soil moisture data with meteoro- logical variables—temperature and precipitation, individually. Scatter plots (not presented) between soil mo is- ture and precipitation or near surface air temperature indicate a stronger association between soil moisture and precipitation than that between soil moisture and temperature, which associations ma y not necessarily be linear. 2.3. Assessment of Linear Association Partial correlation coefficients are calculated to check the strength of the linear association of soil moisture on precipitation (or near surface air temperature), while the effect of temperature (or precipitation) is partial out. The first order partial correlation coefficient between x and y, while the effect of z is partial out is expressed as: ( )( ) 22 .. 11 − = −− xyxz yz xy z xz yz r rr rrr (1) where, , are primary variables and is the variable, which is partial out; , and are the correlation coefficients between the variables given in the subscript (Ley, 1973). Values of first order partial correlation coefficients along with their significance level (95%) are presented in Figure 2(a). It is found that at all stations, first order partial correlation coefficient between soil moisture and precipitation is positive, statisti- cally significant (at 95% significance level) for all the stations and varies over a range of 0.507 to 0.861. How- ever, the partial correlation coefficient for soil moisture and temperature is significant only at Anakapalle, Dur- gapura, Nagpur, Pillamedu and Vellayani. Thus, the linear association between soil moisture and precipitation is 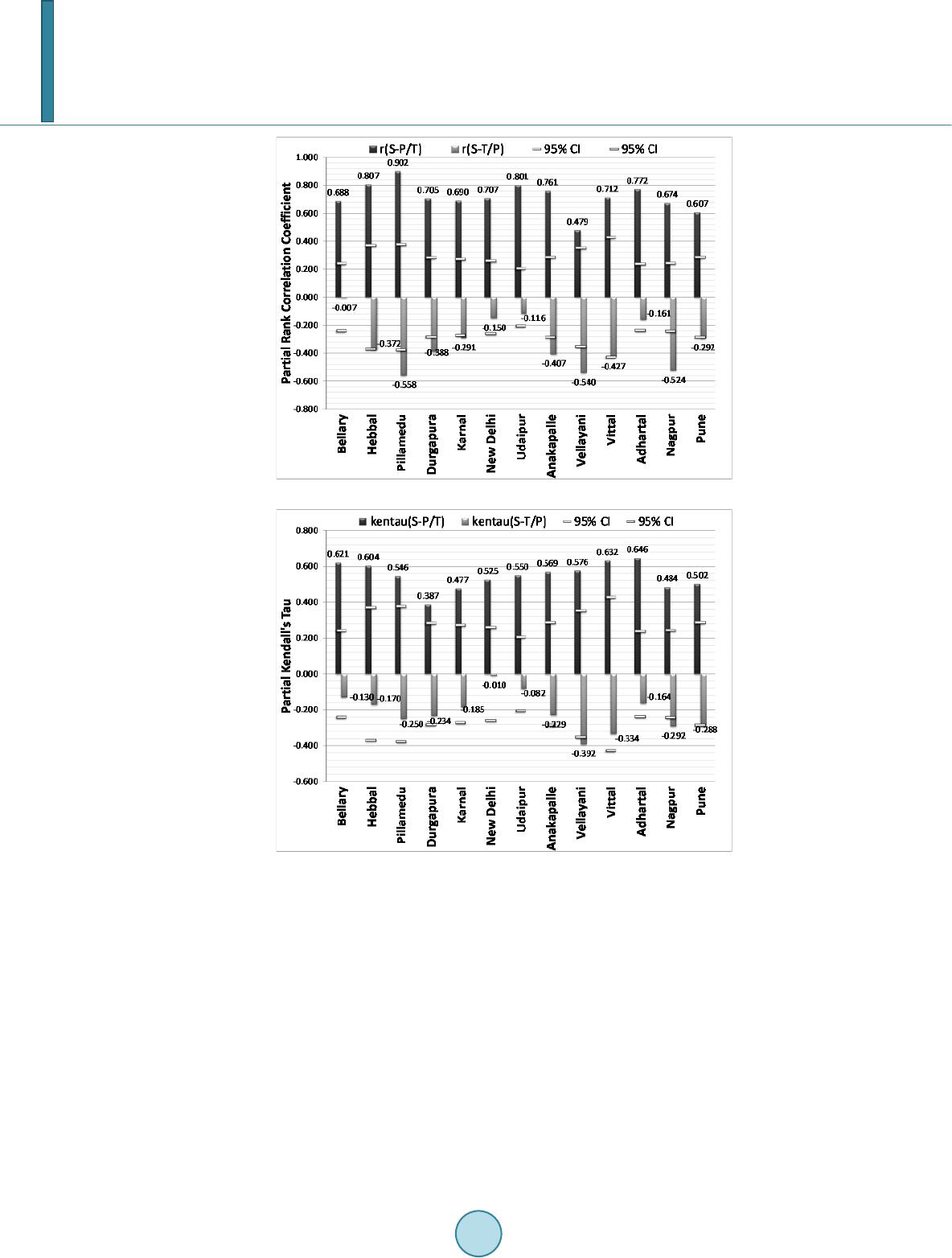 S. K. Das, R. Maity (a) (b) Figure 2. Significance of between Soil Moisture (S), Precipitation (P) and Temperature (T). found stronger than that between soil moisture and temperature. The strength of association is also investigated through a scale-free measure of association. 2.4. Assessment of Scale-Free Association Rank-based, scale-free measures of association such as, Kendall’s Tau ( ) or Spearman’s Rho ( ) are inde- pendent of the individual marginal distribution of the variables, and thus, useful for determining joint distribu- tion without compromising the dependence structure during simulation (Nelsen, 2006). In this study, Kendall’s Tau ( ) is adopted as a measure of such association since it directly determines the dependence parameter for the copula. Partial Kendall’s Tau can be treated as the association between two variables while the effect of third variable is partial out. This is expressed as (Kendall, 1962):  S. K. Das, R. Maity ( )() 22 .. 11 τ ττ τ ττ − = −− xyxz yz xy z xz yz (2) where, , and are the Kendall’s Tau ( ) between the variables shown in the subscript. Partial Kendall’s Tau values, between soil moisture and precipitation while the effect of temperature is partial out, and between soil moisture and temperature while the effect of precipitation is partial out, are computed for all sta- tions and are shown in Figure 2(b). At all stations, partial Kendall’s Tau for soil moisture and precipitation rela- tionship is positive and significant at 95% confidence level, however the soil moisture-temperature relationship is significant only at three (Nagpur, Pune, Vellayani) (Fig ure 2(b)). Thus, based on the linear association and scale-free measures of association, only precipitation is considered hereinafter for simulation of soil moisture. 3. Methodology To remove the effect of seasonality, anomaly values of both monthly precipitation and soil moisture are used in the simulation model. Anomalies for monthly average of soil moisture and monthly cumulative values of pre- cipitation are obtained by deducting the long-term monthly mean from the observed values of the variable for each month in a calendar year. Kolmogorov-Smirnov test is applied to check the fitted distribution and to select the best one from the tentatively eligible pool of distributions. 3.1. Estimation of Joint Probability Distribution Marginal distributions are used to determine the joint distribution by employing a copula based approach. In this study, three different bivariate copula functions viz., Clayton, Frank, and Gumbel-Hougaard (belong to the Archime d e an Class of copulas) are tested. Here, another commonly used bivariate copula, Ali-Mikhail-Haq, is not adopted as the acceptable range of dependence for this copula is narrow ( = −0.182 to 0.333) (Chowdhary et al., 2011), and not suitable for most of the monitoring stations. Details of these copula functions can be found in Nelsen (2006). First, the tentatively eligible copulas are selected based on the Kendall’s Tau ( ) value calcu- lated for association between soil moisture anomaly and precipitation anomaly, separately for each station. When there exists more than one feasible copula family that satisfy the range of dependence for the given data, the final selection of a suitable copula is based on the best fit to the observations. This fit is assessed statistically by goodness-of-fit (GOF) tests prescribed by Genest et al. (2009). The copula showing best fit (denoted as ) is selected to obtain the joint distribution between soil moisture and precipitation anomaly. The developed joint distribution between soil moisture anomaly and precipitation anomaly, denoted as . This is expressed as: ()( )( ) ( ) , , ,. b SPS P FspCF s Fp= (3) where, S and P are the soil moisture anomaly and the precipitation anomaly respectively; and are values. 3.2. Determination of Conditional Distribution Function The joint distribution, is used to get a conditional cumulative distribution for the soil moisture anomaly conditioned on the precipitation. The formulation as given by Schmidt (2006): () ( )() ( ) |1 | ,. = ≤== b SP pSP FSsPpCFs Fp (4) For a particular value of observed precipitation anomaly, this conditional cumulative distribution function (Equation (4)) is used for probabilistic simulation of soil moisture anomaly. This simulated soil moisture anom- aly is then added to the long-term monthly mean of soil moisture to obtain the probabilistic distribution of simu- lated soil moisture. 3.3. Model Performance Evaluation The simulated soil moisture using the methodology proposed here is first compared with in-situ observed data. Further, the proposed model output is compared with the ESA CCI surface soil moisture data set, and CPC model soil moisture data. The statistical comparison, between Proposed model output and CCI soil moisture date  S. K. Das, R. Maity is made in terms of standard and most updated measures for model performance, namely, Correlation Coeffi- cient (CC), normalized unbiased Root Mean Square Error (ubRMSE) (Albergel et al., 2013b), and Refined In- dex of Agreement ( ) (Willmott et al., 2012) etc. The ubRMSE is normalized using the range of in-situ or ob- served data. 4. Results and Discussions 4.1. Development of Simulation Model A few tentatively eligible probability density functions (pdf) with relatively high Kurtosis, such as, Normal and Logistic distribution, which are a pplicab le for the data having both positive and negative values, are tested for the anomaly of average monthly soil moisture and precipitation. Goodness-of-fit tests are carried out using Kolmogorov-Smirnov test. T he se p-values indicate (not presented) that at majority of stations Logistic distribu- tion is best among the distribution functions tested. At nine out of 13 stations for precipitation anomalies and 12 out of 13 stations for soil moisture anomalies Logistic distribution is passing through the KS test. Thus, the probability distributions for both soil moisture and precipitation are accepted to follow Logistic distribution. The results of copula selection procedure reveal that Clayton is the best copula for deriving the joint distribu- tion of soil moisture and precipitation anomalies. Simulation of soil moisture using Clayton copula is carried out for all the stations, across different HSGs. For discussion, the results (time series plots) ob tained at four stations, one from each HSGs (Bellary, Udaipur, Anakapalle and Nagpur) are presented in Figure 3 (left panel) resp ec- tively. Probabilistic estimation of soil moisture is represented through 90% confidence interval (the interval area is shown in grey) along with the expected values (50th quantile) in black line. Observed in-situ soil moisture (red), satellite based ESA CCI soil moisture values (green) and CPC model estimated values (dark blue) are also shown in these figures. 4.2. Checking of Model Performance The simulated soil moisture (50th quantile value), based on the proposed methodology, is first compared with in-situ observed data. As noted earlier, the proposed model provides a probabilistic output and availability of uncertainty information is a strong point of the proposed model. From the probabilistic output of proposed ap- proach, 5th quantile is used as Lower Limit (LL), 95th quantile as Upper Limit (UL). Comparison plots between estimated soil moisture (LL, UL and expected value), in- situ soil moisture data, ESA CCI data and CPC data are prepared. It is important to mention here that CPC model is taken as an existing model which simulates soil moisture based on precipitation and temperature, whereas, Satellite based ESA-CCI data are considered another observed data set for soil moisture to be compared with. Model performances are assessed through three stati s- tics during both model development and testing periods. Results are presented in Table 1. The results reveal that at all monitoring stations, the proposed model performs reasonably well during both model development and testing period. While comparing with in-situ values during model development period, CC varies between 0.744 (New Delhi) and 0.904 (Pillamedu); normalized ubRMSE varies between 0.231 (Karnal) and 0.084 (Vellayani); ranges from 0.626 (Anakapalle) to 0.805 (Pillamedu). However, during testing period the CC values ranges between 0.999 (Bellary) and 0.752 (Pillamedu); normalized ubRMSE varies from 0.211 (Pillamedu) to 0.001 (Bellary); ranges between 0.871 (Vittal) and 0.707 (Nagpur). This relative improvement in model perform- ance for some stations, like Bellary, during testing period can be attributed to the range of in-situ data during that time period. The performance of the proposed model against CPC model is assessed through the perform- ance of the both against in-situ values. This assessment as shown in Table 1 reveals that the proposed model performs relatively better at all the stations during both model development and testing periods, except at station, Karnal during model development period. The significantly poor performance of the CPC model at a few sta- tions—Anakapalle, Bellary, Hebbal etc. can be attributed to the fact that this model assumes a constant soil po- rosity values across the globe which can be far different from the in-situ value as in these cases. The perform- ance of the proposed model against the ESA-CCI data is also found to be reasonably good at all stations, except Anakapalle. The CC values varies between 0.647(Hebbal) and 0.909 (Vittal), normalized ubRMSE varies from 0.243 (New Delhi) to 0.130 (Vittal). However, values found to be negative at almost all the stations, indi- cating the larger variability in the simulated soil moisture data compared to the ESA-CCI data set. 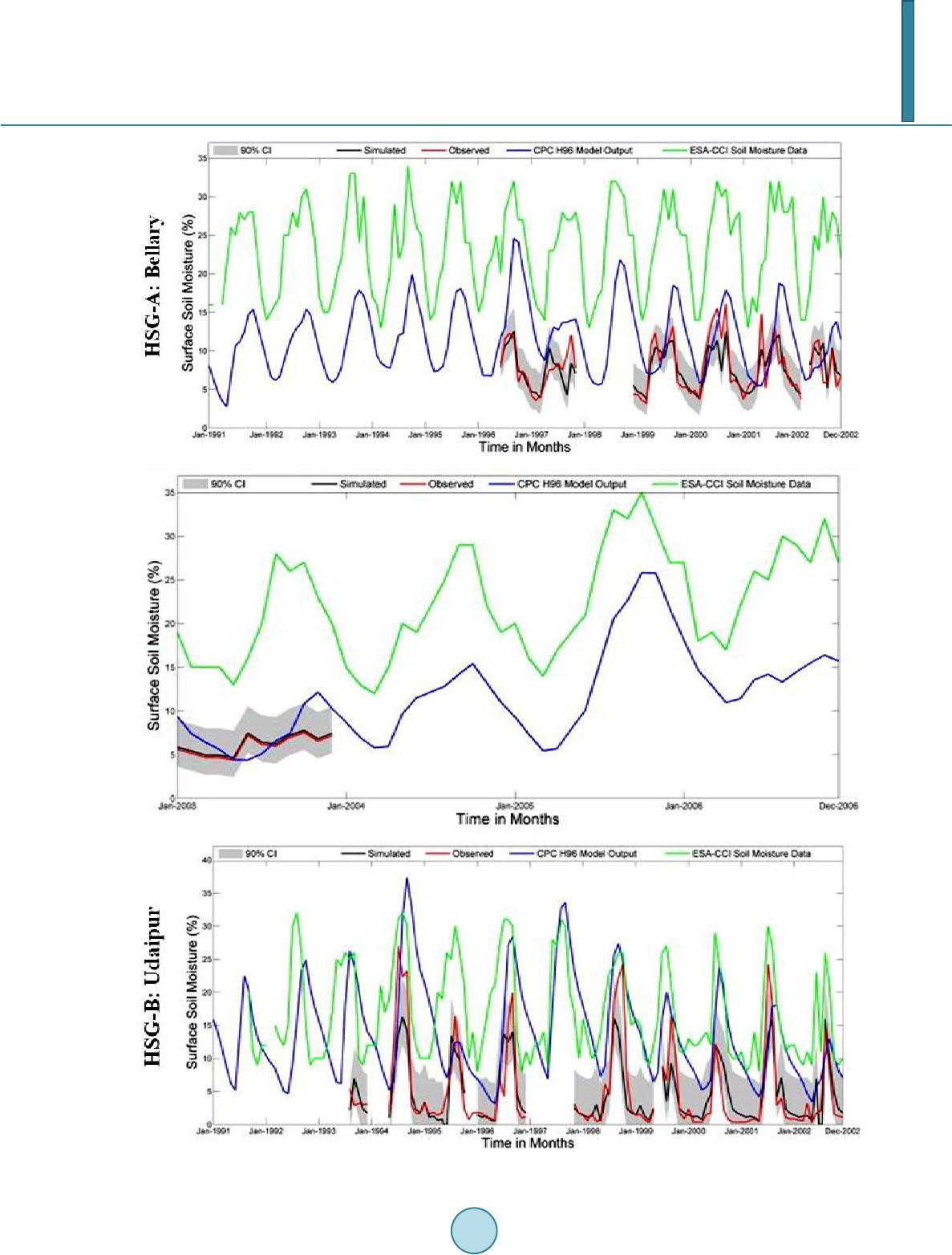 S. K. Das, R. Maity  S. K. Das, R. Maity Figure 3. Time series plots of observed and simulated soil moisture, CPC model output and ESA-CCI Soil Moisture data for both model development and testing periods. 4.3. Model Parameter and Soil Hydrologic Properties Model parameter ( ) of the proposed copula-based soil moisture simulation model represents the dependence between soil moisture and precipitation anomalies. This parameter is applied to the joint distribution of soil moisture and precipitation anomalies. The values of this model parameter at all soil moisture monitoring stations are investigated for any possible link with the soil hydrologic characteristics at monitoring stations. Thi s com- parison (Table 2) provides the necessary evidence of the influence of soil properties on the variation of soil moisture due to variation in precipitation. The comparison, as parameter value is higher for stations belongs to HSG A and B, whereas it is lower for stations belongs to HSG C and D. The soil porosity is maximum for HSG A and gradually drops through HSGs. Thus it emphasizes the fact that the soil-hydrologic properties e.g. soil porosity has a control on the response of soil moistur e variability due to hydrometeorological forcing. 5. Conclusions In this paper, dependence of monthly soil moisture variation on hydroclimatic variables (precipitation and tem- perature) is explored. It is found that the strength of association is higher between soil moisture and precipitation  S. K. Das, R. Maity Table 1. Model Performance during Model Development (top rows) and Model Testing (bottom rows). Station Correlation Coefficient (CC) Normalized Unbiased RMSE (ubRMSE) Refined Index of Agreement (dr) In-situ vs. Proposed model In-situ vs. CCI Data vs. Proposed Model In-situ vs. Proposed model In- CPC model CCI Data vs. Proposed Model In-situ vs. Proposed model In-situ vs. CPC model CCI Data vs. Proposed Model A Bellary 0.999 0.471 0.665 0.001 0.700 0.29 0.734 0.148 −0.432 Hebbal 0.887 0.257 0.647 0.103 0.416 0.202 0.758 −0.634 −0.554 0.998 -0.18 0.504 0.001 0.695 0.296 0.803 −0.619 −0.572 Pillamedu 0.752 0.332 D.N.A. 0.211 0.442 D.N.A. 0.737 −0.056 D.N.A. B Durgapura 0.810 0.18 0.723 0.146 0.737 0.222 0.711 −0.667 −0.361 0.999 0.499 0.871 0.001 0.752 0.23 0.781 −0.618 −0.316 Karnal 0.843 0.695 D.N.A. 0.146 0.195 D.N.A. 0.743 0.627 D.N.A. New Delhi 0.744 0.273 0.671 0.174 0.271 0.243 0.688 0.349 −0.235 0.999 0.399 D.N.A. 0.001 0.481 D.N.A. 0.721 0.255 D.N.A. Udaipur 0.823 0.452 0.731 0.161 0.311 0.221 0.788 0.17 0.04 C Anakapalle 0.834 0.291 0.253 0.13 0.246 0.411 0.626 0.732 −0.138 0.932 0.031 0.372 0.105 0.378 0.395 0.784 −0.194 −0.230 Vellayani D.N.A. D.N.A. D.N.A. D.N.A. D.N.A. D.N.A. D.N.A. D.N.A. D.N.A. Vittal 0.865 0.778 0.909 0.139 0.228 0.13 0.75 0.273 −0.079 0.941 0.839 D.N.A. 0.11 0.234 D.N.A. 0.871 −0.008 D.N.A. D Adhartal 0.91 0.698 0.766 0.138 0.174 0.255 0.798 0.324 −0.139 Nagpur 0.758 0.681 0.869 0.166 0.201 0.166 0.686 0.63 0.451 0.841 0.519 0.762 0.149 0.302 0.207 0.707 0.296 0.071 Pune 0.883 0.755 D.N.A. 0.111 0.169 D.N.A. 0.771 0.526 D.N.A. D.N.A. = Data not available at the time step. Table 2. Model parameter with different HSGs. HSG Station Model parameter (θ) A Bellary Hebbal 0.994 Pillamedu 1.45 B Durgapura 1.086 Karnal 1.252 New Delhi Udaipur 1.535 C Anakapalle 0.803 Vellayani 0.391 D Adhartal Nagpur 0.496 Pune 0.288  S. K. Das, R. Maity compared to that between soil moisture and temperature. Considering the associated uncertainty, a probabilistic model is applied for soil moisture estimation along with uncertainty quantification. The monthly soil moisture computed with the proposed model is found to be promising. Observed in-situ soil moisture variation is found to be well captured between 5th (upper limit) and 95th quantile (lower limit) provided by the proposed approach. 50th quantile of the probabilistic estimate is found to well correspond with the in-situ values for all the stations. The comparison is also carried out between soil moisture estimate by the proposed model and CPC model as well as the ESA CCI soil moisture data. A fairly good correspondence is indicated for all the stations. Finally the relationship between model parameter value and the hydrologic soil properties at monitoring location indicates the possible spatial transferability of the proposed model. Acknowledgements We acknowledge financial support from ISIRD fund of Indian Institute of Technology, Kharagpur through the project, code FSH. References Albergel, C., Dorigo, W., Balsamo, G., Muñoz-Sabater, J., de Rosnay, P., Isaksen et al. (2013a). Monitoring Mu lt i-Decadal Satellite Earth Observation of Soil Moisture Products through Land Surface Reanalyses. Remote Sensing of Environment, in press. Albergel, C., Brocca, L., Wagner, W., De Rosnay, P., & Calvet, J.-C. (2013b). Selection of Performance Metrics for Global Soil Moisture Products: The Case for the ASCAT Soil Moisture Product. In: G. P. Petropoulos (Ed.), Remote Sensing of Energy Fluxes and Soil Moisture Content (pp. 427-444). CRC Press. Bormann, H. (2012). Assessing the Soil Texture-Specific Sensitivity of Simulated Soil Moisture to Projected Climate Change by SVAT Modelling. Geoderma, 185-186, 73 -83. http://dx.doi.org/10.1016/j.geoderma.2012.03.021 Central Ground Water Board (CGWB) (2007). Manual on Artificial Recharge of Groundwater. Ministry of Water Resources, Government of India, Faridabad. Chowdhary, H., Escobar, L. A., & Singh , V. P. (2011). Identification of Suitable Copulas for Bivariate Frequency Analysis of Flood Peak and Flood Volume Data. Hydrology Research, 42, 193-216. http://dx.doi.org/10.2166/nh.2011.065 Das, S. K., & Maity, R. (2013), Probabilistic Simulation of Surface Soil Moisture using Hydrometeorological Inputs. IS H Journal of Hydraulic Engineering, 19, 227-234. http://dx.doi.org/10.1080/09715010.2013.798907 Dripps, W. R., & Bradbury, K. R. (2007). A Simple Daily Soil-Water Balance Model for Estimating the Spatial and Tempo- ral Distribution of Groundwater Recharge in Temperate Humid Areas. Hydrogeology Journal, 15, 433-444. http://dx.doi.org/10.1007/s10040-007-0160-6 Drusch, M. (2007). Initializing Numerical Weather Prediction Models with Satellite-Derived Surface Soil Moisture: Data Assimilation Experiments with ECMWF’s Integrated Forecast System and the TMI Soil Moisture Data Set. Journal of Geophysical Research, 112, D0310 2. http://dx.doi.org/10.1029/2006JD007478 Ek, M. B., & Holtslag, A. A. M. (2004). Influence of Soil Moisture on Boundary Layer Cloud Development. Journal of Hydrometeorology, 5, 86-99. http: //d x.do i .org/ 10. 1175 /15 25 -7541(2004)005<0086:IOSMOB>2.0.CO;2 Entekhabi, D., Rodriguez-Iturbe, I., and Castelli, F. (1996). Mutual Interaction of Soil Moisture State and Atmospheric P ro cesses. Journal of Hydrology, 184, 3-17. http://dx.doi.org/10.1016/0022-1694(95)02965-6 Fan, Y., & van den Dool, H. (2004). Climate Prediction Center Global Monthly Soil Moisture Data Set at 0.5 Resolution for 1948 to Pr esent. Journ al of Geophysical Research, 109, D10102. http://dx.doi.org/10.1029/2003JD004345 Gaur, N., & Mohanty, B. P. (2013). Evolution of Physical Controls for Soil Moisture in Humid and Subhumid Watersheds. Water Research, 4 9, 12 44-12 58. http://dx.doi.org/10.1002/wrcr.20069 GCOS (2010). Global Climate Observing System (GCOS). Implementation Plan for the Global Climate Observing System in Support of the UNFCCC (2010 Update), GCOS-138. UNEP and Intl. Council for Science. Genest, C., Remillard, B., & Beaudoin, D. (2009). Goodness-of-Fit Tests for Copulas: A Review and a Power Study. I nsur- ance: Mathematics and Economics, 44, 19 9. http://dx.doi.org/10.1016/j.insmatheco.2007.10.005 Huang, J, van den Dool, H. M., & Georgakakos, K. P. (1996). Analysis of Model Calculated Soil Moisture over the United States (1931-1993) and Applications to Long Range Temperature Forecasts. J. of Cli., 9, 1351-1362. http://dx.doi.org/10.1175/1520-0442(1996)009<1350:AOMCSM>2.0.CO;2 Kao, S. C., & Govindraju, S. C. (2008). Trivariate Statistical Analysis of Extreme Rainfall Events via the Plackett Family of Copulas. Water Resources Research, 44, W02415. http://dx.doi.org/10.1029/2007WR006261  S. K. Das, R. Maity Kendall, M. G. (1962). Rank Correlation Methods (4th ed.). Lo ndon : Griffin. Maity, R., & Kashid S. S. (2011), Importance Analysis of Local and Global Climate Inputs for Basin-Scale Streamflow Pre- diction. Water Resources Research, 47, W11504. http://dx.doi.org/10.1029/2010WR009742 Maity, R., & Nagesh Kumar, D. (2008). Probabilistic Prediction of Hydroclimatic Variables with Nonparametric Quantifica- tion of Uncertaint y. Journal of Geophysical Research, 113, D14105, 12. Nelsen, R. B. (2006). An Introduction to Copulas (2nd ed.). New York: Springer, 269. Oyedele, D. J., & Tijani, F. O. (2010). Spatial and Temporal Variability of Soil Water Content. International Agrophysics, 24, 171-176. Panareda, A. A., Balsamo, G., & Beljaars, A. (2010). Impact of Improved Soil Moisture on the ECMWF Precipitation Fore- cast in West Africa. Geophysical Research Letters, 37, L20808. Pandey, V., & Pandey, P. K. (2010). Spatial and Temporal Variability of Soil Moisture. International Journal of Geo- sciences, 1, 87 -98. http://dx.doi.org/10.4236/ijg.2010.12012 Porporato, A., Daly, E., & Rodriguez-Iturbe, I. (2004). Soil Water Balance and Ecosystem Response to Climate Change. The American Naturalist, 164, 625-632. http://dx.doi.org/10.1086/424970 Rodriguez-Iturbe, I., Porporato, A., Liao, F., & Ridolfi L. (2001). Plants in Water-Controlled Ecosystem: Active Role in Hy- drologic Process and Response to Water Stress, I. Scope and general outline. Advances in Water Resources, 24, 695-705. http://dx.doi.org/10.1016/S0309-1708(01)00004-5 Rosenbaum, U., Bogena, H. R., Huisman, J. A., Peterson, T. J., Weuthen, A., Western, A. W., & Vereecken, H. (2012). Sea- sonal and Event Dynamics of Spatial Soil Moisture Patterns at the Small Catchment Scale. Water Resources Research, 48, W10544. http://dx.doi.org/10.1029/2011WR011518 Schmidt, T. (2006). Coping with Copulas in “Copulas: From Theory to Applications in Finance”. London: Risk Books. Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., Lehner, I., Orlowsky, B., & Teuling, A. J. (2010). Inves- tigating Soil Moisture–Climate Interactions in a Changing Climate: A Revie w. Earth Science Reviews, 99, 12 5-161. http://dx.doi.org/10.1016/j.earscirev.2010.02.004 USDA (2009). Chapter 7 Hydrologic Soil Groups, Part 630 Hydrology, National Engineering Handbook. National Re- sources Conservation Service, United States Department of Agriculture. 210-VI-NEH. Willmott, C. J., Robesonb, S. M., & Matsuuraa, K. (2012). Short Communication: A Refined Index of Model Performance. Intl. Journal of Climate.
|