 Journal of Biosciences and Medicines, 2014, 2, 63-68 Published Online June 2014 in SciRes. http://www.scirp.org/journal/jbm http://dx.doi.org/10.4236/jbm.2014.24010 How to cite this paper: Li, W., et al. (2014) Role of Mechanical Stimuli in Oral Implantation. Journal of Biosciences and Medicines, 2, 63-68. http://dx.doi.org/10.4236/jbm.2014.24010 Role of Mechanical Stimuli in Oral Implantation Wei Li, Daniel Lin, Junning Chen, Zhongpu Zhang, Zhipeng Liao, Michael Swain, Qing Li School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, Australia Email: Wei.Li@Sydney.edu.au Received June 2014 Abstract Prosthetic implantation has been a prevalent surgical procedure in dentistry. Insertion of dental implant significantly changes local oral conditions and leads to the surrounding bone to remodel to a new morphology. To predict how the bone responds such a biomechanical change, finite ele- ment analysis (FEA) based remodeling simulation has proven effective. For a range of mechanical stimuli, which should be used remains controversial arguable? This paper aims to compare how the different mechanical stimuli, including mechostat model (effective strain), daily stress and strain energy density (SED) affect the predictions of bone remodeling. Keywords Dental Implant, Bone Remodeling, Mech an obiol ogy , Finite Element, Mechanical Stimulus 1. Introduction It has been well recognized that human bone adapts the changes in biomechanical environment and functions. The Wolff’s law signified a major milestone to address the relationship between the distribution of bones and mechanical loading, which is a foundation for numerous biomechanics researches. In general, bone remodeling indicates an ongoing process where bone gradually alters its morphology in terms of resorption and apposition for adapting any new change in external loading. Two different phenomenological descriptions, known as “sur- face” and “internal” remodeling [1], are commonly used in the field [2] [3]. By definition, the former is related to the resorption or deposition on the outer or inner surfaces of the bone [3], whilst the latter is related to the re- sorption or apposition of lamellar bone within the existing osteons [2]. From biological perspective, how bone remodels has drawn significant attention in the field [2]. It is well known that three types of cells, namely osteoblasts, osteocytes, and osteoclasts, are the major constituents that make up the process of bone remodeling. Upon completion of the osteoblastic process, internal changes occur, where the osteoblasts envelop into hollow lacunae, and these are known as the osteocytes. One of the main roles of the osteocytes is to transport calcium and other ions between the bone minerals and the blood plasma, and is also involved in routine turnover of bone matrix [4]. From biomechanics perspective, mechanical loading plays a critical role in driving bone to remodel to a prop- er shape, which has been a basis for many medical and healthcare disciplines, such as orthopedics and orthodon- tics. Over the past four decades, prosthetic dentistry and dental implantology have evolved as a significant field  W. Li et al. of study, which has gained considerable popularity in clinic for an increased aging population. Dental implants alter the oral mechanical environment and change the force transfer from crown to bone bed. As a consequence of this, the bone may engage in a process of biological remodeling, whereby the mandible and/or maxilla bone is self-adapted to the new functional requirements. Such a process may in turn influence the long-term success of the implanted prostheses in either a negative or a positive manner. On the one hand, a prosthetic device may not remain well-supported if its bone bed gradually disappears due to unsuitable or abnormal biomechanical patterns. On the other hand, the adaptive course may strengthen the bone/prosthesis as a whole if a desirably “positive” remodeling can be stimulated [2]. For the above reasons, understanding how bone responds to implantation through force application signifies an important topic of research. This paper aims to address the mechanobiological issue for bone remodeling in- silico. It will take a case scenario of dental implant driven bone remodeling and show the difference of how dif- ferent mechanical stimuli would affect the long term outcome. 2. Methods and Materials 2.1. Mechanical Stimuli There are many different mechanical stimuli proposed for long bone remodeling simulation. Several prevalent theories include: 1) the mechanostat model, where the induced effective mechanical strain is treated as a stimu- lus [1] [5]; 2) daily stress model [6], where the effect of daily cyclic loading pattern is considered; and 3) Strain Energy Density (SED) model [7], where the amount of distortion energy in the bone is extrapolated to be used as a trigger for bone remodeling. These mechanical stimuli can be related to the adaptive process that is driven by the “error signals” between their magnitude and corresponding reference [2] [8] [9]. The mechanostat theory proposed by Frost [1] drives bone remodeling by the error signal arising from the difference between effective strains given by, ( ) () () 22 2 1223 31 1 2 eff ψεεεε εεε ≡ =−+−+− (1) and minimum effective strain (MES) [1], where ε 1, ε 2 and ε 3 are the principal strains. As such, mechanical strains greater than the upper limit of MES leads to bone apposition, and smaller than the lower limit causes bone resorption. These two thresholds (upper and lower thresholds) were identified by Frost [1] to be 0.015% and 0.15%, respectively, whereas the lazy zone between these two thresholds indicates that the remodeling process is inactive or in equilibrium. It is worth noting that although strain itself is highly direction-dependent, there is no directional effect in the mechanostat model. In addition, these MES values may need to be specified for jaw bones to include the site dependency of bone remodeling [10] [11]. The second mathematical model incorporates the effect of daily cyclic loading pattern into the mechanical stimuli formulation [6]. Literature suggests that the average biting force on implant supported prosthesis can vary from 42 to 412 N, with average frequency of 0.23 - 0.3 contact/sec for a total period of 9 - 17 minutes per day [12] [13]. From these data, approximately 207 daily chewing cycles are expected in an average human. However, this gives no indication as how the loading magnitude due to chewing may vary in a human mouth, because it is obvious that the chewing force in the human jaw is not a constant and can vary according to the different foods being chewed. For example, greater chewing force may be used when a person is chewing meat, and lesser force is needed to chew soft rice. The number of loading cycles in human mouths may also vary ac- cording to the different foods being chewed. It is extremely difficult to determine the exact chewing pattern of an “average” human, since this can vary according to culture, age, gender and socio-economic variations amongst human population groups and such data is scarce. For the purpose of this study, the chewing pattern of an average human being from different reference resources was estimated as in Table 1. A daily stress stimulus, σday, can be derived as [6]: 1 1 m Nm dayi i i n ψσ σ = ≡= ∑ (2) where ni is the number of chewing cycles, σi is the corresponding mechanical stress and m is an empirical con- stant (m = 2 is typically chosen in the literature [6] and was used in this study).  W. Li et al. Table 1. Estimated daily chewing pattern. Number of chewing cycles Load (N) 80 42 50 120 40 200 25 300 12 412 The third mechanical stimulus is a scalar quantity known as the strain energy density (SED) advocated by Huiskes et al. [7]. One of the advantages of using this model is that, the directional nature of the stress/strain tensor can be neglected in the analysis, therefore eliminating the ambiguity of the results. The strain energy den- sity model has been used in many bone remodeling studies for dental bone scenarios [14] [15]. In finite element analysis, the strain energy of the element can be mathematically expressed as: (3) where U is the strain energy, σij and εij are the stress and strain tensors, respectively. 2.2. Mechanobiological Remodeling Rule To tackle the proposed dental bone remodeling problem, the implant-induced change in the bone density must be determined, which employ a mechanical stimulus as a mechanobiological trigger. Mathematically, re- modeling-induced density variation ∆ ρ over time increment ∆t can be expressed in terms of the stimulus error (signal), and a lazy zone measure of δ as [2] [14] [15]: ()( )()( )() ()( )()()() ( )()()() ,1, if,1 ,1, if,1 0,if 1,1 Ctt t Ctt t t ρ ψδψψδψ ρ ψδψψδψ ρδψ ψδψ ∆ =−+∆>+ ∆ =−−∆≤+ ∆ =−≤≤+ xx x xx x xx (4) By adding this incremental density onto the existing density, the new density can be updated as, () () () ( ) () () 1 k kk ρ ρρ + = +∆xx x (5) where superscript k denotes the kth time step of remodeling process. 2.3. Finite Element Modeling Two models are generated: Model I simulates the buccual-lingual section of mandible and Model II represents the mesial-distal section, as illustaretd in Figure 1. These two models are used in this study to investigate the difference in bone remodeling results from the different sections. Both the models consist of four parts, the tita- nium dental implant, the crown, a layer of cortical bone and the cancellous bone. The choices of mesh size used in the models were determined based on convergence tests as in [16] [17]. The final finite element (FE) meshes in Fig ure 1 consist of 6570 triangular elements in Model I (plane strain), and 8157 elements in Model II (plane stress) . As in Figure 1, a mechanical load of 200N was applied on top of the crown for the mechanostat and strain energy density cases [2] [8]. In the daily stress case, a unit load of 1N was used. Each FE calculation would produce stress tensors based on this unit load. The real loading magnitudes used for generating the daily stress model would be simply to multiply the unit tensors by the different magnitudes as given in Table 1. The boundary condition for Model I is constrained around the bottom edge, which allows buccal-lingual de- formation in the cervical part, whilst Model II is constrained around the two edges of the model that are attached to its neighboring jaw bone. The material properties of both cortical and cancellous bones were treated as isotropic linear elastic materials as adopted in most dental bone analyses and remodeling studies to date [2] [18]. 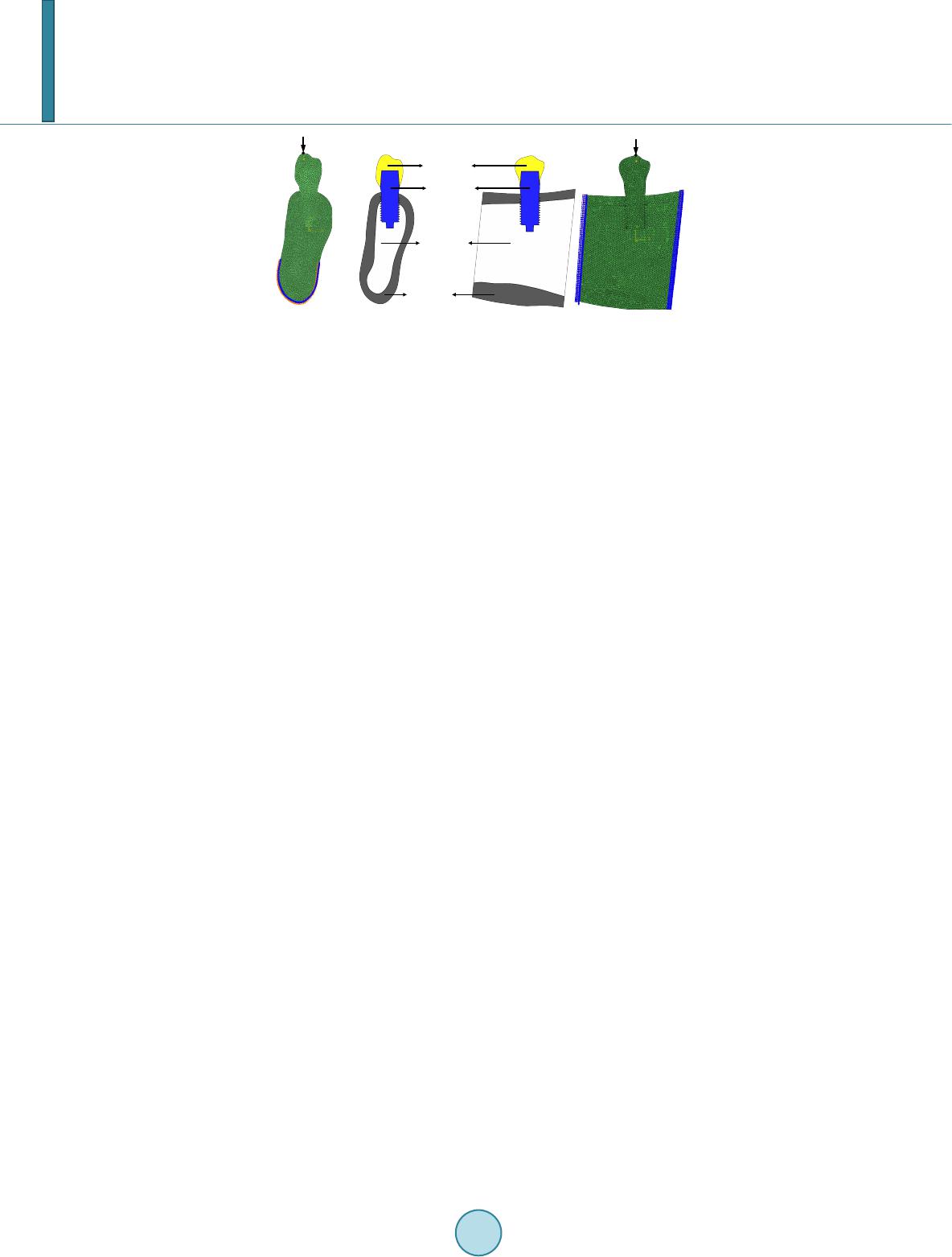 W. Li et al. (a) (b) Figure 1. Finite element Model I and Model II of mandibular section. (a) Model I: buccal-lingual section; (b) Model II: mesial-distal section. 3. Results and Discussion 3.1. Model I—Bu ccal-Lingual Section Figure 2(a) and Figure 2(b) depict the remodeling results of average cortical and cancellous bone densities when these three mechanical stimuli are respectively used in Model I over a 24 month period. It is seen that in general, the overall density of bony tissues increases for these three different mechanical stimuli considered, which signify a positive remodeling processes. Figure 2(a) indicates that the average cortical bone density in- creases in a monotonic fashion. It is suggested that the remodeling activity is relatively low in the cortical region if a daily stress stimulus is used. Furthermore, the average cortical bone density obtained from the mechanostat and daily stress stimuli are almost identical over the entire remodeling processes. However, this does not imply that final density distributions derived by these two stimuli are identical because the density in Figure 2(a) is averaged over the per-implant region and could not differentiate the specific resorption and apposition. It is clear that the remodeling driven by the strain energy density causes more cortical bone growth over the 24 month pe- riod. On contrary, the adoption of the daily stress and mechanostat leads to less overall gain of cortical bone densi t y. Figure 2(b) exhibits the change in the average cancellous bone density over the 24 month period. Again, some degree of similarity between the mechanostat and daily-stress remodeling can be observed, especially after month 14. In addition, the average cancellous densities obtained from the mechanostat and daily stress remode- ling are consistently higher than that obtained from the SED stimuli, which are in contrast to the results in the cortical bone aforementioned. An explanation can be that much stimulation energy (an integration of the multip- lication of stress and strain components) has been absorbed in the stiffer cortical bone region, while large strain occurs in the soft cancellous bone, thereby resulting overall in a more intense mechanostat (strain) field. This also causes the average density from the daily-stress remodeling to be lower in the early healing stage. 3.2. Model II—Mesial-Distal Section The bone remodeling results for the mesial-distal sectional Model II are plotted in Fig ure 3(a) and Figure 3(b). It is evident that the progression with time of the average cortical density for all the stimuli investigated shows the increasing trends. The maximum average cortical bone densities after 24 months are 1.745 g/cm3 and 1.750 g/cm3, 1.742 g/cm3, respectively for SED, mechanostat and daily stress. Figure 3(a) shows a surprising result where the average cortical bone density is the highest when the daily stress stimulus is used, which is different from the results obtained in Model I. This is because the upper cortical bone region in Model II is more like a simply-supported beam where the overall bending stress is lower than a compressive stress in Model I. Figure 3(b) depicts the change in the average cancellous bone density, where the rates of remodeling appear higher than those in the cortical bone for these three stimulus cases. This implies that in Model II, the cancellous bone seems to be more stimulated by the load. After the 24 month remodeling, the SED, mechanostat and daily stress stimuli generate the average densities of 0.930 g/cm3, 0.929 g/cm3 and 0.930 g/cm3 for the cancellous bone, respectively. Interestingly, the amount of cancellous bone remodeling is higher in the daily stress stimuli than that in the mechanostat model. This indicates that Model II provides a more positive overall stress field in the cancellous region due to the direct connection with its kinematic boundaries. Crown Titanium implant Cortical bone Cancellous bone AB 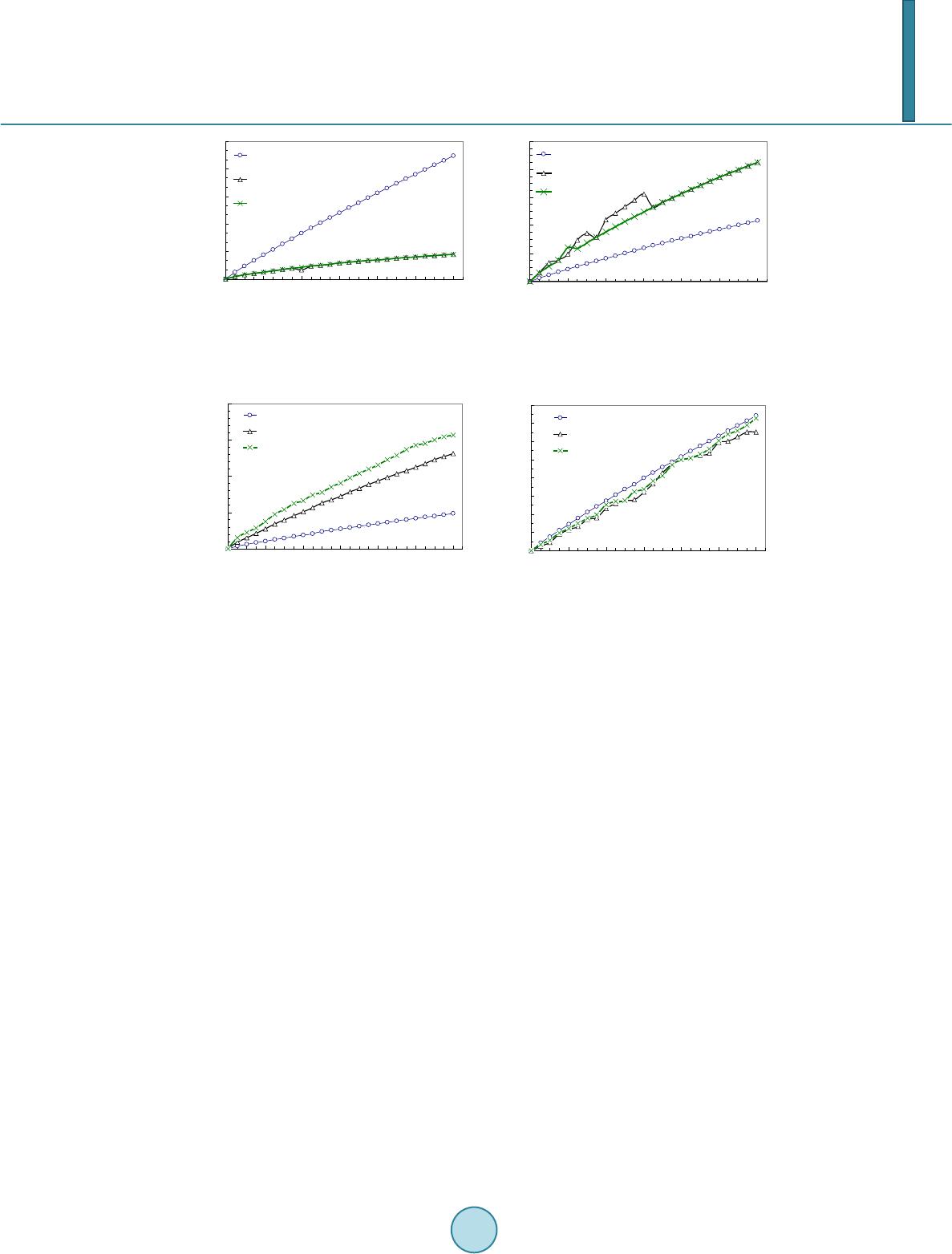 W. Li et al. (a) (b) Figure 2. (a) Change of average cortical bone density; (b) Change of average cancellous bone density (Model I). (a) (b) Figure 3. (a) Progression of average cortical bone d ensity; (b) Progression of average cancellous bone density (Model II). Revelation resulting from the bone remodeling analysis suggests an overall positive bone remodeling pheno- menon. However, no visible signs of equilibrium status can be observed over the 24 months. Upon a first glance, the results do not appear to be sensible, but further interpretation of the results shows that, while positive re- modeling is implicated to the entire structure, certain areas in the bony tissues are subjected to higher stress due to greater exposure to the source of loading, thereby conjugating a higher bone density due to bone remodeling (i.e. implant neck region at the cortical shell). Consequently, certain areas in the structure which are located fur- ther from the source of loading are subjected to a lower stress/strain field, resulting in less bone remodeling or even bone resorption (i.e. bottom of the cortical shell). This leads to the average bone density in both cortical and cancellous tissues being lower compared to their maximum possible density (2.0 g/cm3 for cortical bone and 1.2 g/cm3 for cancellous bone). Therefore, it is likely that the higher stressed zones did reach equilibrium status, while certain regions are still resorbing and hindering the approach towards a steady state of bone remodeling. 4. Conclusion This paper provides a comparative study on prediction of the mandibular bone remodeling based on three wide- ly-used mechanical stimuli developed in long bone research community, namely mechanostat, daily stress and strain energy density. To observe the different aspects of changes that occurs in the bone anatomy, two different sectional models, namely Model I in buccal-lingual section (a plane strain problem) and Model II in mesial-dis- tal section (a plane stress problem) in the mandible created from the CT image data. Under a certain mechanical loading, the density changes in the cortical and cancellous bones are computed from these three stimuli, respec- tively. The differences are clearly shown through plotting the density evolution at different healing time steps. It is observed that a positive remodeling (i.e. apposition) becomes more significant after 6 to 12 months of healing for both the models and these three stimuli, which matches to the clinical observation well [8] [10]. Acknowledgements Financial support from Australian Research Council (ARC) through Discovery Scheme is acknowledged. 1.740 1.743 1.746 1.749 1.752 1.755 04812 16 20 24 Strain energy density mechanostat daily stress 0.900 0.920 0.940 0.960 0.980 1.000 0481216 20 24 strain energy density Mechanostat Daily Stress 1.740 1.744 1.748 1.752 1.756 048 12 1620 24 Cortical bone density (g/cm^3) strain energy density mechanostat daily stress 0.900 0.904 0.908 0.912 0.916 0.920 0.924 0.928 0.932 048 12 1620 24 Cancellous bone density (g/cm^3) strain energy density mechanostat daily stress  W. Li et al. References [1] Frost, H.M. (1987) Bone Mass and the Mechanostat—A Proposal. Anatomical Record, 219, 1-9. http://dx.doi.org/10.1002/ar.1092190104 [2] Lin, D., Li, Q., Li, W. and Swain, M.V. (2009) Dental Implant Induced Bone Remodeling and Associated Algorithms. Journal of the Mechanical Behaviour of Biomedical Materials, 2, 410-432. http://dx.doi.org/10.1016/j.jmbbm.2008.11.007 [3] Chen, J.N., Li, W., Swain, M.V., Darendeliler, M.A. and Li, Q. (2014) A Periodontal Ligament Driven Bone Remode- ling Algorithm for Orthodontic Tooth Movement. Journal of Biomechanics, 47, 1689-1695. http://dx.doi.org/10.1016/j.jbiomech.2014.02.030 [4] McLean, F.C. and Urist, M.R. (1968) Bone. 3rd Edition, University of Chicago, Chicago. [5] Frost, H.M. (1990) Skeletal Structural Adaptations to Mechanical Usage (Satmu), Redefining Wolff Law—The Re- modeling Problem. Anatomical Record, 226, 414-422. http://dx.doi.org/10.1002/ar.1092260403 [6] Beaupre, G.S., Orr, T.E. and Carter, D.R. (1990) An Approach for Time-Dependent Bone Modeling and Remodeling —Theoretical Development. Journal of Orthopaedic Research, 8, 651-661. http://dx.doi.org/10.1002/jor.1100080506 [7] Huiskes, H.R., Weinans, H., Grootenboer, J., Dalstra, M., Fudala, B. and Slooff, T.J. (1987) Adaptive Bone Remode- ling Theory Applied to Prosthetic Design Analysis. Journal of Biomechanics, 20, 1135-1150. http://dx.doi.org/10.1016/0021-9290(87)90030-3 [8] Lin, D., Li, Q., Li, W., Duckmanton, N. and Swain, M.V. (2010) Mandibular Bone Remodeling Induced by Dental Im- plant. Journal of Biomechanics, 43, 287-293. http://dx.doi.org/10.1016/j.jbiomech.2009.08.024 [9] Rungsiyakull, C., Rungsiyakull, P., Li, Q., Li, W. and Swain, M.V. (2011) Effects of Occlusal Inclination and Loading on Bone Remodeling. The International Journal of Oral & Maxillofacial Implants, 26, 527-53 7. [10] Field, C., Li, Q., Li, W., Thompson, M. and Swain, M.V. (2010) Prediction of Mandibular Bone Remodeling Induced by Fixed Partial Dentures. Journal of Biomechanics, 43, 1771-1779. http://dx.doi.org/10.1016/j.jbiomech.2010.02.016 [11] Field, C., Li, Q., Li, W., Thompson, M. and Swain, M.V. (2012) A Comparative Mechanical and Bone Remodeling Study of All-Ceramic Posterior Inlay and Onlay Fixed Partial Dentures. Journal of Dentistry, 40, 48-56. http://dx.doi.org/10.1016/j.jdent.2011.10.003 [12] Stanford, C.M. and Brand, R.A. (1999) Toward an Understanding of Implant Occlusion and Strain Adaptive Bone Mo- deling and Remodeling. Journal of Prosthetic Dentistry, 81, 553-561. http://dx.doi.org/10.1016/S0022-3913(99)70209-X [13] Khrai sat, A., Hashimoto, A., Nomura, S. and Miyakawa, O. (2004) Effect of Lateral Cyclic Loading on Abutment Screw Loosening of An External Hexagon Implant System. Journal of Prosthetic Dentistry, 91, 326-334. http://dx.doi.org/10.1016/j.prosdent.2004.01.001 [14] Lin, D., Li, Q., Li, W. and Swain, M.V. (2010) Bone Remodeling Induced by Dental Implants of Functionally-Graded Materials. Journal of Biomedical Materials Research: Part B—Applied Biomaterials, 92B, 430-438. [15] Lin , D., Li, Q., Li, W., Zhou, S.W. and Swa i n, M.V. (2009) Design Optimization of Functionally Graded Dental Im- plant for Promoting Bone Remodeling. Composites Part B Engineering, 40, 668-675. http://dx.doi.org/10.1016/j.compositesb.2009.04.015 [16] Li, W., Swain, M.V., Li, Q., Ironside, J. and Steven, G.P. (2004) Fibre Reinforced Composite Dental Bridge. Part II: Numerical Investigation. Biomaterials, 25, 4995-5001. http://dx.doi.org/10.1016/j.biomaterials.2004.01.011 [17] Li, W., Swain, M.V., Li, Q., Ironside, J. and Steven, G.P. (2005) Towards Automated 3D Finite Element Modeling of Direct Fiber Reinforced Composite Dental Bridge. Journal of Biomedical Materials Research Part B—Applied Bio- materials, 74B, 520-528. http://dx.doi.org/10.1002/jbm.b.30233 [18] Chen, J.N., Rungsiyakull, C., Li, W., Chen, Y.H., Swain, M.V. and Li, Q. (2013) Multiscale Design of Surface Mor- phological Gradient for Osseointegration. Journal of the Mechanical Behavior of Biomedical Materials, 20, 387-397. http://dx.doi.org/10.1016/j.jmbbm.2012.08.019
|