Paper Menu >>
Journal Menu >>
 Geomaterials, 2011, 1, 1-13 doi:10.4236/gm.2011.11001 Published Online April 2011 (http://www.SciRP.org/journal/gm) Copyright © 2011 SciRes. GM A Coal Mine Dump Stability Analysis —A Case Study Ashutosh Kainthola*, Dhananjai Verma, S. S. Gupte, T. N.Singh Department of Earth Sciences, Indian Institute of Technology Bombay , Mumbai, India E-mail: ashuddn@live.com Received April 12, 2011; revised April 14, 2011; accepted April 18, 2011 Abstract The present paper mainly deals with a case study of failed dump slope in western coalfield limited, Nagpur, India. A huge mass of debris flow had happened during the routine the activity of mining. The failed dump had a height of 75 m with 43˚ slope angle which had slipped forward by 18m. Representative loose dump material samples were collected from the site and tested to determine the physico-mechanical properties of dump material. The dump material consisted of loose fragments and lumps of friable sandstone, shale, clay and carbonaceous shale. To evaluate the condition of failure, a well known, shear strength reduction tech- nique has been applied to achieve the desired factor of safety using two dimensional finite element code. Fi- nally, a economical, sustainable and stable dump angle and height has been suggested for smooth and safe disposal of the dump. Keywords: Dump Stability, Factor of Safety, Shear Strength Reduction, Wardha Valley 1. Introduction With the increasing size of opencast mines and the large stripping ratio associated with these mines, the amount of overburden removal will also increase substantially. Only Coal India Limited (CIL) has removed overburden 21, 160, 462 and 695 million cubic metres during 1976, 1986 - 87, 1999 - 2000 and 2009 - 2010 respectively. Considering the major opencast projects XII Five Year plan, the amount of overburden to be handled in near future will be more than 20 000 million cubic metres for these projects alone. The maximum overburden disposal from an individual mine in the coal sector is likely to be 50 million cubic metres per year (WCL). Overburden dumps can be external dumps created at a site away from the coal bearing area or it can be internal- dumps created by in-pit dumping (IPD) concurrent to the creation of voids by extraction of coal. Practice of dumping overburden in the external dumps have some serious problems [1] foremost amongst them are re- quirement of additional land, involves very high trans- port and rehandling cost which will increase the cost of coal production subs tantially, stability an d reclamation at the site. It is not possible to eliminate the option of the external dumps concept completely, even if we adopt IPD practice. The internal dump concept is very well utilized by various local produ cing countries like Austra- lia, Canada and USA, then there is no fear to adopt this technique to avoid further requirement of land for dumping and aggravate various associated problems. However, the combination of external dumps and inter- nal dumps shall substantially reduce the required land. As a result, it shall reduce the surface land requirement significantly which is very difficu lt task to arrang e in an y area due to growth of population forest cover and associ- ated problem. In this decade few destabilization of in ter- nal dumps have taken place in coal mines. It is necessary to study such cases and find out the cause of destabiliza- tion. 2. Destabilization of Internal Dumps Failure of internal dumps is a complex problem. In addi- tion to environmental considerations, it directly affects the resource recovery, mine safety and mining cost. Overburden has been traditionally disposed off in the most economical way throughout the world. However, some massive spoil pile failures around the world attract the attention of geo-scien tists and engineers to this prob- lem [2-4]. The stability of dump is now reco gnized to be an important aspect of designing large open pit mines. The majority of slope stability analyses performed in  2 A. KAINTHOLA ET AL. practice still use traditional limit equilibrium approaches involving methods of slices that have remained essen- tially unchanged for decades. The finite element method represents a powerful alternative approach for slope sta- bility analysis which is use to accurate, versatile and re- quires fewer a priori assumptions, especially, regarding the failure mechanism. Slope failure in the finite element model occurs ‘naturally’ through the zones in which the shear strength of the dump material is insufficient to re- sist the shear stresses. It is argued that the finite element method of slope stability analysis is a more powerful alternative to traditional limit equilibrium methods and its wide-spread use should be standard in geotechnical practice [5]. Elasto-plastic analysis of geotechnical problems using the finite element method (FEM) has been widely ac- cepted in the research area for many years; however, its routine use in geotechnical practice for slope stability analysis still remains limited. The challenge for an ex- perienced engineer is to know which kind of problem would benefit from a FEM treatment and which would not. In general, linear problems such as the predictions of settlements and deformations, the calculation of flow quantities due to steady seepage or th e study of transient effects due to consolidation are all highly amenable to solution by finite element. 3. Factors Affecting Dump Failure In dump materials, failure is likely to form as a shallow, large radius surface extending from a tension crack close behind the crest to the toe of the slope (Figure 1). It fails in a circular manner as the slope dimensions are substan- tially greater than the dimensions of the rock fragments. The actual shape of the “circular” slide surface is influ- enced by the geological conditions in the slope mass. The slopes with loose, weak and soft rock masses can basically have three different failure geometries viz. slope failure, toe failure and base failure (Figure 2). In the slope failure, the arc of rupture surface meets the slope above the toe. This is possible only when slope angle steep and the soil close to the toe possess high strength. Toe failure occurs when the soil mass of the slope above the base and below the base is mainly ho- mogeneous. There are a number of factors, which affect the dump stability [6-8]. These factors are broadly classified as: ● Geometry and strength of the dump material, ● Hydro geological and rain water condition of dumping area, ● Load bearing capacity of dumping ground, and ● External loading conditions The slope geometry and the geo-mechanical strength of the dump material always control the stability of the dump [2,9,10]. Dump material is anisotropic in their be- havior and its stress-strain behavior is quite erratic, ow- ing to the presence of clay mineral. The visco-elastic behavior due to the presence of water poses serious threat during the rainy season. The shear strength reduc- tion due to rise in pore water pressure leads to the failure. Consolidation and compaction is another key factor be- cause of the uneven size distribution of the dump mate- rial. Bearing capacity of the ground has a direct influence on the stability of the dump slope. A sloping ground with low bearing capacity lead destabilizing of the dump slope stability due to foundation failures [11]. High variation in temperature can cause dump material to spall due to the accompanying dilation. Water freezing in voids may causes damage by further loosening the slope material. Repeated freeze/thaw cycles may result in gradual loss of strength. Except for periodic maintenance requirements, temperature effects are a surface phe- nomenon and are most likely of little concern for final waste dump slopes. However, in a few cases, surface weakening could activate dump slope instability in large scale [12]. Figure 1. View of the failed dump slope. Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. 3 Figure 2. Different type s of failure in waste dump slopes. Ground water and surface water flow condition plays a critical role on the stability of dump slope. Frictional strength is reduced as the height of the dump is raised, due to the presence of water. The pore water pressure reduces the normal stress acting on the material. The cohesive strength of weak geo-material will be further reduced due to presence of pore water pressure. Waste dump placed in a loose state, shear failure is often fol- lowed by static liquefaction which is complete loss of strength [13]. The flow of water may enhance the seep- age force, leading to the formation and migration of ten- sion cracks. Erosion also plays an important role in affecting the stability by surface weathering [14], groundwater or sur- face-water seepage [15,16], toe erosion and slope modi- fication [17], primary is massive scale erosion, such as river erosion at the toe of the river bed. The other one is comparatively localized erosion caused due to ground- water or surface runoff. Erosion changes the waste dump slope geometry and morphological characters. The weathering and attrition of material at the toe of a poten- tial slide reduces the restraining force that may destabi- lize the slope. Erosion of void filling material, or zones of percolation, can efficiently decrease cohesion among grain boundaries. The decease of cohesive strength nota- bly reduces the rock mass shear strength. The decrease in shear strength may allow movement in dump slope along weak plane. In addition, lo calized erosion may also result in increased permeability and ground-water flow either the slope. This may lead to failure due to formation of gully and deep flow channels in dump. 4. Failure Criterion and Geo- Mechanical Strength Parameters of the Dump Material Mohr- Coulomb’s failure criterion was used for the nu- merical analysis of the dump material. The soft and loose mine dumps are mostly fine grained material. The shear failure in dumps is by slippage of particles shear failure. The failure is caused by a critical combination of normal and shear stresses. The dump material fails when the shear stress on the failure plane at failure is an exclusive function of the normal stress acting on that plane. This failure criterion is concerned with the sh ear stress at failure plane at failure. The curve defined by this is known as the failure envelope. The shear strength of a material at a point on a particular plane was expressed by Coulomb as a linear function of the normal stress on that plane, τ = c + tan(φ), where τ is the shear strength, σ is Copyright © 2011 SciRes. GM 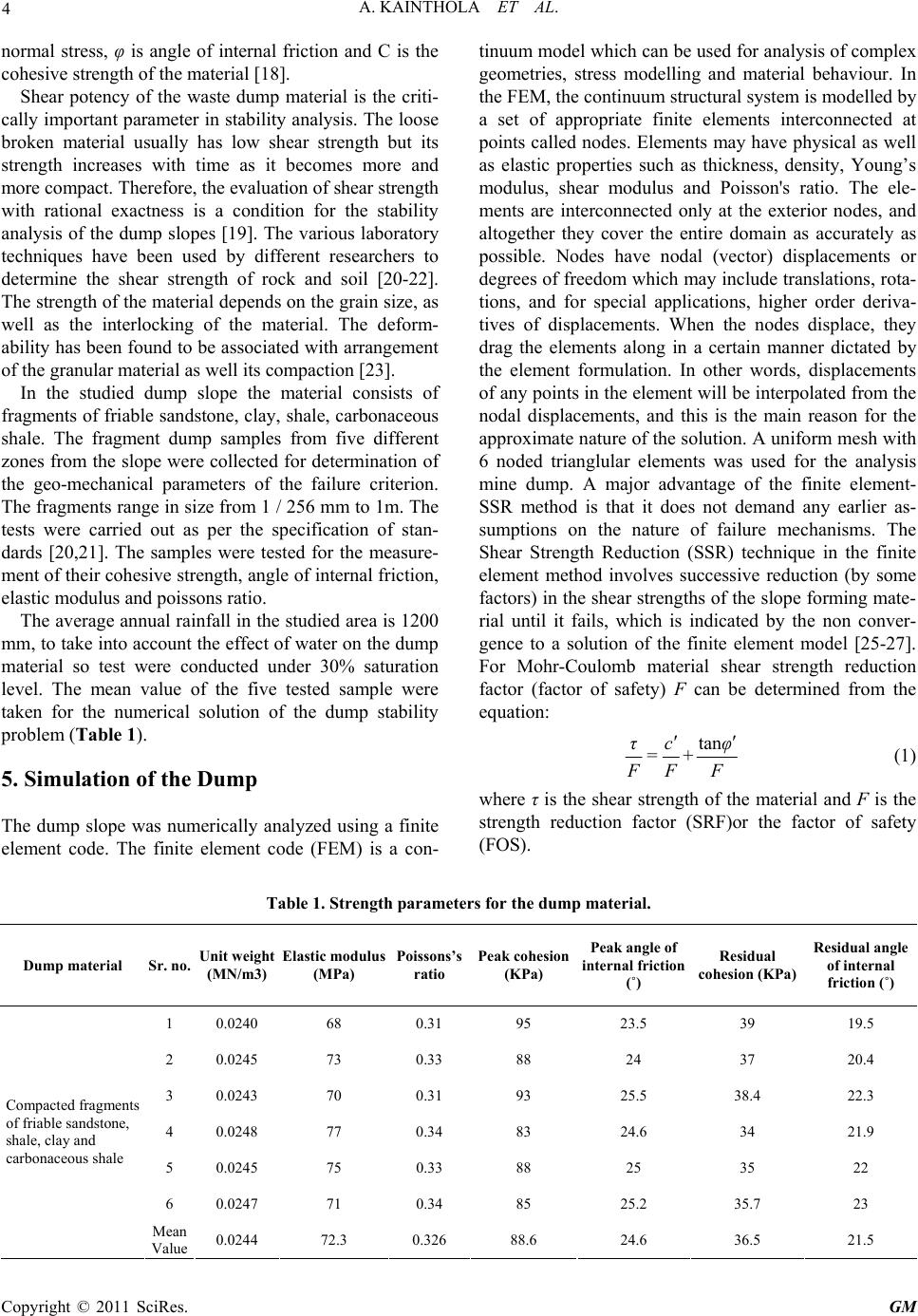 4 A. KAINTHOLA ET AL. normal stress, φ is angle of internal friction and C is the cohesive strength of the material [18]. Shear potency of the waste dump material is the criti- cally important parameter in stability analysis. The loose broken material usually has low shear strength but its strength increases with time as it becomes more and more compact. Therefore, the evaluation of shear strength with rational exactness is a condition for the stability analysis of the dump slopes [19]. The various laboratory techniques have been used by different researchers to determine the shear strength of rock and soil [20-22]. The strength of the material depends on the grain size, as well as the interlocking of the material. The deform- ability has been found to be associated with arrangement of the granular m at e rial as well its compaction [23]. In the studied dump slope the material consists of fragments of friable sandstone, clay, shale, carbonaceous shale. The fragment dump samples from five different zones from the slope were collected for determination of the geo-mechanical parameters of the failure criterion. The fragments range in size from 1 / 256 mm to 1m. The tests were carried out as per the specification of stan- dards [20,21]. The samples were tested for the measure- ment of their cohesive strength, angle of internal friction, elastic modulus and p oisso ns rat i o. The average an nual rainfall in the stud ied area is 1200 mm, to take into account the effect of water on the dump material so test were conducted under 30% saturation level. The mean value of the five tested sample were taken for the numerical solution of the dump stability problem (Table 1). 5. Simulation of the Dump The dump slope was numerically analyzed using a finite element code. The finite element code (FEM) is a con- tinuum model which can be used for analysis of complex geometries, stress modelling and material behaviour. In the FEM, the continuum structural system is modelled by a set of appropriate finite elements interconnected at points called nodes. Elements may have physical as well as elastic properties such as thickness, density, Young’s modulus, shear modulus and Poisson's ratio. The ele- ments are interconnected only at the exterior nodes, and altogether they cover the entire domain as accurately as possible. Nodes have nodal (vector) displacements or degrees of freedom which may include translations, rota- tions, and for special applications, higher order deriva- tives of displacements. When the nodes displace, they drag the elements along in a certain manner dictated by the element formulation. In other words, displacements of any points in the element will be in terpolated from the nodal displacements, and this is the main reason for the approximate nature of the solutio n. A uniform mesh with 6 noded trianglular elements was used for the analysis mine dump. A major advantage of the finite element- SSR method is that it does not demand any earlier as- sumptions on the nature of failure mechanisms. The Shear Strength Reduction (SSR) technique in the finite element method involves successive reduction (by some factors) in the shear strengths of the slope forming mate- rial until it fails, which is indicated by the non conver- gence to a solution of the finite element model [25-27]. For Mohr-Coulomb material shear strength reduction factor (factor of safety) F can be determined from the equation: tanτcφ =+ F FF (1) where τ is the shear strength of the material and F is the strength reduction factor (SRF)or the factor of safety (FOS). Table 1. Strength parameters for the dump material. Dump material Sr. no. Unit weight (MN/m3) Elastic modulus (MPa) Poissons’s ratio Peak cohesion (KPa) Peak angle of internal friction (˚) Residual cohesion (KPa) Residual angle of internal friction (˚) 1 0.0240 68 0.31 95 23.5 39 19.5 2 0.0245 73 0.33 88 24 37 20.4 3 0.0243 70 0.31 93 25.5 38.4 22.3 4 0.0248 77 0.34 83 24.6 34 21.9 5 0.0245 75 0.33 88 25 35 22 6 0.0247 71 0.34 85 25.2 35.7 23 Compacted fragments of friable sandstone, shale, clay and carbonaceous shale Mean Value 0.0244 72.3 0.326 88.6 24.6 36.5 21.5 Copyright © 2011 SciRes. GM 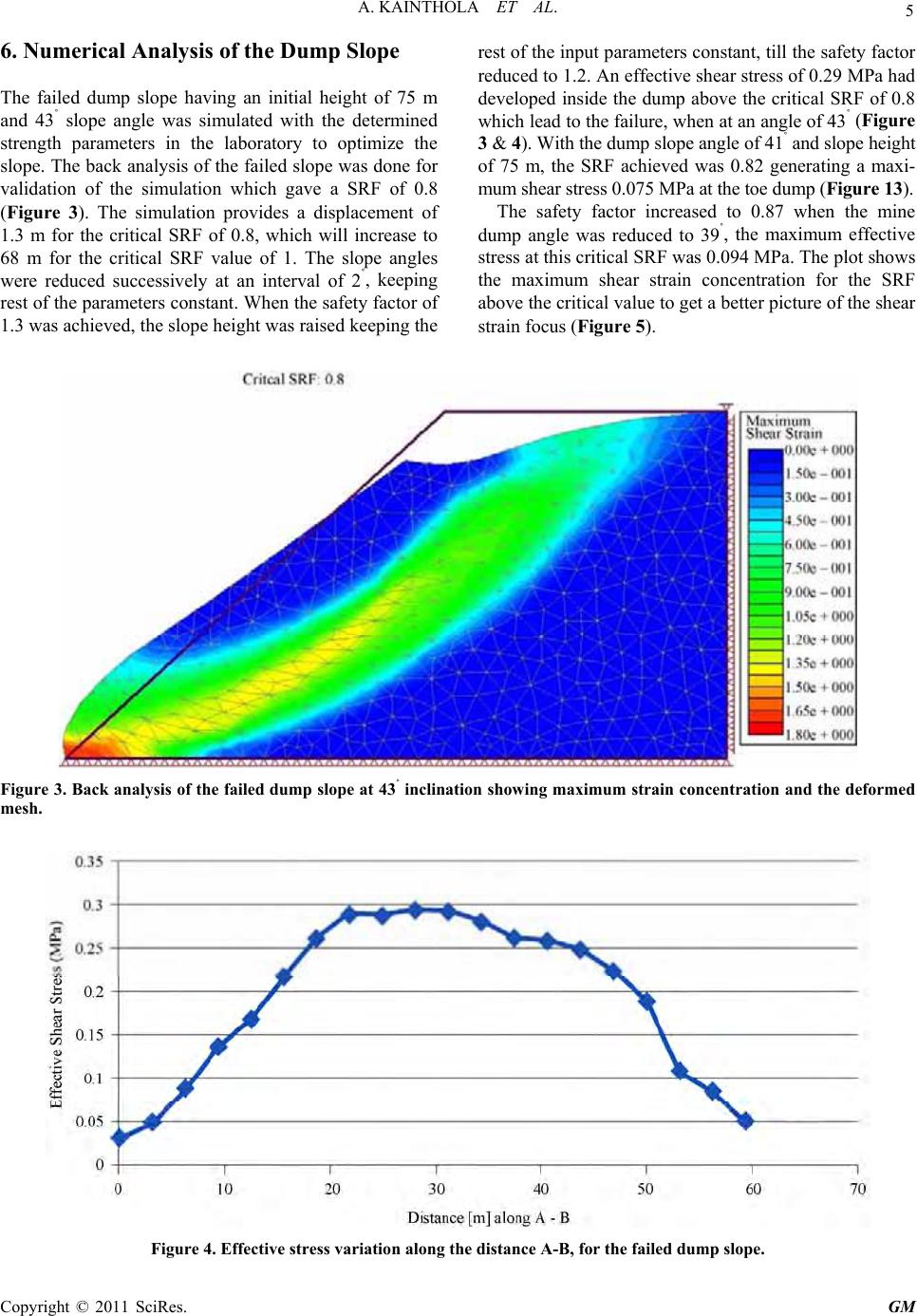 A. KAINTHOLA ET AL. Copyright © 2011 SciRes. GM 5 6. Numerical Analysis of the Dump Slope The failed dump slope having an initial height of 75 m and 43˚ slope angle was simulated with the determined strength parameters in the laboratory to optimize the slope. The back analysis of the failed slope was done for validation of the simulation which gave a SRF of 0.8 (Figure 3). The simulation provides a displacement of 1.3 m for the critical SRF of 0.8, which will increase to 68 m for the critical SRF value of 1. The slope angles were reduced successively at an interval of 2˚, keeping rest of the parameters constant. When the safety factor of 1.3 was achieved, the slope height was raised keeping the rest of the input parameters constant, till the safety factor reduced to 1.2. An effective shear stress of 0.29 MPa had developed inside the dump above the critical SRF of 0.8 which lead to the failure, when at an angle of 43˚ (Figure 3 & 4). With the dump slope angle of 41˚ and slope height of 75 m, the SRF achieved was 0.82 generating a maxi- mum shear stress 0.075 MP a a t t he t oe dump (Figure 13). The safety factor increased to 0.87 when the mine dump angle was reduced to 39˚, the maximum effective stress at this critical SRF was 0.094 MPa. The plot shows the maximum shear strain concentration for the SRF above the critical value to get a better picture of the shear strain focus (Figure 5). Figure 3. Back analysis of the failed dump slope at 43˚ inclination showing maximum strain concentration and the deformed mesh. Figure 4. Effective stress variation along the distance A-B, for the failed dump slope. 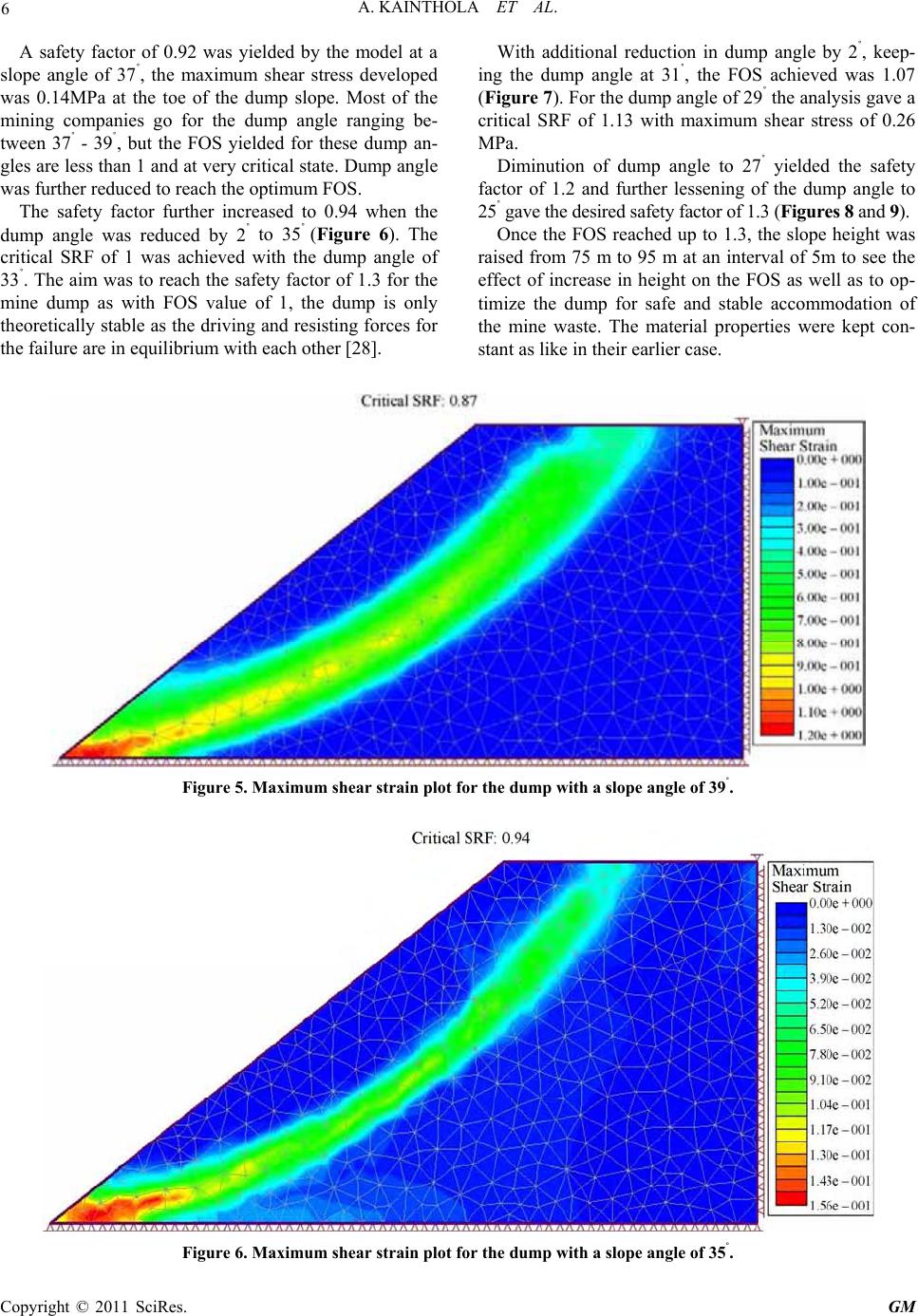 A. KAINTHOLA ET AL. Copyright © 2011 SciRes. GM 6 A safety factor of 0.92 was yielded by the model at a slope angle of 37˚, the maximum shear stress developed was 0.14MPa at the toe of the dump slope. Most of the mining companies go for the dump angle ranging be- tween 37˚ - 39˚, but the FOS yielded for these dump an- gles are less than 1 and at very critical state. Dump angle was further reduced to reach the optimum FOS. The safety factor further increased to 0.94 when the dump angle was reduced by 2˚ to 35˚ (Figure 6). The critical SRF of 1 was achieved with the dump angle of 33˚. The aim was to reach the safety factor of 1.3 for the mine dump as with FOS value of 1, the dump is only theoretically stable as the driving and resisting forces for the failure are in equilibrium with each other [28]. With additional reduction in dump angle by 2˚, keep- ing the dump angle at 31˚, the FOS achieved was 1.07 (Figure 7). For the dump angle of 29˚ the analysis gave a critical SRF of 1.13 with maximum shear stress of 0.26 MPa. Diminution of dump angle to 27˚ yielded the safety factor of 1.2 and further lessening of the dump angle to 25˚ gave the desired safety fact or of 1.3 (Figures 8 and 9). Once the FOS reached up to 1.3, the slope height was raised from 75 m to 95 m at an interval of 5m to see the effect of increase in height on the FOS as well as to op- timize the dump for safe and stable accommodation of the mine waste. The material properties were kept con- stant as like in their earlier case. Figure 5. Maximum shear strain plot for the dump with a slope angle of 39˚. Figure 6. Maximum shear strain plot for the dump with a slope angle of 35˚. 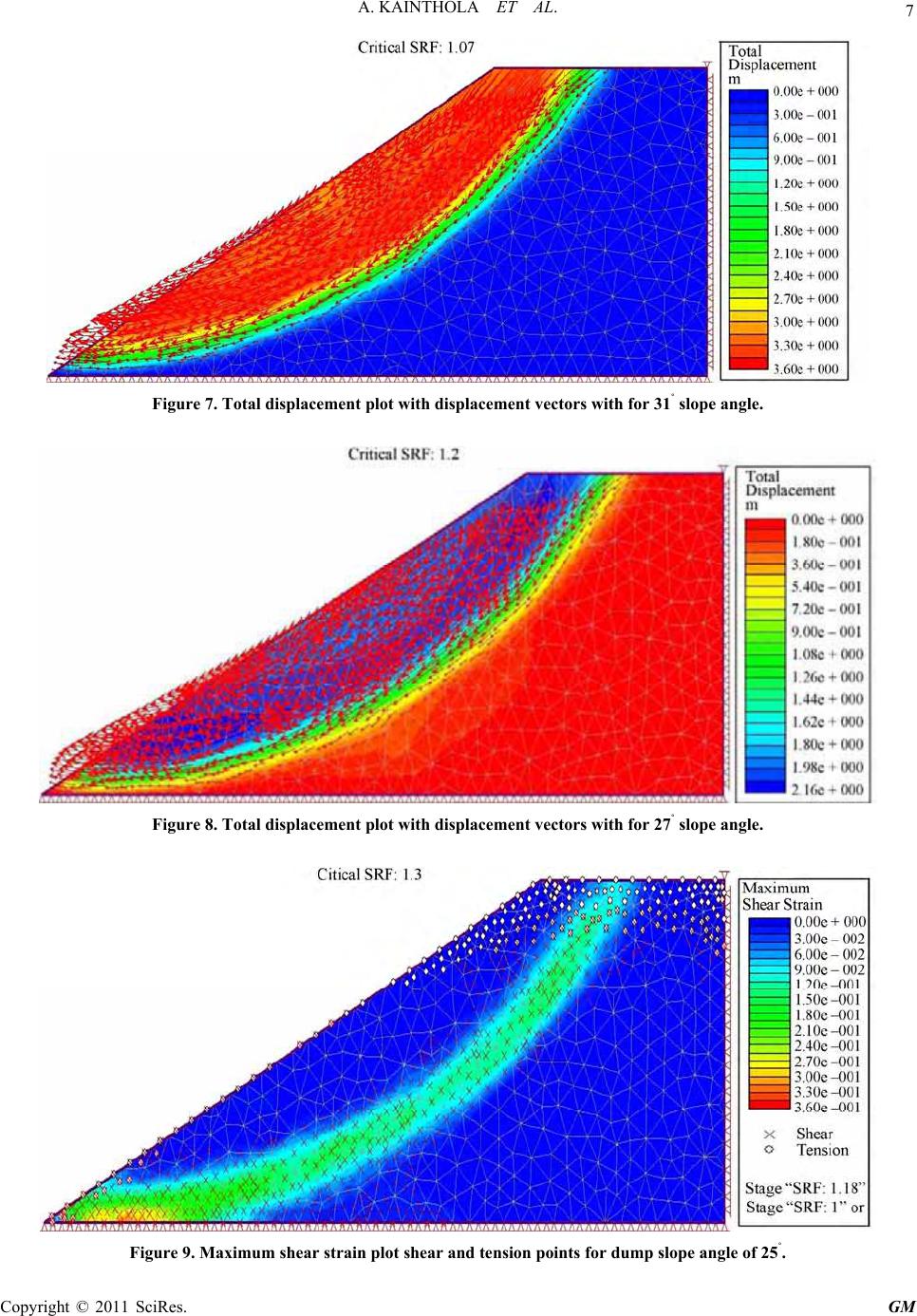 A. KAINTHOLA ET AL. 7 Figure 7. Total displacement plot with displacement vectors with for 31˚ slope angle. Figure 8. Total displacement plot with displacement vectors with for 27˚ slope angle. Figure 9. Maximum shear strain plot shear and tension points for dump slope angle of 25˚. Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. Copyright © 2011 SciRes. GM 8 The FOS reduced by 3% when the dump height was raised by 5 m (Figure 10). Effective shear stress of 0.045 MPa was developed at the toe of the dump with a height of 80 m. A critical safety factor of 1.22 was attained when the dump height was raised to 85m (Figure 11). It is it in- teresting to observe that, even changing the height from 85 m to 90 m does not affect FOS. When the height of the dump was raised further more with slope angle of 25˚, the FOS reduced up to 1.2 (Fig- ure 12). The simulation was stopped at 95 m slope height as raising more height would have given a much lesser value of FOS, which is undesired and not appro- priate. 7. Discussion A 75 m high failed dump slope consisting of low strength material was numerically solved and analyzed for slope angle optimization. The investigated mine dump having weak material strength gave a FOS value of 1 when it was at angle of 33˚ i.e. 10˚ less the original value at which it has already failed. Keeping the Dump height constant at 75 m the FOS varied logarithmically with th e dump slope ang le (Figure 13). FOS can be cor- related with dump angle for the 75 m high studied dump Figure 10. Maximum shear strain plot with tension and shear points for slope angle 25˚ and dump height of 80 m. Figure 11. Maximum shear strain plot with tension and shear points for slope angle 25˚ and dump height of 85 m.  A. KAINTHOLA ET AL. 9 Figure 12. Stress trajectories for dump slope angle 25˚ and dump height of 95 m. Figure 13. Correlation between dump slope angle Vs. FOS with constant slope he ight of 75 m. by the equation FOS= –0.91 ln (slope angle) + 4.215 (2) The aim was to reach a FOS of 1.3 for the optimum stability of the dump which was attained at an angle of 25˚ (Table 2). The effective shear stress along the dump slope length has been calcu lated to increase with FOS of the dump. This increase in stress can be attributed to the fact that, with higher SRF value for the model, the shear strength of the material will reduce significantly above the critical SRF value (Figure 14). The effective shear stresses have a similar trend for the different dump angles and FOS or SRF values along the dump slope length (Figure 15). The effective shear stress variation for different FOS/SRF values has been depicted against slope length which has been divided into 200 equal divisions for each lope length (Figures 14 and 15). s Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. 10 Table 2. Variation of FOS with respect to slope angle with constant height of 75 m. Slope angle FOS or SRF Percentage Increase in FOS 430 0.8 0 41 0.82 2.5 6 0 390 0.87 .09 370 0.92 5.7 350 0.94 2.1 330 1.0 6.3 310 1.07 7 290 1.13 5.6 270 1.2 6.2 250 1.3 8.3 Figure 14. Effective shear strain plot along the slope length for different dump angles. Figure 15. Effective shear strain plot along the slope length for different dump height. Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. 11 For better efficiency of the dump, managements the height was raised to keeping the dump angle constant at 25˚, till the FOS was reduced to 1.2 (Table 3). The FOS again reduced logarithmically with respect to the raise in dump height, Similar observation was expressed previ- ously by an author [30] (Figure 16). For the inve stigated dump with slope angle of 25˚ the FOS can be estimated with respect to the dump height using the empirical equa- tion, FOS= –0.41 ln (dump height) + 3.059 (3) Effective shear stress has increased with rise in dump height reaching a maximum value of 0.16 MPa for the 95 m dump (Figure 15). The results have only minor incon- sistencies, as there was no significant reduction in FOS when the dump height was raised from 85 m to 90 m. But the maximum effectiv ngth was raised 15). The generation of tension and shear zones on the dump slope model when in the critical state gives us a great deal of information about the critical zones which can be used for the stabilization. The rear vicinity and the slope surface of the dump are undergoing tension avoid of failure while the maximum shear strain concentration is at depth of 14 m from the dump surface (Figure 9). Generally, waste dumps are designed for factor of safety of 1.10 to 1.15 have only a minor risk of failure under saturated conditions. Waste dumps with a FOS less than 1.1 are subject to always used great risk, even with accurate data, it is due to the anomalous conditions re- lating to height and strength of dump material or the un- derlay which are likely to be present withthe dump. Such anomalous conditions may result in loal fluctua- e heig F e shear stress along the slope from 0.08 MPa to 0.1 MPa (Figure tion in the FOS by 10%. le c Table 3. Variation of FOS w.r.t slop Dump Height (m) FOS or SR ht with constant 25˚ slope angle. Percentage Reduction in FOS 75 1.3 80 1.26 3.07 85 1.22 3.17 0 1.63 90 1.22 95 1.2 Figure 16. Variation of FOS with respect to the dump height (constant dump angle 25˚) . Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. 12 8. Conclusion In pit dumping , particularly in Wes tern coal field Ltd., is very crucial due to the none availability of land as well as weak rock cond ition as well as heavy rain. In the pre- sent study a failed dump slope problem from India was numerically examined and based on back analysis, an optimum dump angle and height have been suggested for safe and stable dumping. The factor of safety was found to increase logarithmically with red uction in dump angle while keeping the dump height constant at 75 m. The dump slope gave an FOS of 1.3 when at an angle of 25˚ and height of 85 m and hence owing to the weak geo- mechanical strength of the dump it was suggested to keep the flatter slope of 25˚ with a height of 75 m. The FOS also reduced logarithmically when the dump height was raised up till 25 m. The numerical study provides a comprehensive understanding about the slope mecha- nism failure in weak material. led d like to thank the management of at Goonyella mine,” dian Geotechnical Journal, Vol. 18, 1981, pp. 179-194. P. A., “Slope stability analysis by finite elements,” Geotechnique, Vol. 49, No. 3, 1999 T. N., Singh, A. P. and Goyal, M., “Stability of Waste Dump and its Relation to Environment,” Indi nt Review, Vol. 9(2), 1994, pp. 15-21. d Singh, T. N., “Assessing instability of [9] Morgenstern, N. R. and Price, V. E., “The analysis of the stability of general slip surface,” Geotechnique, Vol. 15, No. 4, 1965, pp. 289-290. [10] Dawson, E. M., Roth W.H. and Drescher, A., “Slope Stability Analysis by St rength Reduction”, Geotechnique, Vol. 49, No. 6, 1999, pp. 835-840. [11] Khandelwal M. and Singh, T. N., “Prediction of Blast induced ground vibration using intelligent approach - A Case Study,” I33rd Mine Safety Workshop, Rajasthan, 2009, pp. 45-48. [12] Steiakakis, E., Kavouridis K. and Monopolis, D., “Large scale failure of the external waste dump at the South Field lignite mine,” Northern Greece, Engineering Geol- ogy Vol. 104, 2009, pp. 269-279. [13] Chowdhury, R., “Geotechnical Slope Analysis,” Pub- lished by CRC Press, New York, 2009, [14] Matsukura, Y. and Mizuno, K., “The influence of weath- ering on the geotechnical properties and slope angles of mudstone in the Mineoka earth-slide area,” Japan. Vol. 11, No. 3, 2006, pp. 263-273. [15] Norris, R. M. and Back, W., “Erosion of seacliffs by logy: The role of a, Boulder, Colo., 1990, pp. 283-290. er die Anwendung derselben in der Festig- tabilisation for a rd 9. Acknowgements groundwater. Groundwater Geomorpho he authors woulT Coa WCL, India, for their cooperation and support during the field work. The views expressed in the article are those of the author and are not necessarily any organization or institution. 10. References [1] Upadhyay, O. P., Sharma, D. K. and Singh, D. P., “Fac- tors affecting stability of waste dumps in mines,” Interna- tional Journal of Surface Mining and Reclamation, Vol. 4, 1990, PP. 95-99. [2] Bishop A. W, “The use of the slip circle in the stability analysis of slopes,” Geotechnique, Vol. 5, 1955, pp. 7-17. [3] Calder, P. N. and Workman, J. L., “The design of stable highwalls and spoil piles in strip mining,” SME-AIME Meeting, Minneapolis, Minn., Preprint, 1980, pp. 80-368. [4] Richards, B. G., Coulthard, M. A., and Toh, C. T., “Analysis of slope stability Cana- test method for direct shear test of soils under consoli- dated drained conditions. ASTM D3080-98. Annual book of ASTM Standards. ASTM, 1998, West Conshohocken, PA. [5] Griffiths, D. V. and Lane, , [ pp. 387-403. [6] Singh, T. N. and Chaulya, S. K.,” External Dumping of Overburden in Opencast Mine,” Indian Journal of Engi- neers, Vol. 22 (1 & 2), 1992, pp. 65-73. [7] Singh, posi an [2 Journal of Ceme ] Singh, A. P. an[8 l Mine waste dump,” The Indian mineral industry journal, 2006, pp. 113-118. subsurface water in Earth-surface processes and land forms,” C. G. Higgins and D. R. Coates, eds., Geological Society of Americ [16] Hampton, M., “Gravitational failure of sea cliffs in weakly lithified sediment,” Environmental Engineering Geosciences, Vol. 83, 2002, pp. 175-191. [17] Barton, M. E. and Cresswell, A., “Slope stability in a sand/ sandstone borderline material,” Proc., 2nd Int. Symp., The Geotechnics of Hard Soils—Soft Rocks, Vol. 3, A. Evangelista and L. Picarelli, eds., Balkema, Rotter- dam, The Netherlands, 1998, pp. 1051-1055. [18] Mohr, O., “Ueber die Darstellung des Spannungszustan- des und des Deformationszustandes eines Körperele- mentes und üb keitslehre,” Civilengenieur, Vol. 28, 1882, pp.113-56. [19] Chaulya, S. K., Singh, R. S., Chakraborty, M. K. and Dhar, B.B, “Numerical modelling of bios coal mine overburden dump slope,” Ecological Modelling, Vol. 14, 1999, pp. 275-286. [20] American Society for Testing and Materials, Standa 21] Chakravorty, M. K., Chaulya, S. K. and Singh T. N., “Method of waste dump stability analysis—an overview,” In: Proceeding national symum. Engineering, mining and ground control, technology, Varanasi, 1996, pp. 287-2. 2] Gue S. S. and Tan, Y. C., “The Determination of shear strength in residual soils for slope stability analysis,” Seminar Cerun Kebangsaan, 2001, Cameron Highlands. [23] Singh T. N. and Naidu S., “Influence of strain Rate and cyclic compression on physicmechanical behavior of rocks,” Indian. Journal. of Engineering. and material sci- Copyright © 2011 SciRes. GM  A. KAINTHOLA ET AL. 13 iaxial compression: re- 983, PP.283cience, “A new area in slope stability analysis: Shear ences, Vol. 59, 2000, pp. 482-486. [24] ISRM, “Suggested method for the determining the strength of the rock materials in tr vised version,” International Journal Rock Mining Sci- ence Geo-mechanics Abstract, Vol. 20,1-290 strength reduction finite element technique.” RocNews. 2004. [28] Jha, G. K. and Lal, K. M., “Slope stability of external OB dumps”, Opencast, 1998, pp.119-125. [25] Zhou, W. Y., Xue L. J., Yang Q., and Y. R. Liu, “Rock slope stability analysis with nonlinear finite element method,” Taylor & Francis, 1994, pp. 503-507. [26] Ann, T., SCheang,. W. Hai O. P and D. Ta, “Finite Ele- ment Analysis of A Soil Nailed Slope-Some Recent Ex- perience,” GeoAsia, 2004. [27] Rocs Copyright © 2011 SciRes. GM |

