Journal of Biosciences and Medicines, 2014, 2, 12-18
Published Online June 2014 in SciRes. http://www.scirp.org/journal/jbm
http://dx.doi.org/10.4236/jbm.2014.24003
How to cite this paper: Chen, K.-K., et al. (2014) Data Classification with Modified Density Weighted Distance Measure for
Diffusion Maps. Journal of Biosciences and Medicines, 2, 12-18. http://dx.doi.org/10.4236/jbm.2014.24003
Data Classification with Modified Density
Weighted Distance Measure for Diffusion
Maps
Ko-Kung Chen1, Chih-I Hung1, Bing-Wen Soong2, Hsiu-Mei Wu3, Yu-Te Wu1,4*,
Po-Shan Wang5*
1Department of Biomedical Imaging and Radiological Sciences, National Yang-Ming University, Taip ei, Taiwan
2Department of Radiology, Taipei Veteran General Hospital, Taipei, Taiwan
3Department of Neurology, Taipei Veteran General Hospital, Taipei, Taiwan
4Institute of Biophotonics, National Yang-Ming University, Taipei, Taiwan
5The Neurological Institute, Taipei Municipal Gan-Dau Hospital, New Taipei, Taiwan
Received February 2014
Abstract
Clinical data analysis is of fundamental importance, as classifications and detailed characteriza-
tions of diseases help physicians decide suitable management for patients, individually. In our
study, we adopt diffusion maps to embed the data into corresponding lower dimensional repre-
sentation, which integrate the information of potentially nonlinear progressions of the diseases.
To deal with nonuniformaity of the data, we also consider an alternative distance measure based
on the estimated local density. Performance of this modification is assessed using artificially gen-
erated data. Another clinical dataset that comprises metabolite concentrations measured with
magnetic resonance spectroscopy was also classified. The algorithm shows imp roved resu lts c om-
pared with conventional Euclidean distance measure.
Keywords
Diffusion M ap s, Density Estimation, Spinocerebellar Ataxia
1. Introduction
Exploring the behavior and patterns of clinical data is crucial, and is mostly done with statistics or linear analy-
sis. But several factors may make these approaches incapable of dealing the data effectively and efficiently.
Sometimes the higher dimensional data may actually lie on a lower dimensional space. Generally, classical sta-
tistical methods and linear analysis may not provide insightful information on such kind of data. A new ap-
proach, namely diffusion maps [1], had been proposed to deal with high dimensional data. Based on the stochas-
*
Corresponding authors.

K.-K. Chen et al.
13
tic process on the spectral graph theory, diffusion maps is among the most powerful spectral dimensionality re-
duction tool to locate intrinsic lower dimensional coordinates of a given multi-dimensional dataset [2]. Diffusion
Maps has been applied to diverse applications [3]-[7].
The Diffusion Maps uses a distance measure that preserves local information of a given dataset. The distance
between a pair of data points is short providing there exist some paths connecting them; that is, the affinity for
this pair of points is high. This characteristic is likely in clinical data analysis since the distribution patterns of
the patients do not always behave in a linear sense, and the progression of diseases and symptoms mimics the
concept of local connectivity providing the data exhibits certain longitudinal behavior. In addition to capable
tracking down the nonlinear structure, diffusion maps also reduce the dimensionality of the data, which simpli-
fies characterization and differentiation of different groups. However, the irregular distribution of the data, along
with relative small population size and other factors discussed above, complicate the discerning of the data. Un-
der these conditions, diffusion maps with a naïve distance measure no longer suit for such task.
In this study, we use a self-tuning kernel, which is coupled with a density estimator, to adjust the bias intro-
duced by the underlying distribution of the data. The main advantage of this approach lies in its ability to deal
with false and missing cluster induced by nonuniform density. An artificially generated data using Gaussian dis-
tribution is given in later section to illustrate this phenomenon. Another clinical dataset is also analyzed with the
same method, compr ising spinocerebellar ataxia type 3 (SCA3) patients, multiple system atrophy (MSA) pa-
tients, and normal subjects.
2. Materials and Met ho d s
2.1. Diffusion Maps
For a given measure (Χ, μ), a dataset X consists of N samples with underlying distribution μ being included. The
data points may be characterized as xi = (yi1, yi2, …, yil, …, yim), i = 1, 2, …, N, l = 1, 2, …, m, A kernel k: X × X
→ R is defined to measure the pairwise similarities between every pair of data points. The kernel function is
nonnegative, and it defines certain notion of connectivity between data points pairwisely. Since the design of the
kernel will influence the geometry captured by diffusion maps, the choice of the kernel should be guided by the
characteristics of the data or prior knowledge that one bears in mind. A popular choice for distance measure is
the Gaussian kernel:
()
2
,2
exp
ij
ij
xx
k xx
σ

−−

≡

(1)
Once the choice of kernel is determined, the mass can be defined as:
( )
()( )
,
0
i Xijj
mxk xxdx µ
≡∫ >
(2)
Then a weighting function can be built by normalizing the kernel using mass:
( )( )
( )
,
,
ij
ij i
kxx
pxx mx
≡
(3)
Since the weighting function satisfies ∫X p(xi, xj)dμ(xj) = 1, the constructed graph can be viewed as an asymme-
tric Markov chain built over the data, where the p(xi, xj) is interpreted as the probability for state xi transits to
state xj in a single time step. A square matrix P whose elements are p(xi, xj) is then constructed. Taking powers
of P, which is equivalent to drive the Markov chain forward, will reveal corresponding intrinsic geometry of the
data. If one allow the Markov chain running unceasingly, all the data points will be merged together and re-
garded as a single cluster.
As long as the matrix P is nonsingular, it can be written in quadratic form:
1tt
P νλν
−
=⋅⋅
where ν is the discrete set of eigenfunctions {ν(i): i = 1, 2, …, N} with corresponding eigenvalues {(λ(i))t: i = 1,
2, …, N}. The sequence of eigenvalues has the property such that
(1)(2)( )
10
N
λλ λ = ≥≥…≥≥
. Since the

K.-K. Chen et al.
14
sequence of eigenvalues tends to zero, a few largest eigenvalues and their corresponding eigenfunctions can be
used to approximate the P with minimal truncation error.
The diffusion maps is then defined as:
( )
( )
( )
( )
( )
( )
{ }
j
, 1,2,,
t
tj
ii
xxj N λν Ψ≡ =…
(4)
The dimension of the new embedding depends on only the powers of the P, not that of the original space.
2.2. Weighted Kernel Based on Density Estimation
As mentioned in previous section, the choice of the kernel should be guided by application itself. The design of
the kernel influences the resulting embedding due to the fact that the structure of the constructed Markov chain
is altered. Even if the kernel is drawn from one of the known parametric family of distributions, tweaking its
parameters may yield quite distinct results, this is especially true if the underlying distribution function of the
data is irregular. Different setting of parameters of a global measure, taking the Gaussian kernel for example,
leads to embeddings that differ from one another. If the scaling parameter σ is too small, the resulting graph
would look like a series of mutually disconnected islands; however, setting σ too large would glue all data points
altogether, leaving only a single cluster in the diffusion embedding.
While a global setting captures the intrinsic geometry of the data, it would not be able to effectively address
the nonuniformity of the intrinsic density distribution. When treating data comprises different groups, it is de-
sirable that the kernel can be self-tuning based on the local statistics of the data points. In our case, in order to
compensate the bias and skewness introduced by the distribution of the data, we consider the local density of the
data points. Density plays an important role in statistics; it conveys the distribution pattern to be drawn from the
data. There’s a vast literature focus on density estimation [6]. In our case, consider any point xi in the original
data, let the set
( )
{ }
:,1, ,
i jiji
xx xxjn ξε ≡−< =
being its neighbor. Providing one assume that the data is
drawn from the normal distribution N(u,τ2) and the variance of all dimensions are the same, then the ratio that
the local variance of data points in the set ξ(xi) to the global variance τ2 should depend on the size of the local set,
that is, ni. One may further assume that if this ratio of associated with ξ(xi) surpasses certain predefined value,
then data points in the ξ(xi) are actually discernable. Since the density of ξ(xi) is proportional to its sample size,
we can use ni as a density estimator to formulate the self-tuning kernel.
Alternatively, one can use the following integral to estimate the local density as delineated by Silverman [6]:
( )
( )
( )
,id ij
xi
dxkxxdx
ξ
≡∫
(5)
where kd is a Gaussian function that takes the same form as (1), except for the fact that σ is replaced by σd (In
our case, we assume σd to be the ε). The purpose of kd is to measure the contribution of xj to the local density of
the xi. For normal distribution, it can be shown that estimated d(xi) will converge to ni as the sample size N is
sufficiently large. Then for every pair estimated densities of samples, the lower one will be incorporated into the
Euclidean distance measure to form a weighted version:
( )
( )
( )
( )
{ }
2
2
,min,, 1,,
i jijiljl
xi
Dw xxdxdxyydxlm
ξ
≡∫−= …
(6)
In the same manner as (1), Dw2(xi, xj) is then used as the distance measure of the self-tuning kernel:
( )( )
2
,2
,
exp
ij
ij
Dwx x
axx
τ

−

≡

(7)
This approach is more flexible, and can reduce the possibility that samples with different characteristics being
identified as the same due to nonuniform density of the data. Furthermore, the method is nonparametric; this
feature is desirable since no additional prior or background knowledge is required for clients to obtain meaning-
ful results.
The computation procedure of the aforementioned approach is listed in the following flowchart:

K.-K. Chen et al.
15
A result using artificially generated data is given in Figure 1. We assume that the local density of the gray
zone is generally higher than a clean group, since it is a mixture of subjects from different clusters; also, if there
are multiple clusters with varied density appear at once, it is unlikely that a naïve kernel would be able to treat
the data properly. Each dataset is randomly divided into training set and testing set. The training set is fed to
train the support vector machine (SVM) first, and then evaluating the performance of SVM with the testing set.
The results show that the overall classification ratio has been improved using the modified method.
An important characteristic of such spectral clustering techniques is that they are feasible only if the different
groups can be separated in the lower dimensional representation [8]. This issue arises in our study of the first
clinical dataset, where the classification accuracy of the MSA groups in the diffusion embedding actually de-
creases in comparison to that using original data.
3. Experimental Re s ults
The clinical dataset compris e relative metabolite concentrations measured using magnetic resonance spectros-
copy (MRS). The MRS is carried out on left and right cerebellum, left and right basal ganglia, and vermis. The
relative concentration of three different metabolites, namely N-acetylaspartate (NAA), Choline (Cho), and myo-
inositol (mI), are measured at all five anatomies; these three concentrations have been normalized using the
concentration of creatine (NAA/Cr, Cho/Cr, mI/Cr). The SCA dataset consists of three different groups, namely
the 63 SCA3 patients, 98 MSA patients, and 44 normal subjects. While the SCA and MSA share similar clinical
symptoms, the MRS has been shown to be a potential modality to differentiate SCA and MSA, particularly mul-
tiple system atrophy-cerebellar type (MSA-C) [9]. While the MSA patients are readily separable from the other
two groups, classifying SCA3 patients and normal subjects is more difficult, as shown in Figure 2(A). Using
diffusion maps, we obtain an embedding that separate the original data into three clusters, but all of them are
mixture of different groups. This suggests a naïve distance measure is unsuitable. Density estimation is first
performed on the original data (Figure 2(B) and Figure 2(C)), then incorporated into the distance measure as
self-tuning factor. Figure 3 shows embeddings obtained with simple kernel and density based kernel, respec-
tively. The classification is carried out on four di fferent setting, namely original data, principal component based
representation, diffusion embedding, and diffusion embedding with density based kernel built in, respectively.
The SVM is performed thirty times for each setting. The classification accuracy is listed in the Table 1.
4. Discussion
While the overall classification performance is ameliorated in general, particularly in the case of normal subjects,
the accuracy of the MSA group actually drops. The issue may be caused by a variety of factors, and we suspect
the most likely source being the overly estimated density, namely d(xi). We illustrate this by considering the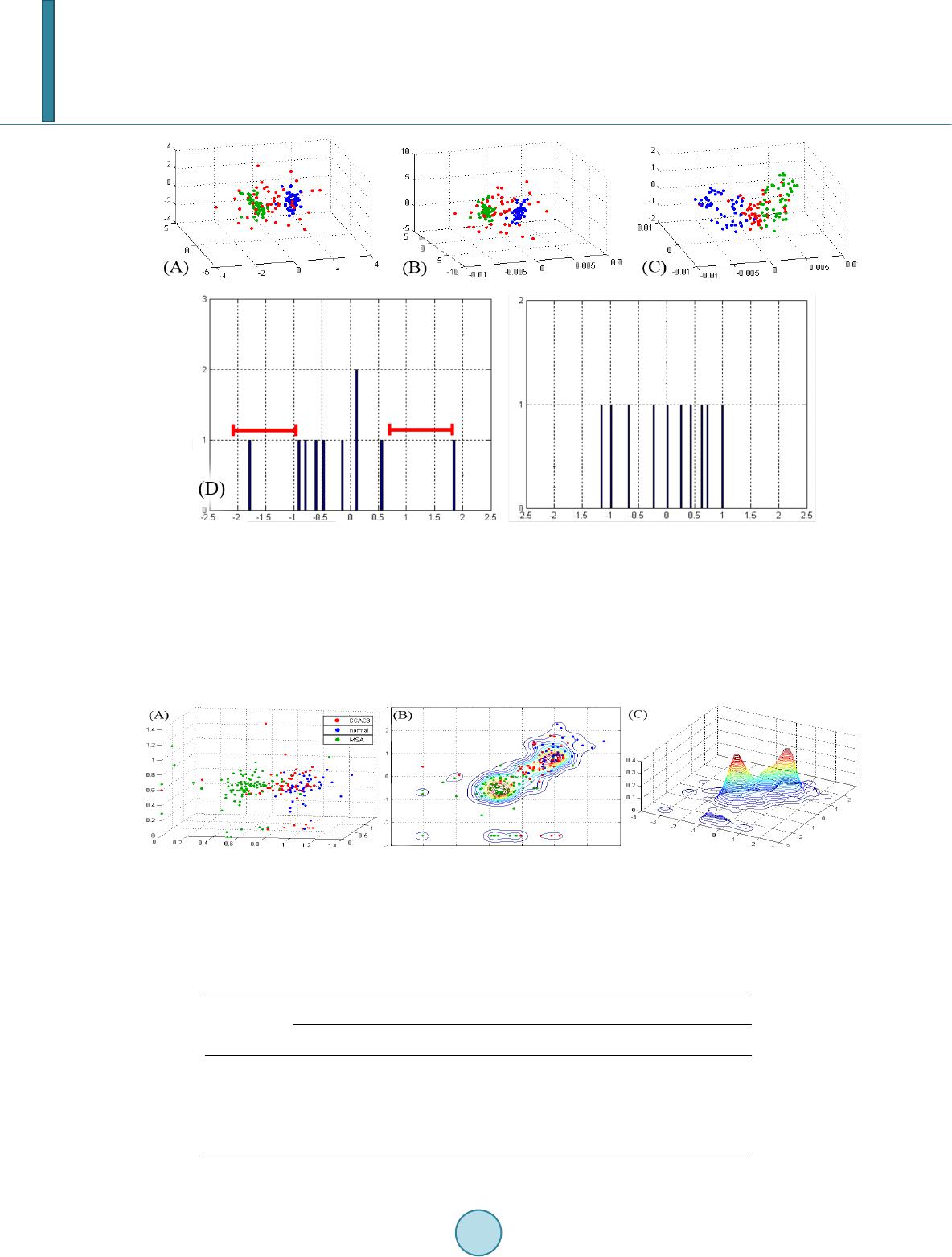

K.-K. Chen et al.
16
Figure 1. Demonstration of two different approaches using artificially generated data. The setup for this data constitutes
three Gaussian distribution: N((1, 0, 0),1), N((−1, 0, 0),1), and N((0, 0, 0), 2). (A) The original data displayed in 3D. The
red group disperses through both the green one and the blue one. One can consider the higher density clusters as typical
representative of certain disease, or the gray zone induced by overlapping interval between different groups; (B) The dif-
fusion coordinate computed using Euclidean distance measure. The red group is incorrectly regarded as the background of
the data due to its lower density; (C) Diffusion coordinate obtained with self-tuning kernel. The dispersive red cluster is
glued altogether and can be easily identified (D) 10 samples randomly generated from normal distribution, originally the
distances between every local pair differ a lot, but the differences have been toned down after the dfensity weighted dis-
tance measure is used.
Figure 2. The Intermediate result of density estimation performed on the clinical dataset. (A) The original data in 3D view.
The dimensions being chosen as coordinates are: NAA/Cr in both left and right cerebellum, and Cho/Cr in left cerebellum;
(B) The contour of bivariate density estimation using NAA/Cr in both left and right cerebellum; (C) The corresponding 3D
contour of the estimated density. It can be inferred that not only SCA3 has lower density, but the gray zone induced by both
normal subjects and SCA3 group complicate the situation further.
Table 1. Classification accuracy using SVM of SCA dataset.
SVM Classification Accuracy
Original Space PCA Based Naïve Kernel Modified Kernel
SCA3 64% - 73% 65% - 74% 79% - 88% 86% - 93%
MSA 81% - 93% 46% - 50% 71% - 82% 73% - 82%
Normal 62% - 73% 74% - 79% 50% - 63% 79% - 88%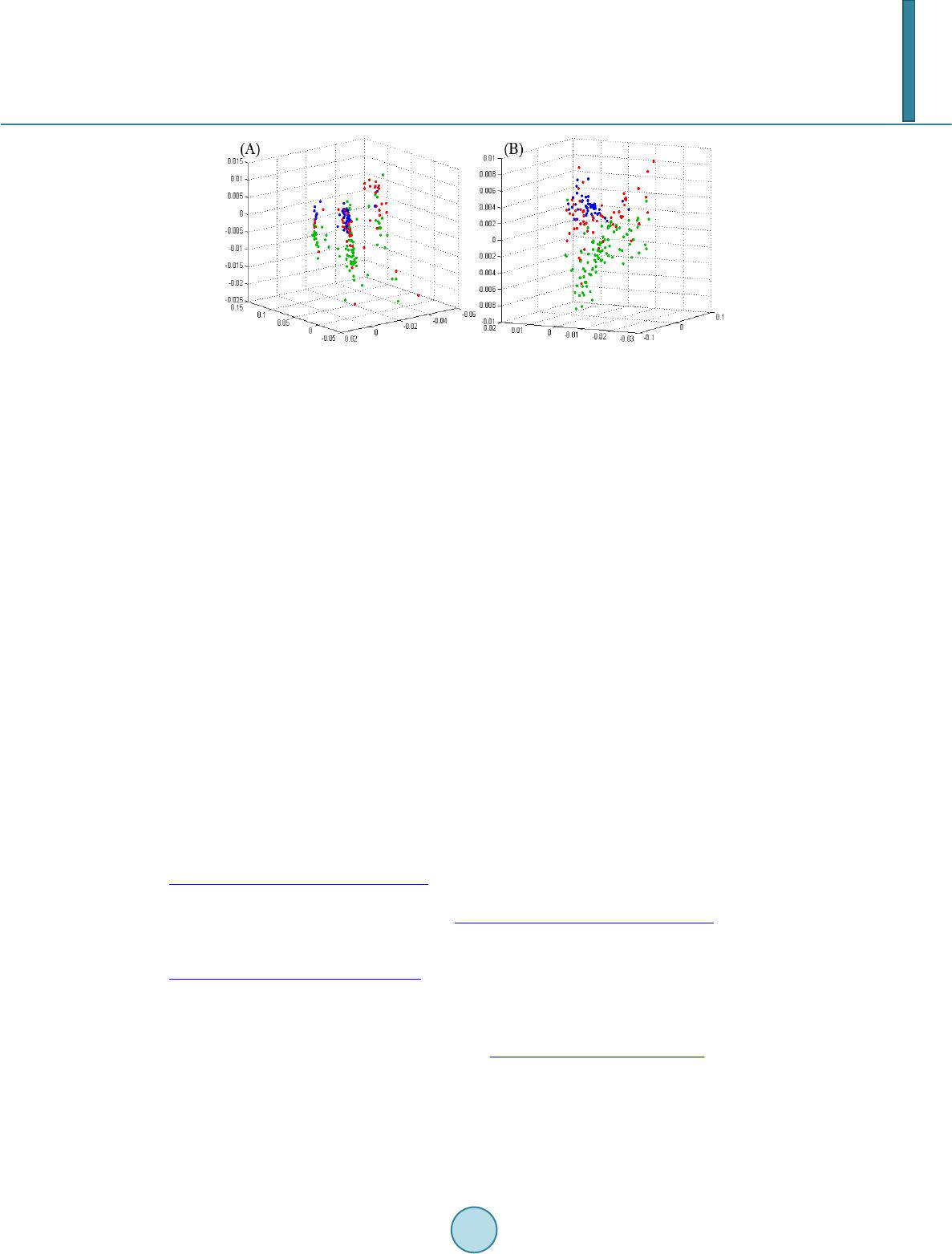

K.-K. Chen et al.
17
Figure 3. Diffusion coordinate of SCA dataset obtained with different approaches. (A)
Embedding computed with the naïve distance measure. The data roughly is divided
into three distinct clusters, all of which are mixture of different groups; (B) Result ob-
tained using self-tuning kernel. The false clusters are now patched altogether.
embedding of simulated data in Figure 1(C). It is evident that the perturbations within green and blue groups are
both magnified as integrating the red group. Based on this observation, we conjecture that ineffective estimation
of local density, which may potentially destroys originally compact and dense structure, can be hazardous; hence
correct density estimation is crucial to the efficacy of the self-tuning kernel. This issue can be formerly charac-
terized as correct estimation of certain intrinsic parameters of the distribution function given the data.
5. Conclusion
Based on the clustering properties of the diffusion maps, we analyze the clinical data in a lower dimensional
space induced by distance measure of the diffusion maps. To adjust the nonuniformity introduced by the under-
lying distribution of the data, we estimate the local density of the data, and use it as self-tuning factor of the dis-
tance measure. This approach shows satisfactory results on both artificial data and metabolite concentrations
obtained with MRS. The results also shows that distance measure with scaling factor based on variance of local
mean generally is more capable than a naïve kernel.
Acknowledgements
This study is supported by National Science Council, Taiwan (NSC 101-2221-E-010-004-MY2 & NSC 101-
2314-B-733-001-MY2) and by the project of Center for Dynamical Biomarkers and Translational Medicine, Na-
tional Central University, Taiwan (NSC 102-2911-I-008-001).
References
[1] Coifman, R.R. and Lafon, S. (2006) Diffusion Maps. Applied and Computational Harmonic Analysis, 21, 5-30.
http://dx.doi.org/10.1016/j.acha.2006.04.006
[2] Si nge r, A. and Coifman, R.R. (2008) No n-Linear Independent Component Analysis with Diffusion Maps. Applied and
Computational Harmonic Analysis, 25, 226-239 . http://dx.doi.org/10.1016/j.acha.2007.11.001
[3] Lafon, S., Keller, Y. and Coifman, R.R. (20 06) Data Fusion and Multicue Data Matching by Diffusion Maps. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 28, 1784-1797.
http://dx.doi.org/10.1109/TPAMI.2006.223
[4] Nadl er, B., Lafon, S., Coifman, R.R. and Kevrekidis, I.G. (2005) Diffusion M aps, Spectral Clustering and Eigenfunc-
tions of Fokker-Plank Operator s. Neural Information Process. System 18, MIT Press, 955-962.
[5] Si nge r, A., Shkolnisky, Y. and Nadler, B. (2009) Diffusion Interpretati on of Nonlocal Neighborhood Filters for Signal
Denosing. SIAM Journal Imaging Science, 2, 118-139. http://dx.doi.org/10.1137/070712146
[6] Silverman, B.W. (19 86) Density Estimation for Statistics and Data Analysis. Monographs on Statistics and Applied
Probability, Vol. 26, Chapman and Hall, London.
[7] Etyngier, P., S’egon n e and Kwriven, R. (20 07) Shape Prior Using Manifold Learning Techniques. Proceedings of the
IEEE International Conference on Computer Vision, 15, 132-141.
[8] Chandola, V., Banerjee, A. an d Kumar, V. (20 09) Anomaly Detection: A Survey. ACM Computing Surveys, 41, 1-58.

K.-K. Chen et al.
18
[9] Liring, J.F., Wang, P.S., Chen, H.C., S oon g, B.W. and Guo, W.Y. Differences between Spinocerebellar Ataxias and
Multiple System Atrophy-Cerebellar Type on Proton Magnetic Resonance Spectroscopy. PLoS ONE, 7, e47925.
http://dx.doi.org/10.1371/journal.pone.0047925