Communications and Network, 2013, 5, 681-687
http://dx.doi.org/10.4236/cn.2013.53B2122 Published Online September 2013 (http://www.scirp.org/journal/cn)
Asymptotic Design and Analysis of Multiuser Detector
for UWB High Data Ra te C h annel Based on Channel
Division Multiple Access
Houda Chihi, Ridha Bouallegue
Higher School of Communications (Sup’Com), Innov’COM, Tunis, Tunisia
Received April 2013
ABSTRACT
In this paper, we study an innovative multiple access scheme that exploits the intrinsic properties of the wireless envi-
ronment to improve the multiuser environment, so-called Channel Division Multiple Access (ChDMA) focusing on
spectral efficiency analysis and system performance. In particular, we show that Simultaneous multiuser accessing to a
common destination is made possible by considering the channel impulse response (CIR) of each user as a signature.
We begin by the assumption of the channel state information available at the receiver. Then, we analyze the perform-
ance of the ChDMA integration in a random environment over UWB high data rate channel. Next, we discuss the de-
sign of MMSE and optimal receiver structu re for such a system. Additionally, we show an asymptotic analysis behavior
taking into account the channel eigenv alues distribution with the associated spectral efficiency.
Keywords: ChDMA; MBOFDM; UWB; Spectral Efficiency; Eigenvalues Distribution; MMSE; Optimal Receiver;
PDP
1. Introduction
UWB is a promising technology that has attracted con-
siderable interest in the research and standardization
communities for wireless communications. For a very
large bandwidth, the capacity derivation for UWB chan-
nel cannot be the same as for a classical narrowband
channel. The main difference results from two frequency
dependent attenuation origins: distance and frequency
selectivity of channel. Indeed, the attenuation due to dis-
tance is proportional to the squared in verse of frequency,
and cannot therefore be considered constant over the full
UWB bandwidth. Besid es, the various realization s of the
channel act as linear filters that attenuate randomly the
transmitted signal at diff erent frequencies.
In this contribution we describe, firstly, the MBOFDM
UWB high data rate system. This must be taken into ac-
count in the capacity computation [1]. Next, we present
ChDMA Characteristics with the channel model. We
shall examine system spectral efficiency in a random
environment with channel state information in the recap-
tion. The key performance measure here is in particular
the eigenvalue distribution of the channel matrix. Then,
in section III, we investigate two receiver structures that
we will study in different system behavior: the optimal
receiver and the linear minimum mean square error
(MMSE) detector. The MMSE linear detector is particu-
larly interesting as it allows maximizing the signal-to-
interference ratio (SIR) among all linear receivers. In
section IV, we present the PDP impact in spectral effi-
ciency. Then, we present the simulation results.
2. System Description
2.1. The Multiband OFDM Solution
The multiband technique proposed in the WiMedia Alli-
ance MBOFDM scheme divides the UWB spectrum into
14 bands of 528 MHz each, as illustrated in Figure 1.
The first 12 bands are then grouped into four band
groups consisting of three bands each. The last two bands
are grouped into a fifth band group [2]. Initially, most of
the studies have been performed on the first three sub-
bands- from 3.1 to 4.8 GHz. An OFDM signal can be
transmitted on each subband using a 128 point inverse
fast Fourier transform (IFFT). Out of the 128 subcarriers
used, only 100 are assigned to transmit data. The multi-
user access is performed with time frequency codes (TFC)
which provide frequency hopping from a subband to
another at the end of each OFDM symbol. Hence, at a
given instant, if we consider a 3 user system, each user
occupies one of the first three subbands [ 2].
In the MBOA solution case, the signal generated at the
output of the IFFT [2] is: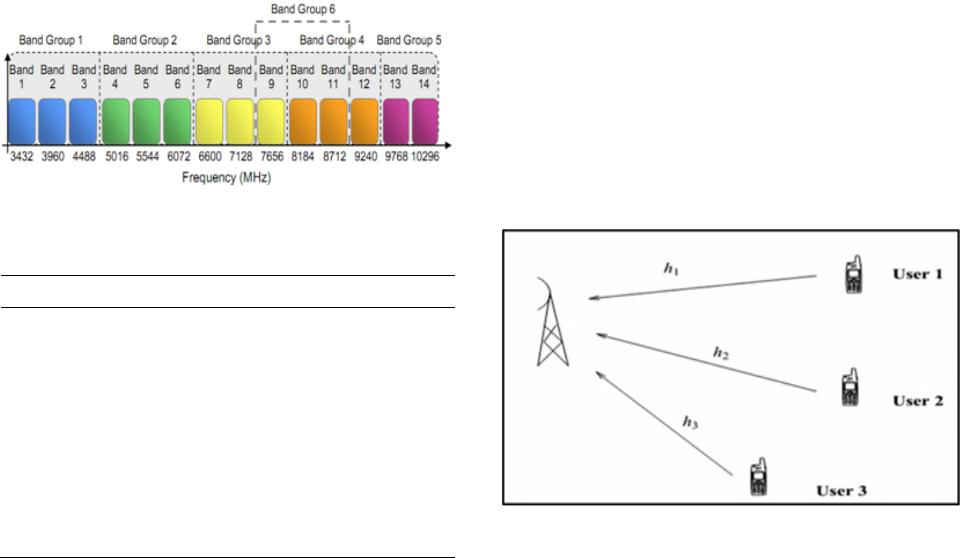

H. CHIHI, R. BOUALLEGUE
Copyright © 2013 SciRe s. CN
682
( )
( )
( )
2()
F cp
Mjnt iT
OFDM
n cCP
iM
Xip t Te
St
π
+∞ +∆−
=−∞ −
= −
∑∑
(1)
ΔF, M and TCP represent respectively the subcarriers
spacing, the total number of used subcarriers and the
spacing between two consecutive OFDM symbols. Xn(i)
is a complex symbol belonging to QPSK constellation
and is transmitted by subcarrier n during the ith OFDM
symbol. It represents a data, a pilot or a reference symbol,
pc(t) is a rectangular window defined by [2] as:
( )
( )
1 for 0
0 for
c FFT
cFFTFFTCP GI
pt tT
ptTtTT T
= ≤≤
=≤≤+ +





Transmitted data rates in each subband vary from 53.3
to 480 Mbit/s, which are listed in Table 1 [2].
2.2. UWB Channel Modeling
The proposed model for MBOFDM is 802.15.3a high
data rate channel which derived from Saleh Valenzuela
model [3]. Mathematically, the impulse response of the
multipath model is given by [4]:
()( )( )( )
()
00
,,
kk
ZB
kk
zb
kk
htXzbzzbtT αδ
= =
− −
∑∑
(2)
where:
Xk is the lognormal shadowing of the kth channel re-
alization, Tk(z) is the dela y of clu ster z, and αk(z, b), τk(z, b)
represent respectively the gain and the delay of multipath
b withincluster z respectiv ely.
Figure 1. UWB spectrum bands in the MBOFDM system.
Table 1. MBOFDM UWB data rates [4].
Data rate Coding rate
53,3 1/3
80 1/2
106,7 1/3
160 1/2
200 5/8
320 1/2
400 5/8
480 3/4
2.3. ChDMA-UWB System Principle Analysis
The idea behind ChDMA is to use the channel impulse
response (CI R) of each user as a signature, i.e . , th e sign a-
ture code is given by the channel and the users are sepa-
rated as a CDMA system. It is important to note that the
signatures are given by the environment and by user’s
position, which means that they are uniquely determined.
This signature location dependent property provides de-
centralized flexible multiple access as the codes are natu-
rally generated by the radio channel [5]. The previous
multiple access schema don’t benefit of using low duty
cycle transmissions. For this reason, in this paper we
consider a multiuser communications system which ex-
ploits the duty cycle assumption and sends a modulated
peaky signal. The new multiple access considered system
is based on the integration of ChDMA in the 802.15.3a
model. The ChDMA proposition works because UWB
channels have a large coherence time (typically about
100 µs) relatively to their delay spread (typically around
15 - 40 ns, depending on the user environment) [6]. Fol-
lowing the clustered ray model, each ray is considered as
a single replica of the sign al due to the distortion accom-
panied the environment, yields that each user occupies an
appropriate position as presented in Figure 2 [6], where
we consider an uplink channel between user K and the
destination. For this reason, the transmitted signal identi-
fication is easily obtained where the receiver benefits of
the different position occupied by each user independ-
ently, as it knows the channel it will be able to detect and
to demodulate the received wavefor m.
3. Spectral Efficiency Performance Analysis
We analyze the performance of ChDMA UWB system in
terms of spectral efficiency using two different receivers:
• The optimal receiver.
• The minimum mean square error receiver.
The spectral efficiency γ is defined as the number of
bits per chip summed over the users that can be reliably
Figure 2. Channel Impulse Division Multiple Access with
three users.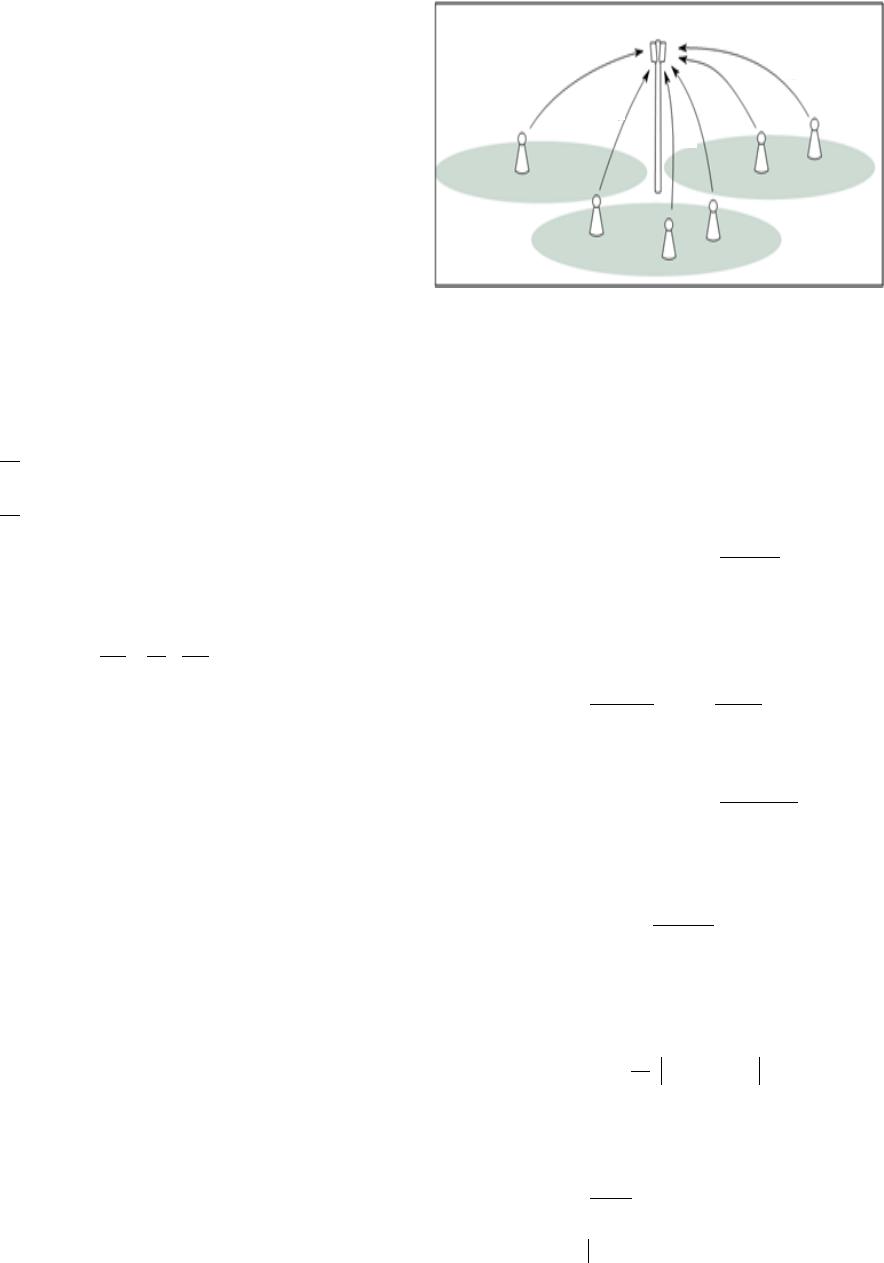

H. CHIHI, R. BOUALLEGUE
683
transmitted [7]. It is expressed as the bits per second per
Hertz (bit/s/Hz) supported by the syst e m.
3.1. Linear Minimum Mean Square Error
Receiver
The concept of MMSE detector originates from turning
the problem of detection of transmitted symbols in a
CDMA system into a problem of linear estimation [8]. In
the following, we consider the uplink communication,
where the SINRk,n at the output of the MMSE detector is
given by [9]:
( )
1
2
, ,,,,
HH
knkn knknkn
SINRhH HIh σ
−
= +
. (3)
where n is related to nth symbol from N and k related to
the kth user from K, Hk,n is the matrix obtained from H
suppressing the column hk,n. The instantaneous spectral
efficiency is given by [5]:
2,
1
21
2, ,,,
1
1log (1)
1log (1()).
N
kn
i
NHH
knkn knkn
i
SINR
N
hHHI h
N
γ
σ
=
−
=
+
= ++
=
∑
∑
(4)
We must mention that the signal to noise ratio 1/σ2 is
related to the spectral efficiency γ following the author in
[7] by:
2
1.
b
o
E N
KN
γ
σ
=
Deeper insight on the linear MMSE spectral efficiency
performance behavior is obtained byK, N → ∞ with con-
stant ratio β where β = K/N.
The study of the eigenvalue distribution of random
matrices has triggered important consideration in many
numerous works. For this reason, the performance of
MBOFDM ChDMA UWB communication system is
determined via the eigenvalues of the covariance matrix
NN
H
N
CHH=
. We study the eigenvalues distribution
performance of linear MMSE multiuser receiver in ran-
dom environment. The eigenvalue distribution is de-
scribed in Figure 3 [10]:
The formula for the MMSE demodulator could be de-
scribed via considering the transformation of CN using
the singular value decomposition (SVD). We denote the
SVD representation of the channel correlation matrix CN:
T
N
C SDS=
.
where S is a unitary matrix containing the eigenvectors
of HHH and D is a diagonal matrix, containing the singu-
lar values λi with i = 1···N representing the eigenvalues
of HHH. Second, following results from random matrix
theory [11], it can be deduced that the empirical distribu-
tion of the eigenvalues of CN converges to some limiting
distribution F, we obtain:
λ11
λ21
λ22
λ23
λK1
λK2
Figure 3. Eigenvalue distribution.
( )
1
2
,, ,
H
knkm ikn
SINRhI h λσ
−
= +
(5 )
We assume a large system, i.e., we let K, N → ∞ while
K/N is finite and converges to a specific value
β
. Yields
in the asymptotic analysis, the spectral efficiency can be
expressed in terms of the eigenvalue distribution of HHH
and it is given by:
22
1log (1)
1/
m
K
ms i ei
i
N
λ
λσ
=++
ϒ= ∑
. (6)
We must mention that in [12] (Lemma 9) if we con-
sider the key performance criterion as SIR of user k un-
der the MMSE detector we obtain:
11
11
KK
kk
ii
kk
SIR
SIR
λ
λ
= =
=
++
∑∑
.
By this way (6 ) c ould be described by:
22
1log
1/(1 )
mm e
Ki
i
s
i
SIR
IR
NS
σ
=
ϒ+ + =∑
.
We should point out that (6) converges in probability
to:
( )
22
log (1)
N
iH
i
mmse
fF
λ
λσ λ
++ ϒ=
∫
. (7)
where
N
H
F
defined by the author in [13] by:
RR→
is
the empirical eigenvalue distribution (e.e.d) of the ran-
dom matrix H, i.e.
( )
{
}
1:
N
H ii
FN λλλ λ =⋅≤
.
Let GA(z) the Stieltjes Transform of
N
H
F
as defined
by [14]:
( )()
1
N
HA
d or
zzFGz f
λ
λ
+
−
= ∈
∫
.
where
[]
{ }
Im 0zz
+
=∈>
Yields:

H. CHIHI, R. BOUALLEGUE
Copyright © 2013 SciRe s. CN
684
( )
( )
( )
( )
( )
2
22
2
2
2
2
log
log 2
log .
mN
ii
H
oi
N
H
o
m
N
o
s
H
e
dF
dF
dF
λσ λλ
λσ
λσ λ
λσ λ
∞
∞
∞

++
=
+

= +
−+
ϒ
∫
∫
∫
(8)
Following Theorem 6 in [15], we have that F converge
if
N→∞
to a distribution function G, we obtain the
SNR of the MMSE receiver convergence to:
( )
21
, ,,,2
1
() .
HH
kmkm kmkm
hH HIhdG σρ λ
λσ
−
+→=+
∫
(9)
Finally we obtain:
( )
2
γlog (1ρ)dG λ.
∞
→+
∫
Additionally, for asymptotically large random matrices
such upper bound s are prov ided by r andom matrix th eory.
If the channel matrix is composed of independent identi-
cally distributed random entries. The eigenvalues of HHH
are asymptotic a l l y upper bounded by [16] :
()
2
1
k
λ β < +
.
By this way the bounds of (8) are given by:
()
( )
( )
( )
2 22
22
o
log 2λσdG λlog 2(1β)σdG λ
∞
+<++
∫∫
( )
()
( )
2 22
22
o
log ()dGλlog (1)σdG λ. λσ β
∞
+< ++
∫∫
Yields:
( )
( )
( )
22
2
22
2
log 2(1)
log (1)d
mmse
G
βσ
βσ λ
++
− ++
ϒ<
∫
We obtain:
( )
( )
22
222
21
log 1
mmse
βσ
σ
γ
β

+
<
+



++


.
Following Theorem 2 presented in [17] we have that
under the condition of large system the minimal value of
eigenvalue is given by:
( )
2
1
k
λ β > −
.
The minimum bounds of (8) are gi ven by:
( )
()
()
()
2 22
22
o
log 2λσdG λlog 2(1β)σdG λ.
∞
+> −+
∫∫
( )
( )
( )
2
22
22
o
log ()dGλlog1dGλ. λσβ σ
∞

+>−+


∫∫
Let the minimal bound is given by:
( )
( )
22
222
21
log 1
mmse
βσ
σ
γ
β

−
>
+



−+


.
If we consider the case of 0 < β < 1, and following the
author in [18], the density of F(x) is given by:
( )
( )( )
22
22
for
(((1)(((1)) )/
0, otherwi
2
s
.
e.
11
k
f
β
λββ λπβλ
ββ
λ
λ
−−+ −


=
<<
−+





Then, if we consider the case of 0 < β < ∞, we obtain:
( )
( )
( )
( )
( )( )
( )
( )
2
2
22
1
2
1 1/01.
() 11
1.
1 1/
1
N
H
N
H
k
H
k
Nk
for
for
whe
dt
n
F
Ff
F
λ
β
β
β
λβ β
β
λβλ
λβ λ
λλ
−
+=− <<
=− +<<

= >

−+


+


∫
3.2. Optimal Receiver
The optimal receiver is defined as the receiver that mi-
nimizes the probability of symbol error among all re-
ceiver structures. It is based on the analysis of the post-
erior probabilities of the transmitted signal [19]. The
spectral efficiency is defined by:
( )
( )
( )
2
2
1/*1/
H
N
Nlog detIHH γσ = +
. (10)
where: σ2 is the noise variance and N the channel vector
length. Equation (10) can also be represented like the
author in [6]:
( )
( )
2
1/ *.
H
N
Nlog detIHH γρ = +
(11)
where ρ is defined in [6] by:
( )
withK N
b
E
No
γ
ρβ
β
==
.
In fact, the asymptotic analysis allows providing a
good understanding of the ChDMA limiting behavior in
MBOFDM-UWB channel.
The author in [6] allows us to write the spectral effi-
ciency represented in (10) in terms of the eigenvalues
(λ1···λm) of HHH like: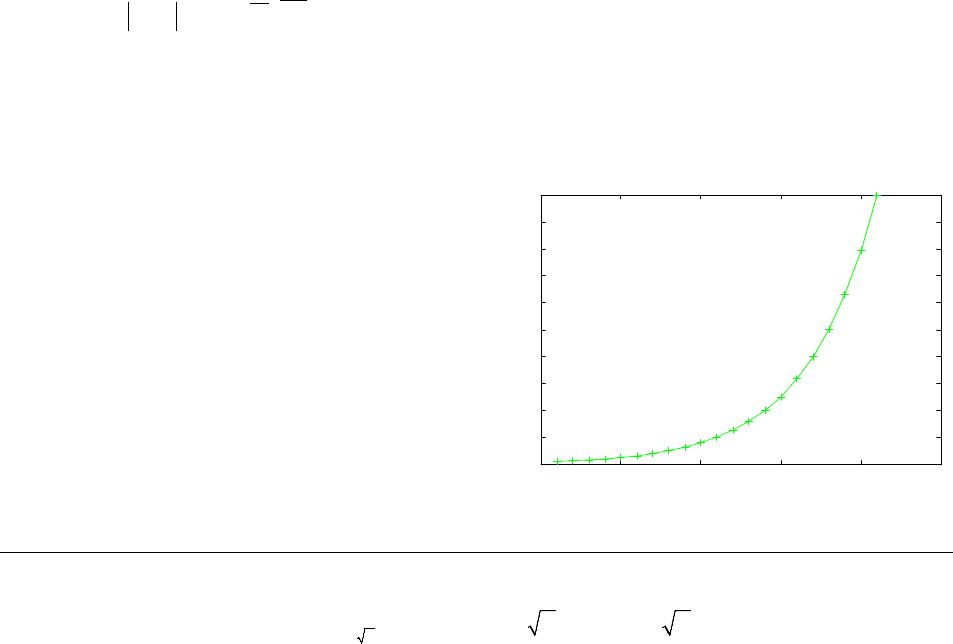

H. CHIHI, R. BOUALLEGUE
685
( )
( )
()
log 1.1/ *
NH
ii
H NH ρλ γ +=
∑
(12)
Following, the author in [20], when N → +∞, the
spectral efficiency can be represented in terms of the
eigenvalue distribution of HHH yields to:
( )
log 1dH
HH
rf γλ
∞= +
∫
. (13)
We conclude that the spectral efficiency is determinis-
tic and only depends on a few macroscopic system pa-
rameters in asymptotic regime.
4. Power Delay Profile
Following the Toeplitz structure of the matrix CN, the
followin g eigendecomposi tion hol ds when N → ∞ [21]:
lim .
NH N N
C DFF
∞ →∞
=
where FN being the Fourier matrix and D could be de-
fined following the decomposition in [22] according to
its elements Dn,n.
where:
PDP refers to power delay profile representing the ex-
ponential decay of each cluster; also it reflects the decay
of the total cluster power with the delay. The detailed
definition is given following the author in [23]:
,
2
,0
kl
l
lk
T
l
Eee
τ
γ
ξβ
−
−
Γ 
= Ω


. (15)
with Ω0 represents the average energy of the first path of
the first cluster, Γ and γ are, respectively, defined as con-
stants that characterize the exponential decay of each
cluster and each ray.
• Wc repre s ents the frequency resoluti on.
• Tl is the arrival time of the first path of the lth cluster
and L is the number of multipath.
We evaluate the impact of a power delay profile (PDP)
on the spectral efficiency. In fact, if we refer to (14) and
replace PDP with his previous expression in (15), we can
represent the results of spectral efficiency with a random
generation of the channel by employing the diagonal
matrix D .We assume, respectively, the number of fre-
quency samples N, the frequency resolution Wc, the
number of multipath L, 128,40 MHz and 100.
Figure 4 presents the impact of the PDP on the spec-
tral efficiency. As the SNR increase, the spectral effi-
ciency of the simulated channel increase and this depend
intimately to the system parameters. The result shows
that the energy is equally spread over all the bandwidth.
In fact, PDP has been shown to be a useful measure, and
we have employed it to identify the optimum number of
parameters to represent the performance. This increase of
spectral efficiency is also due to the attractive choice of
OFDM for UWB communication because it can capture
the multipath energy efficiently.
The obtained result shows that the cluster s are disjoint
because we have an increase of spectral efficiency. How-
ever, we can find generally some overlap between the lth
and (l + 1)th clusters.
5. Results
In this section, we present the simulation r esults obtained
by averaging over 500 Monte Carlo iteration, we consid-
er the mode I of the MBOFDM employing the first three
subbands of 528 MHz. Additionally, each realization of
the channel model related to each user is generated inde-
pendently and assumed to be time invariant during the
transmission of a frame. We simulated the MMSE spec-
tral efficiency using the CM1UWB channel model where
the parameters are present ed in Table 2 [24] which is pre-
sented in Figur e 5.
In Figure 6 we present a comparison of the spectral
efficiency of optimal receiver performance results over
the CM1 UWB model. The obtained results show that the
performance of the MBOFDM ChDMA-UWB high data
rate system is critically dependent of the receiver struc-
ture as the number of users increase, the spectral effi-
ciency increases as well. The increase in spectral effi-
ciency comes from the multiuser diversity effect provided
by ChDMA system; if we consider many users transmit-
ting independently, we could find a user with strong
0510 1520 25
0
10
20
30
40
50
60
70
80
90
100
SNR
S pc tral eff i ciency
Figure 4. Impact of the power delay profile.
( )
() ()
( )
( )
( )
( )
( )( )
2
c lclcl
22
N
H
n
1
,n
PDP*L/W*TwithNW T*l1/Ln1NW T*l/
F
L
1?
D 0.Otherwise
()for 11
k
f dt
β
λ
β
λβ λ λβ β
−


−
−≤ −≤
=+<

<

=
+


∫
(14
)

H. CHIHI, R. BOUALLEGUE
Copyright © 2013 SciRe s. CN
686
channel yields that the channel is used in the most effi-
cient manner where the total throughput is maximized.
By this way, we obtain a maximized multiuser diver-
sity gain .We must mention also that QPSK is the best
practical choice in the MBOFDM ChDMA-UWB chan-
nel coherent regime when the receiver knows the chan-
nel.
6. Conclusions
In this contribution we aim at providing a very good
technical solution to be proposed for UWB physical layer
024 6810 12 14 16 18 20
15
20
25
30
SNR
S pc tral eff i ciency
opti m al receiver
as ymptotic
Figure 5. Validation of ChDMA-UWB channel model with
MMSE detector (Eb/No = 5 dB).
Table 2. MBOFDM UWB system parameters.
WiMedia
Number of data subcarriers 100
number of pilot symbols 12
number of guar d s ymbols 10
Subcarrier frequency spacing (Mhz) 4,125
zero padding duration (ns) 60,61
00.2 0.40.6 0.811.2 1.41.6 1.82
1
2
3
4
5
6
7
8
9
10
11
S pec tral Ef f i ci enc y
K/N
Figure 6. Comparison between optimal and asymptotic
spectral effi ci ency.
high data rate wireless applications called ChDMA. This
approach, simplifies the transmitter ar chitecture allowing
simultaneous access as we assimilate the natural disper-
sion of the channel to code signature. We have studied
the eigenvalues distribution performance analysis of the
MMSE and optimal receiver in MBOFDM ChDMA -
UWB channel in terms of spectral efficiency assuming
that the system size is large. Additionally, we investi-
gated the impact of power delay profile (PDP) on the
spectral efficiency of MBOFDM UWB-ChDMA high
data rate system.
As perspectives, we could investigate other receiver
structure that will be adapted for the considered system.
We are more ambitious in studying mutual information
criteria as well channel es timation mismatches.
REFERENCES
[1] M. Kamoun, S. Chaillouz, J. Gosteau, L. Mazet and M.
de Courville Pierre Duhamel, “Data Rate Upper Bounds
for UWB Link with IEEE802.15.3a Channel Model,”
IEEE International Conference, ICU 2005.
[2] A. Stephan, “Resource Allocation Strategies and Linear
Precoded OFDM Optimization for Ultra-Wideband Com-
munications,” Ph.D. Thesis, National Institute of Applied
Sciences (INSA), 2008.
[3] A. Saleh and R. Valenzuela, “A Statistical Model for
Indoor Multipath Propagation,” IEEE Journal on Selected
Areas in Communications, Vol. 5, No 2, 1987, pp. 128-
137. http://dx.doi.org/10.1109/JSAC.1987.1146527
[4] J. Foerster, “Channel Modeling Sub-Committee Report
Final,” IEEE Document P802.15-02/490r1, Intel R&D,
2003.
[5] Raul L. de Lacerda Neto, Aawatif Menouni Hayar and
Merouane Debbah, “Channel Division Multiple Access:
New Multiple Access Approach for UWB Networks,”
European Ultra Wide Band Radio Technology Workshop
2007, Grenoble, France, 10-11 May 2007.
[6] R. L. De LacerdaNeto, “Exploiting the Wireless Channel
for Communication,” Ph.D. Thesis, Nice-Sophia Antipo-
lis University, 2008.
[7] S. Verdu and S. Shamai, “Spectral Efficiency of CDMA
with Random Spreading,” IEEE Transactions on Infor-
mation Theory, 1999, pp. 622-640.
http://dx.doi.org/10.1109/18.749007
[8] Z. Xie, R. T. Short and C. K. Rushforth, “A Family of
Suboptimum Detectors for Coherent Multiuser Commu-
nications,” IEEE Journal on Selected Areas in Commu-
nications, Vol. 8, No. 4, 1990, p. 683.
[9] L. Cottatellucci, R. R. Muller, M. Debbah, “On the Ca-
pacity of Asynchronous CDMA Systems,” Conference
Record of the Fo rty-First Asilomar 2007.
[10] R. Couillet, “Random Matrices in Wireless Communica-
tions Course 2: System Performance Analysis: Capacity
and Rate Regions,” 2009.
[11] V. A. Marcenko and L. A. Pastur, “Distribution of Eigen-

H. CHIHI, R. BOUALLEGUE
687
values for Some Sets of Random Matrices,” Mathematics
of the USSR, Vol. 1, 1967, pp. 457 -483.
http://dx.doi.org/10.1070/SM1967v001n04ABEH001994
[12] S. V. Hanly and D. N. C. Tse, “Resource Pooling and
Effective Bandwidths in CDMA Networks with Multiuser
Receivers and Spatial Diversity,” IEEE Transactions on
Information Theory, Vol. 47, No. 4, 2001.
[13] M. J. M. Peacock, I. B. Collings and M. L. Honig,
“Asymptotic Spectral Efficiency of Multiuser Multisig-
nature CDMA in Frequency-Selective Channels,” IEEE
Transactions on Information Theory, Vol. 52, No. 3, 2006.
http://dx.doi.org/10.1109/TIT.2005.864427
[14] R. Wegmann, “The Asymptotic Eigenvalue-Distribution
for a Certain Class of Random Matrices,” Journal of Ma-
thematical Analysis and Applications, Vol. 56, 1976, pp.
113-132.
http://dx.doi.org/10.1016/0022-247X(76)90011-1
[15] J. Evans and D. N. C. Tse, “Large System Performance of
Linear Multiuser Receivers in Multipath Fading Chan-
nels,” IEEE Transactions on Information Theory, Vol. 46,
No. 6, 2000. http://dx.doi.org/10.1109/18.868478
[16] R. R. Muller, “Applications of Large Random Matrices in
Communications Engineering,” Statistical Mechanics, 2.
Spin Glasses, 2003.
[17] Z. D. Bai and Y. Q. Yin, “Limit of the Smallest Eigenva-
lue of a Large Dimensional Sample Covariance Matrix,”
Annals of Probability, Vol. 21, No. 3, 1993, pp. 1275-
1294. HTTP://DX.DOI.ORG/10.1214/AOP/1176989118
[18] J. W. Silverstein, “Some Limit Theorems on the Eigen-
vectors of Large Dimensional Sample Covariance Ma-
trices,” Journal of multivariate Analysis, Vol. 15, 1984,
pp. 295-324.
http://dx.doi.org/10.1016/0047-259X(84)90054-X
[19] J. Proakis (2000) Digital Communications. McGraw Hill.
[20] I. E. Telatar, “Capacity of Multi-Antenna Gaussian Chan-
nels,” Technical Report, AT&T Bell Laboratories Tech-
nical Memorandum, 1995.
[21] R. M. Gray, “Toeplitz and Circulant Matrices: A Re-
view,” Technical Report. No. 6504-1, Information Sys-
tems Laboratories: ISL, Stanford University, Stanford,
CA, 1977.
[22] R. de Lacerda, L. Co tt atellucci, A. Hayar and M. Debbah,
“Asymptotic Analysis of Channel Division Multiple Ac-
cess Schema for Ultra Wideband Channel,” 9th IEEE
Workshop (SPAWC’08), 2008.
[23] A. Batra, J. Balakrishnan, G. R. Aiello, J. R. Foerster and
A. Dabak, “Design of a multiband OFDM System for
Realistic UWB Channel Environments,” IEEE Transac-
tions on Microwave Theory and Techniques, Vol. 52, 2004,
pp. 2123-2138.
http://dx.doi.org/10.1109/TMTT.2004.834184
[24] E. Gueguen, M. Crussiere and J.-F. Helard, “An OFDM-
CDMA Scheme for High Data Rate UWB Applications,”
VTC Spring 2007, pp. 2905-2909.