 Int. J. Communications, Network and System Sciences, 2011, 4, 205-218 doi:10.4236/ijcns.2011.44025 Published Online April 2011 (http://www.SciRP.org/journal/ijcns) Copyright © 2011 SciRes. IJCNS 205 Forwarding vs. Network Coding: Efficient Broadcasting in Multihop W ir eless Networks Suranjit Paul1, Thomas Kunz1, Li Li2 1System and Computer Engineering, Carleton University, Ottawa, Canada 2Communications Research Centre Canada, Ottawa, Canada E-mail: spaul2@connect.carleton.ca, tkunz@sce.carleton.ca, li.li@crc.ca Received March 5, 2011; revised March 27, 2011; accepted March 30, 2011 Abstract Broadcasting is used as a building block in many MANET (Mobile Ad hoc Network) routing protocols. In addition, broadcasting is a key primitive in ad hoc networks to support group-based applications. Efficiently supporting broadcasting in multihop wireless networks is therefore important. In this paper, we compare ef- ficient broadcasting protocols based on packet forwarding with those based on network coding. Using a number of network scenarios, we derive lower bounds for the required number of packet retransmissions at the MAC layer to support broadcast with and without applying network coding techniques. We compare these lower bounds with each other, as well as with protocols proposed for each approach. More specifically, we use SMF and PDP as sample forwarding-based broadcast protocols, and a simple XOR-based coding protocol over SMF and PDP as representative network coding solution. The results show that neither packet forwarding protocols nor network coding protocols achieve the theoretical lower bounds, in particular as the size of the network area (at constant density) increases. The comparison of the lower bounds also shows that network coding does have a potential performance advantage over packet forwarding solutions for broad- casting in multi-hop wireless networks, in particular for larger fixed density networks, justifying its inherent increased complexity. Keywords: MANETs, Broadcasting, Multi-hop Networks, SMF, PDP, Network Coding 1. Introduction In recent years, multi-hop wireless networks have at- tracted significant attention due to their potential appli- cations in tactical networks. A multi-hop wireless net- work consists of numerous devices that are equipped with processing, memory and wireless communication capa- bilities, and are linked via short-range ad hoc radio con- nections. There is no pre-installed infrastructure in this type of network, communication is supported by inter- mediate nodes relaying packets between communicating parties. Broadcast communication is an important mechanism to communicate information in such ad hoc wireless networks. In addition, many routing and other network protocols for wireless ad-hoc networks need a broadcast mechanism to update their states and maintain informa- tion between nodes. Many packet forwarding and net- work coding techniques have been proposed so far for improved performance of broadcast communications in packet networks. Recent research has also applied net- work coding to mobile ad hoc networks (MANET) for improved network throughput and robustness. In a mul- ti-hop wireless network, each node has limited energy resources. Reducing the number of transmissions re- quired to broadcast messages to the whole network saves energy and improves spectrum efficiency, which is very critical in bandwidth limited multi-hop radio communi- cations. Different packet forwarding and network coding protocols have been proposed to reduce the number of retransmissions. This paper studies the performance of packet for- warding and network coding broadcast approaches in a multi-hop wireless networks, aka the MANET environ- ment. In particular, we are interested in minimizing the number of packet transmissions at the MAC layer, as this directly translates into reduced energy consumption and more efficient spectrum utilization. We therefore study This work was supported by the Communications Research Centre Canada under Intergovernmental Agreement Number 9003930.  206 S. PAUL ET AL. lower bounds of the packet transmission and compare the performance of actual broadcast protocols against the derived lower bounds. We approximate the lower bound for any packet forwarding solution, using the Minimum Connected Dominating Set (MCDS). We also derive lower bounds for any network coding solution based on a linear program. We then compare these lower bounds with two protocols in each category and with each other. The paper is organized as follows. In Section 2, the re- sults of a literature survey for packet forwarding and network coding approaches are summarized. This section also identifies the packet forwarding and network coding protocols we selected for comparison purposes. In Sec- tion 3, the implemented MCDS heuristic is described, which approximates the lower bound on packet trans- missions for any packet forwarding solution. A linear program that derives the lower bound for network coding is described in Section 4. Section 5 discusses the per- formance of the packet forwarding protocols, with re- spect to their lower bound; Section 6 likewise discusses the performance of the network coding protocols, rela- tive to their lower bound. Section 7 compares the lower bounds themselves, and Section 8 concludes the paper and points to avenues for future research. 2. Related Work The review of related work is broken down in two main sections. We first review work on efficient broadcasting using packet forwarding only, followed by a review of the use of network coding in the context of broadcast communication. 2.1. Broadcasting via Packet Forwarding 2.1.1. The Minimum Connected Dominating Set Efficiently broadcasting packets to all nodes in the net- work can be modeled either as a graph problem or via appropriate routing protocols. In graph theory, the neighbors of a vertex are all the vertices which are con- nected to that vertex by a single edge. A dominating set (DS) for a graph is a set of vertices whose neighbors, along with themselves, constitute all the vertices in the graph. A connected dominating set (CDS) of a graph G = (V,E) is a subset of nodes, S such that S is a dominating set of G and the sub-graph of G induced by S is also connected. The Minimum Connected Dominating Set (MCDS) problem is to find a connected dominating set of minimum cardinality. An MCDS provides an efficient way to broadcast packets to all nodes in a network: as- suming that the wireless links are inherently a broadcast medium, only nodes in the MCDS need to (re-)broadcast packets to ensure that all nodes receive a packet. In addi- tion, as the MCDS itself is connected, once one node within the MCDS knows about the packet, it will propa- gate through the MCDS via broadcasting. Unfortunately, computing a minimum connected dominating set over a given graph is an NP-complete problem [1]. There exist several centralized approximations and exact algorithms in the literature to solve the minimum connected dominating set problem. All exact algorithms are at best only small improvements of the trivial O (2n) solution. The trivial solution requires checking every possible subset of nodes to determine whether this subset constitutes a minimum connected dominating set. Refer- ence [2] proposes an exact algorithm for the MCDS problem of an arbitrary graph with an improved runtime complexity of O (1 .9407n). The algorithm makes use of some new domination rules and reduction rules and its analysis is based on the Measure and Conquer technique. But this algorithm is not practical for networks as small as even only 100 nodes as it will take a long time to find the minimum connected dominating set. Guha and Khuller first proposed a two-stage greedy ln 3 -approximation in [3] for MCDS in general graphs, where is the maximum node degree in the graph. In the first step of this algorithm, a CDS is built from one node, then the search space for the next domi- nator(s) is restricted to the current set of dominatees and the CDS expands until there are no uncovered nodes left. All the possible dominators determined in the first phase are then connected through some intermediate nodes in the second phase. A new efficient heuristic algorithm for the MCDS problem was proposed in [4]. The algorithm starts with a feasible solution containing all vertices of the graph. Then it reduces the size of the CDS by excluding some vertices using a greedy criterion. This algorithm is espe- cially valuable in situations where setup time is costly because it maintains a feasible solution at any time dur- ing the computation. This algorithm provides a better approximation of 2H than that of Guha and Khuller’s. Here, ∆ is the maximum degree of the graph and 112 1 n is the harmonic function. In [5], the authors proposed a new approximation al- gorithm based on Steiner trees, which produces an ap- proximation solution within a factor of 6.8. This ap- proximation algorithm can also be implemented in a dis- tributed manner. This algorithm consists of two steps. In the first step, a maximal independent set is being con- structed. In the second step, a 3-approximation for the ST-MSN (Steiner Tree with Minimum Number of Steiner Nodes) to interconnect the maximal independent set is determined. Note that the size of the optimal solu- tion for the ST-MSN cannot exceed the size of the min- imum connected dominating set since the latter can also Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. 207 interconnect the maximal independent set. A Steiner tree is defined as a subset of the vertices of a graph G which is a minimum-weight connected sub-graph of G that in- cludes all the vertices. It is always a tree. Therefore, the ST-MSN has at most 3*opt Steiner nodes in the second step, where opt denotes the optimal solution (MCDS size). The resulting connected dominating set has a size bounded by 6.8*opt. On the other hand, in [6], another greedy algorithm called S-MIS (Steiner tree with Maximal Independent Set) was proposed. The algorithm, with the help of Steiner trees, constructs a CDS within a factor of 5.8 + ln 4 from the optimal solution. This is also a two-step algorithm. In the first step, a MIS is constructed and in the second step a greedy approximation for the ST-MSN to interconnect the nodes in the MIS was employed. The resulting CDS has a size bounded by (5.8 + ln 4) opt + 1.2. Since NP-hard problems cannot be solved in polyno- mial time, approximation algorithms are more efficient to use. On the other hand, exact algorithms provide the optimal solution; however their running time is very high even for small problem sizes. After reviewing a range of algorithms, we found that the algorithm proposed in [7] has better execution time than others. Also the proposed algorithm produces an MCDS of smaller size than others. In addition, this algorithm is less complex than others. Hence this one has been chosen to be implemented. In Section 3, we discuss the proposed algorithm in detail. 2.1.2. Distributed Efficient Flooding Algorithms In addition to these graph-based approaches, a number of authors have proposed distributed broadcast algorithms to efficiently flood data packets in a network. All these proposals aim to improve on the trivial flooding protocol, where a node rebroadcasts a packet the first time it re- ceives it. In general, research on efficient broadcast sup- port in mobile ad hoc networks has proceeded along two main approaches: deterministic and probabilistic. Deter- ministic approaches predetermine and select the neigh- boring nodes that forward the broadcast packet. On the other hand, probabilistic or gossiping-based approaches require each node to rebroadcast the packet to its neigh- bors with a given forwarding probability. The key chal- lenge with these approaches is to tune the forwarding probability: keeping it as low as possible for maximum efficiency while maintaining it high enough so that all the nodes are able to receive the broadcast packets. In this work, we selected two deterministic protocols SMF and PDP. Both SMF and PDP apply the two-hop neigh- borhood information in selecting relay nodes, which is collected via periodic HELLO messages. SMF is described in detail in [8,9]. The concept of “multipoint relaying” is used to reduce the number of duplicate re-transmissions while forwarding a broadcast packet. This technique restricts the number of re-trans- mitters to a small set of neighbor nodes, instead of all neighbors, as would be the case in flooding. This set is kept as small as possible by efficiently selecting the neighbors which cover (in terms of one-hop radio range) the same network region as the complete set of neighbors. This small subset of neighbors is called multipoint relays of a given network node. The technique of multipoint relays (or MPRs) provides an adequate solution to reduce the flooding of broadcast messages in the network, while attaining the same goal of transferring the message to every node in the network with high probability. The information required to calculate the multipoint relays is the set of one-hop neighbors and the two-hop neighbors, i.e. the neighbors of the one-hop neighbors. To obtain the information about one-hop neighbors, most protocols use some form of HELLO messages that are sent locally by each node to declare its presence. In a mobile environ- ment, these messages are sent periodically to get the most updated information. To obtain the information of two-hop neighbors, one solution may be that each node attaches the list of its own neighbors, while sending its HELLO messages. With this information, each node can independently calculate its one-hop and two-hop neigh- bor sets. Once a node has its one-hop and two-hop neigh- bor sets, it can select a minimum number of one- hop neighbors which covers all its two-hop neighbors. MPRs are dynamically selected by each node and selections are advertised and dynamically updated with hello messages. The variant of SMF we selected is based on the source-specific MPR forwarding. A node will forward packets if and only if it receives a unique multicast pack- et from any of its neighbors and the neighbor from which the packet was received has selected the node as an MPR. The basic algorithm for the S-MPR selection process is described in [8]. N(n) and N(N(n)) indicate one-hop neighbors and two-hop neighbors of node n, respectively. 1) Start with an empty multipoint relay set MPR(n). 2) First select those one-hop neighbor nodes in N(n) as multipoint relays which are the only neighbor of some node in N(N(n)), and add these one-hop neighbor nodes to the multipoint relay set MPR (n). 3) While there still exists some node in N(N(n)) which is not covered by the multipoint relay set MPR(n): a) For each node in N(n) which is not in MPR(n), compute the number of nodes that it covers among the uncovered nodes in the set N(N(n)). b) Add that node of N(n) to MPR(n) for which this number is maximum. Partial Dominant Pruning (PDP) is another algorithm which also utilizes the neighborhood information for re- Copyright © 2011 SciRes. IJCNS  208 S. PAUL ET AL. ducing redundant packet transmissions. In PDP, when a node v receives a packet from another node u, it selects a minimum number of forwarding nodes from the set that can cover all the nodes in the set Nv Nu U NNvNu Nv NNuNv . A node can obtain its one-hop and two-hop neighborhood infor- mation by periodically sending hello messages. Upon receiving the hello messages, each node updates its neighborhood information. Each forwarding node then again follows the same procedure to select its own for- warding nodes. The forwarding stops when all forward- ers have received a packet at least once. The PDP algo- rithm is described below. Details of this algorithm are described in [10]. Step 1: Node v uses NNv, , and Nu Nv to obtain PNNu Nv , UNNvNuNv P, and BNv Nu. Step 2: Node v then calls the selection process to de- termine the set of forwarding nodes, F. Selection Process: Step 1: Let ,Fuv (empty list), z U (empty set), and K = U Si, where for vi ε B. ii SNv Step 2: Find the set Si, whose size is maximum in K. (use the one with the smallest identification i in case of a tie) Step 3: Fv,i ZUS, K = K – Si, and Sj = Sj – Si for all Sj K. Step 4: If Z = U, exit; otherwise, goto Step 2. 2.2. Broadcasting via Network Coding Research in information theory discovered that routing alone is not sufficient to achieve maximum throughput in the general model of data networks. Network coding techniques have been proposed for improved perform- ance for broadcast and multicast traffic. Network coding is a technique which looks beyond the traditional store- and-forward approach followed by routers in communi- cation networks. Network coding is a generalization of routing in which nodes can generate output data by en- coding previously received input data. Thus, network coding allows information to be “mixed” at a node. Ahlswede et al. in [11] first formally introduced the pa- radigm of network coding, where they also demonstrated its use in case of single-source multiple-sink network multicast in a wired network. Additional examples of networks are also presented in [11] where it is shown that network coding can improve the overall throughput of the network which can not otherwise be realized by the conventional store-and-forward approach. Network coding has drawn significant interest, especially for broadcast and multicast traffic. However, it is not obvi- ous whether network coding further reduces the number of packet transmissions for random networks in the case of broadcasting. This section briefly reviews several network coding techniques that were proposed for wire- less networks. The approach proposed in [12] applies network coding to a deterministic broadcast protocol, resulting in a sig- nificant reduction in the number of transmissions in the network. To reduce the number of transmissions, two algorithms that rely only on local two-hop topology in- formation and make use of opportunistic listening were proposed. The first algorithm is a simple XOR-based coding algorithm, similar to the approached described in [13], and the second one is a Reed-Solomon based cod- ing algorithm. The simulation results show that the de- terministic coding approach (Nodes pre-select a few neighbors for rebroadcasting) outperforms the probabil- istic coding approach (Each node rebroadcasts a packet with a given probability). CodeCast, a network coding based ad hoc multicast protocol which is well-suited especially for multimedia applications with low loss and low latency is proposed in [14]. The main component of CodeCast is random net- work coding, which is used to implement both localized loss recovery and path diversity transparently. The au- thors demonstrated through simulation that CodeCast achieves a near perfect packet delivery ratio while main- taining lower overhead than conventional multicast. On the other hand, the authors of [15] present a theo- rem that unifies and generalizes Edmonds’ theorem on routing (i.e. if all nodes other than the source are destina- tions, the cut bound, which is any cut separating the source from a destination, can be achieved by routing) and Ahlswede et al.’s theorem on network coding (i.e. the cut bound can be achieved by performing network coding) by classifying the links in a network into two categories: links entering relay nodes (Steiner edges), and links entering destinations (Terminal edges). The authors show that the multicast capacity can be achieved by performing nontrivial network coding (Mixing) only at links entering relay nodes. Links entering destinations will only require routing, which leads to a saving in the processing/implementation complexity. In [16] the authors develop a network coding scheme for broadcast traffic in ad hoc networks and compare its performance against simpler solutions, based on flooding and deferred broadcast. They show that network coding is advantageous only in certain cases, such as dense net- works, by comparing random linear network coding with two broadcast schemes under a range of scenarios. Their Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. 209 analysis shows that network coding significantly outper- forms other broadcasting schemes in terms of end-to-end packet loss probability and protocol overhead only for large neighborhood sizes (i.e., more than 12 neighbors) and generation sizes smaller than or equal to three. A generation is defined as a collection of packets that can be allowed to be linearly combined. Dividing packets into generations decreases the decoding complexity and allows to decode data faster (And thus to empty the re- spective memory). In [17], random linear network coding for time divi- sion duplexing channels for broadcasting is studied. The authors also studied the mean time to complete the transmission of a block of packets to all receivers. Nu- merical results show that the coding scheme proposed in [17] outperforms a Round Robin broadcast scheme in a time division duplexing channel. Reliability gain as a performance metric for random linear network coding in relay networks is studied in [18]. The work studies the expected number of channel uses per data bit successfully received. By analysis they show that random linear network coding provides limited per- formance gains in comparison to other protocols. Reference [19] explores the efficiency of broadcasting via network coding in general and whether it is beneficial to use network coding over routing. It argues that for wireless networks in the 2D space, the asymptotic coding gain for a single-source broadcast is between 1.642 and 1.684 when both the area and the density of the network converge toward infinity. The paper also provides bounds of 1.432 and 2.035 for networks of the Euclidean space of dimension 3. Reference [20] investigates benefits in terms of energy efficiency that the use of network coding can offer for the problem of broadcasting over ad-hoc wireless net- works. The authors also show that network coding can result in a coding gain of 2 in ring networks and a coding gain of 1.3333 for grid networks and provides protocols that achieve this gain for such specific network topolo- gies, using scenarios where all nodes are sources. Their work also indicates that there is a potential for significant benefits when deploying network coding over a practical wireless ad hoc network environment, especially when we are restricted to use low complexity decentralized algorithms. For comparison purposes, we selected the XOR-based coding approach proposed in [12]. This is a fairly simple protocol, which can extend PDP and SMF and has been shown to reduce the number of MAC packet transmis- sions while achieving good broadcast performance. Each node maintains one-hop and two-hop neighborhood in- formation, based on the HELLO message exchange of the underlying SMF or PDP protocols. For each data packet a node u receives from a neighbor v, it will as- sume that those of its neighbors that are also v’s neigh- bors will also have received that packet. So a node will promiscuously, and without any additional messaging overhead, maintain information about which packets were already received by what neighbor (called the neighbor reception table), to guide its encoding decision. A node u with a set of native packets P in its output queue seeks to find a subset of native packets Q to XOR. Let the set of neighbors of u, each of which can decode a missing packet be N1(u) (determined by Q and the neighbor reception tables). As shown in [12], determin- ing the optimal combination of packets (maximal cardi- nality of N1(u), optimized across all packets in u’s output queue) is NP-hard. So instead, the following greedy heu- ristic is proposed: Start with the packet p at the head of the output queue and sequentially look for other packets in the queue that, when combined with p, will allow all neighbors of node u to decode the packet. If successful, these packets are added to the coded packet. Once such a coded packet is received by a node, it can extract the missing packet by XOR-ing the received packet with the remaining N – 1 packets it already received and buffered. This requires that the coded packet carries with it an in- dication that it is a coded packet, and the unique identifi- ers of its contributing native packets. In case that the neighbor reception table of a node u was inaccurate, a node will be unable to successfully decode a packet. Al- so a node may not gain any new information from this packet, as it already received all constituent native pack- ets. In the following, we refer to the XOR coding over PDP or SMF as PDP/XOR and SMF/XOR. 2.3. Summary Network coding enables more efficient, scalable and reliable wireless networks. Based on the reviewed stud- ies, we conclude that the potential advantages of network coding over routing include a reduction in resource usage (e.g., bandwidth and power), and robustness to network dynamics. Besides, network coding can increase the pos- sible network throughput and, in the multicast case, it can achieve the maximum data rate theoretically possible. In addition to maximizing throughput, network coding can also maximize the energy efficiency by reducing the number of transmissions required to deliver a message to the whole network. But there is also some evidence that network coding is not always beneficial. In this work, we explore a range of network scenarios to study this ques- tion in more detail. We compare the performance of effi- cient packet forwarding approaches and network coding protocols to support broadcasting in multi-hop wireless networks. The comparison is based on both lower bounds Copyright © 2011 SciRes. IJCNS  210 S. PAUL ET AL. derived from analytical models and also the simulation results. More specifically, we compare the following: • A lower bound for packet forwarding based broad- cast protocols generated using the centralized MCDS heuristic proposed in [7]. • The number of PDP forwarders and SMF MPRs, where both PDP and SMF are representative packet forwarding broadcast protocols. • A lower bound for network coding approaches generated using an integer linear program. • The number of data packets forwarded by network coding protocols employing XOR coding as repre- sentative network-coding based broadcast protocols. 3. Packet Forwarding Lower Bound The MCDS algorithm that we implemented is proposed in [7] and it uses a heuristic to find the minimum con- nected dominating set. This algorithm is divided into three phases. In the first phase, a dominating set D is constructed, in the second phase a set of connectors are found which can connect nodes in D, with the help of a Steiner tree, and in the final phase, pruning is done, where the number of nodes in the MCDS is reduced to make it a near-optimal minimum connected dominating set. A black node is a node which is to be present in the Connected Dominating Set or is a Dominator. A gray node is a dominatee and a blue node is a connector which is to be present in the Connected Dominating Set. The algorithm proceeds in three stages. Stage 1: In Stage 1, a dominating set is constructed which consists of the minimum number of nodes. This stage consists of the following steps: 1) An arbitrary unique number say ID is assigned to each Node in the graph G(V,E), 2) Each node is assigned white color, 3) The node u with maximum degree is taken from G(V,E) and colored as black, i.e. it indicates that it is a Dominator, 4) All the neighbor nodes of the node u are colored as gray, 5) Repeat steps 3 and 4 till all the nodes in the graph G(V,E) are colored either as black or gray. Stage 2: In Stage 2, a set of connectors B is found such that all the nodes in the dominating set are con- nected. Let a black node be a node in D and a blue node represent a node in B. A node in B is connected by at most K nodes in the graph G(V, E). The set of blue nodes with given D could be found using a Steiner tree. It is a tree interconnecting all the nodes in D by adding new nodes between them. The nodes that are in the Steiner tree but not in set D are called Steiner nodes. In the minimum connected dominating set, the number of Steiner nodes should be minimal. After this stage a CDS is constructed, which consists of black and blue nodes. This involves the following steps: 1) Select a gray node which is connected to the max- imum (K) number of black nodes, set its color as blue, 2) Check whether the Dominating Set D is connected or not, 3) If D is connected stop, 4) Else go to step 1 with K-1 number of Black nodes. Stage 3: Stage 3 is a pruning stage. In this stage, re- dundant nodes are deleted from the CDS constructed in Stage 2, to obtain the MCDS. Let the CDS constructed in the previous stage be set F. Initially, all nodes in the set are unmarked. 1) Select a minimum degree, unmarked, node u from F. 2) Check if N[u] is a subset of N[1] and N[2] and … N[n] where i belongs to F- {u}. 3) If step 2 returns true then remove node u and goto step 1. 4) Otherwise do not remove node u (but mark it) and goto step 1. After implementing the original algorithm (referred to as Unconstrained MCDS algorithm in the following), we developed a revised version where we enforce that a spe- cific node (node 0) is always in the final MCDS. This reflects more accurately the deployment of protocols in a network, where a specific node (or group of nodes) is chosen as source. Since node 0 is the source node in our simulations, this revised version (referred to as Con- strained MCDS algorithm in the remainder of this paper) allows us to directly compare the results. 4. Network Coding Lower Bound We are determining the lower bound on the number of required packet retransmissions for network coding using the linear program originally proposed in [21]. Here, the lower bound on the number of required packet retrans- missions for network coding is determined by formulat- ing this as an integer linear program and solving it for a range of randomly generated multi-hop wireless networks. The linear program is based on the intuition that, as- suming the NC protocol is optimal, working on genera- tions of size N, than all packet transmissions will be in- novative for all neighbors. So, if each node receives at least N packets, with all of them being innovative, they can then decode and therefore receive all native packets in a generation. In addition, flow constraints have to be met: flows exist from the sender to each receiver; these flows are subject to the typical flow constraints: the amount of flow on an edge cannot exceed the capacity of the edge and a flow must satisfy the restriction that the Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. 211 amount of flow into a node equals the amount of flow out of it, except when it is a source, which has more outgoing flow, or sink, which has more incoming flow. Flow variables Fi,j(d) are introduced which capture the data flow from source 0 over link i, j destined to node d. In a broadcast scenario, all nodes are receivers, but to simplify the formulation, it is assumed that node 0, the implied source, trivially receives all packets and there- fore d ≠ 0. Finally, to correctly capture the broadcast nature of the wireless media, a dummy node is intro- duced where node i will transmit its packets to its dum- my node ī first, and the dummy node will then forward the packets to all neighbors of i. Let Xi be the number of packet transmissions of node i (for a given generation of size N), let N(i) be the set of one-hop neighbors of node i, The integer linear program to determine the minimum number of packet transmis- sions at the MAC layer is: min i Subject to: , ,, ,, ,: for 0 ,: for 0 otherwise ,: 0 :0, is integer i ii ii ji jNi ij ii jNi ii id FdX Ni= id FdFdNi=d idFdFd iX X Here, the first constraint limits the flows out of a real node i (which are all destined to the nodes’ dummy node ī) to the number of physical packet transmissions of that node. The second set of constraints imposes the flow balance condition: if the node is the source node, it gen- erates N more packets than potentially received from the dummy nodes of its neighbors. If the node is a destina- tion, it consumes N more packets than forwarded to its dummy node. For all other nodes, it passes on all re- ceived packets. The third set of constraints expresses flow balance constraints on the newly introduced dummy nodes: as these are neither sources nor destinations, their flow balance is always zero. Finally, the last set of con- straints enforces that the number of physical packet transmissions by each node are always a positive integer or zero. 5. Performance of Packet Forwarding Protocols 5.1. Scenario Descriptions To compare lower bounds and actual routing protocols, we generated a number of multihop wireless network scenarios, distributing a number of nodes in a rectangular area of a given size using a uniform distribution. These scenario files were then used as the basis for NS-2 (NS-2 version 2.29) simulations of SMF, PDP, and the XOR- based coding variants thereof. We also process these scenario files to approximate the MCDS size, using both constraint and unconstrained versions of the MCDS heuristic described in Section 3. Finally, we also used these scenario files to derive integer linear programs that were then solved with glpk, a free LP solver. Before de- scribing the results, we first discuss the simulation setup and relevant parameters. We study both fixed area and fixed density networks. For the fixed area network, we consider an area of 500 × 500 square-meters and then increase the number of nodes from 10 to 100 in steps of 10. For all network sizes, the network diameter was slightly over 3. On the other hand, for fixed density networks, we generated scenarios for an increasing number of nodes (again, from 10 to 100 in steps of 10), but this time we kept the density constant by scaling the network area with the number of nodes. Ta- ble 1 shows the number of nodes, corresponding areas, and average network diameter. In both cases, the gener- ated network scenarios are static. In essence, we consider mobile networks as a sequence of static snapshots, so this simplifies the analysis significantly. The NS-2 simulations were run for 100 seconds. Dur- ing the first 50 seconds, nodes exchange HELLO mes- sages at an interval of 5 seconds, allowing enough time for nodes to learn about their neighborhood, selecting MPRs, and signaling this to the selected nodes. Node 0 starts sending data packets in the 51st second and we are sending a total of 10 data packets (256 bytes each) at a rate of two packets per second. These settings are delib- erately low to not stress the network (except where noted Table 1. Number of nodes, corr esponding networ k size, and network diame ter for fixed density network. Number of NodesNetwork Area Average Network Diameter 10 346 × 346 2.1 20 490 × 490 3 30 600 × 600 4.2 40 693 × 693 4.6 50 774 × 774 5.3 60 848 × 848 5.9 70 916 × 916 6 80 979 × 979 6.4 90 1039 × 1039 7.1 100 1096 × 1096 7.3 Copyright © 2011 SciRes. IJCNS  212 S. PAUL ET AL. later). Additionally, to reduce timer synchronization problems, all packet transmissions are jittered by an ad- ditional random delay, distributed uniformly in a range from 0 to 20 ms. Consequently, and as anticipated, all simulations achieve 100% (or close to it) packet delivery ratio. From the NS2 tracefile, we then extract the number of packet transmissions at the MAC layer, not counting the periodic HELLO messages. For SMF, that number represents the transmission by the source node, and all MPRs that re-transmit a packet. Similarly, for PDP, that number represents again, the transmission by the source node and the forwarding by the selected forwarders, until the packet is delivered to all nodes. In general, we consider only one source, node “0” for simulating packet forwarding algorithms (PDP and SMF). On the other hand, in our simulation for network coding protocols (PDP/XOR and SMF/XOR), we consider four sources, as having only one data source will not generate enough coding opportunities. We confirmed that in- creasing the number of sources further (To six or eight, for example) does not provide additional coding oppor- tunities. Therefore, nodes “0”, “1”, “2”, and “3” are cho- sen as sources in this case and results are presented in terms of the required number of forwards per source. The MAC and PHY settings are based on the default values in NS2 when simulating IEEE 802.11 networks: The transmission range is a perfect circle with a radius of 250 m, carrier sensing range is 550 m, and the raw data rate is 2 Mbps. Again, as the network load is deliberately kept low, these parameters are not expected to impact the findings reported here, except for the case where we stress the network. 5.2. Packet Forwarding Performance for Fixed Area Networks In a first step, we evaluated the performance of the pack- et forwarding protocols in a fixed area network, as we increased the number of nodes. For each network size, 50 different scenarios have been generated and evaluated. Moreover, we generated scenarios for a (Comparatively speaking) sparse and also a (Comparatively speaking) dense network and evaluated the protocol performance. Table 2 shows the average number of forwarding nodes required to cover all nodes in the network for both the unconstrained and constrained MCDS version along with PDP and SMF. The table shows that the uncon- strained MCDS algorithm provides the lower bound for all cases. The constrained version, where we ensure that node “0” is always in the resulting MCDS, also provides a smaller number of re-broadcasting nodes compared to the two distributed algorithms. To evaluate the statistical significance of the differences in the results, we con- ducted a number of t-tests at a 95% confidence level and found the following results: • For small networks (10 to 30 nodes), there is evi- dence of statistically significant difference between the means of the two MCDS versions, with the unconstrained version producing a smaller MCDS size than the constrained version. When the num- ber of nodes increase in the network (up to 100 nodes), the difference becomes statistically insig- nificant. • Comparing SMF and PDP, for all network sizes, the differences between the total numbers of active forwarding nodes for both algorithms are statisti- cally insignificant. • Comparing PDP/SMF to MCDS, unconstrained MCDS always determines a statistically significant smaller MCDS size than the number of active for- warders in PDP/SMF. • Additionally, when we performed t-tests for con - strained MCDS and PDP/SMF, for any network with 10 or 20 nodes, the constrained MCDS will determine an MCDS size that is similar to the number of active forwarding nodes in PDP. How- ever, as the network size grows, constrained MCDS will result in a statistically significant smaller MCDS size, compared to the number of active forwarders in PDP/SMF. We also analyzed scenarios for dense and sparse net- works. For this purpose, we considered two additional network areas. The first one is a (relatively speaking) denser network, i.e. a network with an area of 350 by 350 square-meters. For the second scenario, we consider Table 2. Average number of forwarding nodes for packet forwarding in fixed ar e a ne tworks. No. of Nodes Average # of nodes in unconstrained MCDS Average # of nodes in constrained MCDS Average # of Active Forwarders for PDP Average # of Active MPRs for SMF 10 2.52 3.14 3.30 3.30 20 2.88 3.52 3.82 3.82 30 3.26 3.68 4.54 4.44 40 3.70 3.88 4.60 4.54 50 3.90 3.96 4.78 4.72 60 4.04 4.12 4.82 4.86 70 4.16 4.40 5.20 5.20 80 3.90 4.38 4.94 4.88 90 4.32 4.40 5.12 5.10 100 4.38 4.64 5.48 5.62 Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. 213 a sparser network, i.e. a network with an area of 750 by 750 square-meters. We generated 100 scenarios (10 sce- narios for network size) for both networks and conducted statistical analysis as the number of nodes increases from 10 to 100 in steps of 10 again. In the denser network, for all network sizes, we always find statistically significant differences between the means of unconstrained MCDS compared to constrained MCDS, PDP and SMF. Additionally, we find no evi- dence of statistically significant difference between the means of PDP and SMF. When there are 10 to 30 nodes in the network, t-test results for constrained MCDS vs. PDP as well as constrained MCDS vs. SMF show no evidence of statistically significant difference between the means. But when we added more nodes in the net- work (in our cases, more than 30 nodes), there exists a statistically significant difference between their means. For the sparser network, we could not randomly gen- erate a connected scenario with 10 nodes only. But for all other network sizes (20 to 100 nodes), t-test results indi- cate that there is no evidence of statistically significant differences between the means of unconstrained MCDS and constrained MCDS; and also between PDP and SMF. On the other hand, t-test analysis between unconstrained MCDS and PDP, unconstrained MCDS and SMF, con- strained MCDS and PDP, and constrained MCDS and SMF show that the differences between their means are always statistically significant when the number of nodes in the network is more than 20. For all protocols, as the network area increases, the number of re-broadcasting nodes increases. But for the distributed algorithms (PDP and SMF), the total number of re-broadcasting nodes increases more rapidly in com- parison to the centralized MCDS heuristic as the number of nodes in the network increases. As a final experiment for our fixed size network, we conducted simulations for 200 to 500 nodes and observe how that affects the total number of forwarding nodes. We do not find any significant difference when we add 200 or 300 nodes in the network. But when there are 400 or more nodes, the performance deteriorates severely and PDP and SMF both have more forwarding nodes, as shown in Table 3. Table 3. Average number of forwarding nodes for high- density networks (200 - 500 nodes). Nodes in Network unconstrained MCDS constrained MCDS Active Forwarders (PDP) Active MPRs (SMF) 200 4.9 5.4 6.2 6.5 300 5.0 4.9 6.2 6.7 400 5.4 5.5 11.56 16.43 500 5.2 5.3 17.4 18.67 The performance deteriorates since we now stress/ overload the network. Each node has many neighbors, and all nodes contend for access to the wireless medium to send their (large) HELLO messages and data packets. This results in many observable collisions, despite the added random jitter. Increasing the jitter value does not help the situation. The collisions cause nodes to have only a partial view of their neighborhood, impacting the efficiency of the MPR/forwarder selection. Using SMF as an example protocol, the following diagrams show how inaccurate 2-hop neighborhood information may result in a significantly higher number of active MPRs, which then will forward the data packet originated from node 0. As a result, the protocol performance deteriorates significantly. In the case of SMF, Figure 1 shows that when source 0 has complete and accurate neighborhood information, there is only one active MPR, which is node 1. Once this node (selected by node 0 as its MPR) receives and re- broadcasts the packet, all nodes in the network received the packet, either via the original transmission from node 0 or the retransmission by node 1, resulting in a total of two packet transmissions at the MAC layer. But if node 0 does not have any information of node 1 (lost a succes- sion of HELLO messages because of collisions), nodes will select a different set of MPRs (Figure 2). Once node 0 broadcasts the original data packet, its MPRs (nodes 2 and 3) rebroadcast the packet. Nodes 4 and 5, having been selected as MPRs by nodes 2 and 3, respectively, will then rebroadcast the packet. Depending on whether node 1 did overhear the initial transmission of the packet from node 0, it may rebroadcast the data packet once it Figure 1. MPR selection for a network with 6 nodes (no missing neighborhood information). Figure 2. MPR selection for a network with 6 nodes (node 0 has no knowledge of node 1). Copyright © 2011 SciRes. IJCNS 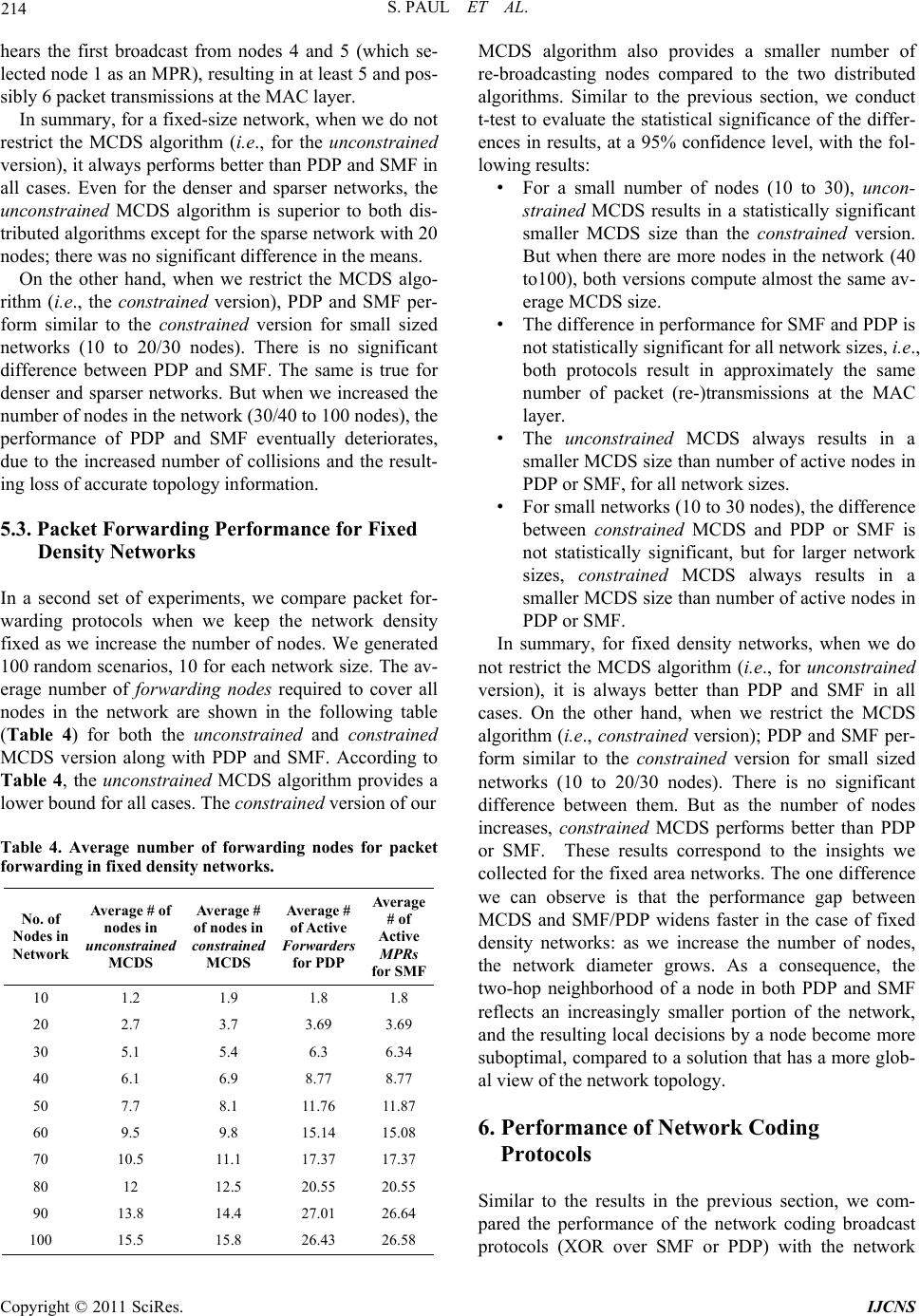 214 S. PAUL ET AL. hears the first broadcast from nodes 4 and 5 (which se- lected node 1 as an MPR), resulting in at least 5 and pos- sibly 6 packet transmissions at the MAC layer. In summary, for a fixed-size network, when we do not restrict the MCDS algorithm (i.e., for the unconstrained version), it always performs better than PDP and SMF in all cases. Even for the denser and sparser networks, the unconstrained MCDS algorithm is superior to both dis- tributed algorithms except for the sparse network with 20 nodes; there was no significant difference in the means. On the other hand, when we restrict the MCDS algo- rithm (i.e., the constrained version), PDP and SMF per- form similar to the constrained version for small sized networks (10 to 20/30 nodes). There is no significant difference between PDP and SMF. The same is true for denser and sparser networks. But when we increased the number of nodes in the network (30/40 to 100 nodes), the performance of PDP and SMF eventually deteriorates, due to the increased number of collisions and the result- ing loss of accurate topology information. 5.3. Packet Forwarding Performance for Fixed Density Networks In a second set of experiments, we compare packet for- warding protocols when we keep the network density fixed as we increase the number of nodes. We generated 100 random scenarios, 10 for each network size. The av- erage number of forwarding nodes required to cover all nodes in the network are shown in the following table (Table 4) for both the unconstrained and constrained MCDS version along with PDP and SMF. According to Table 4, the unconstrained MCDS algorithm provides a lower bound for all cases. The constrained version of our Table 4. Average number of forwarding nodes for packet forwarding in fixed de nsity ne tworks. No. of Nodes in Network Average # of nodes in unconstrained MCDS Average # of nodes in constrained MCDS Average # of Active Forwarders for PDP Average # of Active MPRs for SMF 10 1.2 1.9 1.8 1.8 20 2.7 3.7 3.69 3.69 30 5.1 5.4 6.3 6.34 40 6.1 6.9 8.77 8.77 50 7.7 8.1 11.76 11.87 60 9.5 9.8 15.14 15.08 70 10.5 11.1 17.37 17.37 80 12 12.5 20.55 20.55 90 13.8 14.4 27.01 26.64 100 15.5 15.8 26.43 26.58 MCDS algorithm also provides a smaller number of re-broadcasting nodes compared to the two distributed algorithms. Similar to the previous section, we conduct t-test to evaluate the statistical significance of the differ- ences in results, at a 95% confidence level, with the fol- lowing results: • For a small number of nodes (10 to 30), uncon- strained MCDS results in a statistically significant smaller MCDS size than the constrained version. But when there are more nodes in the network (40 to100), both versions compute almost the same av- erage MCDS size. • The difference in performance for SMF and PDP is not statistically significant for all network sizes, i.e., both protocols result in approximately the same number of packet (re-)transmissions at the MAC layer. • The unconstrained MCDS always results in a smaller MCDS size than number of active nodes in PDP or SMF, for all network sizes. • For small networks (10 to 30 nodes), the difference between constrained MCDS and PDP or SMF is not statistically significant, but for larger network sizes, constrained MCDS always results in a smaller MCDS size than number of active nodes in PDP or SMF. In summary, for fixed density networks, when we do not restrict the MCDS algorithm (i.e., for unconstrained version), it is always better than PDP and SMF in all cases. On the other hand, when we restrict the MCDS algorithm (i.e., constrained version); PDP and SMF per- form similar to the constrained version for small sized networks (10 to 20/30 nodes). There is no significant difference between them. But as the number of nodes increases, constrained MCDS performs better than PDP or SMF. These results correspond to the insights we collected for the fixed area networks. The one difference we can observe is that the performance gap between MCDS and SMF/PDP widens faster in the case of fixed density networks: as we increase the number of nodes, the network diameter grows. As a consequence, the two-hop neighborhood of a node in both PDP and SMF reflects an increasingly smaller portion of the network, and the resulting local decisions by a node become more suboptimal, compared to a solution that has a more glob- al view of the network topology. 6. Performance of Network Coding Protocols Similar to the results in the previous section, we com- pared the performance of the network coding broadcast protocols (XOR over SMF or PDP) with the network Copyright © 2011 SciRes. IJCNS 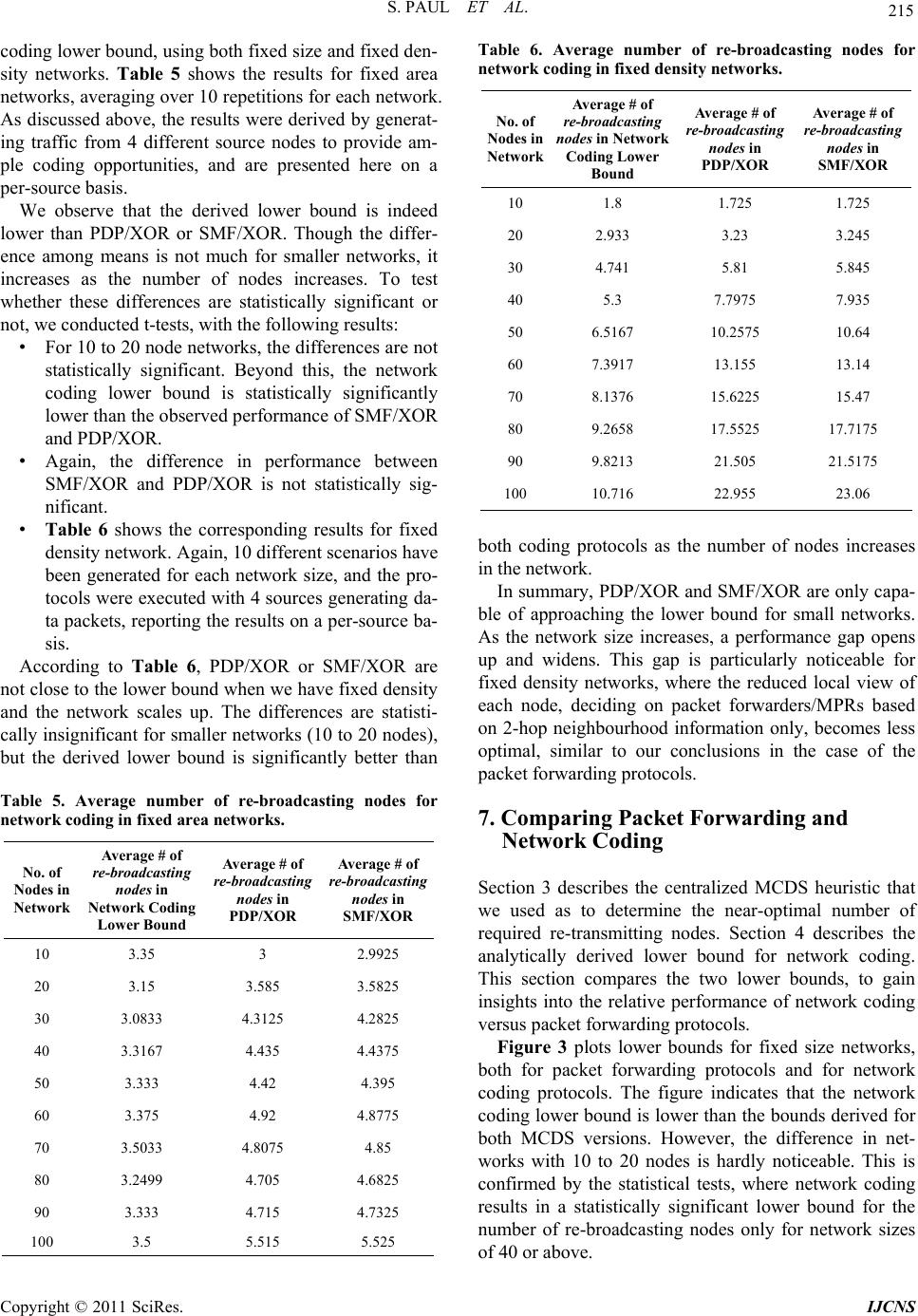 S. PAUL ET AL. 215 coding lower bound, using both fixed size and fixed den- sity networks. Table 5 shows the results for fixed area networks, averaging over 10 repetitions for each network. As discussed above, the results were derived by generat- ing traffic from 4 different source nodes to provide am- ple coding opportunities, and are presented here on a per-source basis. We observe that the derived lower bound is indeed lower than PDP/XOR or SMF/XOR. Though the differ- ence among means is not much for smaller networks, it increases as the number of nodes increases. To test whether these differences are statistically significant or not, we conducted t-tests, with the following results: • For 10 to 20 node networks, the differences are not statistically significant. Beyond this, the network coding lower bound is statistically significantly lower than the observed performance of SMF/XOR and PDP/XOR. • Again, the difference in performance between SMF/XOR and PDP/XOR is not statistically sig- nificant. • Table 6 shows the corresponding results for fixed density network. Again, 10 different scenarios have been generated for each network size, and the pro- tocols were executed with 4 sources generating da- ta packets, reporting the results on a per-source ba- sis. According to Table 6, PDP/XOR or SMF/XOR are not close to the lower bound when we have fixed density and the network scales up. The differences are statisti- cally insignificant for smaller networks (10 to 20 nodes), but the derived lower bound is significantly better than Table 5. Average number of re-broadcasting nodes for network co ding in fixe d area networks. No. of Nodes in Network Average # of re-broadcasting nodes in Network Coding Lower Bound Average # of re-broadcasting nodes in PDP/XOR Average # of re-broadcasting nodes in SMF/XOR 10 3.35 3 2.9925 20 3.15 3.585 3.5825 30 3.0833 4.3125 4.2825 40 3.3167 4.435 4.4375 50 3.333 4.42 4.395 60 3.375 4.92 4.8775 70 3.5033 4.8075 4.85 80 3.2499 4.705 4.6825 90 3.333 4.715 4.7325 100 3.5 5.515 5.525 Table 6. Average number of re-broadcasting nodes for network coding in fixe d de nsity networks. No. of Nodes in Network Average # of re-broadcasting nodes in Network Coding Lower Bound Average # of re-broadcasting nodes in PDP/XOR Average # of re-broadcasting nodes in SMF/XOR 10 1.8 1.725 1.725 20 2.933 3.23 3.245 30 4.741 5.81 5.845 40 5.3 7.7975 7.935 50 6.5167 10.2575 10.64 60 7.3917 13.155 13.14 70 8.1376 15.6225 15.47 80 9.2658 17.5525 17.7175 90 9.8213 21.505 21.5175 100 10.716 22.955 23.06 both coding protocols as the number of nodes increases in the network. In summary, PDP/XOR and SMF/XOR are only capa- ble of approaching the lower bound for small networks. As the network size increases, a performance gap opens up and widens. This gap is particularly noticeable for fixed density networks, where the reduced local view of each node, deciding on packet forwarders/MPRs based on 2-hop neighbourhood information only, becomes less optimal, similar to our conclusions in the case of the packet forwarding protocols. 7. Comparing Packet Forwarding and Network Coding Section 3 describes the centralized MCDS heuristic that we used as to determine the near-optimal number of required re-transmitting nodes. Section 4 describes the analytically derived lower bound for network coding. This section compares the two lower bounds, to gain insights into the relative performance of network coding versus packet forwarding protocols. Figure 3 plots lower bounds for fixed size networks, both for packet forwarding protocols and for network coding protocols. The figure indicates that the network coding lower bound is lower than the bounds derived for both MCDS versions. However, the difference in net- works with 10 to 20 nodes is hardly noticeable. This is confirmed by the statistical tests, where network coding results in a statistically significant lower bound for the number of re-broadcasting nodes only for network sizes of 40 or above. Copyright © 2011 SciRes. IJCNS 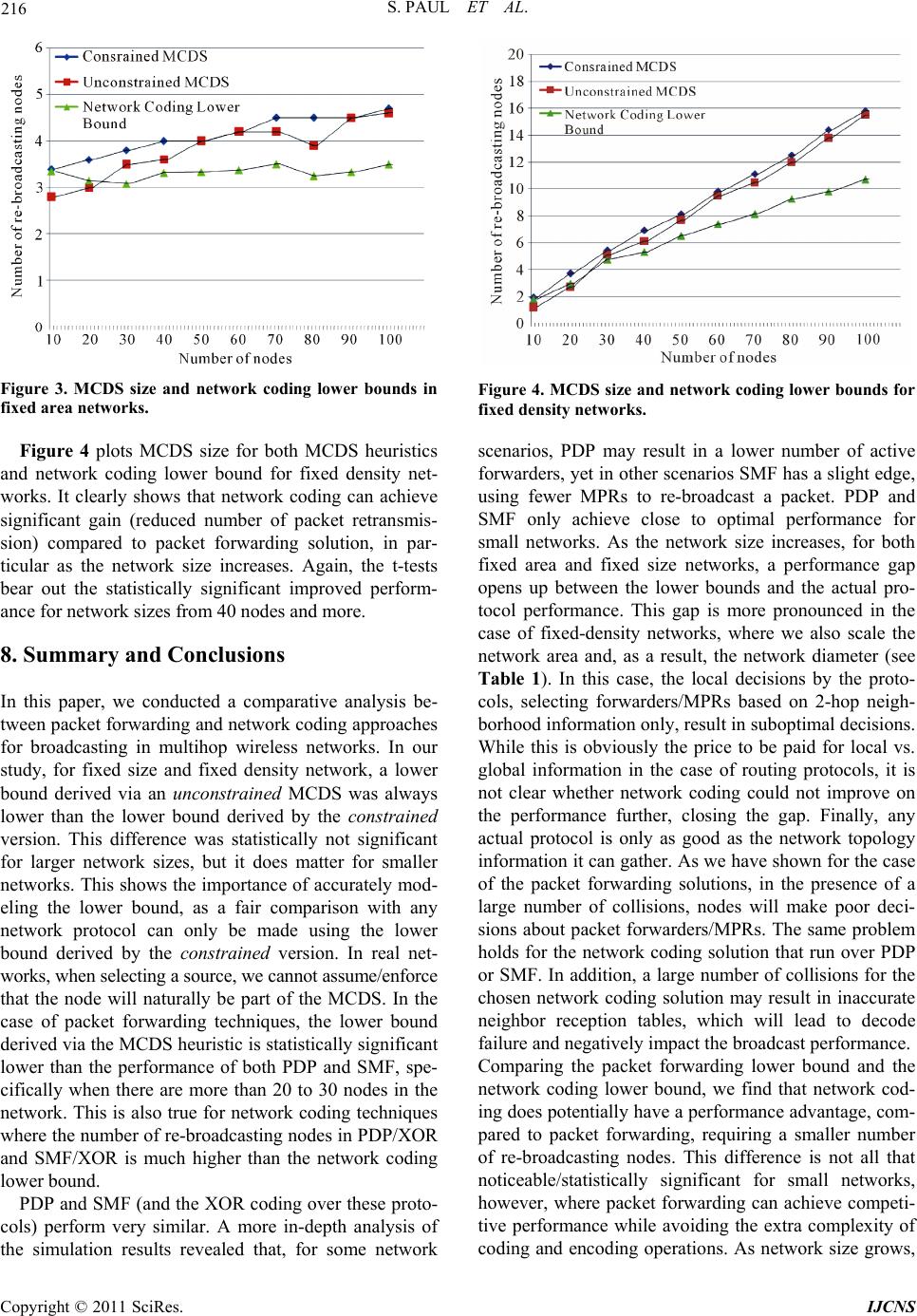 216 S. PAUL ET AL. Figure 3. MCDS size and network coding lower bounds in fixed area networks. Figure 4 plots MCDS size for both MCDS heuristics and network coding lower bound for fixed density net- works. It clearly shows that network coding can achieve significant gain (reduced number of packet retransmis- sion) compared to packet forwarding solution, in par- ticular as the network size increases. Again, the t-tests bear out the statistically significant improved perform- ance for network sizes from 40 nodes and more. 8. Summary and Conclusions In this paper, we conducted a comparative analysis be- tween packet forwarding and network coding approaches for broadcasting in multihop wireless networks. In our study, for fixed size and fixed density network, a lower bound derived via an unconstrained MCDS was always lower than the lower bound derived by the constrained version. This difference was statistically not significant for larger network sizes, but it does matter for smaller networks. This shows the importance of accurately mod- eling the lower bound, as a fair comparison with any network protocol can only be made using the lower bound derived by the constrained version. In real net- works, when selecting a source, we cannot assume/enforce that the node will naturally be part of the MCDS. In the case of packet forwarding techniques, the lower bound derived via the MCDS heuristic is statistically significant lower than the performance of both PDP and SMF, spe- cifically when there are more than 20 to 30 nodes in the network. This is also true for network coding techniques where the number of re-broadcasting nodes in PDP/XOR and SMF/XOR is much higher than the network coding lower bound. PDP and SMF (and the XOR coding over these proto- cols) perform very similar. A more in-depth analysis of the simulation results revealed that, for some network Figure 4. MCDS size and network coding lowe r bounds for fixed density networks. scenarios, PDP may result in a lower number of active forwarders, yet in other scenarios SMF has a slight edge, using fewer MPRs to re-broadcast a packet. PDP and SMF only achieve close to optimal performance for small networks. As the network size increases, for both fixed area and fixed size networks, a performance gap opens up between the lower bounds and the actual pro- tocol performance. This gap is more pronounced in the case of fixed-density networks, where we also scale the network area and, as a result, the network diameter (see Table 1). In this case, the local decisions by the proto- cols, selecting forwarders/MPRs based on 2-hop neigh- borhood information only, result in suboptimal decisions. While this is obviously the price to be paid for local vs. global information in the case of routing protocols, it is not clear whether network coding could not improve on the performance further, closing the gap. Finally, any actual protocol is only as good as the network topology information it can gather. As we have shown for the case of the packet forwarding solutions, in the presence of a large number of collisions, nodes will make poor deci- sions about packet forwarders/MPRs. The same problem holds for the network coding solution that run over PDP or SMF. In addition, a large number of collisions for the chosen network coding solution may result in inaccurate neighbor reception tables, which will lead to decode failure and negatively impact the broadcast performance. Comparing the packet forwarding lower bound and the network coding lower bound, we find that network cod- ing does potentially have a performance advantage, com- pared to packet forwarding, requiring a smaller number of re-broadcasting nodes. This difference is not all that noticeable/statistically significant for small networks, however, where packet forwarding can achieve competi- tive performance while avoiding the extra complexity of coding and encoding operations. As network size grows, Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. 217 however, the added complexity of network coding pays off. In particular for fixed density networks, the per- formance of network coding is potentially much better as we scale the number of nodes, network area, and network diameter, though this is also the scenario where existing packet forwarding and network coding protocols perform most poorly (relative to the lower bounds). In future work, we will address some of the open is- sues. For example, while we selected XOR coding over PDP and SMF due to its performance and direct compa- rability with the underlying packet forwarding protocols, the majority of network coding protocols implement (random) linear network coding. We are currently de- veloping our own random linear network coding protocol that supports coding across data generated from multiple sources and will compare its performance against other protocols and the lower bounds derived here. We will also explore further network characteristics to more clearly identify what networks benefit most from net- work coding, and, conversely, in what scenarios the ad- ditional overhead due to network coding is not worth the limited additional gain. For example, based on our ob- servations to date, it seems that both network density and network diameter are important factors to consider. 9. References [1] M. R. Garey and D. S. Johnson, “Computers and Intrac- tability: A Guide to the Theory of NP-Completeness,” Freeman, San Francisco, 1978. [2] F. V. Fomin, F. Grandoni and D. Kratsch, “Solving Con- nected Dominating Set Faster than 2n,” Algorithmica, Vol. 52, No. 2, 2008, pp. 153-166. doi:10.1007/s00453-007-9145-z [3] S. Guha and S. Khuller, “Approximation Algorithms for Connected Dominating Sets,” Algorithmica, Vol. 20, No. 4, April 1998, pp. 374-387. [4] S. Butenko, X. Cheng and C. A. S. Oliveira, “A New Heuristic for the Minimum Connected Dominating Set Problem on Ad Hoc Wireless Networks,” in: S. Butenko, R. Murphey and P. Pardalos, Eds., Recent Developments in Cooperative Control and Optimization, Kluwer Aca- demic Publishers, Norwell, 2004, pp. 61-73. [5] M. Min, H. Du, X. Jia, C. X. Huang, S. C. H. Huang and W. Wu, “Improving Construction for Connected Domi- nating Set with Steiner Tree in Wireless Sensor Net- works,” Journal of Global Optimization, Vol. 35, No. 1, 2006, pp. 111-119. doi:10.1007/s10898-005-8466-1 [6] Y. Li, M. T. Thai, F. Wang, C. W. Yi, P. J. Wan and D. Z. Du, “On Greedy Construction of Connected Dominating Sets in Wireless Networks,” Wireless Communications and Mobile Computing, Vol. 5, No. 8, December 2005, pp. 927-932. doi:10.1002/wcm.356 [7] M. Rai, S. Verma and S. Tapaswi, “A Heuristic for Minimum Connected Dominating Set with Local Repair for Wireless Sensor Networks,” Proceedings of the 2009 8th International Conference on Networks, Guadeloupe, 1-6 March 2009, pp. 106-111. [8] J. P. Macker, J. Dean and W. Chao, “Simplified Multicast Forwarding in Mobile Ad Hoc Networks,” Proceedings of the Military Communications Conference, Monterey, 31 October-3 November 2004, pp. 744-750. [9] J. Macker, I. Downard, J. Dean and B. Adamson, “Evalu- ation of Distributed Cover Set Algorithms in Mobile Ad Hoc Network for Simplified Multicast Forwarding,” Mo- bile Computing and Communications Review, Vol. 11, No. 3, July 2007, pp. 1-11. [10] W. Lou and J. Wu, “On Reducing Broadcast Redundancy in Ad Hoc Wireless Networks,” IEEE Transactions on Mobile Computing, Vol. 1, No. 2, April-June 2002, pp. 111-123. [11] R. Ahlswede, N. Cai, S.-Y. R. Li and R. W. Yeung, “Network Information Flow,” IEEE Transactions on In- formation Theory, Vol. 46, No.4, 2000, pp. 1204-1216. [12] L. Li, R. Ramjee, M. Buddhikot and S. Miller, “Network Coding Broadcast in Mobile Ad Hoc Networks,” Pro- ceedings of the 26th IEEE International Conference on Computer Communications, Anchorage, 6-12 May 2007, pp. 1739-1747. [13] S. Katti, H. Rahul, W. Hu, D. Katabi, M. Medard and J. Crowcroft, “XORs in the Air: Practical Wireless Network Coding,” Proceedings of the Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Vol. 36, No. 4, October 2006, pp. 243- 254. [14] J. S. Park, D. S. Lun, Y. Yi, M. Gerla and M. Medard, “CodeCast: A Network-Coding Ad Hoc Multicast Proto- col,” IEEE Wireless Communications, Vol. 13, No. 5, October 2006, pp. 76-81. [15] Y. Wu, K. Jain and S. Kung, “A Unification of Network Coding and Tree-Packing (Routing) Theorems,” IEEE/ ACM Transactions on Networking, Vol. 52, No. 6, June 2006, pp. 2398-2409. [16] C. Campolo, C. Casetti, C. F. Chiasserini and S. Tarapiah, “Performance of Network Coding for Ad Hoc Networks in Realistic Simulation Scenarios,” Proceedings of the IEEE International Conference on Telecommunications, Marrakech, 25-27 May 2009, pp. 31-36. [17] D. E. Lucani, M. Medard and M. Stojanovic, “Broad- casting in Time-Division Duplexing: A Random Linear Network Coding Approach,” Proceedings of the Work- shop on Network Coding, Theory, and Applications, Lausanne, 15-16 June 2009, pp.62-67. [18] R. Khalili, M. Ghaderi, J. Kurose and D. Towsley, “On the Performance of Random Linear Network Coding in Relay Networks,” Proceedings of the IEEE Military Communications Conference, San Diego, 16-19 Novem- ber 2008, pp. 1-7. [19] C. Adjih and S. Y. Chon, “Wireless Broadcast with Net- work Coding: Energy Efficiency, Optimality and Coding Gain in Lossless Wireless Networks,” Research Report RR-7011, France, July 2009. [20] C. Fragouli, J. Widmer and J. Le Boudec, “Efficient Broadcasting Using Network Coding,” IEEE/ACM Trans- Copyright © 2011 SciRes. IJCNS  S. PAUL ET AL. Copyright © 2011 SciRes. IJCNS 218 actions on Networking, Vol. 16, No. 2, April 2008, pp. 450-463. [21] T. Kunz, S. Paul and L. Li, “Efficient Broadcasting in Tactical Networks: Forwarding vs. Network Coding,” Pro- ceedings of the Military Communication Conference, San Jose, 31 October-3 November 2010, pp. 1245-1250.
|