 Journal of Applied Mathematics and Physics, 2014, 2, 431-436 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26052 How to cite this paper: Zhang, X.T., Zhong, W., Yang, J.Z. and Liu, M.H. (2014) Dimensional Analysis and Dissipation Rate Estimation in the Near Wake of a Circular Cylinder. Journal of Applied Mathematics and Physics, 2, 431-436. http://dx.doi.org/10.4236/jamp.2014.26052 Dimensional Analysis and Dissipation Rate Estimation in the Near Wake of a Circular Cylinder Xintai Zhang, Wei Zhong, Jiangzhi Yang, Minghou Liu Department of Thermal Science and Energy Engineering, University of Science and Technology of China, Hefei, Anhui 230027, China Email: zhan gxintai@li ve.cn Received March 2014 Abstract A particle image velocimetry (PIV) experiment is performed for dissipation rate estimation in the near wake behind a circular cylinder with diameter D of 12 mm and corresponding Reynolds number of 7100. Considering the limitation of PIV resolution, a large eddy PIV method based on idea of large eddy simulation (LES), is used for more accurate estimation of dissipation rate. Based on the dynamic equilibrium assumption in the inertial subrange, the dissipation rate of the sub- grid scales is approximated by the subgrid scale (SGS) flux, computed from PIV velocity fields and Smagorinsky model for SGS stress. A dimensional analysis about the integral length scale and the Kolmogorov length scale is discussed firstly to verify whether the dynamic equilibrium assump- tion holds or not. Keywords Cylinder, Near Wake, Large Eddy PIV, Dissipation Rate 1. Introduction Turbulence dissipation rate is an important small-scale characteristic of turbulence, which determines kinetic energy transport among multi-scale turbulent structures, segregation, droplet and bubble breakup. Therefore, es- timation of turbulent dissipation rate has attracted significant attention in the past few decades. The conventional approach to measure the dissipation rate is to use a hot-wire probe with invoking Taylor’s hypothesis [1], Particle image velocimetry (PIV) can also be used to measure the dissipation rate, such as Saare- nrinne and Piirto, Sheng et al. [2] and Jong et al. [3]. Compared wi th traditional single-point hot-wire measure- ments, PIV can obtain the full and immediate field without the use of Taylor’s hypothesis. However, the current PIV resolution may still limit its feasibility of estimating the turbulent dissipation rate which lies in the smallest scale, i.e. Kolmogorov scale. To address this problem, Sheng et al. [2] proposed the large eddy PIV method which approximates the dissipation rate with the cascade flux from resolved scales to subgrid scales. They ob- tained a good agreement of results for the flow in a stirred circular tank with Reynolds number of about 9200. 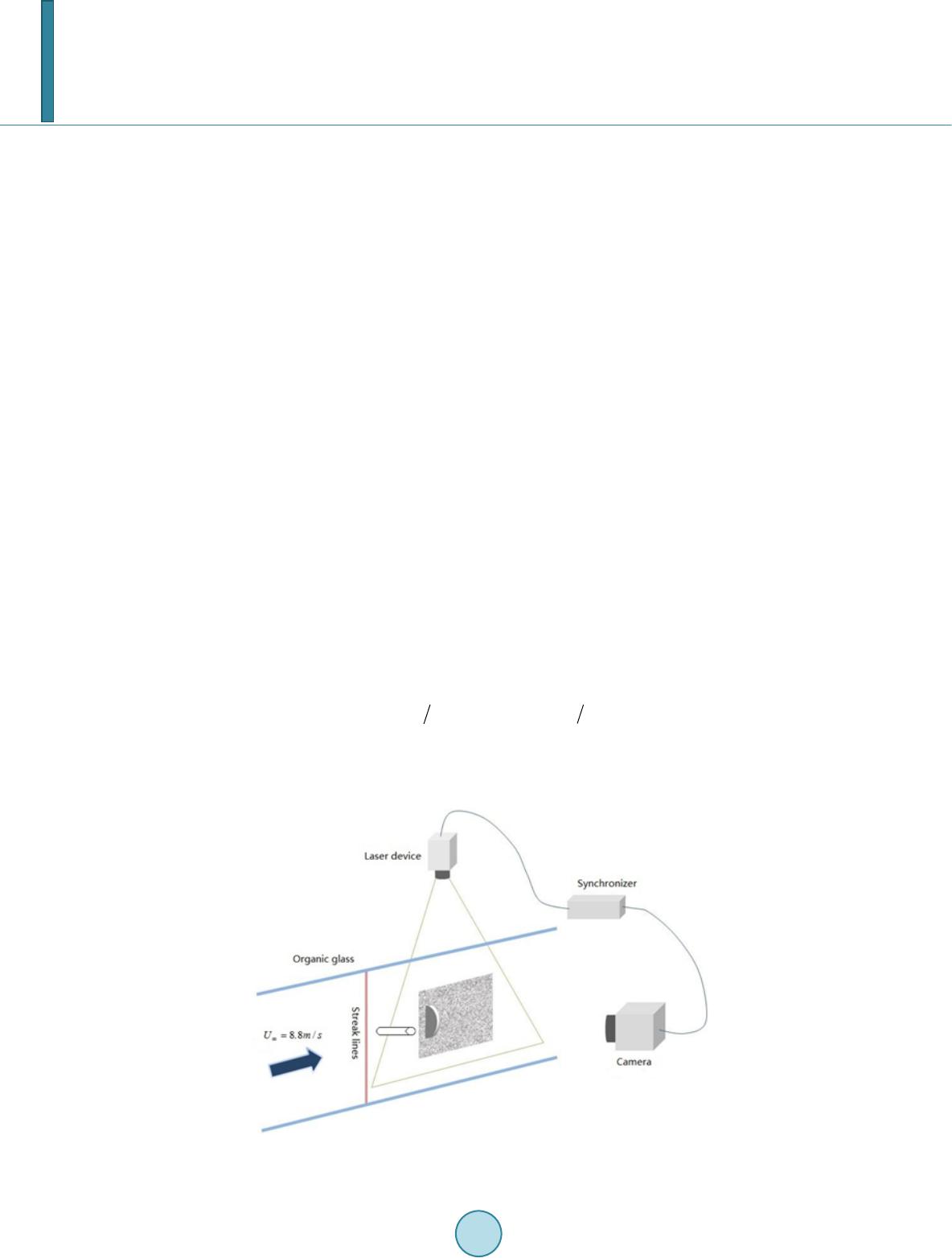 X. T. Zhang et al. The dissipation rate behind a cylinder has been studied in various articles [4]-[7]. For example, Mi and Anto- nia [6] measured the mean turbulent dissipation rate throughout the intermediate wake at Re = 3000 and com- pared the results with those under the simplification of local axisymmetry, local homogeneity and local isotropy, respectively. However, most of these studies are focused on the intermediate wake or self-preserving far wake, there are few which have addressed the near wake region behind a cylinder. In this paper, PIV measurements are conducted in the near wake behind a cylinder at Reynolds number of 7100. Dimensional analysis about the integral length scale and the Kolmogorov scale is made firstly to verify the validity of the dynamic equilibrium assumption for the large eddy PIV method. Then, the dissipation rate is estimated, and results in the near wake are compared with those in the intermediate and far wake to get an over- all view. 2. Experimental Details The experiments are conducted in a closed loop wind tunnel with a test section of 1.0 m (width) × 1.0 m (height) × 1.5 m (long). The cylinder used for the experimental study is a steel hollow pipe of 1.0 m long, with an aspect ratio of 83.3 and an area blockage of about 1.2%. The free stream velocity ∞ is about 8.8 m/s, corresponding to a Reynolds number (Re = ) of about 7100. The entire flow is seeded with atoleine droplets of 1.0 μm in diameter generated by a fog machine placed downstream. The particles are illuminated by a Dantec pulsed Nd: YAG laser, producing a 1-mm-thick light sheet through the front glass window of the channel. The laser wave- length is 532 nm with a pulse duration of 0.01 μs and a separation of 100 μs. To capture the particle image pairs, a CCD camera with a resolution of 1280 × 1024 pixels and a view field of 11.2 D × 11.7 D is applied. The spa- tial resolution is estimated to be 2 mm both vertical and horizontal directions. A schematic model of the experi- mental setup is shown in Figure 1. 3. Dimensional Analysis Among the various scales of turbulent motion, the longitudinal integral length scale L11, defining the scale or size of an average eddy, can be used to characterize the large structures of turbulent field. To obtain this length scale, the longitudinal velocity spatial correlation function f(r) needs to be computed. And the integral length scale L11 is the integration of f(r) about r from zero to infinity theoretically. '2 '''2 11 ()() ()frRuux ruxu==<+>< > (1) With the PIV data, the longitudinal velocity spatial correlation function is calculated at several different origin points, f(r) at the centerline of x/D = 4 is shown as an example in Figure 2(a). Then, L11 is calculated and shown in Figure 2(b). Obviously, the lateral distribution of L11 at x/D = 4, 6 and 8 is far away from keeping a homo- Figure 1. Schematic of PIV experimental setup .  X. T. Zhang et al. (a) (b) Figure 2. Longitudinal velocity autocorrelation function (a) and integral length scales (b) at x/D = 4. geneous constant. However, there is still some similarity in the shear region of 0.5 < y/D < 1.5, which varies between 0.7 and 0.85. Outside of this region, there exists significant discrepancy and the maximum of L11 de- viate as large as 1.56. In order to evaluate the dynamic equilibrium assumption which needs to be held for estimating dissipation rate, the Kolmogorov length scale η, considered as the smallest scale of turbulence, needs to be computed. One approach to estimate η is based on the Reynolds number and the integral length scale, i.e. . Re- sults of η have the same shape as Figure 2(b), with the maximum and minimum values being 16.2 μm and 9.43 μm, respectively. 4. Dissipation Rate Estimation The large eddy PIV method to estimate dissipation rate was firstly proposed by Sheng et al. [2] wi t h the ideas of “large eddy” and “sub -grid scales” from large eddy simulation (LES). The PIV results with an algorithm of low-pass filtering shares a similar physical definition as —the resolved velocity in LES, and should satisfy the LES equation: (2) 2 2 () 1 ji jjij ij i i U UUU p tx xx x τ ν ρ ∂∂∂ ∂ ∂ +=−+ − ∂∂ ∂∂ ∂ (3) where is the subgrid-scale stress tensor which needs to be modeled. The conservation equation of resolved kinetic energy is: 22 ir r jijijijij ijij ij ii UE Ep U SSSS t xx ντ δντ ρ ∂ ∂∂ + −−−=−+ ∂∂∂ (4) where Er is the kinetic energy of the resolved velocity field and is the resolved strain rate tensor. For high Reynolds number turbulence, the turbulent kinetic energy is mainly generated in the large-scale structures and transferred to the small scales where the dissipation process takes place. The term in Equation (4) represents viscous dissipation in the resolved velocity field and is relatively small, while the term acts as the rate of energy transfer from the resolved structures to the smaller scales. If the filter width is in the inertial subrange where no energy production or dissipation occurs, as shown in Figure 3, the flux of energy transfer through the inertial subrange should be equal to the dissipation rate in the dissipation range. According to the previous discussions, the integral scales L11 and Kolmogorov scale η lie within the ranges of [7.32, 12] mm and [9.43, 16.21] μm, respectively. The PIV filter width (Δ = 2 mm) is safely located in the iner-  X. T. Zhang et al. Figure 3. Schematic model of the energy cascade at high Reynolds number. tial subrange. Therefore, the turbulent dissipation rate can be approximated by the SGS dissipation rate: (5) To model the subgrid stress , the Smagorinsky model [8] is introduced: , (6) where Cs = 0.17 and Δ is the PIV window size. Due to the limitation of current PIV method, only five of the nine terms in the strain rate tensor could be directly measured and derived from the continuity equation. Instead of multiplying by a factor of 9/5 in Sheng et al. [2], the rest four off-diagonal terms are approximated here with isotropy relations. As mentioned above, the PIV resolution of Δ = 2 mm in this study satisfies the dynamic equilibrium assump- tion and thus the large-eddy PIV method is applicable. Considering the critical role of Δ in this method, inde- pendence of the large-edd y-PIV results on the PIV resolution is verified quantitatively in Figure 4. Apparently in Figure 4, significant deviation exists only near y/D = ±0.8, which may result from the numerical error due to strong local shear stresses [9] [10]. In all other regions, the large-eddy-PIV results over the four Δs (1.75 mm, 2 mm, 2.25 mm and 2.5 mm) agree with each other very well. In other words, the four Δs lie in the inertial sub- range that the large-eddy-PIV method is reliable. In Figure 5, the non-dimensionless dissipation rate estimated with the large eddy PIV method in this article is compared with the results in [6], the agreement at x/D = 10 is very satisfying except that near the centerline (x/D < 0.6). This underestimation may result from the simplification of the strain rate tensor. Similar underestimation due to the isotropy assumption near the centerline has been reported in the far wake and the intermediate wake [5]. 5. Conclusions In this paper, the turbulent dissipation rate is estimated with the large eddy PIV method in the near wake of a cy- linder at Re = 7100. To verify this method’s availability, dimensional analysis about the longitudinal integral length scale and the Kolmogorov scale is firstly discussed to check the assumption of dynamic equilibrium. The integral scale L11, varies significantly at different spatial locations, indicating that the near wake investigated here is far away from isotropy and rough homogeneity holds only in the shear region (0.5 < y/D < 1.5). The dependence on the PIV resolution Δ is studied considering that the PIV resolution could play a critical role in the large eddy PIV and may potentially influence the calculation results. Based on four cases under dif- ferent PIV resolutions, it is found that the dissipation rate is independent on the choice of PIV resolution if it is within the inertial subrange. By selecting a PIV resolution within the inertial subrange, result of the large eddy PIV with the Smagorinsky model agrees well with that of Mi and Antonia [6] at x/D = 10, indicating the method’s validity in this study. The lateral distribution of estimated dissipation rate in the near wake shows collapse near the centerline, where the largest difference among different locations in the intermediate or far wake appears. Before reaching the self-preserving far wake, the dissipation rate shows a tendency of decay in the downstream direction for the near and intermediate wakes. 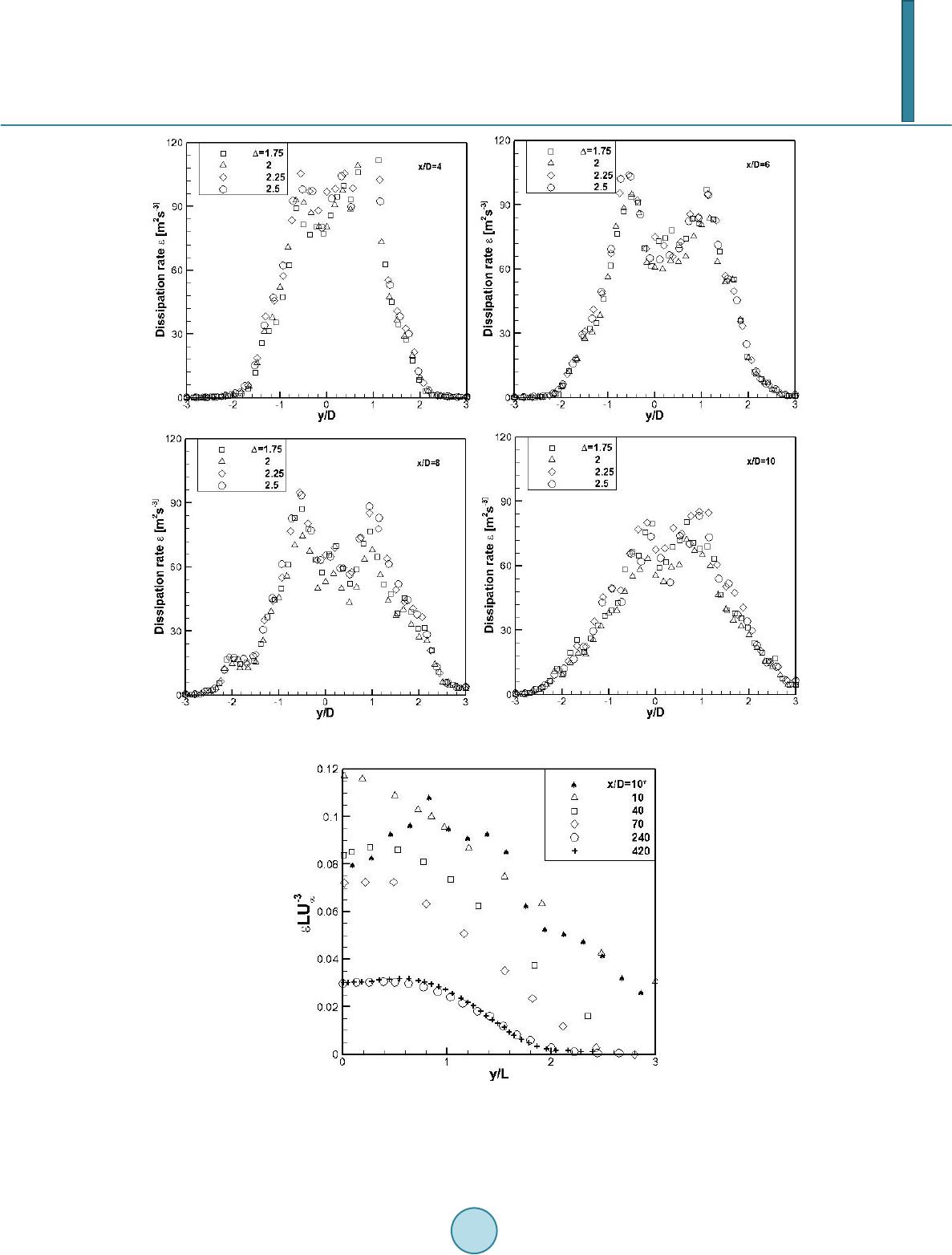 X. T. Zhang et al. Figure 4. Dependence of the large-eddy-PIV results on the PIV resolution. Figure 5. Comparison of results of the dissipation rate estima- tion at different locations: x/D = 10*, estimated with the large eddy PIV method in this article; x/D = 10, 40 and 70, from Mi and Antonia [6] ; x/D = 240 from Zhou et al. [11] .  X. T. Zhang et al. Acknowledgem ents The authors wish to acknowledge the support to this work by the Natural Science Foundation of China (NSFC Grant No. 11172296, 11372302, 50936005). References [1] Saarenrinne, P. and M. Piirto, (200 0) Turbulent Kinetic Energy Dissipation Rate Estimation from PIV Velocity Vector Fields. Experiments in Fluids, 29, S300-S307. http://dx.doi.org/10.1007/s003480070032 [2] Sheng, J., Meng, H. and Fox, R.O. (2000) A Large Eddy PIV Method for Turbulence Dissipation Rate Estimation. Chemical Engineering Science, 55, 4423-4434. http://dx.doi.org/10.1016/S0009-2509(00 ) 0003 9 -7 [3] Jong, J.D., et al. (2009) Dissipation Rate Estimation from PIV in Zero-Mean Isotropic Turbulence. Experiments in Fluids, 46, 499-51 5. http://dx.doi.org/10.1007/s00348-008-0576-3 [4] Aronson, D. and Löfdahl, L. (1993 ) The Plane Wake of a Cylinder: Measurements and Inferences on Turbulence Mod- eling. Physics of Fluids A, 5, 1433-14 37 . http://dx.doi.org/10.1063/1.858579 [5] Hao, Z., et al. (20 08 ) Approximations to Energy and Temperature Dissipation Rates in the Far Field of a Cylinder Wake . Experimental Thermal and Fluid Science, 32, 791-799. http://dx.doi.org/10.1016/j.expthermflusci.2005.08.008 [6] Mi, J. and Antonia, R. (20 10) Approach to Local Axisymmetry in a Turbulent Cylinder Wake. Experiments in Fluids, 48, 933-947. http://dx.doi.org/10.1007/s00348-009-07 79 -2 [7] Browne, L.W.B., Antonia, R.A. and Shah, D.A. (1987) Turbulent Energy Dissipation in a Wake. Journal of Fluid Me- chanics, 179, 307 -32 6. http://dx.doi.org/10.1017/S002211208700154X [8] Smagorinsky, J. (1963 ) General Circulation Experiments with the Primitive Equation I the Basic Experiment. Monthly Weather Review, 91, 99-164. http://d x. doi .or g/1 0. 1175 /15 20 -0493(1963)091<0099:GCEWTP>2.3.CO;2 [9] Ong, L. andWallace, J. (1996) The V elocity Field of the Turbulent Very Near Wake of a Circular Cylinder. Exp eri- ments in Fluids, 20, 441-45 3. ht tp: // dx. do i.o rg/1 0. 1007 / BF 0018 93 83 [10] Ma, X., Karamanos, G.S. and Karniadakis, G.E. (2000 ) Dynamic and Low-Dimensionality of a Turbulent Near Wake. Journal of Fluid Mechanics, 410 , 29-65. http://dx.doi.org/10.1017/S0022112099007934 [11] Zhou, T., et al. (2006 ) Comparisons between Different Approximations to Energy Dissipation Rate in a Self-P reser- ving Far Wake. Physical Review E, 74, 056308. http://dx.doi.org/10.1017/S0022112099007934
|