 Journal of Applied Mathematics and Physics, 2014, 2, 418-424 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26050 How to cite this paper: Wu, G.F., He, Z.G. and Liu, G.H. (2014) A Well-Balanced Numerical Model for the Simulation of Long Waves over Complex Domains. Journal of Applied Mathematics and Physics, 2, 418-424. http://dx.doi.org/10.4236/jamp.2014.26050 A Well-Balanced Numerical Model for the Simulation of Long Waves over Complex Domains Gangfeng Wu1, Zhiguo He1,2*, Guohua Liu1 1Institute of Hydraulic Structures and Water Environment, Zhejiang University, Hangzhou, China 2Ocean College, Zhejiang University, Hangzhou, China Email: *hezhiguo@zju.edu.cn, zjdxwgf@gmail .com Received March 2014 Abstract This paper presents a well-balanced two-dimensional (2D) finite volume model to simulate the propagation, runup and rundown of long wave. Non-staggered grid is adopted to discretize the governing equation and the intercell flux is computed using a central upwind scheme, which is a Riemann-pr oblem-s olver -free method for hyperbolic conservation laws. The nonnegative recon- struction method for water depth is implemented in the present model to treat the appearance of wet/dry fronts, and the friction term is solved by a semi-implicit scheme to ensure the stability of the model. The Euler method is applied to update flow variable to the new time level. The model is verified against two experimental cases and good agreements are observed between numerical results and observed data. Keywords Long W av e, Central Upwind Scheme, Well -B al anc e d , Wetting and Drying 1. Introduction Long waves, such as storm surges, tides, or tsunamis, will cause huge casualties and considerable property damage. So it is important to develop an accurate and robust numerical model to predict and understand the pro- pagation and runup of long wave. The nonlinear shallow water (NLSW) equations are widely employed to mod- el the physical process of long wave [1-5]. Although the models based on NLSW omit dispersive effects, these models are able to provide the general characteristics of the wave runup process [4]. A good long wave model should have two major properties, which are crucial for the stability of numerical model [6]: 1) The model should be able to be well balanced; 2) The model should preserve the water depth to be nonnegative. Therefore, this paper presents a 2D well-balance shallow water model to simulate the propagation, runup and rundown of long wave. The model is able to preserve the “lake at rest” steady states and guarantee the positivity of the computed water depth. *  G. F. Wu et al. 2. Governing Equation The two-dimensional NLSW equations can be written as: (1) in which , 22 1 2 hu hu gh huv =+ f , 22 1 2 hv huv hv gh = + g , 0 b fx b fy z gh S x z gh S y ∂ −− = ∂ ∂ −− ∂ S (2) where, q represents the vector of conserved variables; f and g are the flux vectors associated with the conserved variables in the x- and y-directions, respectively. S represents the vector of source terms. t indicates time; x and y are Cartesian coordinates; η is water surface elevation; h is water depth; zb represents bed elevation over the da- tum where η = h + zb; u and v are depth-averaged velocity components in the x- and y-directions, respectively; g is the gravitational acceleration; Sfx and Sfy are the friction source terms in the x and y directions, respectively. In this paper, the friction source terms are estimated by using the Manning’s formula: , (3) where n is the Manning coefficient. 3. Numerical Method 3.1. Finite Volume Discretization for NLSW Equations The discretization of Equation (1) is based on the finite volume method. As shown in Figure 1, the model adopts the non-staggered structure grids, in which the conserved variables and bottom bed elevation are defined at the cell center and represent the average value of each cell. Integrating Equation (1) over the cell ij and ap- plying Green’s theorem yields: 1 ,,1/2,1/2,, 1/2, 1/2, ( )( ) kk ijiji ji jijijij tt t xy + +− +− ∆∆ = −−−−+∆ ∆∆ qqffggS (4) where the superscript k is the time level, subscrip ts i and j are indices of the cell, Δt, Δx, and Δy are the time step, and cell sizes in the x and y directions, respectively. fi+1/2, j, fi−1/2, j, gi, j−1/2 and gi, j+1/2 are the flux at the interface of the cell ij. Si, j represents the source terms evaluated at the cell center. Figure 1. Sketch of control volume and struc- ture grids.  G. F. Wu et al. 3.2. Central Upwind Scheme In the present Godunov-type framework, the interface fluxes are calculated using a central upwind scheme, which requires the correct reconstruction of the Riemann states at the interface. The method of nonnegative re- construction of water depth method proposed by Liang [7] is used to calculate the Riemann states. One can refer to [7] for more details. Then the interface flux can be calculated using central upwind scheme [8]: 1 2,1/2,1/2,1 2,1/2,1/2,1 2,1 2, 1 2,1/2,1/2, 1 2,12,1 2,12, (,( ))(,( ))() LR ij ijbijij ijbijijij RL ij ijij ijij ijij azazaa aa aa + −+− +++ +++++ + ++ +− +− ++ ++ − = +− −− fq fq f qq (5) , 1/2, 1/2, 1/2,1/2, 1/2, 1/2,1/2 , 1/2 , 1/2, 1/2,+1/2 , 1/2, 1/2, 1/2, 1/2 (,( ))(,( ))() LR ijijb ijijijb ijijijRL ijij ij ij ijij ij bzbzbb bb bb + −+− +++ +++++ ++ +− +− ++ ++ − = +− −− gq gq g qq (6) where , are the reconstructed Riemann states on the left and right hand side of cell interface (i + 1/2, j), respectively. , represent the reconstructed Riemann states on the left and right hand side of cell interface (i, j + 1/2), respectively. , are the one-sided local wave speeds in the x and y di- rections, respectively, and can be calculated as: 1/2,1/2,1/2, 1/2,1/2, max{,, 0} R RLL ijij ijij ij au ghu gh + + ++++ =++ (7) 1/2,1/2,1/2, 1/2,1/2, min{,,0} R RL L ijij ijijij au ghugh − + ++++ =−− (8) , 1/2, 1/2,+1/2, 1/2,1/2 max{,, 0} R RL L ijijij ijij bvgh vgh + + +++ =++ (9) , 1/2, 1/2,1/2, 1/2,1/2 min{,, 0} R RL L ijij ijij ij bvgh vgh − + ++++ =−− (10) where , are the velocity in x direction on the left and right hand side of cell interface (i + 1/2, j), respectively. , are the velocity in y direction on the left and right hand side of cell interface (i, j + 1/2), respectively. 3.3. Discretization of the Source Terms The source term, as shown in Equation (2), can be split into the bed slope terms and friction terms. It is impor- tant to discretize the bed slope terms appropriately to ensure the scheme to be well balanced. Hence, the bed slope terms are approximated as follows: 1/2,1/2, 1/2,1/2, () () 2 LR bi jbi jiji j bzz hh z gh g xx +−+ − −+ ∂= ⋅ ∂∆ (11) , 1/2, 1/2, 1/2, 1/2 ()() 2 LR b ijb ijijij b zz hh z gh g yy +−+ − −+ ∂= ⋅ ∂∆ (12) In general, a simple explicit discretization of friction term may cause numerical instability when the water depth is very small. To overcome this problem, the friction terms are discretized by using the semi-implicit treatment in this study. So the friction terms are discretized as follows: 2 222 22 1 13 43 ()( ) kk fx guuvngu vn S hu hh + ++ = = (13) 2 222 22 1 13 43 ()( ) kk fy gvu vngu vn S hv hh + ++ = = (14) 3.4. Stability Criteria The current numerical scheme is explicit and its stability is governed by the Courant-Friedr ichs -Lewy (CFL) criterion. It had been proved that the model could preserve the positivity of the water depth when the Courant 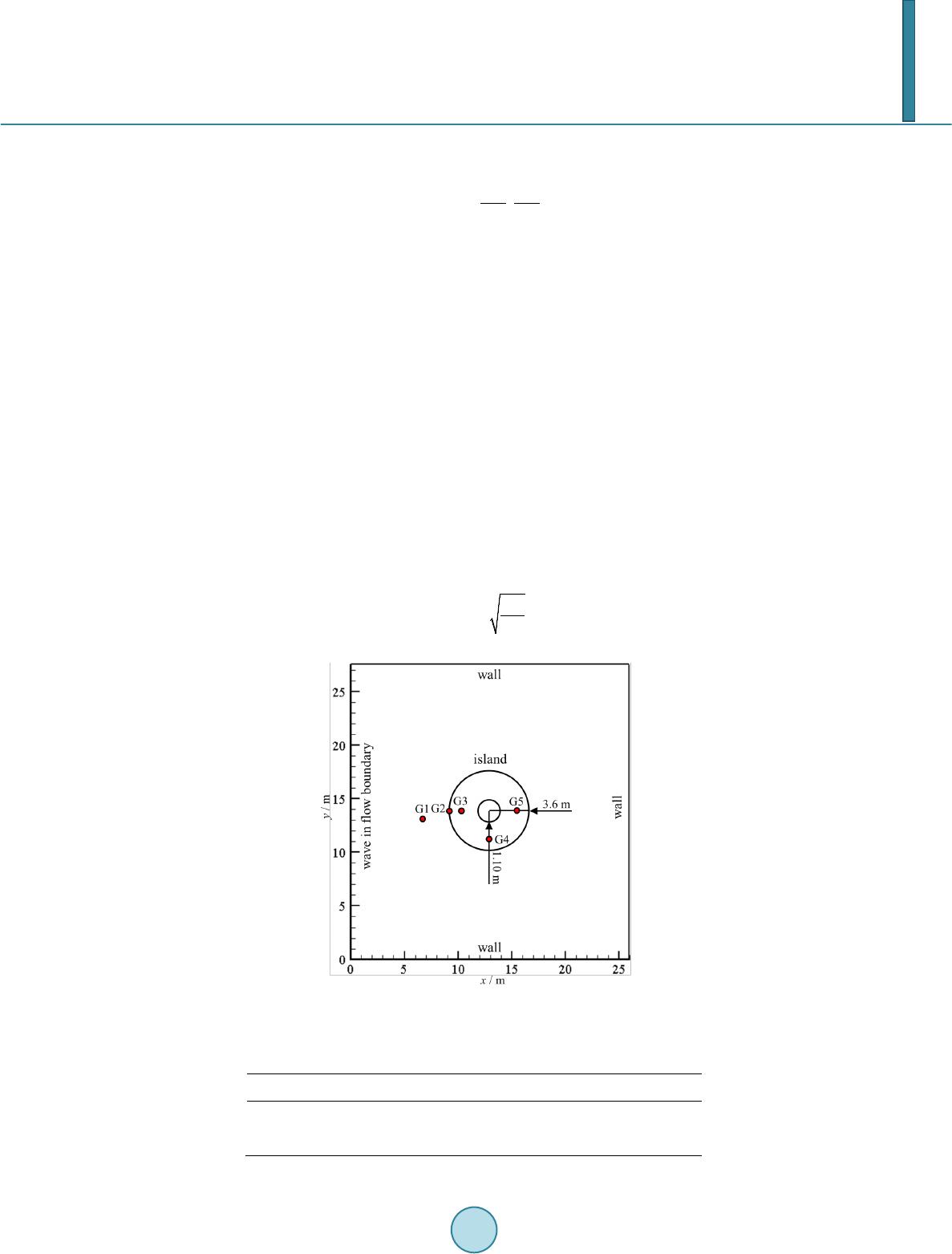 G. F. Wu et al. number is less than 0.25. One can refer [8] to for more details. Therefore, the CFL restriction for the current model is: CFL max{,} 0.25 atbt Nxy ∆∆ = ≤ ∆∆ (15) where NCFL represents the Courant number, and a and b are given by: 1/2, 1/2, , max{ max{,}} ij ij ij a aa +− ++ = − , , 1/2, 1/2 , max{ max{,}} ij ij ij b bb +− ++ = − (16) 4. Numerical Results 4.1. Run-Up of a Solitary Wave on a Conical Island A series of experiments were performed by Briggs et al. [9] in a large scale basin at the US Army Engineer Wa- terways Experimental Station to study the run-up tsunami waves on a conical island. This case has been widely used to validate the wave runup model. The conical island, which had a base diameter of 7.2 m, a top diameter of 2.2 m, and a height of 0.625 m, was located nearly the center of a 30 m × 25 m basin. Planar solitary waves were produced by a directional wave-maker. Since the reflected wave by the wall opposite to the wave makers is not investigated, a simplified 26.0 m × 27.6 m computational domain is selected, as shown in Figure 2. Five water level gauges G1-G5 are located around the island to record the time histories of water surface elevation and their locations are given in Table 1. The island is submerged by the still flow with the depth of 0.32m at the beginning. Following Nikolos et al. [1 0], the left boundary is set to be wave inflow boundary where the water level η (herein water level is related to the still water) and velocity u are given by 2 3 ( )sech[()] 4 H tHCt T D η = − (17) Figure 2. Computational domain, boundary conditions and the locations of the selected gauges. Table 1. Locations of water level gauges. Gauges G1 G2 G3 G4 G5 x/m 6.82 9.36 10.36 1 2.96 1 5. 56 y/m 13.05 13. 80 13.80 1 1.22 1 3. 80 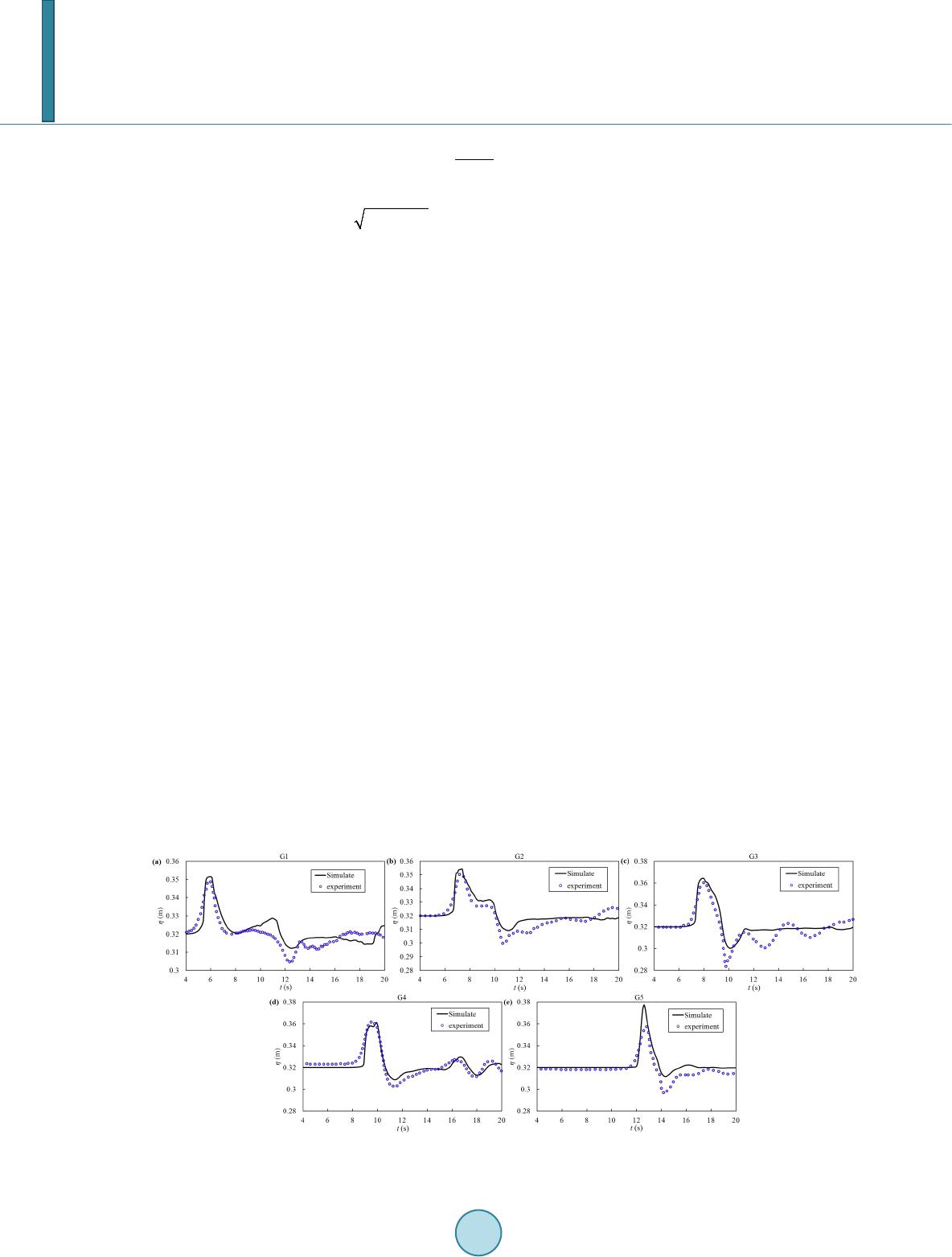 G. F. Wu et al. , (18) where H is the amplitude of the incident wave, D is the still water depth, T represent the time at which the wave crest enters the domain and is the wave celerity. In this study, a non-breaking incident wave is chosen with H = 0.032 m, D = 0.32 m and T = 2.45 s. The rest boundaries are set to be closed as shown in Fig- ure 2. The computational domain is approximated by 260 × 276 grids with a uniform grid size of 0.1 m. The simulation is carried out until 20s and the time step is determined by the CFL criteria. The computed and meas- ured water levels at five gauges are shown in Figure 3. It can be found that the lead wave height and arrival time are well predicted by our model in most gauges. Some discrepancies between the simulated and measured water level may be attributed to the three-dimensionality of the wave in reality cannot be exactly captured by a depth- averaged 2D model. Overall the present model is capable to simulate the wave runup over complex topography with a satisfactory accuracy. 4.2. Tsunami Runup onto a Complex 3D B each This experiment is proposed and suggested as a benchmark test for numerical model in The Third International Workshop on Long Wave Run-up Models in 2004. The experiment was performed in a 1:400 scale wave tank, which approximated the coastline topography near Monai in Japan. As shown in Figure 4, the tank was 5.488 m long and 3.402 m wide. The incoming wave was generated by the movements of wave paddles and three gauges Ch5, Ch7, and Ch9 (see Figure 4) were setup to record the time history of water elevation. For this case, the computational domain is approximated by 392 × 243 grids with a uniform grid size of 0.014 m. At the beginning, the tank is filled with a still water of 0.135m depth. The left boundary is wave inflow boundary, in which the time history of measured surface elevation was specified. The other three sides’ bounda- ries are set to be closed. The total simulation time is 22.5 s and the manning coefficient is n = 0.0025. The com- puted surface elevation at different time is plotted in Figure 4. Figure 5 shows the computed water elevation at three gauges compared with the observation data. In general, the movement of wave is well predicted by our model. Some discrepancies are found between numerical and experimental results due to the fact that the three- dimensionality of the flow cannot be exactly captured by a depth-averaged 2D model. Nevertheless, the lead wave height and arrival times are predicted with a good accuracy at these gauges. 5. Conclusion In this paper, a well-balanced numerical model is developed to simulate the long wave runup process. The cen- tral upwind scheme, which is a Riemann-problem-solver-free method, is used to calculate the flux at the inter- face. The model is able to preserve the “lake at rest” steady states and guarantee the positivity of the computed water depth when the Courant number is less than 0.25. The model is validated against a solitary wave runup Figure 3. Time histories of water level at different gauges. 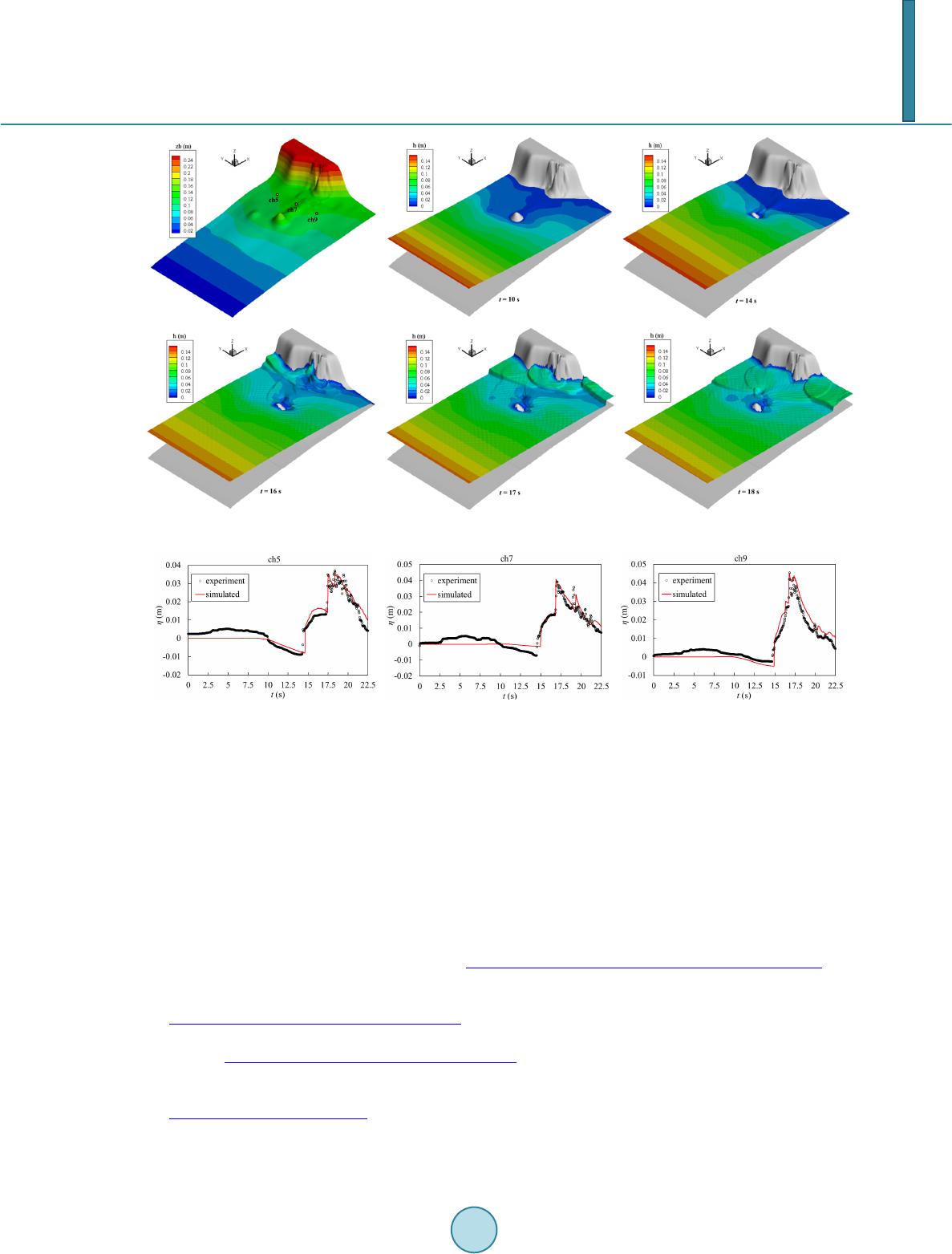 G. F. Wu et al. Figure 4. Bed elevation, the locations of gauges and the inundation map at different time. Figure 5. The computed water elevation at different gauges. experiment and tsunami runup experiment. For both experiments, the simulated results agree very well with measurement data, which confirm the applicability of the present model for long wave runup applications. Acknowledgements This work is part of the research project sponsored by the National Basic Research Program of China (973 Pro- gram) (No 2013CB035900), Natural Science Foundation of China (51009120), Zhejiang Province Ocean and Fisheries Bureau (2010210), and Zhejiang University (2012HY012B). References [1] Dodd, N. (1998) Numerical Model of Wave Run-Up, Overtopping, and Regeneration. ASCE Journal of Waterway, Port, Coastal and Ocean Engineering, 124 , 73-81. http://dx.doi.org/10.1061/(ASCE)0733-950X(1998)124:2(73) [2] Hu, K., Mingham, C.G. and Causon, D.M. (2000) Numerical Simulation of Wave Overtopping of Coastal Structures Using the Non-linear Shallow Water Equations. Coastal Engineering, 41, 433-465. http://dx.doi.org/10.1016/S0378-3839(00)00040-5 [3] Hubbard, M.E. and Dodd, N. (2002) A 2D Numerical Model of Wave Run-up and Overtopping. Coastal Engineering, 47, 1-26. http://dx.doi.org/10.1016/S0378-3839(02 ) 0009 4 -7 [4] Delis, A. I., Kazol ea, M. and Kampanis, N. A. (20 08 ) A Robust High-Resolution Finite Volume Scheme for the Simula- tion of Long Waves over Complex Domains. International Journal for Numerical Methods in Fluids, 56, 419-452. http://dx.doi.org/10.1002/fld.1537 [5] Li an g, Q., Wang, Y. and Archetti, R. (20 10) A Well-Balanced Shallow Flow Solver for Coastal Simulations. Int e r n a- tional Journal of Offshore and Polar Engineering, 20, 41-47.  G. F. Wu et al. [6] Bryson, S., Epshteyn, A., Kurganov, A. and Petro va, G. (2010) Well-Balanced Positivity Preserving Central-upwind Scheme on Triangular Grids for the Saint-Venant System. ESAIM: Mathematical Modelling and Numerical Analysi s, 45, 423-446. http://dx.doi.org/10.1051/m2an/2010060 [7] Li an g, Q. (2010) Flood Simulation Using a Well-Balanced Shallow Flow Model. ASCE, Journal of Hydraulic Engi- neerin g, 136 , 669 -67 5. http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000219 [8] Kurganov, A. and Petrova, G. (2007) A Second -Order Well-Balanced Positivity Preserving Scheme for the Saint-Ve- nant System. Communications in Mathematical Sciences, 5, 133-160. http://dx.doi.org/10.4310/CMS.2007.v5.n1.a6 [9] Br iggs, M., Synolakis, C., Ha rkin s, G. and Green, D. (1995) Laboratory Experiments of Tsunami Runup on a Circular Island . Pure and Applied Geophysic s, 144, 569-593. http://dx.doi.org/10.1007/BF00874384 [10] Nikolos, I. and Delis, A. (2009) An Unstructured noDe-Centered finite Volume Scheme for Shallow Water Flows with Wet/Dry Fronts over Complex Topography. Computer Methods in Applied Mechanics and Engineering, 198, 3723- 3750. http://dx.doi.org/10.1016/j.cma.2009.08.006
|