 Journal of Applied Mathematics and Physics, 2014, 2, 411-417 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26049 How to cite this paper: Xu, R., Hou, J.L., Wang, L., Yu, Y.F., Wei, J.X. and Li, C.F. (2014) Fluid Flow and Heat Transfer Chara- teristics in a 180-deg Round Turned Channel with a Perforated Divider. Journal of Applied Mathematics and Physics, 2, 411-417. http://dx.doi.org/10.4236/jamp.2014.26049 Fluid Flow and Heat Transfer Charateristics in a 180-deg Round Turned Channel with a Perforated Divider Rui Xu, Jinliang Hou, Li Wang, Yanfei Yu, Jiaxing Wei, Changfeng Li* School of Energy and Power Engineering, Jiangsu University, Zhenjiang, China Email: *cfli@ujs. edu.cn Received March 2014 Abstract This study provided a new configuration of the 180-deg round turned channel with a perforated divider, as well as numerically investigated the effect of perforations, including the diameter of perforation and the angel of perforation, on the fluid flow and heat transfer. The numerical results appeared in good agreement with previous experimental data under the same operating condi- tions. The results indicated that large size and positive angle of perforation changed the fluid flow pattern and the local Nusselt-number distribution fundamentally. It is noteworthy that a more uniform distribution of Nusselt-number was achieved by increasing the diameter of perforation. Keywords 180-deg Turned Channel, Perforated Divider, Heat Transfer, Computational Fluid Dynamic 1. Introduction To improve the thermal efficiency, gas-turbine blades are being designed to operate at increasingly higher working temperatures. Without cooling design, overly high temperature will lead to the deformation, inaccuracy, and even damage of the power machine. Leading coolant into the internal passages of the blade is widely used in the power machine design. Jeng et al. [1]-[3] proposed the configuration of intermediate divider with multiple perforations in the 180-deg turned channel. The coolant in the first duct entered the second duct ahead of time through perforations due to the bypass effect, so that the temperatures of upstream and downstream hot wall surfaces were relatively consistent, to avoid local high temperature at the wall surface of downstream channel. In addition, the perforations had additional perturbation effect on the air flow, the bypass air flew through the perforations mix with the main flow, that may improve the overall heat transfer capacity. Flow visualization technique and steady state heat transfer experimentation were used to investigate the fluid flow and heat transfer characteristics of 180-deg round turned channel with perforated divider [2]. The experimental results indicated that large size and positive angle of perforations influenced local Nusselt number distribution significantly, and the overall heat transfer declined as the perforation size increased, especially when the perforation was at posi- tive angle. However, when the perforation size was small, the overall heat transfer was higher than that without *  R. Xu et al. perforations by about 10%, and the influence of perforation angle was insignificant. In addition to the experimental studies mentioned above, several studies have been made to numerically pre- dict the flow and heat transfer in 180-deg turned channel. Iacovides et al. did a review of computer fluid dy- namic applied to the internal gas-turbine cooling [4]. Rigby et al. [5] use d the turbulent model to simu- late heat transfer and fluid flow phenomenon in a statio na r y straight duct with ribs no rmal to the mainstream flow. Prakash and Zerkle [6] used high Reynolds model to study three d imens ion fluid flow and heat transfer between two ribs in a straight duct. Its Reynolds-number attained as high as 30,000 to 100,000 and the wall functio n was adopted to figure out the near wall effects. This study conduct numerical research based on RANS methods to investigate the flow and heat transfer of the 180-deg round turned channel with perforated divider. The Realizable turbulent model is adopted, since it has a better performance than the standard model when confronted complex flow condition, such as secondary flow, flow sepa r atio n, jet impingement and so on. Numerical results provide more detailed fluid flow structure and local Nusselt-number distribution than the former experimental data, which can be used for industrial cooling design. 2. Numerical Analysis The detailed size of this physical model is identical to that of former experiment [2]. And the flow is governed by Reynolds averaged Navier-Stokes (RANS) equations and the energy equation. In the Cartesian tensor system these equations can be written as follows: Continuity equation: (1) Momentum equation: () () i iji j jij j u p uuu ug xxx x ρµ −ρρ ∂ ∂ ∂∂ ′′ =−+ + ∂∂∂ ∂ (2) Energy equation: 2 () j jp jj T uT xC xx λ ρ ∂∂ = ∂ ∂∂ (3) where is air velocity, , , stands for dynamic visc osity, specific heat and coefficient of thermal conductivity, respectively. T and P is the temperature and pressure. The Reynolds-averaged approach to turbu- lence modeling requires that the Reynolds stresses, in Equation (2) need to be modeled. The Boussi- nesq hypothesis relates the Reynolds stresses to the mean velocity gradients as seen in the equation below: '' 2 3 j ik ij tt ji k u uu uu k xx x ρ µρµ ∂ ∂∂ − =+−+ ∂∂ ∂ (4) where k is the turbulent kinetic energy, as defined by , is the Kronecker delta. The Realizable model, which is an example of the two-equation models that use the Boussinesq hypothesis, was selected for closure of the RANS equations. And the , transport equations are as follows: () )] () j it ii t ijkjj jj u kuu u k xxxx xx ρµ µ +µρε σ ∂ ∂ ∂∂ ∂∂ = [(++− ∂∂∂∂ ∂∂ (5) 2 12 () )] it ij j uCE C xx xk ε ρεµ εε µ+ρε ρ σνε ∂∂∂ = [(+− ∂∂ ∂+ (6) whe r e, 2 1/2 21 1 1.0,1.2,1.9,max(0.43,/ (5)),(2)(/),(),= 2 j i kij ijijt ji u uk CCEEk EC xx εµ σσηηηεµρ ε ∂ ∂ === =+=⋅=+ ∂∂ 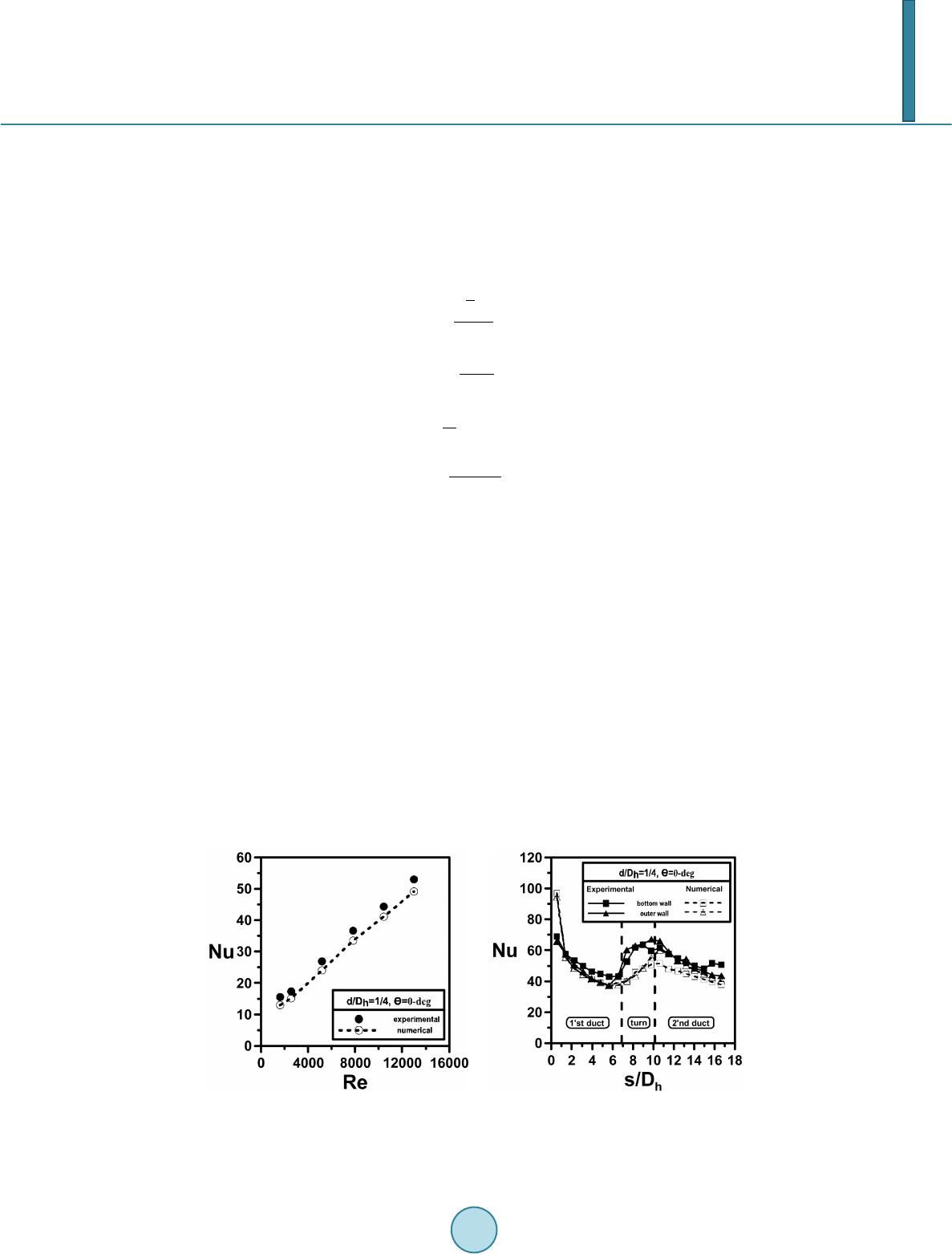 R. Xu et al. In Realizable turbulence model is not a constant, and its expression is much more complicated which can be found in ref [7]. All the equations above were discretized by the Second Order Upwind numerical scheme, decoupling with the SIMPLE algorithm and solved using a finite volume method (FVM) [8]. The solutions were considered to be converged when the normalized residual values were less than 10−5 for all variables but the energy equation, which is set to 10−6. The dimensionless parameters of interest in the present work are the Reynolds number, friction factor, local and averaged Nusselt number, Colburn factor, which are defined by the following equations: (7) (8) (9) (10) In this study, the commercial software FLUENT was adopted to execute the computing work. Enhanced wall treatment in this software was selected to handle the near wall effects. The working fluid was air at ordinary temperature and pressure (300 K, Pr = 0.707), whose physical properties being kept constant throughout the whole computation. I mpermeable boundary and no-slip wall conditions have been implemented over the duct walls as well as a uniform heat flux ranging from 3000 W/m2 to 20,000 W/m2 according to the flow inlet veloc- ity. Pressure-outlet was selected for the outflow condition. Due to the employment of the enhanced wall treat- ment, which contain a two-layer model to calculate the flow directly from the core turbulent region to the sub- layer viscous region, the grid near the wall should be refined according to the various Reynolds numbers so as to keep the first cell’s dimensionless wall distance . 3. Results and Discussion 3.1. Validation Figure 1 compares the averaged Nusselt number and local Nusselt number distribution of the present numerical study with those of experimental data under the same operating conditions. It is found that the numerical result have a good agreement with the experi mental data. As it shows in Figure 1( b) , the 180-deg turned channel can be divided into three sections: the first duct, the turn region and the second duct. (a) (b) Figure 1. Comparison with previous experimental results [2]: (a) averaged Nusselt-number as a function of Re; (b) local Nusselt-number distribution along the flow direction  R. Xu et al. 3.2. Flow St ru ct u re Figure 2 dep icts the flow structure of the half-hei ght (z = 1/2 Dh) main stream plane and three different trans- verse planes for the non-perforation system. The arrows, colored by temperature, indicate the flow direction. It can be found that the near wall fluid have a higher te mperature. Figure 2(a) shows an obvious vortex above the tip of the rectangular. Most of the air impinged on the outer wall, after that the cool air would flow near the out- er zone due to the inertia. Figure 2(c) indicates a strong secondary flow in the middle of the turn region, which contains a pair of counter rotating vortex near the top and bottom wall. Figure 3 shows the flow structure for various perforation sizes and angles. When the perforation diameter is Figure 2. Flow structure for the non-perforation configuration: (a) z = 10 mm; (b) x = 140 mm, y = 0 - 20 mm; (c) y = 30 mm; (d) x = 140 mm, y = 40 - 60 mm. (a) (b) (c) (d) Figure 3. Fluid flow structure for: (a) d/Dh = 1/4, θ = 0-deg; (b) d/Dh = 3/4, θ =0-deg; (c) d/Dh = 3/4, θ = +30-deg; (d) d/Dh = 1/4, θ = −30-deg.  R. Xu et al. small (d = 5 mm), as it shows in Fig ur e 3(a), and only a small amount of air passed through the perforation. Thus the effect of perforation on the fluid flow of the second duct was weak. However, when the perforation diameter increased to 15 mm and the angle kept the same, it had more amount of bypass air flowing through perforations into the second duct and a vortex existed in each perforation, as depicted in Figure 3(b) . When the angle of perforation changed from 0-deg to +30-deg and the perforation diameter kept large, most of air would flow through the first two perforations to the second duct, as it shows in Fig ur e 3(c). Besides, when the bypass flow was adverse to the main flow in the second duct, a more chaos flow state appeared. It can be found in Fig- ure 3(d) that only a small part of air flowed through perforations even though the perforation diameter was large. 3.3. Heat Transfer Figure 4 shows the contours of wall surfaces Nusselt number of the non-perforation configuration. At the first duct, the distribution of Nusselt number declined along the main flow direction due to the thermal developing flow. In downstream of the turn region and upstream of the second duct, Nusselt numbers roused remarkably, due to the secondary flow brought by the 180-deg bend. Figure 5 displays the contours of wall surface Nusselt number for differ ent configurations at Re = 13,000. The contours shows great differences from the non-perforation one when the size of the perforations was big. In the case of small perforation diameter, as depicted by Figure 5(a), the contours of Nusselt number were gener- ally the same as that of the non-perforation one. When the diameter increased to 15 mm, it is obvious from Fig- ure 5(b) that the extreme high Nusselt number zones located on the bottom and outer wall disappeared. This was resulted from the fact that bigger perforation size allowed more amounts of bypass flow as well as de- creased the amount of corresponding main flow passing through the turn region. In the case of negative perfora- tion angle, as it displays in Figure 5(c) , the Nusselt number contours of the bottom surface also keeps uniform. Figure 6 represents ratio of Nu/Nu0 as a function of Re, where Nu0 stands for the averaged Nusselt number of the non-perforation one. The results indicated that when the size of perforation was big and perforation angle was non-negative, the averaged Nusselt numbers for the perforation ones were smaller than that of the non-per- foration one. 4. Conclusion Fluid flow and heat transfer characteristics in a 180-deg round turned channel with perforated divider are nu- merically investigated for Re = 1609 to 13,000. Three perforations of different sizes (d/Dh = 1/4 and 3/4) and angles (θ = −30-deg, 0-deg and +30-deg) were located on the divider with equal interval. The numerical results had a good agreement with previous experimental data under the same operating conditions. The results indi- cated that the big size and positive angle of perforation influenced the flow behavior as well as the distribution of local Nusselt number remarkably. Furthermore, the heat transfer results demonstrated that small size of per- foration (d/D h = 1/4) led to slight improvement of the averaged Nusselt number and certain configuration (d/Dh = 3/4, θ = 0-deg) would result in a more uniform distribution of local Nusselt number. Figure 4 . Distribution of local Nusselt number (Nux) for the non-perforation configuration.  R. Xu et al. (a) (b) (c) Figure 5. Distribution of local Nusselt number (Nux) for: (a) d/Dh = 1/4, θ = 0-deg ; (b) d/Dh = 3/4, θ = 0-deg ; (c) d/Dh = 1/4, θ = −30-deg. Figure 6. Variation of Nu/Nu0 with Reynolds number. Acknowledgem ents The authors would like to thank the National Natural Science Foundation of China (11072091) and Key Sci- Tech Project from Ministry of Education, China (210078) for financially supporting this research. References [1] Jeng, T.M. , Tzeng, S.C. and Yang, Y.C. (2011) Detailed Measurements of Heat Transfer Coefficients in a 180-Deg Rectangular Turned Channel with the Perforation Divider. International Journal of Heat and Mass Transfer, 54,  R. Xu et al. 4823-4833. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2011.06.036 [2] Jeng, T. M., Tzeng, S.C. and Xu, R. (2013) Fluid Visualization and Heat-Transfer Tests in a 180-Deg Round Turned Channel with the Perforated Divider. International Communications in Heat and Mass Transfer, 44, 45-51. http://dx.doi.org/10.1016/j.icheatmasstransfer.2013.03.016 [3] Jeng, T. M., Tzeng, S.C., Chen, Y.C. and Chang, J.H. (2012) Thermal Behavior in a 180-Deg Turned Channel with the Perforation Divider Under rotational Condition. International Communications in Heat and Mass Transfer, 39, 803- 810. http://dx.doi.org/10.1016/j.icheatmasstransfer.2012.05.006 [4] Iacovides , H. and Launder, B.E. (1995) Computational Fluid Dynamics Applied to Internal Gas-Turbine Cooling: A Revie w. International Journal of Heat and Mass Transfer, 16, 454 -470. http://dx.doi.org/10.1016/0142-727X(95)00072-X [5] Rigb y, D.L., Steinthorsson, E. and Ameri, A.A. (1997) Numerical Prediction of Heat Transfer in a Channel With Ribs and Bleed, 1997. ASME J. Turbomach., 97, 431-447 . [6] Prakash , C. and Zerkle, R. (1995 ) Prediction of Turbulent Flow and Heat Transfer in a Ribbed Rectangular Duct With and Without Rotation. ASME J. Turbomach., 177, 255-264. http://dx.doi.org/10.1115/1.2835654 [7] Shih, T.H. , Liou, W.W. and Shabbir, A. (1995) A New Eddy Viscosity Model for High Reynolds Number Turbulent Fl ows. Computers Fluids, 24, 227-241. http://dx.doi.org/10.1016/0045-7930(94)00032-T [8] Patankar, S.V. (1980 ) Numerical Heat Transfer and Fluid Flow. McGraw-Hill, New York.
|