 Journal of Applied Mathematics and Physics, 2014, 2, 349-358 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26042 How to cite this paper: Ponnuswamy, V. and Govindaraj, S. (2014) Behaviour of Couple Stress Fluids in Porous Annular Squeeze Films. Journal of Applied Mathematics and Physics, 2, 349-358. http://dx.doi.org/10.4236/jamp.2014.26042 Behaviour of Couple Stress Fluids in Porous Annular Squeeze Films Vimala Ponnuswamy1, Sumathi Govindaraj2 1Department of Mathematics, Anna University, Chennai-600025, Tamil Nadu, India 2Department of Mathematics, Adhiparasakthi Engineering College, Melmaruvathur-603319, Tamil Nadu, India Email: vimalap@annauniv.edu Received March 2014 Abstract The laminar squeeze flow of an incompressible couple stress fluid between porous annular disks is studied using hydrodynamic lubrication theory. The modified Reynolds’ equation is derived us- ing Stokes microcontinuum theory and is solved analytically. Analytical expressions for the squeeze film pressure and the load carrying capacity are obtained in terms of Fourier-Bessel se- ries. Numerical results are obtained for the sinusoidal motion of the upper disk. The effect of cou- ple stresses and that of porous facing on the squeeze film behaviour are analysed through the squeeze film pressure and the load carrying capacity. Further, the equation for the gap width be- tween the disks is obtained from the inverse problem. Keywords Squeeze Films, Hydrodynamic Lubrication, Couple Stresses, Non-Newtonian Fluid 1. Introduction Squeeze film technology is widely applied in many areas of Engineering and Applied Sciences such as clutch plates in automotive transmission, impact film in bio-lubricated joints and turbo-machinery. The classical con- tinuum theory focuses on the use of a Newtonian lubricant in various squeeze film mechanisms [1-4]. The non- Newtonian characteristics of lubricants become important, when the lubricants contain additives with large quantity of high molecular weight polymers as the viscosity index improvers. Grease, emulsion, liquid crystals and body fluids like blood and synovial are examples of such lubricants. As the classical continuum theory of fluids neglects the size effects of particles, a microcontinuum theory has been developed by Stokes [5] to take into account the particle size effects of such non-Newtonian fluids. Many researchers have applied the micro- continuum theory of couple stress fluids in various squeeze film investigations [6-8]. Self lubricating porous bearings have been widely used in industry for a long time due to their special feature of self contained oil reservoir apart from low cost and other aspects of lubrication mechanism. In such bearings, as two surfaces approach each other, a part of the fluid will be squeezed out and the remaining part will flow through the porous media. This will reduce the time required for the oil to reach a prescribed thickness and will change the nature of the flow pattern. There have been numerous studies on various types of such porous bear- ings with a Newtonian or a non-Newtonian lubricant [9]-[12]. 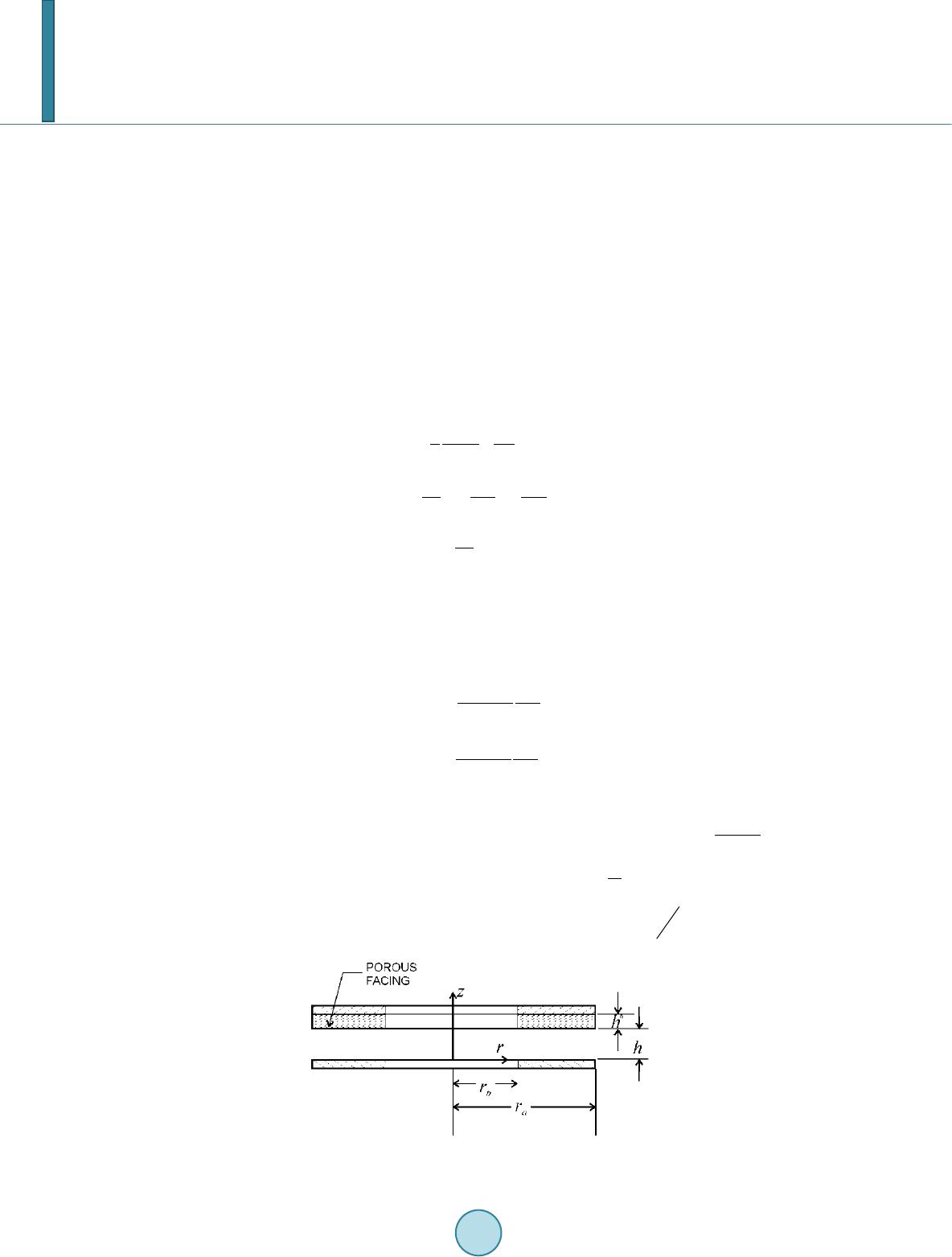 V. Ponnuswamy, S. Govindaraj Naduvinamani et al. [13] have examined the rheological effects of the couple stress fluids in porous journal bearings. Several investigations reveal the combined effects of couple stresses and surface roughness between various porous geometries [14]-[16]. In this paper, the couple stress fluid flow between porous annular disks is considered. On the basis of hydro- dynamic lubrication theory and Stokes microcontinuum theory the modified Reynolds’ equation is derived and is solved analytically. The effects of couple stresses and the porous facing on the squeeze film pressure, load carrying capacity and film thickness as a function of response time are studied. 2. Mathematical Formulation The axisymmetric laminar flow of an incompressible couple stress fluid between porous annular disks is consid- ered as shown in Figure 1. The upper disk with porous facing at z = h(t) is approaching the lower non-porous disk at z = 0 with a squeezing velocity of dh/dt. On the basis of Stokes microcontinuum theory and the assump- tion that the body forces and body couples are absent, the governing equations of motion of couple stress fluids take the form (1) (2) (3) where u and w are the velocity components in the radial and axial directions respectively, p the squeeze film pressure, ρ the fluid density, µ the shear viscosity and η is the new material constant responsible for the couple stress property with the dimension of momentum. The flow of couple stress fluid in a porous matrix is governed by the modified form of Darcy’s law which accounts for polar effects given by (4) (5) where u* and w* are respectively the radial and axial components of the fluid velocity in the porous region, p* the film pressure in the porous region, κ the permeability of the porous facing and . The parameter β represents the ratio of microstructure size to the pore size. The ratio has a dimension of square of length and this length may be regarded as the chain-length of the polar additives. If , then the mi- Fig ure 1. Annular squeeze film geometry.  V. Ponnuswamy, S. Govindaraj crostructure additives present in the lubricant block the pores in the porous layer and thus reduce the Darcy flow through the porous matrix. When the microstructure size is very small when compared to the pore size, i.e. β ≪ 1, the additives percolate in the porous matrix. Due to the continuity of flow in the porous region, the velocity components in the porous region, given by Equations (4) and (5), satisfy the continuity Equation (1). This result in Laplace equation in polar form for the squeeze film pressure in the porous region is given by 0 1 2 *2* = ∂ ∂ + ∂ ∂ ∂ ∂ z p r p r rr (6) The boundary conditions for the velocity components are the no-slip condition on z = 0 and slip condition on z = h(t) given by )(on ,0 0 on0,0 * thz dt dh ww u zw u =+== === (7) and the no-couple stress conditions are given by )( on0 and 0 on02 2 2 2 thz z u z z u== ∂ ∂ == ∂ ∂ (8) The boundary conditions for the squeeze film pressure are (9) (10) where ra and rb are the outer and inner radii of the annular disks respectively. The film pressure p* in the porous matrix satisfies the following conditions (11) (12) (13) where is the thickness of the porous layer. Also the continuity condition on the squeeze film pressure at the disk film interface is given by (14) 3. Solution Methodology From the axial momentum Equation (3), it is clear that the pressure p in the film region is independent of z. Solving the radial momentum Equation (2) and using the boundary conditions for u given in Equations (7) and (8), expression for the radial velocity component u is obtained as − −+− ∂ ∂ =)2/cosh( ]2/)2cosh[( 22 2 1222 lh lhz ll hzz r p u µ (15) where . Substitution of the expression of u from Equation (15) into the continuity Equation (1) and integration yields =− == dr dp r dr d r lhf ww zth z 1 12 ) ,( 0 0)( µ (16) where 32 3 0 (, )1224tanh2 h f hlhlhll =−+ . Substitution of the boundary conditions for the axial velocity com-  V. Ponnuswamy, S. Govindaraj ponent from Equation (7) into Equation (16) results in * 0 1 12 ),( w dt dh dr dp r dr d r lhf += µ (17) Using the expression for w* from Equation (5), the modified Reynolds equation is derived as () ∂ ∂ − − = h z p dt dh l h fdr dp r dr d r * 0 1 ) ,( 12 1 β µ κ µ (18) Equation (6) is solved for the film pressure in the porous matrix using the variable separable method and us- ing the boundary conditions for film pressure in the porous matrix from Equations (11)-(13). Thus, the pressure in the porous matrix is obtained as ( ) ( ) ( ) rUeecp n N n zhhz n nn α αα 0 1 2 * * 1 ∑ = −+ += (19) where is the nth eigenfunction defined by ( )()( )()() rYaJrJaYrU nnnnn ααααα 00000 −= (20) and αn is the nth eigenvalue that satisfies the equation given by ()()()() 0 0000 =− bYaJbJaY nnnn αααα (21) Equation (19) on differentiation gives ( ) () rUe ec z p n N n hh n n hz nn α α αα 0 1 2 * * 1 ∑ = = + = ∂ ∂ (22) On using from Equation (22), the modified Reynolds Equation (18), yields ( ) ( ) ( ) + − −= ∑ = rUeec dt dh lhfdr dp r dr d r n N n hz nn nn αα βµ κµ αα 0 1 2 0 * 1 1),( 121 (23) Integrating Equation (23) twice with respect to r with the use of pressure boundary conditions given in Equa- tions (9) and (10), the squeeze film pressure is obtained as ()() ( ) ( ) ( ) () ( ) rUe e c lhf rr rr rrr r dt dh l hf p n N n h n h n b a b bab n n α αβ κ µ α α 0 1 2 0 2 222 0 * 1 1 ),( 12 /log /log ) ,( 3 ∑ = − − + −− −= (24) Use of Equations (19) and (24) in the interface condition (14) yields ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) −−−= − − −+ ∑ = ba b bab n N n h n hh n rr rr rrrr dt dh lhf rUe lhf eec nnn /log /log ),( 3 1 1 1),( 12 1 2222 0 0 1 2 0 2 * µ α αβ κ ααα (25) The constants cn in Equation (25) can be determined using the orthogonality of eigen functions and are given by ( ) ( ) () 1 2 0 2 2 0 * * 1 1),( 12 1 1 ),( 24 − − − −+ − = h n hh nan n nn n e lhf ee r dt dh l hf c ααα β α κ ξα µ (26) where ( )( )()( )( )() 0 11011nna anabnbna anabnb YrrJr rJrJrrYrrYr ξαααααα =+− + .  V. Ponnuswamy, S. Govindaraj The following quantities are introduced to non-dimensionalize the flow variables: ( )() 2 2 0 3 0 * 3 0 0 * 0 0 * * 0 , , ,, , , , ,,, , b n bn b a b b r p h P h h r r r h l h f LHf h l L tT r h H h h H r r R µω κ ψ α αα ω = == == = === = (27) Here h0 is the initial film thickness and 1/ω is the characteristic time. Substituting Equation (26) in Equation (24) and applying the non-dimensional quantities given in Equation (27), the squeeze film pressure in the non- dimensional form is obtained as ( )( ) ( ) ( ) ( )() ( )() ( )() 1 1 * *** 0 3* 0 0 22 * 0 1 2exp1 2exp1 12 1),( ),( 24 log log 11 ),( 3 − = ∑ − − +− − −−−= N nn nn nn n n H HHLHf dT dH LHf RU R R dT dH LHf P α α ψ αβ ξα α αα α (28) The squeeze film force is found by integrating the squeeze film pressure over the disk surface (29) The non-dimensional form of the squeeze film force is given by () ( ) ( ) ( ) ( )() ( )() 1 1 * *** 0 4* 0 2 2 4 * 0 1 2exp1 2exp1 12 1),( ),( 48 log 1 1 ),(2 3 − = ∑ − − +− − − −−−= N nn nn n n n sq H HHLHf dT dH LHf dT dH LHf F α α ψ αβ ξ ζ α π α α α π (30 ) where ()( )( )()( )() 0 11011nnnnnnn YJJJY Y ζαααααααααα αα =−− − and The squeeze film pressure and force are obtained for a sinusoidal motion h(t)= h0 + esinωt of the upper por- ous disk, where h0 is the initial film thickness, e is the amplitude and ω is the angular frequency of the sinusoidal motion. On using the non-dimensional quantities given in Equatio n (27), the dimensionless form of h(t) is given by (31) where . Constant Force Squeezing State Considering a constant force squeezing state, the film thickness and time relation can be obtained as ( ) ( )() ( )() dT dH H H HLHf LHfLHf N n n n n n − − + − +−=± − = ∑ 1 1 * * ** 0 4* 0 * 0 1 2exp1 2exp1 12 1),( ),( 48 ),(2 3 1 α α ψ αβ ξ ζ α ππ (32 ) where the non-dimensional time is . Equation (32) is solved numerically for H(T) by fourth order Runge Kutta method using the initial conditions given by (33) 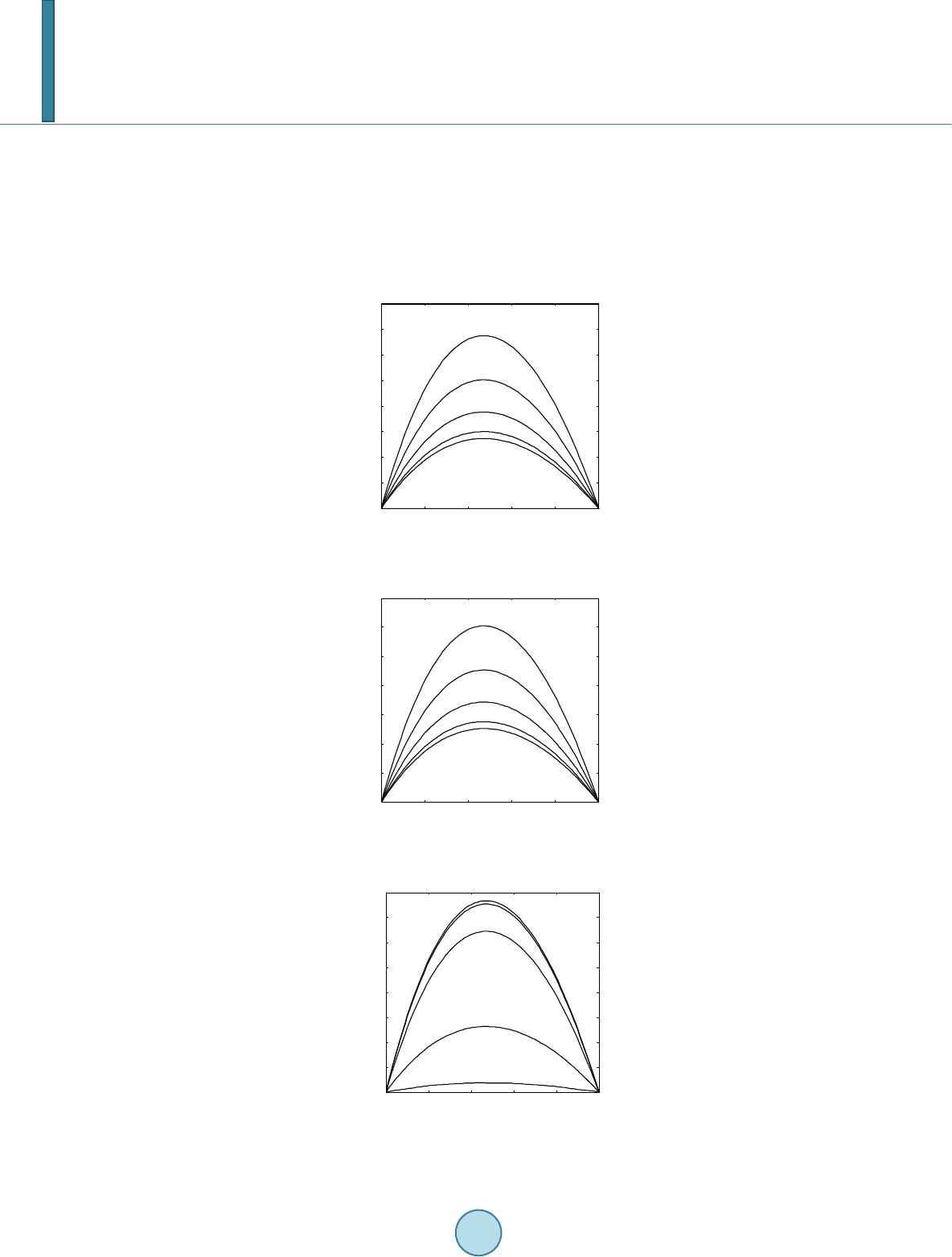 V. Ponnuswamy, S. Govindaraj 4. Results and Discussion In this analysis, the effects of couple stresses on the squeeze film behaviour between porous annular disks have been studied on the basis of Stokes microcontinuum theory. The couple stress effect on the squeeze film charac- teristics is observed through the non-dimensional couple stress parameter L and the effect of permeability is studied through the non-dimensional permeability parameter ψ. The squeeze film pressure and load carrying ca- pacity have been computed using Equations (28) and (30) for the sinusoidal motion of the upper porous disk. Figures 2-5 show the variation of non-dimensional squeeze film pressure P as a function of radial co-ordinate Figure 2. Couple stress effects on the film pressure (E = 0.2). Figure 3. Couple Stress Effects on the Film Pressure (E = 0.4). Figure 4. Effects of permeability on the film pressure (E = 0.2). 11.2 1.4 1.6 1.82 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 P R 5 4 3 2 L 1 0 2 0.1 3 0.2 4 0.3 5 0.4 ψ =0.001,E=0.2,T=3, β =0.2,H*=0.01 1 11.2 1.4 1.6 1.82 0 0.2 0.4 0.6 0.8 1 1.2 1.4 P R L 1 0 2 0.1 3 0.2 4 0.3 5 0.4 ψ =0.001,E=0.4,T=3, β =0.2,H*=0.01 4 5 3 2 1 11.2 1.41.6 1.82 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 P R L=0.2,E=0.2,T=3, β =0.2,H*=0.01 ψ 1 1 2 0.1 3 0.01 4 0.001 5 0 5 4 3 1 2  V. Ponnuswamy, S. Govindaraj Figure 5. Effects of permeability on the film pressure (E = 0.4). R for T = 3, β = 0.2, H* = 0.01 and α = 2. Figure 2 and Figure 3 present the squeeze film pressure P as a func- tion of R with ψ = 0.001 for different values of the couple stress parameter L, taking the amplitude of the sinu- soidal motion as E = 0.2 and E = 0.4 respectively. It is observed that the squeeze film pressure P increases for increasing values of couple stress parameter L and that the squeeze film pressure in enhanced for larger values of the amplitude E of sinusoidal motion. Figure 4 and Figure 5 present the variation of non-dimensional squeeze film pressure P as a function of R with L = 0.2 for different values of the permeability parameter ψ. Figur e 4 shows that there is a significant re- duction in pressure with increasing permeability of the porous facing for the amplitude of the sinusoidal motion E = 0.2. Also, it is observed that there is no significant difference in the pressure distribution between ψ = 0 and ψ = 0.001. Thus ψ = 0.001 indicates a very low permeability almost bordering on the non-porous case. Similar trend is observed in Figure 5 for E = 0.4. Comparison of Figure 4 and Figure 5 shows that the squeeze film pressure is more significant for higher values of E. Figures 6-9 display the variation of non-dimensional load carrying capacity Fsq as a function of response time T at β = 0.2, H* = 0.01and α = 2. Fig ure 6 and Figure 7 present the variation of non-dimensional load carrying capacity Fsq as a function of response time T with ψ = 0.001 for different values of the couple stress parameter L when E = 0.2 and E = 0.4 respectively. A significant increase in the load carrying capacity is observed with an increase in the value of couple stress parameter L. Further, it is observed that the increase in the load carrying capacity is more pronounced for larger values of the amplitude of sinusoidal motion. Figure 8 and Figure 9 describe the variation of non-dimensional load carrying capacity Fsq as a function of response time T for different values of the permeability parameter ψ with L = 0.2 when E = 0.2 and E = 0.4 re- spectively. It is observed from Figure 8 and Figure 9 that the effect of permeability parameter ψ is to decrease the load carrying capacity when compared to the case of ψ = 0 and that an increase in the load carrying capacity is obtained by increasing the amplitude of sinusoidal motion. The variation of non-dimensional squeeze film thickness H as a function of response time T has been obtained using Equatio n (32). Figure 10 presents the gap width as a function of response time for different values of the couple stress parameter L with H* = 0.01, ψ = 0.001, β = 0.2 and α = 2. It is observed that, for attaining a partic- ular height there is an increase in the response time with an increase in the couple stress parameter L, i.e. the couple stress fluids sustain a higher load for a longer time. Figure 11 shows the gap width as a function of re- sponse time for various values of the permeability parameter ψ with H* = 0.01, L = 0.2, β = 0.2 and α = 2. It is found that the time required for the film thickness to reach any particular value is greatly reduced as the perme- ability parameter is increased. Conclu sion The theoretical study of rheological effects of squeeze film flow of a non-Newtonian couple stress fluid between porous annular disks is presented. On the basis of Stokes microcontinuum theory, the modified Reynolds equa- tion is derived and is solved analytically. The numerical results are presented for a sinusoidal motion of the up- 11.2 1.4 1.61.82 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 P R 1 L=0.2,E=0.4,T=3, β =0.2,H*=0.01 4 5 3 2 ψ 1 1 2 0.1 3 0.01 4 0.001 5 0 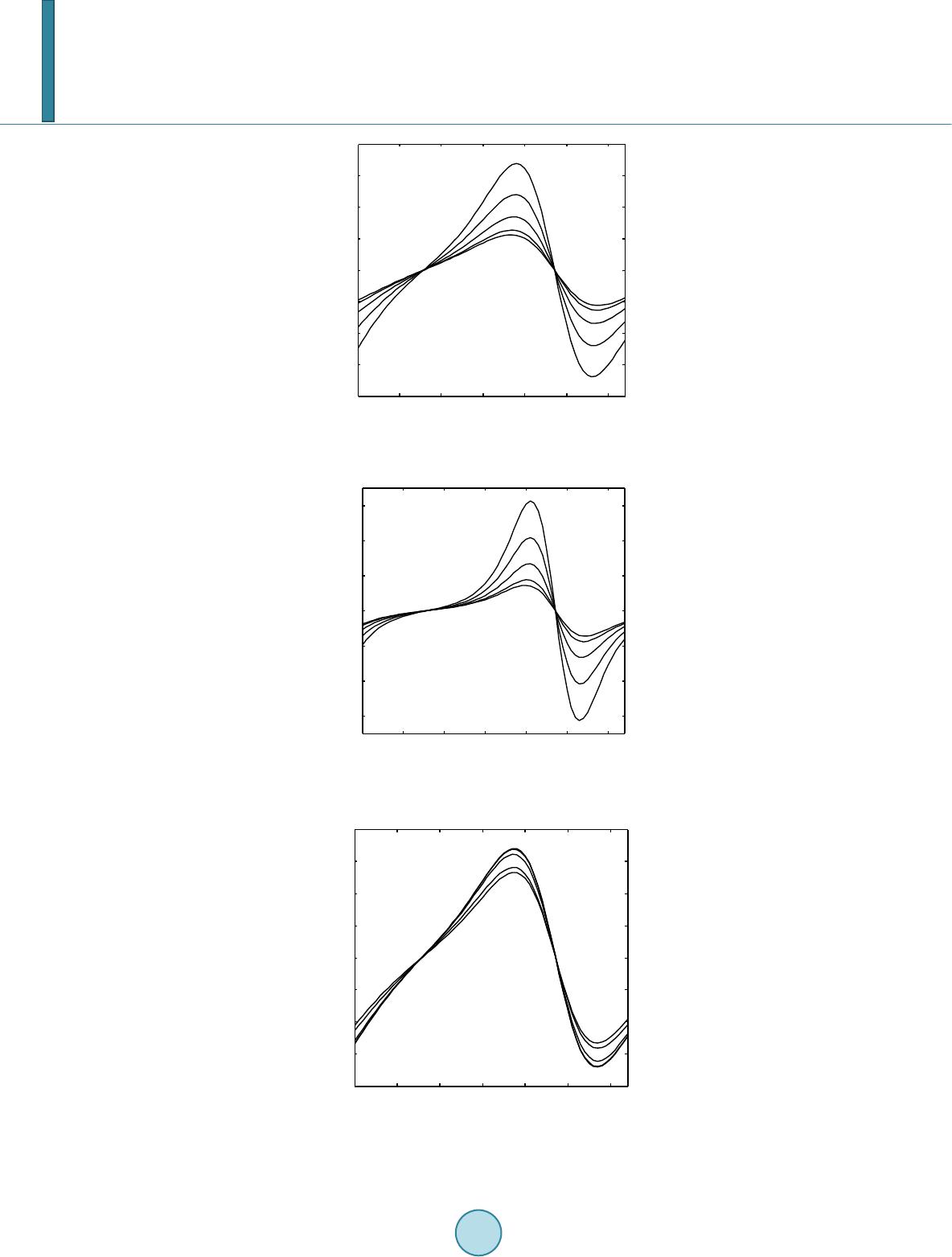 V. Ponnuswamy, S. Govindaraj Figure 6. Effect of couple stresses on the film force (E = 0.2). Figure 7. Effect of couple stresses on the film force (E = 0.4). Figure 8. Effects of permeability on the film force (E = 0.2). 0 1 2 3 4 5 6 -8 -6 -4 -2 0 2 4 6 8 Fsq T L 1 0 2 0.1 3 0.2 4 0.3 5 0.4 4 3 2 1 ψ =0.001,E=0.2, β =0.2,H*=0.01 5 01 2345 6 -30 -20 -10 0 10 20 30 Fsq T L 1 0 2 0.1 3 0.2 4 0.3 5 0.4 ψ =0.001,E=0.4, β =0.2,H*=0.01 5 3 4 2 1 0123456 -4 -3 -2 -1 0 1 2 3 4 Fsq T ψ 1 1 2 0.1 3 0.01 4 0.001 5 0 L=0.2,E=0.2, β =0.2,H*=0.01 3 2 1 54 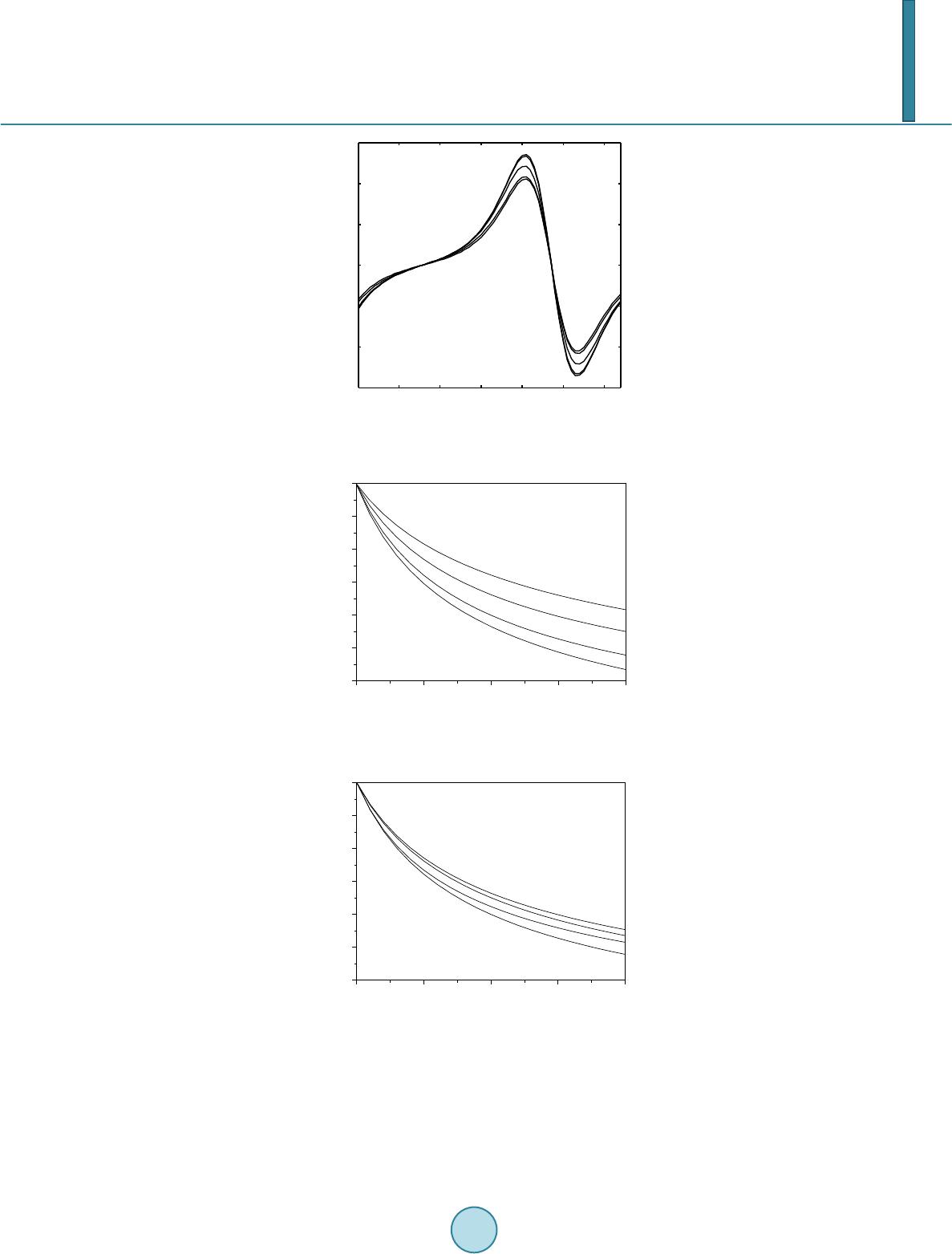 V. Ponnuswamy, S. Govindaraj Figure 9. Effects of permeability on the ilm force (E = 0.4). Fig ure 10. Effects of couple stresses on the film thick- ness. Figure 11. Effects of permeability on the film thick- ness. per disk. Enhancements in the squeeze film pressure and load carrying capacity are observed for larger values of the couple stress parameter. Further enhancements in squeeze film pressure and load carrying capacity are ob- tained by increasing the amplitude of sinusoidal motion. Although the effect of porosity decreases the squeeze film force, the use of couple stress fluids as lubricants improves the squeeze film behavior by increasing the 0123456 -15 -10 -5 0 5 10 15 Fsq T 1 3 45 ψ 1 1 2 0.1 3 0.01 4 0.001 5 0 L=0.2,E=0.4, β =0.2,H*=0.01 2 05 10 15 20 0.4 0.5 0.6 0.7 0.8 0.9 1.0 4 23 1 H * =0.01, ψ =0.001, β =0.2, α =2 1 L=1 2 L=0.1 3 L=0.2 4 L=0.3 T H 05 10 15 20 0.4 0.5 0.6 0.7 0.8 0.9 1.0 H * =0.01,L=0.2, β =0.2, α =2 1 23 4 H T 1 ψ =1 2 ψ =0.01 3 ψ =0.001 4 ψ =0  V. Ponnuswamy, S. Govindaraj squeeze film force. Also, it is observed from the inverse problem that the effect of permeability decreases the film thickness and the effect of couple stresses provide a longer response time. On the whole, the performance of porous squeeze film bearings can be improved by a proper choice of lubricants blended with microstructures. References [1] Archibald, F.R. (1956 ) Load Capacity and Time Relations for Squeeze Films. Transactions of the ASME, 78, 29-35. [2] Jones, A. F. and Wilson, S.D. R. (1975) On the Failure of Lubrication Theory in Squeezing Flows. ASME Transactions Journal of Lubrication Technology, 97, 101-104. http://dx.doi.org/10.1115/1.3452513 [3] Pinkus, O. and Sternlicht, B. (1961) Theory of Hydrodynamic Lubrication. Mc-Graw Hill Book Company Inc., New York. [4] Tich y, J. A. and Winer, W.O. (1970) Inertial Considerations in Parallel Circular Squeeze Film Bearings. ASME Trans- actions Journal of Lubrication Technology, 92, 588-592. http://dx.doi.org/10.1115/1.3451480 [5] Stokes, V.K. (19 66 ) Couple Stress in Fluids. Physics of Fluids, 9, 1709-1715 . http://dx.doi.org/10.1063/1.1761925 [6] Ramanaiah, G. and Sarkar, P. (1978) Squeeze Films and Thrust Bearings Lubricated by Fluids with Couple Stresses. Wear, 48, 309 -316. http://dx.doi.org/10.1016/0043-1648 (78 )90 22 9-6 [7] Naduvinamani, N.B., Fathi ma, S.T. and Hiremath, P.S. (2003) Hydrodynamic Lubrication of Rough Slider Bearing with Couple Stress Fluids. Tribology International, 36, 949-959. http://dx.doi.org/10.1016/0043-1648(78 )90 22 9 -6 [8] Elsharkawy, A.A. and Guedouar, L.H. (2001 ) An Inverse Solution for Finite Journal Bearings Lubricated with Couple Stress Fluids. Tribology International, 34, 107-118. http://dx.doi.org/10.1016/S0301-679X(00 )00 14 5-6 [9] Wu, H. (19 70 ) Squeeze Film Behaviour for Porous Annular Disks. ASME Transactions Journal of Lubrication Tech- nology, 92, 593-596. http://dx.doi.org/10.1115/1.3451481 [10] Bhat, V. and Deheri, G.M. (1991) Squeeze Film Behaviour in Porous Annular Disks Lubricated with Magnetic Fluid. Wear, 1 51 , 123 -128. http://dx.doi.org/10.1016/0043-1648( 91 )90 352-U [11] Cusano, C. (1972) Lubrication of Porous Journal Bearings. ASME Transactions Journal of Lubrication Technology, 94, 69-73. http://dx.doi.org/10.1115/1.3451638 [12] Murti, P.R.K. (1974) Squeeze Film Behaviour in Porous Circular Disks. ASME Transactions Journal of Lubrication Technology, 96, 2 06-209. http://dx.doi.org/10.1115/1.3451923 [13] Naduvinamani, N.B., Hiremath, P.S. and Gurubasavaraj, G. (2001) Squeeze Film Lubrication of a Short Porous Journal Bearing with Couple Stress Fluids. Tribology International, 34, 739-747. http://dx.doi.org/10.1016/S0301-679X(01)00064-0 [14] Naduvinamani, N.B. and Siddangouda, A. (2007) Combined Effects of Surface Roughness and Couple Stresses on Squeeze Film Lubrication between Porous Circular Stepped Plates. Proceedings of IMechE Part J: Journal of Engi- neering Tribology, 221, 52 5-534. [15] Naduvinamani, N.B. and Siddangouda, A. (2007) Effects of Surface Roughness on the Hydrodynamic Lubrication of Porous Step Slider Bearings. Tribology International, 40, 780-793. http://dx.doi.org/10.1016/j.triboint.2006.07.003 [16] Bujurke, N.M. and Basti, D.P. (2008) Surface Roughness Effects on Squeeze Film Behaviour in Porous Circular Disks with Couple Stress Fluid. Transactions of Porous Media, 71, 185-197. http://dx.doi.org/10.1016/j.triboint.2006.07.003
|