 Journal of Applied Mathematics and Physics, 2014, 2, 335-341 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26040 How to cite this paper: Lee, K.-L., Meng, C.-H. and Pan, W.-F. (2014) The Influence of Notch Depth on the Response of Local Sharp-Notched Circular Tubes under Cyclic Bending. Journal of Applied Mathematics and Physics, 2, 335-341. http://dx.doi.org/10.4236/jamp.2014.26040 The Influence of Notch Depth on the Response of Local Sharp-Notched Circular Tubes under Cyclic Bending Kuo-Long Lee, Ching-Hsun Meng, Wen-Fung Pan Department of Engineering Science, National Cheng Kung University, Tainan, Taiwan Email: z7808034 @email. ncku. edu.tw Received January 2014 Abstract In this paper, the mechanical behavior and buckling failure of SUS304 stainless steel tubes with different local sharp-notched depths subjected to cyclic bending were experimentally investigated. It can be seen that the experimental moment-curvature relationship exhibits cyclic hardening and becomes a steady loop after a few cycles. However, the experimental ovalization-curvature rela- tionship exhibits an increasing and ratcheting manner with the number of th e bending cycles. In addition, higher notch depth of a tube leads to a more severe unsymmetrical trend of the ovaliza- tion-curvature relationship. It has been observed that the notch depth has almost no influence on the moment-curvature relationship. But, it has a strong influence on the ovalization-curvature re- lationship. Finally, the theoretical model proposed by Kyriakides and Shaw [1] was used in this study for simulating the controlled curvature-number of cycles to produce buckling relationship. Through comparison with the experimental data, the theoretical model can properly simulate the experimental findings Keywords Circular Tube, Local Sharp Notch, Notch Depth, Cyclic Bending 1. Introduction The circular tube components in a number of practical industrial applications, such as offshore structures, nuc- lear reactor components, earthquake resistant structures, transporting tubes of heat exchanger, …etc., must be designed to resist cyclic bending. The major characteristic of the circular tube under bending is the nonlinear behavior of ovalization of the tube cross-section. The ovalization of the tube cross-section is the change of the outside diameter divides by the original outside diameter. It is known that the magnitude of the tube ovalization increases when the bending moment increases. If the bending moment increases cyclically, the magnitude of the ovalization also increases in ratcheting manner with the number of cycles. Such increase in ovalization of tube cross-section causes a progressive reduction in its bending rigidity, which can ultimately result in buckling or fracture of the circular tube. Therefore, studies concerning the response and buckling of circular tubes subjected to cyclic bending are very important for many industrial applications.  K.-L. Lee et al. Beginning in the 1980, Kyriakides and his co-workers constructed the tube bending machine and conducted a series of experimental and theoretical investigations. Kyriakides and Shaw [1] investigated the 6061-T6 alumi- num and 1018 steel tubes to the stability conditions under cyclic bending. Corona and Kyriakides [2] experi- mentally studied the degradation of circular tubes subjected to cyclic bending and external pressure. Vaze and Corona [3] experimentally investigated the elastic-plastic degradation and collapse of steel tubes with square cross-sections under cyclic bending. Corona et al. [4] used a set of bending experiments to conduct on aluminum alloy tubes for investigating the yield anisotropy effects on the buckling. Limam et al. [5 ] studied the inelastic bending and collapse of tubes in present of the bending and internal pressure. Pan and his co-workers also constructed a similar bending machine with a newly invented cur va t ure-ovaliza- tion measurement apparatus (COMA), which was designed and set up by Pan et al. [6] to study various kinds of tubes under different cyclic bending conditions. Lee et al. [7] studied the influence of the Do/t ratio on the re- sponse and stability of circular tubes subjected to symmetrical cyclic bending. Lee et al. [8] experimentally in- vestigated the effects of the Do/t ratio and curvature-rate on the response and stability of circular tubes subjected to cyclic bending. Chang and Pan [9] discussed the estimation of the buckling life of circular tubes subjected to cyclic bending. In practical industrial applications, tubes are under the hostile environment, so the material in the environment may corrode the tube surface and produce notches. The mechanical behavior and buckling failure of a notched tube differs from that of a tube with a smooth surface. In 2010, Lee et al. [10] studied the variation in ovaliza- tion of sharp-notched circular tubes subjected to cyclic bending. Lee [11] investigated the mechanical behavior and buckling failure of sharp-notched circular tubes under cyclic bending. Lee et al. [12] experimentally dis- cussed the viscoplastic response and collapse of sharp-notched circular tubes subjected to cyclic bending. How- ever, all investigations of the sharp notch were the circumferential sharp notch. If the sharp notch is a local sharp notch, the mechanical behavior and buckling failure subjected to cyclic bending should be different with that of a circumferential sharp notch. Therefore, the response of local sharp-notched SUS304 stainless steel tubes with different notch depths subjected to cyclic bending is discussed in this paper. 2. Experiment 2.1. Bending Device Figure 1(a) is a schematic drawing of the bending device. It is designed as a four-point bending machine, capa- ble of applying bending and reverse bending. The device consists of two rotating sprockets resting on two sup- port beams. Heavy chains run around the sprockets and are connected to two hydraulic cylinders and load cells forming a closed loop. Each tube is tested and fitted with solid rod extension. The contact between the tube and the rollers is free to move along axial direction during bending. The load transfer to the test specimen is in the form of a couple formed by concentrated loads from two of the rollers. Once either the top or bottom cylinder is contracted, the sprockets are rotated, and pure bending of the test specimen is achieved. Reverse bending can be achieved by reversing the direction of the flow in the hydraulic circuit. Detailed description of the bending de- vice can be found in Kyriakides and Shaw [1] and Pan et al. [6]. 2.2. Curvature-Ovalization Measurement Apparatus (COMA) The COMA, shown schematically in Figure 1(b), is an instrument used to measure the tube curvature and ova- lization of a tube cross-section. It is a lightweight instrument, which is mounted close to the tube mid-span. There are three inclinometers in the COMA. Two inclinometers are fixed on two holders, which are denoted side-inclinometers. These holders are fixed on the circular tube before the test begins. From the fixed distance between the two side-inclinometers and the angle change detected by the two side-inclinometers, the tube cur- vature can be derived. In addition, a magnetic detector in the middle part of the COMA is used to measure the change of the outside diameter. A more detailed description of the bending device and the COMA is given in Pan et al. [6] . 2.3. Materials and Specimens The circular tubes used in this study were made of SUS304 stainless steel. The tubes’ chemical composition is Cr (18.36%), Ni (8.43%), Mn (1.81%), Si (0.39%), …., and a few other trace elements, with the remainder being 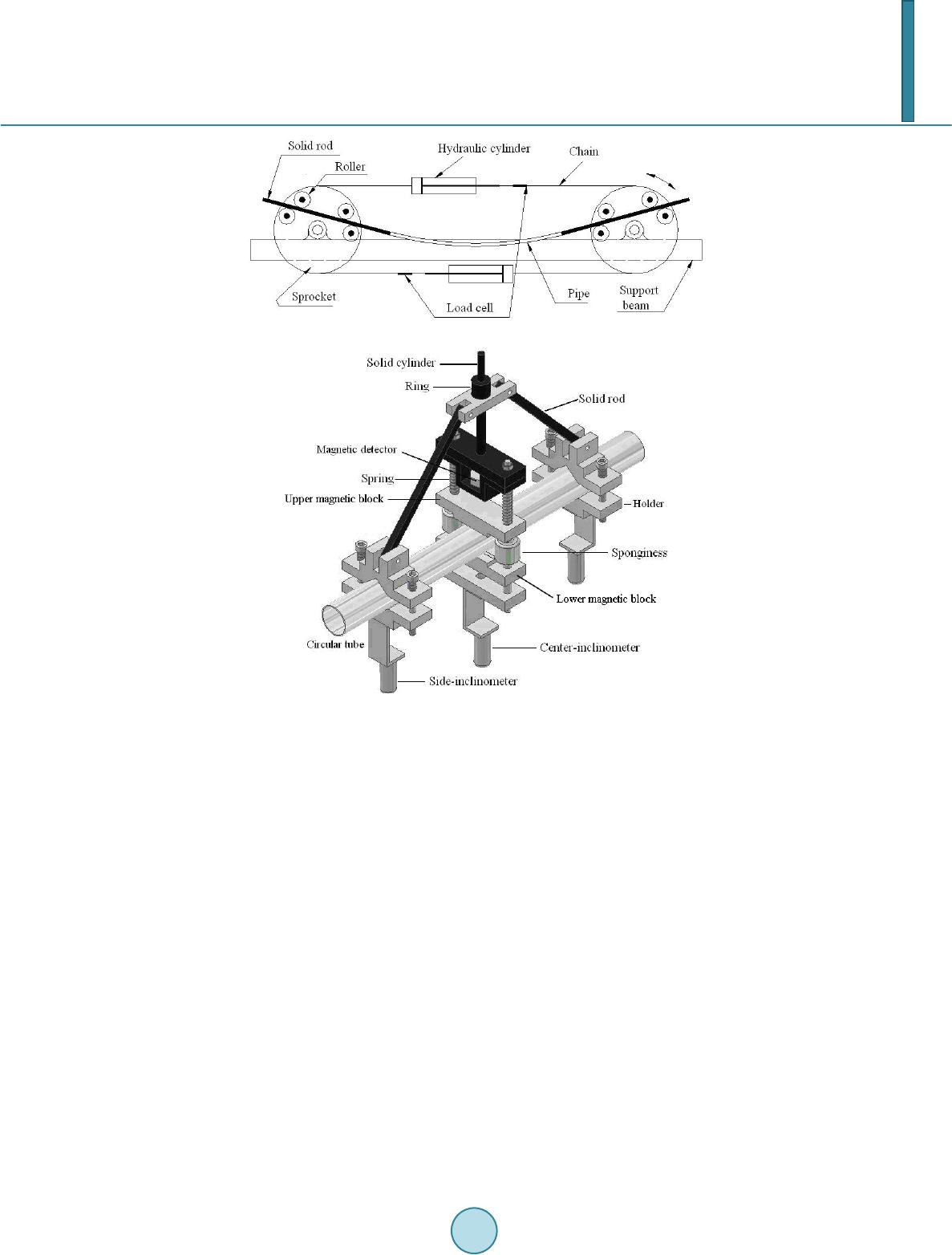 K.-L. Lee et al. (a) (b) Figure 1. (a) Schematic drawing of the Bending device and (b) schematic drawing of the COMA. Fe. The ultimate stress, 0.2% strain offset the yield stress and the percent elongation are 626 MPa, 296 MPa and 35%, respectively. The raw smooth SUS304 stainless steel tube had an outside diameter Do of 36.6 mm and wall-thickness t of 1.5 mm. The raw tubes were machined on the outside surface to obtain the desired local notch depth a of 0.2, 0.4, 0.6, 0.8 and 1.0 mm. Figure 2 shows a schematic drawing of the local sharp-notched tube. According to the drill of the machine, the corresponding surface diameters b were 0.6, 1.2, 1.8, 2.4 and 3.0 mm, respectively. 2.4. Test Procedures The test involved a curvature-controlled cyclic bending. The controlled-curvature ranges were from ±0.2 to ±0.5 m−1 and the curvature-rate of the cyclic bending test was 0.035 m−1·s−1. The magnitude of the bending moment was measured by two load cells mounted in the bending device. The magnitudes of the curvature and ovalization of the tube cross-section were controlled and measured by the COMA. In addition, the number of cycles neces- sary to produce buckling was also recorded. 3. Experimental Result and Discussion 3.1. Response of Local Sharp-Notched SUS304 Stainless Steel Tubes under Cyclic Bending Figure 3 shows the experimentally determined cyclic moment (M)-curvature (κ) for local s har p -notched SUS304 stainless steel tubes under cyclic bending with a notch depth a of 0.2 mm. It can be seen that the tube exhibit 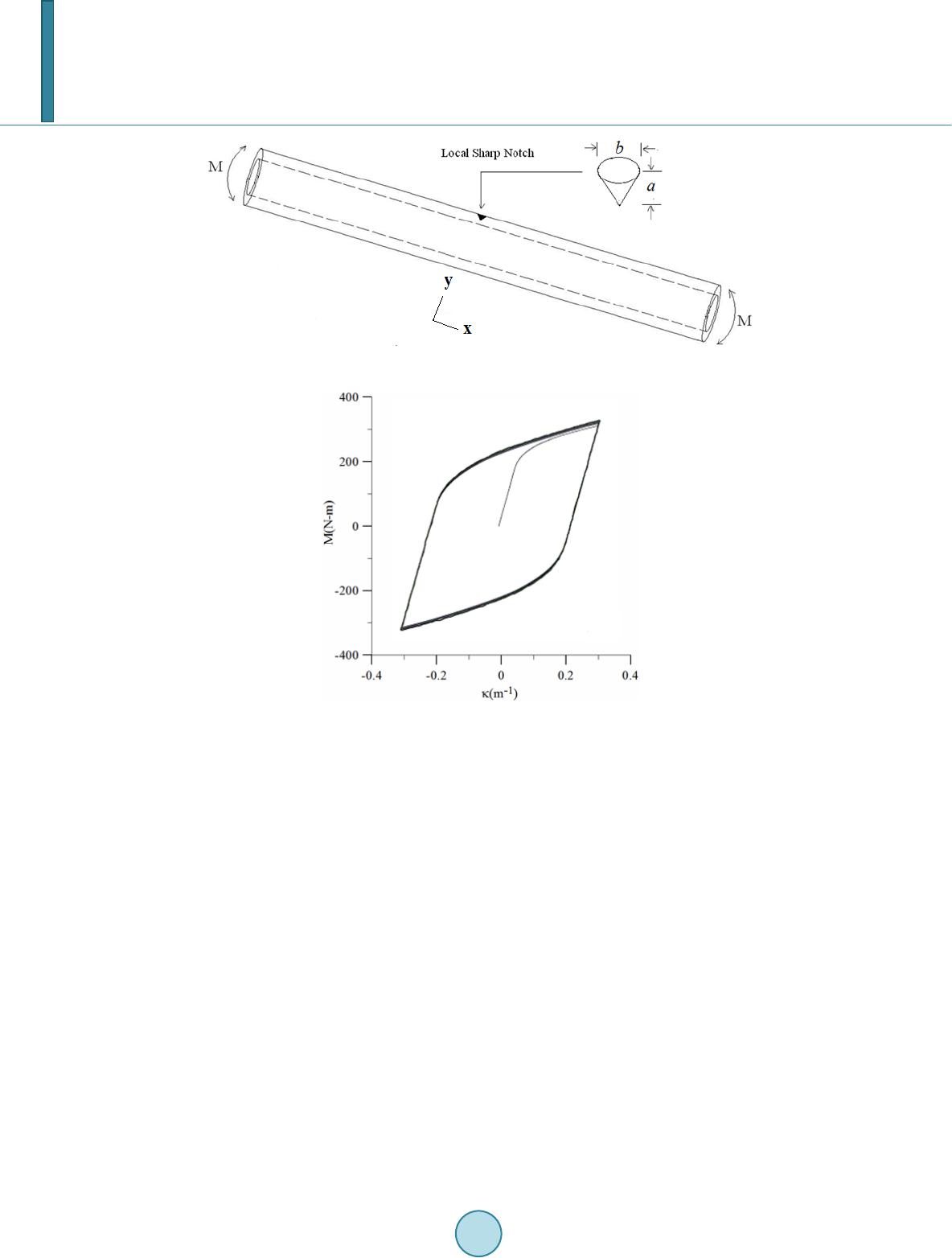 K.-L. Lee et al. Figure 2. Schematic drawing of the local sharp-notched tube. Figure 3. Experimental moment (M)-curvature (κ) curve for local sharp-notched SUS304 stainless steel tubes under cyclic bending with a = 0.2 mm. cyclic hardening and become stable after a few cycles. Because the type of notch is small and local, the notch depth has almost no influence on the M-κ curve. Therefore, the M-κ curves for other different values of a are not shown in this paper. Figures 4(a)-(e) depict the experimentally determined cyclic ovalization (ΔDo/Do) -curvature (κ) for a = 0.2, 0.4, 0.6, 0.8 and 1.0 mm, respectively. It can be seen that the ovalization increases in a ratcheting manner with the number of bending cycles. Higher a of the notch tube leads to a more severe unsymmetrical trend of the ΔDo/Do-κ curve. In addition, higher a of the notch tube causes greater ovalization. 3.2. Collapse of Local Sharp-Notched SUS304 Stainless Steel Tubes under Cyclic Bending Figure 5(a) shows the experimental cyclic curvature (κc) versus the number of cycles necessary to produce buckling (Nb). For a given curvature, tubes with a higher value of a display a lower number of cycles necessary to produce buckling. The results of Figure 5(a) are plotted on a double logarithmic coordinate in F igure 5(b). The five straight lines in this figure are least square fits of the data. The five fits are almost parallel straight lines. Kyriakides and Shaw [1] have proposed a formulation of the relationship between κc and Nb for the material they tested as or (1a, b) where C and α are the material parameters, which are related to the material properties and the Do/t ratio. The material parameter C is the controlled cyclic curvature magnitude at Nb = 1, and α is the slope in the log-log  K.-L. Lee et al. Figure 4. Experimental ovalization (ΔDo/Do)-curvature (κ) curves for local sharp-notched SUS304 stainless steel tubes under cyclic bending for a = (a) 0.2; (b) 0.4; (c) 0.6; (d) 0.8 and (e) 1.0 mm. Figure 5. Experimental cyclic curvature (κc) versus the number of cycles to produce buckling (Nb) on (a) de- cimal and (b) double logarithmic coordinates plot. Since the five straight dotted lines are almost parallel to one another, the value of α can be determined to be 0.69. According to the experimental data, five quantities of C, 5.72, 4.04, 2.47, 1.79 and 1.14, can be determined for a = 0.2, 0.4, 0.6, 0.8 and 1.0 mm, respectively. Figure 6(a) shows the relationship between value of logC and (a/t). Based on these results, the following relationship is proposed: (2) where a1 and a2 are material parameters. The magnitudes of a1 and a2 can be determined to be −1.37 and 0.97, respectively. The fitted and experimental results are shown in Figure 6(b) in dotted and solid lines, respectively, and good agreement between these two results has been achieved.  K.-L. Lee et al. Figure 6. (a) Experimental and simulated relationships between logC and a/t and (b) experimental and simulated cyclic curvature (κc) versus the number of cycles to produce buckling (Nb) on double logarithmic coordinates. 4. Conclusions The response and collapse of the local sharp-notched SUS304 stainless steel tubes with different notch depths subjected to cyclic bending are experimentally and theoretically investigated in this study. Based on the experi- mental and theoretical results, the following important conclusions can be drawn: 1) From the experimental M-κ curves, the local sharp-notched SUS304 stainless steel tubes with any notch depth exhibits cyclical hardening and gradually steady after a few cycles under symmetrical curvature-con- trolled cyclic bending. In addition, the shape and size of the steady M-κ loop are very similar for any notch depth. 2) From the ΔDo/Do-κ curves, the ovalization of the tube’s cross-section increases in a ratcheting manner with the number of cycles. Higher a leads to more severe unsymmetrical trend and greater ovalization of the tube’s cross-section. 3) The formulation (Equation (1)) proposed by Kyriakides and Shaw [1] was used to simulate the relationship between κc and Nb for local sharp-notched SUS304 stainless steel tubes with a = 0.2, 0.4, 0.6, 0.8 and 1.0 mm under cyclic bending. The formulation of the parameter C was proposed in Equation (2). It can be seen that the simulation by Equations (1) and (2) is in good agreement with the experimental result as shown in Figure 6(b). Acknowledgements The work presented was carried out with the support of the National Science Council under grant NSC 101- 2221-E-006-022. Its support is gratefully acknowledged. References [1] K yriakides, S. and Shaw, P.K. (1987) Inelastic Buckling of Tubes under Cyclic Bending. ASME Journal of Pressure Vessel and Technology, 109, 169-178. http://dx.doi.org/ 10.1115/1.3264891 [2] Corona, E. and Kyriakides, S. (1991) An Experimental Investigation of the Degradation and Buckling of Circular Tubes under Cyclic Bending and External Pressure. Thin -Walled Structures, 12, 229-263. http://dx.doi.org/10.1016/0263-8231(91)90048-N [3] V aze, S. and Corona, E. (1998) Degradation and Collapse of Square Tubes under Cyclic Bending. Thin-Walled Struc- tures, 31, 325 -341. http://dx.doi.org/ 10.1016/S0263-8231( 98) 00018 -4 [4] Corona, E., Lee, L.H. and Kyriakides, S. (2006) Yield Anisotropic Effects on Buckling of Circular Tubes under Bend- ing. International Journal of Solids and Structures, 43, 7099-7118. http://dx.doi.org/ 10.1016/j.ijsolstr.2006.03.005 [5] Limam, A., Lee , L.H. and Kyriakides, S. (20 12 ) On the Collapse of Dented Tubes under Combined Bending and In-  K.-L. Lee et al. ternal Pressure. International Journal of Solids and Structur es, 55, 1-12. http://dx.doi.org/10.1016/j.ijmecsci.2011.10.005 [6] Pan, W.F., Wang, T. R. and Hsu, C.M. (1998) A Curvature-Ovalization Measurement Apparatus for Circular Tubes under Cyclic Bending. Experimental Mechanics, 38, 99-102. http://dx.doi.org/ 10.1007/BF02321651 [7] Lee, K.L. , Pan , W.F. and Kuo, J.N. (2001) The Influence of the Diameter-to-Thickness Ratio on the Stability of Circu- lar Tubes under Cyclic Bending. International Journal of Solids and Structures, 38, 2401-2413. http://dx.doi.org/10.1016/S0020-7683(00)00116-5 [8] Lee, K.L., Pan, W.F . and Hsu, C.M. (2004) Experimental and Theoretical Evaluations of the Effect between Diame- ter-to-Thickness Ratio and Curvature-Rate on the Stability of Circular Tubes under Cyclic Bending. JSME Interna- tional Journal, Series A, 47, 212-222. http://dx.doi.org/ 10.1299/jsmea.47.212 [9] Chang, K.H. and Pan, W.F. (2009) Buckling Life Estimation of Circular Tubes under Cyclic Bending. International Journal of Solids and Structures, 46, 254-270. http://dx.doi.org/ 10.1016/j.ijsolstr.2008.08.024 [10] Lee, K. L. , Hung, C.Y. and Pan, W.F. (2010) Variation of Ovalization for Sharp-Notched Circular Tubes under Cyclic Bending. Journal of Mechanics, 26, 403-411. http://dx.doi.org/ 10.1017/ S17 27 71 9100 00 3968 [11] Lee, K.L. (2010) Mechanical Behavior and Buckling Failure of Sharp-Notched Circular Tubes under Cyclic Bending. Structural Engineering and Mechanics, 34, 367-376. http://dx.doi.org/ 10.12989/sem.2010.34.3.367 [12] Lee, K.L. , Hsu, C.M. and Pan, W.F. (2013) Viscoplastic Collapse of Sharp-Notched Circular Tubes under Cyclic Bending. Acta Mechanics Solida Sinica, 26, 629-641. http://dx.doi.org/10.1016/S0894-9166(14)60007-0
|