 Journal of Applied Mathematics and Physics, 2014, 2, 253-263 Published Online May 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.26030 How to cite this paper: Gaponov, S.A. (2014) Linear Instability of the Supersonic Boundary Layer on a Compliant Surface. Journal of Applied Mathematics and Physics, 2, 253-263. http://dx.doi.org/10.4236/jamp.2014.26030 Linear Instability of the Supersonic Boundary Layer on a Compliant Surface S. A. Gaponov Khristianovich Institute of Theoretical and Applied Mechanics SB RAS, Novosibirsk, 630090, Russia Email: gapon ov@itam.n sc.ru Received January 2014 Abstract In the paper the influence of flexible covering properties on the linear development of distu r- bances in a supersonic boundary layer is investigated for Mach numbers M = 1.0, 2.0, 5.3, 6.0. As a model of a covering the porous plate closed by a flexible film is used. In the absence of gas in pores it is established that the flexible covering stabilizes boundary layer in the area of large Reynolds numbers and destabilizes it at small Reynolds numbers. Joint influence of the thickness and ten- sion of a film leads to an appearance of additional unstable waves. For filled with gas pores the researches are conducted as taking into account losses of energy of d istu rban ces in pores and in their absence. Calculations without power losses indicate possibility of existence of an absolute instability of the boundary layer on the flexible surface. The damping properties of a flexible cov- ering connected with power losses in pores reduce their stabilizing role. Keywords Compressible Boundary Layers, Laminar-Turbulent Transition, Hydrodynamic Stability 1. Introduction Interest in the use of compliant walls for laminar flow control dates back to the seminal papers of Kramer [1] [2]. He achieved drag reductions of up to 60% in experimental tests on bodies of revolution covered with his spe- cially designed compliant coatings. Tests were carried out for various compliant coverings, and considerable a drag reduction was received. As a result the assumption was coming out that damping in a covering prevents development of Tollminn-Shlichting waves. Theoretical researches of the stability of incompressible fluid flows were conducted in [3]-[6]. There it was established that in addition to Tollmin-Shlichting disturbances the new waves were revealed which were caused by an interaction of a flow with a surface. Besides they came to con- clusion that only very flexible coverings which density differs little from density of a streamline liquid can be the effective. With this they should have low damping that contradicted to the initial assumption. The first suc- cessful experiments on the stability of boundary layer on a flexible surface were carried out in [7]. It was found that decreasing the tension produced a significant increase of the stability region, increasing the critical Rey- nolds number by about a factor of two. For more information on questions related to the interaction of flexible coatings with the incompressible fluid boundary layer can be found in reviews [8]-[12].  S. A. Gaponov As to possibility of using of flexible coverings for stabilization of a supersonic boundary layer, this question remains open because of the limitation of the corresponding studies. There are two works [13] [14] where the stability of the supersonic boundary layer on a flexible surface was studied. In the first of them the stability of a supersonic boundary layer above a flexible surface is considered in the limit of large Reynolds number and for Mach numbers O(l). Asymptotic theory of viscous—inviscid interaction has been used in it. It was found that for a simple elastic surface the boundary-layer flow remains stable as it is for a rigid wall. However when either damping or surface inertia is included the flow becomes unstable. The lack of these studies was the following. Due to the fact that the problem is considered in the limit of large Rey- nolds number and for Mach numbers O(l), its conclusions may be incorrect for flows with a finite Reynolds number and large Mach numbers. In [14] researches are conducted on the basis of the stability eq uation s of Dunn-Lin (see [15]). There the In- fluence of a flexible covering on the stability of a supersonic boundary layer without its damping properties was studied. Within the framework of the linear theory the supersonic boundary layer stability is considered for the Mach number M = 2; 5.3. It was established that flexible coverings influences on the boundary layer stability even at a gas flow. At moderate supersonic speeds, M = 2.0, application of thin flexible coverings leads to the flow stabilization, at least in the field of large Reynolds numbers. At the same time in the domain of small Rey- nolds numbers the insignificant destabilization can be observed. Influence of flexible coatings on the boundary layer stability at М = 5.3 and М = 2.0 is different because at high Mach numbers there are two unstable modes. At Mach number М = 5.3 the area of low Reynolds numbers, where the destabilization of the first mode is observed, extends in comparison with a case of М = 2.0. However the second mode was stabilized by a flexible covering at Reynolds numbers, when the greatest instability on a rigid surface is observed. In the present paper researches of [14] were continued. Here new data are presented both without damping properties of a flexible covering and with their account for different Mach numbers. Calculations carried out at Mach numbers М = 1.0, 2.0, 5.5, 6.0. 2. Problem Formulation 2.1. Linear Stability Equations The flow of a compressible gas in a boundary layer on a flat plate is taken as an initial undisturbed flow. Distur- bances in a boundary layer we shall consider in orthogonal coordinate system [16] connected with stream-surfaces of basic flow and look like () () , expaiiz it ξ ψαξβω +− (1) Here —flow function; for a plate ; ; —speed and kinematical viscosity of a running stream; x, y, z—longitudinal, normal to a wall and transversal co-ordinates of the Carte- sian system with the beginning on an edge of a plate. Gas is perfect with a constant Prandtl number, Pr. Result- ing a set of Navier-Stokes eq uatio n s to a linear view, using estimations on the whole degrees of a Reynolds number, Re, rejecting the members order Re−2 respect to the main ones, the properties of a critical layer it is possible to obtain the following equations. ()( ) ( ) 2 21111 ln ln, cm vv iuuiwugupu TT ρ αβρρ ∂=− ∂−−∂+∂−−−∂+∂ () () 20112 23 2 23, t pi uiwehudvii µ αβρατβτ ∂++−=−+++ ()() ( ) ( ) 2 1212111113 , t ipuvud uuuii ταρρρ ατβτ ∂=+∂ +∂+∂++∂−− () () 21212 ,ui vu αµµ τµ ∂=−+∂− ∂+ 2231333, t ipdw ii τβ ρατβτ ∂= +−− (2) ( )() ()() ( ) ( ) 22 222111 13 Pr , t qipHiuvHuuhdHu ii ωραµρραβ µρατβτ ∂=+∂−∂+ ∂+++++−+ ( )( )() 22 212 PrPr ,huuhqu µµτ µ ∂ =−∂−∂+−  S. A. Gaponov where: ( ) 11 0 2 3;iu e τ µα = − ( ) 33 0 2 3; iw e τ µβ = − ( ) 02 ln ; c e vu ρ ρρ =−∂− u—velocity; T—temperature; —density; p—pressure; —full enthalpy; μ—viscosity; , —complex amplitudes normal to a surface and transversal components of velocity disturbances; ; ; ; ; ; —specific heat of gas at constant pressure. The view of equations will not change after normalizing with the help of following scales: —length, —time, —viscosity and flow function, —velocity and its disturbances, —temperature, —density, —enthalpy, —pres- sure and disturbances of viscous stresses, —value , —specific heat (the index ∞ corresponds to values in the ram airflow). In this case: , where —relation of heat capacities; M—Mach number. Entering independent variables , and using notations: ( )() 11 1 Reaafa ′ ∂ =∂+ , ( where ); the stroke means a derivative on η, , Eq uatio n (2) are adduced to a view: () ( ) 02 12 , m wc vguTpTvTfuuuiTrfTuTf T ufT ρρ ′′ ′′′′ =−∂+−+∂−−−− ∂−++ ( ) 12 23 2, c hxzrw piruviiu ττµ ′′ =−++ + − ()() 12122 , xc T iTpifuuufurif uuv τρ ′′′ ′′ =+∂+++∂+− ++ 12 , xt r uiv uT µ τµ ′′ =−− + ( ) 23 2 , zcazrw ipiuw iufw τ µµ ′′ =+ − +∂−+ (3) ( ) ( ) 2 21222 Pr , tc ca qiRT pHvfHruiiufHfuuuf hfuuiuh ωρ µ ′′′′′′′ =++−++ ++∂+++−+∂ ( ) 12 Pr Pr, tR huuhTqu µ τµ ′ ′′ =−− +− where ; ; ; ( ) 0 22 3;piu iwe π µαβ =− +− ; ; . Equation (3) have the following structure: (4) Here prime stands for derivative with respect to η, , , , ( ) 12 23 ,,, ,,,,pvuwh q ττ =Z , —quadratic matrixes of given functions of . are ampli- tudes of pressure; normal to a surface of a plate, longitudinal and transversal speeds; enthalpy disturbances. The expressions for can be found in the paper [17]. Reduced above a systems (2,4) are systems of pa- rabolized equatio ns. According to [16] except the full parabolize Equatio n (4) at high Reynolds numbers it is possible to limit by the approximate equations of two types. The first approximation is connecting with a neglect by the perturba- tions amplitude deformation in (4) (∂Z = 0), but taking into account terms which are proportional f1. It was called as the locally nonparallel approach. The second one can be received neglecting by members of D∂Z and f1. Such approach is called by the Lees-Lin parallel approach. At some additional Dunn-Lin assumptions it is possible to receive the truncated system of the equations (see, for example [15] [18]). Dunn-Lin approach was used in [14]). 2.2. Boundary Conditions and Impedance on a Flexible Surf ac e Similar to conditions on a porous surface [19] for disturbances on a flexible coating the boundary conditions are 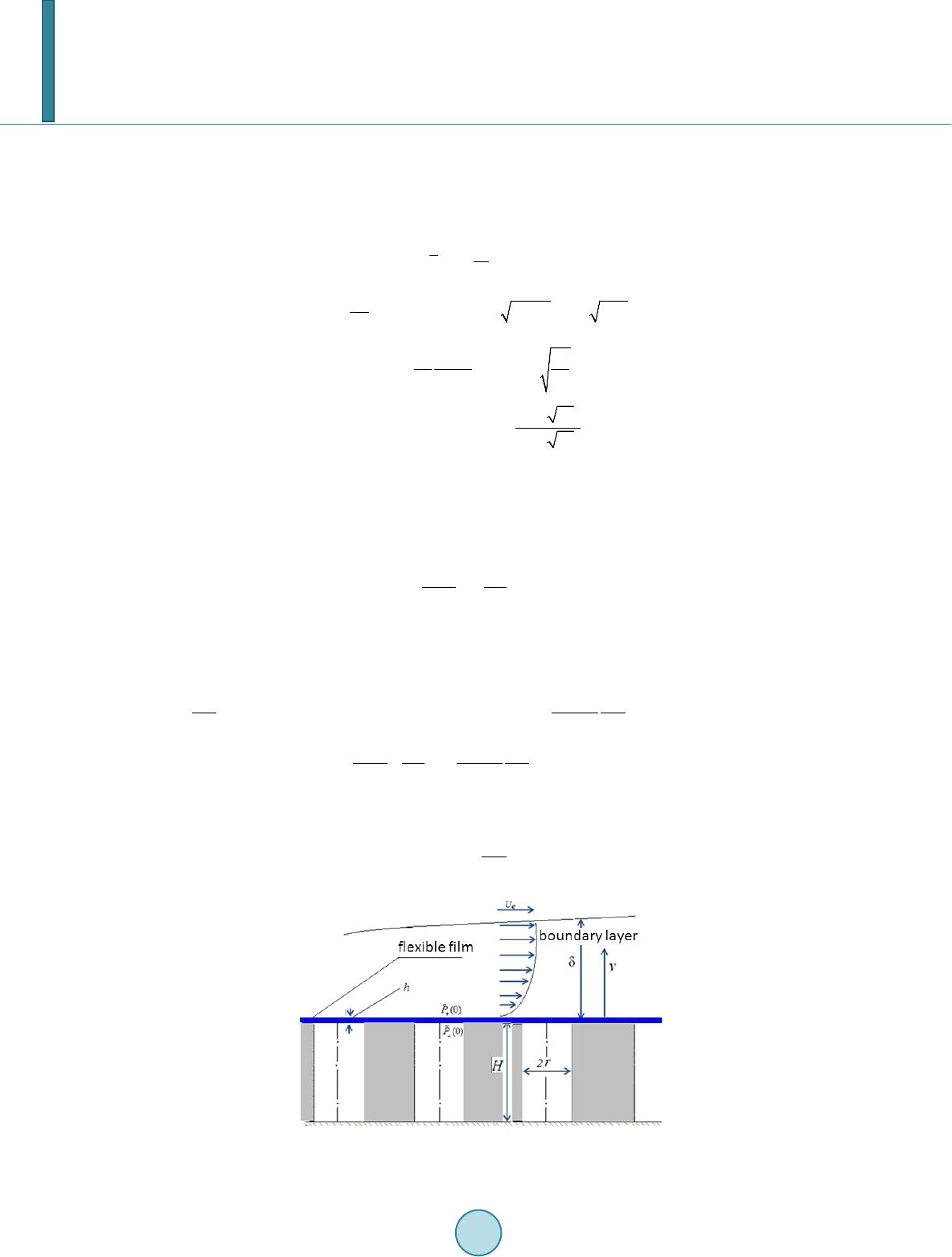 S. A. Gaponov defined as follows: u, v, w, ϑ = 0 at η = ∞; u, w, ϑ = 0, on the wall. For definition of we consider the forced oscillations of the membrane tense on one end of a pipe when the other end is closed by a rigid plug, Figure 1. Damped waves propagate in a round pore. According to [20] average on the area of a pore section a dimensionless velocity and a pressure near a membrane are defined by a ratio: (5) 01 111 0 tanh(Re), ZZ/, Z, H n K YY Z = Λ=Λ= 0 1 2 () , k=Re, () r ww Jk ii ZTJk ωω ν = 20 1 2 (Pr) (1) (Pr) e Jk Y iMJk ω γγ =− +− . Here ρ is gas density; ; J0, J2—Bessel functions of the corresponding or- der; an index w serves for designation of the corresponding quantities in a pore, n—porosity (the ratio of the occupied by the pores area to the total area), γ—the ratio of thermal capacities, dimensional quantities are des- ignated by an asterisk. We write down the movement equation of a membrane in a view: 2 2 ( )exp() c mc dy Nk hyppit dt S ρω ∗ ∗∗∗∗ ∗ −+ ∗∗ =−+−− (6) Here h—a membrane thickness. —density of a membrane material , N is a tension force of unit length [21], yc—a mass center coordinate of a membrane, k—the factor depending on a form of a section contour of a pore, —pressure on the outside of the closed tube, —the pressure on the inside the pore. Because of the correlation (5) can be written in a view: and (6) as follows: 2 2exp( ) cee c mc d ynUdy Nk hyp it K dt Sdt ρ ρω ∗∗∗ ∗ ∗∗ ∗∗ + ∗∗ ∗ +−=− − The common solution of the last equation is defined by the sum of the solution of homogeneous, fading over time, and particular one, which is proportional to . We are looking for a solution in the form and the velocity amplitude . Therefore the dimensionless form of the last Figure 1. Scheme of the flexible coating. 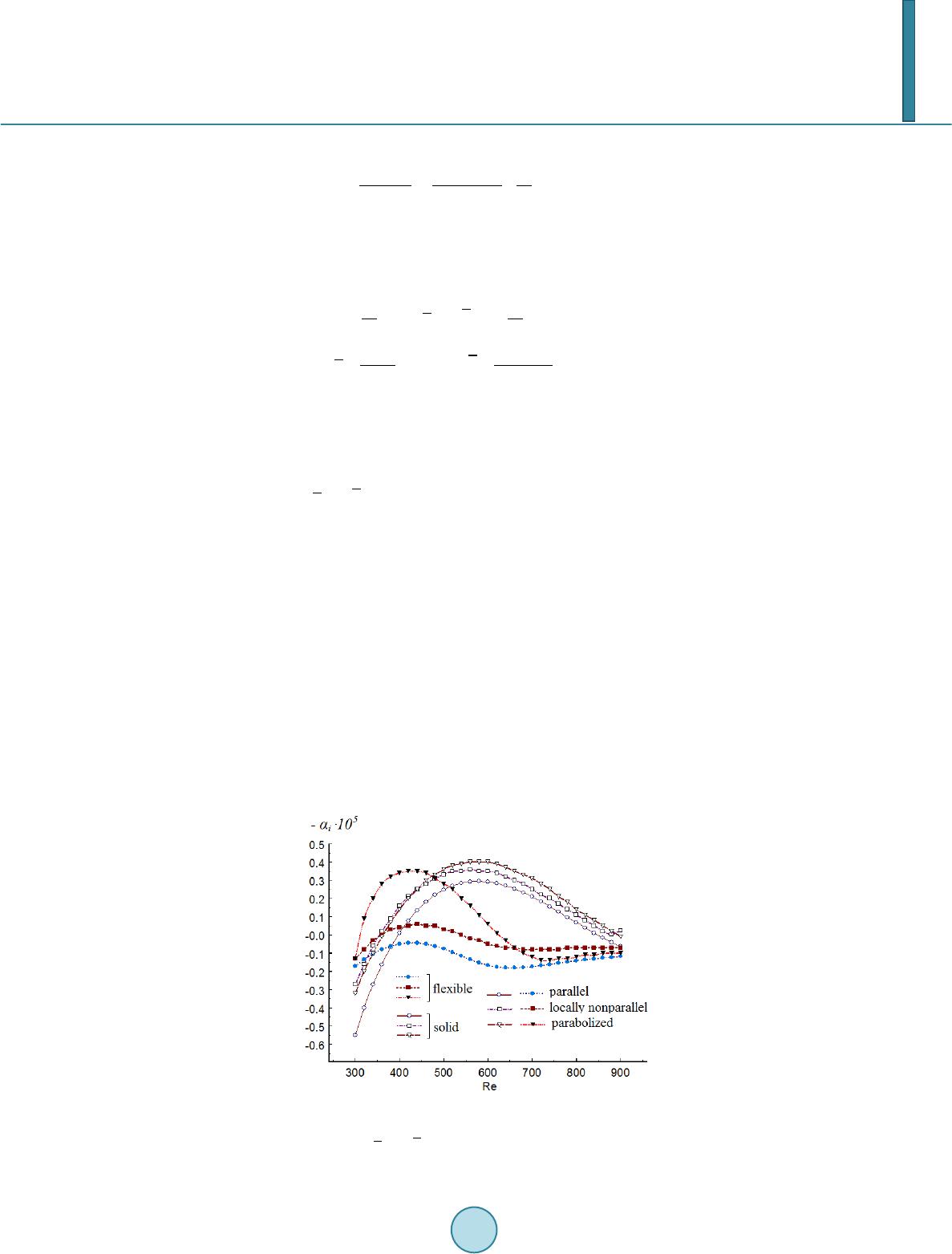 S. A. Gaponov equation has a view: 2 (), /, / m c ee ee cc eee hNk n i ivp K U US v vUppU ωρ ρ ρω ρ ∗∗∗ + ∗∗ ∗∗∗∗ ∗ ∗∗ ++ − +−=− = = Assuming that an average velocity of a gas in a boundary layer near a surface we obtain: 2 (0)(0), (0)(0)/, 1(/ )/ (/), (/). m eee e e ee AvppvpAKp n Aia ibn K K hNk a UbU US ωω ρνν ρρ + ∗∗ ∗∗∗ ∗ ∗∗∗∗ = === = =−−+− = = 3. Results 3.1. A Case of Empty Pores Calculations are carried out for a case of the blank by gas pores (in the vacuum assumption in a pore). In this case c = d = 0 . Dependences of spatial rate amplification on Reynolds’s number for solid and flexible surfaces are calculated for three theories: parallel approach, locally not parallel flow, parabolized stability equations is shown in Fig ure 2. Both on solid and on a flexible surface the greatest stability corresponds to parallel approach. For a flexible surface in the parallel and locally nonparallel approach the amplification rate is negative that indicates to stabi- lizing role of a flexible covering. Though the calculations which have been carried out on the basis of the para- bolized equations indicate on some decrease in efficiency flexible coverings in a suppression of disturbances, as a whole, they confirm a possibility of their application for increase of a Reynolds number of a laminar-turbulent transition. In view of the fact that parallel approach, as a whole, describes stability characteristics not too badly, given below results were received by this method. When it will be a need, for example, for a confirmation of the theory by an experiment, it is possible to specify the received results. In Fig ur e 3 dependence of the amplitude of disturbances of the longitudinal velocity, received in a linear pa- rallel approach, on Reynolds number is presented. It is visible essential suppression of disturbances under the influence of a compliant surface. Thus application of flexible coverings can be used successfully for a tightening of process of the laminar-turbulent transition. Figure 2. Dependence of spatial amplification rates of dis- turbances on Reynolds number (M = 2, ω = 0.5 × 10−4, β = 0.1 × 10−3; for a flexible surface). 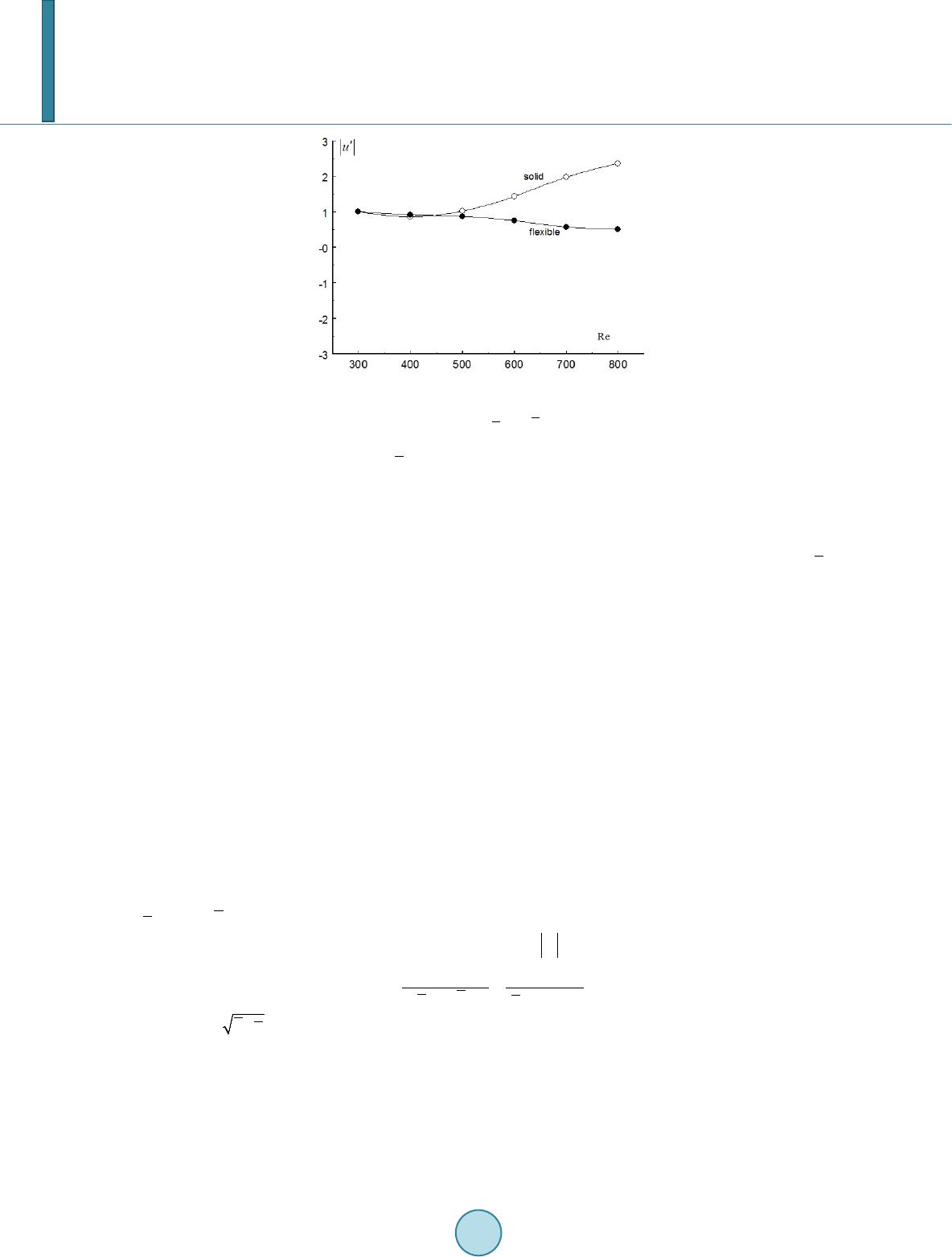 S. A. Gaponov Figure 3. Dependence of a disturbance amplitude of longitudinal velocity on Reynolds’s number (M = 2, ω = 0.5 × 10−4, β = 0.1 × 10−3, ). In Figure 4 influence of parameter on an amplification rate is shown. The boundary layer stabilization is observed in the area of large Reynolds numbers and its destabilization at low Reynolds numbers with decreasing of the film tension. In Figure 5 the dependence of the amplification rate on the Reynolds’s number is shown at difference para- meters of which is proportional to thickness of a film. From these data it is possible to conclude that with a film thickness increase results approach to rigid surface data. Another important result is the following. At there are two amplifying waves. Near Re ≈ 800 the wave (1) disappears. It means that in the region of Re < 800 there are two growing waves and in the area of Re > 800 there is only one unstable wave. Shown in Figure 4 and Figur e 5 results for M = 1.0 are similar to data of the paper [14] for the M = 2.0. Investigation of two amplifying waves was studied in more detail at the Mach number M = 2.0. The results of these studies are shown in F igure 6. In case of a flexible covering along with a wave which is similar the wave at a rigid surface, there are additional disturbances which fade in the area of small Reynolds’s numbers. It is shown in Fig ur e 6(a). However on long distances these waves increase intensively. It should be noted that in the area of large Reynolds’s numbers waves lengths (2π/αr) of two types of disturbances approach. It is visible well in Figure 6(b). Influence of a film thickness and its tension degree on stability of a boundary layer was investigated also at Mach number M = 6.0, 5.35. Influence of a film tension on the amplification rate is shown in F igure 7 (M = 6.0). At high Mach numbers the boundary layer destabilization is observed in the area of low Reynolds numbers as in case of M = 1.0. However at large Reynolds numbers, where instability is defined by the second mode, the flexible covering stabilizes the flo w. Figure 8 shows the effect of a film thickness on the amplification rate of disturbances (M = 6.0). It is possible to see that increasing of the film thickness (its inertia) destabilizes a flow that is consistent with the results of work [13]. However its stability increases in comparison with a case of a rigid surface. Dependence of an amplification rate on frequency parameter is studied also, see Figure 9 (M = 5.3, Re = 103, = 10 3, = 10 −5). Because of the fact that the frequency Eigen disturbances of boundary layer ω = 10−4 is in resonance with a Eigen frequency of a stretched film, approach to infinity when . Really, 22 /() c nn Kiaibia ωωωω − = = −+ − where —frequency of Eigen oscillations of a stretched film. However, it was obtained that values of an amplification rate on the right and on the left of a resonant frequency doesn’t undergo a jump. So it is possible to determine its value by interpolation. 3.2. The Influence of Energy Losses on the Stability of the Boundary Layer on a Porous Surface Coated by a Flexible Film Above it was considered the influence of the flexible cover on the boundary layer stability in the case of empty 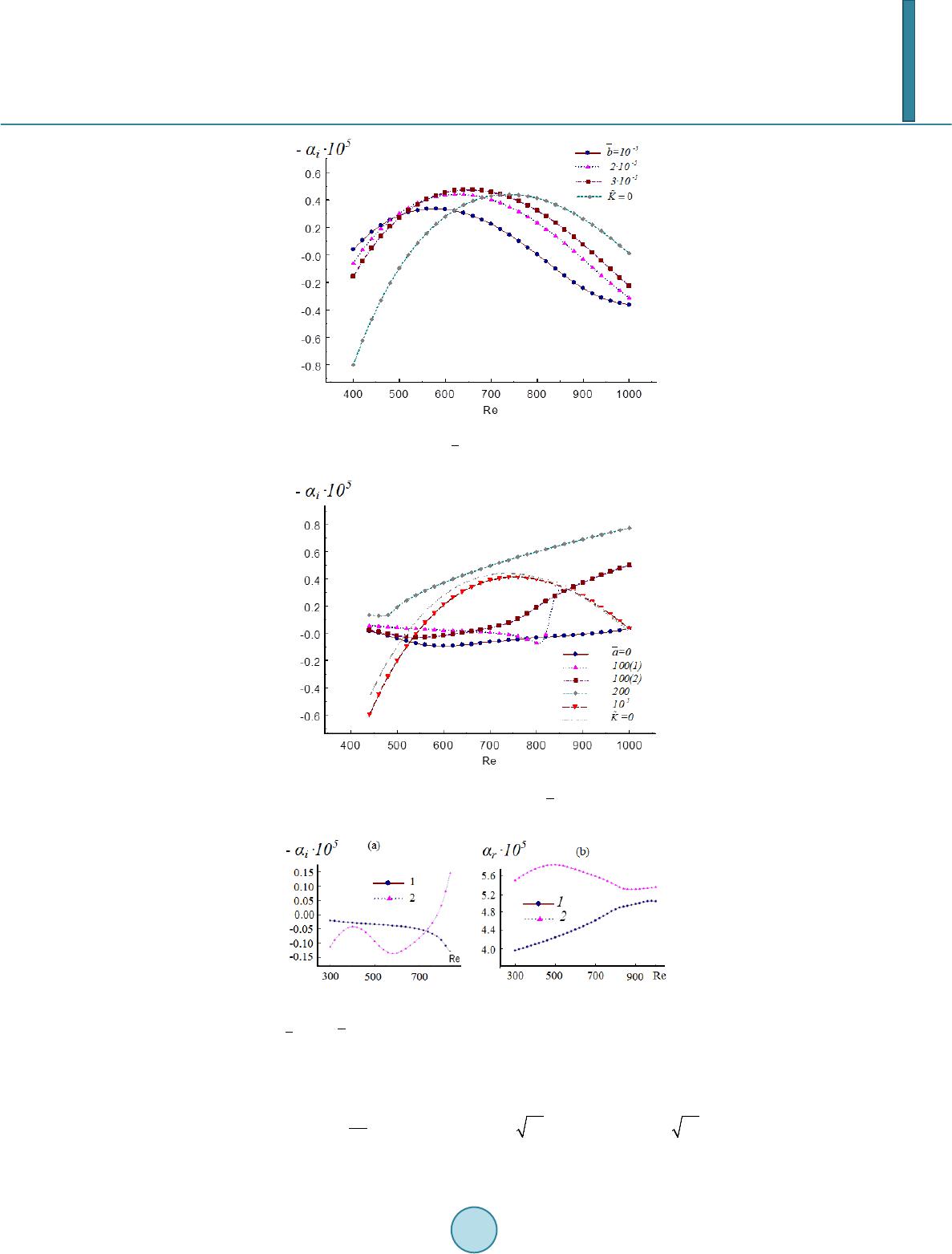 S. A. Gaponov Figure 4. Influence of a film tension on an amplification rate of disturbances (M = 1.0, , ω = 0.5 × 10−4, β = 0 ). Figure 5. Influence of a film thickness on a amplification rate of disturbances. (M = 1.0, ω = 0.5 × 10 −4, β = 0). Figure 6. Amplification rates (a) and wave numbers (b) of two Eigen fluctuations (ω = 0.5 × 10−4, M = 2.0, β = 0.1 × 10−3, ). pores. Before consider its impact on the stability in the case of gas-filled pores it is necessary to study the boun- dary layer stability in the absence of energy losses in the pores. In this case the sound wave propagates inside pores with parameters: Relationship between 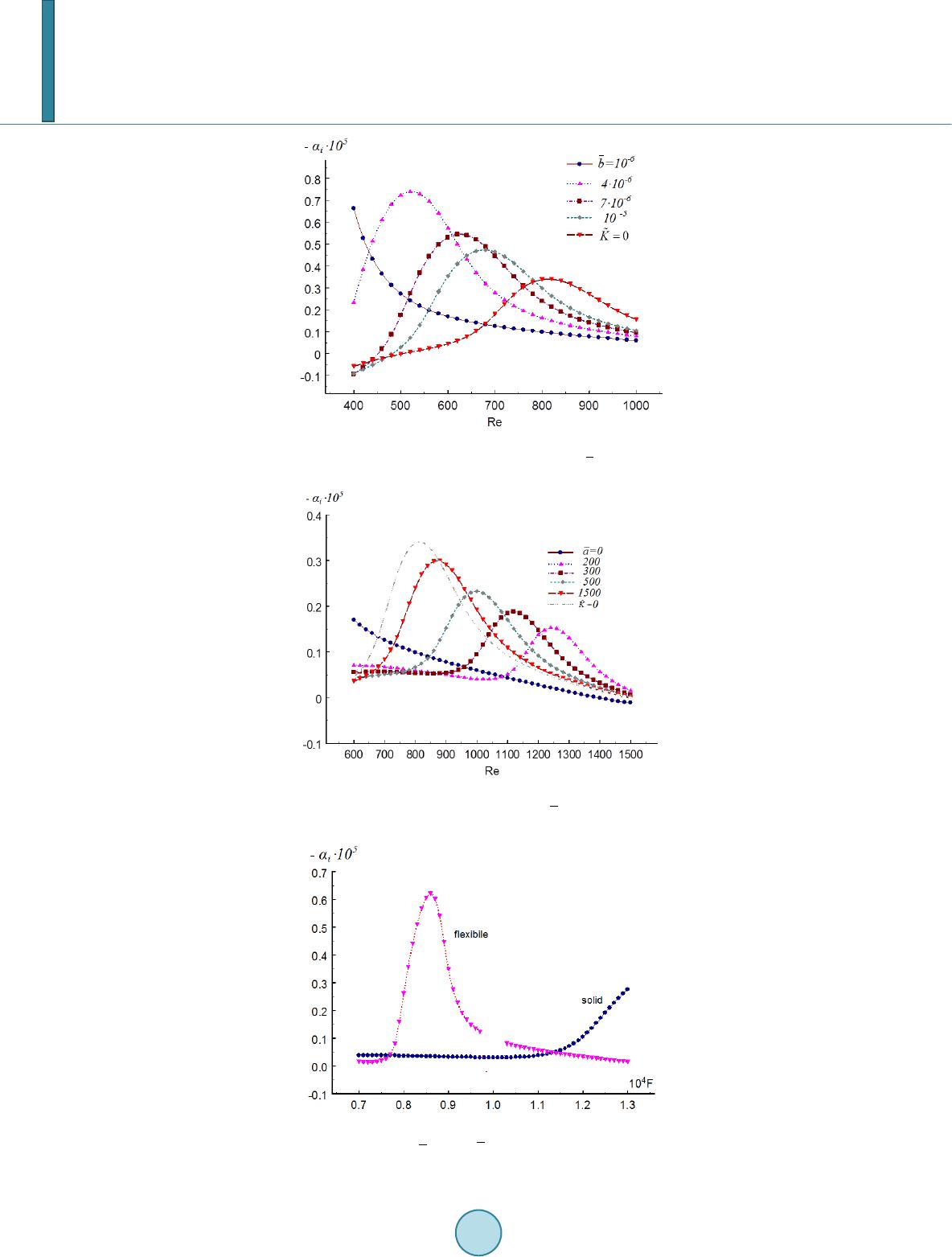 S. A. Gaponov Figure 7. Influence of a film tension on an amplification rate of disturbances (M = 6.0, β = 0, ω = 1.3 × 10−4, = 0). Figure 8. Effect of a film thickness on the amplification rate of disturbances (M = 6.0, ω = 1.3 × 10−4; ). Figure 9. Dependence of amplification rate on frequency at Re = 103, M = 5.3, , .  S. A. Gaponov fluctuating velocity and pressure takes the form: (0)/(/Re )(0) w eewH vnTMtgMTp ω = . Figure 10 shows the dependence of the spatial amplification rates on the thickness of the porous coating. You can see that in the range 0 < ReH < 19,500 the stability increases with the boundary layer thickness. However a furt her increase of ReH leads to the appearance of a new type of oscillations with large amplification rates. For example the amplification rate at ReH = 21,000 is greater than the corresponding value for the solid impermeable surfaces (ReH = 0) about by 10 times. A new type of oscillations requires further study. Calculations show that its group velocities are complex and its absolute value is close to zero. Special studies will help to determine the propagation character of such disturbances. Probably the found instability is absolute, similar instability of a boundary layer of incompressible liquid on a flexible surface [6]. Neglect by energy losses is equivalent to increasing of Rer to infinity. In Figure 11 and Figur e 12 the influ- Figure 10. Dependence of the spatial amplification rates on the thickness of the porous coating. Einfluss der Dämpfung auf die Stabilität der Grenzschicht. Influence of damping on the stability of boundary layer. You must consider the stability of boundary layer in the absence of energy losses in the pores You must consider the stability of boundary layer in the ab- sence of energy losses in the pores You must consider the sta- bility of boundary layer in the absence of energy losses in the pores Positive (M = 2.0, ω = 0.5 × 10−4, β = 10−3, Re = 600). Figure 11. Influence of damping properties of the coating on the boundary layer stability (M = 2.0, ω = 0.5 × 10−4, β = 10−3, , ReH = 104).  S. A. Gaponov Figure 12. Influence of damping properties of the coating on the boundary layer stability (M = 5.3, ω = 1.3 × 10−4, β = 0.0, , ReH = 0.5 × 104). ence of damping properties of the coating on the boundary layer stability is show for Mach numbers M = 2.0 and 5.3. Figure 11 shows that the maximum value of a spatial amplification rate of disturbances in the boundary layer on a flexible surface at M = 2.0 and ReH = 104 in absence of energy losses is less than the corresponding value received on a solid impermeable surface ( ). Energy losses in the pores (Rer = 1000) lead to the destabili- zation of the boundary layer, the maximum value of spatial amplification rate of disturbances increases. Another important fact is that in the absence of energy losses in the pores (Rer = ∞) you can find the value of the coating thickness (in our case ReH = 19500) when the stability at filled pores by a perfect gas is not different from the stability at empty pores. Influence of damping properties of flexible coating on spatial perturbation increments of the second mode with M = 5.3 is shown in Figur e 12. As well as at M = 2.0 at the accounting of power losses (Rer = 1000) in the region of Reynolds numbers Re > 1000 increments are less than in case of their absence (Rer = ∞). Again in the absence of energy losses in the pores (Rer = ∞) you can find the value of the coating thickness (in our case ReH = 5000) when the stability at filled pores by a perfect gas is not different from the stability at empty pores. However unlike a case with M = 2.0 at M=5.3 always increments of disturbances on flexible coverings are less than on a solid impenetrable surface ( ) in this area of Reynolds numbers. In the field of Re Reynolds numbers Re < 1000 influence of flexible covering properties on the boundary layer stability is ambiguous. 4. Conclusions In the case of empty pores, it is established that the supersonic boundary layer stabilization is observed in the area of large Reynolds numbers and its destabilization at low Reynolds numbers with decreasing of the film ten- sion. At finite thicknesses of the film along with a wave a similar to waves at a rigid surface, there is the addi- tional disturbance which fades in the area of small Reynolds numbers. However on long distances this wave in- creases intensively. In the case of gas-filled pores and the absence of energy losses in the pores, there are waves whose group ve- locities are close to zero. Another important fact is that in the absence of energy losses in the pores there are flexible coating thickness when the stability is not different from the stability at empty pores. Energy losses in the pores lead to the destabilization of the boundary layer. At last it is necessary to notice that the impact of flexible coverings on the stability of a supersonic boundary layer have different directions, on the one hand it allows to hope for their successful use for the laminar-turbu- lent transition control and on the other hand it is necessary to apply them carefully. Acknowle dgment s It has been supported by Russian Foundation for Basic Research (grant 12-01-00158а).  S. A. Gaponov References [1] Kramer, M.O. (1957) Bound ary Layer Stabilization by Distributed Damping. Journal of the Aeronautical Sciences, 24, 459-460. [2] Kramer, M.O. (1960) Boundary Layer Stabilization by Distributed Damping. Journal of the American Society for Na- val Engineers, 72 , 25-33. http://dx.doi.org/10.1111/j.1559-3584.1960.tb02356.x [3] Benjamin, T. B. (1960) Effects of a Flexible Boundary on Hydrodynamic Stability. Journal of Fluid Mechanics, 9, 513-532. http://dx.doi.org/10.1017/S0022112060001286 [4] Benjamin, T.B. (19 63 ) The Threefold Classification of Unstable Disturbances in Flexible Surfaces Bounding Inviscid Fl ows. Journal of Fluid Mechanics, 16, 436 -450. http://dx.doi.org/10.1017/S0022112063000884 [5] Landahl, M.T. (1962 ) On the Stability of a Laminar Incompressible Boundary Layer over a Flexible Surface. Journal of Fluid Mechani cs, 13, 609-632. http://dx.doi.org/10.1017/S0022112063000884 [6] Carpenter, P.W. and Garrad, A. D. (1985 ) K ramer-Type Compliant Surfaces. Part 1. Tollmien-Schlichting Instabilities. Journal of Fluid Mechanics, 155, 465-510. http://dx.doi.org/10.1017/S0022112085001902 [7] Babenko , V.V. and Kozlov, L.F. (1973) Experimental Study of Hydrodynamical Stability on Rigid and Elastically Damping Surfaces. Fluid Dynamics, 8, 109-11 4 . [8] Benjamin, T. B. (1964) Fluid Flow with Flexible Boundaries. In: Gortler, H., Ed., Proc. II-th Int. Congr. Appl. Math, Springer-Verlag, Berlin, 109-128. [9] Bushnell, D.M., Hefner, J.N. and Ash, R.L. (1977) Effect of Compliant Wall Motion on Turbulent Boundary Layers. Physics of Fluids, 20, 31-48. http://dx.doi.org/10.1063/1.861756 [10] Riley, J.J., Gad-el-Hak. and Metcalfe, R.W. (1988) Compliant Coatings. Annual Review of Fluid Mechanics, 20, 393- 420. [11] Carpen ter, P.W. (2008) Recent Progress in the Use of Compliant Walls for Laminar Flow Control. Progress in Indus- trial Mathematics at ECMI 2006, Mathematics in Industry, 12, 178-187. http://dx.doi.org/10.1007/978-3-540-719 92 -2_13 [12] Manuilovich, S.V. (2003 ) Propagation of Perturbations in Plane Poiseuille Flow between Walls of Nonuniform Com- plian ce. Fluid Dynamics, 38, 529-544. http://dx.doi.org/10.1023/A:1026317710292 [13] Walker, J.D.A., Fletcher, A. and Ruban, A.I. Instabilities of a Flexible Surface in Supersonic Flow. The Quarterly Journal of Mechanics and Applied Mathematics, 59, 253-27 6. [14] Gaponov, S.A. and Terekhova, N.M. (2012) Influence of a Compliant Surface on a Supersonic Boundary Layer Stabil- ity. In: Arslan, O. and Oprisan, S, Eds., Resent Advances in Mechanical Engineering and Automatic Control. Proceed- ings of the 3rd European Conference of MECHANICAL ENGINEERING (ECME '12), Paris, WSEAS, 87-92. [15] Gaponov, S.A. and Maslo v A.A. (1980) Development of Disturbances in Compressible Flows. Science, Novosibirsk, 144 p. (In Russian). [16] Petrov, G. V. (2000) New Parabolized System of Equations of Stability of a Compressible Boundary Layer. Journal of Applied Mechanics and Technical Physics, 41, 55-61. http://dx.doi.org/10.1007/BF02465237 [17] Gaponov, S.А. and Yudin, A.V. (2002) Interaction of Hydrodynamic External Disturbances with the Boundary Layer. Journal of Applied Mechanics and Technical Physics, 43, 83-89. [18] Gaponov, S.A. and Smorodsky, B.V. (2012) Acoustics and Instability of High -Sp eed Boundary Layers. International Journal of Mechanics, 6, 9-16 [19] Gaponov, S.A. and Smorodsky, B.V. (20 09) Linear Stability of Supersonic Boundary Layer on Porous Surface. Pro- ceedings of the 7th IASME/WSEAS International Conference on Fluid Mechanics and Aerodynamics (FMA'09), Mos- cow, WSEAS, 68-73. [20] Gaponov, S.A. (1977) Stability of Supersonic Boundary Layer on Permeable Surface with Heat Exchange. Fluid Dy- namics, 41-46 [21] Landau, L.D. and Lifshitz, E.M. (1970) Theory of Elasticity. 2nd Engl. Edition, Revised end Enlar ged , Pergamon Press, 165 pp (Vol. 7 of Course of Theoretical Physics).
|