 Journal of Biosciences and Medicines, 2014, 2, 50-56 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jbm http://dx.doi.org/10.4236/jbm.2014.22008 How to cite this paper: Lu, Y.L., et al. (2014) Converging Parallel Plate Flow Chambers for Studies on the Effect of the Spa- tial Gradient of Wall Shear Stress on Endothelial Cells. Journal of Biosciences and Medicines, 2, 50-56. http://dx.doi.org/10.4236/jbm.2014.22008 Converging Parallel Plate Flow Chambers for Studies on the Effect of the Spatial Gradient of Wall Shear Stress on Endothelial Cells Yiling Lu1*, Wei-Qi Li2, Ilias Oraifige1, Wen Wang2 1School of Engineering and Technology, University of Derby, Derby, UK 2School of Engineering and Materials Science, Queen Mary, University of London, London, UK Email: *y.lu@derby.ac.uk Received February 2014 Abstract Many in vitro studies focus on effects of wall shear stress (WSS) and wall shear stress gradient (WSSG) on endothelial cells, which are linked to the initiation and progression of atherosclerosis in the arterial system. Limitation in available flow chambers with a constant WSSG in the testing region makes it difficult to quantify cellular responses to WSSG. The current study proposes and characterizes a type of converging parallel plate flow chamber (PPFC) featuring a constant gra- dient of WSS. A simple formula was derived for the curvature of side walls, which relates WSSG to flow rate (Q), height of the PPFC (h), length of the convergent section (L), its widths at the entrance (w0) and exit (w1). CFD simulation of flow in the chamber is carried out. Constant WSSG is ob- served in most regions of the top and bottom plates except those in close proximity of side walls. A change in Q or h induces equally proportional changes in WSS and WSSG whereas an alteration in the ratio between w0 and w1 results in a more significant change in WSSG than that in WSS. The current design makes possible an easy quantification of WSSG on endothelial cells in the flow chamber. Keywords Parallel Plate Flow Chamber; Wall Shear Stress; Wall Shear Stress Gradient; Atherosclerosis; Endothelial Cell 1. Introduction Atherosclerosis occurs preferentially in curved and bifurcation regions of arterial tree. Its initiation and progres- sion are at least in part attributed to the blood flow induced wall shear stress [1] [2]. Endothelial cells (ECs) lin- ing the luminal surface of the entire circulatory system directly experience blood flow-induced WSS. Prompted by the low wall shear stress theory [1] and aided with the computational fluid dynamics, different WSS meas- ures, such as the spatial gradient of WSS [3], temporal gradient of WSS [4] and oscillatory shear index [5], have * 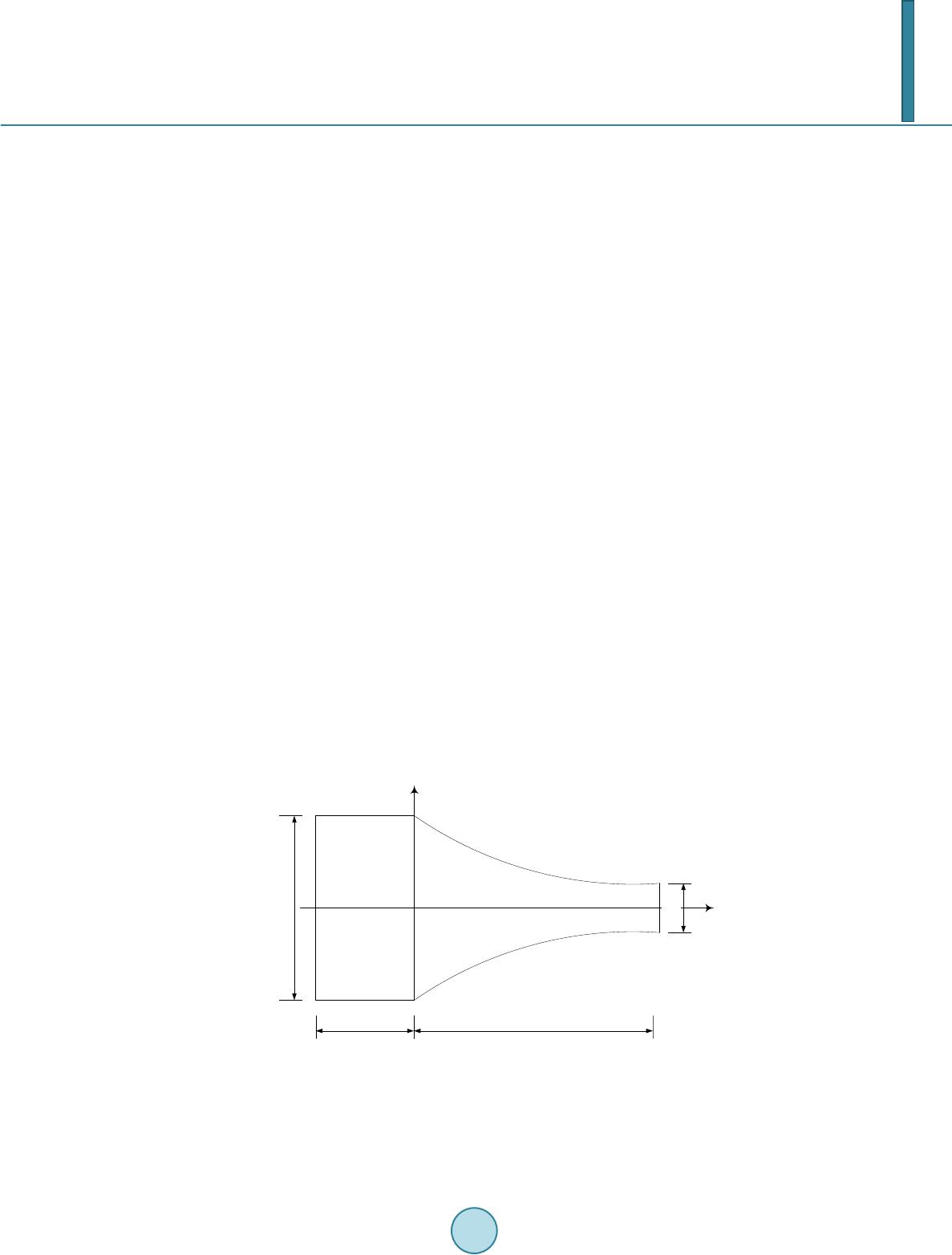 Y. L. Lu et al. been proposed as indicators leading to atherosclerosis. Among them, the spatial gradient of WSS has attracted much interest [6] [7] and has recently been incorporated in a newly-proposed indicator for cerebral aneurysm formation [8]. ECs elongate by reorganizing cytoskeletons along the flow direction, and simultaneously modify intracellular signalling, gene and protein expression and cell functions [9] [10]. These findings are largely made by in vitro studies which feature well controlled biomechanical and biochemical environment for ECs. Different flow systems have been proposed, e.g. cone and plate systems [11], radial-flow chambers [12], and parallel plate flow chambers (PPFCs) [13] [14]. PPFCs are most widely used due to their simplicity and ease of operation [15]. Traditionally a rectangular PPFC is used to generate a uniform WSS on the bottom/top plates. It has later been adapted to investigate effects of WSSG. “Backstep” PPFC uses an additional stair to purposely induce flow separation and make WSS distri- bution non-uniform downstream the step. Differential responses of ECs before and after the reattachment point have been revealed [16 ] [17]. To focus on the effect of WSSG, it is desirable to design a flow chamber that fea- tures a constant WSSG for cells cultured in the testing region. Converging PPFCs with a varying channel width are capable of such specification. Qin et al. [18] tilted the straight side walls of a PPFC to form a converging channel. The simple system was easy to manufacture but did not generate a uniform WSSG. Another converging PPFC with curved side walls was used to investigate the combined effect of WSS and WSSG by LaMack & Friedman [7]. The authors used CFD to pre-determine WSS and WSSG at selected locations in the chamber. No attempt was made to achieve a uniform WSSG in the chamber, nor an explicit formula for the side wall given in that study. Usami et al. [19] proposed a diverging flow chamber with a linear change in WSS. The shape of side walls was derived based on Hele-Shaw flow in the PPFC. They used the streamline function from a 2D stagnant flow to delineate the side wall. This chamber was initially designed as a single flow system to compare effects of different WSS magnitudes, and recently used to study cell adhesion under different WSS [20]. Flow chamber of constant WSSG was also created by varying the chamber height while keep the uniform width, which has been used to investigate the WSSG on endothelial proliferation, survival and alignment [21]. The current study investigates a converging PPFC that produces a constant WSSG. We derive the exact shape of side walls using a similarity approach based on the plane-Poiseuille solution. WSS and WSSG on top/bottom plates are given. CFD simulation of flow in the converging chamber is performed to validate the predicted WSS and WSSG. 2. Flow Chamber Design In the converging PPFC, the width (w) decreases in the flow direction. The height of the chamber (h) is constant and is much less than its length (L) and w. In the coordinates, shown in Figure 1, the x-axis coincides with the Figure 1. Schematic drawing of the converging parallel plate flow chamber. The length of the converging section is L. The width of the chamber, w, de- creases from w0 at the entrance to w1 at the exit. A leading section of the length Le and constant width w0 is added at the entrance for inflow to become fully developed. The height of the chamber between the top and the bottom plates, h, is constant (not shown in the figure).  Y. L. Lu et al. longitudinal direction and the origin locates at the middle point of the beginning section of the converging chamber. The exact solution for steady Newtonian fluid in a duct is available [21], but is too complicated to use in the design of converging PPFC. Since h << w and L, flow can be approximated by the plane-Poiseuille solu- tion, , (1) where umax is the peak velocity at the mid-height plane and is a function of x and y. Since flow is predominantly in the x direction, velocity and WSS are referred to as their x components only for convenience, unless otherwise stated. . (2) A similarity approach, most appropriate for a duct of slow varying cross-section is adopted [22]. The same velocity profile as in (1) is assumed for all cross-sections of the converging chamber. The velocity magnitude, however, changes with local cross-sectional area for a given Q. After neglecting effects of the side wall, flow rate per unit width 2 /2 max max 2 /2 42 13 h h Qz udz hu wh − = −= ∫ . (3) Using the above Equation in (2), . (4) For a converging flow chamber, w is a function x and takes the following expression to achieve a constant WSSG, , (5) where a and b are constants. When the widths of the chamber at the entrance (x = 0) and exit (x = L) of the con- verging section are w0 and w1 respectively, and . (6) The formula (or position) of the side wall takes the half width of the chamber, 0 10 ( )0.5 21 11 wx yx w wwL == +− . (7) The corresponding WSS 20 10 6 111 w Qx w wwL h τµ = +− , (8) and WSSG, . (9) Effect of side walls is neglected in aforementioned derivation. To verify the above formulations, CFD soft- 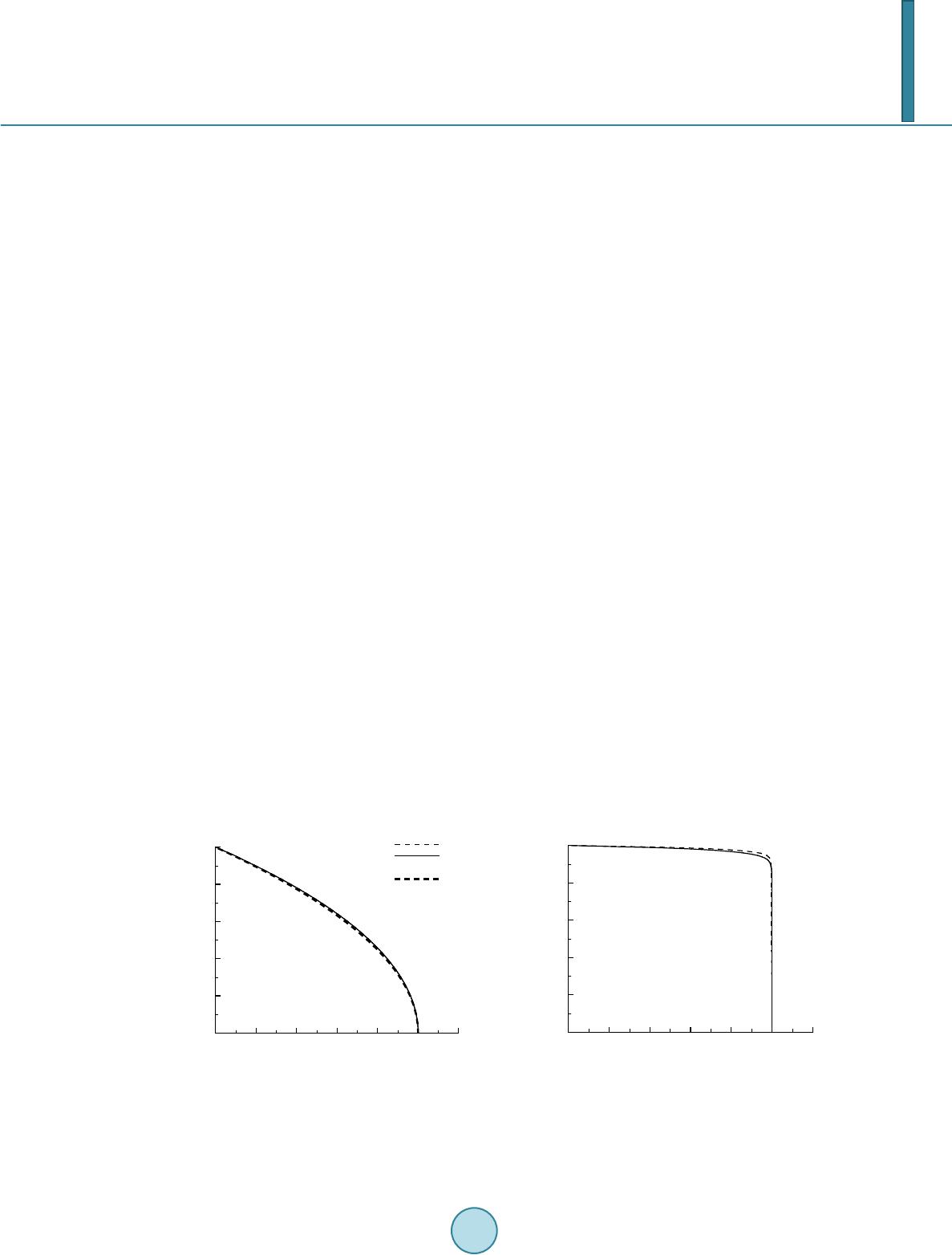 Y. L. Lu et al. ware Fluent (Ansys, Inc. PA, USA) is used to simulate flow and calculate WSS distribution in the converging chamber. In the practical design, a leading section with length Le is added to minimize the entrance effect. A fully developed flow is assumed at the entrance and a pressure outlet boundary condition prescribed at the exit. Exploiting symmetries in the flow chamber, only a quarter of the chamber is taken for computational domain. Standard validation and mesh independence test are completed. In following results: L = 30 mm, Le = 5 mm, w0 = 10 mm, w1 = 4 mm and h = 0.2 mm. At Q = 1.0 ml/s and µ = 1.02 × 10−3 Pa·s, WSSG is approximately 0.752 Pa/mm according to Equation (9). 3. Flow Chamber Characterization When the width decreases, overall flow velocity is expected to increase in the converging PPFC. For the con- venience of comparison, velocity profile in a cross section is normalized by its respective peak value. On the mid-width plane, i.e. y = 0, normalised velocity profiles in the z direction at x = 5, 15 & 25 mm collapse onto the theoretical parabola in Figure 2. This confirms the validity of adopting the plane-Poiseuille solution and the si- milarity approach in the derivation. Velocity profiles cross the width on the mid-height plane z = 0 (shown in Figure 2(b)) deviates markedly from the parabolic shape. A steep velocity gradient forms near the side wall while the central region exhibits an almost constant velocity. Nevertheless this significant velocity gradient is limited to less than 10% of the width of the converging chamber. From numerical simulation, a parabolic veloc- ity profile can be envisaged between the top and bottom plates with a good uniformity of velocity spanning most region of the rectangular cross section. Accordingly WSS on the bottom/top plate shows a uniform distribution across the width (except in close proximity of the side wall) and an increasing magnitude along the x direction (see Figure 3(a)). Narrowing in the width of the chamber induces an increase in the velocity and hence an elevated WSS. Longitudinal profiles of WSS at different widths of the chamber are extracted in Figure 3(b). At the centreline, y = 0.0, WSS increases in perfect linearity from the entrance to the exit. A constant WSSG of 0.756 Pa/mm is confirmed, which is close to the nominal value of 0.752 Pa/mm estimated from Equation (9). The linearity remains at off-centre locations (i.e. y = 0.5, 1.0, 1.5 mm) and more importantly, all curves have nearly identical slopes in most regions of the chamber. Close to the side wall, WSS decreases sharply, i.e. WSSG is no longer constant near the exit at y = 1.9 mm. A converging flow chamber needs to be adjustable in order to meet different requirements for WSS gradient in experiments. The flow rate (Q) has a direct effect on the flow field. Figure 4(a) shows the change of WSS along the centre line. At x = L/2, WSS increases from 13.589 Pa at Q = 0.5 ml/s to 27.533 and 56.483 Pa at Q = 1.0 and 2.0 ml/s. This quasi-proportional increase is consistent with prediction in (8). Similar change in WSSG is also seen: the highest WSSG (1.567 Pa/mm) at Q = 2.0 ml/s, is reduced to nearly 1/4th the value (0.371 Pa/mm) at Q = 0.5 ml/s. Adjustment of h induces a significant change in WSS and WSSG in the converging chamber. When h increases from 0.1 to 0.2 mm, WSS and WSSG are both decreased by approximately four (a) (b) Figure 2. Velocity profiles at selected cross sections in the converging flow chamber. (a). Normalized profiles on the mid-width plane, i.e. y = 0, together with the analytical solution; (b). Normalized velocity distribution on the mid-height plane, i.e. z = 0. In the figure, L = 30 mm, w0 = 10 mm, w1 = 4 mm, h = 0.2 mm and Q = 1 ml/s. u/u max z/h 0 0.2 0.4 0.6 0.8 1 1.2 0 0.1 0.2 0.3 0.4 0.5 x=5 mm x =15 mm x =25 mm analytical u/umax y/w 00.2 0.4 0.6 0.811.2 0 0.1 0.2 0.3 0.4 0.5 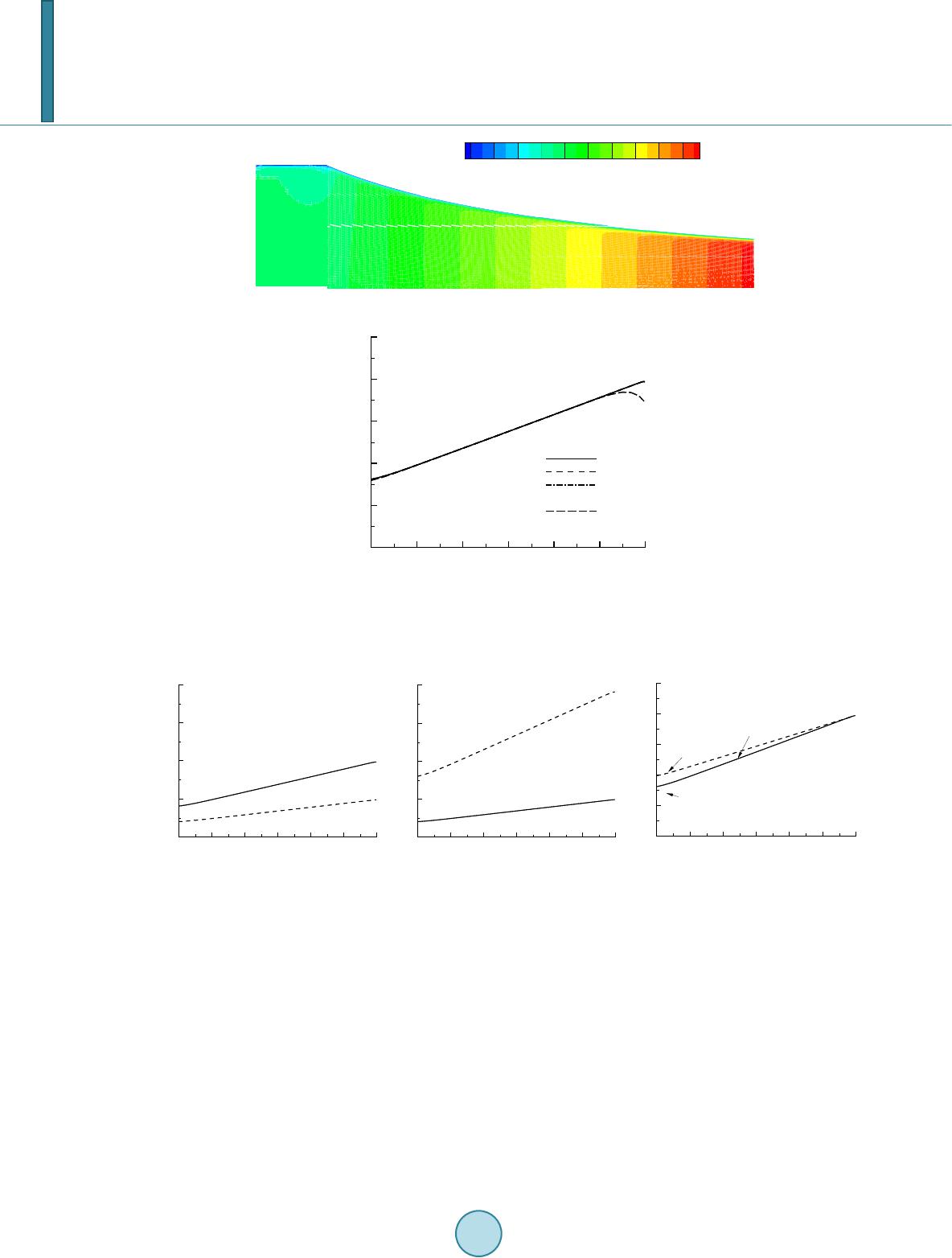 Y. L. Lu et al. (a) (b) Figure 3. Wall shear stress distribution in the converging flow chamber. (a) WSS contours on the bottom/top plate; (b) Longitudinal profiles of WSS on the bottom/top plate. In the figure, L = 30 mm, w0 = 10 mm, w1 = 4 mm, h = 0.2 mm and Q = 1 ml/s. (a) (b) (c) Figure 4. Effects of parameters on WSS and WSSG in the converging flow chamber. WSS distribution is plotted along the central line on the bottom/ top plate. Control parameters are L = 30 mm, w0 = 10 mm, w1 = 4 mm, h = 0.2 mm and Q = 1 ml/s. (a). Effect of Q; (b) Effect of h; (c) Effect of w0. times, as predicted by the inverse-square relation in (8) and (9). However, as h increases further to 0.4 mm, the average WSSG decreases to 0.214 Pa/mm, which is 12% lower than the prediction from equation (9). The con- vergence of the flow chamber is controlled by the ratio between the entrance and exit widths, w0/w1, and the length of the converging section L. Here, we present results with given w1 and L, but different w0 values. WSS changes moderately with the variation of w0. At x = L/2, WSS in the centreline decreases from 29.391 to 26.264 Pa (i.e. by 10.6%) as w0 is expanded from 8 mm to 12 mm (i.e. an increase of 50%). A more significant change is observed in WSSG. It is 0.631 Pa/mm at w0 = 8 mm but is augmented to 0.835 Pa/mm at w0 = 12 mm. This change accounts for a 32.3% increase in WSSG. Change in the width of the flow chamber is, therefore, an effec- tive way to modify WSSG without altering WSS significantly. Needless to say, that when the entrance width is fixed, adjustment of the exit width has opposite effects on WSSG as to above. 159 13 17 21 2529 33 37 τ w Pa x (mm) τ w (Pa) 0510 15 20 25 30 0 10 20 30 40 50 y= 0.0mm y =0.5 mm y =1.0 mm y =1.5 mm y =1.9 mm x (mm) τw(Pa) 0510 15 20 25 30 0 20 40 60 80 Q =2ml/s Q =0.5 ml/s Q =1ml/s x (mm) τw(Pa) 0510 15 20 2530 0 40 80 120 160 h = 0.1mm h = 0.4mm h = 0.2mm x (mm) τ w (Pa) 0510 15 20 25 30 0 10 20 30 40 50 w 0 = 8 mm w 0 = 12 mm w 0 = 10 mm  Y. L. Lu et al. 4. Discussion In this study, a converging PPFC is proposed that provides a controlled flow environment with a constant WSSG. An explicit formula for the curved side walls is given, together with expressions for resultant WSS and WSSG in the flow chamber. CFD simulation confirms that most regions in the converging chamber, except those in close proximity of side walls, experience a constant WSSG. Flow in the chamber is predominately in the longitudinal direction. However, cross-flow exists close to side walls. This is accentuated by the narrowing of the flow chamber and has important implications to experimentalists when they consider the testing region for in vitro studies. Compared to “backstep” flow chambers [16] [17], our converging chamber generates a monotonically varying WSS from the entrance to the exit. Unlike the simple converging chamber with straight-side-walls by Qin et al. [18], WSS variation in the present design is linear with the distance in the flow direction. The present PPFC is converging thus yields an increasing WSS from the entrance to the exit, which is contrary to the divergent flow chamber proposed by Usami et al. [19]. Both can easily be converted by swapping the entrance end with the exit end. The curved side wall based on our formula is a truncation of streamline at the distance L/(w0/w1 − 1) fol- lowing the coordinates in Usami et al.’s design. But the formulating process we pursued here starts with the ba- sic plane-Poiseuille solution and is much easier to follow. WSSG in the converging chamber can be altered with or without significant change in WSS. Q and h can be adjusted to achieve desired magnitude of WSSG, but they also induce similar degree of changes in WSS. On the other hand, the ratio between the entrance and exit widths of the converging chamber provides a means to alter WSSG without significant change in the magnitude of WSS. This provides versatility in controlling the range of WSS and WSSG in the flow chamber, and enables systematic studies on their individual and combined effects on endothelial cells [7]. CFD characterization confirms the validity of similarity approach to derive the side wall shape. It also reveals a varying extent of underestimation of actual WSS and WSSG by analytical solutions (8) and (9), which should not be overlooked by experimentalist when to use this converging flow chamber. It needs to be noted that the similarity approach applied in the derivation usually holds for slowly varying ducts. Under conditions used in the present study, a close likeness in velocity profiles is observed, confirming its validity. When the ratio between the entrance and exit widths increases significantly, similarity assumption be- comes less satisfied and the size of effective testing region with a constant WSSG in the flow chamber is re- duced. Nevertheless, the proposed converging flow chamber enables an easy and direct quantification of WSS and WSSG on cells cultured in the chamber. Acknowledgements W.Q.L thanks the Chinese Scholar Council and Queen Mary, University of London for supporting his PhD study. References [1] DeBakey, M.E., Lawrie, G.M. and Glaeser, D.H. (1985) Patterns of Atherosclerosis and Their Surgical Significance. Annals of Surgery, 201, 115-131. http://dx.doi.org/10.1097/00000658-198502000-00001 [2] Caro, C.G., Fitz-Gerald, J.M. and Schroter, R.C. (1971) Atheroma and Arterial Wall Shear Observation, Correlation and Proposal of a Shear Dependent Mass Transfer Mechanism for Atherogenesis. Proceedings of the Royal Society B: Biological Sciences, 177, 109-159. http://dx.doi.org/10.1098/rspb.1971.0019 [3] Lei, M., Kleinstreuer, C. and Truskey, G.A. (1995) Numerical Investigation and Prediction of Atherogenic Sites in Branching Arteries. ASME Journal of Biomechanical Engineering, 117, 350-357. http://dx.doi.org/10.1115/1.2794191 [4] Ojha, M. (1994) Wall Shear Stress Temporal Gradient and Anastomotic Intimal Hyperplasia. Circulation Research, 74, 1227-1231. http://dx.doi.org/10.1161/01.RES.74.6.1227 [5] He, X. and Ku, D.N. (1996) Pulsatile Flow in the Human Left Coronary Artery Bifurcation: Average Conditions. ASME Journal of Biomechanical Engineering, 118 , 74-82. http://dx.doi.org/10.1115/1.2795948 [6] Buchanan, J.R., Kleistreuer, C., Truskey, G.A. and Lei, M. (1999) Relation between Non-Uniform Hemodynamics and Sites of Altered Permeability and Lesion Growth at the Rabbit Aorta-Celiac Junction. Atherosclerosis, 143, 27-40. http://dx.doi.org/10.1016/S0021-9150(98)00264-0 [7] LaMack, J.A. and Friedman, M.H. (2007) Individual and Combined Effects of Shear Stress Magnitude and Spatial Gradient on Endothelial Cell Gene Expression. American Journal of Physiology—Heart and Circulatory Physiology,  Y. L. Lu et al. 293, H2853-H2859. http://dx.doi.org/10.1152/ajpheart.00244.2007 [8] Shimogonya, Y., Ishikawa, T., Imai, Y., Matsuki, N. and Yamaguchi, T. (2009) Can Temporal Fluctuation in Spatial Wall Shear Stress Gradient Initiate a Cerebral Aneurysm? A Proposed Novel Hemodynamic Index, the Gradient Os- cillatory Number (GON). Journal of Biomechanics, 42, 550-554. http://dx.doi.org/10.1016/j.jbiomech.2008.10.006 [9] Davies, P.F. (1995) Flow Mediated Endothelial Mechanotransduction. Physiological Reviews, 75, 519-560. [10] Chien, S. (2008) Effects of Disturbed Flow on Endothelial Cells. Annals of Biomedical Engineering, 36, 554-562. http://dx.doi.org/10.1007/s10439-007-9426-3 [11] Dewey, C.F. (1994) Effects of Fluid Flow on Living Vascular Cells. ASME Journal of Biomechanical Engineering, 106, 31-35. http://dx.doi.org/10.1115/1.3138453 [12] Goldstein, A.S. and DiMilla, P.A. (1998) Comparison of Converging and Diverging Radial Flow for Measuring Cell Adhesion. AIChE Journal, 44, 465-473. http://dx.doi.org/10.1002/aic.690440222 [13] Frangos, J.A., Eskin S.G., McIntire, L.V. and Ives, C.L. (1985) Flow Effects on Prostacyclin Production by Cultured Human Endothelial Cells. Scienc e, 227, 1477-1479. http://dx.doi.org/10.1126/science.3883488 [14] Zeng, L., Xiao, Q., Margariti, A., Zhang, Z., Zampetaki, A., Patel, S., Capogrossi, M. C., Hu, Y. and Xu, Q. (2006) HDAC3 is Crucial in Shear- and VEGF-Induced Stem Cell Differentiation toward Endothelial Cells. Journal of Cell Biology, 174, 1059-1069. http://dx.doi.org/10.1083/jcb.200605113 [15] Brown, T.D. (2000) Techniques for Mechanical Stimulation of Cells in vitro: a Review. Journal of Biomechanics, 33, 3-14. http://dx.doi.org/10.1016/S0021-9290(99)00177-3 [16] DePaola, N., Gimbrone, M.A., Davies, P.F. and Dewey, C.F. (1993) Vascular Endothelium Responds to Fluid Shear Stress Gradients. Arteriosclerosis, Thrombosis, and Vascular Biology, 12, 1254-1257. http://dx.doi.org/10.1161/01.ATV.12.11.1254 [17] Watkins, N.V., Caro, C.G. and Wang, W. (2002) Parallel-Plate Flow Chamber for Studies of 3D Flow-Endothelium Interaction. Biorheology, 39, 337-342. [18] Qin, K., Jiang, W., Li, X. and Liu, Z. (1998) On Analysis of the Steady Flow in an Irrectangular Paral-lel-Plate Flow Chamber. Applied Mathematics and Mechanics, 19, 851-859. http://dx.doi.org/10.1007/BF02458240 [19] Usami, S., Chen, H.H., Zhao, Y., Chien, S. and Skalak, R. (1993) Design and Construction of a Linear Shear Stress Flow Chamber. Annals of Biomedical Engineering, 21, 77-83. http://dx.doi.org/10.1007/BF02368167 [20] Tsou, J.K., Gower, R.M., Ting, H.J., Schaff, U.Y., Insan, M.F., Passerini, A.G. and Simon, S.I. (2008) Spatial Regula- tion of Inflammation by Human Aortic Endothelial Cells in a Linear Gradient of Shear Stress. Microcirculation, 15, 311-323. http://dx.doi.org/10.1080/10739680701724359 [21] Dolan, J.M., Meng, H., Singh, S., Paluch, R. and Kolega, J. (2011) High Fluid Shear Stress and Spatial Shear Stress Gradients Affect Endothelial Proliferation, Survival, and Alignment. Annals of Biomedical Engineering, 39, 1620-1631. http://dx.doi.org/10.1007/s10439-011-0267-8
|