 Journal of Applied Mathematics and Physics, 2014, 2, 225-234 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.25028 How to cite this paper: Aridi, M.R., et al. (2014) Mode Stresses for the Interaction between Straight and Curved Cracks Problem in Plane Elasticity. Journal of Applied Mathematics and Physics, 2, 225-234. http://dx.doi.org/10.4236/jamp.2014.25028 Mode Stresses for the Interaction between Straight and Curved Cracks Problem in Plane Elasticity M. R. Aridi1, N. M. A. Nik Long1,2, Z. K. Eshkuvatov1, 2 1Institute for Mathematical Research, Universiti Putra Malaysia, Serdang, Selangor, Malaysia 2Department of Mathematics, Universiti Putra Malaysia, Serdang, Selangor, Malaysia Email: radz7cr@gmail.com, n masr i@u pm.ed u. my, ezaini@upm.edu.my Received January 2014 Abstract In this paper, the complex variable function method is used to obtain the hypersingular integral equations for the interaction between straight and curved cracks problem in plane elasticity. The curved length coordinate method and suitable quadrature rule are used to solve the integrals for the unknown function, which are later used to evaluate the stress intensity factor, SIF. Three types of stress modes are presented for the numerical results. Keywords Hypersingular Integral Equation, Complex Variable Function Method, Stress Intensity Factor 1. Introduction In order to predict the safety and stability of components, many researchers paid attention to the crack geometry. Several types of integral equations have been developed to formulate the single crack problem such as singular integral equation [1], Fredholm integral equation [2], hypersingular integral equation [3] and interaction integral equation [4]. Formulation for the multiple cracks problem are also obtained in terms of singular integral equa- tion [5], Fredholm integral equation [6] and hypersingular integral equation [7] for various set of cracks posi- tions. These integral equations can be solved numerically using the polynomial approximation of the dislocation distribution. This approach was achieved by taken the crack opening displacement (COD) as the unknown and the resultant forces as the right term in the equations [8]. In this paper, the formulation for the interaction between straight and curved cracks in term of hypersingular integral equations is obtained using the complex potential method. Then, the cracks are mapped into a straight line using the curved length coordinate method. In order to solve the equations numerically, the quadrature rules are applied with M + 1 collocation points. The obtained unknown coefficients will later be used in calculating the SIF. In this paper, we consider three types of loading modes: Mode I, Mode II and Mode III for the numeri- cal computations. 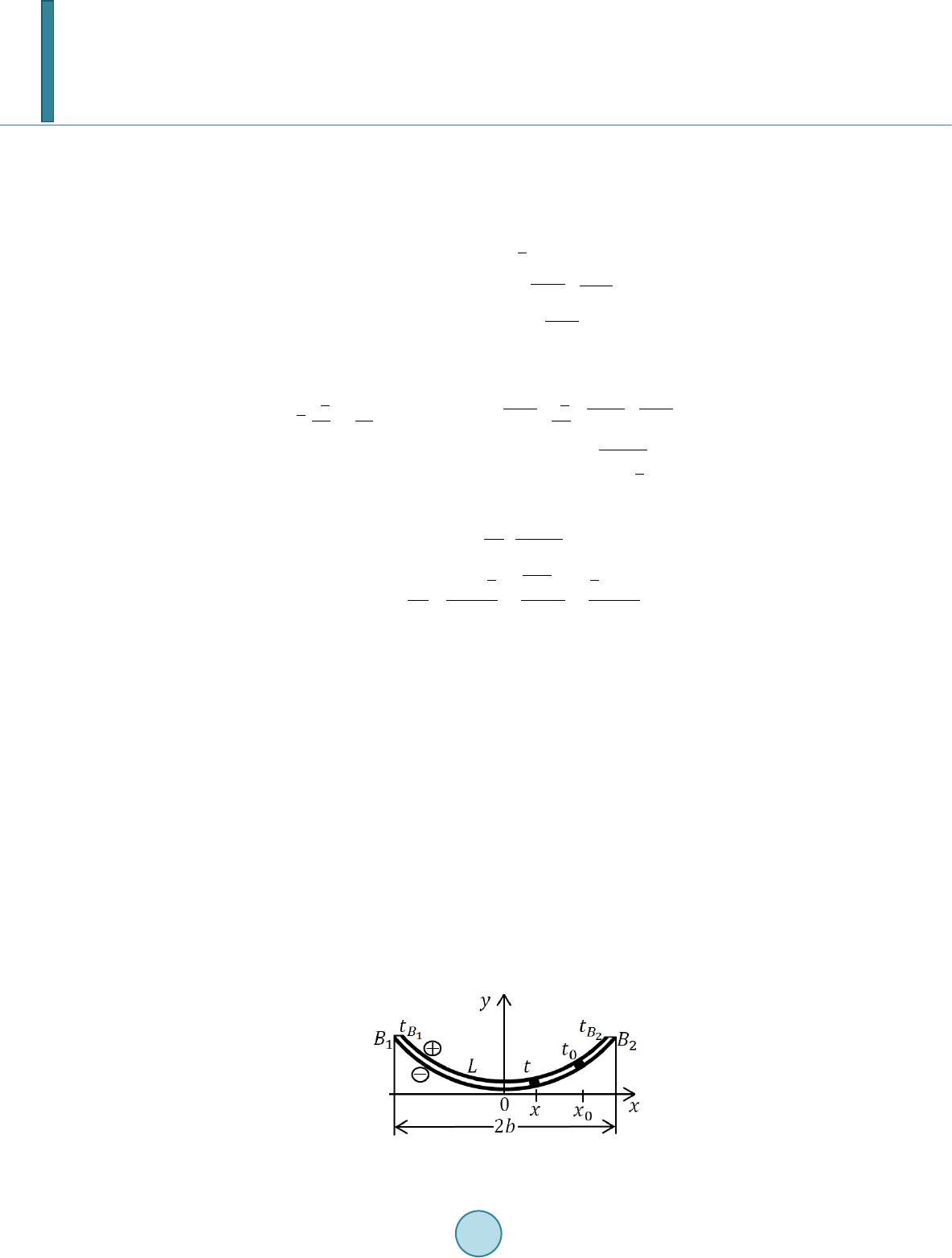 M. R. Aridi et al. 2. Complex Variable Function Method Let and be two complex potentials. Then the stress , the resultant function and the displacement are related to and as [9] (1) () ( ) ' 22 ΦΨ y xxy izz z σσ σ −+ =+ (2) ( )( )( ) ' fY iXzzzzc φ φψ =−+ =+++ (3) ()( )( )() ' 2G uivKzzzz φ φψ +=−+ (4) whe r e G is shear modulus of elasticity, for plane strain, for plane stress and is Poisson’s ratio and . The derivative in a specified direction (DISD) is defined as {}( )( )() () () ,, Φ ΦΦ Ψ dz ddz Jz zYiXzzzzzNiT dz dzdz ′ =−+=+++=+ (5) whe r e J denotes the normal and tangential tractions along the segment . Note that the value of J not only depends on the position of point z, but also on the direction of the segment [3]. Let the complex potentials and be ( )( )()( ) ( ) 2 1 2 L LL gtdt gtdtgtdt ztztztz t ψπ = +− −− − ∫ ∫∫ whe r e denotes the crack configuration and substitute into (4). By letting approaches and , which are located on the upper and lower sides of the crack faces (see Figure 1), then using the Plemelj equations [3], and rewriting as t, the following result is obtained [3] ( )( ) ( ) ()( ) () 21, G u tiv tikg ttL+=+ (6) and ( )( ) ( ) ( )( ) () ()( ) ( ) u tiv tu tiv tu tiv t +− + =+−+ denotes the crack opening displacement (COD) for the curved crack. It is well known that the COD possesses the following properties: ( ) ( ) 1/2 at the crack tip ,1,2 j Bj gtOt tBj =−= (7) 3. Hypersingular Integral Equation The hypersingular integral equation for a curved crack problem is obtained by placing two point dislocations at point and . It is given by [3] Figure 1. A crack configuration. 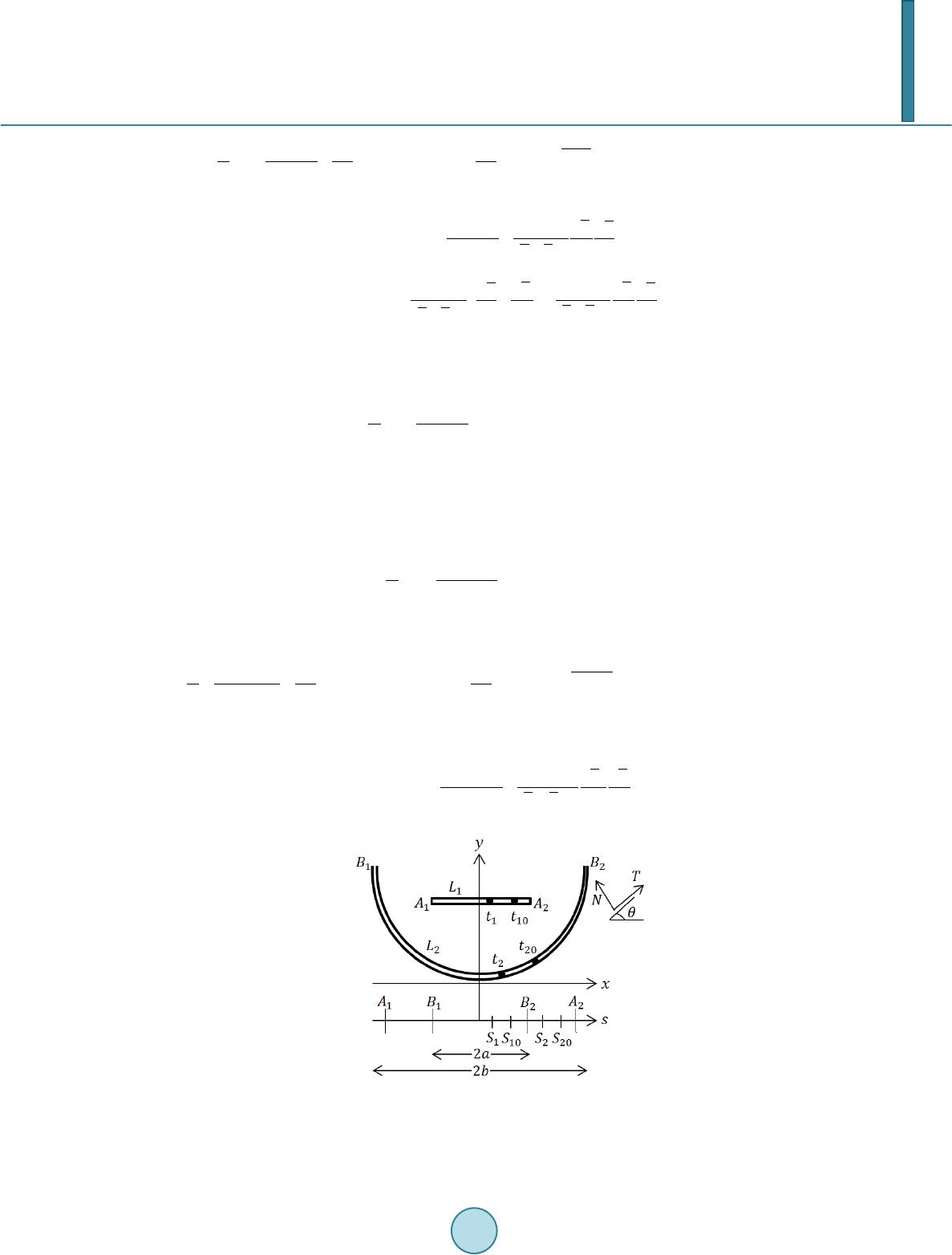 M. R. Aridi et al. () ( )( ) () ( ) ( ) () ( ) 1 020000 2 0 11 1 .. ,,, 22 LL L g t dt hpKttgt dtKttgtdtN tiTttL tt ππ π ++=+∈ − ∫∫ ∫ (8) whe r e ()( ) 0 10 22 0 0 0 11 ,, () dt dt K ttdt dt tt tt − =+ − − () () ( ) 0 00 20 23 00 0 0 2 1 ,() tt dt dt dt dt K ttdtdtdt dt tt tt − − = +− − − and is the dislocation distribution along the curved. In Equ a tio n (8), the first integral with h.p. denotes the hypersingular integral and should be defined in the sense of Hadamart finite part integral. It easy to see that for a straight crack, Equation (8) is reduced to ( ) ( )( )( ) 0 00 2 0 1.. , L g t dt h pNtiTttL tt π =+∈ − ∫ (9) and it can be solved analytically. Now consider the interaction between straight and curved cracks problem (see Figure 2). For the crack-1, if the point dislocation is placed at point and and is the dislocation doublet distribution along crac k- , and the traction is applied on the then the hypersingular integral equa- tion for crack- is ( ) ( )()( ) 1 11 111 1011 10 2 1 10 1.. L g t dt h pNtiTt tt π = + − ∫ (10) where denotes the traction influence on crack-1 caused by dislocation doublet distribution, , on crack-1. The influence from the dislocation doublet distribution on crac k-2 gives ( ) ( )( ) ( ) ( ) () ( )( ) 22 2 22 212102 222 2102 2212101210 2 2 10 11 1 ,, 22 LL L g t dtKttgtdtKt tgt dtNtiTt tt ππ π ++=+ − ∫∫ ∫ (11) whe r e denotes the traction influence on crack- caused by dislocation doublet distribution, , on crack-2 and () ( ) 10 2 121022 10 2 2 10 2 10 11 ,, () dt dt Kttdt dt tt tt − =+ − − Figure 2. Straight and curved cracks in plane elasticity with configurations on a real axis-s. Cracks with length 2a (straight) and 2b (curved) are known as crack-1 and crack-2 resp ectivel y.  M. R. Aridi et al. ()() ( ) ( ) 2 10 10 10 22 22 1023 21010 2 2 102 10 2 1 ,. tt dt dt dt dt K ttdtdtdtdt tt tt − − = +− −− Note that since , all three integrals in (11) are regular and that and satisfy (7). By superposition of the dislocation doublet distr ib ution, along the crack-1 and dislocation doublet dis- tribution, along the crack-2, we obtained the following hypersingular integral equation for crack-1 ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( )() 12 2 1112 221210222 2102 22110110 22 1 102 10 1 11 .., , 2 LL L g t dtgtdt hpKttg tK ttg tdtNtiTt tt tt π ππ +++ =+ −− ∫∫ ∫ (12) whe r e ( )( )( )( )()() ( ) 1 101 1011 10121011 1012 10 NtiTt NtNtiTtiTt+= + ++ is the traction applied at point of crack-1, which is derived from the boundary condition. The first integrals represents the effect on crack-1 caused by the dislocation on the crack-1 itself, whereas the second three inte- grals represent the effect of the dislocations on crack-2. Similarly, the hypersingular integral equation for crack-2 is ( ) ( )() ( ) ( ) ( )( ) ( )( )() 2221 2 22111 1220 2222220 22 2220220 22 2201 20 111 1 .. ,, 22 LLL L gtdtg t dt hpKttg t dtK ttg tdtN tiTt tt tt πππ π ++ +=+ −− ∫∫∫ ∫ (13) whe r e ( )( )()()( )() ( ) 2 202 20212022 2021202220 NtiTt NtNtiTtiTt+= +++ is the traction applied at point of crack-2 and ()( ) 20 2 122022 20 2 2 20 2 20 11 ,, () dt dt Kttdt dt tt tt − =+− − ()( ) ( ) ( ) 2 20 20 20 22 22 2023 22020 2 2 202 20 2 1 ,. tt dt dt dt dt K ttdtdtdt dt tt tt − − = +− −− The first three integrals in (13) represent the effect on crack-2 caused by the dislocation on crack-2 itself, and the fourth integral represents the effect of the dislocation on crack-1. Equations (12) and (13) are to be solved for and It is obvious that if the two cracks are far apart, the last three integrals in Equation (12) and the fourth integral in Equ atio n (13) vanish. Then the solutions for Equations (12) and (13) approach the so- lution for a single crack problem, and a closed form solution is available [10]. By mapping the two cracks configurations on a real axis s with an interval 2a and 2b respectively, the map- ping functions and are expressed as ( ) ( ) 111 22 111 11 | () t ts gtasH s == − (14) ( ) ( ) 222 22 22222 | () t ts gtbsHs = = − (15) whe r e 1 111 112 1 ()() () H sHsiHs= + and 2 2212222 ()() ()H sHsiHs = + . In solving the integral equations, we used the following integration rules [11], for the hypersingular and regu- lar integrals, respectively, ( ) ( )( ) ( ) ( ) 22 00 21 0 1, M a jj aj a sGsdsWsG ssa ss π + −= −= < − ∑ ∫ (16) ( ) ( ) ( ) ( ) 1 222 20 1 11,, 2 aM jj j a a sGsdsa sGssa M π + = − −=− < + ∑ ∫ (17)  M. R. Aridi et al. whe r e G(s) is a given regular function, , 0 a cos,1,2,3,,1, 2 jj j ssj M M π === …+ + and ( ) ( ) 0 00 21, 2 Mn j jn n s W snVU Ma = =−+ + ∑ whe r e () 1 sin sin. 22 n j nj j VMM π π + = ++ Here is a Chebyshev polynomial of the second kind, defined by ( ) ( 1) sin,cos . sin n n Ut t θθ θ + = = and can be evaluated using ( ) 11 0 , M nn n s H scUsa a = = ≤ ∑ (18) and ( ) 22 0 , M nn n s H scUsb b = = ≤ ∑ (19) whe r e ( ) 1 1 11 1 2, 2 Mn nj j cVH s M + = =+ ∑ (20) ( ) 1 2 22 1 2 2 Mn nj j cVH s M + = =+ ∑ (21) and and are defined from (14) and (15) respectively. 4. Numerical Results The stress intensity factor (SIF) of inner and outer cracks can be calculated respectively ()( ) ' 121 2 lim jj jAj AA Att KKiKttg t π → =−=− (22) and ()( ) ' 12 2 2 lim jj jBj BB Btt KKiKt tg t π → =−=− (23) where and can be obtained by using Equations (12) and (13) simultaneously. As the two cracks are far apart, the formulations in Equatio ns (12) and (13) become an equation for a straight and a curved crack respectively. For the straight crack with length 2a, we obtain which is simi- lar to the exact solution . Whereas, for the curved crack, we compare the result of the curved crack with the exact solution using the remote traction , given by [9] ( )( ) 1/21/2 12 22 cos sin 22 , 1 sin1 sin 22 aa aa KK aa ππ = = ++ (24) 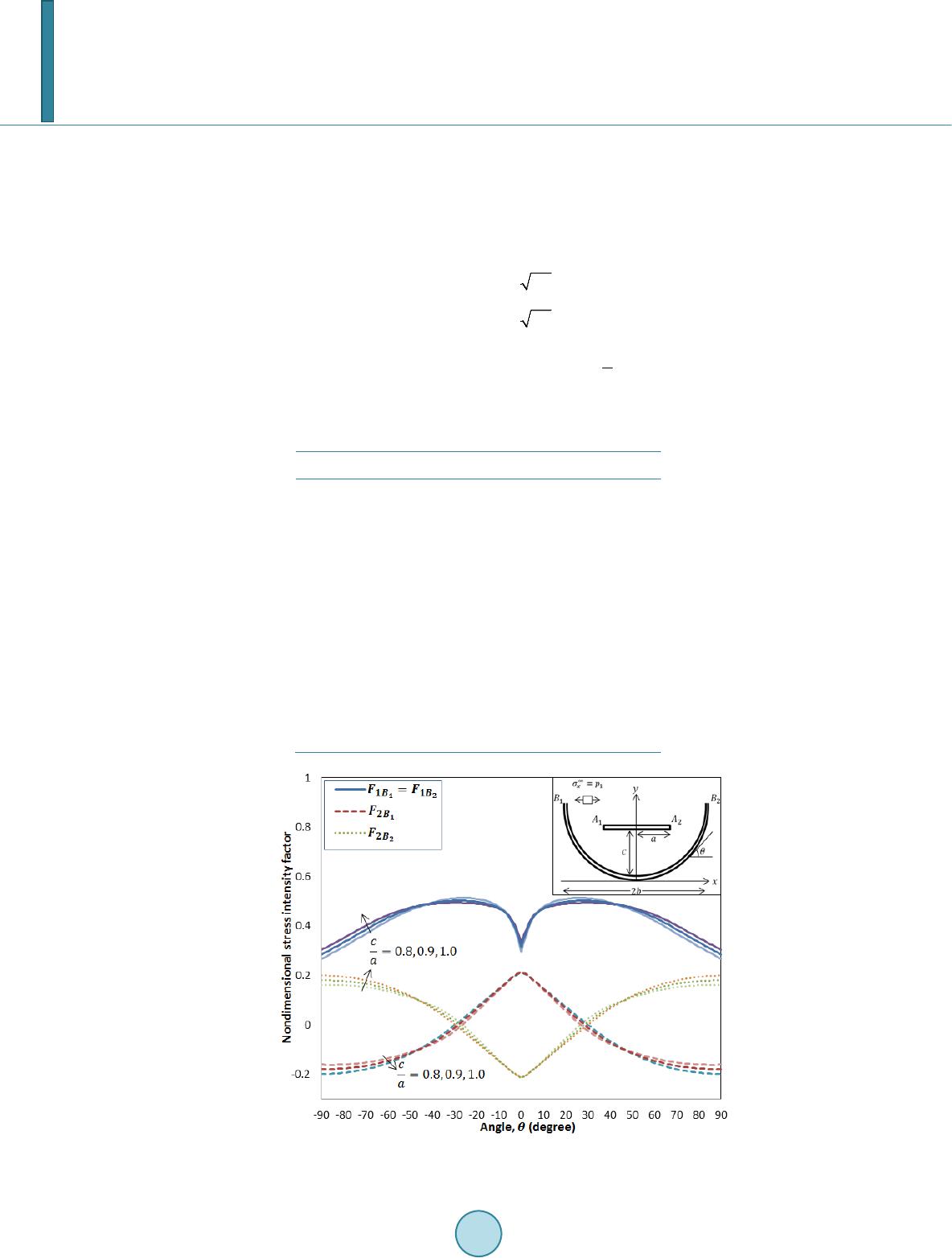 M. R. Aridi et al. The numerical results are tabulated in Table 1. It can be seen that maximum error is not more than 1.0% and the results show very good agreement. 4.1. Example 1: Mode I Consider the traction applied is and the calculated results for SIF at the crack tips and are respectively expressed as () 1 /,,1,2 jj iA iA KFb apaij π = = ( ) 1 /,,1,2 jj iB iB KFb apaij π = = Figure 3 shows the nondimensional SIF for a curved crack whe n . It is found that the real Table 1. The SIF for single curved crack: A comparison be- tween exact and numerical results. (exact) (exact) 0 0.9972 0.9956 0.0435 0.0413 10 0.9887 0.9840 0.0 865 0.0777 20 0.9748 0.9677 0.1 283 0.1091 30 0.9560 0.9493 0.1 686 0.1584 40 0.9326 0.9308 0.2 068 0.2046 50 0.9053 0.9133 0.2 426 0.2420 60 0.8746 0.8966 0.2 758 0.2560 70 0.8413 0.8788 0.3 062 0.3058 80 0.8059 0.8240 0.3 338 0.3411 90 0.7690 0.7786 0.3 806 0.3798 Figure 3. Nondimensional SIF when θ is changing. 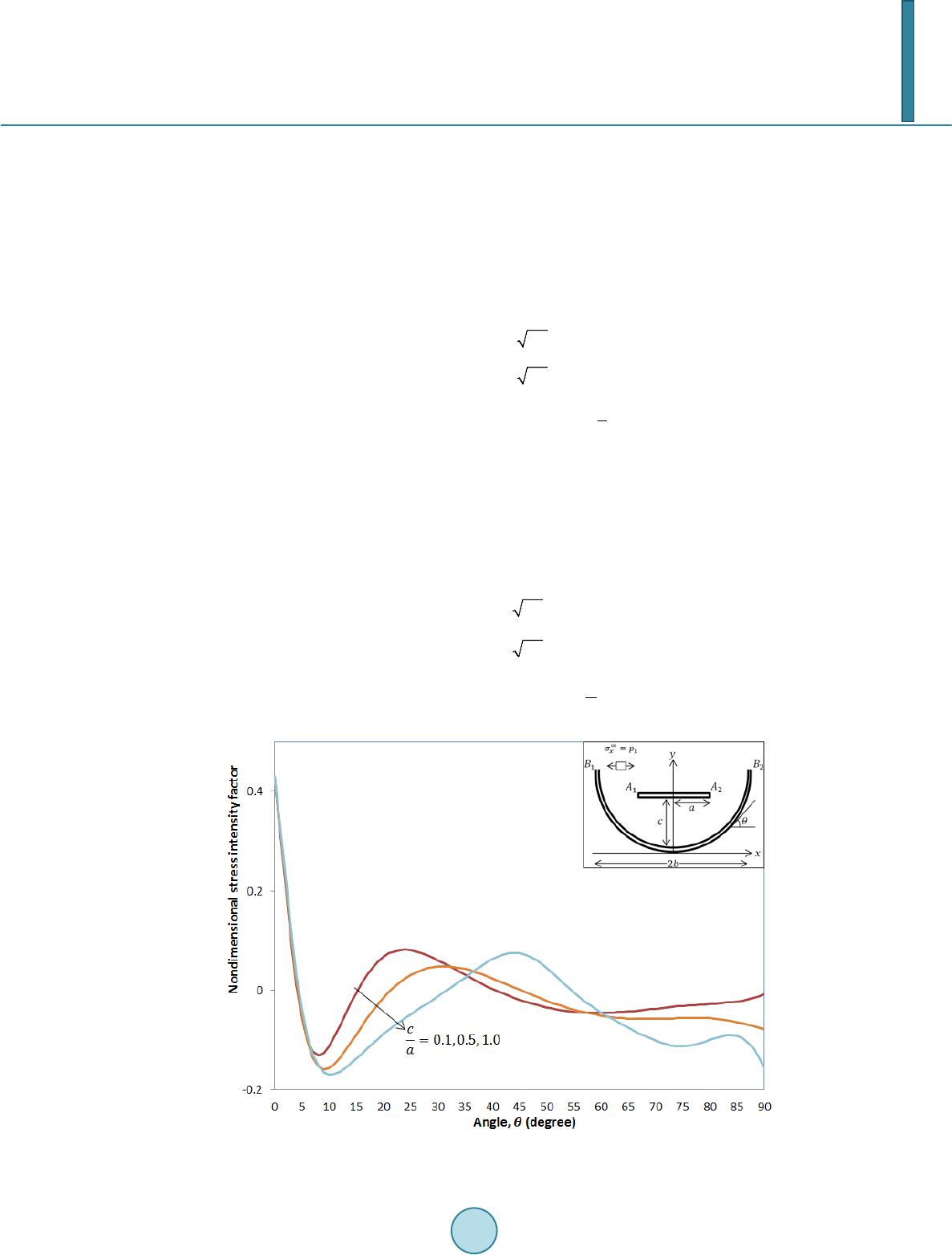 M. R. Aridi et al. parts of SIF at the left crack tip is equal to its right crack tip , whereas the imaginary parts give opposite sign . The effect of the distance between both cracks is also studied and the result is shown in Fig ure 4. The nondimensional SIF for the straight crack is decreased at the same rate when whereas increased with different rates when and the SIF becomes higher as the two cracks are close together. 4.2. Example 2: Mode II The traction applied for this mode is and the calculated results for SIF at the crack tips and are respectively expressed as ( ) 2 /,,1,2 jj iA iA KFb apaij π = = ( ) 2 /,,1,2 jj iB iB KFb apaij π = = Figure 5 shows the nondimensional SIF for a curved crack when and the effect of the dis- tance between both cracks is shown in Figure 6. The nondimensional SIF for the straight crack is decreased with different rates at the considered domain. As the two cracks are close together, the nondimensional SIF at the crack tip is higher. 4.3. Example 3: Mode III Consider the traction applied is and the calculated results for SIF at the crack tips and are respectively expressed as ( ) /,,1,2 jj iA iA KFb aqaij π = = () /,,1,2 jj iB iB KFb aqaij π = = Figure 7 shows the nondimensional SIF for a curved crack when . It is found that the imagi- Figure 4. Nondimensional SIF when θ is changing.  M. R. Aridi et al. Figure 5. Nondimensional SIF when θ is changing. Figure 6. Nondimensional SIF when θ is changing. nary parts of SIF at the left crack tip is equal to its right crack tip , whereas the real parts give opposite sign . The effect of the distance between both cracks is shown in Figure 8. For the nondimensional SIF is decreased at the same rate but later increased at the different rates. 5. Conclusion In this paper, the different types of loading modes have been applied to the interaction between straight and curved cracks problem in plane elasticity. As the result, we obtained different results of nondimensional SIF due to the different loading modes. We also observed that the SIF increases as both cracks become closer. For a  M. R. Aridi et al. Figure 7. Nondimensional SIF when θ is changing. Figure 8. Nondimensional SIF when θ is changing. symmetry shape crack problem, the real parts of SIF for the left side of the crack is equal to its right side while the imaginary parts give the opposite sign. Acknowledgements The second author would like to thank Ministry of Science, Technology and Innovation (MOSTI), Malaysia for the Science Fund, Vot No. 5450657. References [1] Helsing, J. (2011) A Fast and Stable Solver for Singular Integral Equations on Piecewise Smooth Curved. SIAM Jour- nal on Scientific Computing, 33, 153-174. http://dx.doi.org/10.1137/090779218  M. R. Aridi et al. [2] Helsing, J. and Peters, G. (1999) Integral Equation Methods and Numerical Solutions of Crack and Inclusion Problems in Planar Elastostatics. SIAM Journal on Applied Mathematics, 59, 965-982. [3] Chen, Y.Z., Hasebe, N. and Lee, K.Y. (2003) Multiple Crack Problems in Elasticity. WIT Press, Southampton. [4] Johnson, J. and Qu, J. (2007 ) An Interaction Integral Method for Computing Mixed Mode Stress Intensity Factors for Curved Biomaterial Interface Cracks in Non -Uniform Temperature Fields. Engineering Fracture Mechanics, 74, 2282- 2291. http://dx.doi.org/10.1016/j.engfracmech.2006.10.008 [5] Chen, Y.Z. and Lin, X.Y. (2010) Numerical Solution of Singular Integral Equation for Multiple Curved Branch-Cracks. Structural Engineering and Mechanics, 34, 85-95. http://dx.doi.org/10.12989/sem.2010.34.1.085 [6] Chen, Y.Z. and Hasebe, N. (1997) Fredholm Integral Equation for the Multiple Circular Arc Crack Problem in Plane Elasticity. Archieve of Applied Mechanics, 67, 433-446. http://dx.doi.org/10.1007/s004190050129 [7] Nik Long, N.M .A. and Eshkuvatov, Z.K. (2009) Hypersingular Integral Equation for Multiple Curved Crack Problem in Antiplane Elasticity. International Journal of Solids and Structures, 46, 2611-2617. http://dx.doi.org/10.1016/j.ijsolstr.2009.02.008 [8] Chen, Y.Z., Gross, D. and Huang, Y.J. (1991) Numerical Solution of the Curved Crack Problem by Means of Polynomial Approximation of the Dislocation Distribution. Engineering Fracture Mechanics, 39, 791-797. http://dx.doi.org/10.1016/0013-7944(91)90184-3 [9] Muskhelishvili, N.I. (1957) Some Basic Problems of the Mathematical Theory of Elasticity. Noordhoff International Publishing, Leyden. [10] Cotterell, B. and Rice, J.R. (1980) Slightly Curved or Kinked Cracks. International Journal of Fracture, 6, 155-169. http://dx.doi.org/10.1007/BF00012619 [11] Mayrhofer, K. and Fischer, F.D. (1992) Derivation of a New Analytical Solution for a General Two Dimensional Fi- nite-Part Integral Applicable in Fracture Mechanics. International Journal of Numerical Method in Engineering, 33, 1027-1047. http://dx.doi.org/10.1002/nme.1620330509
|