Journal of Applied Mathematics and Physics, 2014, 2, 219-224
Published Online April 2014 in SciRes. http://www.scirp.org/journal/jamp
http://dx.doi.org/10.4236/jamp.2014.25027
How to cite this paper: Das, P. and Kundu, A. (2014) Bifurcation and Chaos in Delayed Cellular Neural Network Model.
Journal of Applied Mathematics and Physics, 2, 219-224. http://dx.doi.org/10.4236/jamp.2014.25027
Bifurcation and Chaos in Delayed Cellular
Neural Network Model
Pritha Das, Amitava Kundu
Department of Mathematics, Bengal Engineering and Science University, Shibpur, Howrah, India
Received February 2014
Abstract
This paper deals with control of chaotic behavior of a delayed Cellular Neural Network (DCNN)
model which is a one-dimensional regular array of four cells with continuous activation function.
We investigate different dynamical behaviors including limit cycle, torus, and chaos for different
range of weight parameters of the system. Regarding synaptic weight as parameter, Hopf bifurca-
tions are obtained in the system without delay. In the delayed model condition for the Global as-
ympto ti c stability of the equilibrium point is presented. Numerical simulation and results are
given to show the role of delay in chaos control of the CNNs.
Keywords
Delayed Cellular Neural Networks, Chaos, Bifurca tion, Global Stability
1. Introduction
An artificial neural network (ANN) is a mathematical model that can mimic the biological process of human
brain. An ANN can be presented by a directed graph composed of neurons as nodes and synapses or nerves as
edges with an algorithm that show how impulses are conducted through the network. There are various types of
network architecture. Cellular Neural Net wo rk s (CNNs) introduced by Chua and Yang [1] is one dimensional
regular array of locally connected circuits (called cells), they are able to display various dynamics, such as limit
cycle, torus, especially chaos. Neural oscillation can arise from interactions between different brain areas. Time
delays can play an important role here because nerve impulse takes a time to travel the length of the axon to the
target neuron which in turn takes the time to summate their inputs and produce response. Brain areas are as-
sumed to be bidirectionally (BAM) coupled forming delayed feedback loops. An example of such a feedback
loop is the connection between the thalamus and cortex [2] [3]. The malfunctioning of the neural system is often
related to changes in the delay parameter causing unmanageable shifts in the phases of the neural signals. Some
of the visible mechanical consequences could be explained: such as tremor in the fingers, difficulties in balanc-
ing; the increased danger of falling over for elderly people or even motion disorders in the case of bursts of epi-
lepsy, Parkinson disease and so on [4].
Physiological experiments suggest that the main components of neural activity in olfactory systems are chao-
tic. In the olfactory system, the phase transition has the appearance of a change in the EEG from a chaotic, ape-
riodic fluctuation to a more regular nearly periodic oscillation. Chaotic activity enables the rapid state transitions

P. Das, A. Kundu
220
essential for information processing. Without this ability, the brain could not quickly concern itself with a new
task. Thus, we can assume chaos for the rapid transitions between perceptual states. Without it, observation
could be extremely slow. It is supposed that brains injured by Alzheimer’s disease have electrophysiologically
inactive neurons and/or synapses and show decreased chaotic behavior. Results of various research works in this
area support the assumption that chaos plays an important role in brain function, for instance, learning and
memory [5]-[13].
This paper is structured as follows: In Section 2 we analyze a new family of simplified 4-CNNs, as shown in
Figure 1. In Section 3, we investigate different dynamical behaviors including chaos for different range of
weight parameters of the system. Using Matlab software we can observe limit cycle, torus and chaos in a new
family of 4-CNNs for different range of adjustable parameters of main diagonal of the weight matrix. Numerical
results are discussed showing changes of dynamics of the system from unstable to stable (chaos control) one
through bifurcation due to variation in the individual weight parameter. In Section 4, a delayed Cellular Neural
Networks (DCNNs) is considered where the chaotic dynamics is controlled [see Figure 2]. A sufficient
condition for the Global asymptotic stability of the equilibrium point in the delayed model is found. Finally
some concluding remarks have been drawn on the implication of our results in the context of related work
mentioned above.
2. Limit Cycle, Torus and Chaos in 4-CNNs
In this section, the dynamics of this system can be described by the following ordinary differential equations:
( )( )
4
1
1,2,3,0 4,
ii iijji
j
xcxtW fxitc
=
=

=−+ >

∑

(1)
where
()
ij
WW=
is a
44×
weight matrix describing the strength of the connection from
j
th neuron on the
i
th neuron.
[( )]
i
fxt
is the output state of the
i
th neuron at time t .
For numerical simulation we consider
[1.1, 1.5,4.5, 15]
T
c=
,
( )tanh( )
ii
fx x=
and the weight matrix
W
to be
3
2.1 2.1700
3.51 13.11 0
0 31.1
0020 30
Wp


−

=
−−


(2)
where
3 33
pW=
is an adjustable parameter.
The phase portraits (Figures 3-5) show the evidence that there exist limit cycles, torus and chaotic attractors
with different values of
3
p
. In Figure 6, chaotic nature is controlled by taking
3
6.4( 6.1)p= >
which is also
confirmed by bifurcation diagram (see Figure 7) with respect to parameter
3
p
.
Figure 1. Architecture of the network model 4-cell Cellular Neural
Networks.
Figure 2. Architecture of the network model 4-cell delayed Cellular
Neural Networks.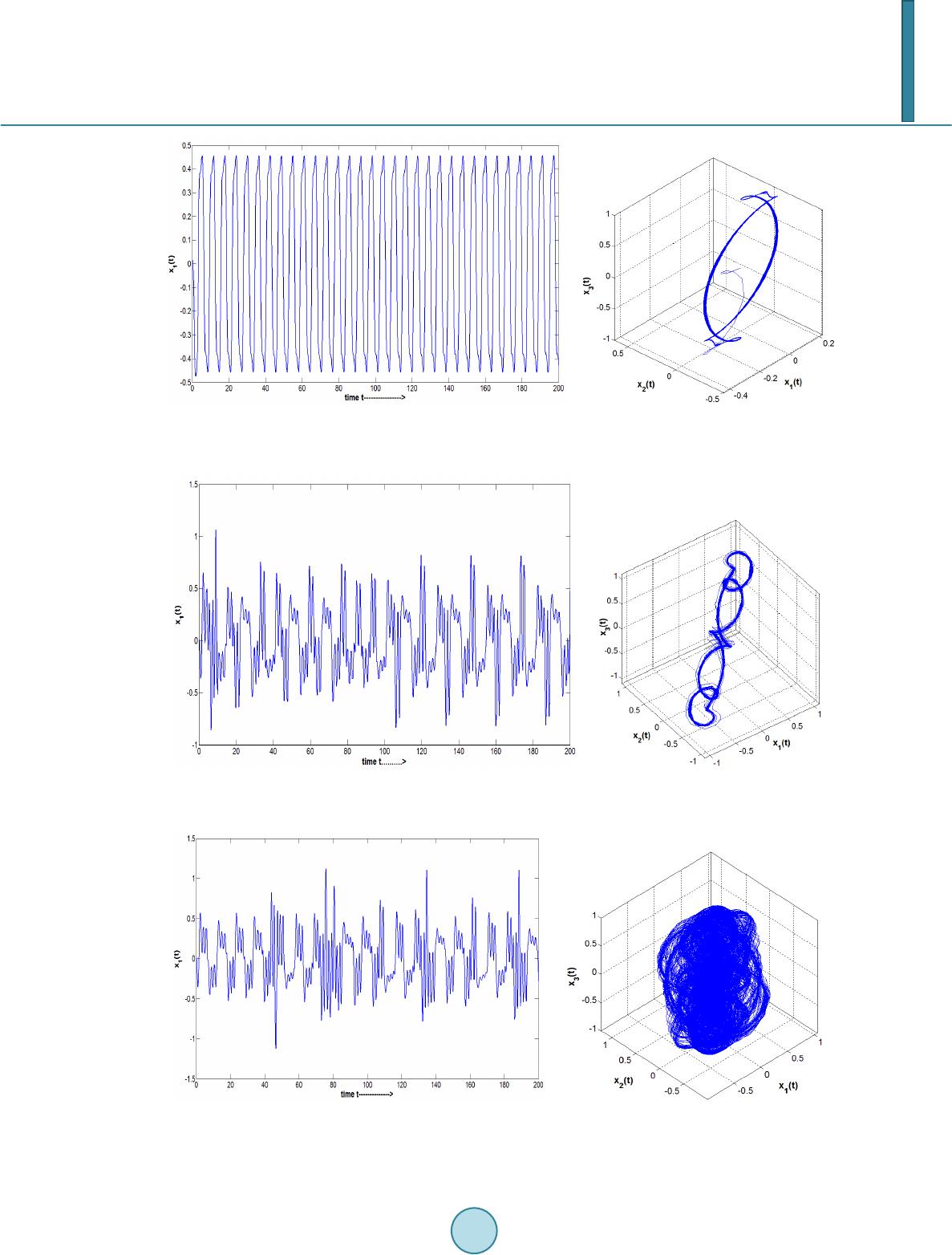

P. Das, A. Kundu
221
Figure 3. Solution trajectory showing periodic behavior and corresponding phase portrait in
123
(, , ) xxx
space with
parameter
32p=
.
Figure 4. Solution trajectory showing chaotic behavior and corresponding phase portrait in
123
(, , )xxx
space with
parameter p3 = 4.4.
3
6.4p=
.
Figure 5. Solution trajectory showing chaotic behavior and corresponding phase portrait in
123
(, , )xxx
space
with parameter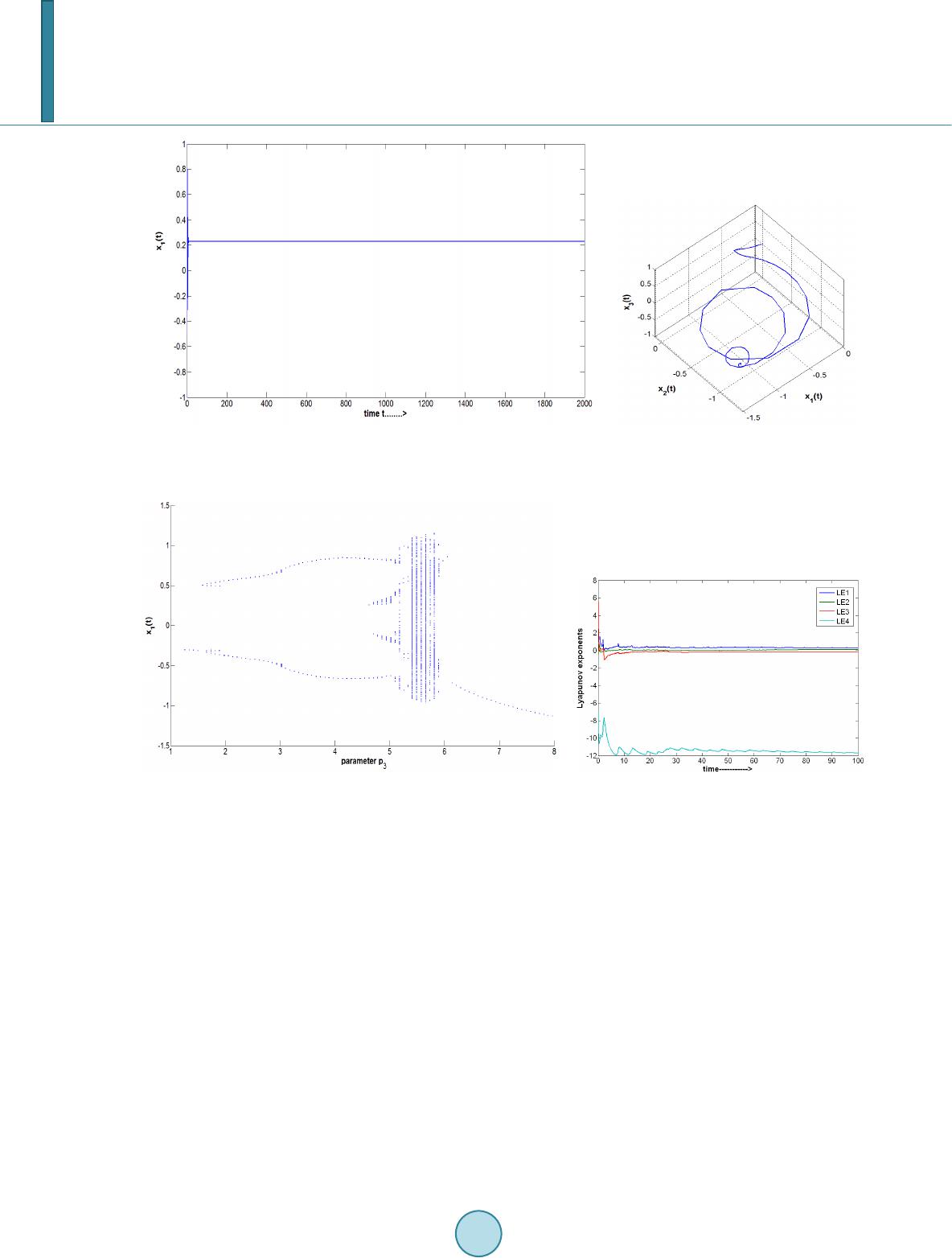
3
5.4p=
.

P. Das, A. Kundu
222
Figure 6. Solution trajectory showing stable behavior and corresponding phase portrait in
123
(, , )xxx
space with pa-
rameter
3
6.4p=
.
(a) (b)
Figure 7 . (a) Bifurcation diagram with respect to parameter
3
p
, (b) The four Lyapunov exponents when
3
5.4p=
.
Again, if we consider all other self-synaptic weights like
4 44
pW=
as adjustable parameter, then we get sim-
ilar type of behavior which is shown in the following Figure 8.
3. Mathematical Model with Time Delay and Global Stabilit y
We consider an artificial 4-neuron network model of Cellular Neural Networks time delayed connections
between the neurons by the delay differential equations:
( )( )()
4
1
,0 1,2,3,4
ii iiiiijji
j
ij
xcxt afxtbfxitc τ
=
≠
= 
=−++− > 
 
∑

(3)
with
()
i
xt
is the activation state of
i
th neuron at time t,
[( )]
i
fxt
is the output state of the
i
th neuron at time
t,
ii
a
is self-synaptic weight,
ij
b
is the strength of the
j
th neuron on the
i
th neuron at time
()t τ −
,
τ
is the signal transmission delay and
i
c
(decay rate) is the rate with which the
i
th neuron will reset its potential
to the resting state in isolation when disconnected from the network. In the following, we assume that each of
the relation between the output of the cell
f
and the state of the cell possess following properties:
(H1)
f
is bounded on
R
;

P. Das, A. Kundu
223
(H2) There is a number
0 µ >
such that
() () fufvu v µ − ≤−
for any
,.uv R∈
It is easy to find from (H2) that
f
is a continuous function on
R
. In particular, if output state of the cell is
described by
( )tanh( )
ii
fx x=
, then it is easy to see that the function
f
clearly satisfy the hypotheses (H1)
and (H2).
Theorem 1 For the DCNN (3), suppose output of the cell
[( )]
i
fxt
satisfy the hypotheses (H1) and (H2)
above and there exist constants
*
ij
α
,
*
ij
β
,
*
ij
η
,
*
ij
ξ
,
ij
α
,
ij
β
,
ij
η
,
ij
R ξ ∈
such that
**
** *
2
4
22
2
22 22
1
( )2
ij
ij j
ij ij ijijji
i
ijiiij jii
j
ij
a abbc
η
ηξ
ξ
αβ αβ
µµ µµ
=
≠
+++ <
∑
(4)
1,2,3,4i=
, in which
*
ij
α
,
*
ij
β
,
*
ij
η
,
*
ij
ξ
,
ij
α
,
ij
β
,
ij
η
,
ij
ξ
( ,1,2,3,4)ij=
are any real constants with
**
1
ij ij
αβ +=
,
**
1
ij ij
ηξ +=
,
1
ij ij
αβ +=
,
1
ij ij
ηξ +=
,
µ
is a constant number of the hypothesis (H2) above.
Then the equilibrium
*
x
of the DCNN (3) is also globally asymptotically stable independent of delays.
4. Conclusion
This paper addresses chaos control by varying the adjustable parameter (self-connection weights) and
introducing time delay [see Figure 9] in original model of 4-cell CNNs. These two approaches stabilize unstable
Figure 8 . Bifurcation diagram with respect to parameter
4
p
.
Figure 9. Control of chaos: Solution trajectory showing periodic behavior corresponding phase portrait in
123
(, , )xxx
space
with parameter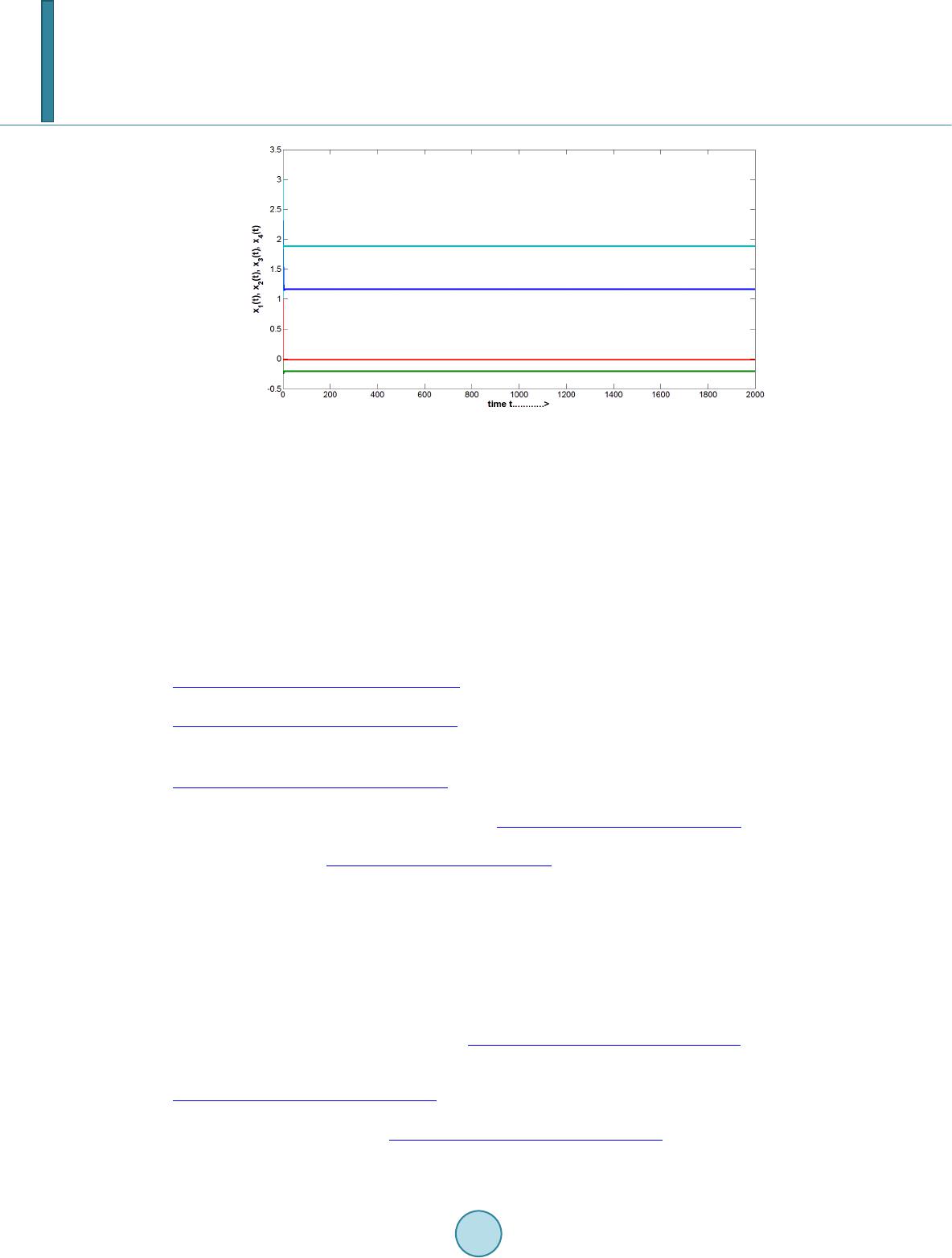
5.4p=
.

P. Das, A. Kundu
224
Figure 10. Solution trajectory showing stable behavior satisfying globally asymptotically
stable conditions.
periodic orbits that a chaotic attractor encompasses. Furthermore, different from the work of Yang and Huang
[14] where adjustable parameter lies off the main diagonal (self-connection weights), we consider it on the main
diagonal which seems more meaningful for controlling chaos in CNNs. Besides global stability criteria ensures
asymptotically stable behavior for DCNN model [see Figure 10]. The results obtained enforce more restrictions
on synaptic weight and decay parameters.
References
[1] Chua, L.O. and Yang, L. (1988) Cellular Neural Networks: Theory. IEEE Transactions on Circuits and Systems I, 35,
1257-1272.
[2] Aihara, K., Ta k abe, T. and Toyoda, M. (1990) Chaotic Neural Networks. Physics Letter A, 6, 333 -340.
http://dx.doi.org/10.1016/0375-9601(90)90136-C
[3] P yragas, K. (1992) Continuous Control of Chaos, by Self-Controlling Feedback. Physics Letters A, 170, 4 21 -428.
http://dx.doi.org/10.1016/0375-9601(92)90745-8
[4] Wu, J. (2001) Introduction to Neural Dynamics and Signal Transmission Delay. de Gruyter, New York.
[5] Ott, E., Grebogi, C. and Yor ke, J.A. (1990) Controlling Chaos. Physical Review Letters, 64, 1196-119 9 .
http://dx.doi.org/10.1103/PhysRevLett.64.1196
[6] Babloyantz, A. and Destexhe, A. (1986) Low-Dimensional Chaos in an Instant of Epilepsy. Proceedings of the Na-
tional Academy of Sciences of the USA, 83, 3513 -35 17 . http://dx.doi.org/10.1073/pnas.83.10.3513
[7] Free man, W.J. (1987) Simulation of Chaotic EEG Patterns with a Dynamic Model of the Olfactory System. Biological
Cybernet ics, 56, 139 -150. http://dx.doi.org/10.1007/BF00317988
[8] Jeong, J. and Kim, S.Y. (1997) Nonlinear Analysis of Chaotic Dynamics Underlying the Electroencephalogram in Pa-
tients with Alzheimer’s Disease. Journal of the Korean Physical Society, 30, 320-327.
[9] Skar da , C.A. and Freeman, W.J. (1987) How Brains Make Chaos in Order to Make Sense of the World. Behavioral
and brain Sc., 19, 161-195.
[10] Skard a, C.A. an d F reeman, W.J. (1990) Chaos and the New Science of the Brain. Neurosci ence, 1, 275-285.
[11] Chen, L. and Aihara , K. (1999) Global Searching Ability of Chaotic Neural Networks. IEEE Transaction on Circuits
and Systems I, 46, 974-993.
[12] Das, A., Roy, A.B. and Das, P. (2002) Chaos in a Three Dimensional General Model of Neural Network. International
Journal of Bifurcation and Chaos, 12, 2271-2281 . http://dx.doi.org/10.1142/S0218127402005820
[13] Kundu, A., Das, P. and Roy, A. B. (2014) Complex Dynamics of a Four Neuron Network Model Having a Pair of
Short-Cut Connections with Multiple Delays. Nonlinear Dynamics, 72, 643 -662.
http://dx.doi.org/10.1007/s11071-012-0742-2
[14] Yang, X.S. and Huang, Y. (2007) Chaos and Two-To r i in a New Family of 4-CNNs. International Journal of
Bifurcation and Chaos, 17, 953 -963. http://dx.doi.org/10.1142/S0218127407017677