 Journal of Applied Mathematics and Physics, 2014, 2, 204-213 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.25025 How to cite this paper: Liu, Y.M., et al. (2014) Reconstructions for Continuous-Wave Diffuse Optical Tomography by a Globally Convergent Method. Journal of Applied Mathematics and Physics, 2, 204-213. http://dx.doi.org/10.4236/jamp.2014.25025 Reconstructions for Continuous-Wave Diffuse Optical Tomography by a Globally Convergent Method Yueming Liu1, Jianzhong Su1*, Zi-Jing Lin2, Steven Teng1, Aubrey Rhoden1, Natee Pantong1, Hanli Liu2 1Department of Mathematics, University of Texas at Arlington, Arlington, Texas, USA 2Department of Bioengineering, University of Texas at Arlington, Arlington, Texas, USA Email: *su@uta.edu Received January 2014 Abstract In this paper, a novel reconstruction method is presented for Near Infrared (NIR) 2-D imaging to recover optical absorption coefficients from laboratory phantom data. The main body of this work validates a new generation of highly efficient reconstruction algorithms called “Globally Conver- gent Method” (GCM) based upon actual measurements taken from brain-shape phantoms. It has been demonstrated in earlier studies using computer-simulated data that this type of reconstruc- tions is stable for imaging complex distributions of optical absorption. The results in this paper demonstrate the excellent capability of GCM in working with experimental data measured from optical phantoms mimicking a rat brain with stroke. Keywords Inverse Problems, Diffuse Optical Tomography, Medical and Biological Im agi ng , Globally Convergenc e Meth od 1. Introduction The studies using Near Infrared light (NIR) for biomedical imaging have become quite extensive in the past 15 - 20 years. Earlier applications of NIR imaging started with breast imaging [1-3], since NIR has better penetration depths in soft tissues than visible light. Applications of NIR technologies have made tremendous progress, in- cluding the detection of brain injury/trauma [4], the determination of cerebrovascular hemodynamics and oxy- genation [5-8], and functional brain imaging in response to a variety of neurological activations [9-11]. Recently, the technique was also successfully used for measuring the efficacy of photodynamic therapy for prostate cancer [12]. Among several common NIR imaging mechanisms Frequency Domain (FD) imagers were developed and used in patients [13], and Time Domain (TD) methods were used for brain studies in [14,15]. As a low-cost al- ternative to the TD and FD imaging systems, Continuous-Wave (CW) NIR imaging systems have become more *  Y. M. Liu et al. commonly used in recent years. To spatially quantify brain hemodynamic activities resulting from functional neuronal signals, it is desirable to extract distributions of light absorption from light intensity measurements through mathematical models. Since these optical properties are described by coefficients in the light diffusion model [16,17], one needs to solve an inverse problem of the corresponding partial differential equation, the diffusion equation, to obtain dif- fuse optical tomography (DOT). The inverse reconstruction for DOT has been mathematically challenging. The problem is nonlinear as well as ill-posed. As reviewed by Hielscher in [18], the majority of the inverse reconstruction algorithms used for DOT has utilized a perturbation approach involving the inversion of large Jacobian matrices, for examples [19-21]. The successful reconstruction of the unknown coefficients depends highly on the initial guess being close to the true solution since the least-square residues might have multiple local minima [22]. Our current focus of theoretical research is on numerical methods that have no restrictions on the initial guess, namely, the development of a Globally Convergent Method (GCM) as initiated by Klibanov and Timonov [22], [23]. Our earlier generation of a GCM is called a “convexification method,” as introduced in [23], based on modified residual error estimates. When a proper Carleman weight function is added to the error terms, those re- sidues depend on the unknown variable in a convex manner. Our current approach (2nd generation of a GCM) is called a continuation method or homotopy method, as defined in [24]. The homotopy connects the sought sys- tem with a similar system that is easier to solve. In this approach, our inverse reconstruction is a continuation of reconstructions from a DOT problem where light sources are far away yielding a “tail function” [25,26]. This new generation method has achieved satisfactor y results in reconstructions of simulated CW data [27]. A similar GCM was developed for the case of the reconstruction of a coefficient in a wave-like time dependent partial differential equation by Beilina and Klibanov [28,29]. This work proceeds to show the validity of this method based on physical measurements using laboratory optical phantoms with the shape of a rat head. In [30], we presented the preliminary results where we proved the convergence of the method and showed a few examples using phantom data. The focus there was to show the convergence of the method is mathematically guaranteed by the “Approximate Globally Convergent Theorem” and it is feasible to reconstruct in phantom experiments. The current paper is a more in-depth and comprehensive study of the reconstruction method based on phantom data. It contains the capability and limitations of the proposed method, error analysis in using the GCM in prac- tical experiments. The study shows that there are two major areas that GCM clearly is superior to the conven- tional DOT methods. 1. GCM can reconstruct the absolute value of absorption coefficient vs. conventional me- thod can only reconstruct the relative change of absorption coefficient. 2. GCM can tolerate discrepancy and fluctuation of reduced scattering coefficient, and still give quality reconstructions of absorption distribution. In practice, it gives the justification of use DOT in stroke and other applications where the scattering does fluctuate. This is the main contribution of the method to the DOT research community. We present the model in Section 2. Section 3 presents the experimental setup for the optical phantom study and its data acquisition scheme in 3-D geometry to be processed for 2-D tomography. In Section 4 we present results of reconstructed absorption coefficients. We summarize by conclusions and discussions in Section 5. 2. The Mathematical Model 2.1. The Optical Diffusion Model An optical light source can be used in three forms in DOT: 1) the light is amplitude-modulated at a radio fre- quency (RF) in Frequency-Domain NIR imaging, 2) the light has a short pulse with a pulse width of a few pico- seconds used in Time-Domain NIR imaging, and 3) the light has a Continuous-Wave (CW) form and the ampli- tude is independent of time. In this paper we only discuss the CW-based problem. The time-independent diffu- sion equation and boundary conditions of the CW case can be found in [16]: 0 (()(, ))()(, )(,),(,), am Dx,y x,ys μx,y x,ysxxysxy δ ∇⋅∇Φ−Φ=− −−∈Ω (1) 0 ( ,)(,)0,( ,), x,y sx,y sxy n ∂Φ +Φ=∈ ∂Ω ∂ (2) whe r e . The distributions and are the absorption and reduced scattering coefficients in the tissue, respectively, and is the photon fluence rate or photon density. The locations of the light 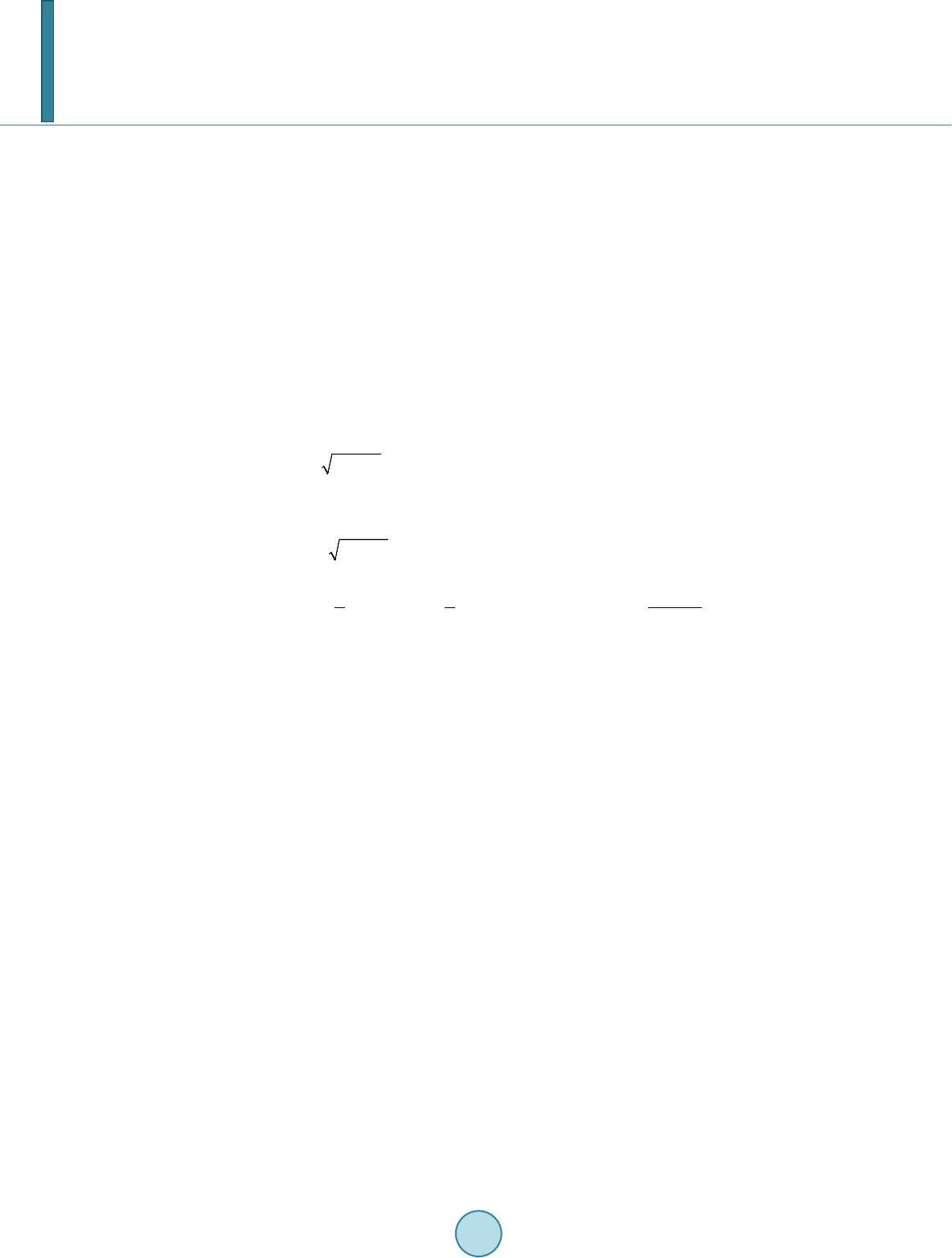 Y. M. Liu et al. sources can be chosen at several points by varying . For 2-dimenional inverse problem of Equation (1), the source is modeled by a Dirac function in the domain in the same 2-demensional plane. The forward problem domain should in theory be the entire 2-dimensional plane, but in calculation it is a truncated rec- tangle [29]. We call the background domain throughout this paper. Equation (1b) is commonly known as Robin boundary condition [16]. In real applications, the domain of interest is a bounded and irregularly shaped domain contained in the back- ground domain . We call it t he physical domain and write it as , e.g. the cross section of a rat brain. The distribution of the absorption parameter is unknown in the physical domain . It is closely related to oxygenated (HbO) and deoxygenated (HbR) hemoglobin concentrations [15], which is an important index for imaging in functional brain research. The locations of the light sources are outside of the physical domain . When the forward problem (1) is restricted into the physical domain we have ((, )(, ,))(, )(, ,)0,(, ), a Dxyxysxy xysxy µ ∇⋅∇Φ−Φ =∈Ω (2a) (, ,)(, ,),(, ),xysxysxy ϕ Φ=∈ ∂Ω (2b) where is the light intensities which can be measured on the boundary of domain . The right hand side of (2a) is equal to 0 since the light sources are located outside of the physical domain . Let ( ,)( ,)(,)x,y sx,y sD xyΦ=Φ . Then Equation (2) becomes (, ,)(, )(, ,)0,(, ),xysaxyxysxy∆Φ− Φ=∈Ω (3a) (, ,)(,,),(, ),xysxysxy ϕ Φ=∈ ∂Ω (3b) where ()() ,,,, (,)xysxysDxy ϕϕ = on the boundary of and is a new unknown coefficient, defined as: (, ) 11 ( ,)(ln(,))(ln(,))(ln( ,)), 24(, ) axy axyDxyDxyDxy Dx y µ =∆+ ∇⋅∇+ (4) where represents the Laplacian operator. For the rest of this paper the focus is on the reconstruction of the parameter distribution . This parameter reflects both the light absorption and the reduced scat- tering coefficients. When the scattering coefficient is uniform in space, the unknown coefficient reduces to ' ()(,)/ 3(,) a sa a x,yμxy Dμμxy = = with a unit of cm−2. The Influence of inhomogeneity and dis- crepancy of scattering coefficient will be di scussed in the last section. 2.2. The Idea of Reconstruction If is known in the whole physical domain we can compute the coefficient in Equati on (3) in a str aight forward way by computing the second order derivative of . A better and more stab l e solution [25], which involves only the first order derivative of utilizes a finite element version of Equation (3) (,)()(,)0, x,ys ax,y x,ysdxdy ηη Ω ∇ ⋅∇Φ−Φ= ∫∫ (5) where is taken as any quadratic finite element function. However, we only know on the boundary of in real applications. So the idea of the recon- struction for the coefficient is to construct an approximation of in the whole physical do- main from the boundary measurement data. In order to achieve this goal, a sequence of transformations of Equation (3) is performed. The transformed equation can be solved in a regular domain, e. g. a rectangle domain which contains the physical domain [31]. Once we have an approximation of , we use Equatio n (5) to compute the coe fficie nt . 2.3. Transformations The first transformation is to let . Then Eq uatio n (3a) becomes the nonlinear elliptic equation (, ,)(, ,)(, ,)(, )0.uxysuxysuxys axy∆+∇⋅∇− = (6) The second transformation is to let and , where is the second coordi-  Y. M. Liu et al. nate of the light source . We obtain that () 2 22 22 (,,) 2(,,)4(,,)2. ss ss qqxy dsqxy dsqxy dTsTqT ss ττ ττττ ∆−∆−∇+−∇+∇+∇⋅∇= −∆ ∫∫ (7) The term is the so-called “tail function” and is defined to be . This is an inte- gral-differential equation without the unknown coefficient . If we are able to approximate well both functions and , and their derivatives, then we can approximate well the target coefficient via Equation (5). We use the asymptotic relation to approximate and then solve a discrete version of Equa- tion (7) to solve the problem. As discussed in the introduction, the mathematical underpinning of transforming the inverse problem into Equatio n (7) is the mathematical method of Homotopy, i.e., using a free parameter (in our case, the light source location s), we create a continuous passage from one difficult problem at one end of the parameter to another “easier” problem at the other end. Once we have solved the relatively easier problem, we change the free parameter continuously and continue to solve the perturbed problem until we reach the other end. The relatively easier mathematical problem here is that the light source moves to infinity, where the light intensity (photon flux) at the unknown medium has an asymptotical formula to be discussed below. This is the additional information required to solve Eq uatio n (7). For more details about the algorithm, we refer to [32]. 3. The Phantom Experiments Our DOT imaging system is set for surface data collection and 3-D reconstruction through 2-D tomography of parallel cross-sections. The envisioned scenario is that of a rat brain which is covered with an optical mask that is filled with a “matching material”, a gelatin tissue phantom that has similar optical properties to those of the rat’s skull/skin. The purpose of the experiment is to determine the unknown location and severity of a stroke in the rat brain phantom. Figure 1(a) is a photo of the measurement setup. The center of the picture displays the optical phantom which contains the hidden inclusions that are not visible in the photo. The four thin tube-like probes are laser fibers that provide the light sources. A diode laser (Coherent Inc. wavelength at 808 nm) is multiplexed to serve as the source by a multiplexer (Avantes Inc. Multiplex Channels 1 × 16), which delivers and controls light at four loca- tions through the four laser fibers. The fiber on the right-hand side of Figur e 1(a) can be moved to other posi- tions by adjusting the mechanical arm that controls the lateral distance. A Charge-Coupled Device (CCD) cam- era for light intensity measurements is mounted directly above the setup. A schematic drawing of the experi- mental setup is shown in Figu re 2(b). Two optical phantoms are specifically designed and made for testing GCM-based imaging reconstructions, as a feasibility study for GCM applications in rat stroke models. The 3-D geometry of the phantoms is depicted in Figure 2. Both phantoms are shaped as a hemisphere with a diameter of 13 mm on top of a cube with dimen- sions 30 mm × 30 mm × 30 mm. The top hemisphere, the meshed shape in Figure 2(a), mimics a rat head, and the cube of the phantom emulates an optical mask filled with the “matching material”. Spherical hollows of 2.5 - 3.0 mm diameter are within the phantoms. Because the said cross section is obstructed by the top surface of the hemisphere in the CCD’s field of view, we can only collect the light intensity data at the boundary of a 2-D cross section of the presumed “animal head" as depicted in Figure 2(b). In our experiments the optical coefficients of the phantoms are cm uniformly, cm−1 for the background phantom (excluding the inclusions), and ranging from 0.18 to 0.4 cm−1 Figure 1. (a) A photograph of the experimental setup (b) A 3-D schematic drawing of experimental setup for phantom study.  Y. M. Liu et al. Figure 2. (a) A schematic drawing for the 3-D geome- try of an optical phantom. (b) The data acquisition pro- cess of on the boundary of the physical domain (meshed area) for Equation (2b), from light intensity measure- ments of 3-D phantom surface. for the inclusions by adjusting the ink-Intralipid mix. An inclusion with pure black ink has a theoretical value of that tends towards infinity. These optical parameters are standard values used for our rat brain phantom ex- peri ments. 4. Reconstruction Results The reconstruction is done without assuming any prior knowledge of the total number, location or optical para- meter values of the inclusions. We collected six groups of “phantom data” with inclusions and an additional group of measurement data for the phantom without any inclusion as the background reference. The data are the light intensity at the boundary of the physical domain collected by a CCD camera. They served as Dirichlet boundary condition while solving the inverse models. Within the six groups, the first three have one inclusion each of which has different absorption contrasts; see the upper panel of Fig ur e 5. The last three groups have two inclusions; see the lower panel of Figure 3, also with three different contrasts. Let be the peak value of the inclusion, and be the background value. Then the contrasts in our experiments are and 4, respectively. Figure 3 shows the reconstructed images of all six groups of data. The recovered positions in the first three groups are within the circle of the actual position of the single inclusion, the dashed circle. The recovered posi- tions in the last three groups are also approximate to the actual locations of the inclusions; the two dashed circles, except that the distance between the two reconstructed inclusions is closer than the actual distance. However, we observe from the lower panel of Figure 3 that the distance between two reconstructed inclusions becomes larger when the contrast of the inclusions increases (from left to right in the figure). Especially, in the figure of two in- clusions with contrast 4:1, the lower right panel, the two inclusions can be better resolved from each other. Listed in Table 1 are the maximal contrast values and relative errors for all six cases. It shows that we have imaged the contrast values of the inclusions in the same scale of magnitude. These contrast values are important as they can be further used to calculate HbO and HbR levels. In Table 2, we show the localization errors of our reconstructions. The absolute localization error is defined as the distance between the actual center and the center location of a reconstructed inclusion where attains a maximal contrast value. The relative localization error is defined as where is radius of . We have observed that the localization errors tend to increase with the number of inclusions. 5. Conclusions and Discussions We have applied the GCM algorithm of [32] for a Coefficient Inverse Problem to DOT phantom measurements. These data mimic imaging of a blood clot in a rat brain. Reconstructions are performed without any prior know- ledge of the inclusions. In our 6 cases, we found that reconstructed images of inclusions from NIR experimental data are quite accurate, including both locations of inclusions and inclusions-to-background contrasts. The main contribution of this paper is the validation of GCM by acquiring the phantom data from phantom boundary measurements, and reconstructing without assuming any prior knowledge of the total numbers, locations and the optical parameter values of inclusions. Our GCM compares favorably with other conventional locally convergent methods. We have tested the same data sets with a conventional DOT reconstruction method which is a Tikhnov regularization based method with  Y. M. Liu et al. Figure 3. Reconstructed a (x,y) for the six groups of data. Upper panel: one inclusion cases. Lower panel: two inclusions cases. The contrasts are arranged in the order 2:1, 3:1 and 4:1 from left to right. The actual locations of inclusions are marked out in the dashed circles. Table 1. Reconstructed maximal contrast values within imaged inclusions and relative errors of a(x, y) in terms of maximal contrast values. Actual contrast (# of inclusions) Reconstructed contrast Relative Errors 2:1 (One inclusion) 2.33 16.7% 3:1 (One inclusion) 3.29 9.86% 4:1 (One inclusion) 4.57 14.3% 2:1 (Two inclusions) 2.29 14.8% 3:1 (Two inclusions) 3.49 16.4% 4:1 (Two inclusions) 4.58 14.7% Table 2. Localization errors of reconstructed a(x,y) by GCM method. Actual contrast One Inclusion Two Inclusion Left Right 2:1 0.50 mm 5.3% 1.6 mm 17.1% 2.4 mm 25.6% 3:1 0.70 mm 7.5% 1.7 mm 18.2% 2.3 mm 24.6% 4:1 0.60 mm 6.4% 1.4 mm 15.0% 1.3 mm 13.9% depth compensation [33,34] and the regularization parameter is 0.001. The conventional DOT method was per- formed using a publicly available software HomER (http://www.nmr. mgh.harvard.edu/P MI/resources/ homer/home. htm) [35]. The computational times for both methods are similar, about 1 - 2 minutes [29]. In Figure 4, we show the reconstructed images by the conventional DOT reconstruction method for the one- inclusion cases. The locally convergent method can ident ify the changes in the absorption coefficient well; however, note that the conventional DOT algorithm cannot reconstruct the absolute value of due to the limitations of the method. The images in Figure 4 depict , the change of the coefficient in convention- 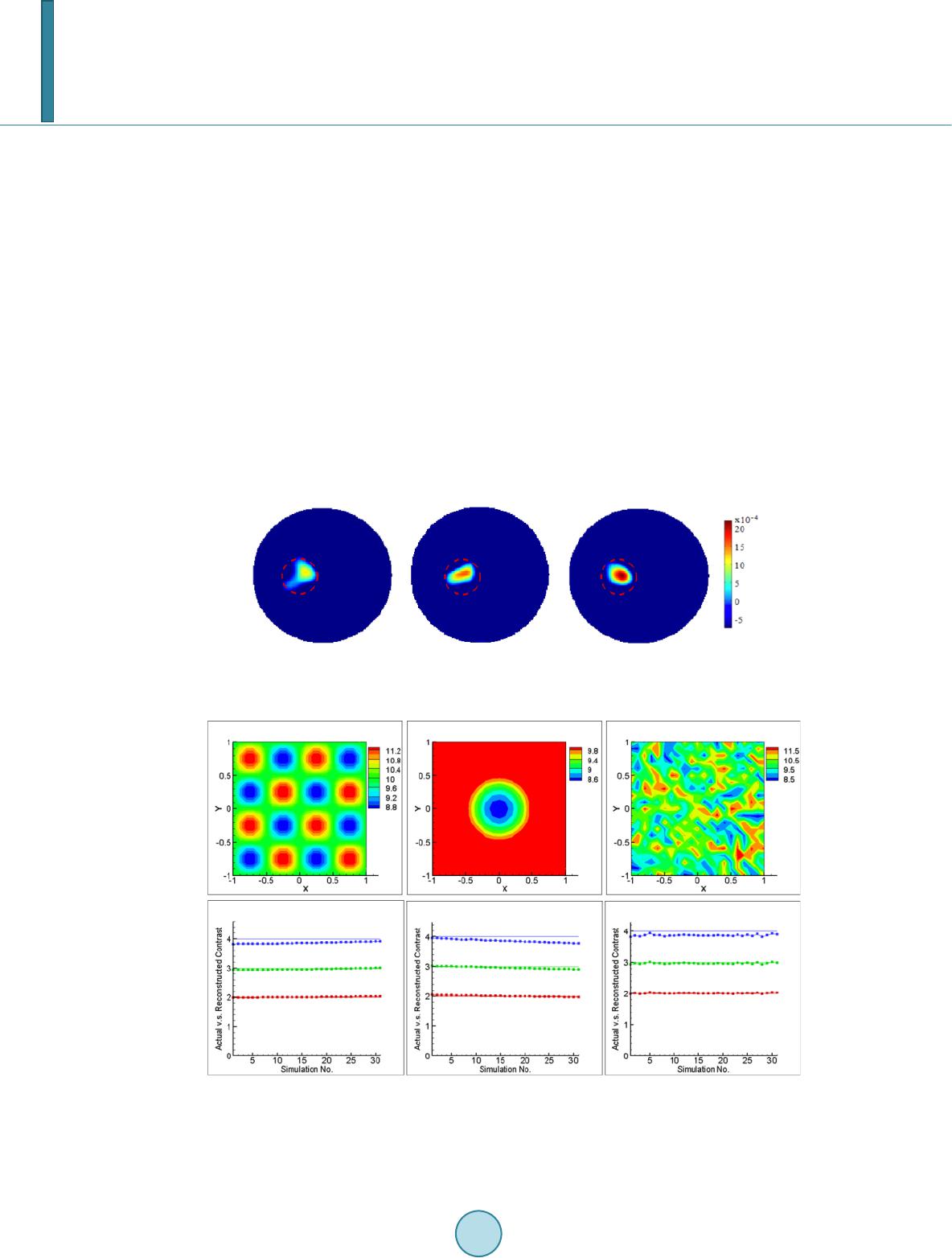 Y. M. Liu et al. al DOT from the background in the range [−5 × 10−4, 20 × 10−4], while the images in Figure 3 by GCM depict in the range [1,10] which is in the same range as actual change. For the two-inclusion cases, the con- ventional DOT did not differentiate the two inclusions. As stated in Section 2, we assume the scattering coefficient is known and uniform in our experi- ments. We also assume that keeps unchanged during the background measurements and measurements with inclusions. The reconstructed contrast reflects the change in absorption coeffi ci e nt . How- ever, in application for small animal measurements the scattering coefficient is neither homogeneous nor un- changed with time. In order to quantify the errors in recovered contrasts in with respect to discrepan- cies in the assumed background scattering coefficient, numerical simulations have been done to provide the comparison. Commonly, 5% additive noise is included in the simulated light intensities of the forward problem. Light sources are located at (x,y) = (−2,0), (2,0),(0,−2), (0,2), (0.2,2), (0.4,2) in the background domain. The first 4 sources are used for obtaining the initial tail function. The last 3 sources are used for solving the i nte- gral-differential equation in Equation (7). The detector is supposed to be a CCD camera taking in the Dirichlet boundary value, the simulated light intensity data with noise on the boundary of the physical domain are the measurement data in Equation (2b). The background domain for forward problem is and the mesh is a 120 by 120 rectangular grid. The interested physical domain for inverse problem is and the mesh for inverse problem is a 40 by 40 rectangular grid. Three different error patterns in scattering coefficient have been studied, as shown in the upper panel of Figure 5. The amount of errors Figure 4. Reconstruct ed results (changes of a(x,y) from background) for the first t hree groups of data by the conventional DOT algorithm. The contrasts are arranged in the order 2:1, 3:1 and 4:1. Actual positions of inclusions are marked out by dashed circles. Figure 5. Upper panel: three typical error patterns in the background scattering coefficient are shown. Lower panel: the recovered contrasts (lines with square symbols) and actual contrasts in are shown in each figure for tests with contrasts 2, 3 and 4. In each case, 31 simulations are done with re- spect to the errors in the scattering coefficient that range from −15.0% to 15.0%. 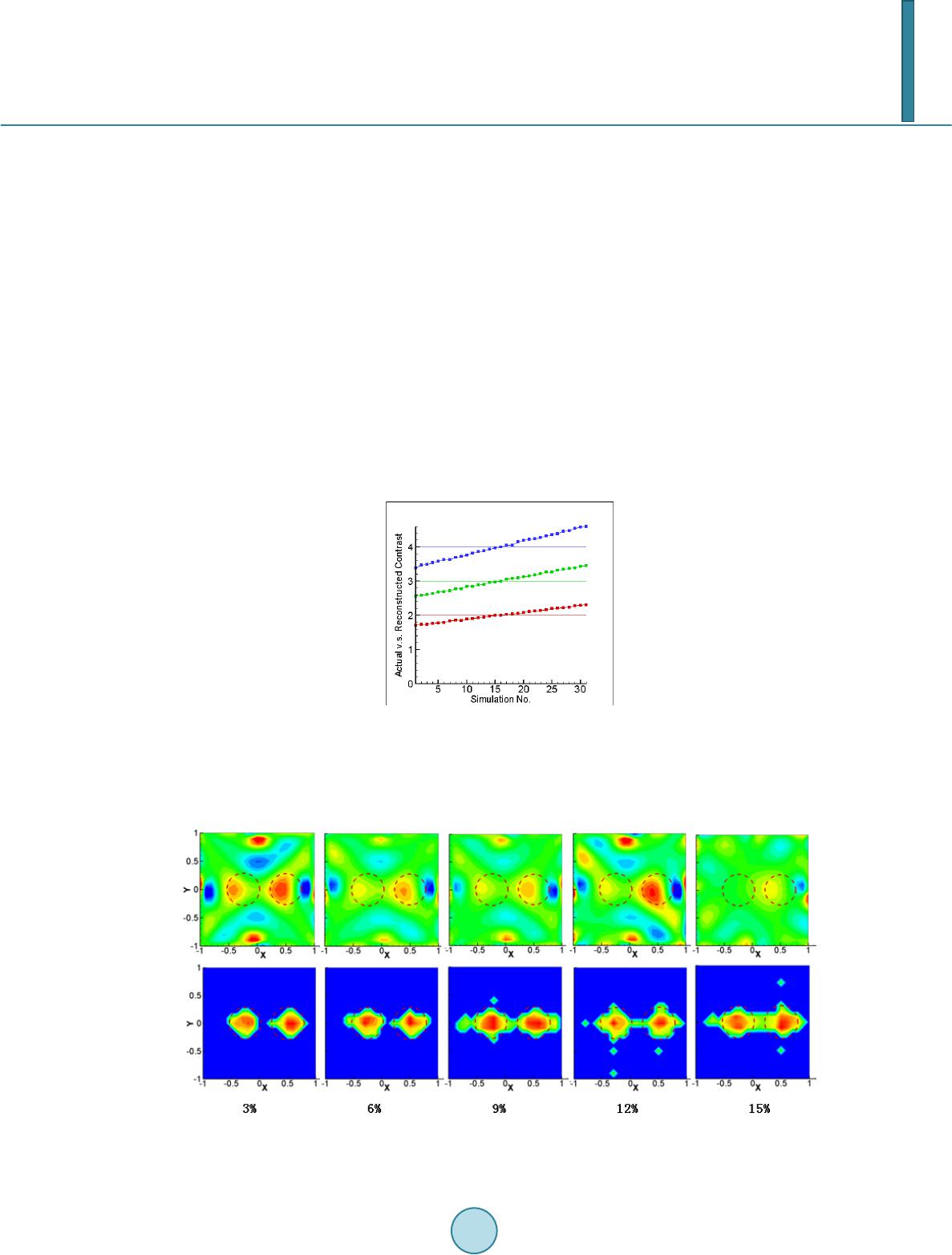 Y. M. Liu et al. ranges from −15.0% to 15.0%. The reconstructed contrasts are shown in the lower panel of Figure 5. The results show that the errors in the recovered contrasts in are pretty accurate (less than 3.0%) for all the test cases. We then studied the case where the scattering coefficient changes after the background measurements were done. Its purpose is to test the capability of the method in dealing with animal data where scattering coefficient fluctuate with time during experiments. The changes of scattering coefficients occur in locations whe r e inc lu- sions are at. The error pattern is the same as the pattern shown in the middle of the upper panel in Figure 5. The reconstructions were also successful: the locations of the inclusions are precise. However the relative peak errors change with the magnitude of fluctuations in scattering coefficients. The recovered contrasts in are shown in Figure 6. It shows that in this case, the errors in the recovered contrasts depend on the errors in the scattering coefficient linearly. The increase of reconstruction errors is due to the sensitivity of the solution to the scattering coefficient variance. In order to investigate the effect of cross talk for the locations of the reconstructed inclusions under the influ- ence of random errors in scattering coefficient, a comparative study of GCM method and conventional method has been performed. Two circular inclusions centered at (−0.25,0) and (0.5,0) with radius 0.3 are considered. The maximum value of in the inclusions is 0.3. The upper panel of Fig ur e 7 shows the reconstructed loca- tions by using the conventional method and the lower panel shows the results by our GCM method. The accurate locations are marked out by dotted circles. It should be noted that in order to give a better understanding for the Figure 6. The recovered contrasts (lines with square symbols) and actual contrasts in in the cases of that the scattering coefficient changes after the background measurements Figure 7. The reconstructed locations of the two inclusions by the conventional method (upper panel) and the GCM method (lower panel). From left to right, the error levels in scattering coefficient are 3% to 15%.  Y. M. Liu et al. results of the conventional method, the results are not cut by a threshold. For GCM method, it requires a cut at the stage of computing the tail function. We can see that at the 15% error level in scattering coefficient, the conventional method failed to reconstruct the two inclusions, while our GCM is able to give the locations of the two inclusions despite of some artifacts in between the two inclusions. In summary, we have validated our GCM reconstruction algorithm based on real data acquired by a NIR CCD Camera using optical phantoms, after testi ng successfully the GCM method on computer simulated data in pre- vious papers [27,31,32]. This study has confirmed the ability of GCM to reconstruct improved DOT images us- ing laboratory rat-head phantoms. Acknowledgements The work of all authors was supported by the National Institutes of Health grant number No. 5R33CA101098. References [1] Sri nivasan , S., Pogue, B.W., Br ooksb y, B., Jiang, S., Dehghani, H., Kogel, C., Pop lack, S.P. and P aul s e n, K.D. (20 05) Near-Infrared Characterization of Breast Tumors in V ivo Using Spectrally-Constrained Reconstruction . Technology in Cancer Research & Treatment, 4, 513-52 6. [2] Xu, Y., Gu , X., Fajardo , L. and Ji a ng, H. (20 03) In Vivo Breast Imaging with Diffuse Optical Tomography Based on Highe r-Order Diffusion Equations. Applied Optics, 42, 3163-3169. http://dx.doi.org/10.1364/AO.42.003163 [3] Godavart y, A., Thompson, A.B., Roy, R., Gurfinkel, M., Ep p s te in , M.J., Zhang, C. and Sevick-M ur aka, E.M. (20 04) Diagnostic of Breast Cancer Using Fluorescence-Enhanced Optical Tomography: Phantom Studies. Journal of Bio- medical Optics, 9, 488-496. http://dx.doi.org/10.1117/1.1691027 [4] Gopinath, S., Robertson, C.S., Grossman , R.G. and Chan ce, B. (1993) Near-Infrared Spectroscopic Localization of In- tracranial Hematomas. Journal of Neurosurgery, 79, 43-47. http://dx.doi.org/10.3171/jns.1993.79.1.0043 [5] Bluestone, A.Y., St ewart, M., Lasker, J., Abdoulaev, G.S. and Hielscher, A.H. (2004) Thre e-Dimensional Optical To- mographic Brain Imaging in Small Animals, Part 1: Hypercapn ia. Journal of Biomedical Optics, 9, 1046-1062. http://dx.doi.org/10.1117/1.1784471 [6] Zhang, G., Kat z, A., Alfa no , R.R., Kofinas, A.D., Stubblefield, P.G., Ro senfeld , W., Beyer, D., Maulik, D. and Stank- ovic, M.R. (2000) Brain Perfusion Monitoring with Frequ ency-Domain and Continuous-Wave Near-Infrared Spec- troscopy: A Cross-Correlation Study in N e wb orn Piglets. Physics in Medicine and Biology, 45, 3143-3158. http://dx.doi.org/10.1088/0031-9155/45/11/303 [7] Yodh, A.G. and Boas, D.A. (2003) Functional Imaging with Diffusing Light. In: Vo-Dinh, T., Ed., Biomedical Photonics Handbook, CRC Press, New York, 1-45. [8] Josep h, D.K., Huppert, T.J., F ranceschi ni, M.A. and Bo as, D.A. (2006) Diffuse Optical Tomography System to Image Brain Activation with Improved Spatial Resolution and Validation with Functional Magnetic Resonance Imaging. Ap- plied Optics, 45, 8142-815 1. http://dx.doi.org/10.1364/AO.45.008142 [9] Boas , D. A., Gaudet te, T., S trangman , G., Cheng, X., M arota, J.J.A. and Mandeville, J.B. (2001) The Accuracy of Near Infrared Spectroscopy and Imaging during Focal Changes in Cerebral Hemodynamics. NeuroImage, 13, 76-90. http://dx.doi.org/10.1006/nimg.2000.0674 [10] Chan ce, B. anday, E., Nio ka, S., Zhou, S., Hong, L., Worden, K., Li, C., Murray, T., Ovetsky, Y., Pidikiti, D. and Thomas, R. (1998) A Novel Method fo r Fast Imaging of Brain Function, Non-Invasively, with Li gh t . Optics Express, 2, 411-423. http://dx.doi.org/10.1364/OE.2.000411 [11] Boas, D.A., Gaud ette, T., Str angman, G., Cheng, X., Marota, J.J.A. an d Mandeville, J. B. (2001) The Accuracy of Near Infrared Spectroscopy and Imaging during Focal Changes in Cerebral Hemodynamics. NeuroImage, 13, 76-90. http://dx.doi.org/10.1006/nimg.2000.0674 [12] Wan g, K.K. and Zhu, T.C. (2009) Reconstruction of In-Vivo Optical Properties for Human Prostate Using Interstitial Diffuse Optical Tomography. Optics Express, 17, 11665-11 67 2. http://dx.doi.org/10.1364/OE.17.011665 [13] McBride, T. O., Pogue, B.W., Jian g, S., Ös terber g, U.L. and P aulsen, K.D. (2001) Initial Studies of in Vivo Absorbing and Scattering Heterogeneity in Near-Infrared Tomographic Breast Imaging. Optics Letters, 26, 822-824. http://dx.doi.org/10.1364/OL.26.000822 [14] Koleh mainen, V., Prince, S., Arridge, S.R. and Kaip i o , J.P. (2000) A State Estimation Approach to Non-Stationary Optical Tomography Problem. Journal of the Optical Society of America, 20, 876-884. http://dx.doi.org/10.1364/JOSAA.20.000876 [15] Zhang, Q., Broo ks, D.H. and Boas, D. A. (2005) A Haemodynamic Response Function Model in Spatio-Temporal Dif-  Y. M. Liu et al. fuse Optical Tomograp h y. Physics in Medicine and Biology, 50, 4625-4644. http://dx.doi.org/10.1088/0031-9155/50/19/014 [16] Arridge, S.R. and Sch otland, J.C (2009) Op tical Tomography: Forward and Inverse Problems. Inverse Problems, 25, 123010. http://dx.doi.org/10.1088/0266-5611/25/12/123010 [17] Arridge, S.R. and Hebden, J.C. (1997) Optical Imaging in Medicine: II. Modeling and Reco nst ruction. Phys. Med. Boil., 42, 841-853. http://dx.doi.org/10.1088/0031-9155/42/5/008 [18] Hielsch er, A. H., Klo se, A. D. and Hanson, K.M. (1999 ) Gradient-Based Iterative Reconstruction Scheme for Time - Resolved Optical Tomograph y. IEEE Transactions on Medical Imaging, 18, 262-271. http://dx.doi.org/10.1109/42.764902 [19] Schotland, J.C. (1997) Continu ous-Wave Diffusion Imaging. Journal of the Optical Society of America, 14, 275 -279. http://dx.doi.org/10.1364/JOSAA.14.000275 [20] O’Lear y, M.A., Boas D.A., C hance, B. and Yo dh, A.G. (1995) Experimental Images of Heterogeneous Turbid Media by Freq uen cy-Domain Diffusion-Photon Tomography. Optics Letters, 20, 426-428. http://dx.doi.org/10.1364/OL.20.000426 [21] Gryazin, Y.A., Klibanov, M.V . and Lucas, T.R. (2001) Numerical Solution of a Subsurface Imaging Inverse Problem. SIAM Journal on Applied Mathematics, 62, 664-683. http://dx.doi.org/10.1137/S0036139900377366 [22] Klibanov, M.V. and Timonov, A. (2004 ) Carleman Estimates for Coefficient Inverse Problems and Numerical Appli- cation s. Brill Academic Publishers, VSP, Imprint Brill. [23] Klibanov, M.V. and Timonov, A. (2007) Numerical Studies on the Globally Convergent Convexification Algorithm in 2D. Inverse Problems, 23, 123-138. http://dx.doi.org/10.1088/0266-5611/23/1/006 [24] Keller, H.B. and Perozzi , D.J. (1983 ) Fast Seismic Ray Tracin g. SIAM Journal on Applied Mathematics, 43, 981-992. http://dx.doi.org/10.1137/0143064 [25] Su, J., S han , H., Liu , H. and Klibanov, M.V. (2006) Reconstruction Method with Data from a Multiple-Site Continu- ous-Wave Source for Thre e-Dimensional Optical Tomography. Journal of the Optical Society of America, 23 , 2388- 2395. http://dx.doi.org/10.1364/JOSAA.23.002388 [26] Shan , H., Klibanov, M.V., Liu, H., Pantong, N. and Su, J. (2008) Numerical Implementation of the Convexification Algorithm for an Optical Diffusion Tomograph . Inverse Problems, 24, 025006. http://dx.doi.org/10.1088/0266-5611/24/2/025006 [27] Shan , H., Klibanov, M.V., Su, J., Pa nton g, N. and Liu, H. (2008 ) A Globally Accelerated Numerical Method for Opti- cal Tomography with Continuous Wave Source. Journal of Inverse and III-posed Problems, 16, 763-790. http://dx.doi.org/10.1515/JIIP.2008.048 [28] Beilina, L. and Klibanov, M.V. (2008) A Globally Convergent Numerical Method for a Coefficient Inverse Problem. SIAM Journal on Scientific Computing, 31, 478-509 . http://dx.doi.org/10.1137/070711414 [29] Beilina, L. and Klibanov, M.V. (2012) Approximate Global Convergence and Adaptivity for Coefficient Inverse Prob- lems. http://dx.doi.org/10.1007/978-1-4419 -78 05-9 [30] Su, J., Klibanov, M.V., Liu , Y., Lin , Z., P antong, N. and Liu , H. (2013) Optical Imaging of Phantoms from Real Data by an Approximately Globally Convergent Inverse Algorithm. Inverse Problems in Science and Engineering, 21, 1125-1150. http://dx.doi.org/10.1080/17415977.2012.743126 [31] P anton g, N., Su , J., Shan, H., Klibanov, M.V. and Li u , H. (2009) A Globally Accelerated Reconstruction Algorithm for Diffusion Tomography with Continuous-Wave Source in Arbitrary Convex Shape Domain. Journal of the Optical So- ciety of America, 26, 456-472. http://dx.doi.org/10.1364/JOSAA.26.000456 [32] Klibanov, M.V., Su, J., Pantong, N., Shan , H. and Liu, H. (2010) A Globally Convergent Numerical Method for an In- verse Elliptic Problem of Optical To mography. Appl. Anal., 6, 861-891. http://dx.doi.org/10.1080/00036811003649157 [33] Niu, H., Ti an , F., Lin, Z. and Liu H. (20 10 ) Development of a Compensation Algorithm for Accurate Depth Localiza- tion in Diffuse Optical Tomography. Optics Letters, 35, 429-431. http://dx.doi.org/10.1364/OL.35.000429 [34] Niu, H., Lin, Z., Tian, F., Dhamne, S. and Liu, H. (20 10 ) Comprehensive Investigation of Three -Dimensional Diffuse Optical Tomography with Depth Compensation Algorithm. Journal of Biomedical Optics, 15, 046005. http://dx.doi.org/10.1117/1.3462986 [35] Huppert, T.J., Diamond, S.G., Franceschi ni, M.A. and Boas , D.A. (2009) HomER: A Review of Tim e Series Analysis Methods for Near-Infrared Spectroscopy of the Brain. Applied Optics, 48, D2 80-D298. http://dx.doi.org/10.1364/AO.48.00D280
|