Journal of Applied Mathematics and Physics, 2014, 2, 163-169
Published Online April 2014 in SciRes. http://www.scirp.org/journal/jamp
http://dx.doi.org/10.4236/jamp.2014.25020
How to cite this paper: Ding, W.S. and Sun, Z. (2014) Wavelet-Based Response Computation for Base-Isolated Structure
under Seismic Excitation. Journal of Applied Mathematics and Physics, 2, 163-169.
http://dx.doi.org/10.4236/jamp.2014.25020
Wavelet-Based Response Computation for
Base-Isolated Structure under Seismic
Excitation
Wensheng Ding1, Zhi Sun2
1Department of Bridge Engineering, Tongji University, Shanghai, China
2State Key Laboratory for Disaster Reduction in Civil Engineering, Shanghai, China
Received January 2014
Abstract
This paper presents a wavelet-based approach for estimating the response of the base-isolated
structure under seismic ground motions. The seismic ground motion record is expressed as the
multi-scale wavelet coefficients which presents the time-frequency characteristics of the seismic
excitation. The wavelet domain governing differential equation between the wavelet coefficients
of the excitation and response is derived. Numerical study on a one-storey base isolated structure
is performed. The result shows that the wavelet based response computation method is of high
precision.
Keywords
Wavelet Transform, Seismic Excitation, Time-Frequency Characteristic, Input-Response
Relationship, Wavelet Basis
1. Introduction
Earthquakes will usually induce huge disasters to the civil structures. The way to compute structural responses
under seismic ground motions has been of continued interest to researchers over the past few decades. Base iso-
lation is a passive device used to reduce earthquake load effect of structures [1]. Compared with other seismic
resistant measures, base isolation has good applicability, safety and reliability. Seismic ground motions are gen-
erally amplitude and frequency modulated time records [2]. Their evolutions in the time-frequency domain are
their main characteristics [3]. The recently developed wavelet analysis has emerged as a powerful tool to ana-
lyze variations in time-frequency content [4,5]. It has been widely used for engineering vibration analysis [6].
This paper presents a wavelet-based approach for estimating the response of the equivalent linear base-iso-
lated frame under seismic ground motions. The seismic ground motion record is expressed as the multi-scale
wavelet coefficients which presents the time-frequency characteristics of the seismic expression. The wavelet
domain governing differential equation between the wavelet coefficients of the excitation and response is de-
rived. Numerical study on a one-storey base isolated structure is performed and presented below.

W. S. Ding, Z. Sun
164
2. Wavelet Transform and Mother Function
For any function
2
()( )t LR ψ ∈
, if it satisfies the admissible condition
2
()
R
Cd
ψ
ψω ω
ω
= <∞
∫

(1)
where
() ψω

is the Fourier transform of
()t ψ
, the function
()t ψ
is called the “mother wavelet”. A series of
wavelet functions
,() ab t
ψ
, as the dilated and translated version of
()t ψ
using scale (or dilation) parameter
a
and translation parameter
b
, can then be constructed as
,1
(),; 0
ab tb
tab Ra
a
a
ψψ
−

= ∈≠


(2)
The wavelet transform of the function,
2
()( ) ftL R∈
, with respect to the basis
()t ψ
, is defined as
1
2
,
( ,),()
ab R
tb
Wfa bfaftdt
a
ψ
ψψ
−−

=< >=

∫
(3)
It can be also expressed in another form as
( )
,,
(,),( )
ab ab
R
Wf abfaFd
ψ
ψωψω ω =<>= ∫
(4)
Here, the
()F ω
is the fourier form of the
()ft
. It is possible to reconstruct
()ft
from its wavelet coeffi-
cients
(,)Wf ab
ψ
2
11
()( ,)tb ftWfa bdadb
Ca a
ψ
ψ
ψ
∞∞
−∞ −∞
−

=

∫∫
(5)
This integral has to be discretized for numerical evaluation.
Assuming that
,(1)
j
jj
abj b σ == −∆
(6)
() ()() ()
1 111
2, 2
jjjjjjj jjj
aaaaabb bbbb
+ −+−
 
∆=−+−∆=− + −=∆
 
(7)
discretizing the Equation (5) in such a way, the discretized version is thus obtained as
,
()(, )()
ji
j iab
ij j
Kb
ftWfa bt
a
ψ
ψ
∆
=
∑∑
(8)
whe re
K
is a constant with a value equal to
3
8
KC
ψ
π
=
.
In this study, the LittleWood-Paley (L-P) mother wavelet function is used as it provides an orthogonal basis
with excellent frequency localization characteristics. Its time-domain expression is
1sin 2sin
() tt tt
ππ
ψπ
−
=
(9)
the frequency-domain expression is
( )
1
ˆ2
2
ψωπ ωπ
π
= ≤≤
(10)
As a comparison, the Morlet wavelet mother function and the harmonic wavelet mother function would be
chosen. The Morlet wavelet basis is expressed as
( )()
2
2cos 5 t
te t ψ
−
=
(11)
The frequency-domain expression is
( )
( )
2
15
2
1
ˆ2e
ω
ψω π
−−
=
(12)

W. S. Ding, Z. Sun
165
And the Harmonic wavelet basis is expressed as
( )
42
2
it it
ee
tit
ππ
ψπ
−
=
(13)
The frequency-domain expression is
( )
1
ˆ24
2
ψωπ ωπ
π
= ≤<
(14)
3. Wavelet-Based Response Computation of Base-Isolated Structure
Considering a base-isolated structure subjected to the seismic ground acceleration
()zt
, if the base-isolation
system is set to be equivalent to a linear system, the equation of motion of the structure can be expressed as fol-
low
[]
{}
[ ]
{}
[]
{}
[ ]
{}
m xc xkxm Iz ++ =−
 
(15)
where
[] []
,mc
and
[ ]
k
are the
nn×
mass, damping and stiffness matrixes respectively,
{ }
I is the
1n×
ground displacement influence vector;
{ }
x is the
1n×
displacement vector relative to the ground motion.
Assuming the damping is the classically damping [8]. Equation (15) can be transformed into the following n un-
coupled equations. The displacements response could then be represented as mode shape vector
{ }
()
(1, 2)
j
jn φ =
and generalized modal coordinate
()(1,2)
jtj n
η =
{ }
{ }
()
1
() ()
njj
j
xt t φη
=
=
∑
(16 )
Then, the original equation can be decoupled as a series of equation describing the motion in a particular
mode of vibration
2
2;1,2
jjjjjjj
zj n ης ωηωηα ++=− =
 
(17 )
where,
{ }
[][ ]
{ }
[ ]
{ }
()() ()
,,( )
TT
j jj
jj j
mI m ωςα φφφ =
represent the jth mode natural frequency, damping ratio
and participation factor.
Taking the wavelet transform on the both sides of Equation (16), the following relationship is obtained for the
respo nse [7]
()
1
(,) (,)
nj
i pqij pq
j
WxabW ab
ψψ
φη
=
=∑
(18)
where, the
()j
i
φ
is the ith element of mode shape
{ }
()j
φ
. Taking the wavelet transform of both sides of Equa-
tion (17) with the chosen wavelet basis
,() ab t
ψ
,
2
(,) 2(,)(,)(,)
jjj jjjj
W abW abW abWzab
ψψψ ψ
ηςωηωηα + +=−
 
(19)
Considering the fast decaying property of the wavelet basis in time domain and it can be shown
2
1
(,)(,)W abW ab
a
ψψ
ηη =


(20)
The right side of the Equation (20) can be written as
2
,
2
(,)() ()
ab
Wa bxtdt
b
ψ
η ηψ
∞
−∞
∂
=∂∫

(21)
Exchanging the integral with the double differentials and applying the Leibnitz rule of differential,
2
22
1
(,) (,)W abW ab
ba
ψψ
ηη
∂=
∂

(22)
Substituting the Equation (20) into Equation (22), it can be obtained that
2
2
(,) (,)
jj
W abWab
b
ψψ
ηη
∂
=∂

(23)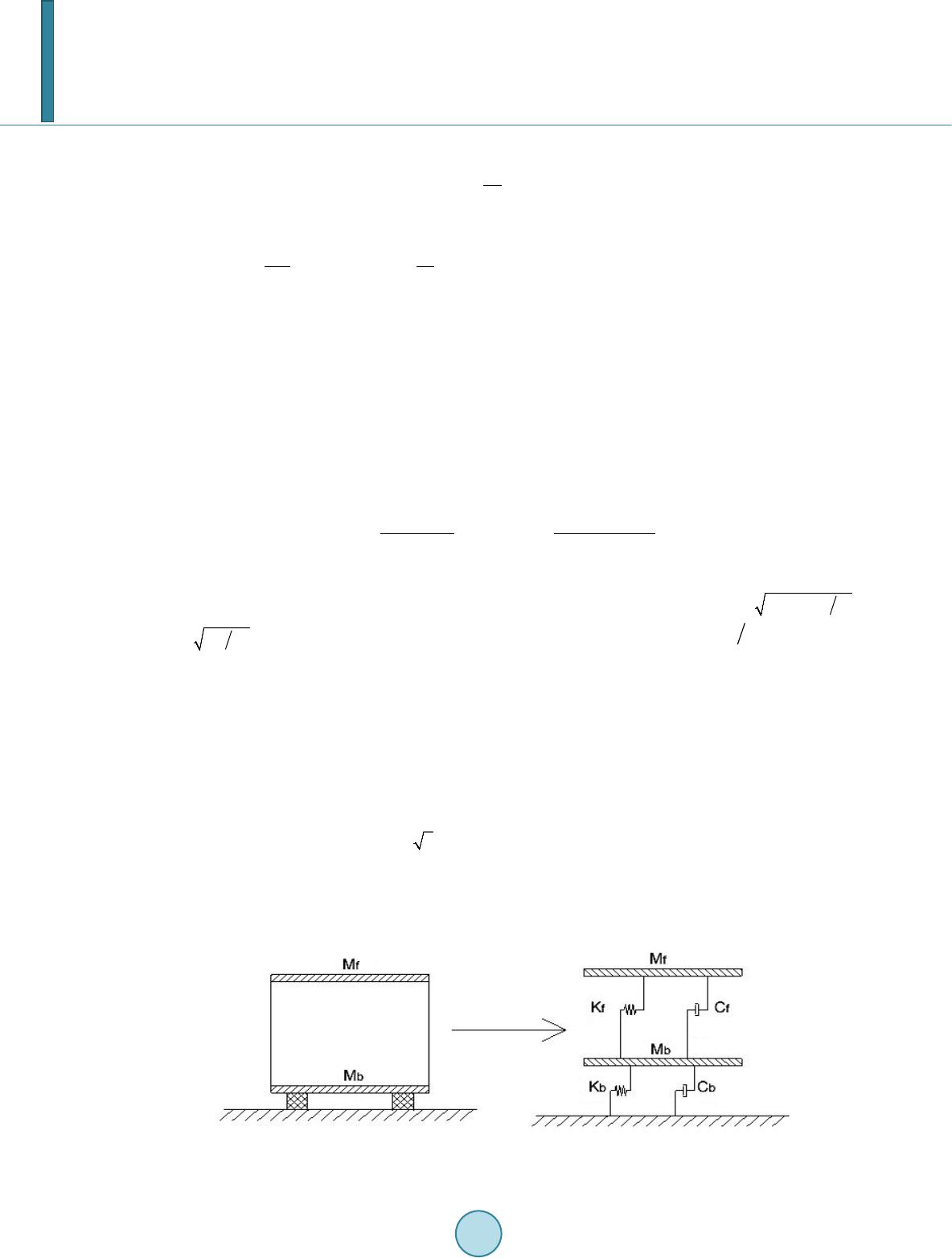

W. S. Ding, Z. Sun
166
Similarly, the following expression can be obtained
(,) (,)
jj
W abWab
b
ψψ
ηη
∂
=∂

(24)
Substituting the Equation (23) and Equation (24), the Equation (19) is expressed as [9]
22
2
(,) 2(,)(,)(,)
jjjjj jj
W abW abW abWzab
b b
ψψψ ψ
ηςωηωηα
∂∂
+ +=−
∂ ∂
(25)
The differential equation shows the relationship between the input wavelet coefficients and the response
wavelet coefficients. For a particular
j
a
，the Equation (25) can be easily solved, so the wavelet coefficients for
the given frequency band can be obtained. It should be noted that the coefficients contain both time and fre-
quency information to understand the time-frequency characteristic of the excitation and response.
4. Numerical Study
For a one storey base-isolated structure, Figure 1 shows, the base-isolation system can be equivalent as a linear
system. For a base-isolation system of shear displacement ductility ratio
µ
, strain hardening ratio
α
, and
elastic stiffness
u
K
, the equivalent stiffness and damping could be expressed as below according to the
AASHTO guide specifications [10]
0
1 ( 1)2(1 )( 1)
,[1 ( 1)]
b ub
kK
αµαµ
ξξ
µπµα µ
+−− −
=−=+−
Therefore, the one storey base-isolated structure can be simplified as a 2DOF system with the lumped masses
,
bf
mm
, the stiffnesses
,
bf
kk
, and the damping
,
bf
cc
. Denoting that
2( )
bb fb
T mmk π = +
,
2
f ff
T mk π =
which is the vibration period of the non-isolated structure, and . The damping
ratio is set to be and .
The seismic ground motion considered is the seismic ground motion recorded during 1971 San Fernando
earthquake. Figure 2 shows the first 15s of ground motion time record and the corresponding wavelet
time-fr eq ue nc y c haracteristic. As presented, the seismic is of an energy concentration in the time duration
around 8s and in the frequency band of 1-3Hz.
To compute structural response under earthquake, the wavelet coefficients of structural response in each scale
are computed firstly and then transformed into time domain via wavelet reconstruction. For different mother
wavelet function, the following parameters are set during the computation: for L-P wavelet mother function,
2 σ =
, for
2
j
a π ωπ ≤≤
, so
j= −5,−4,...4
; for Harmonic wavelet mother function,
2, j σ == −4,−3,...5
;
for Morlet wavelet mother function,
2, j σ == −9,−8,...5
. Fi gure 3 shows the computed time history of ab-
solute acceleration and relative displacement response of
f
m
by wavelet based computation and time-int e gr a-
tion with
1, 2
b
vT s==
and
1
fs
Τ=
. As presented, the computed response histories based on different wave-
let basis functions match very well with the computed history by the time-integra ti o n.
Varying the natural periods
f
T
from 0.10 s to the 3.0 s and fixing
1, 2
b
vT s= =
, the absolute acceleration
Fig ure 1. The base-isolated structure.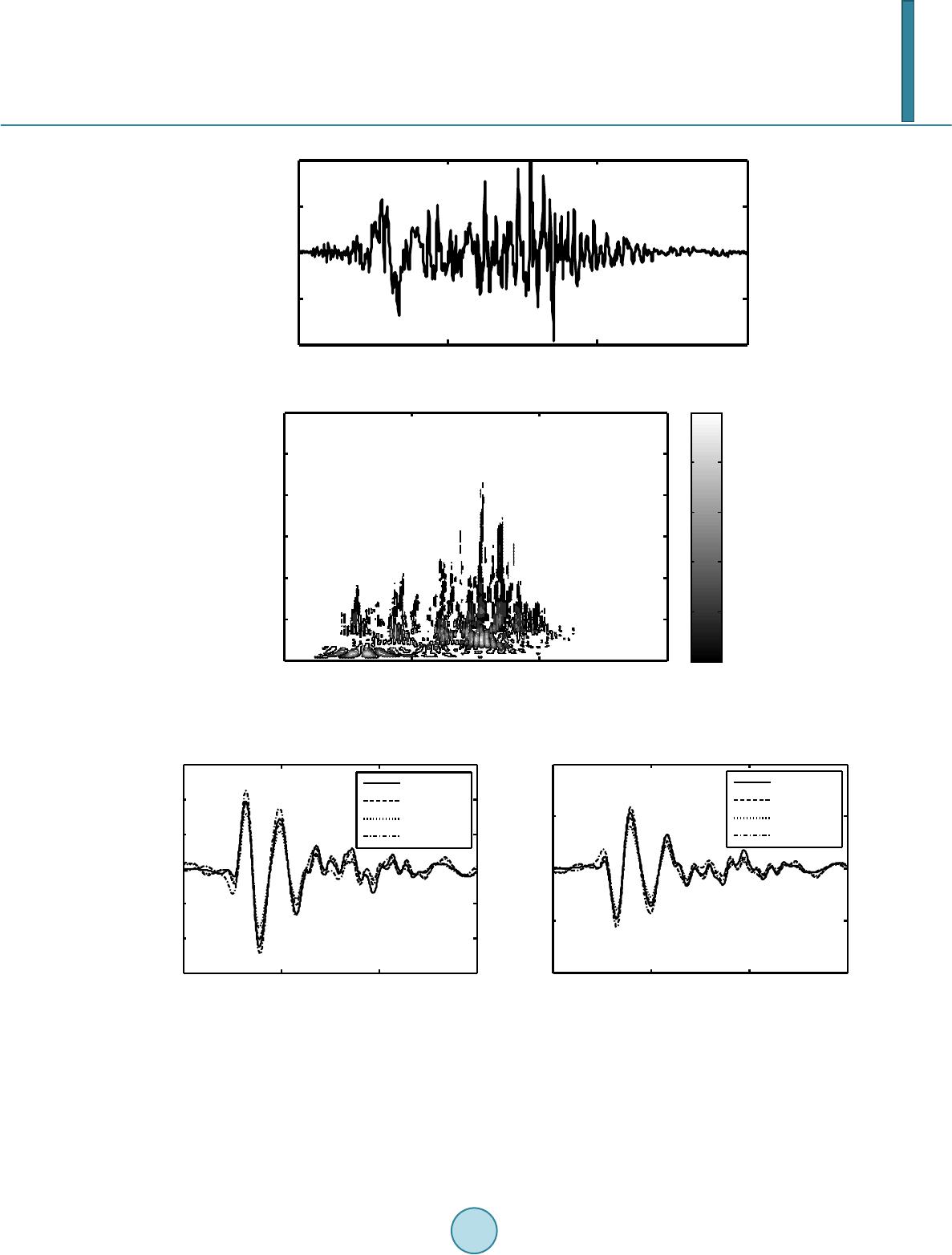
fb
vmm=
0.10
b
ς =
0.03
f
ς =

W. S. Ding, Z. Sun
167
Figure 2. The San Fernando ground motion record and its wavelet representation.
(a) (b)
Fig ure 3. Comparison of computed acceleration (a) and relative displacement (b) response with
1, 2
b
vT s= =
and
1
fsΤ=
using the time-integration and wavelet based methods.
and relative displacement response spectrum are computed using different methods and different mother wavelet
functions. Figure 4 shows the result. As presented for this study, the response calculated from Morlet wavelet
0510 15
-10
-5
0
5
10
acceleration (m/s
2
)
t (s)
f (Hz)
0510 15
0
5
10
15
20
25
30
0.05
0.1
0.15
0.2
0.25
0.3
0510 15
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
t (s)
acceleration (g)
integration
L-P
harmonic
m orlet
0510 15
-0.2
-0.1
0
0.1
0.2
t (s)
relative displacement (m)
integration
L-P
harmonic
m orlet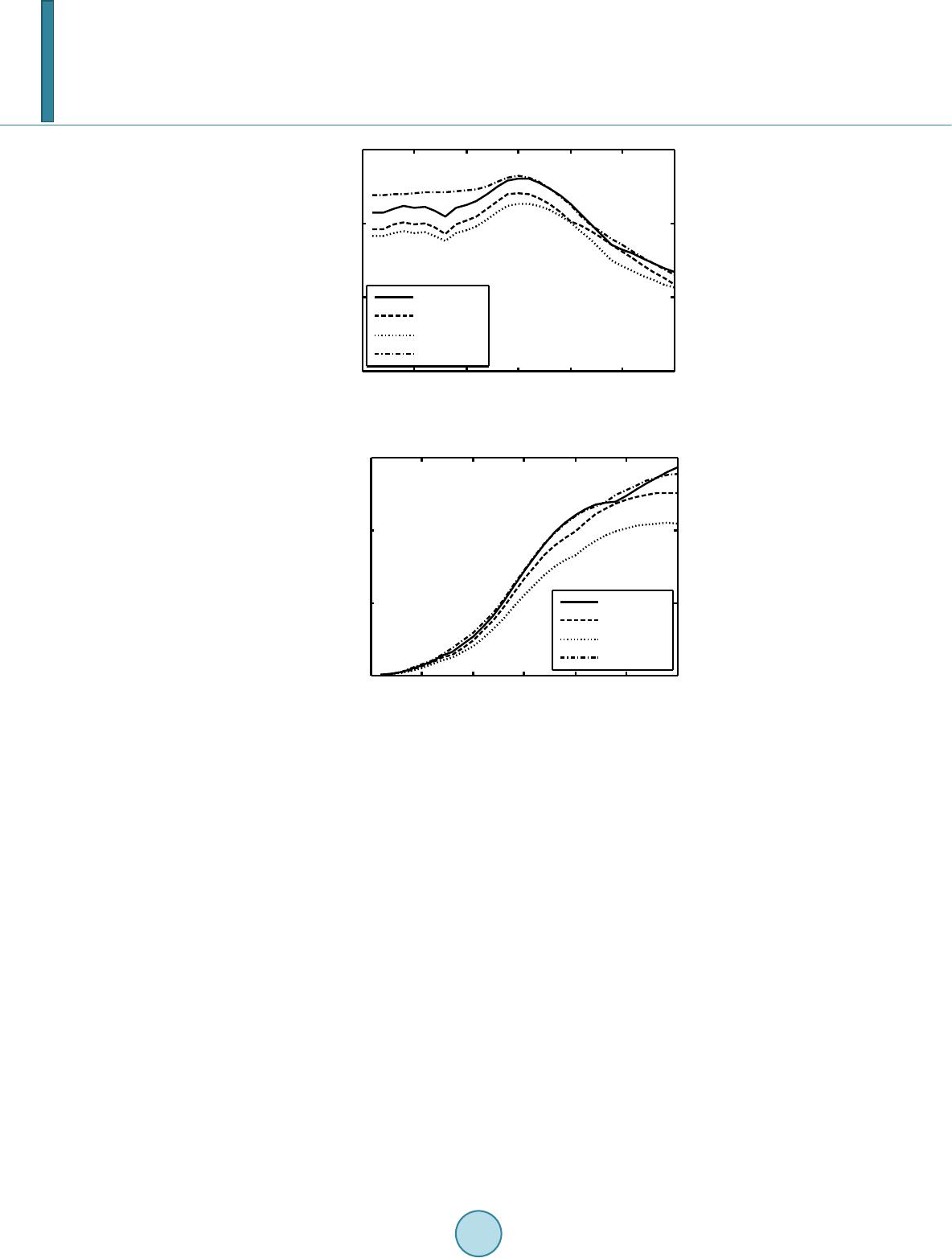

W. S. Ding, Z. Sun
168
(a)
(b)
Figure 4. Comparison of computed acceleration (a) and relative displacement (b) spectra using time-integration and wavelet
based methods.
will generally provide an over-estimation and the response calculated from L-P and harmonic wavelet will gen-
erally provide an under-estimation; the computation errors for acceleration response spectrum are generally lar-
ger than the computation errors for relative displacement response spectrum; the response calculated using L-P
wavelet is generally of the best accuracy.
5. Summary
This paper presents a wavelet-based approach for estimating the response of the base-isolated structure under
seismic ground motions. Numerical study on a one-storey base isolated structure is performed. The results show
that the wavelet decomposition can provide orthogonal multi-scale expression of structure governing equation of
motion and can be used for structural vibration response computation; the L-P mother wavelet function is of
good fast decaying property in time domain and precise localization property in frequency domain and can pro-
vide good precision on nonstationary seismic excitation expression as well as on structural seismic response
computatio n.
References
[1] Tak ed a , J. (1997) Building Isolation and Vibration Control. China Architecture & Building Press, Beijing.
[2] Caughey, T.K. and Stumpf, H.J. (1961) Transient Response of a Dynamic System under Random Excitation. Journal
00.51.0 1.52.0 2.53.0
0
0. 2
0. 4
0. 6
perio d(s)
accel spectral (g)
integrat i on
L-P
harmon i c
morlet
00.5 1.0 1.52.0 2.53.0
0
0. 2
0. 4
0. 6
perio d(s)
relative displacement(m)
integrat i on
L-P
harmonic
morlet

W. S. Ding, Z. Sun
169
of Applied Mechanics, 28, 563-566. http://dx.doi.org/10.1115/1.3641783
[3] Basu, B. and Gupta, V.K. (19 98 ) Seismic Response of SDOF System by Wavelet Modeling of Non-Stationary Process.
Journal of Engineering Mechanics, 1142-1150. http://dx.doi.org/10.1061/(ASCE)0733-9399(1998)124:10(1142)
[4] Newla nd , D.E. (1994 ) Wavelet Analysis of Vibration, Part 1: Theory. Journal of Vibration and Acoustics, ASME, 11 6,
409-416. http://dx.doi.org/10.1115/1.2930443
[5] Daub echies, I. (1992) Ten Lectures on Wavelets. Society for Industrial & Applied Mathematics. Philadelphia, Penn-
sylvania.
[6] Newla nd , D.E. (1994) Wavelet Analysis of Vibration, Part 2: Wavelet M aps. Journal of Vibration and Acoustics,
ASME , 116.
[7] Chopra, A.K. (2007) Dynamics of Structures, Theory and Applications to Earthquake Engineering. Higher Education
Press, Beijing.
[8] Basu, B. and Gupta, V.K. (1997) Seismic Response of MDOF System by Wavelet Transform. Earthquake Engineering
and Structures Dynamics, 26, 1243-1258.
http://dx.doi.org/10.1002/(sici)1096-9845(199712)26:12<1243::aid-eqe708>3.0.co;2-p
[9] Du, P. and Sun, Z. (2010) Wavelet-Based Instantaneous Roo t -Mean-Square Response Estimation for sdof Systems
under Seismic Excitation. Academic Engineering Mechanics, 27, 122-126 .
[10] (1991) Guide Specifications for Seismic Isolation Design, American Association of State Highway and Transportation
Officials, Washington D.C.