 Journal of Applied Mathematics and Physics, 2014, 2, 32-38 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.25005 How to cite this paper: Pato, M.P. and Bohigas, O. (2014) Structure and Curvatures of Trajectories of a 2D Log-Gas. Journal of Applied Mathematics and Physics, 2, 32-38. h t tp://d x.d oi.org/10.4236/ jam p. 2014.25005 Structure and Curvatures of Trajectories of a 2D Log-Gas M. P. Pato1, O. Bohigas2 1Instituto de FÍsica, Universidade de São Paulo Caixa Postal, São Paulo, S.P., Brazil 2CNRS, Université Paris-Sud, UMR8626, LPTMS, Orsay Cedex, France Email: mpato@if.usp.br Received December 2013 Abstract A model is constructed to study the statistical properties of irregular trajectories of a log-gas whose positions are those of the complex eigenvalues of the unitary Ginibre ensemble. It is shown that statistically the trajectories form a structure that reveals the eigenvalue departure positions. It is also shown that the curvatures of the ensemble of trajectories are Cauchy distributed. Keywords Statistical Mechanics, Random Matrix Theory, Quantum Hall Effect 1. Introduction The question of the formation of structures in the evolution of a 2D log-gas whose particle positions are those of the eigenvalues of non-Hermitian random matrices [1] moving in the complex plane under the action of an ex- ternal parameter, recently has been addressed [2,3]. It has been shown that, in the transition from the Hermitian to the non-Hermitian unitary class of the Gaussian ensemble of random matrix theory (RMT) [4], eigenvalues keep memory of their position in the real axis as they progressively evaporate into the complex plane. As a sequel of Ref. [2], we here investigate what happens with the trajectories after they reach the final stage when the Hermiticity is completely broken, that is when the eigenvalues belong to the Ginibre ensemble [5]. By using the stability property of the Gaussian distribution, a model is constructed in which the nature of the en- semble is preserved during the evolution. The question addressed is then the same: do they keep memory of their initial relative positions? In other words, eigenvalues initially at the edge or near the origin statistically move in- side these initial regions? If so, their trajectories form a structure in the 2D space. The electrostatic analogy between eigenvalues and a coulomb gas can be traced back to the consideration by Stieljes of the distribution of the roots of polynomials as those of unidimensional charges (wires) interacting via a logarithmic potential. The ground state of the 1D Girardeau gas [6,7 ] and that of the 2D electron gas described by the Laughlin wave function [8,9] can be considered physical realizations of log-gases. If we suppose an ex- ternal parameter acting without disturbing the nature of the gas, then we have a physical situation in which our results would apply. We remark that eigenvalues moving in the complex has also been experimentally studied [10].  M. P. Pato, O. Bohigas Parametric correlations have been matter of investigation in the RMT as a signature of the universality of quantum chaos statistics. Specially the level curvatures has been studied both theoretically [11-16] and experi- mentally [15,16]. Recently, these studies have been extended to the case of eigenvalues at the spectral edge [20]. Here we are investigating curvature distributions of the complex eigenvalues as another way of looking to fea- tures of their trajectories. 2. The Equations of Motion Consider a non-Hermitian complex matrix H, of size N, which depends on a real positive parameter λ. To inves- tigate the properties of the trajectories followed in the complex plane by its eigenvalues as the parameter changes, we resort to a system of equations which describes their motion [21]. Taking the derivative (denoted by a dot) with respect to λ of the decomposition equation (1) we obtain (2) where (3) and (4) The diagonal part of (2) gives (5) while the off-diagonal gives (6) or (7) Further, for the derivative of P we have (8) On the other hand, combining Equations (4) and (7) the equations (9) and (10 ) describe the evolution of the eigenvectors. Finally, to complete the derivation, the arbitrariness of the matrix U is used to impose the necessary condition that its diagonal elements are zero, that is The above equa- tions form a complete system which, in principle, numerically can be solved once initial conditions are given. 3. The Model As no hypothesis about the nature of the matrix elements has been made, the set of equations derived in the pre- vious section is general. In particular, they show that repulsion between pair of eigenvalues is a conspicuous feature of generic matrices. Now we particularize it to the kind of matrices we are interested in, that is to those of the Ginibre ensemble. Namely, to random matrices whose joint distribution of elements is given by  M. P. Pato, O. Bohigas (11) such that the elements are Gaussian distributed. It is known that eigenvalues of these matrices are located inside a disk of radius of the order of square root of the size of the matrices. A result that can be derived from the joint distribution of the eigenvalues ( ) ( ) 1 1,. ... exp.. NN Pz ,,z=CWz,z − (12) where () () 1 ²2 log N k ji k= l>i W=zz z −− ∑∑ (13) This expression shows that eigenvalues move under the action of a confining potential and a two-body repul- sive logarithmic interaction between the eigenvalues. This logarithmic interaction justifies the log-gas analogy. If two matrices, S and T, are taken out of this ensemble to construct a new matrix H whose elements are given by ( )( ) cos sin ij ijijijij H =sω λ+T ω λ (14) then, from the stability property of the Gaussian distribution, it follows that H (λ) itself also belongs to the en- semble. With frequencies ωij real and positive, the elements of Hij will oscillate as λ evolves and, if the frequen- cies are equal or satisfy some rational relation, the matrix H and, as a consequence, its eigenvalues will have a periodic motion. If, on the other hand, frequencies are incongruate, the matrix H will have an irregular evolution, and its eigenvalues will describe irregular trajectories. A simple way of having the incongruate frequencies is to take them randomly out of an uniform band of frequencies of width W, for instance from the distribution ( )( ) ( ) 1 2 02 W , if ωω < W Pω={ W , if ωω > − − (15) By doing this, we are imposing an extra external source of randomness which puts our model in the context of the disordered ensembles [22]. 4. The Trajectories In order to avoid regularity caused by some periodicity in the evolution of the matrix, the model with incongru- ent frequencies is adopted in the calculation of the trajectories. In this case, as matrix elements undergo their in- dependent variation, correlations between eigenvalue and eigenvector evolutions prevent the use of the set of equations describing only eigenvalue motions as done in Ref. [2]. This difficulty easily can be circumvented by using instead Equations (5), (9), and (10), with the matrix elements of P given by (1 6) These equations form a complete set which describes the combined evolution of the set of eigenvalues and eigenvectors. The initial values of the eigenvalues and of the Q matrix are given by the matrix S. While the ini- tial matrix Q−1 is obtained from the adjoint matrix S✝ . To integrate these equations is equivalent to diagonaize the matrix H (λ) at each intermediate value of the pa- rameter λ during its evolution. The advantage of using them is to be able to follow the trajectory of each indi- vidual eigenvalue. In this respect, they provide a way of studying the behavior of individual eigenvalues, a kind of approach which has aroused interest recently [23,24]. However, considering the complete set of eigenvalues, both procedures should give the same result. That this is indeed the case is shown in Figure 1, in which the two set of trajectories are obtained using the two proce- dures. The accurate agreement between these trajectories attests the reliability of the equations of motion and vice versa of the diagonalization method. As a proof the utility of the equations of motion, we focus in the Fig- ure 2, the event of a frontal collision of a pair of eigenvalues seen in Figure 1 around the point (−1.5, −1.5). 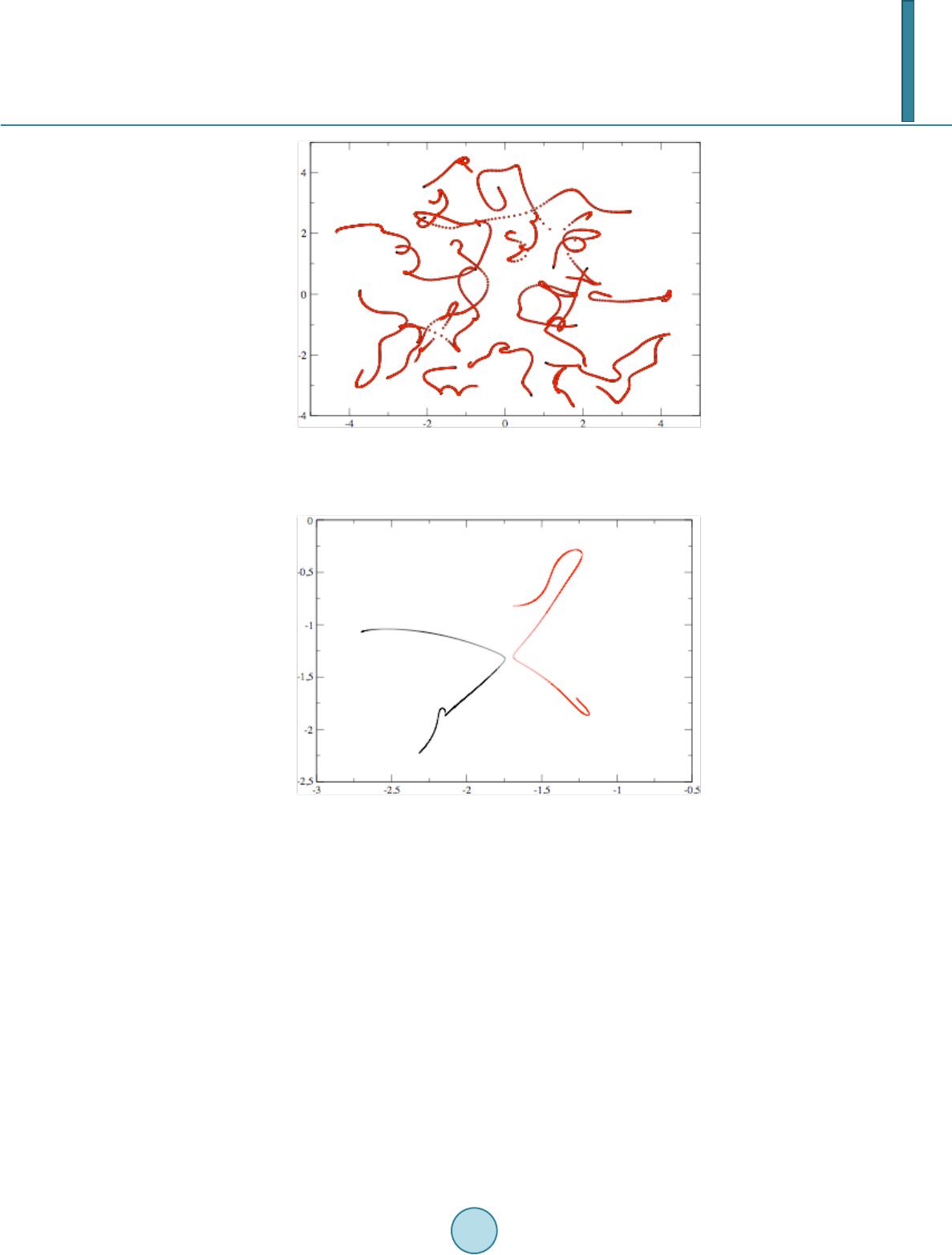 M. P. Pato, O. Bohigas Figure 1. The comparison between the set of N = 20 eigenvalue trajectories calculated integrating the equations of motion and by di- agonalizing the matrices is shown. Figure 2. The frontal collision between two trajectories seen around the point (−1.5, −1.5) in Figure 1 is shown. To see the formation of structures it is necessary to superpose many trajectories. We have calculated from an ensemble of matrices trajectories constituted of the two ones starting closest and the two ones starting farthest to the origin. The average value of the band is taken to be ω0 = 1, while two width of the band W = 0.5 and W = 1.5 were used. The results are shown in Figures 3 and 4. It is clear that the trajectories statistically tend to remain in the re- gion of their initial positions. The picture that emerges from these figures is that eigenvalues are forced to remain at the border or at the center of the gas. Eventually, a trajectory in one of these regions escapes and moves towards the other. This can be understood as the result that each eigenvalue move under the combined action of the confining harmonic po- tential and the mean field produced by the others. This combination forces them to remain in the region where they are, though, eventually, a close encounter can throw them out of where they are. 5. The Curvatures An important measure of the behavior of the trajectories is the statistical distribution of their curvatures. The ex- pression of the curvature κ(x, y) at a point of a 2D trajectory is, in terms of its parametric equation of motion, 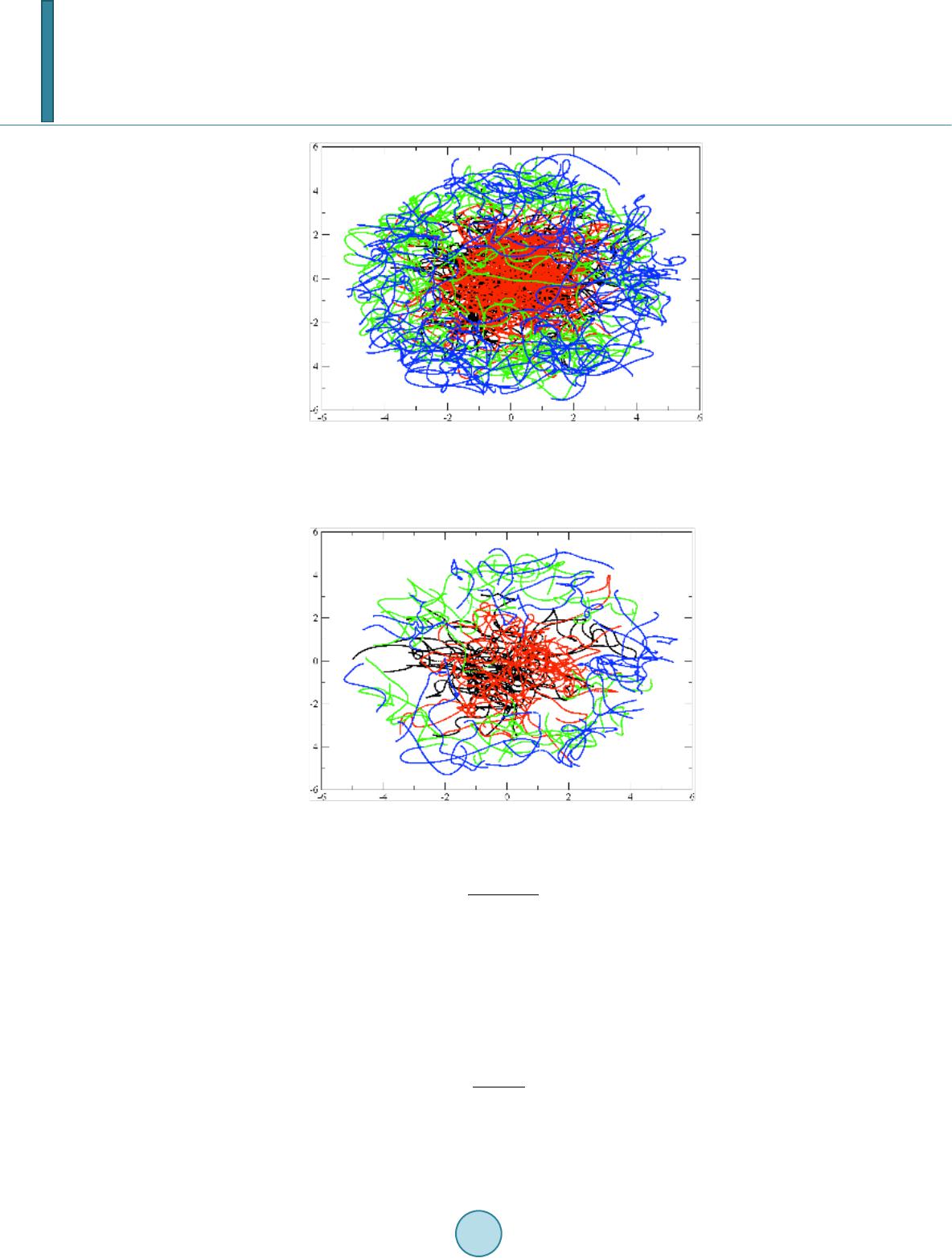 M. P. Pato, O. Bohigas Figure 3. Ensemble of trajectories of 100 matrices of size N = 20 generated evolving two eigenvalues initially at the edge and two at the center is shown. The band of frequencies has parameters ω0 = 1 and W = 0.5. Figure 4. The same as Figure 4 for 50 matrices and band of fre- quencies with parameters ω0 = 1 and W = 1.5. ( ) 1.5 ² ² xy xy κ=x +y − (1 7 ) For our equation of motions, the “velocities”, are given by the real and the imaginary parts of Equation (5) and the “accelerations”, by the real and the imaginary parts of the diagonal elements of the derivative of P, that is by Equation (8). Explicitly, we have (18) and 2 2P ¹ km mk kkkijij jk m kij km P z =P=ωQ HQ zz ≠ − − ∑∑ ( 19 ) We have found that the distributions obtained by collecting curvatures of all eigenvalues of an ensemble of matrices are well fitted by the Cauchy distribution 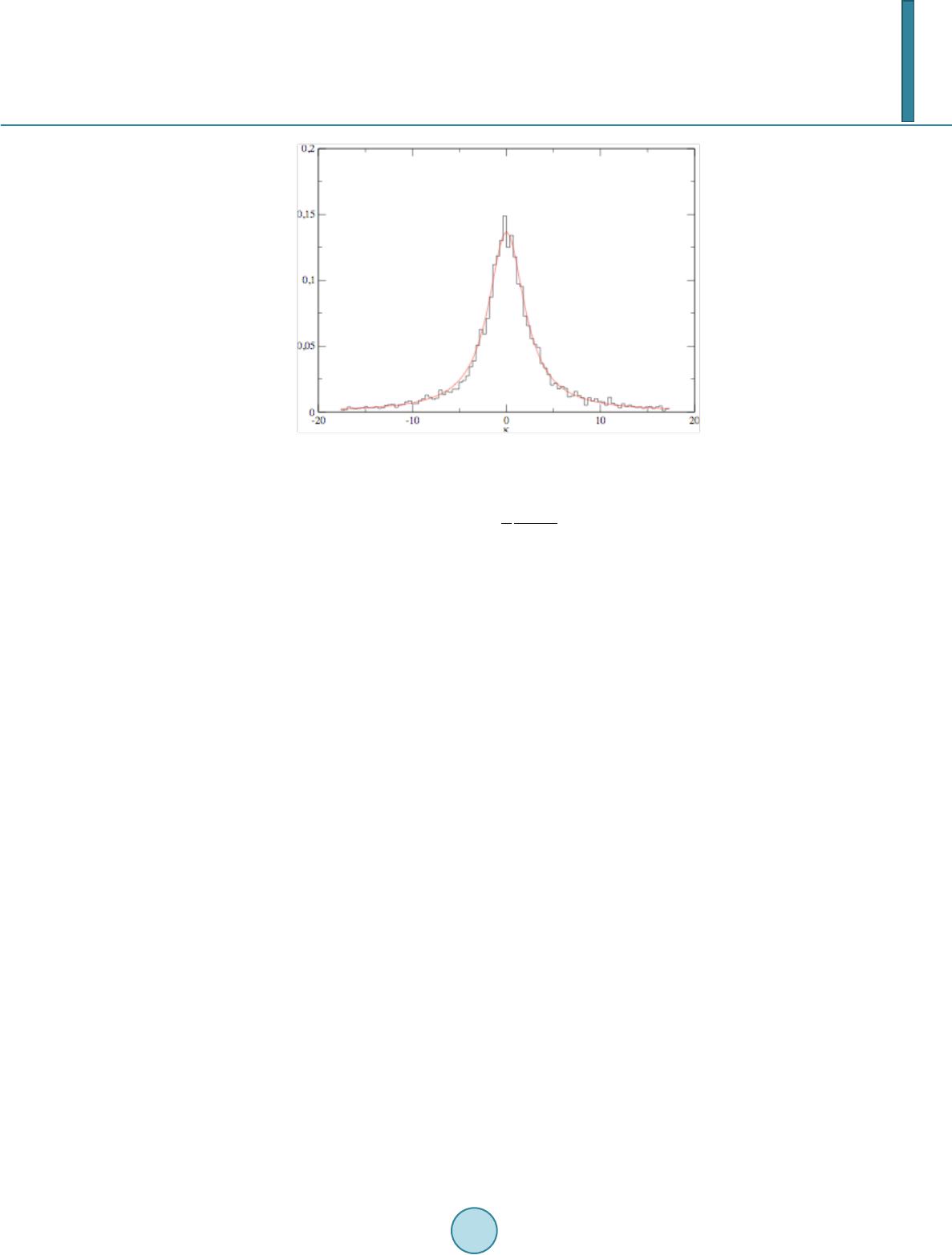 M. P. Pato, O. Bohigas Figure 5. Distribution of curvatures with N = 20 is plotted against a Cauchy distribution with parameter γ = 2.32. (20 ) where the parameter γ depends on the choice of frequencies distribution. This result is illustrated in the Figure 5. 6. Conclusion We have investigated the statistical properties of the tra jectories in the complex plane of the eigenvalues of the unitary class of the Ginibre ensemble. This study complements the results obtained in Ref. [2] in which eigen- values evaporated from the real axis into the complex plane in the transition from the Hermitian unitary to the Ginibre ensemble. As in Ref. [2], also eigenvalue trajectories show a structure determined by their departure po- sitions. This structure suggests that the combination of the mean field and the confining potential force eigenva- lues to remain at the border or at the proximities of the center. Eventually, though, a close encounter can throw them out of these regions. We also have found that curvatures of the ensemble of the trajectories are Cauchy distributed. Acknowledgements This work is supported by the Brazilian agencies CNPq and FAPESP. References [1] Forrester, P.J. (2010) Log-Gases and Random Matrice s. Princeton University Press. [2] Bohigas, O., de Carvalho, J.X. and Pato, M.P. (2013) Physical Review E, 86, 031118. [3] Pato, M.P., Bohigas, O. and de Carvalho, J.X. (2013) Proc. of the 4th Interational Interdisciplinary Chaos Symposium, Springer-Verlag. [4] Mehta, M.L. (2004) Random Matrices. 3rd Edition, Academic Press, London. [5] Ginibre, J. (1965) Journal of Mathematical Physics, 6, 440. [6] Girardeau, M. (1960) Journal of Mathematical Physics, 1, 516. [7] Kolomeisky, E.B., Newman, T.J., Straley, J.P. and Qi, X. (2000) Physical Review Letters, 85, 1146. [8] Laughlin, R.B. The Quantum Hall Effect. Springer-Verlag, New York. [9] Di Francesco, P., Gaudin, M., Itzykson, C. and Lesage, F. (1994) International Journal of Modern Physics A, 9, 4257. [10] Persson, E., Rotter, I., Stockmann, H.-J. and Bat h, M. (2000) Physical Review Letters, 85, 2478.  M. P. Pato, O. Bohigas [11] Wilkinson, J. (1988) Journal of Physics A, 21, 4021. [12] Zakrzewski, J. and Delande, D. (1993) Physical Review E, 47, 1650. [13] Simons, B.D., Hashimoto, A., Courtney, M., Kleppner, D. and Altshuler, B. L. (1993) Physical Review Letters, 71, 2899. [14] von Oppen, F. (1995) Physical Review E, 51, 2647. [15] Leboeuf, P. and Siebert, M. (1999) Physical Review E, 60, 3969. [16] Hussein, M.S., Malta, C.P., Pato, M.P. and Tufaile, A.P.B. (2002) Physical Review E, 65, 057203. [17] Ellegaard, C., Guhr, T., lindemann, K., Nygard, J. and Oxborrow, M. (1999) Physical Review Letters, 77, 4918. [18] Ellegaard, C., Guhr, T., Oxborrow, M. and Schaadt, K. (1996) Physical Review Letters, 83, 2171. [19] Pato, M.P., Schaadt, K., Tufaile, A.P.B., Ellegaard, C., Nogueira, T.N. and Sartorelli, J.C. (2005) Physical Review E, 71, 037201. [20] Fyodorov, Y.V. (2012) Acta Physica Polonica A, 120, 100-113. [21] Pato, M.P. (2002) Physica A, 312, 153. [22] Bohigas, O. and Pato, M.P.J. (2010) Physical Review E, 77, 011122. [23] O’Rourke, S. (2010) Journal of Statistical Physics, 138, 1045. [24] Terence, T. and Vu Van (2011) Acta Mathematica, 206, 127.
|