 Journal of Power and Energy Engineering, 2014, 2, 687-693 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24092 How to cite this paper: Long, D.L. and Wei, H. (2014) Extended Sequential Truncation Technique for Adaptive Dynamic Programming Based Security-Constrained Unit Commitment with Optimal Power Flow Constraints. Journal of Power and Energy Engineering, 2, 687-693. http://dx.doi.org/10.4236/jpee.2014.24092 Extended Sequential Truncation Technique for Adaptive Dynamic Programming Based Security-Constrained Unit Commitment with Optimal Power Flow Constraints Danli Long, Hua Wei Guangxi key Laboratory of Power System Optimization and Energy Technology, Guangxi University, Nanning, China Email: longdanli@163.com Received February 2014 Abstract Considering the economics and securities for the operation of a power system, this paper presents a new adaptive dynamic programming approach for security-constrained unit commitment (SCUC) problems. In response to the “curse of dimension” problem of dynamic programming, the ap- proach solves the Bellman’s equation of SCUC approximately by solving a sequence of simplified single stage optimization problems. An extended sequential truncation technique is proposed to explore the state space of the approach, which is superior to traditional sequential truncation in daily cost for unit commitment. Different test cases from 30 to 300 buses over a 24 h horizon are analyzed. Extensive numerical comparisons show that the proposed approach is capable of ob- taining the optimal unit commitment schedules without any network and bus voltage violations, and minimizing the operation cost as well. Keywords Power System Operation and Planning; Priority Order; Adaptive Dynamic Programming; Unit Commitment 1. Introduction Security-constrained unit commitment (SCUC) is a crucial issue for power system generation scheduling. The most difficult issue for SCUC with optimal power flow constraints is its computational difficulties. Mathemati- cally, SCUC is a nonconvex, nonlinear, large-scale, mixed-integer optimization problem. Since it involves a large number of 0/1 variables that represent up/down status of the unit. From the viewpoint of computational complexity, SCUC is in the class of NP-hard problems and cannot be solved in the polynomial time [1]. Hence, the key to SCUC problems is to handle the 0/1 variables. Up to now, many approaches are proposed to solve SCUC problems, such as decomposition approach [1], branch-and -bound algorithm [2], MILP-based approach [3] and Semi-definite programming [4]. Nevertheless,  D. L. Long, H. Wei all of the methods mentioned above have to obtain a high calculation speed at the expense of sacrificing the op- timal solution, which means more cost for the generation scheduling just because of the low accuracy of the al- gorithm for SCUC problems [2]. Among the existed unit commitment methods, dynamic programming is a clas- sical optimization method, which can deal with the 0/1 variables directly and get global optimum solution [5]. But the calculation efficiency needs to be improved further for unit commitment due to the “curse of dimension” problem. In response to this situation, the truncation technique [6] is proposed, which cut combinations of 0 - 1 variables based on priority order [7]. Then a heuristic improvement of adjusting truncated window size accord- ing to the incremental load demands in adjacent hours is presented in [8]. On the other hand, researchers began to explore the possibility of applying artificial intelligence to solve dynamic programming problems, and then adaptive dynamic programming (ADP) was developed, which do not require global exploration of the state space at each iteration [9]. For the particular case of unit commitment, Momoh et al. [10] constructed a two- stage neural network to learn how to commit the generators according to the heuristic states and the generation cost at each period. In this paper, the power flow equations, transmission flow constraints, and limitations of the bus voltage are taken into account in the unit commitment problem. As the nonlinear degree of optimization model brought higher, it can solve the optimization model with remarkable increases in difficulties and calculations. Therefore it will be significant to extend ADP to solve the SCUC problems. This paper proposes an ADP approach based on in-depth analysis on the characteristics of SCUC. It solves the Bellman’s equation approximately by solving a sequence of simplified single stage optimization problems. The key part of the approach is “extended sequen- tial truncation technique”, which can explore the optimization space of SCUC for ADP, and accelerate the cal- culation in the premise of guaranteeing the optimality of the solution. The rest of the paper is organized as follows. Section 2 provides the formulation model of SCUC. Section 3 introduces the proposed approach for the model. Two cases utilizing data from four test systems are taken as cases studied in Section 4. Section 5 concludes the paper. 2. SCUC Problem Formulation The objective of SCUC is to determine a day-ahead UC to minimize the total cost of supplying the load, while meeting the operational and power flow constraints G 1 GU Cost [( )(1)] min. t tttt ii iiii t Ti S dfPdd C F − ∈∈ +− =∑∑ (1) subject to: 1) Power balance constraints (power flow equations) B B GD B RD [ ()()],, [ ()()] ttttt ttt iijijjijijijj iji jS ttttt ttt iijijjijijijj iji jS PeeGfBffGeBPiStT QfeGfBefGeBQ ∈ ∈ −−++ = ∈∈ −−−+ = ∑ ∑ (2) 2) Transmission flow constraints (3) whe re 22 L[()()](), , ttttttttt tt ijiiijijijijj iijL Pefe effGefefBijStT=+−−+ −∈∈ 3) System spinning and operating reserve requirements G GG (), ttt t ii ii iS dPdPRt T ∈ − ≥∈ ∑ (4) 4) Ramp rate limitations 1up 1 GG G 1 down1 GG G (1) (1 ) tt tt i iiiii tt tt iii iii P PPdPd PP PdPd −− −− −≤+− −≤+− (5) 5) Startup and shutdown characteristics of units  D. L. Long, H. Wei 11 on 11 off ()() 0 ()() 0 t tt i ii i tt t iii i d dT T ddT T −− −− − −≥ −−−≥ (6) 6) Limits of active power GG GG , t tt iii ii dPPdPiS≥≥ ∈ (7) 7) Limits of reactive power RR RR , t tt iiiii dQQdQi S≥≥ ∈ (8) 8) Limits of voltage at each bus 2 222B ()(), , tt ii ii UefU iStT≥ +≥∈∈ (9) where is the total scheduling period which is 24 h; is the index for time; , , and are the set of buses, thermal plants, reactive power sources and transmission lines separately; are the transfer admittance between buses and ; is the up/down status of unit ; and are the schedulable active and reactive power output of bus at time ; is the active power of transmission line; , , Q, , , Lij , , are the upper and lower limit of , , and the node voltage ; and are the active and reactive power demand; is the system spinning reserve re- quirement; and are the ramp up and ramp down limit of unit ; and are the fuel cost and startup cost, defined as 2 G GG () () t tt ii iiiii fPa PbPc= ++ (10) hot offoffcold Ucoldoffcold : : t tiiii i it iii i CTTT T CCTT T ≤− ≤+ =−> + (11) , , represent the unit cost coefficients, and are the cold start cost and hot start cost, and are the minimum up and down time, is the cold start time, is the continuously on (posi- tive)/down (negative) time of unit up to time . 3. SCUC Solution 3.1. The Principle of Adaptive Dynamic Programming Basically, ADP is a decision-making procedure, executed via computing the value associated with each state approximately. The entire procedures for SCUC problem solving based on ADP in this study is as follows. Step 0: Read in system data. Set , where , : iteration count and its maximum. Step 1: Choose the initial state by priority list method (PL) [7], and initialize the value func- tion of . WHILE ( ) DO: Step 2: Set , and update the state space by extended sequential truncation technique. Step 3: For each feasible state in the state space, solve the following minimization problem to evaluate the value at approximately. G 11 G U1 ()min.[()(1)] t tk ttttt tt k kiiiiik aiS VSd fPdCV −− − ∈∈ =+− + ∑ (12) subject to (2), (3), (7)-(9), where is a decision at time , is the feasible decision space. Step 4: Let be the value of that solves the minimization problem. Step 5: If , set and go to step 3; else proceed to next step.  D. L. Long, H. Wei Step 6: If , let be the resulting decisions that solves the minimum problem and stop; else set , go to step 2. END DO. 3.2. Extended Sequential Truncation Technique The key technique of the proposed ADP approach is “extended sequential truncation technique”, which allows the exploration of the value of a better estimate of the value function. Unlike traditional sequential truncation, it selects truncated window not only through a combination of priority order and load variation, but also through aggregating the units into groups according to the minimum up/down time. Figure 1 shows the principle of the “extended sequential truncation technique” by a 6 units system. Let be the solution obtained in iteration . Assume the minimum up/down time of the units are {5 5 1 3 3 1} pe- riods separately and define . The heavy line in Figure 1 represents the up/down line of , which di- vides the priority list into two sections. The units in the upper and lower section are the off and up status units of respectively. According to the minimum up/down time, the units are divided into 3 classes. In period 1, the heavy line is in the border of class 1 and class 2. Unit 2 and 5, as well as unit 3 in class 3, whose priorities are the closest to the heavy line in each class, may be on or off. The remaining unit 1 below the heavy line must be on and unit 4 and 6 above the heavy line must be off. In period 2, class 1 units must be on to bear basic load. The heavy line is in class 2. Unit 4 and 5, as well as unit 3 in class 3, whose priorities are the closest to the heavy line in each class, may be on or off. The remaining unit 6 below the heavy line must be off. In period 3, the maximum number of up status units arises to bear peak load, so the units have no partitioning. The partition method in following periods is the same as period 1 and 2. After determining the unit up/down status selection, a set of composite states is available through the startup of units that may be on or off in the order of highest to lowest in priority. It forms the state space of each dis- patch period as long as put in the status of units that must be on or off. Last but not the least, we rule out the un- promising states as follow steps: 1) Remove states unsatisfied the reserve requirements from state space. 2) Assure units with the same minimum up/down time start in order of priority. 3) Limit the number of operation units close to the number of optimal operation units obtained in last itera- tion. 4. Case Studies We apply four test systems consisting of the IEEE 30-bus system [11], IEEE 118-bus system [12], IEEE 300- bus system [12] and a modified IEEE 118-bus system [13] to illustrate the performance of SCUC with optimal power flow constraints. The value parameters for system scales are depicted in Table 1. To discuss the efficien- cy of the proposed approach, we consider the following two cases: Case 1: traditional UC model without any network and bus voltage constraints. Case 2: SCUC model described in Section 2. 4.1. Efficiency Test This part tests the efficiency of the proposed ADP approach improved by the “extended sequential truncation Figure 1. Unit up/down status selection.  D. L. Long, H. Wei technique” on SCUC problems. Let the spinning reserve requirements be 10% of hourly load demand and the ramp up (down) limit of each unit be 20% of its maximum power output [14]. We implement the proposed ap- proach by MATLAB-2013a on a 3.2 GHz Intel Core i3 dual core, IBM-compatible PC with 4GB of RAM and employ the MATLAB interior point method solver [15] to solve nonlinear programming problem. Table 2 compares the iterations and CPU time of the proposed approach for both case 1 and case 2. Obvious- ly, the proposed approach is efficient and converges fast for all of the test systems. The Bellman error is a very important measure to judge the optimality of solutions and its change reflects the characteristic of the approach. Figure 2 shows the variation of Bellman error with iterations for the four test systems, which is the difference in the value iteration between current value and the updated value. It can be seen from Figure 2 that the iteration process made 100% and 97% Bellman errors away from zero in case 1 and case 2 respectively. This certainly verifies that the proposed approach has favorable stability and the decline of value function (12) is permanent in the searching process. 4.2. Economic Benefit Figure 3 provides the comparison of the daily costs obtained by SDP [4], PL [7], DP [8], SF [16] and the pro- posed ADP approach for the modified IEEE 118-bus system in case 1. The less cost indicates that the proposed approach can provide high-quality solutions in comparison with other methods. To clarity the effects of “extended sequential truncation technique” in detail, Table 3 compares the daily cost of ADP by traditional sequential truncation and extended sequential truncation. As can be seen from Table 3 with extended sequential truncation technique, the daily cost of the four systems decrease by 1.58%, 0.61%, 0.13%, 0.03% in case 1 and 1.46%, 0.27%, 0.11%, 1.89% in case 2 separately. This confirms that extended se- quential truncation is superior to traditional sequential truncation in daily cost for unit commitment problems. Table 1. Value parameters for system scales. Name of System Buses Units Lines IEEE-30 30 6 41 IEEE-118 118 54 186 IEEE-300 300 69 411 Modified IEEE-118 188 54 177 Table 2. Performance of the proposed approach. Name of Syste m Iterations CPU Time (s) Case 1 Case 2 Case 1 Case 2 IEEE-30 3 3 1 7 IEEE-118 13 20 4 177 IEEE-300 5 6 4 1711 Modified IEEE-118 5 5 2 238 Table 3. Daily cost of ADP by traditional & extended sequential truncation. Name of System Traditional Sequential Truncation ($) Extended Sequential Truncation ($) Case 1 Case 2 Case 1 Case 2 IEEE-30 12587 12594 12388 12410 IEEE-118 3571736 3600043 3550091 3590273 IEEE-300 22104882 22141570 22076537 22117784 Modified IEEE-118 1643681 1740040 1643263 1707114 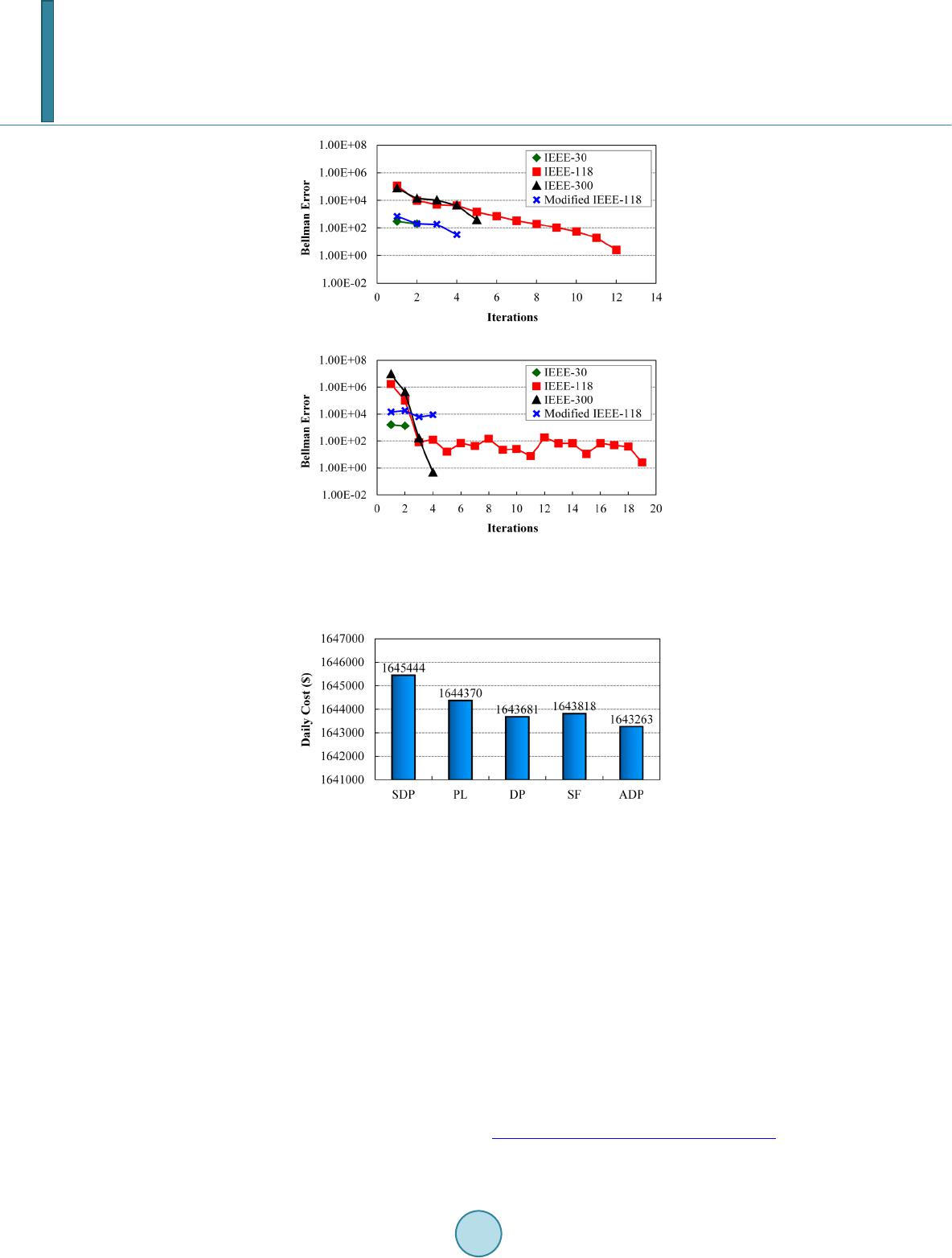 D. L. Long, H. Wei (a) (b) Figure 2. Bellman error with iterations in case 2. (a) Bellman error with iterations in case 1; (b) Bellman error with itera- tions in case 2. Figure 3. Results of different approaches for the same case. 5. Conclusion In response to the computational difficulties brought by SCUC problem with optimal power flow constraints, a novel “extended sequential truncation technique” was proposed to solve the problem by improving the adaptive dynamic programming approach. Two cases utilizing data from four test systems ranging in size from 30 to 300 buses were studied. Extensive calculation and comparative analysis between the two cases demonstrate the effectiveness and applicability of the proposed approach for SCUC with optimal power flow constraints. Acknowledgements This work was jointly supported by National 973 Program of China (2013CB228205) and National Natural Science Foundation of China (51167001). References [1] Fu, Y., Li, Z. and Wu, L. (2013) Modeling and Solution of the Large -Scale Security-Constrained Unit Commitm e nt . IEEE Transactions on Power Systems, 28, 3524-353 3. http://dx.doi.org/10.1109/TPWRS.2013.2272518 [2] Wan g, P., Wang, Y. and Xia, Q. (2012) Fast Bounding Technique for Br anch-And -Cut Algorithm Based Monthly  D. L. Long, H. Wei SCUC. 2012 IEEE Power and Energy Society General Meeting, San Diego. http://dx.doi.org/10.1109/PESGM.2012.6345349 [3] Hamed, A. and Hassan, G. (2014) Securit y-Constrained Unit Commitment with Linearized System Frequency Limit Constraints. IEEE Transactions on Power Systems, in Press. [4] Bai, X. and Wei , H. (2009) Semi-Definite Programming-Based Method for Security-Constrained Unit Commitment with Operational and Optimal Power Flow Constraints. IET Generation Transmission & Distribution, 3, 182-197. http://dx.doi.org/10.1049/iet-gtd:20070516 [5] Li e W. N., Le e C.M., Yeh, C.H. and Gao, Z.W. (2014) Motion Vector Recovery for Video Error Concealment by Using Iterative Dynamic-Programming Optimization. IEEE Transactions on Power Systems, 16, 216-22 7. [6] P ang, C.K., Sheble, G.B. and Albuyeh, F. (1981 ) Evaluation of Dynamic Programming Based Methods and Multiple Area Representation for Thermal Unit Commitments. IEEE Transactions on Power Apparatus and Systems, PAS 100, 1212-1218. [7] Senjyu, T., Shimabukuro, K., Uezato, K. and Funabashi, T. (2003) A Fast Technique for Unit Commitment Problem by Ex-Tended Priority List. IEEE Transactions on Power Systems, 18, 882-888. http://dx.doi.org/10.1109/TPWRS.2003.811000 [8] Ouyang, Z. and Shahidehpour, S.M. (1991) An Intelligent Dynamic Programming for Unit Commitment Application. IEEE Transactions on Power Systems, 6, 1203-1209 . http://dx.doi.org/10.1109/59.119267 [9] Murray, J.J., Cox, C.J., Lendaris , G. G. and Saeks, R. (2002) Adaptive Dynamic Programmin g . IEEE Transactions on Systems, Ma n , and Cybernetics, Part C: Applications and Reviews, 32, 140-153. http://dx.doi.org/10.1109/TSMCC.2002.801727 [10] Momoh, J.A. and Zhang, Y. (2005) Unit Commitment Using Adaptive Dynamic Programmi ng . Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, 523-526. http://dx.doi.org/10.1109/ISAP. 200 5.15 99 318 [11] Alsac, O. and Stott, B. (1974 ) Optimal Load Flow with Steady State Security. IEEE Transactions on Power Apparatus and Systems, PAS 93, 745-751. [12] Christie, R.D. (1999) Power Systems Test Case Archive. http://www.ee.washington.edu/research/pstca [13] Fu, Y., Shahidehpour, M. and Li, Z. (2005) S ecuri ty-Constrained Unit Commitment with AC Constraints. IEEE Transactions on Power Systems, 20, 1538-1550. http://dx.doi.org/10.1109/TPWRS.2005.854375 [14] Han, D., Jian, J. and Yang, L. (2013) Outer Approximation and Ou t -Inner Approximation Approaches for Unit Com- mitment Problem. IEEE Transactions on Power Systems, in Press. [15] Zimmerman, R.D., Murillo-Sanchez, C.E. and Gan, D. (2013) Matpower a Matlab Power System Simulation Package. http://www.pserc.cornell.edu/matpower [16] Hosseini, S.H., Khodaei, A. and Ami nifar , F. (2007) A Novel Straightforward Unit Commitment Method for Large- Scale Power Systems. IEEE Transactions on Power Systems, 22, 2134-2143. http://dx.doi.org/10.1109/TPWRS.2007.907443
|