 Journal of Power and Energy Engineering, 2014, 2, 647-655 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24087 How to cite this paper: Yang, Q., Xiong, X.F., Wang, J. and Weng, S.J. (2014) Short-Term Reliability Evaluation of Transmis- sion System Using Lightning Strike Probability Prediction. Journal of Power and Energy Engineering, 2, 647-655. http://dx.doi.org/10.4236/jpee.2014.24087 Short-Term Reliability Evaluation of Transmission System Using Lightning Strike Probability Prediction Qing Yang1, Xiaofu Xiong2, Jian Wang2, Shijie Weng2 1Yunnan Power Grid Corporation, Kunming, China 2State Key Laboratory of Power Transmission Equipment & System Security and New Technology, Chongqing University, Chongqing, China Email: wang rela y@foxmail.com Received February 2014 Abstract The transmission lines are exposed to the atmosphere nature and will be affected by adverse weather such as lightning storm, so that it will affect the reliability of transmission system. This paper studies the fault probability model of transmission line during the lightning storm, and evaluates the short-term reliability of transmission system in the forecasting weather condition. Firstly, build the lightning strike fault probability model of the transmission line based on histor- ical lightning record information, then calculate the lightning strike probability under the fore- casting weather conditions, furthermore evaluate the reliability index of transmission system. Uti- lizing IEEE RTS-79 system to verify the validity of the proposed model and the results show that lightning has great negative influence on the transmission lines and the reliability of transmission system. The reliability evaluation model proposed in this paper can guide the short-term opera- tion and online scheduling for transmission system operators. Keywords Lightning; Transmission Line; Reliability Evaluation; Information Diffusion 1. Introduction Overhead transmission lines are exposed to nature for a long time, so they are easily affected by adverse weather. Though the duration of adverse weather is short, the failure rate of electrical element will apparently increase under adverse weather. Therefore, the effect of adverse weather on power grid should be considered. The operation experience of power system indicates that lightning current may cause electrical disturbances such as short-circuit and flashover, which will affect the safety and stability of power system. Statistics show that with the expansion of power grid, the harm of fault caused by lightning on transmission lines and electrical equipment is more and more great. For transmission lines of 500 kV and below, lightning trip accidents account for 50% of the total trip accidents [1], and for UHV transmission lines, the proportion increases to 75% - 90% [2]-[4].  Q. Yang et al. Researches on the influence of lightning disasters on transmission line fault are extensively carried out. The analysis models for transmission lines of lightning withstand level of shielding failure mainly are electric geo- metry method, improved electric geometry method and the leader progression model. Literature [5] puts forward the “necessary and sufficient condition of shielding failure” according to the characteristic of shielding failure of lightning leader, and develops protective measures against lightning shielding failure. Literature [6] discusses the research on correlation between lightning trip of transmission line in Zhejiang power grid and factors such as ground flash density, flash intensity, elevation and ground slope, and on the basis of the research, a multi-factor comprehensive evaluation model for external lightning risk of transmission line is established. On the other hand, the influence of bad weather on power system reliability has been paid great attention. Literature [7] raises three states model, where the weather conditions are divided into normal weather, adverse weather and extreme weather. Literature [8] considers strong wind, ice and lightning are the most destructive meteorological factors, and studies the influence of wind speed on the assessment result of system reliability. Literature [9] simulates the influence process of large-scale ice disaster to transmission system with the meteorological model that changes over time, and calculates the reliability index. Literatures [10] [11] using the comprehensive risk as- sessment method, presents mathematical model and early warning method for the evaluation of catastrophic events of power grid based on the entropy method. Therefore, this paper establishes a model to calculate the lightning strike failure probability of transmission line from the perspective of probability, based on lightning weather information, and to predict the lightning strike failure probability of lines under thunder weather, then to study the effect of lightning strike probability on the short-term reliability of power system. 2. Selection of Failure Rate under Lightning Weather Lightning is a kind of adverse weather that is easy to happen. Analysis shows that the failure rate of line under lightning weather is related to lightning strike trip times, lightning duration and so on. The basic method to assess the reliability of power grid under lightning weather is Monte Carlo sampling method, and it is needed to make sure the failure probability of each transmission line when sampling the state. One way is adopting statistical method, to count the lightning strike failure probability of transmission line un- der lightning weather specially; the other one is to search for the relationship between lightning strike failure probability and lightning meteorological parameters, namely, lightning strike probability distribution model, which is to predict lightning strike failure probability through the meteorological parameters. Because the exist- ing statistical methods of calculating the reliability don’t distinguish the weather type that causes fault from oth- er types, it is unable to obtain the failure rate of transmission line under lightning weather. The second way will be used in this paper to predict the failure probability of line under lightning weather, as the failure rate of each transmission line. 3. Lightning Strike Probability Model 3.1. Lightning Strike Failure Analysis Electro-geometric model (EGM) indicates that, transmission line lightning shielding failure probability is related to the lightning current amplitude (LCA) and striking distance. It is hard to determine striking distance because the lightning strike position is varied, while a large number of statistical data demonstrate that lightning dis- charge path is approximately vertical downward. Therefore, lightning current amplitude (LCA) and lightning side distance (LSD) are selected as two parameters to calculate the lightning shielding failure probability of transmission line. The m times of fault events occurred on n times of transmission lines at the same voltage class should be got through statistics, and lightning current amplitudes and lightning side distances when m times of fault events occurred can be obtained, where the lightning current amplitude is averaged. Parameters of m times of fault are record as follows: 112 2 (, ){(,),(,),,(,)} mm XYx yxyxy= (1) where X represents lightning current amplitude, Y represents lightning side distance. Information diffusion method is a kind of data processing technique that can learn the rules from samples to get rid of the restraints of subjective mathematical assumptions. The method estimates the probability density  Q. Yang et al. function of the sample based on the drive of sample data. The two-dimensional Gaussian diffusion model is as follows: ( )( ) 22 22 1 12 11 1 ( ,)exp 222 mjj mj ux vy f uvmh hhh π = −− = −− ∑ (2) where h1 and h2 are diffusion factors, which can be determined based on the maximum of samples b, the mini- mum of samples a and the sample number M using the Equations (3) [12]. 1 2 - 1.4230 9 M-1 - 1.4208 10 M-1 ba hM ba hM =×≤ =×≥ (3) 3.2. Calculation of Lightning Failure Probability The physical meaning of f(u,v) is the joint probability density function of lightning current amplitude and lightning side distance when trip out fault occurs on lines. It is conditional probability density function essen- tially, and can be represented as f(BC|A), where A represents shielding failure event, B represents lightning cur- rent amplitude and C represents lightning side distance. The condition probability density is as follows: (4) Thus, ()()() ( )== ()()( ) fABCfBC |AfA fA| BCfBC fBfC × (5) So the conditional probability is: ( )() ( )==( )dB()dC fBC |AdBdCpA pA| BCfB fC × ∫∫ ∫∫ (6) where p(A|BC) represents the transmission line shielding failure probability in particular lightning current am- plitude and lightning side distance conditions. p(A) represents the probability of the transmission line shielding failure, f(B) represents the probability of lightning current amplitude, f(C) is the lightning side distance distribu- tion probability, the events B and C are considered independent. In transmission line shielding failure probability model, the lightning trip probability can be derived from the rate of shielding failure [13]: (7) where λ is the rate of shielding failure, t represents the time span between M times of faults. The probability density function of lightning current amplitude uses the IEEE standard, shown as follow [14]: (2.6 1) 2.62.6 2 2.6 () 31[1(/ 31)] I fI I − =× + (8) The lightning side distance distribution adopts even distribution, and can be calculated using Equation (9). (9) where L is the maximum of lightning side distances. 4. Prediction of Lightning Strike Probability In the analysis of lightning weather influence on power system short-term reliability assessment, the probability 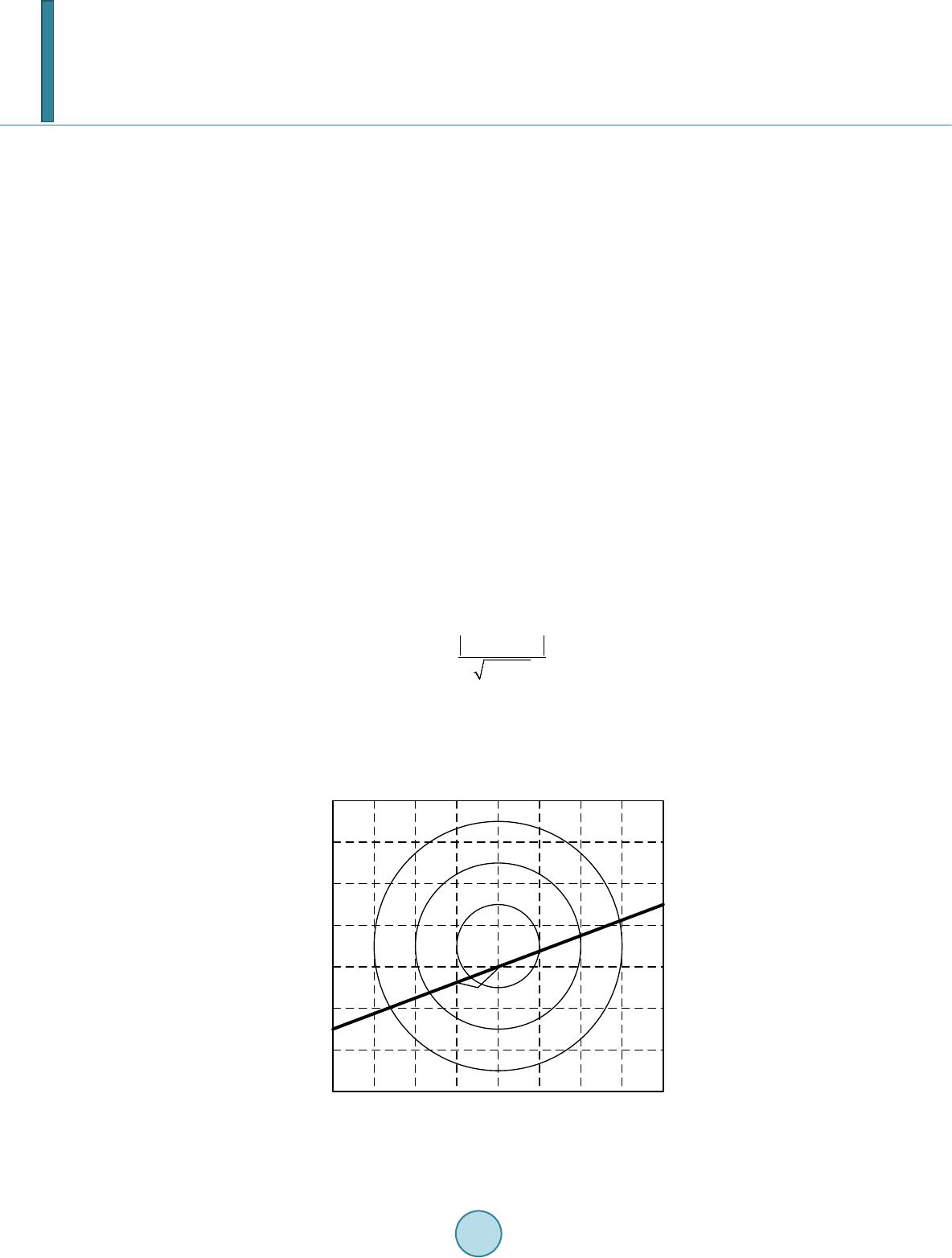 Q. Yang et al. of transmission line lightning strike fault under lightning weather should be determined primarily, and lightning strike fault model of transmission line which has discussed in Section 2 is related to lightning current amplitude and lightning side distance. So, the key point of prediction of lightning strike probability is to get the predicted value of the two characteristic parameters. 4.1. Acquisition of Radar Parameters On the one hand, study shows that lightning current amplitude is related to radar echo intensity, radar echo top, and vertical integrated liquid content and so on [15], and these parameters can be got from weather forecast of lightning. On the other hand, lightning side distance is the side distance between lightning and transmission line, thus it can be calculated through thundercloud move direction and move speed. Therefore, the key meteorologi- cal parameters to predict the lightning strike probability are radar echo intensity, radar echo top, vertical inte- grated liquid content, and move direction and move speed of the thundercloud. The data got from the weather radar is divided into 0.01˚ × 0.01˚ grid, as shown in Figure 1, where circle represents detection range of the weather radar and straight line represents the transmission line. 4.2. Calculation of LSD 1) Determine the line equation According to the latitude and longitude information of grid inside where is transmission line, the coordinates of the transmission line can be determined. The two endpoints is denoted by M1(x1, y1) and M2(x2, y2), and then the linear equation of the transmission line is got, recorded as aX + bY + c = 0. 2) Calculation of side distance The center of grid inside where is thundercloud can be approximately considered as the lightning discharge point, and it is recorded as M0(x0, y0). So the equation to calculate the side distance between lightning discharge point and line is as follows: (10) 4.3. Prediction of LCA Using BP Neural Network The relevance model between lightning current amplitude and radar echo intensity, radar echo top and vertical integrated liquid content is established through historical data, as shown in Equation (11). And then the pre- 118.50 118.51 118.52 118.53 118.54 118.55 118.56 118.58118.57 32.10 32.11 32.16 32.15 32.14 32.13 32.12 32.17 probe point Longitude (E) Latitude M 0 M 1 M 2 (N) Figure 1. Coordinate figu r e by longitude and latitude.  Q. Yang et al. dicted value of lightning current amplitude can be obtained according to the predicted value of the relevant pa- rameters. (11) Here, y is the lightning current amplitude, x1 is the radar echo intensity, x2 is the radar echo top, and x3 is the vertical integrated liquid content. To get the concrete expression of the Equation (11), the historic M times of transmission line shielding failure events are selected as sample to be studied. The input variables are the three parameters recorded by weather radar, such as echo intensity and so on, and the output is the maximum of lightning current amplitudes when the line trips out. Due to the nonlinearity of the relationship between inputs and output, it is hard to express it in ex- plicit expression, while the artificial neural network has strong ability of nonlinear mapping, self-adaption and self-learning. Therefore, the BP neural network [16] is used in this paper to identify the relationship between lightning current amplitude and radar echo intensity, radar echo top, vertical integrated liquid content, and the specific steps are as follows. 1) Get the information of parameters when the M times of lightning strike occur, as the training sample data. 2) Establish the three layer feed-forward BP neural networks using neural network function in MATLAB, and initialize the weights and thresholds. 3) Use BP algorithm to train the network, and save the training results. 4) Compare the training results and historical data to verify the accuracy of trained network. 4.4. Prediction of Lightning Strike Probability Based on radar detection, the parameter values such as radar echo intensity and radar echo top of each grid are got, and the predicted amplitude of lightning current in corresponding grid can be obtained according to the pre- diction model of lightning current amplitude, then the coordinate position of the corresponding grid is got to calculate the side distance. Finally, the lightning strike failure probability of transmission line in corresponding grid can be obtained through the lightning strike failure probability model. If a section of transmission line had k times of grid under lightning weather, then the lightning strike failure probability of line is as follows: (12) where P is the failure probability of transmission line under lightning weather, and pi is the lightning strike fail- ure probability of line in the ith grid. 5. Short-Term Reliability Evaluation of Transmission System under Lightning Weather The short-term reliability evaluation of power system considering the probability of lightning strike is to predict the lightning strike failure probability of transmission line through the models described above as its forced outage probability, while the transmission lines that don’t suffer lightning weather will use the original reliabili- ty data, and then the system state will be obtained through the Monte Carlo sampling method, in order to analyze the reliability of power system. In the process of assessment, the DC load flow model is used to calculate the load flow, the depth first search algorithm is used to judge whether the system is splitting or not, and the optimal cutting model is used to minimize the load curtailment. In this paper, loss of load probability (LOLP) and expected demand not supplied (EDNS) are used to represent the reliability indexes of power system. The loss of load probability is the probability of system which can’t meet the load demand in a given time, that is: (13) where M is the total sampling number of system state and m(s) is the occurrence number of the system state s. The expected demand not supplied is the expected value of load shedding caused by insufficient generating capacity of system or constraint of power grid in a given time, that is:  Q. Yang et al. (14) where C(s) is the amount of load curtailment at system state s. The assessment process of analyzing the influence of transmission line lightning strike probability on power system short-term reliability is shown in Figure 2. The basic steps of the algorithm are as follows: 1) get radar echo parameters of each grid; 2) predict the lightning current amplitude of the grid using neural network model; 3) calculate the side distance between lightning discharge point and transmission line; 4) calculate lightning strike failure probability of transmission line in the grid; 5) form the failure probability of each transmission line, that is forced outage probability; 6) sample the state using Monte Carlo method; 7) analyze system state and calculate the amount of load curtailment; 8) form reliability indexes; 9) judge whether it achieves convergence condition, if not, do the next sample; 10) form total reliability indexes of the system. 6. Example Analysis 6.1. Example Introduction In this paper, IEEE RTS-79 system is taken as an example. The system is divided into area 1 and 2 by voltage grade, and its wiring is shown in Figure 3. Figure 2. Reliability assessment pro cess. Start Input data Sample the lines Under lightning weather? Get reliability parameters Get meteorological parameters Calculate lightning current amplitude and side distance Calculate failure probability Get operating state of lines All the lines are sampled? Determine the state of other electrical components Assessment system state, calculate reliability indexes End Yes No No Y es  Q. Yang et al. ~~~ ~ ~ ~ ~ ~ ~~~ 18 17 16 21 22 23 2019 15 24 1112 6 10 93 12 7 8 45 14 13 Area 2 230kV Area 1 138kV lightning happening area Figure 3. Electric wiring diagram of the IEEE RTS-79. It is assumed that transmission lines 24 - 15, 11 - 14, 12 - 23, 11 - 13, 12 - 13 and 13 - 23 are under lightning weather. The data needed for the lightning weather model can be got from weather forecast, as shown in Table 1. According to Table 2, p1 = 0.01, p2 = 0.38, p3 = 0.12. So the lightning strike failure probability of line 24 - 15 is P24-15 = 0.45. Similarly, the failure probability of other transmission lines can be predicted, as shown in Table 3. 6.2. Reliability Indexes of the Test System The results of reliability assessment of IEEE RTS-79 test system under lightning weather and normal weather are shown in Table 4. The result in Table 4 shows that the reliability of the test system will worsen under lightning weather: LO LP becomes from 0.086 under normal weather to 0.137 under lightning weather, and EDNS becomes from 15.04 MW/a to 29.75 MW/a. The results indicate that lightning weather will make great influence on reliability index- es. Therefore, it is necessary to consider the influence of bad weather on short-term reliability assessment of power system, to make the reliability indexes closer to the actual value. 6.3. Influence of Lightning Strike Failure Rate on System Reliability If the lightning strike failure rate of transmission line is different, then the failure probability is different accor- dingly under the same lightning parameters. To analyze the influence of failure rate on system reliability, the re- liability indexes of the test system are as shown in Table 5 when λ is 0.001, 0.005 and 0.01 (1/hour·km). According to the result in Table 5, it is obvious that the influence of different failure rate on system reliability is very different. When λ is 0.001, the failure probability of system is as small as under normal weather; while when λ is 0.001, the failure probability of transmission line is higher and the corresponding reliability indexes vary apparently: for example, the LOLP of test system is up to 0.607. 7. Conclusion The influence of lightning strike failure on reliability of transmission line is studied in this paper, and the short- term reliability evaluation model of power system under lightning weather is presented. It is determined that the  Q. Yang et al. Table 1. Val ue of radar forecast para meters. Grid Radar echo intensity (dB z) Maximum of echo top (km) vertical integrated liquid content (kg/m 2) Grid 1 54 13.7 37 Grid 2 40 9.1 27 Grid 3 48 11.2 35 Table 2. Failure probability of line section in each grid. Predictive variables Grid 1 Grid 2 Grid 3 LCA (kA) 67. 2 ± 3.5 22. 3 ± 3.5 44. 3 ± 3.5 LSD (m) 89 ± 5 56 ± 5 102 ± 5 failure probability p 0.01 0.38 0.12 Table 3. Failure probability of transmission lin e. Line Line 24 - 15 Line 11 - 14 Line 12 - 23 Line 11 - 13 Line 12 - 13 Line 13 - 23 Failure probability 0.45 0.25 0.3 0.35 0.40 0.45 Table 4. Reliability indexes of the test system. Weather condition LOLP EDNS (MW) Normal 0.086 15.04 Lightni ng 0.137 29.75 Table 5. Reliability indexes under different failure rate. Failure rate LOLP EDN S (M W) Normal 0.086 15.04 λ = 0.001 0.092 15.68 λ = 0.005 0.137 29.75 λ = 0.01 0.607 238.86 lightning current amplitude and the lightning side distance can be obtained using weather parameters detected by radar through analyzing the distribution model of transmission line lightning strike probability, and then the lightning strike failure probability is predicted to assess the short-term reliability of power system. Result of the IEEE RTS-79 test system shows that the influence of lightning weather on system reliability indexes is great, so if it is neglected, the reliability of system may be higher than the actual value and get over-optimistic assessment. The model proposed in this paper can react to the influence of lightning weather on the transmission line failure rate and the system reliability, and it can easily identify the weak links of power system reliability in order to prepare risk prevention and control measures well in advance and improve the ability of power system to with- stand the adverse weather. References [1] Yang, Q., Si ma , W.X., Feng, J. and Yua n, T. (2008) Research on the Lightning Shielding Performance of the Yun- Guang UHVDC Transmission Lines. High Voltage Engineering, 34, 442-446. [2] Li, P. (2000 ) A New Viewpoint about Lightning Trip-Out of UHV Transmission Lines. Power System Technology, 24, 63-65.  Q. Yang et al. [3] Xia, W.-H. (19 98 ) The Analysis of Lightning Protect ion for EHV and UHV Transmission Lines in Russia. High Vol- tage Engineering, 24, 76-79. [4] Zh ou , H. and Yu, Y.H. (2005) Discussion on Several Important Problems of Developing UHV ac Transmission in China. Power System Technology, 29, 1-9. [5] Wan g, H.-C. (1999) Mechanism of Lightning Shielding Failure. High Voltage Engineering, 25, 52-54. [6] Tong, H.-W., C hen , L.-Y. and Zhang, B. (2013 ) External Lightning Risk Assessment Model for Transmission Line. East China Electric Power, 9, 1906-1910. [7] Billiton, R. and Achar ya, J.R. (2006) Weather-Based Distribution System Reliability Evaluation. Proceedings of IEEE Generation, Transmission and Distribution Conference, Stevenage, 4 99-50 6. [8] Zh ou , Y.J., Pa wh a , A. and Yang, S. (2006 ) Modeling Weather -Related Failures of Overhead Distribution Lines. IEEE Transactions on Power System, 21, 1683-1690. http://dx.doi.org/10.1109/TPWRS.2006.881131 [9] Wan g, J.X., Zhang, Y. and Sun, Y. (2011 ) Influence of Large-Scale Ice Disaster on Transmission System Reliability. Proceedings of the CSEE, 31, 49-56. [10] Feng, J., Xiao, X.-Y., Cui, Z., Feng, G. and Ma, C. (20 12 ) Synthetic Risk Assessment of Catastrophic Failures in Pow- er System Based on Entropy Weight Method. East China Electric Power, 7, 1144-1147 . [11] Cui, Z., Xi ao, X.-Y., F eng, G. and LI, C.S. (2012) Assessment of Power Grid Catastrophic Event Forewarning Based on Comprehensive Risk. East China Electric Power, 9, 1507-15 11 . [12] Huang, C. and Wang, J. (19 95 ) Fuzzy Information Optimum Processing Techniques and Its Application. Beijing Uni- versity of Aeronautics and Astronautics Press, Beijing. [13] Billinton, R. and Allan, R.N. (199 2 ) Reliability Evaluation of Engineering Systems: Concepts and Techniques. Plenum Publishers. http://dx.doi.org/10 . 100 7/97 8-1-48 99-06 85 -4 [14] Transmission and Distribution Committee of the IEEE PES. IEEE Std-12 43-19 97 (1997) IEEE Guide for Improving the Lightning Performance of Transmission Lines. [15] Chang, Y., Chen, D.S. and Guo, Z.H. (2010) Research on the Relationship of Doppler Radar and the Lightning Warn- ing. Meteorological and Environmental Sciences, 33, 36-39. [16] Li, W., Sheng, D.-R., Chen , J.-H., et al. (2007 ) The Application of Double BP Neural Network Combined Forecasting Model in Real-time Data Pred icting. Proceedings of the CSEE, 27, 94-97.
|