 Journal of Power and Energy Engineering, 2014, 2, 639-646 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24086 How to cite this paper: Ravi, K., Shilaja, C., Babu, B.C. and Kothari, D.P. (2014) Solving Optimal Power Flow Using Modified Bacterial Foraging Algorithm Considering FACTS Devices. Journal of Power and Energy Engineering, 2, 639-646. http://dx.doi.org/10.4236/jpee.2014.24086 Solving Optimal Power Flow Using Modified Bacterial Foraging Algorithm Considering FACTS Devices K. Ravi1, C. Shilaja1, B. Chitti Babu2, D. P. Kothari3 1School of Electrical Engineering, VIT University, Vellore, India 2NIT, Rourkela, India 3Former IIT Director, Delhi, India Email: ravikeee@yahoo.co.in Received February 2014 Abstract In this paper, a new Modified Bacterial Foraging Algorithm (MBFA) method is developed to incor- porate FACTS devices in optimal power flow (OPF) problem. This method can provide an enhanced economic solution with the use of controllable FACTS devices. Two types of FACTS devices, thyris- tor controlled series compensators (TCSC) and Static VAR Compensator (SVC) are considered in this method. The basic bacterial foraging algorithm (BFA) is an evolutionary optimization tech- nique inspired by the foraging behavior of the E. coli bacteria. The strategy of the OPF problem is decomposed in two sub-problems, the first sub-problem related to active power planning to mi- nimize the fuel cost function, and the second sub-problem designed to make corrections to the voltage deviation and reactive power violation based in an efficient reactive power planning of multi Static VAR Compensator (SVC). The specified power flow control constraints due to the use of FACTS devices are included in the OPF problem. The proposed method decomposes the solution of such modified OPF problem into two sub problems’ iteration. The first sub problem is a power flow control problem and the second sub problem is a modified Bacterial foraging algorithm (MBFA) OPF problem. The two sub problems are solved iteratively until convergence. Case studies are presented to show the effectiveness of the proposed method. Keywords Flexible AC Transmission System (FACTS); Modified Bacterial Foraging Algorithm (MBFA); Optimal Power Flow (OPF); TCSC; SVC 1. Introduction The solution of an OPF problem determines the optimal settings for control variables in a power network ob- serving various constraints. In the last 30 years’ development, many different solution approaches have been proposed to solve the OPF problems [1]. Recent developments in power electronics have opened a new world in power systems control. Several control devices are being developed under this new concept, known as FACTS 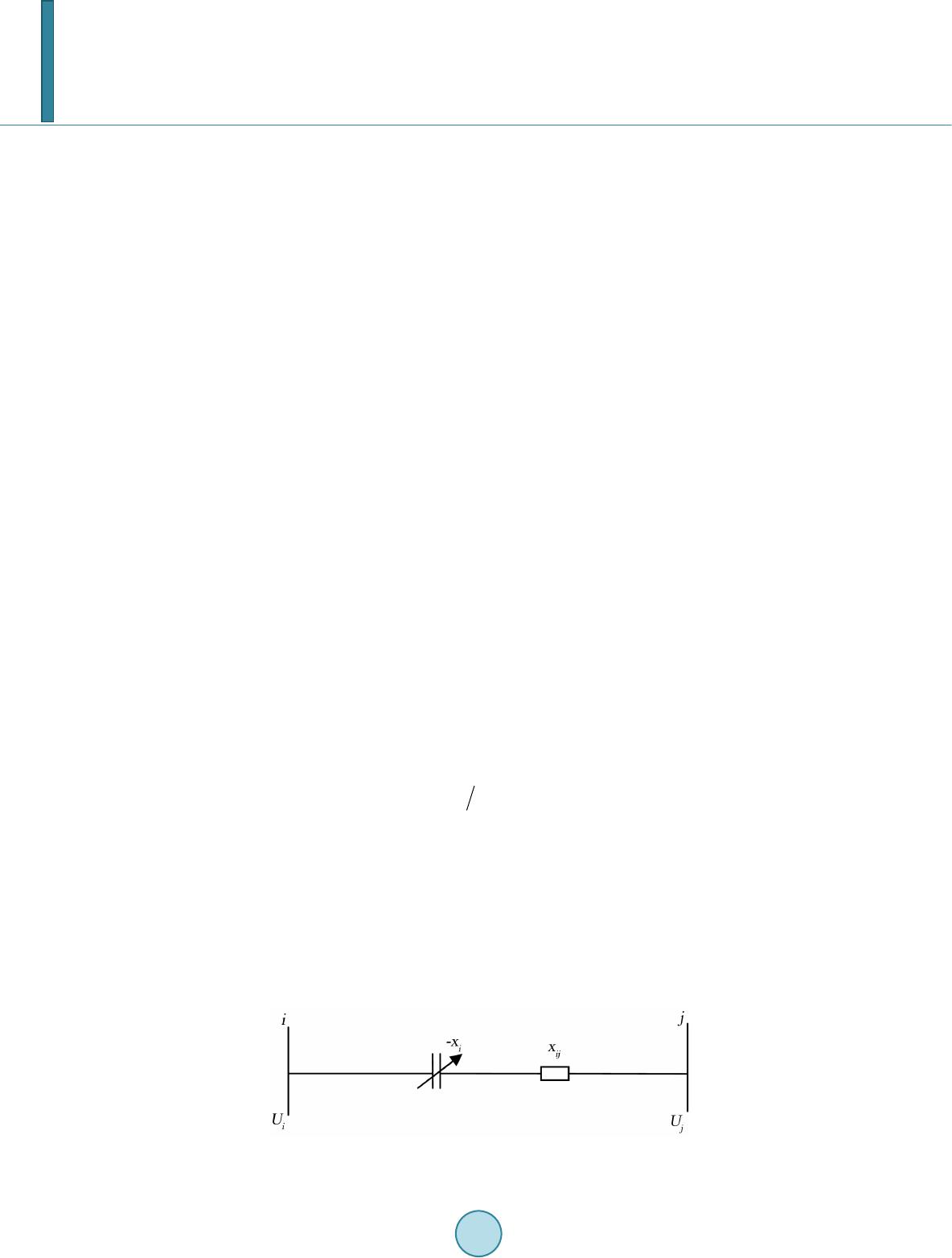 K. Ravi et al. (Flexible AC Transmission System) [2]. These FACTS devices can make the power systems operating in a more flexible, more secure and economic way. However, these FACTS devices also make the power system operating in a more complicated way. In [3], the Benders decomposition method was first proposed to solve the optimal active power flow dispatch problem incorporating FACTS devices. This method can deal with the representation of series compensators and phase shifters, but this method did not consider the specified line flow constraints. In [4], a method for solving the power flow control problem incorporating FACTS devices was proposed based on decomposition. However, this method did not combine tilt OPF problem with the power flow control problem, hence the solution probably may not be the overall optimal solution. In [5] author presented the solution of op- timal power flow using linear programming method for power system network security application. Gotham and Heydt [6] have presented the modeling of FACTS devices for power flow studies and the role of that mod- eling in the study of FACTS devices. The presence of discrete control variables, such as switch able shunt de- vices, transformer tap positions, and phase shifters, further complicates the problem solution [7,8]. The global optimization techniques known as genetic algorithms (GA) [9], simulated annealing (SA), tabu search (TS) [10], evolutionary programming (EP), improved particle swarm optimization (IPSO) [11], a novel crazy swarm optimi- zation (NCSO) [12] and a hybrid genetic algorithm approach based on differential evolution (IGA-DE) [6], in [13] the authors proposed a simple genetic algorithm fuzzy system and evolutionary programming applied to the OPF problem in large-scale power systems. Author in [14] presents a particle swarm optimization (PSO) to solve the economic dispatch with consideration of many nonlinear characteristics of the generator, such as ramp rate limits, prohibited operating zones, and non smooth cost functions. In [15] authors present a novel string structure for solving the economic dispatch through genetic algorithm (GA) with consideration of practical generators con- straints. In [16] authors proposed optimal power dispatch for large scale power system using stochastic search al- gorithms. To accelerate the search process authors in [10] proposed a multiple tabu search algorithm. To overcome the drawbacks of the conventional methods related to the form of the cost function, and to reduce the computa- tional time related to the large space search required by GA, this paper presents a modified BFA for the solution of large-scale OPF with practical generators constraints and with consideration shunt FACTS devices. This paper is organized as follows: Modeling of FACTS device is given in Section 2; Problem Formulation is given in Section 3. Modified Bacterial Foraging algorithm for proposed method is given in Section 4. Results and discussion are given in Section 5, the conclusion is drawn in Section 6 and references are given in Section 7 2. Modeling of Fact Device 2.1. Thyristor Controlled Series Compensator (TCSC) When the DC network model is used, the model of the transmission line with TCSC is shown in s. The total susceptance of the transmission line can be formulated as: (1) Which is directly used as the control variable to be implemented in the bus susceptance matrices (Figure 1). The power flow equations of the branch can be formulated as follows: (2) 2.2. Static VAR Compensator (SVC) The steady-state proposed model is used to incorporate the SVC on power flow problems. This model is based on representing the controller as a variable impedance, assuming an SVC configuration with a fixed capacitor (FC) and Thyristor-controlled reactor (TCR) as depicted in Figure 2. Applying simultaneously a gate pulse to Figure 1. Equivalent circuit of TCSC. 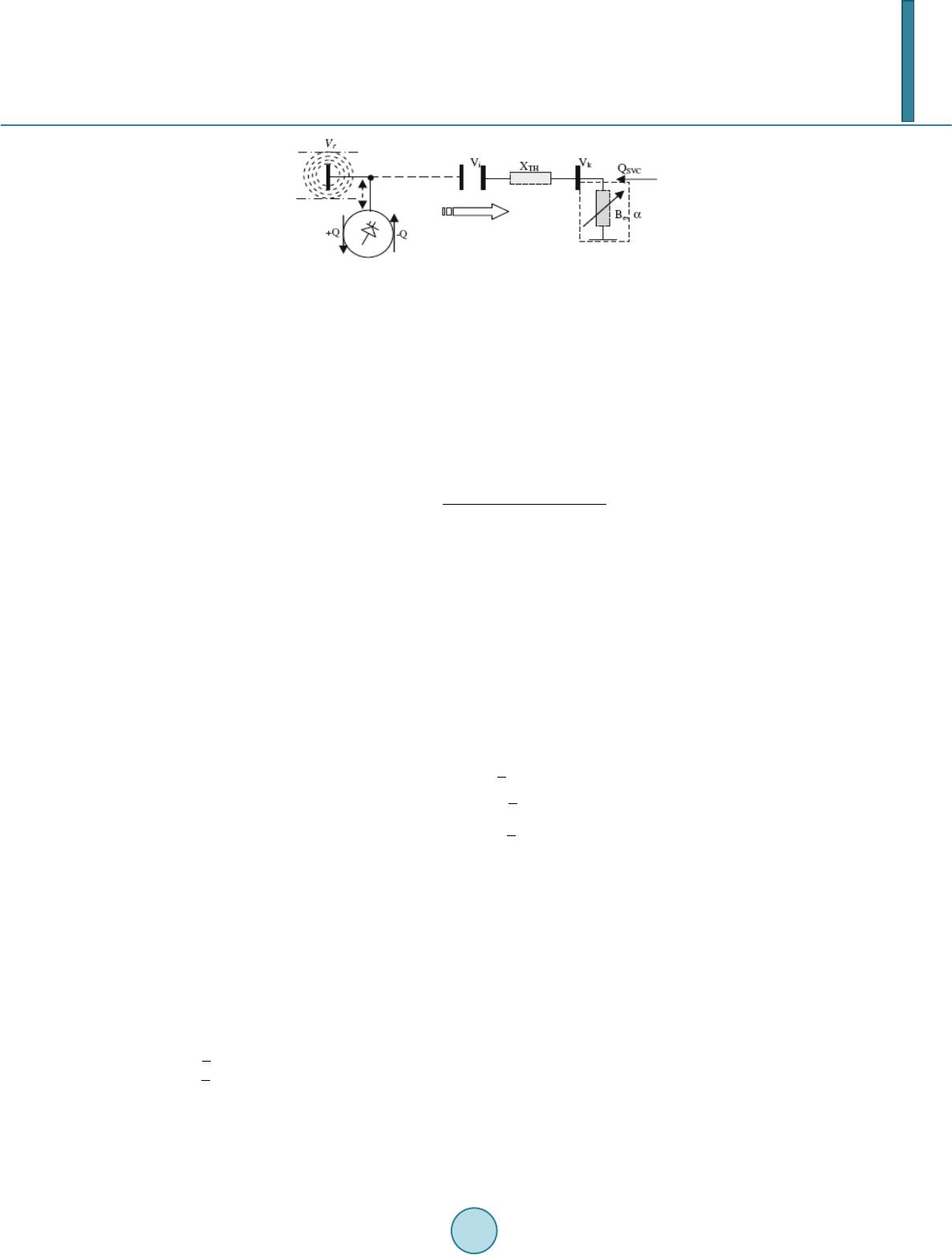 K. Ravi et al. Figure 2. SVC steady state circuit representation. all thyristor of a thyristor valve brings the valve into conduction. The valve will block approximately at the zero crossing of the ac current, in the absence of firing signals. Thus, the controlling element is the Thyristor valve. The thyristors are fired symmetrically, in an angle control range of 90 - 180 with respect to the capacitor (in- ductor) voltage. (3) Xsl are in the range of 0.02 - 0.05 p.u. with respect to the SVC base. The slope is needed to avoid hitting limits. At the voltage limits the SVC is transformed into a fixed reactance. The total equivalent impedance Xe of SVC may be represented by / sin 22(21/) x eC x k XX k π α απ =−+ − (4) where 3. Problem Formulation In this paper, as our attention is focused on the optimal active power flow problem, the liberalized (DC) power flow model is used. When the n − 1 security constraints were considered, the OPF problem can be formulated as follow: To minimize CP, (5) (6) whe r e , C: is the generation cost vector P: is the vector of active bus generation s': is the transpose of bus-branch incidence matrix : is the diagonal matrix of circuit susceptance : is the vector of angle across branch F (0) is the vector of base state active power flour in lines F (/) is the vector of active power flow in lines when branch I is break out : Is the active power loss in the system L: is the vector of active bus loads F and is the circuit flow limits P and are the generation limits This conventional optimization problem can be solved by the LP-based algorithm efficiently [5,17]. Next, two additional control variables and a set of power flow control equality constraints will be introduced into this op- timization.  K. Ravi et al. Because the FACTS devices parameters can be controlled in very small steps, the new additional control va- riables can be seen as continuous and limited by lower and upper bounds. The modified optimal active power flow problem can be formulated as follows: (7) (8) (9) whe r e , is the diagonal matrix of controlled line susceptance and sc is the bus-branch incidence matrix re- lated to controlled line. While is the vector of controlled line phase shifter angle and is a vector of specified line flows. is the vector of bus generation including the compensation injection power of phase shifter. It can be seen that this OPF problem is no longer a linear optimization problem due to the new control variable and the specified power flow equality constraints. Thus, it is not possible to use conventional LP technique [5,17] directly, and it becomes necessary to develop a new method to solve this optimization problem. 4. The Proposed Mbfa 4.1. Bacterial Foraging Algorithm BFA is an optimization technique motivated by the foraging behavior of the E coli. Bacteria. The biological as- pects of the bacterial foraging strategies and their motile behavior as well as their decision making mechanisms can be found in [9]. BFA is designed to solve non-gradient optimization problems and to handle complex and non-differentiable objective functions. Searching the hyperspace is performed through three main operations, namely; chemotaxis, reproduction and elimination dispersal activities [18]. The chemotaxis process is performed through swimming and tumbling. The bacterium spends its life alternating between these two modes of motion. In the BFA, a tumble is represented by a unit length in a random direction, Ф(j), which specifies the direction of movement after a tumble. The size of the step taken in the random direction is represented by the constant run-length unit, C(i). For a population of bacteria, the location of the ith bacterium at the jth chemotactic step, kth reproduction step and lth elimination/dispersal event is represented by At this location the cost function is denoted by ( 1,,)(,,)(,)() ii jkljkl Cijj θθ φ += + (10) When, the cost function J (i, j + 1, k, l) better (lower) than J(i ,j k, l), another step of size C(i, j) in the same direction is taken. This swimming operation is repeated as long as a lower cost is obtained until a maximum preset number of steps, Ns, is reached. The cost function of each bacterium in the population is af- fected by a kind of swarming that is performed by the cell-to-cell signaling released by the bacteria groups to form swarm patterns. This swarming is expressed as follows: ( ) 2 11 1 2 11 ,(..),,(,,)exp() exp( ) ss P ii i attract attractm ii m sP i repellent repellentm im JPjkljj kld h θθθωθ θ ω θθ ∞∞ ∞ = == ∞ = = ==−− − =−− − ∑∑ ∑ ∑∑ (11) where dattract, attract, hrepellant and repellant are coefficients that represent the characteristics of the  K. Ravi et al. attractant and repellant signals released by the cell and is the mth component of ith bacterium position is the position of each member of the population of the S bacteria and defined as: { } (,, )(,, )1,2,......, i P jkljkliS θ = = (12) where S is the size of the bacteria population. The function (9) which represents the cell-to-cell signaling effect is added to the cost function (13) A reproduction process is performed after taking a maximum number of chemotactic steps, Nc. The popula- tion is halved so that the least healthy half dies and each bacterium in the other healthiest one splits into two bacteria which takes the same position. (14) After Nre reproduction steps an elimination/dispersal event takes place for Ned number of excisions. In this operation each bacterium could be moved to explore other parts of the search space. The probability for each bacterium to experience the elimination/dispersal event is determined by a predefined fraction Ped. 4.2. Modified Bacterial Foraging Algorithm The unit step length of the basic BFA is constant which may guarantee good searching results for all optimiza- tion problems. However, when applied to complex problems with high dimensionality it shows poor perfor- mance. The run length parameter is the key factor for controlling the local and global search ability of the BFA. From this perspective, balancing the exploration and exploitation of the search could be achieved by adjusting the run-length unit. In this paper we propose a nonlinear decreasing dynamic function to perform the swim walk instead of the constant step. This function is expressed as: (, )() ( ,1)() () CC CC Ci jCN Ci jNj N CN − += − + (15 ) where j is the chemotactic step and Nc is the maximum number of chemotactic steps while C(Nc) is a predefined parameter. Control parameters of the MBFA are given in Table 1. The algorithm of the proposed technique is as follows: Step 1: Initialization of the following parameters: p: Dimension of the search space S: The number of bacteria in the population Nc: Number of chemotactic steps Ns: The length of a swim when it is on a gradient Nre: The number of reproduction steps Ned: The number of elimination-dispersal events ped: The probability that each bacterium will be eliminated/dispersed C(i, j)|j = 1: Initial run-length unit C(Nc): The run-length unit at the end of the Table 1. Control Parameter of the MBFA. Sl. No PARAMETER VALUE 1 Number of bacteria’s 4 2 Maximum number of steps, Ns 4 3 Number of chemotactic steps, Nc 5 4 Number of reproduction steps, Nre 4 5 Number of elimination–disperse steps, Ned 2 6 Probability, Ned 0.2 7 Size of the step, C(i) 0.1  K. Ravi et al. chemotactic steps (j = Nc). : The initial random location of each bacterium Step 2: Elimination/dispersal loop, l = l + 1 Step 3: Reproduction loop, k = k + 1 Step 4: Chemotaxis loop, j = j + 1 For i = 1, 2, …, S, execute the chemotactic step for each bacterium as follows: - Evaluate the cost function J(i, j, k, l) using (9) and (11). - Let Jlast= J (i, j, k, l) so that a lower cost could be found. - Tumble: generate a random vector ℜand is a random number in the range [−1, 1]. - Compute - Move using (8) - Compute and use (9) to Compute then use (11) to find the new -Swim: let m=0 (counter for swim length) While m< Ns (no climbing down too long) Let m=m+1. If let then take another step in the same direction and compute the new - Go to the next bacterium (i = i + 1 if i ≠ S). - Update the run length unit using (15). Step 5: If j < Nc go to step 4 (j = j + 1). Step 6: Reproduction: For the given k, l, evaluate the health of each bacterium i as follows: 1 1 (, , ,) c N i health j JJijkl + = =∑ (16) health of the bacterium i measures how many nutrient it got over its lifetime. Sort bacteria according to their health in ascending order. The bacteria with the highest values, computed by (16) die while the other Sr with the lowest values split and take the same location of their parents. Step 7: if k < Nre, go to step 3 (k = k + 1) Step 8: Elimination/ dispersal With probability ped, randomly eliminate and dispersal each bacterium i, keeping the size of the population const ant. Step 9: if l < N, go to step 2 (l = l + 1), otherwise end 5. Simulation Results The proposed algorithm is developed in the Matlab programming language using 7.5 versions. The proposed MBFA is tested using modified IEEE 30-Bus system. The test example has been run on a 2.6-Ghz Pentium-IV PC. Case Studies on the IEEE 30-Bus System IEEE 30-Bus, 41-branch system is tested, for the voltage constraint the lower and upper limits are 0.9 p.u and 1.06 p.u., respectively, (expect for PV buses where Vmax = 1:1 p.u). The efficiency of the proposed approach, we made a comparison of our algorithm with others competing OPF algorithm. In [9 ], they presented a standard GA, in [19], the authors presented an enhanced GA, and then in [20], they proposed an Ant colony optimization (ACO). In [13] they presented an optimal power flow solution using GA-fuzzy system approach. In [21], they pre- sented an efficient parallel GA (EPGA). The operating cost in our proposed approach is 800.1585 and the power loss is 8.4625 which are better than other methods reported in the literature. Results in Table 2 show clearly that  K. Ravi et al. Table 2. Results of minimum cost and power generation with SGA, EGA, ACO, FGA and EPGA for IEEE 30 bus. Variable SGA [9] EGA [19] ACO [20 ] FGA [13] E PGA [21] Proposed method (MBFA) P1 (MW) 179.367 176.20 181.945 175.137 180.12 164.501 P2 (MW) 44. 24 4 8. 75 47.001 0 5 0. 353 44.18 3 2. 423 P5 (MW) 24. 61 2 1. 44 20.553 0 2 1. 451 19.64 2 1. 459 P8 (MW) 19. 90 2 1. 95 21.146 0 2 1. 176 20.96 1 1. 130 P11 (MW) 1 0. 71 12.42 1 0. 433 0 12.667 1 4. 90 2 3. 872 P13 (MW) 1 4. 09 12.02 1 2. 173 0 12.11 1 2. 72 3 8. 470 Q1 (MVAR) −3.156 - - −6.562 −4.50 −3.609 Q2 (MVAR) 42.543 - - 22.356 30.71 3 7. 423 Q5 (MVAR) 26. 292 - - 30.372 22.59 24.985 Q8 (MVAR) 22. 768 - - 18.89 3 7. 85 19.530 Q11 (MVAR) 29. 923 - - 21.737 −2.52 15.821 Q13 (MVAR) 32. 346 - - 22.635 −13.08 7.598 θ1 (deg) 0.000 - - 0.00 0.00 0.00 θ2 (deg) −3.674 - - −3.608 −3.448 −3.375 θ5 (deg) −1 0. 14 - - −10.509 −9.858 −9.596 θ8 (deg) −1 0. 00 - - −8.154 −7.638 −7.012 θ11 (deg) −8.851 - - −8.783 −7.507 −4.789 θ13 (deg) −10. 13 - - −10.228 −9.102 −4.584 Ploss (MW) 9 .5 177 9 .3 900 9.8520 9.494 9.120 8.4625 Cost ($/h) 803.699 802.06 802.578 802.00 03 801.34 45 800.15 85 the proposed approach gives better results and the best solution of shunt compensation obtained at the standard load demand (Pd = 283.4 MW) using reactive power planning [18,22], line flows obtained are well under secu- rity limits compared to other algorithm such as FGA, SGA, ACO and other algorithms. First of all, the total real power loss of the system is calculated with shunt FACTS device and the result is 8.4625 MW. And to improve the performance of reactive power planning of the system shunt FACTS device in- cluded at different locations. The power loss is optimized by the MBFA with the combination of improving the bus voltage profile and generator reactive power 6. Conclusion A modified bacterial foraging algorithm (MBFA) for solving large scale OPF Problem has been demonstrated in this paper. Simulation results have demonstrated the effectiveness of the proposed algorithm and Comparison with other computational methods has shown that the MBFA achieved better results. A new method to incorp o- rating FACTS devised in OPF problem has been presented in this paper. The proposed method separates the modified optimization problem into problems’ iteration. The power flow control problem while the sub problem is a conventional OPF problem. The method incorporates the power flow control needs due to FACTS devices into the OPF Problem, and the optimization results can satisfy the power flow control needs and the economic operation at the same time. The case studies of an adapted IEEE 30-bus system have been presented to show the efficiency of the proposed method. References [1] Huneault and Galiana, F.D. (1991 ) A Survey of the Optimal Power Flow Literature. IEEE Transactions on Power,  K. Ravi et al. Systems, P WR S -6, 762-770. [2] Hingorani, N.G. (1993) Flexible ac Transmission. IEEE Spectrum, 40-45. http://dx.doi.org/10.1109/6.206621 [3] Taranto , G.N., Pinto, L.M.V.G. and Perei ra, M.V. F. (1992) Representation of FACTS Devices in Power System Eco- nomic Dispatch. IEEE Tran sactions on Power Systems, 7, 572-576. [4] Noroozian, M. and Andersson, G. (1993) Power Flow Control by Use of Controllable Series. IEEE Tran sactions on Power Deliver, 8, 1420-1429. http://dx.doi.org/10.1109/61.252669 [5] Stott, B. and Marinho, J.L. (1979) Linear Programming for Power System Network Security Application. IEEE Tran s- actions on Power Apparatus and Systems, PAS-98, 837-848 . [6] Gotham, D.J. and Heydt, G.T. (1998) Power Flow Control and Power Flow Studies for Systems with FACTS Devices. IEEE Transactions on Power and S ystems, 13, 60-65. http://dx.doi.org/10.1109/59.651614 [7] Sttot, B. an d Mari nho, J.L. (197 9) Linear Programming for Power System Network Security Applications. IEEE Transactions on Power Apparatus and Systems, PAS-98, 837 -848. [8] Als ac , O. and Stott, B. (1974 ) Optimal Load Flow with Steady State Security. IEEE Transactions on Power Apparatus and Systems, 745-751. [9] Sivan andam, S.N. and Deep a, S.N. (2008) Introduction to Genetic Algorithm. Springer-Verlag, Berlin, Heidelberg. [10] Pothiya, S., Nagamroo, I. and Kongprawechnon, W. (2008) Application of Multiple Tabu Search Algorithm to Solve Dynamic Economic Dispatch Considering Generator Constraints. Journal of Energy Conversion Manage, 49, 506-516. http://dx.doi.org/10.1016/j.enconman.2007.08.012 [11] Baskar, G. and Mohan, M.R. (200 8) Security Constrained Economic Load Dispatch Using Improved Particle Swarm Optimization Suitable for Utility System. Electric Power and Energy Systems, 30, 60 9-613 . http://dx.doi.org/10.1016/j.ijepes.2008.09.001 [12] Bouktir, T., Slimani, L. and Mahdad, B. (2008 ) Optimal Power Dispatch for Large-Scale Power System Using Sto- chastic Search Algorithms. International Journal of Electrical Power & Energy Systems, 28, 1-10. [13] Sain i, A., Chaturvedi, D.K. and Saxena, A.K. (2006) Optimal Power Flow Solution: A GA-Fuzzy System Approach. International Journal of Electrical Power & Energy Systems, 5, 1-21. http://dx.doi.org/10.2202/1553-779X.10 91 [14] Gai ng, Z.L. (2003) Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Con- straints. IEEE Transactions on Power and Systems, 18, 11 87-1195. http://dx.doi.org/10.1109/TPWRS.2003.814889 [15] Chien Kuo, C. (2008) A Novel String Structure for Economic Dispatch Problems with Practical Constraint’s. Energy Conversion Manage, 49, 3571 -3577. http://dx.doi.org/10.1016/j.enconman.2008.07.007 [16] Bouktir, T., Slimani, L. and Mahdad, B. (2008) Optimal Power Dispatch for Large-Scale Power System Using Sto- chastic Search Algorithms. International Journal of Electrical Power & Energy Systems, 28, 1-10. [17] Alsac, O., Bright, J., P rais, M. and Stott, B. (19 90) Further Developments in LP-Based Optimal Power Flow. IEEE Transactions on Power System, 5, 697-710. [18] Passi no, K.M. (2002) Biomimicry of Bacterial Foraging Algorithm for Distributed Optimization and Control. I E EE System Magazine, 22, 52-67. [19] Bakistzis, A.G., Biskas, P.N., Zoumas, C.E. and Pet r id i s, V. (2002) Optimal Power Flow by Enhanced Genetic Algo- rithm. IEEE Transactions on Power Systems, 17, 229-236. http://dx.doi.org/10.1109/TPWRS.2002.1007886 [20] Slimani, L. and Bouktir, T. (2007 ) Economic Power Dispatch of Power System with Pollution Control Using Multi Objective ant Colony Optimization. International Journal of Computational Intelligence Research, 3, 145-153. [21] Mahd ad, B., et al. (2009) Optimal Power Flow for Large Scale Power System with Shunt FACTS Devices Using Effi- cient Parallel GA. International Journal of Electrical Power & Energy Systems, 1-11. [22] Mahd ad, B., Bouktir, T. and Srairi, K. (2007 ) Methodology Based in Practical Fuzzy Rules Coordinated with Asy m- metric Dynamic Compensation Applied to the Unbalanced Distribution Network . International Review of Electrical Engineering (IREE), 3, 145-153 .
|