Applied Mathematics, 2011, 2, 487-495
doi:10.4236/am.2011.24063 Published Online April 2011 (http://www.SciRP.org/journal/am)
Embedding-Based Sliding Mode Control for Linear Time
Varying Systems
Mohammad Reza Zarrabi1, Mohammad Hadi Farahi1, Ali Jafar Koshkouei2, Sohrab Effati1,
Keith Burnham2
1Department of Applied Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran
2Control Theory and Applications Centre, Coventry University, Coventry, UK
Received February 20, 2011; revised March 10, 2011; accepted March 13, 2011
Abstract
In this paper, a novel strategy using embedding process and sliding surface is proposed. In this method, a
state trajectory starting from a given initial point reaches a definite point on a sliding surface in the minimum
time, and then tends to the origin along the sliding surface (SS). In the first, a SS is designed, then using an
appropriate measure, an embedding is constructed to solve a time optimal control problem such that the sys-
tem trajectory reaches the SS in minimum time, after that a control is designed such that the system trajecto-
ry tends to the origin along the SS. It is well-known that the main disadvantage of the use of sliding mode
controls (SMCs) is a phenomenon, the so-called chattering. The proposed SMC here is piecewise continuous
and chattering free. Some numerical examples is presented to illustrate the effectiveness and reliability of the
proposed method.
Keywords: Time Optimal Control Problem, Measure Theory, Sliding Mode Control, Sliding Surface Design,
Equivalent Control
1. Introduction
The concept of sliding mode control (SMC) introduced a
second order system by Emel’yanov [1] in the late 1960s
based on the conceptions of variable structure control
(VSC) in which the second order system trajectories has
been driven towards a line in the state space termed as
the sliding line and enforcing the trajectories to the origin.
However, Flügge-Lotz [2] was the first to present the
concept of sliding motion, and Filippov [3] was the first
to consider the solution of differential equations with a
discontinuous right-hand side. Filippov’s pioneering work
still serves as the basis for work in sliding mode control
which was essentially developed by Utkin [4] and
Emel’yanov [1,5], Draženović [6] and their co-workers.
The pioneering work had not been presented the out-
side of Russia until the mid 1970s when a book by Itkis
[7] and a survey paper by Utkin [8] were published in the
west. SMC which is a particular type of control, known
as variable structure control (VSC), is a powerful and
robust control, and it has been extensively studied in the
last three decades for many classes of linear and nonli-
near systems, from theoretical concepts to industrial ap-
plications, including autonomous underwater robot [9],
continuously stirred tank reactor [10], PUMA 560 robot
[11], finger for a prosthetic hand [12], cable suspended
loads [13] and four rotors helicopter [14].
Utkin [4] has developed the concept of sliding mode
control to guarantees the existence of a sliding mode
motion. In the classical SMC approach, infinite frequen-
cy control switching between different sub-controllers is
required to maintain the trajectories on a prespecified
surface in the state space and to eventually enforce the
state trajectories to the equilibrium point along the sur-
face. Therefore, the system stability and behaviour de-
pend on the selection of sliding surface [8,15]. Several
methods have been proposed to design a stable SS, such
neural network [9], fuzzy SMC [16], SMC a system with
mismatched uncertainties [17], discrete-time SMC [18],
minimizing integral absolute error [19], passivity-based
SMC [10,20] and flatness, back stepping with SMC [21].
SMC approach is well known as one of powerful and
effective robust control approaches to reject the matched
disturbances, to reduce the influence of unmatched un-
certainties and insensitivity to parameter variations. How-

M. R. ZARRABI ET AL. 488
ever, the repetitious control switching creates a phenome-
non, the so-called chattering, which may be dangerous
and exhibits high-frequency vibrations of the controlled
plant [22,23]. To overcome this unwanted behaviour,
many methods including several continuous approxima-
tions of the discontinuous SMCs have been proposed, in
which the switching function enforces the trajectories to
stay within a boundary layer of the sliding surface. The
main disadvantage of such approximation is that the ro-
bustness of SMC may be lost inside the boundary layer if
the size of the boundary layer is not sufficiently small. In
fact, the uncertainties and disturbances may influence the
system behaviour. Other methods for eliminating the
chattering are based on high order sliding mode control
concepts in which the higher order time derivative of the
switching function is used. The traditional discontinuous
sliding mode control enforces the state trajectories on the
sliding surface while the continuous part of sliding mode
control imposes the trajectories remain on the surface
after a finite time. The continuous part has a particular
structure which leads to the invariance conditions for the
sliding motion and in the average sense; it is termed the
equivalent control.
On the other hand, many methods based on sliding
mode and output feedback control schemes have been
also proposed for robust stabilisation of uncertain sys-
tems [24,25]. El-Khazali and DeCarlo [25] have de-
signed sliding surfaces for linear time-invariant systems
without disturbances using eigenvalue assignment and
eigenvector techniques. Żak and Hui [24] have devel-
oped a geometric condition to guarantee the existence of
a SS and the stability of the reduced order sliding motion.
Most established results are based on the matched dis-
turbances, i.e. the disturbances acts in the channels of the
inputs. Even when there are uncertainties in the system
with unknown structure, SMC is an appropriate control
design method. When the system is in a sliding mode,
the dimension of the system is reduced and it is the same
the SS. This subsystem is termed the reduced-order sys-
tem, and the stability of the original system depends on
the stability of this subsystem.
In this paper, a novel strategy based on measure theory
and sliding surface is proposed to design an almost time
optimal control as well as a sliding mode control to en-
force the system trajectories from an initial point to a
definite point on the designed SS in minimum time, and
then force the trajectories tend to the equilibrium points
along the SS. In fact, the entire of control design is com-
pleted in three steps. In the first step, the SS is designed.
In the second step, the minimum time optimal control
problem from an initial point to a given point on the SS,
is solved. In the third step, an equivalent control is de-
signed such that the system trajectories tend to the equi-
librium point along the SS. In fact, the trajectory moves
along the SS and eventually reaches the equilibrium
point (say origin) in infinite-horizon. The proposed con-
troller is piecewise continuous and yields a chattering
free motion. Furthermore, this method guarantees a slid-
ing mode motion and system stability. Moreover, the
proposed approach is straightforward without requiring
any predication or conditions on the initials and using
any iterative algorithm.
This paper is organised as follows: Section 2 briefly
introduces SMC. Section 3 addresses the functional space
and measure theory facts which are used in this paper.
Section 4 addresses the proposed SMC approach. In Sec-
tion 5, some examples are presented to illustrate the pro-
cedure and validity of the proposed control design. Fi-
nally, conclusions are given in Section 6.
2. SMC Design
Consider the linear time varying system






x
ttxttut
AB, (2.1)


0
0
x
x

, and the equilibrium point is the origin,
where nn


A
, nm


B, while

xt is the
state and


ut


is the control input. The sets 
and

are bounded, closed subsets respectively in n 
and m . It is assumed that 1mn and the input
distribution matrix B has full rank. Define the sliding
function as:


s
xGx, (2.2)
where mn
G

 and the sliding surface as:



:0
n
Sx sx

. (2.3)
It is also assumed that


GB t is a nonsingular matrix.
Suppose there exists a finite time
s
t such that the so-
lution of (2.1) represented by

x
t satisfies




0 for all
s
s
xtt t

,
then an ideal sliding motion is said to be taking place for
all
s
tt. Time
s
t is termed the reaching time and it is
the time that the system trajectories (2.1) lie on the sur-
face (2.3). This fact can be mathematically expressed as




0st Gxt

 and


0st Gxt  for all
s
tt.
In this paper an almost optimal control

ao
u is de-
signed to ensure the trajectories hits the SS in minimum
time. Then using the sliding mode conditions


0st

and


0st

 as two extra boundary conditions, a sub-
control


eq
u is designed such that the trajectories con-
verge to the equilibrium point. Thus the traditional SMC
is defined as:
if 0
if
ao s
eq s
utt
uutt





 (2.4)

M. R. ZARRABI ET AL. 489
where
s
t is the reaching time to theSS, i.e.


0
s
St

.
In fact, ao u is a sub-controller which impose the trajec-
tory that moves from an initial point hits the sliding sur-
face at point C in minimum time and eq u is the equi-
valent control which forces the trajectory moves from
C to the equilibrium point along SS.
The sliding surface is selected such that the reduced-
order system, i.e. the system during the sliding mode, is
stable and crosses from the point C. To find the beha-
viour of the sliding mode system, the system may be
decomposed into two subsystems as it is presented here.
If the states are partitioned so that
1
2
x
x
x



(2.5)
where 1
nm
x  and 2
m
x, then the linear system
(2.1) can be written as the following regular form
 
1111122
x
txttx t
AA
(2.6)
 
221122 22
x
txttx ttut
AAB, (2.7)
where the sub-matrices


11 tA,


12 tA,


21 tA,

22 tA, and

2tB are defined appropriately. (See [26]
for more details)
Equation (2.6), which is independent of the control,
considers as a system that shows sliding motion (the re-
duced-order system or the system in the sliding mode).
In the next section, we briefly introduce the functional
space used in embedding method.
3. Functional Space
To describe our embedding method, consider the general
following control system:
 
,,
x
tgtxu
 (3.1)
 
.. ,
ab
s
txaxxb x, (3.2)
where a and b are two nonnegative numbers with ab

,

.tab, the trajectory function

.
x
satisfies

xt and is absolutely continuous, the control func-
tion

.u is Lebesgue measurable and

ut

, where
 and

are respectively closed, and bounded sub-
sets in n
 and m , and


:, n gab is a
continuous time varying vector function.
Clearly the operating regions  and

are com-
pact sets and ,
ab
xx. It is desired to design the con-
trol u such that the system trajectory starting from the
initial state a
x
reaches the final state b
x
at tb

.
An optimal control problem is presented as the following:
Minimise:
 
0
,,,d
b
a
J
xuf txut (3.3)
subject to:

 
,,
x
tgtxu
 (3.4)


,
ab
x
axxbx

, (3.5)
where


0:,fab is a continuous function.
The pair






,wxu


satisfying the conditions
(3.4) and (3.5) is termed admissible. The set of all ad-
missible pairs, is denoted by W. Now, one seeks to find
an optimal pair




** *
,wxu W


which gives the
minimum value of


,
J
xu defined in (3.3). In general
the minimisation of the functional (3.3) over W may
not always possible. The set W may be empty, even if
W is not a null set, the functional measuring the per-
formance of the system may not achieves its minimum in
this set. It appears that the situation may become more
promising if the set W could somehow be made larger.
In the following a transformation is used to enlarge the
set W. Let






,wxu


be an admissible pair and
B an open ball containing I where


,
I
ab. Let


CB 

 where


CB
 denotes the space of real-
valued continuously differentiable functions on B. De-
fine the function
g

as
    
      
d
,, ,
d
,,, ,,
g
xt
txt uttxt
t
txtgtxt uttxt




(3.6)
with






,,txt utI

 
for all tI

. The
function
g

is in the space

C, the set of all con-
tinuous functions on the compact set . For each ad-
missible pair,
 






,, d,,
.
bg
atxt uttbxbaxa
CB

 






(3.7)
Let


0
DI be the space of infinitely differentiable
real-valued functions with a compact support in 0
I
,
where


0,
I
ab. Define
    

  

0
d
,, d
,, ,
, 1,2,,.
jj
jj
txt uttx t
t
tx ttgtxt ut
DI jn






 
(3.8)
Then, if






,wxu

 is an admissible pair, for
every


0
DI  ,
 

,,d0, 1,2,,.
b
j
atxt uttjn
 
 (3.9)
Let


1
C

be a subspace of the space


C

of all
bounded continuous functions on  depending only on
the variable t. Now, by selecting the function


1
fC

,
it is obtained

M. R. ZARRABI ET AL. 490
    
1
,,d
b
f
aftxt uttafC
, (3.10)
the set of Equalities (3.7), of which we have singled out
the special cases (3.9) and (3.10), are properties of the
admissible pairs in the classical formulation of the op-
timal control problem. In the following a transformation
is developed to a non-classical problem to obtain en-
hanced properties in some aspects (see [27] for the de-
tails).
For each admissible pair w, there is a positive linear
continuous functional w
 on

C such that


   
:,,d
wI
FFtxtuttFC  
.
By the Riesz representation theorem (see [28]) there
exists a unique positive Borel measure

on Ω such
that
   


,, dd
.
wI
F
Ftxt uttFF
FC





(3.11)
Thus, the optimal control problem (3.3)-(3.5) is equi-
valent to the minimisation of



00
dJff 


 (3.12)
over the set of measures

, associated with the ad-
missible pair w, which satisfy



 
 
0
1
,
0, , 1,2,,
, .
g
j
f
CB
DI jn
fafC
 
 


 
 

 (3.13)
Let

M be the set of all positive Borel measures
on Ω. Define the set


QM

 of all positive Borel
measures on Ω which satisfy (3.13). Now if the space

M is topologised by the weak*-topology, it can be
shown that Q is compact with the topology induced
(see [28]). In the sense of the weak*-topology, the func-
tional

0:fQ
  defined as in (3.12), is a linear
continuous functional on the compact set Q. Thus it
attains its minimum on Q, and therefore, the measure-
theoretical problem, which consists of finding the mini-
mum of the functional (3.12), over the subset of


M

,
possesses a minimising solution, say *

, in Q.
The set I  is covered with a grid, where
the grid will be defined by taking all points in

as

,,
j
jjj
ztxu. Instead of the infinite-dimensional li-
near programming problem (3.12) and (3.13), the fol-
lowing finite dimensional linear programming (LP)
problem is considered where j z

 in which

is an
approximately dense subset of  (see [29] and its ref-
erences for more details). The finite dimensional LP
problem, which approximates the action of the infinite
dimensional LP problem (3.12) and (3.13) for a suffi-
cient large integer N is as follows.

0
1
min N
j
j
j
f
z 


..
s
t



 


1
1
0
2
1
1
1
, 1,2,,,
0, 1,2,,,
, 1,2,,,
0, , 1,2,,
Ng
ji jii
j
N
jr j
j
N
js jfss
j
jj
ziMCB
zr MDI
fzasLf C
zj N
 
 





  
 
 








(3.14)
Now, using the solution of this problem, one can ob-
tain the coefficients


1, 2,,
jjN
 , and also from
the analysis of the problem as in Rubio (see [27]), it is
possible to obtain the piecewise-constant control func-
tion


u

which approximates the action of the optimal
measure. As a final stage, from the dynamical system
(3.4) and (3.5), one can obtain the state trajectory


x

.
4. Applying Embedding Method
In this section a time optimal control, a sliding surface,
and a so-called equivalent control, for a system such as
(2.1) is considered.
4.1. Step 1: Sliding Surface Design
Consider the regular form of the linear dynamical system
(2.6) and (2.7). Define the sliding surface (2.3) as:




11112 20sxx x

IA A, (4.1)
from (4.1),
 
1
212 111
x
x

 AIA ,
where 1
2
x
x



x,

1
12
L

A is the left inverse of the ma-
trix


12
A
, and I is the identity matrix.
The SS as (4.1) guarantees the stability of the system.
One can see this in the following theorem.
Theorem 1. The sliding motion (2.6) is asymptotically
stable (by Lyapunov sense) on sliding surface (4.1).
Proof. To show the stability of dynamical system (2.6)
and (2.7) on SS (4.1), one can define a suitable Lyapu-
nov function


Vx from nm R to R as:

11
1
2
T
Vx xx,
then,
 
111111221
T
T
Vx xxxx x 
AA,
By considering SS Equation (4.1), we have


1111122
x
xx AA.
Hence,

M. R. ZARRABI ET AL. 491

11 112211 1122
T
Vxx xx x 
AA AA
and so
 
0VxVx
.
That is, while trajectory lies on sliding surface (4.1),
one have
 
0VxVx
, and this procedure, guarantees
the asymptotically stability of sliding motion (2.6) with
respect to SS (4.1). □
4.2. Step 2: Time Optimal Control
Now, use of embedding technique is suggested to solve a
time optimal control problem. Using this method, the
sub-control ao u is designed such that a state trajectory
starting from the initial point B reaches the point C on
the SS in minimum time. By considering Section 3, this
time optimal control problem governed by dynamical
system (2.6) and (2.7) is metamorphosed to the following
linear programming problem:
1
min N
j
j



subject to:








1
1
0
2
1
1
1
1
1,2,,
0 1,2,,
1,2,,
0
0, 1,2,,.
Ng
ji jii
j
N
jr jr
j
N
js jfss
j
N
jj
j
jj
ziMCB
zrMDJ
fzasLf C
sz s
zjN
 
 








 
 
 











(4.2)
The last equality guarantees the trajectory starting
from B, hits the SS at the C in minimum time
4.3. Step 3: Equivalent Control Design
In order to design the equivalent control, consider the SS
as (4.1). The derivative of

1211 1122
,
s
xxx x IAA
is as follow:
 

11112 2
11 1111122122
dd
dd
sSxx
tt
x
xxx
 
 



IA A
AIAAA
.
Now by considering (2.6) and (2.7), one have:


11 11111 1122122
1221 12222eq
Sxxxx
xxu
 

 
AIAAAA
AA AB,
to guarantee the stability of the system on SS, we need to
have, 0s
. So we get Equation (4.3):
This control forces the trajectories stay on the SS, and
the motion is chattering free.
Remark: It is well-known that SMCs are robust
against the matched disturbance and unmodelled dynam-
ics. Note that the system (2.1) with disturbance term is





 
x
ttxttutDt
AB , (4.4)
where


n
Dt. Assume that the matched disturbance


Dt influences the system after a certain time
D
t
where
s
D
tt

, and its effect on the system before this
time is insignificant. Then the proposed method inhe-
rently has the robustness property because the system in
the sliding mode is given by (2.6) in which the term


Dt is absent. If
D
s
tt

one may select
s
t such that
the condition
s
D
tt

is fulfilled. Then the cost func-
tional (3.3) is minimised from 0t to
s
t. If such in-
formation is unavailable, but the disturbance term is
bound to a known function

ht , i.e.




Dt ht,
then the term




T
htRht where R is a positive defi-
nite symmetric matrix is included in the integrand of the
cost functional (3.3). However, in the presence of dis-
turbances, an appropriate method is to use a best estimate
of


Dt which is available or can be designed. Assume
that


Dt is a piecewise continuous and bounded sig-
nal and only a constant bound on the disturbance signal


Dt may be available, i.e. there is a positive number
0
h such that


0
Dt h

. Let

be a small positive
number, two appropriate estimates of

Dt are
 
2
1
1dif 2
ˆ
0otherwise
t
tDt tt
Dt












(4.5)
and
 
2
2
maxif 2
ˆ
0otherwise
tttDt t
Dt 







(4.6)
Both estimates 1
ˆ
D and 2
ˆ
D are computable at the
current time and a designer may select one of them de-
pending on the nature of a disturbances. Therefore, in
both options, the term
 
ˆˆ
T
ii
DtRDt

1 or 2ii
where nn R


 is an arbitrary positive definite sym-
metric matrix, is included to the integrand of the cost
functional (3.3) i.e.



0ˆˆ
,,, d
bT
ii
a
J
xuftxuDt RDtt
 (4.7)
Note that in both scenarios (4.5) and (4.6),

0
ˆi
Dth

,
and the cost functional (4.7) is minimised subject to






ˆi
x
ttxttutDt
AB (4.8)

 
0,
asb
x
xxt x

.
 

1
12211 1111111221221221 1222eq L
uxIxxxxx

 

ABAAAAAA AA. (4.3)

M. R. ZARRABI ET AL. 492
5. Numerical Example
Example 1. Consider the following dynamical system:
112 3
2
x
xx x

212
2
x
xx

313
3
x
xxu

 
02.25,5.25,4.2x , and the origin is equilibrium
point.
It is desired to design an almost time optimal control
ao
u such that the trajectory starting from the initial point

2.25,5.25, 4.2B reaches the point

2, 5, 4.5C
on the SS in minimum time, then derive the system from
C to the origin (equilibrium point) along the SS in an
infinite time. Assume






2.5, 1.54.5,5.54,5  
and


1.1,1.1

. By solving the LP problem (4.2),
the optimal time is found as 0.03
s
t

. In next two steps,
the SS and equivalent control eq u are designed such
that the system is stable and the trajectories remain on
the SS for all 0.03
s
tt.
To design SS, From (4.1) we have:
 
11
312 11
2
L
x
x
x

 

AIA ,
or,

123
0.5 0sxxx x . Now by (4.3), the equi-
valent control achieves as follow:
123
30.53
eq
uxxx .
This control causes

0sx 
, so guarantee the trajec-
tories stay on sliding surface. Now by the procedure dis-
cussed in this article, the whole trajectory functions can
be found. The entire trajectories using the control
if 0
if
ao s
eq s
utt
uutt





 (5.2)
are designed through the steps 1 and 3. Figure 1 shows
the action of the optimal controls (5.2), and the beha-
viour of the states using these controls.
Example 2. Consider the following dynamical system:




 
 
11
2
3
0.150.02sin0.12sin 10
0.70.01cos
0.2060.014sin2
x
ttx
tx
tx



 







  
 
21
2
3
1.45 0.1sin
2.10.05cos0.2cos5
1.030.07sin2
xtx
ttx
tx




 





 
312
3
0.40.5sin1.7
0.610.014sin
x
tx x
x
tu


 






00.1,0.69, 1.8x , and the origin is equilibrium
point.
The above example is from [17], and is implemented
by the method considered have, to compare outcome
with the results appeared in [17]. It is desired to design
an almost time optimal control ao u such that the trajec-
tory starting from the initial point

0, 3,2B
reaches
the point


0.1,0.69,1.8C on the SS in minimum
time, then derive the system from C to the origin
(equilibrium point) along the SS in an infinite time. As-
sume






1, 01,36, 0  and


1.5,1.5

.
By solving the LP problem (4.2), the optimal time is
found as 0.88
s
t

. In next two steps, the SS and equiv-
alent control eq u are designed such that the system is
stable and the trajectories remain on the SS for all
0.88
s
tt.
To design SS, from (4.1) we have:
 
11
312 11
2
L
x
xI
x

 

AA,
hence,


 




312
10.02sin0.12sin101.150.01cos0.7
1.030.07sin 2
x
ttxtx
t
 



,
and eq u is found from (4.3).
Figure 2 shows the action of the optimal controls (5.2),
and the behaviour of the states using these controls. The
trajectory hits SS at 0.88
s
t and reaches the neigh-
bour of equilibrium point (origin) in the time less than 3,
and the behavior is chattering free. The result show that
the method used in this article is more accurate than the
method in [17]. Since trajectories reach SS in shorter
time, nevertheless, the method is very easy to use.
Example 3. Consider the following linear dynamical
system with disturbance:





112
3
2sin cos
10.1sin2cos3
xtxtx
tx t


 
 





21 23
cos2 sin0.2cos2sin
x
txt xt xt

 




3123
1cos sin2cos
40.1sin2
x
ttxx tx
ut

 






02,5,9x

, and the origin is equilibrium point.
Without loss of generality, we assume


x

lies on
SS. By (4.1) the SS defines as: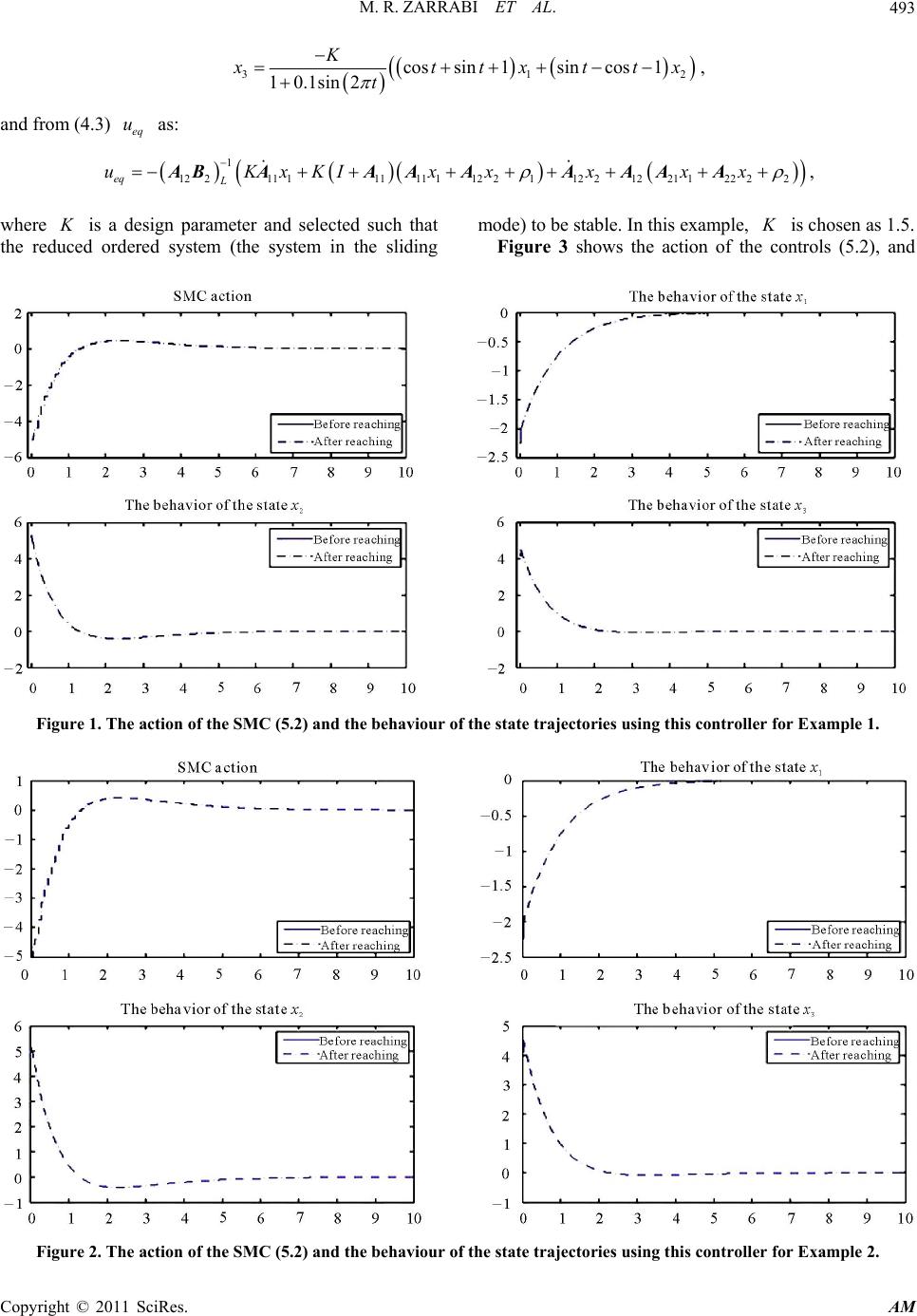

M. R. ZARRABI ET AL. 493



312
cossin1sincos1
10.1sin2
K
x
ttx ttx
t



,
and from (4.3) eq u as:
 


1
12211 11111112211221221 12222eq L
uKxKIxxxxx





ABAAAAAA AA,
where
K
is a design parameter and selected such that
the reduced ordered system (the system in the sliding
mode) to be stable. In this example,
K
is chosen as 1.5.
Figure 3 shows the action of the controls (5.2), and
Figure 1. The action of the SMC (5.2) and the behaviour of the state trajectories using this controller for Example 1.
Figure 2. The action of the SMC (5.2) and the behaviour of the state trajectories using this controller for Example 2.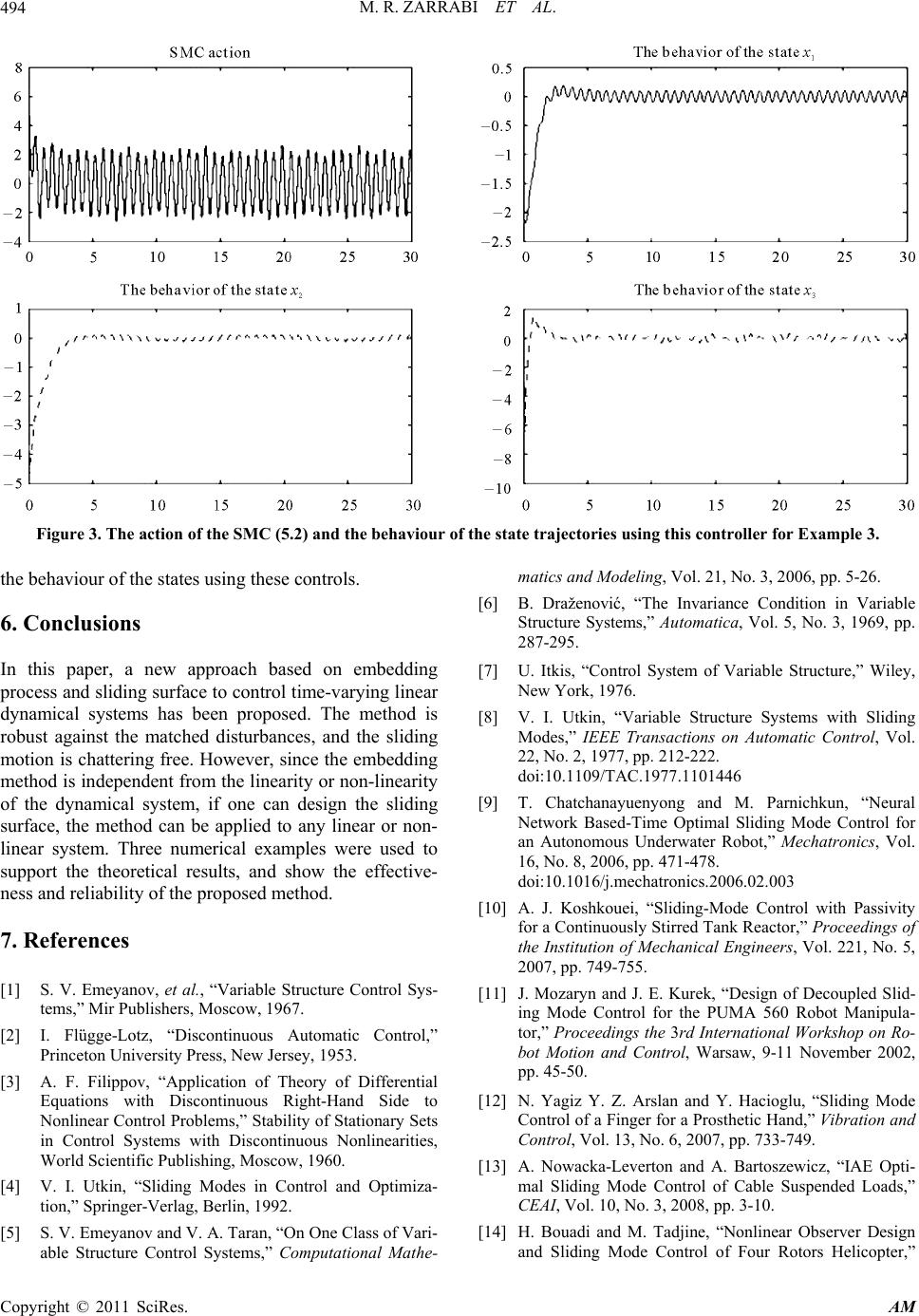

M. R. ZARRABI ET AL. 494
Figure 3. The action of the SMC (5.2) and the behaviour of the state trajectories using this controller for Example 3.
the behaviour of the states using these controls.
6. Conclusions
In this paper, a new approach based on embedding
process and sliding surface to control time-varying linear
dynamical systems has been proposed. The method is
robust against the matched disturbances, and the sliding
motion is chattering free. However, since the embedding
method is independent from the linearity or non-linearity
of the dynamical system, if one can design the sliding
surface, the method can be applied to any linear or non-
linear system. Three numerical examples were used to
support the theoretical results, and show the effective-
ness and reliability of the proposed method.
7. References
[1] S. V. Emeyanov, et al., “Variable Structure Control Sys-
tems,” Mir Publishers, Moscow, 1967.
[2] I. Flügge-Lotz, “Discontinuous Automatic Control,”
Princeton University Press, New Jersey, 1953.
[3] A. F. Filippov, “Application of Theory of Differential
Equations with Discontinuous Right-Hand Side to
Nonlinear Control Problems,” Stability of Stationary Sets
in Control Systems with Discontinuous Nonlinearities,
World Scientific Publishing, Moscow, 1960.
[4] V. I. Utkin, “Sliding Modes in Control and Optimiza-
tion,” Springer-Verlag, Berlin, 1992.
[5] S. V. Emeyanov and V. A. Taran, “On One Class of Vari-
able Structure Control Systems,” Computational Mathe-
matics and Modeling, Vol. 21, No. 3, 2006, pp. 5-26.
[6] B. Draženović, “The Invariance Condition in Variable
Structure Systems,” Automatica, Vol. 5, No. 3, 1969, pp.
287-295.
[7] U. Itkis, “Control System of Variable Structure,” Wiley,
New York, 1976.
[8] V. I. Utkin, “Variable Structure Systems with Sliding
Modes,” IEEE Transactions on Automatic Control, Vol.
22, No. 2, 1977, pp. 212-222.
doi:10.1109/TAC.1977.1101446
[9] T. Chatchanayuenyong and M. Parnichkun, “Neural
Network Based-Time Optimal Sliding Mode Control for
an Autonomous Underwater Robot,” Mechatronics, Vol.
16, No. 8, 2006, pp. 471-478.
doi:10.1016/j.mechatronics.2006.02.003
[10] A. J. Koshkouei, “Sliding-Mode Control with Passivity
for a Continuously Stirred Tank Reactor,” Proceedings of
the Institution of Mechanical Engineers, Vol. 221, No. 5,
2007, pp. 749-755.
[11] J. Mozaryn and J. E. Kurek, “Design of Decoupled Slid-
ing Mode Control for the PUMA 560 Robot Manipula-
tor,” Proceedings the 3rd International Workshop on Ro-
bot Motion and Control, Warsaw, 9-11 November 2002,
pp. 45-50.
[12] N. Yagiz Y. Z. Arslan and Y. Hacioglu, “Sliding Mode
Control of a Finger for a Prosthetic Hand,” Vibration and
Control, Vol. 13, No. 6, 2007, pp. 733-749.
[13] A. Nowacka-Leverton and A. Bartoszewicz, “IAE Opti-
mal Sliding Mode Control of Cable Suspended Loads,”
CEAI, Vol. 10, No. 3, 2008, pp. 3-10.
[14] H. Bouadi and M. Tadjine, “Nonlinear Observer Design
and Sliding Mode Control of Four Rotors Helicopter,”

M. R. ZARRABI ET AL. 495
Vorld Academy of Science, Engineering and Technology,
Vol. 25, 2007, pp. 225-229.
[15] A. S. I. Zinober, “Variable Structure and Lyapunov Con-
trol,” Springer Verlag, London, 1994.
doi:10.1007/BFb0033675
[16] J.-C. Le, and Y.-H. Kuo, “Decoupled Fuzzy Sliding Mo-
de Control,” IEEE Transactions on Fuzzy Systems, 1998,
Vol. 6, No. 3, pp.426-435. doi:10.1109/91.705510
[17] S. H. Jang and S. W. Kim, “A New Sliding Surface De-
sign Method of Linear Systems with Mismatched Uncer-
tainties,” IEICE Transactions on Fundamentals of Elec-
tronics, Vol. E88-A, No. 1,2005, pp. 387-391.
[18] B. Bandyopadhyay and S. Janardhanan, “Discrete-Time
Sliding Mode Control,” Springer-Verlag, Berlin, 2005.
[19] M. Thoma, F. Allgöwer and M. Morari, “Time-Varying
Sliding Modes for Second and Third Order Systems,”
Springer-Verlag, Berlin, 2009.
[20] A. J. Koshkouei, “Passivity-Based Sliding Mode Control
for Nonlinear Systems,” International Journal of Adap-
tive Control and Signal Processing, Vol. 22, No. 9, 2008,
pp. 859-874. doi:10.1002/acs.1028
[21] A. J. Koshkouei, K. Burnham and A. S. I. Zinober,
“Flatness, Backstepping and Sliding Mode Controllers for
Nonlinear Systems,” In: G. Bartolini, L. Fridman, A.
Pisano and E. Usai, Eds., Modern Sliding Mode Control
Theory, Springer-Verlag, Berlin, 2008, pp. 269-290.
doi:10.1007/978-3-540-79016-7_13
[22] B. Friedland, “Advanced Control System Design,” Pren-
tice-Hall, Englewood Cliffs, 1996.
[23] A. J. Koshkouei and A. S. I. Zinober, “Sliding Mode
Controller-Observer Design for SISO Linear Systems,”
International Journal of Systems Science, Vol. 29, No. 12,
1998, pp. 1363-1373. doi:10.1080/00207729808929622
[24] S. H. Żak and S. Hui, “On Variable Structure Output
Feedback Controllers for Uncertain Dynamic Systems,”
IEEE Transactions on Automatic Control, Vol. 38, No.
10, 1993, pp. 1509-1512. doi:10.1109/9.241564
[25] R. El-Khazali and R. DeCarlo, “Output Feedback Vari-
able Structure Control Design,” Automatica, Vol. 31, No.
6, 1995, pp. 805-816. doi:10.1016/0005-1098(94)00151-8
[26] C. Edwards and S. K. Spurgeon, “Sliding Mode Control:
Theory and Applications,” Taylor & Francies, London,
1998.
[27] J. E. Rubio, “Control and Optimization; The Linear
Treatment of Nonlinear Problems,” Manchester Univer-
sity Press, Manchester, 1986.
[28] W. Rudin, “Real and Complex Analysis,” 3rd Edition,
McGraw-Hill, New York, 1987.
[29] S. Effati, A. V. Kamyad and R. A. Kamyabi-Gol, “On
Infinite-Horizon Optimal Control Problems,” Journal for
Analysis and Its Applications, Vol. 19, No. 1, 2000, pp.
269-278.