Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 475-481 doi:10.4236/am.2011.24061 Published Online April 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Boundary Layer Flow and Heat Transfer of a Dusty Fluid over a Stretching Vertical Surface Bijjanal Jayanna Gireesha, Gosikere Kenchappa Ramesh, Hatti Jayappa Lokesh, Channabasappa Shanthappa Bagewadi Department of St u die s an d Re searc h in Mat h emat i cs , Kuvempu University, Shimoga, India E-mail: bjgireesu@rediffmail.com Received February 20, 2011; revised March 7, 2011; accepted March 9, 2011 Abstract This paper presents the study of convective heat transfer characteristics of an incompressible dusty fluid past a vertical stretching sheet. The governing partial differential equations are reduced to nonlinear ordinary dif- ferential equations by using similarity transformation. The transformed equations are solved numerically by applying Runge Kutta Fehlberg fourth-fifth order method (RKF45 Method). Here obtained non-dimensional velocity and temperature profiles has been carried out to study the effect of different physical parameters such as fluid-particle interaction parameter, Grashof number, Prandtl number, Eckert number. Comparison of the obtained numerical results is made with previously published results. Keywords: Boundary Layer Flow, Dusty Fluid, Stretching Sheet, Grashof Number, Fluid-Particle Interaction Parameter, Numerical Solution 1. Introduction The behavior of boundary layer flow due to a moving flat surface immersed in a quiescent fluid was first stu- died by Sakiadis [1], who investigated it theoretically by both exact and approximate methods. Crane [2] presented a closed form exponential solution for the planar viscous flow of linear stretching case. Later this problem has been extended to various aspects by considering non-Newton- ian fluids, more general stretching velocity, magnetohy- drodynamic (MHD) effect, porous sheet, porous media and heat or mass transfer. Andreson et al. [3] extended the work of crane [2] to non-Newtonian power law fluid over a linear stretching sheet. Chakrabarti and Gupta [4] have discussed the hydromagnetic flow and heat transfer over a stretching sheet. Grubka and Bobba [5] analyzed heat transfer studies by considering the power law varia- tion of surface temperature. Cortell [6] studied the mag- netohydrodynamics flow of a power-law fluid over a stretching sheet. Chen [7] analyzed mixed convection of a power law fluid past a stretching surface in the pres- ence of thermal radiation and magnetic field. Power law model has some limitations as, it does not exhibit any elastic properties such as normal stress diffe- rences in shear flow. In certain polymer processing appli- cations, flow of a viscoelastic fluid over a stretching sheet is important. For that reason Cortell [8] studied the effe- cts of viscous dissipation and work done by deformation on the MHD flow and heat transfer of a viscoelastic fluid over a stretching sheet. Abel et al. ([9,10]) extended the work and studied the viscoelastic MHD flow and heat transfer over a stretching sheet with viscous and ohmic dissipation, non-uniform heat source and radiation. Tsai et al. [11] studied an unsteady flow over a stretching sur- face with non-uniform heat source. Ishak et al. [12] ob- tained the solution to unsteady laminar boundary layer over a continuously stretching permeable surface. These investigations deal with the flow and heat trans- fer induced by a horizontal stretching sheet, but there ari- se some situations where the stretching sheet moves ver- tically in the cooling liquid. Under such circumstances the fluid flow and the heat transfer characteristics are deter- mined by two mechanisms, namely the motion of stret- ching sheet and the buoyant force. The thermal buoyancy resulting from heating/cooling of a vertically moving str- etching sheet has a large impact on the flow and heat transfer characteristics. Effects of thermal buoyancy on the flow and heat transfer under various physical situa- tions have been reported by many investigators (see [13- 16]). To study the two-phase flows, in which solid spherical  B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 476 particles are distributed in a fluid are of interest in a wide range of technical problems, such as flow through packed beds, sedimentation, environmental pollution, centrifugal separation of particles, and blood rheology. The study of the boundary layer of fluid-particle suspension flow is important in determining the particle accumulation and impingement of the particle on the surface. In view of these applications, Chakrabarti [17] analyzed the boun- dary layer in a dusty gas. Datta and Mishra [18] have in- vestigated boundary layer flow of a dusty fluid over a semi-infinite flat plate. Further, researches in these fields have been studied by many investigators such as Evgeny and Sergei [19], XIE Ming-liang et al. [20], Palani et al. [21], Agranat [22] and Vajravelu et al. [23]. Abdul Aziz [24] obtained the numerical solution for laminar thermal boundary over a flat plate with a convective surface boundary condition using the symbolic algebra software Maple. Motivated by the above investigations, we present in this paper the boundary layer flow and heat transfer of a dusty fluid over a stretching vertical surface. The govern- ing partial differential equations are transformed into or- dinary differential equations using similarity transforma- tion, before they are solved numerically by Runge Kutta Fehlberg fourth-fifth order method. Comparison of the results are to be in excellent agreement those reported by Grubka and Abel. The RKF45 algorithm in Maple has been well tested for its accuracy and robustness. The analysis of obtained results showed that the fluid particle interaction parameter, Grashof number, Prandtl number and Eckert number have significant influence on the flow and heat transfer. 2. Flow Analysis of the Problem Consider a steady two dimensional laminar boundary layer flow of an incompressible viscous dusty fluid over a vertical stretching sheet. The flow is generated by the action of two equal and opposite forces along the x-axis and y-axis being normal to the flow. The sheet being stretched with the velocity w Ux along the x-axis, keeping the origin fixed in the fluid of ambient tempera- ture T. Both the fluid and the dust particle clouds are suppose to be static at the beginning. The dust particles are assumed to be spherical in shape and uniform in size and number density of the dust particle is taken as a con- stant throughout the flow. The momentum equations of the two dimensional boundary layer flow in usual notation are [23]: 0 uv xy (2.1) 2 * 2p uv u xyy KN uvv uugTT (2.2) p pp pp uu K xy uv muu (2.3) p pp pp vv K xy uv mvv (2.4) 0 pp Nu Nv xy (2.5) where ,uv and , p p uv are the velocity compo- nents of the fluid and dust particle phases along x and y directions respectively. u, and N are the co-effi- cient of viscosity of the fluid, density of the fluid, num- ber density of the particle phase, K is the stokes’ resis- tance (drag co-efficient), T and T are the fluid tem- perature within the boundary layer and in the free stream respectively. g is the acceleration due to gravity, * is the volumetric coefficient of thermal expansion, m is the mass of the dust particle respectively. In deriving these equations, the drag force is considered for the iteration between the fluid and particle phases. The boundary conditions are , 0 at 0, 0, 0, , as . w pp Uxv y uu u vvN y (2.6) where w Ux cx is a stretching sheet velocity, 0c is stretching rate, is the density ratio. To convert the governing equations into a set of similarity equations, we introduce the following transformation as mentioned below, , , , , pp r c ucxfvvc fy v u cxFvvcGH (2.7) which identically satisfies (2.1), and substituting (2.7) into (2.2) to (2.5), we obtain the following non-linear ordinary differential equations: 2 *0 fff fGr lH Ff (2.8) 20GFFF f (2.9) 0GGf G (2.10) 0HF HGGH (2.11) where a prime denotes differentiation with respect to and * lmN , mk is the relaxation time of the particle phase, 1c is the fluid particle interaction parameter, *2 w GrgTTc x is the Grashof num- ber and rN is the relative density. The boundary conditions defined as in (2.6) will take  B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 477 the form, 0, 0 at 0ff (2.12) 0, 0, ,fFGf as H If 0 and 0Gr the analytical solution of (2.8) with boundary condition (2.12) can be written in the form: 1 f e 3. Heat Transfer Analysis The dusty boundary layer heat transport equations in the presence of non-uniform internal heat generation/ab- sorption for two dimensional flows are given by [25]: *2 2 2 PP pT pv TTkTN N xy y uvTT uu cc (3.1) pp pp T p mP uTT xTT yc vc (3.2) where T and P T is the temperature of the fluid and temperature of the dust particle, P c and m c are the specific heat of fluid and dust particles, T is the ther- mal equilibrium time and is time required by the dust cloud to adjust its temperature to the fluid, v is the relaxation time of the of dust particle i.e., the time re- quired by the a dust particle to adjust its velocity relative to the fluid, * k is the thermal conductivity. In order to solve the (3.1) and (3.2), we consider non dimensional temperature boundary condition as follows 2 at 0 , as w p x TT TAy l TTTT y (3.3) where A is a positive constant, v lc is a characteris- tic length. Now we define the non-dimensional fluid phase tem- perature and p dust phase temperature as , p p ww TT TT TT TT (3.4) where 2 x TTA l Using (3.4) into (3.1) to (3.2), we obtain the following non-linear ordinary differential equations 2 Pr 2 p Tv ff NPrNPrEc Ff c (3.5) 2 0 pp pp mT FG c cc (3.6) where * p c Pr k is the Prandtl number, 2 p cl Ec A c is the Eckert number. The corresponding boundary conditions for and p as 1 as 0 0, 0 as p (3.7) 4. Results and Discussion The system of coupled ordinary differential Equations (2.8) to (2.12) and (3.5) to (3.7) has been solved numeri- cally using Runge-Kutta-Fehlberg fourth-fifth order me- thod. To solve these equations we adopted symbolic al- gebra software Maple which was given by Aziz [24]. Maple uses the well known Runge-Kutta-Fehlberg fourty- fifth order (RFK45) method to generate the numerical solution of a boundary value problem. The boundary conditions were replaced by those at 5 in accordance with standard practice in the boundary layer analysis. Numerical computation of these solutions have been carried out to study the effect of various physical parameters such as fluid particle interaction parameter , Grashof number Gr , Prandtl number Pr and Eckert number Ec are shown graphically. In order to verify the accuracy of our present study, the values for wall temperature 0 gradient for vari- ous values of Prandtl number are given in Table 1, which shows the excellent agreement with those reported by Grubka and Bobba [5] and Abel and Mahesha [10]. Further, the Table 2 shows the results of thermal charac- teristics at the wall for different values of influenced physical parameters. Figure 1 shows the effect of Grashof number Gr on the velocity profile. From this plot it is observed that the effect of increasing values of Grashof number is to increases the velocity distribution in the flow region. Physically 0Gr means heating of the fluid or cooling of the boundary surface, 0Gr means cooling of the fluid or heating of the boundary surface and 0Gr corresponds to the absence of free convection current. From the Figure 2 shows the effect of fluid particle 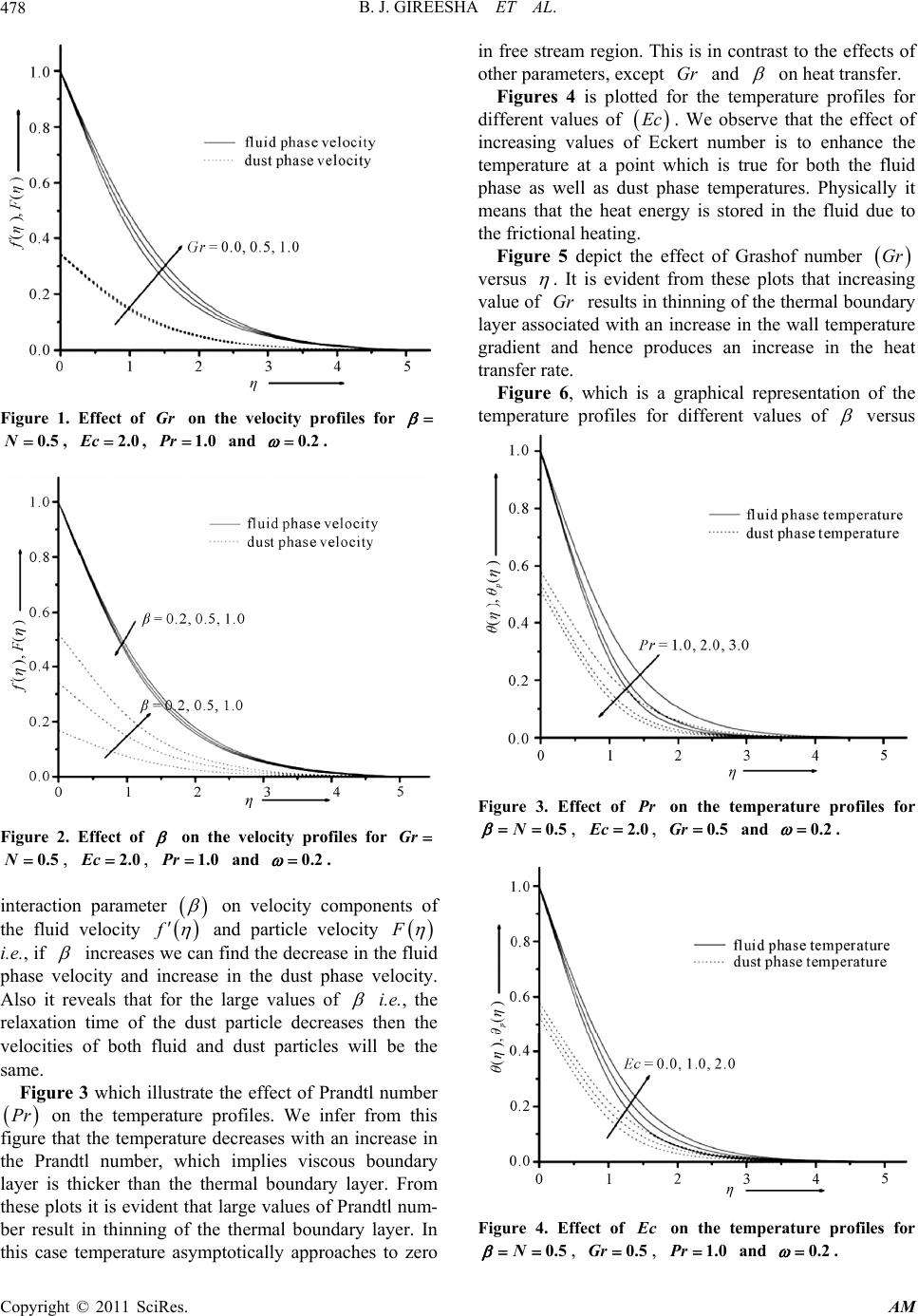 B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 478 Figure 1. Effect of Gr on the velocity profiles for 0.5N, 2.0Ec , 1.0Pr and 0.2 . Figure 2. Effect of on the velocity profiles for Gr 0.5N, 2.0Ec, 1.0Pr and 0.2 . interaction parameter on velocity components of the fluid velocity f and particle velocity F i.e., if increases we can find the decrease in the fluid phase velocity and increase in the dust phase velocity. Also it reveals that for the large values of i.e., the relaxation time of the dust particle decreases then the velocities of both fluid and dust particles will be the same. Figure 3 which illustrate the effect of Prandtl number Pr on the temperature profiles. We infer from this figure that the temperature decreases with an increase in the Prandtl number, which implies viscous boundary layer is thicker than the thermal boundary layer. From these plots it is evident that large values of Prandtl num- ber result in thinning of the thermal boundary layer. In this case temperature asymptotically approaches to zero in free stream region. This is in contrast to the effects of other parameters, except Gr and on heat transfer. Figures 4 is plotted for the temperature profiles for different values of Ec . We observe that the effect of increasing values of Eckert number is to enhance the temperature at a point which is true for both the fluid phase as well as dust phase temperatures. Physically it means that the heat energy is stored in the fluid due to the frictional heating. Figure 5 depict the effect of Grashof number Gr versus . It is evident from these plots that increasing value of Gr results in thinning of the thermal boundary layer associated with an increase in the wall temperature gradient and hence produces an increase in the heat transfer rate. Figure 6, which is a graphical representation of the temperature profiles for different values of versus Figure 3. Effect of P r on the temperature profiles for 0.5 N, 2.0Ec , 0.5Gr and 0.2 . Figure 4. Effect of E c on the temperature profiles for 0.5 N, 0.5 Gr , 1.0Pr and 0.2 . 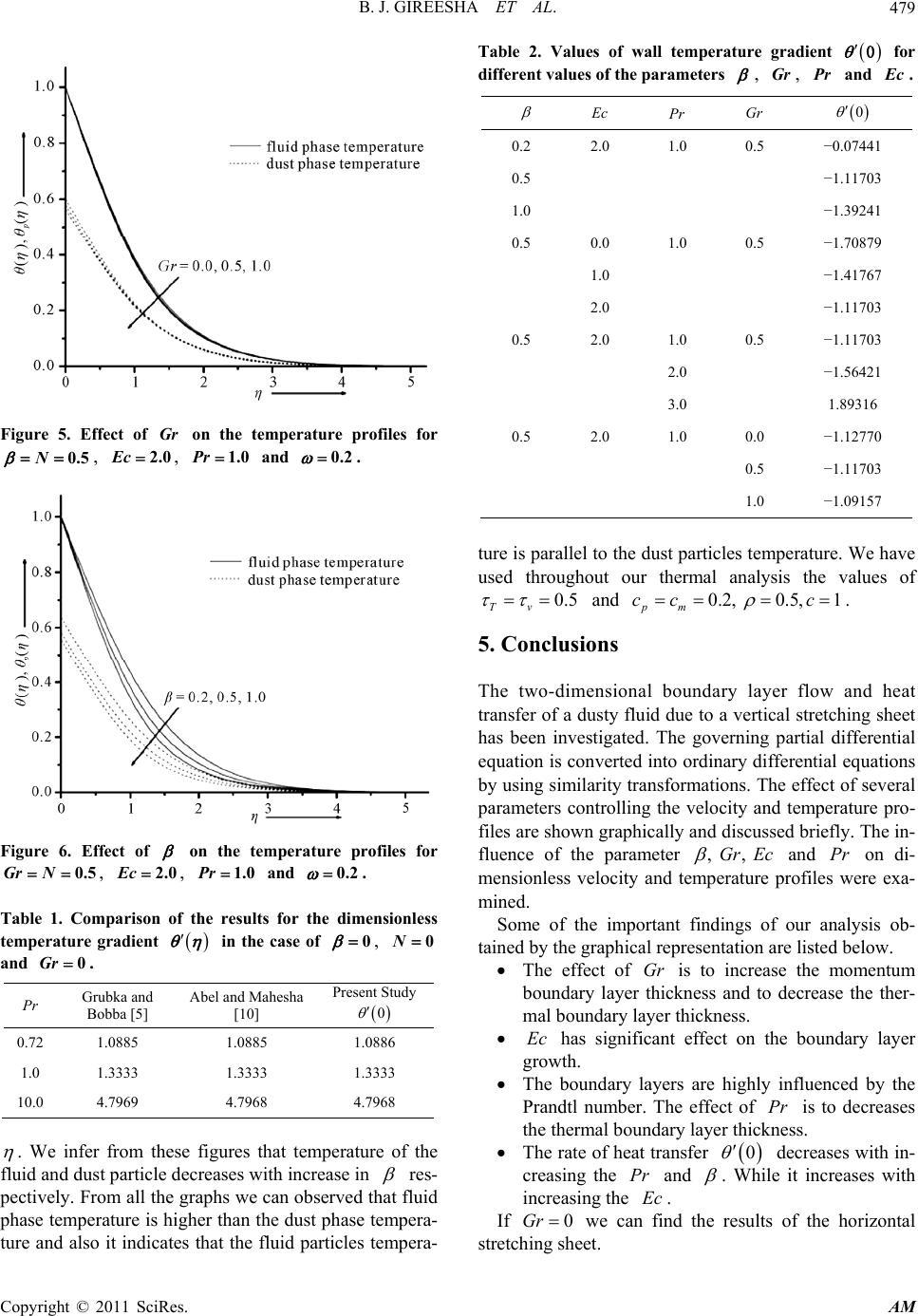 B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 479 Figure 5. Effect of Gr on the temperature profiles for 0.5 N, 2.0Ec, 1.0Pr and 0.2 . Figure 6. Effect of on the temperature profiles for 0.5 Gr N, 2.0Ec , 1.0Pr and 0.2 . Table 1. Comparison of the results for the dimensionless temperature gradient in the case of 0 , 0 N and 0 Gr . Pr Grubka and Bobba [5] Abel and Mahesha [10] Present Study 0 0.72 1.0885 1.0885 1.0886 1.0 1.3333 1.3333 1.3333 10.0 4.7969 4.7968 4.7968 . We infer from these figures that temperature of the fluid and dust particle decreases with increase in res- pectively. From all the graphs we can observed that fluid phase temperature is higher than the dust phase tempera- ture and also it indicates that the fluid particles tempera- Table 2. Values of wall temperature gradient for different values of the parameters , Gr , P r and E c. Ec P r Gr 0 0.2 2.0 1.0 0.5 −0.07441 0.5 −1.11703 1.0 −1.39241 0.5 0.0 1.0 0.5 −1.70879 1.0 −1.41767 2.0 −1.11703 0.5 2.0 1.0 0.5 −1.11703 2.0 −1.56421 3.0 1.89316 0.5 2.0 1.0 0.0 −1.12770 0.5 −1.11703 1.0 −1.09157 ture is parallel to the dust particles temperature. We have used throughout our thermal analysis the values of 0.5 Tv and 0.2, 0.5,1 pm cc c . 5. Conclusions The two-dimensional boundary layer flow and heat transfer of a dusty fluid due to a vertical stretching sheet has been investigated. The governing partial differential equation is converted into ordinary differential equations by using similarity transformations. The effect of several parameters controlling the velocity and temperature pro- files are shown graphically and discussed briefly. The in- fluence of the parameter , , Gr Ec and Pr on di- mensionless velocity and temperature profiles were exa- mined. Some of the important findings of our analysis ob- tained by the graphical representation are listed below. The effect of Gr is to increase the momentum boundary layer thickness and to decrease the ther- mal boundary layer thickness. Ec has significant effect on the boundary layer growth. The boundary layers are highly influenced by the Prandtl number. The effect of Pr is to decreases the thermal boundary layer thickness. The rate of heat transfer 0 decreases with in- creasing the Pr and . While it increases with increasing the Ec. If 0Gr we can find the results of the horizontal stretching sheet.  B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 480 6. References [1] B. C. Sakiadis, “Boundary Layer Behaviour on Conti- nuous Solid Surface,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108 [2] L. J. Crane, “Flow Past a Stretching Sheet,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695 [3] H. I. Anderson, K. H. Bech and B. S. Dandapat, “Mag- netohydrodynamic Flow of a Power-Law Fluid over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 27, No. 6, 1992, pp. 929-936. doi:10.1016/0020-7462(92)90045-9 [4] A. Chakrabarti and A. S. Gupta, “Hydromagnetic Flow and Heat Transfer over a Stretching Sheet,” Quarterly of Applied Mathematics, Vol. 37, No. 1, 1979, pp. 73-78. [5] L. J. Grubka and K. M. Bobba, “Heat Transfer Characte- ristics of a Continuous Stretching Surface with Variable Temperature,” Journal of Heat Transfer, Vol. 107, No. 1, 1985, pp. 248-250. doi:10.1115/1.3247387 [6] R. Cortell, “A Note on Magnetohydrodynamic Flow of a Power-Law Fluid over a Stretching Sheet,” Applied Ma- thematics and Computation, Vol. 168, No. 1, 2005, pp. 557-56. doi:10.1016/j.amc.2004.09.046 [7] C. H. Chen, “MHD Mixed Convection of a Power Law Fluid Past a Strtching Surface in the Presence of Thermal Radiation and Internal Heat Generation/Absorption,” In- ternational Journal of Nonlinear Mechanics, Vol. 44, No. 6, 2009, pp. 596-603. [8] R. Cortell, “Effects of Viscous Dissipation and Work Done by Deformation on the MHD Flow and Heat Trans- fer of a Viscoelastic Fluid over a Stretching Sheet,” Phy- sics Letters A, Vol. 357, No. 4-5, 2006, pp. 298-305. doi:10.1016/j.physleta.2006.04.051 [9] M. S. Abel, E. Sanjayanand and M. M. Nandeppanavar, “Viscoelastic MHD Flow and Heat Transfer over a Stre- tching Sheet with Viscous and Ohmic Dissipation,” Com- munications in Nonlinear Science and Numerical Simula- tion, Vol. 13, No. 9, 2008, pp. 1808-1821. [10] M. S. Abel and N. Mahesha, “Heat Transfer in MHD Viscoelastic Fluid Flow over a Stretching Sheet with Va- riable Thermal Conductivity, Non-Uniform Heat Source and Radiation,” Applied Mathematical Modelling, Vol. 32, No. 10, 2008, pp. 1965-1983. doi:10.1016/j.apm.2007.06.038 [11] R. Tsai, K. H. Huang and J. S. Haung, “Flow and Heat Transfer over an Unsteady Stretching Surface with Non- uniform Heat Source,” International Communications in Heat and Mass Transfer, Vol. 35, No. 10, 2008, pp. 1340-1343. doi:10.1016/j.icheatmasstransfer.2008.07.001 [12] A. Ishak, R. Nazar and I. Pop, “Heat Transfer over an Unsteady Stretching Permeable Surface with Prescribed Wall Temperature,” Non-Linear Analysis, Real World Applications, Vol. 10, No. 5, 2009, pp. 2909-2913. doi:10.1016/j.nonrwa.2008.09.010 [13] A. Ishak, R. Nazar and I. Pop, “Boundary Layer Flow and Heat Transfer over an Unsteady Stretching Vertical Sur- face,” Meccanica, Vol. 44, No. 4, 2009, pp. 369-375. doi:10.1007/s11012-008-9176-9 [14] F. Aman, A. Ishak and R. Nazar, “Boundary Layer Flow and Heat Transfer Adjacent to a Stretching Vertical Sheet with Prescribed Surface Heat Flux,” Matematika, Vol. 26, No. 2, 2010, pp. 197-206. [15] S. M. Alharbi, M. A. A. Bazid and M. S. E. Gendy, “Heat and Mass Transfer in MHD Visco-Elastic Fluid Flow through a Porous Medium over a Stretching Sheet with Chemical Reaction,” Applied Mathematics, Vol. 1, No. 6, 2010, pp. 446-455. doi:10.4236/am.2010.16059 [16] I. Olajuwon, “Heat and Mass Transfer in MHD Vis- co-Elastic Fluid Flow through a Porous Medium over a Stretching Sheet with Chemical Reaction,” International Journal of Nonlinear Science, Vol. 7, No. 1, 2009, pp. 50-56. [17] K. M. Chakrabarti, “Note on Boundary Layer in a Dusty Gas,” AIAA Journal, Vol. 12, No. 8, 1974, pp. 1136-1137. doi:10.2514/3.49427 [18] N. Datta and S. K. Mishra, “Boundary Layer Flow of a Dusty Fluid over a Semi-Infinite Flat Plate,” Acta Me- chanica, Vol. 42, No. 1-2, 1982, pp. 71-83. doi:10.1007/BF01176514 [19] E. S. Asmolov and S. V. Manuilovich, “Stability of a Dusty Gas Laminar Boundary Layer on a Flat Plate,” Journal of Fluid Mechanics, Vol. 365, No. 1, 1998, pp. 137-170. doi:10.1017/S0022112098001256 [20] M.-L. Xie, J.-Z. Lin and F.-T. Xing, “On the Hydrody- namic Stability of a Particleladen Flow in Growing Flat Plate Boundary Layer,” Journal of Zhejiang University SCIENCE A (Springer), Vol. 8, No. 2, 2007, pp. 275-284. doi:10.1631/jzus.2007.A0275 [21] G. Palani and P. Ganesan, “Heat Transfer Effects on Dusty Gas Flow past a Semi-Infinite Inclined Plate,” Forsch Ingenieurwes (Springer), Vol. 71, No. 3-4, 2007, pp. 223-230. doi:10.1007/s10010-007-0061-9 [22] V. M. Agranat, “Effect of Pressure Gradient on Friction and Heat Transfer in a Dusty Boundary Layer,” Fluid Dynamics, Vol. 23, No. 5, 1988, pp. 729-732. doi:10.1007/BF02614150 [23] K. Vajravelu and J. Nayfeh, “Hydromagnetic Flow of a Dusty Fluid over a Stretching Sheet,” International Jour- nal of Non-Linear Mechanics, Vol. 27, No. 6, 1992, pp. 937-945. doi:10.1016/0020-7462(92)90046-A [24] A. Aziz, “A Similarity Solution for Laminar Thermal Boundary Layer over a Flat Plate with a Convective Sur- face Boundary Condition,” Communications in Nonlinear Science and Numerical, Vol. 14, No. 4, 2009, pp. 1064- 1068. doi:10.1016/j.cnsns.2008.05.003 [25] H. Schlichting, et al., “Boundary Layer Theory,” McGraw-Hill, New York, 1968.  B. J. GIREESHA ET AL. Copyright © 2011 SciRes. AM 481 Nomenclature A constant c stretching rate m c specific heat of dust phase p c specific heat of fluid Ec Eckert number Gr Grashof number K stokes resistance * k thermal conductivity l characteristic length N number density of the dust phase Pr Prandtl number T temperature of the fluid p T temperature of the dust phase w T temperature at the wall T temperature at large distance from the wall w Ux stretching sheet velocity ,uv velocity components of the fluid along x and y directions , p p uv velocity components of the dust particle along x and y directions x coordinate along the stretching sheet y distance normal to the stretching sheet Greek symbols coefficient of the viscosity of the fluid density of the fluid density ratio relaxation time of the dust phase fluid particle interaction parameter r relative density T thermal equilibrium time v relaxation time of the dust phase fluid phase temperature p dust phase temperature dimensionless space variable Subscripts w properties at the plate free stream condition |

