 Journal of Power and Energy Engineering, 2014, 2, 423-431 Published Online April 2014 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2014.24057 How to cite this paper: Guo, Y.J., et al. (2014) Loss-of-Main Monitoring and Detection for Distributed Generations Using Dynamic Principal Component Analysis. Journal of Power and Energy Engineering, 2, 423-431. http://dx.doi.org/10.4236/jpee.2014.24057 Loss-of-Main Monitoring and Detection for Distributed Generations Using Dynamic Principal Component Analysis Yuanjun Guo, Kang Li, D. M. Laverty School of Electronics, Electrical Engineering and Computer Science, Queen’s University Belfast, Belfast, UK Email: yguo01@qub.ac.uk, k.li@qub.ac.uk, david.laverty@qub.ac.uk Received Dec emb er 2013 Abstract In this paper, our previous work on Principal Component Analysis (PCA) based fault detection method is extended to the dynamic monitoring and detection of loss-of-main in power systems using wide-area synchrophasor measurements. In the previous work, a static PCA model was built and verified to be capable of detecting and extracting system faulty events; however the false alarm rate is high. To address this problem, this paper uses a well-kn ow n ‘time lag shift’ method to include dynamic behavior of the PCA model based on the synchronized measurements from Pha- sor Measurement Units (PMU), which is named as the Dynamic Principal Component Analysis (DPCA). Compared with the static PCA approach as well as the traditional passive mechanisms of loss-of-main detection, the proposed DPCA procedure describes how the synchrophasors are li- nearly auto- and cross-correlated, based on conducting the singular value decomposition on the augmented time lagged synchrophasor matrix. Similar to the static PCA method, two statistics, namely T2 and Q with confidence limits are calculated to form intuitive charts for engineers or op- erators to monitor the loss-of-main situation in real time. The effectiveness of the proposed me- thodology is evaluated on the loss-of-main monitoring of a real system, where the historic data are recorded from PMUs installed in several locations in the UK/Ireland power system. Keywords Loss-of-Main Detection; Phasor Measurement Units; Big Data; Dynamic Principal Component Analysis 1. Introduction During the last decade, detecting and monitoring power system events have emerged as a focused and promising research topic, which also forms a key part of the Wide-area Monitoring and Control Systems (WAMCS) [1]. Loss -of-main monitoring and detection is one of the most important and hot issues. There are two major concerns when dealing with the loss-of-main problem. The first one is the “Big Data” issue. By virtue of deploying a wide range of smart grid infrastructures, the utilities are gathering tremendous volumes of data on a much more granular level than ever before. This enables the utilities to potentially design  Y. J. Guo et al. better response programs, forecast and control the loads, integrate renewable energy and plan the system opera- tion, etc. However, they are facing new analytic challenges in dealing with the big data, and using them to im- prove decision-making. A recent report on the big data issue in the power system is presented in [2], in which the big data is defined as increasing large volume, high velocity, increasing variety, or all the three. Moreover, the data volumes in the power industry are growing faster than many power utilities may be prepared to handle [3]. The second concern is the variety and multiformity of the power generations. In UK and Ireland, the power networks operate with greater than 10% of power supplied by distributed generations, especially wind farms. Due to common weather patterns, the wind power will exhibit reasonably strong statistical dependency within a certain regional area. Therefore, a statistically efficient process monitoring and control techniques have been chosen for power system transient analysis, loss-of-main detection and extraction to address the above men- tioned concerns. Burke and O’Malley [4] applied principal component analysis (PCA) to the covariance matrix of distributed wind power data from existing Irish wind farms, with eigenvalue analysis generating a lower number of uncorrelated alternative variables. The same idea was also implemented in our previous work [5], but with an extended application in power system islanding detection as well as a fault reconstruction method that have been used to identify the islanding site based on the data collected from synchrophasors in a real system. Similarly, in a recent paper by Barocio et al. [6], PCA was used for detecting and extracting unusual or anomal- ous events from wide-area monitoring data, demonstrating the ability to detect and extract system events based on a transient stability model of the New England Test System. All these researches adopt the PCA method to reduce the dimensionality of the big data to a certain extent. However, it is worth noting that the PCA works well under three assumptions: 1) data follows a multivariate normal distribution, 2) there exist no autocorrelation among observations, and 3) the variables are stationary (keep constant mean and standard deviation over time). From our previous work in [5], it concluded that static PCA based fault detection method could address the problem of redundant and high dimensional data. However, challenges still exist due to the dynamic, and muti-timescale synchronized measurements, which is the most common situation that undergoes slow and normal process changes in real systems. In case of processes with small disturbances, the autocorrelation in variables is taken into account, incorpo- rating the time lags of time series during the modelling stage, this extension is called dynamic principal compo- nent analysis (DPCA). The purpose of this paper is to show how static PCA tools could be extended for the dy- namic multivariate systems and to examine their use for disturbance analysis and loss-of-main detection in the electrical power system. This is achieved by building a dynamic PCA model through singular value decomposi- tion method on the covariance matrix of the time lagged ‘trajectory data’. Similar to static PCA, the data is then projected into principal component subspace and residual space, and two statistics are used to detect loss-of- main situations. This paper is organized as follows. Section 2 introduces the dynamic PCA approach in combination with the power system synchrophasor measurements, including the trajectory data matrix formation as well as the dis- turbance analysis and extraction by the dynamic PCA technique. Section 3 gives a brief introduction of the real system framework. Section 4 presents the data analysis results according to different variables and PMU com- bination cases step by step, to give a clear insight of how DPCA works in the application of loss-of-main detec- tion and monitoring. Finally, Section 5 concludes the paper and discusses the future work. 2. Dynamic Principal Component Analysis 2.1. Data Matrix of DPCA Let matrix X be a set of historical data made up of n observations from p variables, which is taken from a PMU recordings of a distributed power system dynamic process. When the process is under nominal conditions and operates around an operating point, it can be described by the matrix. (1) Each column in X represents an auto-correlated time series, where a current value depends on the past values. In order to include the serial correlation of data, the so called “trajectory matrix” is constructed applying a time lag shift of order w on each of the p columns of the matrix X. The trajectory matrix lagged from one variable  Y. J. Guo et al. column is given as follows ( )()( ) ()( )( ) ( )()() () 12 231 11 ii i ii i w i iii nw X XXw X XXw X Xn XnXnw × + = + +− (2) therefore, the complete trajectory matrix with p variables is (3) where m = pw. The choice of w is made establishing a compromise between the information content and the sta- tistical confidence. To avoid the situation that some particular variables dominate the modelling process, it is conve nient to carry out data standardization on matrix Xw in relation to its means and standard deviations. Thus, the means of Xw are given by [ ] ( ) 12 1 11 w T wT mm X X n µµµ µ × = = (4) where . On the other hand, the covariance matrix of Xw is given by ( )( ) 111 1 w ww T ww X XX SX X n µµ =−− − (5) from which the standard deviations can be obtained as follows ( )()( ) () ,j ˆ,j w w w wX X Xi j Xi j µ σ − = (6) where and . The data formed as trajectory matrix both for off-line model training and for assessing new coming data. Applying PCA to is so called DPCA. 2.2. Disturbances Detection via DPCA The principal component are linear transformation of the original variables, such principal components consti- tutes a new set of variables Z of dimension which are uncorrelated to each other. They are obtained by (8) where the orthonormal transformation matrix is composed of an appropriate selection of l eigenvec- tors, called loading vectors, associated to the correlation matrix . The data matrix can be expressed as (9 ) whe r e is the information captured by the l principal components and E is the information in the neglected m-l components. So for the detection purpose it is possible to use the Hotelling static T2 from Z and/or the squared prediction error (SPE) from E. Calculation for T2 is given by (10) where S is the covariance matrix of Z. Finally, a threshold of normal condition from the probability density function of the set of parameters is calculated. In literature [7], for the data set T2 that follows a beta distribution, the threshold Upper Control Limit (UCL) is given by ( ) 2 1 1(; :1) 12 1 1(; :1) 12 nFln l nl UCL nFln l nl α α − −− −− = + −− −− (11)  Y. J. Guo et al. where n and l are the dimensions of Z and α is a level of significance. A complementary test on the Q statistic, defined as the sum of the squared residual of the selected PCs, is used to measure the variation in the residual space not accounted for by the PCA model. (12) which is also interpreted as a measure of the “best fit” of the PCA model, showing the distance between the ac- tual and the predicted data. A suitable threshold for statistical significance of Q is given by [8]. 0 1 02 20 0 12 11 2( 1) 1 h i ch hh QQ α α θθ θθθ − < =++ (13) with and where Qα is the upper confidence limit for the residual model Qi with significance level and cα is the normal de- viation corresponding to the upper (1 − α) percentile. Used together, both the two statistical tests are able to identify whether the event is associated with unusual variability within the principal subspace defined by the selected PCs or by variations not explained by the re- tained PCs. 3. Synchrophasor Based Loss-of-Main Detection Framework Li et al. [9] developed a novel distributed adaptive real-time learning framework for wide area monitoring of power systems integrated with distributed generations using synchrophasor technology. The framework com- prises distributed agents (synchrophasors) for autonomous local condition monitoring and fault detection, and a central unit for generating global view for situation awareness and decision making. The local agent PMUs, which have been deployed by Laverty et al. [10] in the system of British/Irish utility networks, were developed and manufactured in conjunction with the Open PMU project in Queen’s University of Belfast (QUB) [11] [12] and Scottish & Southern Energy. An overview of the proposed approach in a physical interpretation is given in Figure 1. As shown in Figure 1, several PMUs are installed in different locations of UK/Ireland power grid, including distributed generation level as well as main power stations to collect data including GPS time signatures, voltage magnitude, frequency and phase angle. A reference signal is acquired from a dependable utility site and trans- mitted to the generator site by means of Internet Protocol (IP) telecommunications [13]. At the generator site, the reference signal is compared to the synchrophasors acquired at the generator terminals. The synchronized measurements with a sampling rate of 10 Hz are then transmitted to QUB server and stored for further analysis. The time signatures of the synchrophasors are aligned in order to compare and analyse the phasors taken at the same instant. The phase difference between the generator and the reference site are compared against known typical operating conditions. The traditional mechanism of loss-of-main detection is to find the abnormally large phase difference between the generator and the reference site, which is then considered to be in loss-of-main situation. This passive technique faces a difficulty for time-varying operation conditions. Detection based on current single window of power system conditions may fail either to detect the islanding condition or to cause nuisance trip-ping. Therefore, the aforementioned dynamic PCA method along with the incremental learning framework provides a great potential in improving the near real-time monitoring and detection performance. 4. Loss-of-Main Detections Based on Dynamic PCA Cases 4.1. Analysis of Sin gle -Variable and Sin gle -PMU Ca se For the case of single-variable and single-PMU, frequency data recorded by the main site PMU was used in or- der to test the ability of dynamic PCA to detect the abnormal disturbances such as frequency dip caused by an inter-connector tripping. To extract the dynamic relations from the PMU synchrophasors by the use of dynamic PCA, the necessary number of time lags should be determined. A method called Parallel Analysis on the time shifted time could be found in [14]. 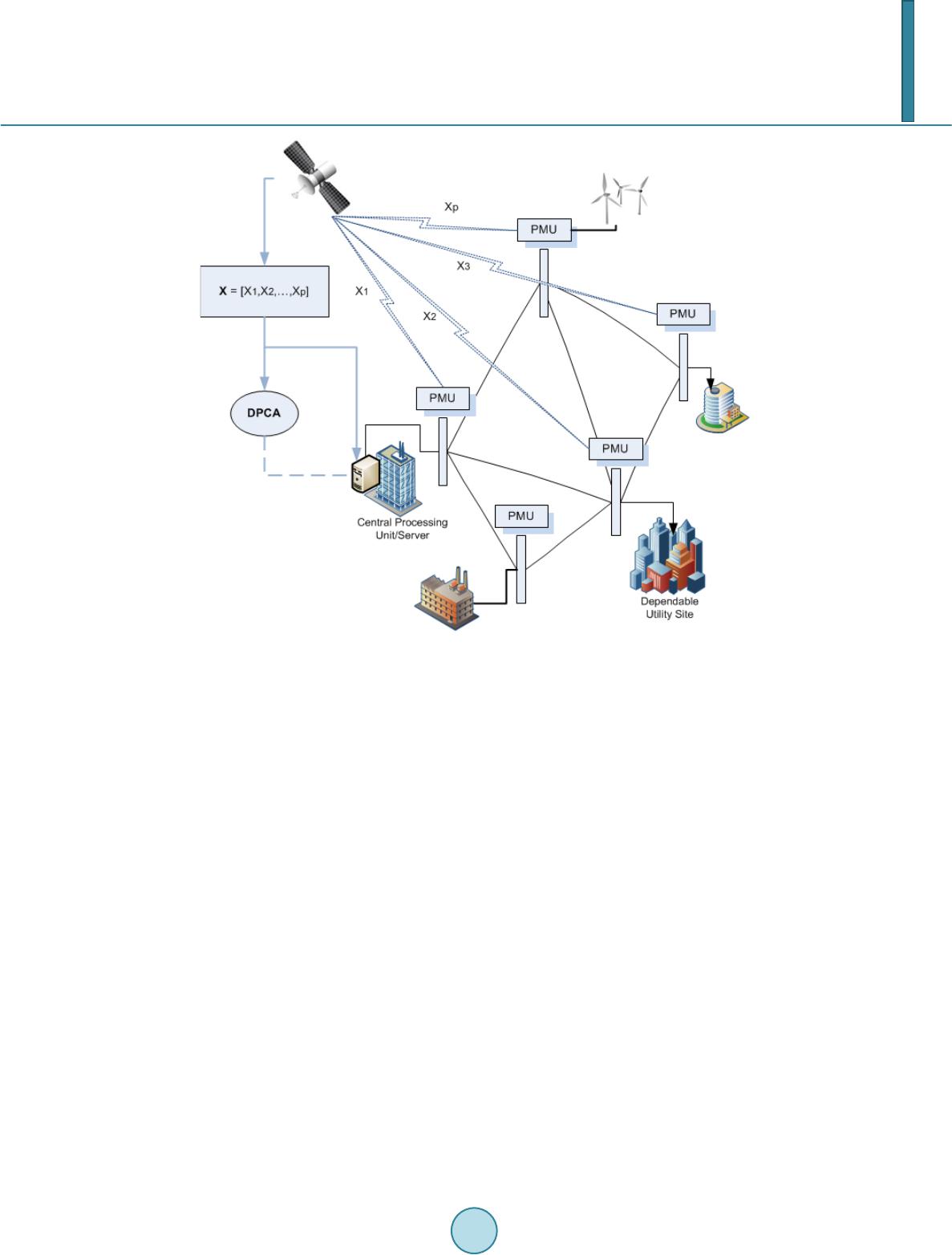 Y. J. Guo et al. Figure 1. Overview of the proposed synchrophasor based loss-of-main detection scheme using DPCA method. The trajectory data matrix was set up according to the time lag of 20 seconds with observations of 1000 nominal samples without disturbances to build the dynamic PCA model. A transient event occurred from the sample point of 1306, which was caused by an instantaneous loss of 1 GW power imported to the GB power grid caused by an interconnector tripping between Great Britain (GB) and France, details of the event could be found in [5]. The dynamic PCA model of single-variable and single-PMU data was tested using the data con- taining the transient event data as well as the nominal data, with the result given in Figure 2. Figure 2 presents the monitoring results using T2 and Q chart for single-variable and single-PMU data. The red dashed lines in the two charts are the 95% control limits of the two statistics. The enlarged view of T2 is given in order to clearly show the normal operating region with no false alarms before the transient event hap- pened. Due to the single variable data, only the variance within the principal model can be detected by the T2 chart, leaving no information in the residual subspace, which explains the clear situation in the Q chart in this case. 4.2. Analysis of Sin gle -Variable and M ult i-PMU Case During the inter-connector failure event, the frequency of the main power system had fallen from 50.08Hz to 49.70 Hz. The result of rate-of-cha nge -of-frequency (ROCOF) exceeded the current ROCOF setting, which falsely triggered an islanding operation on one of the sites and led to further loss-of-main situation. The training and testing data in this case consist of three PMU data, only the frequency variable is used for each PMU. A dynamic PCA model has been built based on the nominal condition data and monitoring result is given in Fig- ure 3. It is worth to mention that due to the multi-timescale synchronized measurements corresponding to the different GPS time format and computational precision, the total data number is different when the multi-PMU data are aligned according to the same UTC time instant. Nevertheless, the converted local time is in accordance with that of the single-PMU case, the only difference is the number of sample points. 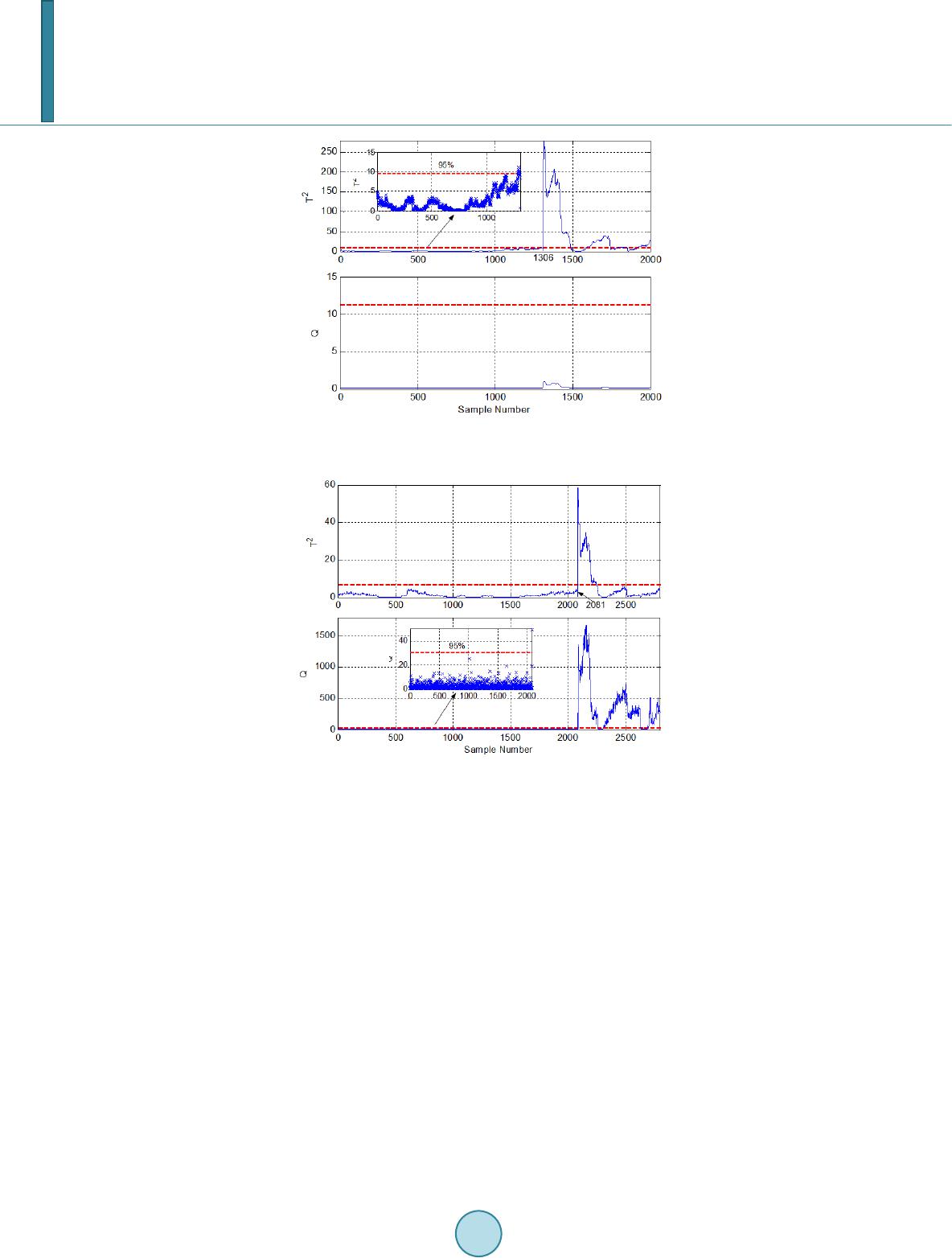 Y. J. Guo et al. Figure 2. Dynamic PCA based monitoring results using T2 and Q charts for single-variable and single-PMU data. Figure 3. Dynamic PCA based monitoring results using T2 and Q charts for single-variable and multi-PMU data. Figure 3 shows the same behaviour in T2 control chart, which clearly differentiate the frequency dip event with normal operation at the sample point of 2081. The relationship between the different PMU agents can be shown through the Q chart, where two high values exceed the Q control limit. One exceeding value at the same position with T2 represents the frequency dip event, the other points exceeding the confidence limit continuously reveals a loss-of-main situation. For further analysis of the islanding site identification, fault reconstruction method proposed by Dunia and Qin in [15] was performed in the central unit. The identification result is given in Figure 4, which clearly shows the loss-of-main data came from the PMU at the forth site which has the most contribution to the reconstructed fault result. 4.3. Analysis of Mult i-Variable and Single-PMU Case As mentioned above, there are other useful variables included in the synchronized phasor measurements, such as magnitude and phase angles. In order to make the best use of the dynamic PCA approach, the magnitude and frequency were chosen to form the training and test data because of their normal distribution property. Figure 5 shows the similar behaviour as Fig ure 2 except some fluctuations around the 95% confidence limit in T2 control chart due to the dynamic changes within voltage magnitude. In addition, the small disturbance indicates that the dynamic change did not significantly affect the nominal magnitude. Similar to case A, the single PMU data has no exceeding information shown in the Q c ha rt .  Y. J. Guo et al. Figure 4. Loss-of-main identification results of 5 different sites. Figure 5. Dynamic PCA based monitoring results using T2 and Q charts for multi-variable and single-PMU data. 4.4. Analysis of Mult i-Va riable and M ult i-PMU Cas e It is important for engineers to monitor the entire grid in order to get the complete information of the status and timely detect any abnormal disturbances. An advantage of applying the PCA-based techniques is to process the high dimensional multi-variate data simultaneously and extract key features of the process. In this section, the trajectory matrix consists of data from 5 different PMUs with magnitude and frequency for each PMU. The dy- namic PCA monitoring result is illustrated in Figure 6. This monitoring result integrates the aforementioned different cases, which also shows a good ability to detect both the generation loss trip from T2 control chart, and the loss-of-main status form Q chart with a neglectable low rate of false alarm. Further analysis by fault reconstruction method can identify the islanding site with a re- sult similar to F igure 4. In summary, the complementary case studies have shown that the proposed dynamic PCA method for the wid e -area power system incremental learning framework can offer great potential in fast and dynamical captur- ing of loss-of-main events while reducing the rate of false alarms and effectively and efficiently deal with the big data issue in the power systems. 5. Conclusions This paper has shown that the dynamic PCA statistical process control approach is a powerful tool for automatic loss-of-main detection. This method is capable of analysing the auto- and correlations between the variables through decomposition of the covariance matrix of the time-lagged trajectory matrix. Similar as static PCA pro- cedure, the data matrix has been projected into principal subspace and residual space. Two statistics of Hotel- ling’s T2 and Q are calculated to monitor the variations in the trajectory data. Through the step-by-step analysis of different real system data cases of variables and PMUs, it is clear that most of the abnormal disturbance can be captured by the T2 control chart, while the loss-of-main event can be intuitively seen through a continuously exceeding trend within the Q control limit. With dynamic PCA approach, the false alarms have been signifi-  Y. J. Guo et al. Figure 6. Dynamic PCA based monitoring results using T2 and Q charts for multi-variable and multi-PMU data. cantly reduced due to the dynamic characteristic been interpreted well through the properly chosen time lag and number of principal components. The proposed methodology is practically applicable and efficient from the tests on real system cases. The work however has some limitations such as the dynamic PCA will fail to detect the loss-of-main situation completely when the multi-timescale data are aligned together which may filter out small but important sections of data. More research needs to be done to investigate the relationship between different time lags and the num- ber of principal components under different abnormal power system disturbances. Moreover, dynamic exten- sions will be applied to more advanced methodologies to make use of the phase angles in the future work to ad- dress the non-linearity issues. Acknowledgements This work was partially funded by Engineering and Physical Sciences Research Council (EPSRC) under grants EP/L001063/1 and EP/G042594/1. Y Guo would like to thank China Scholarship Council for the financial sup- port. References [1] Kamwa, I., Grondin, R. and Hebert, Y. (20 01 ) Wide-Area Measurement Based Stabilizing Control of Large Power Systems—A Decen tral ized/Hierarchical Approach. I EEE Transactions on Power Systems, 16, 136 -153 . http://dx.doi.org/10.1109/59.910791 [2] IBM Softwares (2012) Managing Big Data for Smart Grids and Smart Meters. [3] Kezun ovic, M. , Xie, L. and Grijalva, S. (2013 ) The Role of Big Data in Improving Power System Operation and Pro- tection. IEEE of Bulk Power System Dynamics and Control-IX Optimization, Security and Control of the Emerging Power Grid (I R EP ), 1-9. [4] Burke, D.J. and O’Malley, M.J. (2011) A Study of Principal Component Analysis Applied to Spatially Distributed Wind Power. IEEE Transactions on Power Systems, 26, 2084-2092. http://dx.doi.org/10.1109/TPWRS.2011.2120632 [5] Guo, Y., Li, K. and Laverty, D. M. (2013) A Statistical Process Control Approach for Automatic Anti-Islanding Detec- tion Using Synchrophasors. IEEE of Power and Energy Society General Meeting, Vancouver, 21-25 July 2013, 1-5. [6] Baroci o, E., Pal, B.C., Fab ozzi, D. and Thornhill, N.F. (2013) Detection and Visualization of Power System Distur- bances Using Principal Component Analysis. 2013 IREP Symposium of Bulk Power System Dynamics and Control-IX Optimization, Security and Control of the Emerging Power Grid (IREP), 1-10. [7] Tracy, N., Yo ung, J. and Mason, R. (19 92) Multivariate Control Charts for Individual Observations. Journal of Quality Technology, 24. [8] Wise , B.M. and Gallagher, N.B. (1996) The Process Chemometrics Approach to Process Monitoring and Fault Detec-  Y. J. Guo et al. tion. Journal of Process Control, 6, 329-348 . http://dx.doi.org/10.1016/0959-1524(96) 0000 9 -1 [9] Li, K., Guo, Y., Laverty, D., He, H. and Fei, M. (2013) Distributed Adaptive Learning Framework for Wide Area Moni- toring of Power Systems Integrated with Distributed Generations. Energy and Power Engineering, 5, 962. http://dx.doi.org/10.4236/epe.2013.54B185 [10] Laverty, D. M., Morrow, D.J., Bes t, R. and Crossley, P.A. (2009) Performance of Phasor Measurement Units for Wide Area Real-Time Control. IEEE of Power & Energy Society General Meeting, 1-5. http://dx.doi.org/10.1109/PES.2009.5275578 [11] Lav er ty, D.M., Morrow, D.J., McKinley, A. and Cregan, M. (2011) Openpmu: Open Source Platform for Synchro- phasor Applications and Research. IEEE of Power and Energy Society General Meeting, 1-6. http://dx.doi.org/10.1109/PES.2011.6039607 [12] Lav er ty, D.M., Best, R.J., Brogan, P., Khatib, I.A. and Vanfret ti, L. (2013) The Openpmu Platform for Open -Source Phasor Measurements. IEEE Transactions on Instrumentation and Measurement, 62, 701-7 09. http://dx.doi.org/10.1109/TIM.2013.2240920 [13] Balabin, M., Go’Irner, K., Li, Y., Naumkin, I. and Rehtanz, C. (2010) Evaluation of Pmu Performance during Tran - sients. 2010 IEEE International Conference on Power System Technology (POWERCON), 1-8. [14] Ku, W., Storer, R.H. and Georgakis, C. (1995) Disturbance Detection and Isolation by Dynamic Principal Component Analysis. Chemometrics and Intelligent Laboratory Systems, 30, 179 -196 . http://dx.doi.org/10.1016/0169-7439(95)00076-3 [15] Dunia, R. and Joe Qin, S. (1998) Subspace Approach to Multidimensional Fault Identification and Reconstruction. AIChE Journal, 44, 1813-18 31 . http://dx.doi.org/10.1002/aic.690440812
|