Journal of Power and Energy Engineering, 2014, 2, 416-422
Published Online April 2014 in SciRes. http://www.sc irp.org/journal/jpee
http://dx.doi.org/10.4236/jpee.2014.24056
How to cite this paper: Hu, H.M., et al. (2014) Dynamic Equivalent Method of Motor Loads for Power Systems Based on the
Weighted. Journal of Power and Energy Engineering, 2, 416-422. http://dx.doi.org/10.4236/jpee.20 14.24056
Dynamic Equivalent Method of Motor Loads
for Power Systems Based on the Weighted
Hanmei Hu1, Bo Hong1, Ting Chen2, Qinfeng Li1
1College of Electrical Engineering and New Energy, China Three Gorges University, Yichang, China
2College of Electrical Engineering, Wuhan University, Wuhan, China
Received Dec emb er 2013
Abstract
Dynamic equivalence can not only largely reduce the system size and the computation time but
also stress the dominant features of the system [1]-[3]. This paper firstly recommends the basic
concept of dynamic equivalent and the status of both domestic and abroad development in this
area. The most existing equivalent methods usually only deal with st atic load models and neglect
the dynamic characteristics of loads such as induction motors. In addition, the existing polymeri-
zation method which is based on the frequency domain algorithm of induction electric machines
parameters takes a long time to equivalent for the large system, then the new method based on the
weighted is proposed. Then, the basic steps for dynamic equivalence with the weighted method
are introduced as follows. At first, th e clustering criterion of motor loads based on time domain
simulation is given. The motors with similar dynamic characteristics are classified into one group.
Then, the simplication of the buses of motors in same group and network is carried out. Finally,
parameters of the equivalent motor are calculated and the equivalent system is thus obtained
based on the weighted. This aggregation method is applied to the simple distribution system of 4
generators. Simulation results show that the method can quickly obtain polymerization parame-
ters of generator groups and the aggregation model retains the dynamic performance of the orig-
inal model with good accuracy, the active and reactive power fitting error is smaller as well.
Keywords
Power System; Dynamic Equivalent; Induction Moto rs; Parameter A gg reg atio n; The Weighted
Method
1. Introduction
With the increasing growth of power grid interconnection, the scale of power system becomes larger and larger.
Power systems consist of many synchronous generators and each generator includes many elements. In the study
of power system dynamics, employing all of the detailed elements of generators in modeling creates a sophisti-
cated and large system which put a heavy computational burden in simulation. Generally we only interested in
one local system which is called research system (also called internal system). For external subsystem far side,
we just need to keep its dynamic effects on research system unchanged in the study. There is no need to investi-

H. M. Hu et al.
417
gate its internal structure in detail, at the same time we can simplify the system by making appropriate equiva-
lent. This area we want to simplify is the so-called external equivalent system. These are the fundamentals of
dynamic equivalents.
Dynamic equivalents are used to reduce the computing effort and manifest the principal characteristics of
Power systems. In general it consists of coherency method, mode method and identification method so far. The
coherency method is widely used for its advantages in physical transparence, adaptation to non-linear systems
and big disturbances, and it can be used directly in transient stability analysis. It is also fit for equivalent of large
scale system with a great velocity and a controllability of precision.
Many research works have been carried out in the dynamic equivalence area [4]-[17]. Researchers in China
also have made important contributions. The most existing equivalent methods usually only deal with static load
models and neglect the dynamic characteristics of loads such as induction motors. In addition, most equivalence
methods existing in the domestic adopt the frequency domain aggregation algorithm. This approach assumes
that the transfer function of the generator and its control system are divided into several links which are aggre-
gated respectively. Since the polymerization of coherent generators is complex, it takes a long time to equivalent
for the large system. In order to solve this situation, in this paper, a dynamic equivalent method based on the
weighed which considers motor dynamics is presented. The basic principle and procedure for aggregation are
described. Clustering criterion of motors and parameter aggregation for the equivalent motor are also discussed
in detail. Simulation results with a simple distribution system have validated the proposed method. During the
disturbance, the power generation unit has the same speed, voltage, total mechanical power and total active
power as the original group.
2. Clustering of the Motors
Most generator clustering is based on the coherency principle. It depends on whether the rotor angle of each ge-
nerator can swing coherently. In fact it demands the synchronous rotors speed to be the same in a group.
Similarly, the clustering of motors may be determined according to whether each motor rotor speed
r
ω
is the
same.
The spectral coefficient clustering analysis method is applied to motor clustering. It can be done as follows.
1) Forming the parametric index set
{ }
12
,XX
, where
1rJ
X TR=
,
2L
XK=
2) Normalizing the original indexes.
{}
12
, XX
′′
is used to represent the parametric index set after normaliza-
tion.
3) Preliminary clustering. At the beginning each motor is clustered into a group. It can be written as
{ }
(0)
i
0,,,1,2,,,
Mi M
l mNGXiN
′
==== 
where
l
is used to count the loops,
m
is the number of motor groups and
M
N
is the number of motor bus-
es.
4) Calculating the parametric distance between each group. The parametric distance is calculated by
(, )
c ij
DijX X
′ ′′
= −
A
mm×
symmetric parametric distance matrix
c
D′
is available after this step.
5) Finding out the closest groups in the distance space.
The parametric distance
c
D′
and electrical distance
e
D′
are comprehensively considered.
6) Checking the number of motor groups
m
. Generally speaking, the simulation results will have satisfying
accuracy when the motors are classified into two groups. So, if
m
is greater than 2, then return to step 4) to
repeat the clustering of motors; otherwise stop.
3. The Simplication of Buses and Network
3.1. The Simplication of Motor Buses
The motor buses will be combined and simplified first after identification of the coherent motor group. Assume
the bus set of the motor group which is used for combine as
{ }
c
, and the system bus set associated with
{ }
c
as
{ }
b
, and the system bus set not related to
{ }
c
as
{ }
a
. In the simplify, use an equivalent bus set
{ }
t
to

H. M. Hu et al.
418
replace bus set
{ }
c
and retain bus set
{}
b
, but the associated branch of
{}
c
need to be converted into the
associated branch of equivalent bus set
{}
t
, keep the bus set
{}
a
and all of its power system the same before
and after simplification. The node equation of original system is obtained as follows (the subscripts A, B, C re-
spectively represent bus
{}
a
,
{}
b
,
{ }
c
):
0
.
0
AAA ABA
BBA BBBCB
CCBCCC
I YYU
IYYY U
IYY U
  
  
=
  
  
  
(1)
the node equation for the new system after the simplification of the coherent motor bus is as follows:
0
.
0
AAA ABA
BBA BB BtB
ttB ttt
I YYU
I YYYU
I YYU
∗
 
 
=
 
 
 
(2)
Remain
AA
Y
,
AB
Y
,
BA
Y
the same in the equivalent and calculate
Bt
Y
,
tB
Y
,
tt
Y
. And the diagonal element
of
BB
Y
in the original system node equation need to correct as
BB
Y
∗
accordingly. The equivalent need to sa-
tisfy the constraint conditions for
A
U

and
B
U

in the steady state. The exchanged power between different bus
in
{ }
b
and
{ }
c
is unchanged in the steady state, so it is also called identical power transformation.
3.2. Network Simplication
The key of network simplification is the elimination of nonlinear load. The network steady trend deviation can
be reduced to zero and the dynamic error can be as small as possible by displacing the nonlinear load to the re-
mained bus equally in the process of elimination .The common methods just like REI (Radial Equivalent Inde-
pendent) .
4. Aggregation of Motor Parameters Based on the Weighted
The traditional frequency domain polymerization is rigorous in theory, but it also has some weaknesses as below:
aggregation algorithm is complex, and it takes a long time to equivalent for the large system. The following
weighted method simplifies the parameter aggregation process under the condition of guaranteeing accuracy,
which can save the calculation time and advantageous to project realization.
We can get one motor group
{}
1 , , , j
M
G=
by the correlation recognition. Since the capacity of the synthe-
sis equivalent motor is the sum of the capacity of each motor, namely
n
Mj
jM
SS
∀∈
=
∑
(3)
the subscript
M
represents equivalent motor, then we can export the parameters for the model of equivalent
motor and its control system in detail.
4.1. Basic Principle
The so-called equivalent means that the external characteristic of equivalent motor is the same or similar as the
overall external characteristic of the
m
motors in parallel. Each motor adopts the T-end equivalent circuit, as
shown in Figure 1, now simplify the
m
parallel circuits to an equivalent circuit.
4.2. The Equivalent of Inertia Time Constant
Assume that the kinetic energy of equivalent motor in synchronous speed is the sum of that of each motor. Ac-
cording to the definition of inertia time constant,
J
T
is the value that kinetic energy in synchronous speed mul-
tiply two then divide by capacity, so
1
11
22
m
JMNMJi Ni
i
T STS
=
= ∑
(4)
where
iJ
T
is inertial time constant of ith asynchronous motor;
JM
T
is the inertial time constant of the equiva-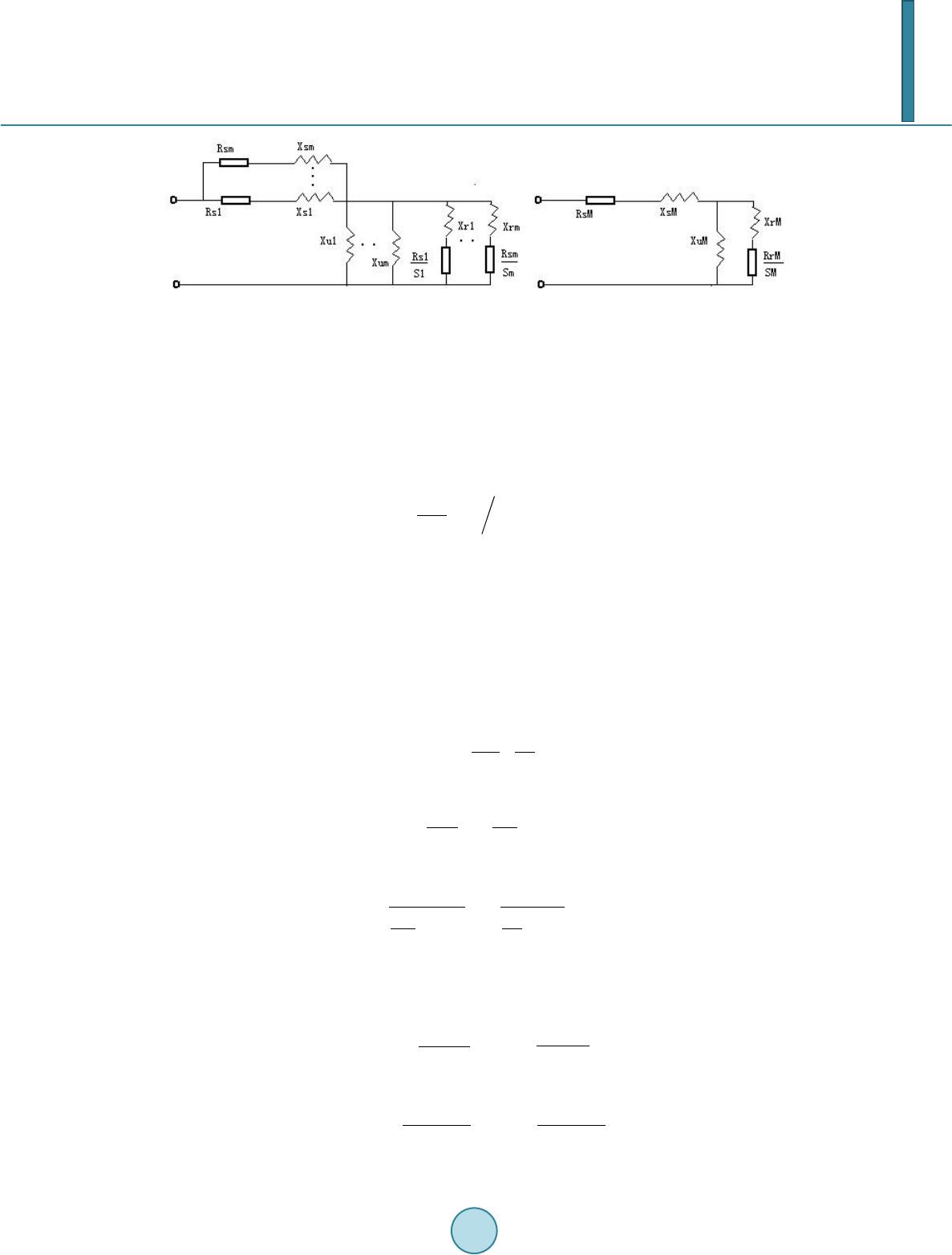

H. M. Hu et al.
419
(a) (b )
Figure 1. Equivalent T–end Circuit of Motor. (a) Equivalent Circuit before simplified (b) Equivalent Cir-
cuit after simplified.
lent motor;
Ni
S
is the rated capacity of ith asynchronous motor;
NM
S
is the capacity of the equivalent motor.
Since
1
m
NM Ni
i
SS
=
=∑
(5)
suppose
1
m
Ni
iNi Ni
NM i
SSS
S
ρ
=
= =
∑
(6)
with the both sides of Equation (10) divided by the half of
NM
S
, we get
1
m
JMi Ji
i
TT ρ
=
=
∑
(7)
4.3. The Equivalent of Electrical Parameters
Equivalent excitation reactance
um
X
is the value of excitation reactance in parallel of the m motors. It should
be noted that the impedance
i
Z
in figure are all per unit values under the total capacity, and the impedance
i
Z′
are per unit values under the capacity of each motor. The connection between
i
Z
and
i
Z′
is as follows:
(8)
from what has been discussed above, we get
1
1mi
i
uM ui
XX
ρ
=
=∑
(9)
in the same way, we get
1
1mi
rm ri
i
IM li
Mi
RR
jX jX
SS
ρ
=
=
++
∑
(10)
where
i
S
,
M
S
is the slip of ith motor and the equivalent motor respectively;
ri
R
,
rm
R
is the rotor resistance
of them;
li
X
,
IM
X
is the sum of the stator leakage reactance and the rotor leakage reactance of them .
When
1(1, 2,,,)
i
S imM= =
, the same is true for Equation (14), thereby
, (11)
where
, (12)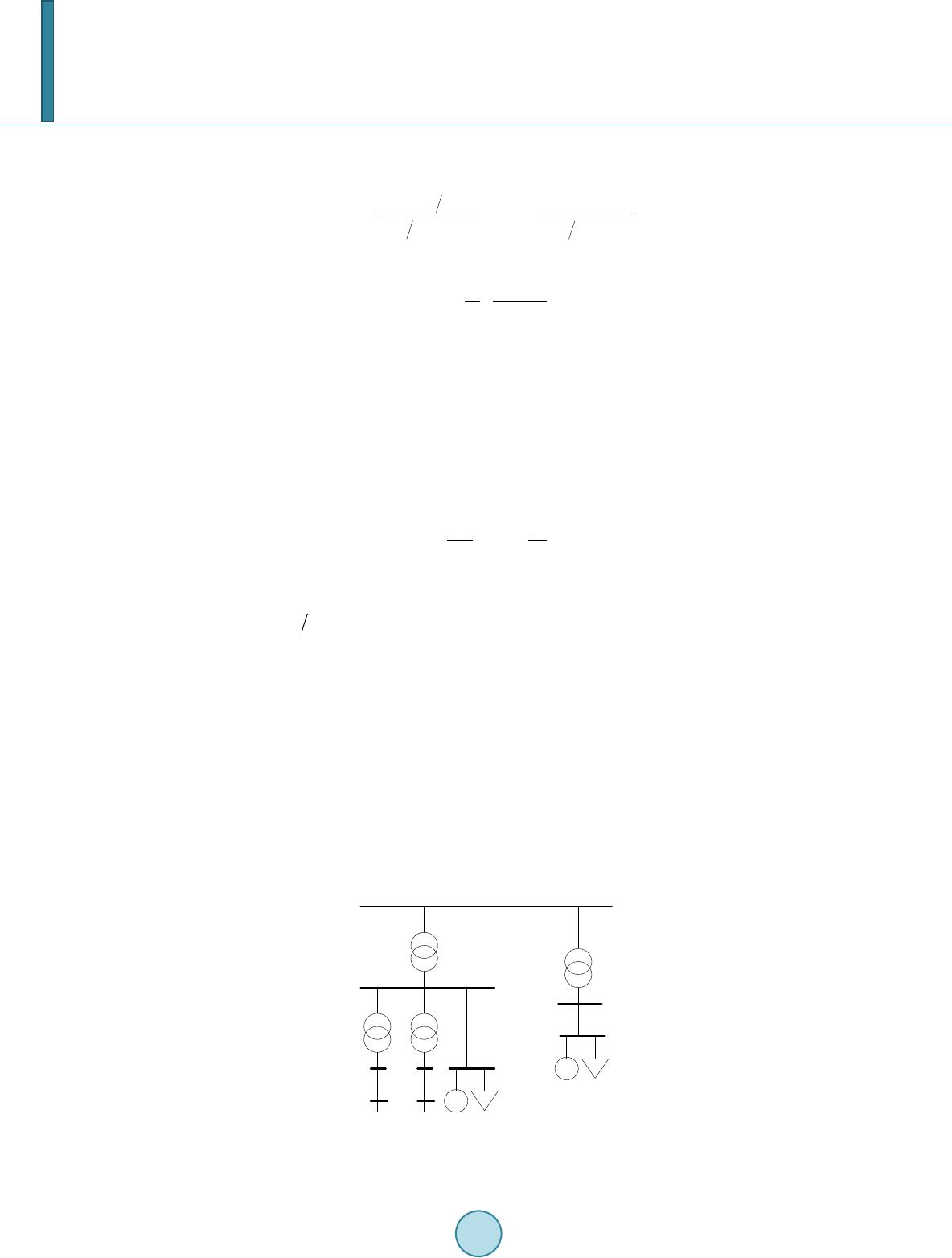
i
i
Ni
NM
ii
Z
S
S
ZZ
ρ
′
=×
′
=
22 ba
a
RrM + =
22
ba
b
X
IM
+
=
∑
=
+
=
m
iliri
rii
XR
R
a
12
2
ρ
∑
=
+
=
m
iliri
rii
XR
X
b
12
2
ρ

H. M. Hu et al.
420
4.4. The Equivalent of Slip
Assume that the motor runs at a constant slip
i
S
, set
, (13)
we get
22
22
''
'
M
aa b
Saab
+
= ×+
(14)
4.5. The Weighted Sum Method
Equivalent inertia time constant and equivalent admittance is the weighted sum of inertia constant and admit-
tance of each motor, weights is the proportion
i
ρ
that each motor capacity accounts in total capacity. In order
to simplify the analysis and calculation, the method that add them together after multiply weights is sometimes
extended to the calculation of the equivalent slip, equivalent mechanical torque and the equivalent parameters.
When the motor takes the T–end equivalent circuit as shown in figure, the Weighted Sum Method may be
adopted approximatively to calculate the equivalent electrical parameters. Then we can assume that inner node
K
in each motor equivalent circuit is in parallel, so
(15)
where
i
Z
is the electrical branch impedance of the ith electric motor;
M
Z
is electrical branch impedance of
the equivalent motor. For the branch of stator,
ss
Z RjX= +
; for excitation branch,
Z jX
µ
=
and for the
branch the rotor,
rr
ZR sjX= +
.
5. Simulation Example
A simple power distribution network is shown in Figure 2, all the impedance of the transformer and line shown
in the figure is per unit values. Table 1 lists the four electric motor parameters. The active and reactive power
models both use the power function model, and the power function adopt the IEEE recommended parameters.
Equivalent motor parameters is shown in Table 2. Make the mistress line voltage drop 50%, monitor the total
output active and reactive power of mistress line 1 respectively before and after polymerization. The curve is
shown in Figures 3 and 4.
Use the fitting degree of active and reactive power absorbed in motor before and after polymerization as the
basis for aggregation effect judgment. From the curve, we can conclude that the aggregation model retains the
dynamic performance of the original model with good accuracy, the active and reactive power fitting error is
smaller as well.
Figure 2 . A sample distribution network.
( )
∑
=
+
=
′
m
ili
iri
iri i
X sR
sR
a
12
ρ
( )
∑
=+
= ′m
iliiri
lii
XsR
X
b
12
ρ
i
m
ii
M
Z Z
11
1
∑
=
= ρ
M4 M3
M2
M1
0037+j0132
0.024+j0.053 0.042+j0017
0.001+j0.002
0.0023+j0.08
1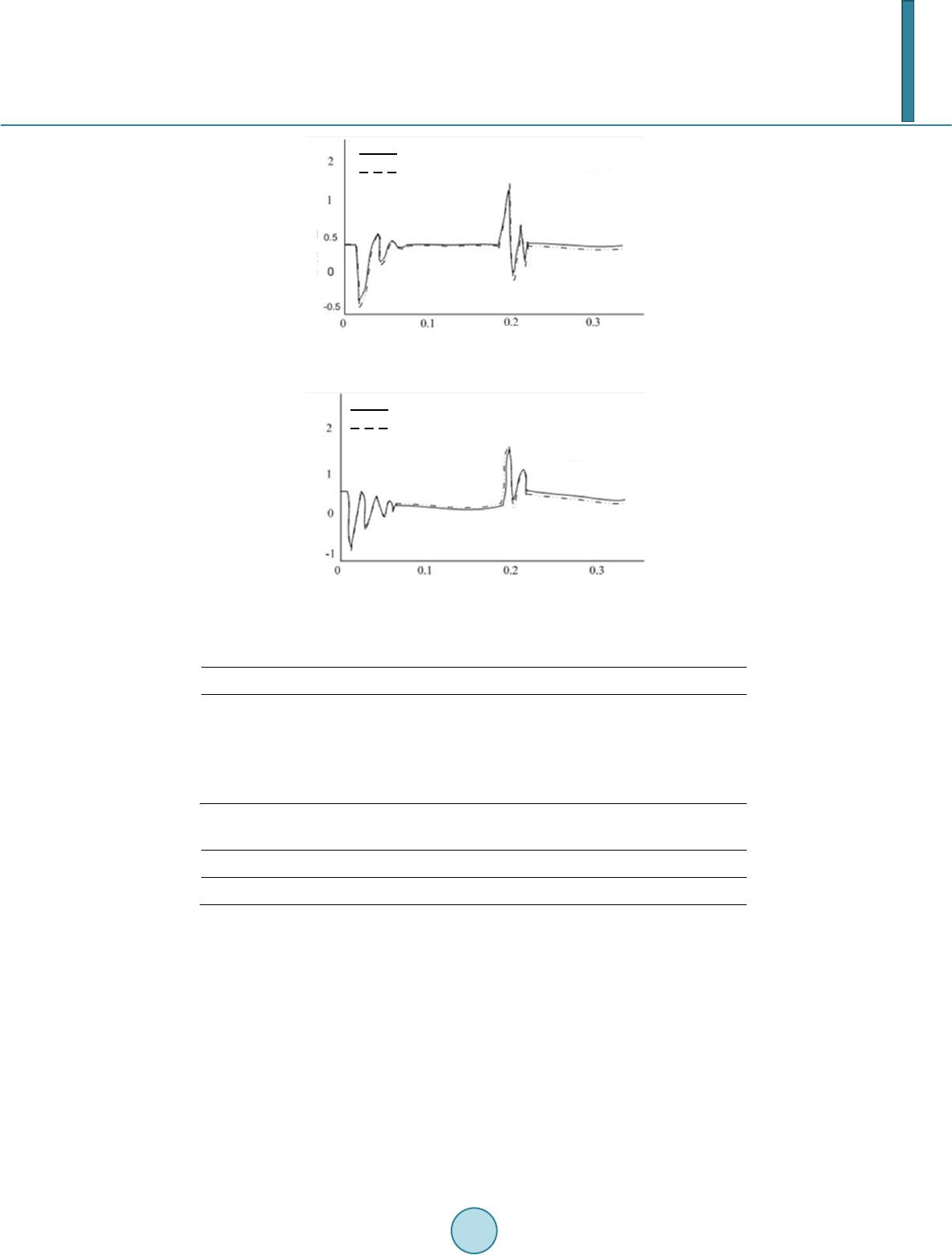

H. M. Hu et al.
421
Figure 3. Active curves before and after polymerization.
Figure 4. Reactive curves before and after polymerization.
Table 1. Motor parameters.
Motor Rs Xs Xm Rr Xr Tj/s Sb/KVA Ub/KV
1 0.0163 0.0816 2.25 0.0287 0.0836 1 597 4.16
2 0.0022 0.0759 2.62 0.0288 0.1037 0.66 3420 4.16
3 0.0235 0.1353 2.58 0.044 0.143 0.2 4269 1.1
4 0.0235 0.1353 2.58 0.044 0.143 0.2 2712 1.06
Table 2. Equivalent moto r parameters.
Equivalent motor Rs Xs Xm Rr Xr Tj/s Sb/KVA Ub/KV
Para m eters 0.0165 0.114 2.57 0.0384 0.1 276 0.39 10998 13.8
6. Conclusion
This paper proposes the weighted method which follows the principle that the total output active and reactive
power of distribution network respectively remains unchanged before and after polymerization to calculate the
equivalent parameter of the distribution network. By adding the coherency identification to motors and intro-
ducing the calculation method of the weighted summation on the basis of traditional equivalence calculation,
aggregation model of active and reactive power of the steady-state error is very small and it can accurately
maintain oscillation mode of the original system, in addition, the deviation of oscillation amplitude is also small.
Acknowledgements
I would like to express my gratitude to all those who helped me during the writing of this thesis. I gratefully ac-
knowledge the help from my supervisor, Ms. Hu Hanmei, who has offered me valuable suggestions in the aca-
before polymerization
after polymerization
active power in per unit (pu)
time (s)
before polymerization
after polymerization
reactive power in per unit (pu)
time (s)

H. M. Hu et al.
422
demic studies. In the preparation of the thesis, she has spent much time reading through each draft and provided
me with inspiring advice. Without her patient instruction, insightful criticism and expert guidance, the comple-
tion of this thesis would not have been possible. In addition, I deeply appreciate the contribution to this thesis
made in various ways by my friends and classmates.
References
[1] Zh ou , X.X. (1997) To Develop Power System Technology Suitable to the Need in 21st Century. Power System Tech-
nology, 21, 11-15.
[2] Ni, Y.X. (20 02) Dynamic Power System Theory and Analysis. Tsinghua University Press, Beijing.
[3] Yu, Y.X. and Che n , L.Y. (1988) Power System Security and Stability. Science Press, Beijing.
[4] Ch en, L.Y. and Sun , D.F. (1989) Aggregation of Generating Unit Parameters in the System Dynamic Equivalents.
Proceedings of the CESS, 9, 30-39.
[5] Min, Y. and Han, Y.D. (1991) Co-Frequency Dynamic Equivalence Approach for Calculation of Power System Fre-
quency Dynamics. Proceedings of the CESS, 11, 29-36.
[6] Zh ou , Y.H., Li, X.S., Hu, X.Y., et al. (1999) Dynamic Equivalents Based on the Transient Power Flow of the Con-
necting Lines. Proceedings of the CSU-EPSA, 11, 29-33.
[7] Xu, J.B., Xue, Y.S., Zhang, Q.P., et al. (2005) A Critical Review on Coher ency-Based Dynamic Equivalences. Au to -
mation of Electric Power Systems, 29, 92-95.
[8] Wan g, G. and Zang, B.M. (2006) External Online Dynamic Equivalents of Power System. Power System Technology,
30, 21-26.
[9] Wen , B.J., Zhang, H.B. and Zhang, B.M. (2004) Design of a Real-Time External Network Auto-Equivalence System
of Subtransmission Networks in Guangdong. Automation of Electric Power Systems, 28 , 77-79.
[10] Jiang, W.Y., Wu, W.C., Zhang, B.M., et al. (2007) Network model reconstruction in online security eEarly warning
system,” Automation of Electric Power Systems, 31, 5-9.
[11] Hu, J. and Yu, Y.X. (2006) A Practical Method of Parameter Aggregation for Power System Dynamic Equivalence.
Power System Technology, 30, 24-30.
[12] Ju, P., Wang, W.H., Xie, H.J., et al. (2007) Identification Approach to Dynamic Equivalents of the Power System In-
terconnected with Three Areas. Proceedings of the CESS, 27, 29-34.
[13] Price, W.W., Chow, J.H. and Haqgave , A.W. (1998) Lar ge-Scale System Testing of Power System Dynamic Equiva-
lence Program. IEEE Transactions on Power Systems, 13, 768-77 4 . http://dx.doi.org/10.1109/59.708595
[14] Sebast iao, E.M., Oliveira, D. and De Queiroz, J.F. (1988 ) Modal Dynamic Equivalent for Electric Power Systems.
IEEE Transactions on Power Systems, 3, 1723-17 30 . http://dx.doi.org/10.1109/59.192987
[15] Joe, H.C., Galarza, R., Accari, P., et al. (19 95 ) Inertial and Slow Coherency Aggregation Algorithms for Power System
Dynamic Model Reduction. IEEE Transactions on Power Systems, 10, 680-685. http://dx.doi.org/10.1109/59.387903
[16] Wallace do, C.B., Reza, M.I. and Amauri, L. (2004) Robust Sparse Network Equivalent for Large Systems: Part
I-Methodology. IEEE Transactions on Power Systems, 19, 157-163 . http://dx.doi.org/10.1109/TPWRS.2003.818603
[17] Zh ou, H.Q., Ju, P., Yang, H., et al. (2010) Dynamic Equivalent Method of Interconn ected P o we r Systems with Con-
siderati on of Motor Loads. Science China Technological Sciences, 53, 902-908.
http://dx.doi.org/10.1007/s11431-010-0110-8